Abstract
Maritime vision sensing can be applied to maritime unmanned systems to perform search and rescue (SAR) missions under complex marine environments, as multiple unmanned aerial vehicles (UAVs) and unmanned surface vehicles (USVs) are able to conduct vision sensing through the air, the water-surface, and underwater. However, in these vision-based maritime SAR systems, collaboration between UAVs and USVs is a critical issue for successful SAR operations. To address this challenge, in this paper, we propose a long-endurance collaborative SAR scheme which exploits the complementary strengths of the maritime unmanned systems. In this scheme, a swarm of UAVs leverages a multi-agent reinforcement-learning (MARL) method and probability maps to perform cooperative first-phase search exploiting UAV’s high altitude and wide field of view of vision sensing. Then, multiple USVs conduct precise real-time second-phase operations by refining the probabilistic map. To deal with the energy constraints of UAVs and perform long-endurance collaborative SAR missions, a multi-USV charging scheduling method is proposed based on MARL to prolong the UAVs’ flight time. Through extensive simulations, the experimental results verified the effectiveness of the proposed scheme and long-endurance search capabilities.
1. Introduction
Maritime accidents have risen with the growth of maritime activities such as transportation and resource exploitation. Consequently, maritime search and rescue (SAR) operations play a crucial role in saving lives and protecting property [1,2]. Meanwhile, advancements in unmanned system technology, such as unmanned aerial vehicles (UAVs) and unmanned surface vehicles (USVs), have been used for a variety of maritime activities, including data transmission [3], maritime communications [4,5], and emergency rescue [6]. However, a single type of USV faces challenges in SAR missions. Generally, the traditional USV search approaches obtain target information through sensor equipment, such as cameras and radars, but their perception range is limited due to their low viewing angles. In contrast, UAVs have unique advantages in acquiring information due to the high-altitude viewing angle and wide sensing range. Thus, UAVs can be utilized to design UAV–USV collaborative SAR systems by leveraging their complementary strengths [7].
Although the collaboration search systems of UAVs and USVs have made significant progress in multiple areas, they still face many challenges in information sharing and task collaboration, especially in complex marine conditions or large-scale search missions. Wang et al. [8] studied the visual navigation and control of cooperative unmanned vehicles in maritime SAR missions, and extracted target location information from images captured by UAV, aiming to improve the visual positioning accuracy and computational efficiency of UAVs. However, the real-time performance could be further investigated. Yang et al. [9] used UAVs and USVs to form a collaborative SAR cognitive mobile computing network, and used reinforcement learning to plan search paths and improve communication throughput. However, they only focus on the optimization of communication network and do not analyze the core search problems such as target recognition and search path optimization. Krishna et al. [10] proposed an approach for monitoring collaborative USVs using an UAV. Although this approach improves the efficiency of target observation, it still relies on manual control, and lacks effective collaboration and information sharing between the UAV and the USV, resulting in poor coordination. Xiao et al. [11] proposed an UAV-assisted USV visual navigation approach. However, the lack of cooperation makes it difficult for UAV and USV to flexibly adjust to real-time conditions, which affects the effectiveness of collaborative search missions.
Furthermore, UAV battery energy limitations are also a major bottleneck in collaborative SAR missions. Particularly in long-endurance missions, limited battery capacity will significantly restrict the system’s working time and mission execution efficiency. Meanwhile, performing complex and persistent operations via UAVs may consume significant battery power, such as video streaming and image processing [12]. This significantly reduces the search time and area. To address the energy limitation issue of UAVs, wireless charging technology [13,14] provides a feasible solution. Unmanned ground vehicles (UGVs) typically serve as energy carriers to carry out regular rendezvous with the UAV for long-term air-to-ground charging. For planning the cooperative routing between UAVs and UGVs, Mondal et al. [15] proposed that UAV can be charged on UGV and thus used a heuristic method to determine the location of the UGV charging stations. Yu et al. [16] investigated the routing problem of energy-limited UAVs accessing a set of locations in minimum time. UAVs can recharge on their way either by landing on fixed charging stations or by utilizing UGVs as mobile charging stations. However, this method with a fixed route is not appropriate for complex maritime search scenarios as the marine environment is unpredictable and diverse. Wang et al. [17] proposed a novel air–ground cooperative UAV recharging framework, in which a group of UAVs compete for charging operations within the mission area. However, this centralized approach may lead to unpredictable charging services and disrupted task execution with maritime search scenarios.
Inspired by these pioneering works, this paper leverages the complementary advantages of both UAV and USV, and proposes a cooperative search and rescue scheme for UAVs and USVs based on a multi-agent reinforcement-learning (MARL) approach. Compared with existing methods, this scheme exploits the full potential of the UAVs and USVs and conducts the first-phase cooperative search using the large field of view of UAVs. The second-phase SAR mission is carried out by taking advantage of the high search accuracy and long cruise capability of the USVs to conduct further search and real-time operation on the detected target. It not only improves the search efficiency through MARL method and probability maps, but also prolongs the flight time of UAVs through the multi-USV charging scheduling method, thereby achieving long-endurance cooperative search [18]. To summarize, the main contributions of this paper are listed as follows.
- We propose a multi-UAV cooperative search (ACS) algorithm leveraging MARL and probability map for the first-phase search. Then, we design a second-phase further search (SFS) algorithm for multi-USV by refining the probabilistic map provided the first-phase search of UAVs.
- To deal with the energy constraints of UAVs and perform long-endurance cooperative maritime search operations, we design a multi-USV charging scheduling (SCS) algorithm based on MADDPG and utilize multiple USVs as mobile charging stations to prolong the flight time of UAVs.
- We conduct extensive simulations to evaluate the feasibility and effectiveness of the proposed scheme.
The rest of this paper is organized as follows. In Section 2, we briefly review the relevant literature. Section 3 provides the system model. In Section 4, we describe the overall scheme and design the algorithm. We evaluate the effectiveness of the proposed algorithm in Section 5. Finally, we conclude our work in Section 6.
2. Related Work
In maritime search operations, UAVs are often employed to collaborate with USVs due to the flexibility and large field of view of UAVs [7,10]. Dufek et al. [19] presented a marine casualty incident SAR strategy using the USV–UAV system. However, its navigation and control works were completed by operators. Zhang et al. [20] combined the long endurance capability of USVs with the wide-area coverage of UAVs, improving rescue efficiency in flood disasters. However, the USV relies on the global information provided by the UAV for navigation and mission execution, which may lead to difficulties when performing tasks in harsh environments. Whereas, most min-UAVs (powered by lithium-ion or lithium polymer batteries) have a flight time of approximately 90 min [21]. This greatly restricts the extent and duration of their search operation. Notably, increasing the battery capacity of an UAV beyond a certain point can degrade its flight time due to excessive weight. Therefore, designing effective approaches for battery recharge is critical to sustaining the life cycle of UAV flight.
To address these challenges, it is crucial to consider the energy constraints of UAVs, particularly with maritime search operations, to ensure efficient task completion. Currently, the advancement of wireless power transmission (WPT) technology offers a contactless and fully automated wireless charging solution for UAVs, allowing them to recharge during task execution [21]. This contactless charging method can be achieved through radio frequency (RF) [22], enabling the UAV to achieve wireless directional charging near the ground charging station. Chen et al. [23] introduced a WPT technology represented by the resonant beam charging (RBC), which facilitates convenient recharging of UAVs located far from the coastline. These WPT technologies can be integrated into maritime search scenarios.
Due to the ability of multiple agents for collaborate tasks, MARL has become one of the most popular research methods [24]. Zhou et al. [25] proposed a solution of using a charging UAV (CUAV) to charge mission UAVs (MUAVs) through wireless media while optimizing the deployment of MUAVs and then studied the charging scheduling problem of CUAV. Zhu et al. [26] utilized a reinforcement-learning (RL) algorithm to investigate the scheduling problem of CUAVs. However, CUAVs may consume more energy while flying over the sea to counter factors, such as sea breezes, which can reduce the energy reserve. Messaoudi et al. [27] proposed a multi-agent deep Q-network (MADQN) approach that utilizes unmanned ground vehicles (UGVs) to provide a demand-based charging facility for UAVs, which minimizes the average age of information (AoI) in Internet of Things (IoT) devices. However, the existing works on UAV charging mainly focus on the one-to-one charging pattern [28] or the many-to-one charging pattern [29], neither of which is an appropriate solution for the multi-UAV and multi-USV scenarios.
3. System Model
As shown in Figure 1, the UAV–USV collaborative search system in the marine environment combines the aerial mobility capability of the UAVs and the advantages of USV’s surface operation to carry out efficient search tasks in the marine environment through cooperation, in which the UAVs are responsible for a quick search task of covering a large area and updating the search probability map. The USVs, as followers, perform a refined search based on the probability map provided by the UAVs. The system consists of U USVs and M UAVs, and the set of USVs and UAVs is represented as and , respectively. The communication range of each USV is defined as , which is a connecting constraint between USVs. If the distance between USVs is greater than , they cannot communicate with each other. Moreover, we define the communication range of UAVs as . The transmission of information between the USV and the UAV, as well as between the USV and the USV, is achieved through radio communications [30].
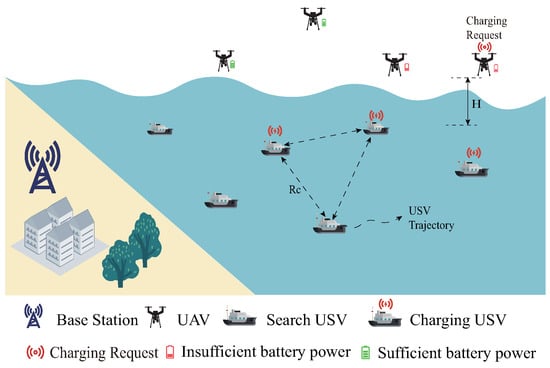
Figure 1.
Illustration of the multi-UAV–USV cooperative search system.
3.1. Probability Map Model
Due to the uncertainty of the target in a wide range of environments, the modeling method based on probability map has been widely used [31]. We divide the task area into grids, and the central position coordinate of each grid is . and represent the presence or absence of a target in a grid, respectively. While indicating otherwise possible scenarios, such as the search device failing to obtain the value of , the probability map remains as it was at the previous moment. As the mission proceeds, the probability map of the mission area is dynamically updated by the UAVs according to predetermined rules [32]. The update equation for the target probability is designed as follows.
where d and f are detection probability and false probability, respectively.
Due to the high speed, the UAVs can take the lead in probabilistic detection of the mission area, i.e., UAV keeps an individual probability map at time step t. When and , the relation in (1) is equivalent to
We use a nonlinear transformation instead of to perform the calculation more effectively.
Once each UAV updates the probability map according to the observation results, the resultant map is broadcast to the adjacent UAVs for the fusion of information. Let us define the neighbors of UAV as .
3.2. Energy Consumption Model
The movement of the USV is accompanied by its energy consumption. We define as the traveled distance of the USV at time slot t, which can be expressed as [33],
Therefore, energy consumption of USV can be written as follows.
where is a coefficient and is the resistance of the USV to travel under maritime conditions. Therefore, the energy consumption of U USVs until time T is given by
The energy consumption of UAVs is mainly divided into two categories: communication energy consumption and flight energy consumption. Since the communication energy consumption is much lower than the flight energy consumption, the communication power is fixed to simplify the system. The flight power of the UAV at a uniform speed v is as follows [34].
where and represent the blade profile power and induced power in hovering condition, respectively. denotes the tip speed of the rotor blades, and is the mean rotor-induced velocity in the hovering state. and represent the fuselage drag ratio and rotor solidity, respectively, while and denote the air density and rotor disc area, respectively. Therefore, the energy consumption of UAV up to time slot t is expressed as
3.3. Wireless Charging Model
We adopt electromagnetic induction wireless charging technology in this study [35]. When an UAV’s battery is lower than the preset threshold, it sends out an energy supply request. After finishing a response of an USV, the UAV performs landing through GPS or visual integration positioning systems. After successful landing of the UAV, the USV battery recharging system converts the input voltage into a high-frequency alternating current, driving the transmitting coil to generate an alternating magnetic field. The UAV’s receiving coil captures the magnetic field energy and converts it into direct current, which is then adjusted to a battery-adaptive voltage, enabling efficient charging.
Based on the input voltage and working current of the power supply, calculate the input power before voltage boost as . Then, estimate the output power after voltage boost by conversion efficiency is . After the magnetic field energy captured by the receiving coil is rectified, the output DC power is , where is the magnetic coupling efficiency and is the rectification efficiency.
According to the charging time and the receiving power, the calculated charging energy is . We assume that the maximum energy capacity of each UAV is . Therefore, the residual energy of the UAV is expressed as follows.
where the energy of UAV at time t satisfies the , where is the minimum reserved battery energy to prolong the battery lifetime [36].
Meanwhile, we define the charging urgency of UAV to reflect the importance of the UAVs charging sequence, which can be calculated as
If the remaining energy of the current UAV is low, it has a high charging emergency, and hence the USV gives priority service to the UAV with a high charging emergency.
4. The Proposed Scheme
In this section, we first briefly describe the framework of long-endurance collaborative SAR scheme. Then, we provide the ACS and SFS algorithm designs. Finally, we present the multi-USV charging scheduling algorithm.
4.1. General Description
In the search mission, the air-mobility capability of the UAV is combined with the advantage of the surface USV. The UAVs are responsible for quickly covering a large area and updating the search probability map for the first-phase search, while the USVs carry out second-phase SAR missions according to the probability map provided by the UAVs. To solve the energy limitation problem of UAVs, multiple USVs are dedicated to providing charging service for UAVs. Due to the continuous changes in the position and residual energy of the UAVs, the USVs should constantly interact with the nearby USVs, optimize the scheduling process, and ensure that the UAVs get sufficient energy to perform long-endurance SAR missions.
4.2. Search Algorithms of Multi-UAV and Multi-USV
4.2.1. ACS Algorithm
With its fast moving speed and wide field of view, an UAV is able to quickly cover large mission areas for extensive target detection. After updating the probability map according to the observation results, each UAV broadcasts the information to its neighbors for probability map fusion. The UAV records the number of target detections and the false detections for each cell. When holds, is increased by 1, otherwise, it remains unaltered. Conversely, when holds, is incremented by 1, otherwise, it also remains unaltered. These target detections and the false detections numbers are used as interactive information between UAVs [37]. and of UAV at time slot t after sufficient fusion of information can be derived as
where is the neighbor set of the UAV. Finally, it is obtained that the probability of target existence in the cell of the time step t after the fusion information is
In this subsection, the multi-actor-attention-critic (MAAC) algorithm [38] is adopted for the multi-UAV collaboration search process. Each UAV independently executes an actor-attention-critic model, utilizing a centralized critic equipped with a shared attention mechanism to select pertinent information for each UAV at every time step. This helps the corresponding UAV to extract meaningful information from the observation–action pairs of other UAVs to construct the input for its critic. This approach addresses the scalability issue and aids UAVs in selectively finding important environmental information while ignoring irrelevant data. We model the search process of each UAV as a partially observable Markov decision process (POMDP), represented by the tuple as follows.
- State space : To search the task area, each UAV searches the target and observes the state information of other UAVs, where is the state space of UAV i, i.e.,where represents the set of location information of all UAVs, indicates the probability map information, and represents the energy consumption of the UAV.
- Observation space : is the set of observed values of all UAVs. represents the observations of UAV i, including the observed position information of UAV i, the position information of other UAVs, and the energy consumption of UAVs. Thus, the observation information can be expressed aswhere denotes the position coordinates of the UAV i and represents observed position information of its neighbor UAV. indicates the probability of detecting the grid and is the energy consumption of the UAV i.
- Action space : includes all actions that all the UAVs may undertake. In the search activities, the actions to be taken by the UAV include moving direction and moving distance. The action taken by UAV i at time t is expressed aswhere is the position of the UAV i at the next time slot.
- State Transition Probability represents the probability of reaching the next state after executing the action in that state.
- Reward function : An appropriate reward function can help the UAVs explore better actions. The main objective of the exploration pursued by the UAV is to cover the unexplored area as soon as possible, minimize the energy consumption of the UAVs, and avoid collision with other UAVs. Therefore, the reward function is defined as follows.Target reward: This reward function encourages the UAV to find the target as soon as possible and mark the location of the target. We set that when , it means that the UAV has determined the target location, where is a threshold. The reward that the UAV can get when marking a target location is as follows.where is a positive constant.Coverage reward: This reward guides the UAVs to quickly cover the mission area, with fewer repetitive searches, and to cover as much unexplored area as possible. Therefore, the UAV search reward iswhere is the number of visits to the grid and is a penalty coefficient.Collision penalty: We use a penalty mechanism to guide UAV not to collide with other UAVs, and the collision penalty is [39]where is the safe distance between UAVs.In summary, the whole reward function is derived aswhere and are the reward correlation coefficients.
The attention mechanism employs a key-value memory model [38]. In this model, each agent queries other agents for information regarding their observations and actions and then uses this information as input to its critic. Specifically, the Q-function of agent i can be expressed as follows.
where and represent the set of observations and the set of actions of all agents, respectively. Both and represent the MLP layer, where is used for embedding operations on the observation-action pair of the agent. represents environmental information from other agent observation–action pairs, expressed as
where is the attention weight of agent i on agent j, and is the embedding of the observation–action pair of agent j, i.e., is first used to code the observation–action pair, and then linear matrix V is used for linear transformation, and finally non-linear operation h (such as leaky ReLU).
The attention weight of is obtained by comparing the similarity between the embedding vector and of agent i and agent j. Since the parameters are shared between the critics of different agents, each critic is trained with a joint loss function, namely
where
The actor policy of each agent is updated by the following formula.
where is the multi-agent baseline. The brief description of this process is shown in Algorithm 1. We first initialize the network parameters and the experience replay buffer D. According to the initial position of the UAV, the observed state of the environment is obtained. Then, the UAV selects actions through the actor network and performs the actions according to Equation (26) to obtain the reward of environmental feedback. Subsequently, the algorithm stores the current state, action, reward, and transfer information as transformation tuples in the experience replay buffer, thereby improving the utilization efficiency of the data and reducing the correlation among samples. In each training iteration, a small batch of transformation tuples is randomly sampled from the buffer, and the two critic networks are updated according to Equations (24) and (25). Finally, update the parameters of the target network to complete the policy optimization within the round and prepare for the next round of training.
| Algorithm 1 The proposed ACS Algorithm. |
|
4.2.2. SFS Algorithm
In maritime search missions, USVs serve as critical executors for precision search operations, leveraging their high-resolution sensor systems and proximity operation advantages to function as key platforms for target detection in refined search scenarios. To optimize search efficiency, USVs must dynamically adjust their search strategies based on target probability maps provided by UAVs, enabling precise coverage of high-probability regions. This paper proposes a cooperative search method based on genetic algorithm (GA) [40], designed to optimize USV navigation paths in complex environments, ensuring maximal coverage of high-probability areas while simultaneously minimizing search path length.
The USV first preprocesses the acquired UAV probability map to identify high-probability target points exceeding threshold , subsequently constructing a distance matrix to characterize the spatial relationships between USVs and waypoints as well as inter-waypoint connections, where U denotes the number of USVs and represents the quantity of waypoints, where each matrix element is computed via the Euclidean distance formula,
During the initialization phase, the system randomly generates an initial population comprising N feasible paths, with each path consisting of multiple interconnected sub-paths. The core of the GA lies in its composite fitness function, mathematically formulated as follows.
where K denotes the number of sub-paths, represents the node count of the j-th sub-path, indicates the cruising speed of the USV, indicates the distance between adjacent nodes in the path, and signifies the search execution time required at each path node.
During the evolutionary process, the algorithm employs improved genetic operators for path optimization. In the selection phase, the roulette wheel strategy based on fitness is employed. For the crossover operation, the ordered crossover method is utilized, and the crossover probability determines the exchange of parent path fragments, and the fine-grained search algorithm for a USV is described in Algorithm 2.
| Algorithm 2 The proposed SFS Algorithm. |
|
4.3. SCS Algorithm
To deal with the energy constraint issue of UAVs and perform long-endurance maritime search missions, we develop a multi-USV charging scheduling algorithm to prolong the flight time of UAVs in this subsection. We deploy N USVs as mobile charging stations specifically to provide wireless charging services for UAVs. When an UAV battery is low, a charging request will be sent to the USVs. Then, the allocated USV plans a path according to the remaining energy level of the UAV and minimizes the moving distance of the USV. Therefore, we propose an USV charging scheduling algorithm based on the multi-agent deep deterministic policy gradient (MADDPG) [41] method. MADDPG is an extension of the deep deterministic policy gradient (DDPG) algorithm by using a centralized training and distributed execution (CTDE) method to use global information in the training process, which is not visible to a single agent. On the other hand, each agent pursues its operations based only on local information. At each time slot , the USV tracks the current state of the environment and pursues action according to the specified policy . Then, environment status is updated and the agent receives reward . We model the motion of USV as a partially observed Markov decision process (POMDP) represented by the quintuple as follows.
- State Space: is the global environment information in the system, including the position coordinates of the USV and UAV, the energy level and the current working state of the USV, which is represented as a binary variable . If is set to 1, it indicates that the USV is engaged in the charging process; otherwise, equals 0. We use to represent the state of USV i at time slot t, i.e.,
- Observation Space: is the set of observations for all USVs. In a multi-agent system, each USV determines the action based on its current state as well as the current state of its nearby USVs. The observed values include the location information of itself and its neighbors, the location information and the charging urgency of the UAV. The observation space of USV i iswhere indicates the position coordinates of the neighbor USV and represents the energy consumption of USV i.
- Action Space: contains all actions that all USVs may take during the course of exploration, including direction and distance of movement. The action space of USV i is represented aswhere is the movement direction of USV i at time slot t and is the distance traveled.
- State Transition Probability : This describes the probability that the system transits to another state after performing an action in a state.
- Reward function: denotes the reward of USV i at time slot t given that the agent observes a system state and takes an action . The objective of the USVs is to learn the optimal strategy , which is to maximize the cumulative reward while interacting with the environment. Therefore, we design a reward function based on the local information of each agent as well as the collaborative information to incentivize the USVs to search the target and maintain the UAV battery level while minimizing the energy consumption due to the movement.Therefore, the reward function of USV i at time t is expressed aswhere represents the energy consumption of USV i for executing the corresponding task. represents a reward that the USV receives when it charges an UAV at time t. and are the penalty term for the USV failing to charge the UAV on time as well as for the collision, respectively.The energy consumed by each USV is determined by the distance it travels. Our objective is to devise an optimal path that minimizes energy consumption. Therefore, the reward for energy consumption is formulated asThe item is a reward component indicating the profit obtained by successfully charging an UAV at time slot t, which is defined as follows.where is the charging energy to the UAV at time t and k is a positive coefficient, representing a basic reward that encourages energy charging of the USV regardless of the charging outcome. represents the charging urgency of UAV . When a USV receives multiple charging requests from UAVs, its charging decision is prioritized based on the charging urgency of each UAV. By assessing the current battery level, the USV determines the charging urgency of UAVs and prioritizes charging service accordingly.The represents a penalty to an USV if it fails to charge any UAV in time and the remaining battery falls below the Eth. We define asIf there is a collision between USVs, there is a penalty, which we define aswhere represents the safe distance between USVs.
In the MADDPG-based charging scheduling algorithm, each agent i maintains its own actor network and critic network , whose network parameters are and , respectively. The actor network is responsible for interacting with the environment and making action decisions based on the current state. The update strategy for the actor network is as follows.
where is the experience reply buffer which contains past decision of the agents as a tuple during the course of training.
For the critic networks, we update the loss function of the model by minimizing the squared time difference of the soft Bellman function, which is defined as follows.
The target network is used to avoid training instability. The method of soft update is adopted to update the parameters of the target network, which can be written as
where represents the soft update factor. The brief description of this process is shown in Algorithm 3. First, initialize the parameters of the actor network, critic network, and the target network of each agent, and initialize the experience replay buffer . Each agent selects and performs actions based on the current state, interacts with the environment, and obtains corresponding rewards and the next state. Subsequently, the agent stores the tuples of the experienced states, actions, rewards, and the next state in the . Each agent uses the to update its own critic and actor by sampling mini-batches. After each update, the network parameters of the agent are adjusted to enhance its decision-making ability. When the UAV’s battery power is insufficient, the USV makes a movement decision based on the current state, adjusts the movement direction and distance, then replenish the battery power of the UAV in time, and minimize the movement energy consumption.
The goal of each agent is to maximize its expected cumulative reward as follows.
where is a discount factor.
| Algorithm 3 The proposed SCS Algorithm. |
|
5. Experiments
In this section, we first provide a description of the parameter settings, then we conduct simulations to demonstrate the effectiveness of the proposed algorithms.
5.1. Simulation Setup
We set the target area as a square area of 10 km × 10 km [42], and the remaining battery capacity of current UAVs follows a uniform distribution of [30%,100%] [17]. The output layer of the critic network is linearly activated, while the actor network uses the tanh function for its output layer to restrict the action range. The hidden layers in all the networks are activated using the ReLU function. For the UAV and USV search algorithms, we perform 20,000 episodes with 300 steps per episode. For the USV charge scheduling algorithm, we perform 20,000 episodes with 100 steps per episode. We implement these algorithms using PyTorch 2.1.2 in python 3.9, which runs on Nvidia 4050 (Santa Clara, CA, USA). The relevant parameters of the algorithm are shown in Table 1.

Table 1.
Simulation parameters.
5.2. The Effectiveness of the Proposed Scheme
Based on the Bayesian network framework of probability map model, the uncertainty of the detection system can be modeled by the entropy function [37] , where is determined by the probability distribution of the detection probability d and the false probability f. With an initial probability of 0.5, we systematically analyze the effect of different parameter combinations on the uncertainty of the system, as shown in Table 2. The system uncertainty shows a monotonically decreasing relationship with d and a monotonically increasing relationship with f, which verifies the key role of improving detection performance and suppressing false alarm in reducing system uncertainty. In particular, when both d and f are taken as 0.5, the uncertainty of the system reaches the maximum value of 1. At this time, the system degenerates into a completely random guessing state. When the detection probability and the false probability , the system uncertainty reaches the minimum value of 0.305. This parameter combination shows the optimal performance in all test configurations.

Table 2.
The uncertainty under the combination of different detection probabilities (d) and false probabilities (f).
To verify the effectiveness of the ACS algorithm, we use heat map analysis to check the change in target probability in different time steps in the task area, as shown in Figure 2. Initially, each grid has a prior probability of 0.5, and the color intensity reflects the target probability value of each grid, where the darker the color means the higher the probability when the target is present. On the contrary, a lighter color means that the possibility of the existence of the target in this area is low. The analysis shows that with the increase in time, the agent’s search region expands gradually, but the target probability in the no-target region decreases significantly. The target probability graph provides important information for the subsequent USV fine-grained search target.
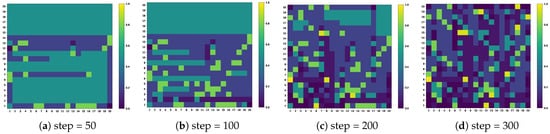
Figure 2.
The target probability in the task area changes at different time steps.
Figure 3 compares the performance of different search algorithms in terms of coverage. The lawnmower algorithm (LMA) [1] achieves rapid initial coverage but plateaus later, reaching a final coverage rate of 64.5%, consistent with its fixed-path planning limitations in dynamic environments. In contrast, MADDPG shows slower initial improvement due to agent exploration but demonstrates steady growth over time, reflecting its adaptability in multi-agent collaboration. Our proposed ACS algorithm outperforms both, achieving fast initial coverage and continuous optimization, culminating in a final coverage rate of 98%. Its success stems from efficient collaboration mechanisms and effective balance between exploration and exploitation.
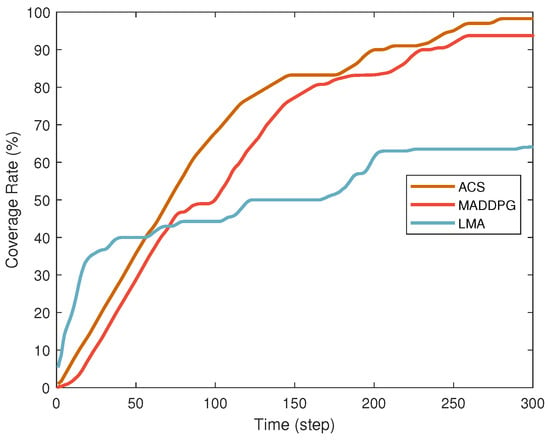
Figure 3.
Comparison of coverage under different search algorithms.
We further compare the total path length performance of the greedy algorithm, K-means clustering algorithm, and SFS algorithm under different number of USVs. As illustrated in Figure 4, the proposed algorithm demonstrates superior path planning performance with significant optimization advantages over conventional methods. The intelligent optimization mechanism of our algorithm, inspired by natural evolutionary processes, effectively overcomes the local optimum trap inherent in greedy algorithms and avoids the adaptability constraints caused by the fixed partitioning pattern of K-means. Particularly noteworthy is the enhanced robustness displayed by our SFS algorithm when handling increased task complexity, attributable to its global optimization characteristics that enable adaptive path allocation. In contrast, traditional methods show varying degrees of performance degradation during scale expansion.
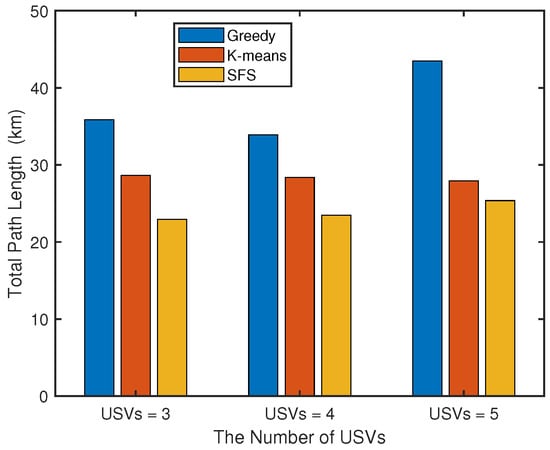
Figure 4.
Comparison of path lengths of different algorithms under different number of USVs.
Figure 5a–c respectively show the comparison of path planning results of the greedy algorithm, K-means clustering algorithm, and the proposed SFS algorithm. It can be seen from the visualization results that the three algorithms show significantly different path characteristics in exploring high-probability regions: the path of the greedy algorithm has obvious path crossing and load imbalance, and the path length of the USV 1 is significantly larger than that of other USVs; the K-means algorithm realizes partition path planning through spatial clustering. Each USV forms a compact path in the specified area, but there are individual detour points at the cluster boundary. The path generated by the SFS algorithm is the smoothest and uniform, and the length difference of each USV path is the smallest and there is no crossover phenomenon, showing the best global optimization capability.
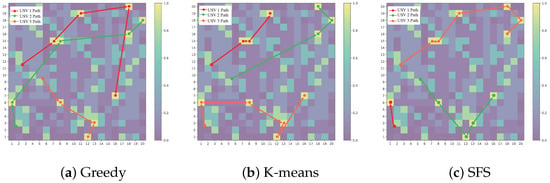
Figure 5.
Search path diagram of USVs under different search algorithms.
Figure 6 shows the change in USV energy consumption with the number of UAVs in the SCS algorithm. The discrete points represent energy consumption at different time steps, with diamond markers for the initial time step. It shows that the energy consumption of USVs initially increases and then decreases. Overall, in the initial stage, due to the random positions of UAVs and USVs as well as the random charging demands, the scheduling strategy needs to learn a better policy. Over time, USVs gradually optimize their movement direction through collaborative communication to minimize energy consumption while meeting the battery charging requirements of UAVs. Moreover, it can be seen that the energy consumption of USVs increases with the increasing number of UAVs because of serving more charging demands, requiring USVs to travel a longer distance and increasing energy expenditure.
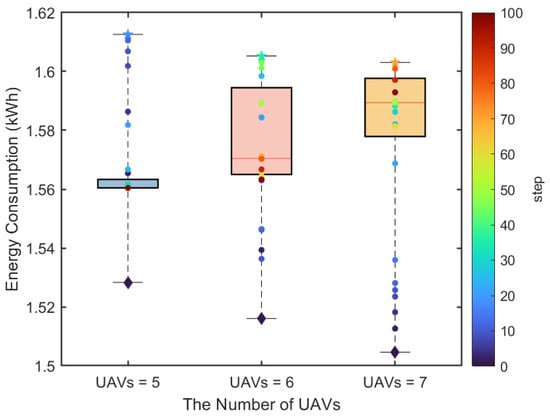
Figure 6.
The USV energy consumption for different numbers of UAVs.
We further compare the average charging energy with different algorithms under varying number of UAVs. Average charging energy [43] refers to the average of the energy received by all UAVs in a single charging service. As illustrated in the Figure 7, the proposed SCS algorithm has significant advantages: when the number of UAVs increases from 5 to 7, the algorithm can keep the average charging energy at a high level. While the highest bidder gets the best bidding mechanism based on the online auction (OA) method [17] achieves a medium level, but its performance decreases significantly when the number of UAVs increases due to resource competition and suboptimal allocation in the bidding process. Compared with the independent deep deterministic policy gradient (IDDPG) [44], the independent decision mechanism may cause multiple USVs to repeatedly select an UAV service object, showing the lowest charging energy effect. With the expansion of the system scale, the SCS algorithm shows stronger adaptability, and the learned cooperative strategy can realize more reasonable path planning.
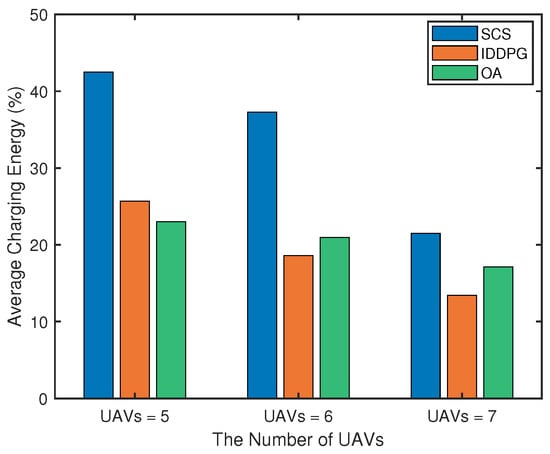
Figure 7.
Comparison of average charging energy among different algorithms under different numbers of UAVs.
Figure 8 verifies the comparison results of average charging response time under different UAVs and USVs, where the response time is defined as the time interval from the UAV issuing the charging request to the actual charging start. The experimental results show that with the increase in the number of UAVs, the average charging response time of the system presents an upward trend, and there are obvious performance differences under different USV configurations. The higher the number of USVs, the shorter the response time, and the lower the number of USVs, the longer the response time, indicating that the number of USVs plays a key role in regulating the endurance capability of multi-UAVs. The data curve shows that as the number of UAVs increases to nine or more, the growth trend in system response time increases, indicating that there may be some reduction in synergy efficiency under the current configuration. This phenomenon suggests that under the existing system architecture, when the scale of UAVs reaches this critical value, it may be necessary to further optimize the resource scheduling strategy to maintain the ideal operational efficiency.
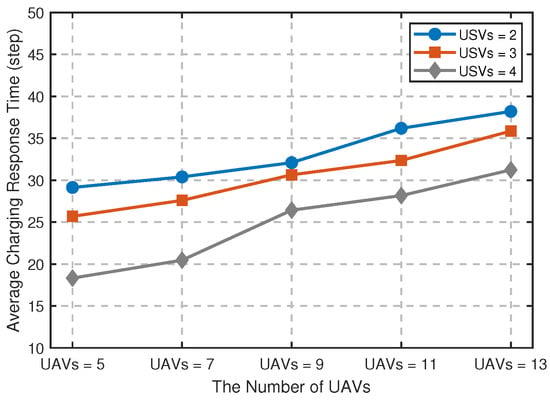
Figure 8.
Comparison of average charging response time under different numbers of UAVs and USVs.
6. Conclusions
In this paper, we proposed a long-endurance collaborative SAR scheme leveraging the complementary advantages of UAV and USV, and deep reinforcement-learning techniques. This scheme includes a multi-UAV first-phase search algorithm and multi-USV second-phase search algorithm. In addition, to carry out long-endurance collaborative search, we designed a multi-USV mobile charging scheduling algorithm to prolong the flight time of UAVs. Numerical simulations are conducted to validate the effectiveness of the proposed scheme. Furthermore, for the operation of the UAV–USV search system in harsh environments, such as ocean currents or environments with variable communication requirements, the effectiveness of the proposed scheme should be further studied by adding more complex algorithms or methods. We leave it as our future research to enhance the robustness of the proposed scheme.
Author Contributions
Conceptualization, P.D., H.T., H.L. and Z.F.; methodology, P.D. and H.T.; software, P.D., J.L. and Y.Z.; validation, P.D. and H.T.; formal analysis, P.D. and H.T.; resources, H.L.; data curation, P.D. and H.T.; writing—original draft preparation, P.D.; writing—review and editing, P.D., H.T. and Z.F.; visualization, P.D., J.L. and Y.Z.; supervision, H.L. and Z.F.; project administration H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the project ZR2024MF024 supported by Shandong Provincial Natural Science Foundation, and in part by the National Natural Science Foundation of China under Grant U24A20215 and 62072287.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors thank the National Natural Science Foundation of China and the Shandong Provincial Natural Science Foundation of China for their financial support and the anonymous reviewers for their valuable comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, J.; Zhang, G.; Jiang, C.; Zhang, W. A survey of maritime unmanned search system: Theory, applications and future directions. Ocean Eng. 2023, 285, 115359–115371. [Google Scholar] [CrossRef]
- Chen, L.; Yu, S.; Chen, Q.; Li, S.; Chen, X.; Zhao, Y. 5s: Design and in-orbit demonstration of a multifunctional integrated satellite-based internet of things payload. IEEE Internet Things J. 2024, 11, 12864–12873. [Google Scholar] [CrossRef]
- Luo, H.; Ma, S.; Tao, H.; Ruby, R.; Zhou, J.; Wu, K. Drl-optimized optical communication for a reliable uav-based maritime data transmission. IEEE Internet Things J. 2024, 11, 18768–18781. [Google Scholar] [CrossRef]
- Wang, J.; Luo, H.; Ruby, R.; Liu, J.; Wang, S.; Wu, K. Enabling reliable water?air direct optical wireless communication for uncrewed vehicular networks: A deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2024, 73, 11470–11486. [Google Scholar] [CrossRef]
- Luo, H.; Wang, J.; Bu, F.; Ruby, R.; Wu, K.; Guo, Z. Recent progress of air/water cross-boundary communications for underwater sensor networks: A review. IEEE Sens. J. 2022, 22, 8360–8382. [Google Scholar] [CrossRef]
- Peng, X.; Lan, X.; Chen, Q. Age of task-aware aav-based mobile edge computing techniques in emergency rescue applications. IEEE Internet Things J. 2025, 12, 8909–8930. [Google Scholar] [CrossRef]
- Queralta, J.P.; Taipalmaa, J.; Pullinen, B.C.; Sarker, V.K.; Gia, T.N.; Tenhunen, H.; Gabbouj, M.; Raitoharju, J.; Westerlund, T. Collaborative multi-robot search and rescue: Planning, coordination, perception, and active vision. IEEE Access 2020, 8, 191617–191643. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, W.; Liu, J.; Sun, C. Cooperative usv–uav marine search and rescue with visual navigation and reinforcement learning-based control. ISA Trans. 2023, 137, 222–235. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, Z.; Sun, R. Maritime search and rescue based on group mobile computing for UAVs and USVs. IEEE Trans. Ind. Inform. 2020, 99, 1–8. [Google Scholar] [CrossRef]
- Krishna, C.L.; Cao, M.; Murphy, R.R. Autonomous observation of multiple usvs from uav while prioritizing camera tilt and yaw over uav motion. In Proceedings of the 2017 IEEE International Symposium on Safety, Security and Rescue Robotics (SSRR), Shanghai, China, 11–13 October 2017; pp. 141–146. [Google Scholar]
- Xiao, X.; Dufek, J.; Woodbury, T.; Murphy, R. Uav assisted usv visual navigation for marine mass casualty incident response. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6105–6110. [Google Scholar]
- Wang, Y.; Su, Z.; Xu, Q.; Li, R.; Luan, T.H.; Wang, P. A secure and intelligent data sharing scheme for uav-assisted disaster rescue. IEEE/ACM Trans. Netw. 2023, 31, 2422–2438. [Google Scholar] [CrossRef]
- Liu, X.; Ansari, N.; Sha, Q.; Jia, Y. Efficient green energy far-field wireless charging for internet of things. IEEE Internet Things J. 2022, 9, 23047–23057. [Google Scholar] [CrossRef]
- Ma, X.; Liu, X.; Ansari, N. Green laser-powered uav far-field wireless charging and data backhauling for a large-scale sensor network. IEEE Internet Things J. 2024, 11, 31932–31946. [Google Scholar] [CrossRef]
- Mondal, M.S.; Ramasamy, S.; Humann, J.D.; Reddinger, J.-P.F.; Dotterweich, J.M.; Childers, M.A.; Bhounsule, P. Optimizing fuel-constrained uav-ugv routes for large scale coverage: Bilevel planning in heterogeneous multi-agent systems. In Proceedings of the 2023 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), Boston, MA, USA, 4–5 December 2023; pp. 114–120. [Google Scholar]
- Yu, K.; Budhiraja, A.K.; Tokekar, P. Algorithms for routing of unmanned aerial vehicles with mobile recharging stations. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5720–5725. [Google Scholar]
- Wang, Y.; Su, Z. An envy-free online uav charging scheme with vehicle-mounted mobile wireless chargers. China Commun. 2023, 20, 89–102. [Google Scholar] [CrossRef]
- Dong, P.; Liu, J.; Tao, H.; Ruby, R.; Jian, M.; Luo, H. An optimized scheduling scheme for uav-usv cooperative search via multi-agent reinforcement learning approach. In Proceedings of the 20th International Conference on Mobility, Sensing and Networking (MSN 2024), Harbin, China, 20–22 December 2024; pp. 172–179. [Google Scholar] [CrossRef]
- Dufek, J.; Murphy, R. Visual pose estimation of usv from uav to assist drowning victims recovery. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 147–153. [Google Scholar]
- Zhang, J.; Xiong, J.; Zhang, G.; Gu, F.; He, Y. Flooding disaster oriented usv & uav system development & demonstration. In Proceedings of the OCEANS 2016-Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–4. [Google Scholar]
- Wang, Y.; Su, Z.; Zhang, N.; Li, R. Mobile wireless rechargeable uav networks: Challenges and solutions. IEEE Commun. Mag. 2022, 60, 33–39. [Google Scholar] [CrossRef]
- Mahbub, I.; Patwary, A.B.; Mahin, R.; Roy, S. Far-field wireless power beaming to mobile receivers using distributed, coherent phased arrays: A review of the critical components of a distributed wireless power beaming system. IEEE Microw. Mag. 2024, 25, 72–94. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, S.; Shi, Q.; Zhang, R. Resonant beam charging-powered uav-assisted sensing data collection. IEEE Trans. Veh. Technol. 2019, 69, 1086–1090. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Multi-agent reinforcement learning: A selective overview of theories and algorithms. In Handbook of Reinforcement Learning and Control; Springer: Cham, Switzerland, 2021; pp. 321–384. [Google Scholar]
- Yi, Z.; Xiang, C.; Huaguang, S.; Zhanqi, J.; Nianwen, N.; Fuqiang, L. Multi-objective coordinated optimization for uav charging scheduling in intelligent aerial-ground perception networks. Chin. J. Electron. 2023, 32, 1203–1217. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, J.; Zhang, Y.; Nie, J.; Lim, W.Y.B.; Zhang, H.; Xiong, Z. Aerial refueling: Scheduling wireless energy charging for uav enabled data collection. IEEE Trans. Green Commun. Netw. 2022, 6, 1494–1510. [Google Scholar] [CrossRef]
- Messaoudi, K.; Oubbati, O.S.; Rachedi, A.; Bendouma, T. Uav-ugv-based system for aoi minimization in iot networks. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 4743–4748. [Google Scholar]
- Zhao, M.; Shi, Q.; Zhao, M.-J. Efficiency maximization for uav-enabled mobile relaying systems with laser charging. IEEE Trans. Wirel. Commun. 2020, 19, 3257–3272. [Google Scholar] [CrossRef]
- Shin, M.; Kim, J.; Levorato, M. Auction-based charging scheduling with deep learning framework for multi-drone networks. IEEE Trans. Veh. Technol. 2019, 68, 4235–4248. [Google Scholar] [CrossRef]
- Jiang, S. Fostering marine internet with advanced maritime radio system using spectrums of cellular networks. In Proceedings of the 2016 IEEE International Conference on Communication Systems (ICCS), Shenzhen, China, 14–16 December 2016; pp. 1–6. [Google Scholar]
- Yao, P.; Gao, Z. Uav/usv cooperative trajectory optimization based on reinforcement learning. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 4711–4715. [Google Scholar]
- Liu, Y.; Peng, Y.; Wang, M.; Xie, J.; Zhou, R. Multi-usv system cooperative underwater target search based on reinforcement learning and probability map. Math. Probl. Eng. 2020, 2020, 7842768–7842780. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Hof, J. An adaptive vns algorithm for vehicle routing problems with intermediate stops. OR Spectr. 2015, 37, 353–387. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Han, Y.; Ma, W. Automatic monitoring of water pollution based on the combination of UAV and USV. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 420–424. [Google Scholar]
- Wang, Y.; Luan, H.T.; Su, Z.; Zhang, N.; Benslimane, A. A secure and efficient wireless charging scheme for electric vehicles in vehicular energy networks. IEEE Trans. Veh. Technol. 2022, 71, 1491–1508. [Google Scholar] [CrossRef]
- Shen, G.; Lei, L.; Zhang, X.; Li, Z.; Cai, S.; Zhang, L. Multi-UAV cooperative search based on reinforcement learning with a digital twin driven training framework. IEEE Trans. Veh. Technol. 2023, 72, 8354–8368. [Google Scholar] [CrossRef]
- Iqbal, S.; Sha, F. Actor-attention-critic for multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2961–2970. [Google Scholar]
- Qu, X.; Gan, W.; Song, D.; Zhou, L. Pursuit-evasion game strategy of USV based on deep reinforcement learning in complex multi-obstacle environment. Ocean Eng. 2023, 273, 114016. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6379–6390. [Google Scholar]
- Lyu, L.; Chu, Z.; Lin, B. Joint association and power optimization for multi-uav assisted cooperative transmission in marine iot networks. Peer Peer Netw. Appl. 2021, 14, 3307–3318. [Google Scholar] [CrossRef]
- Simolin, T.; Rauma, K.; Viri, R.; Mäkinen, J.; Rautiainen, A.; Järventausta, P. Charging powers of the electric vehicle fleet: Evolution and implications at commercial charging sites. Appl. Energy 2021, 303, 117651–117663. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).