Feasibility and Accuracy of an RTMPose-Based Markerless Motion Capture System for Single-Player Tasks in 3x3 Basketball
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
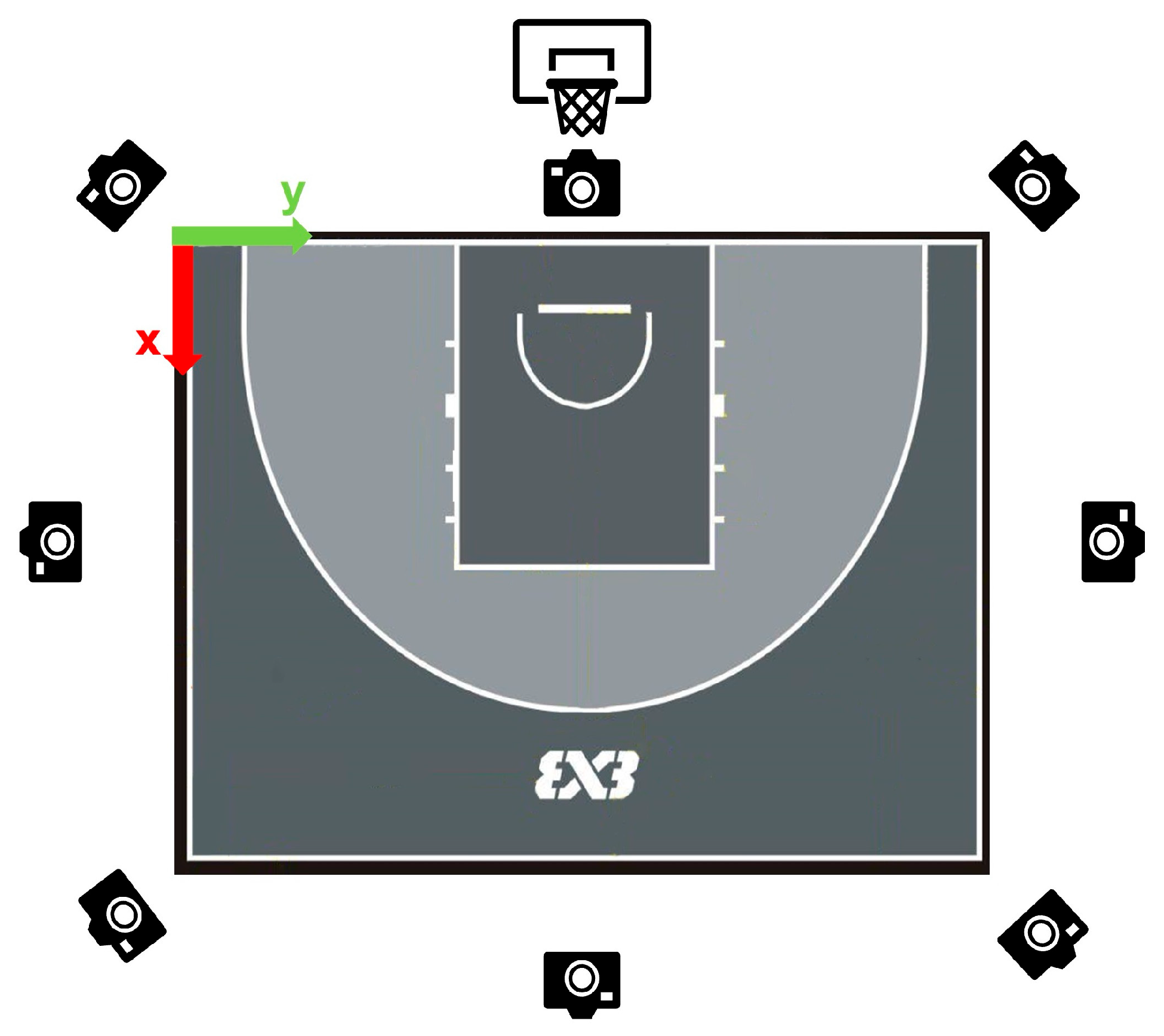
2.2. Equipment and Venue
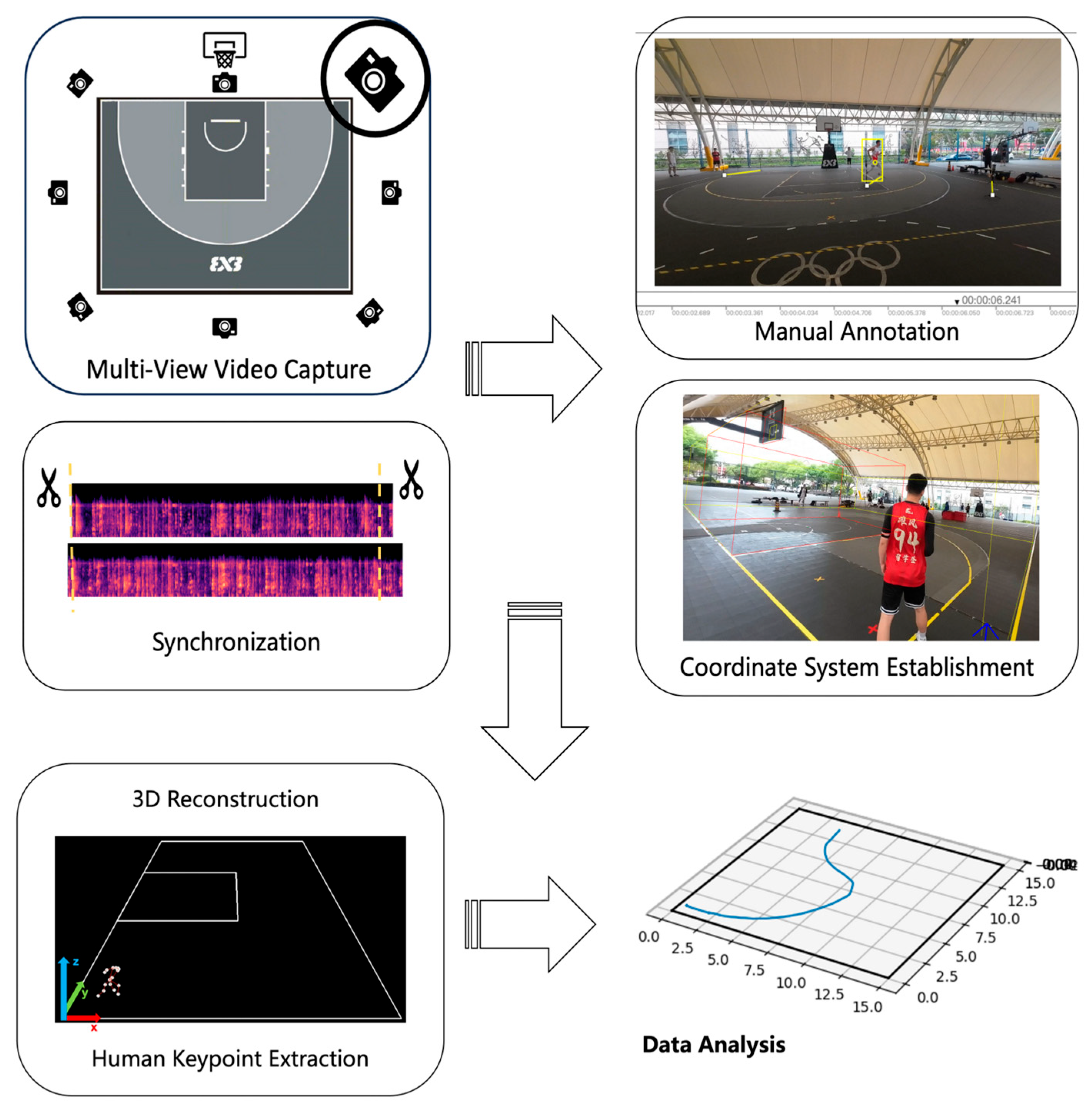
2.3. Algorithm Workflow
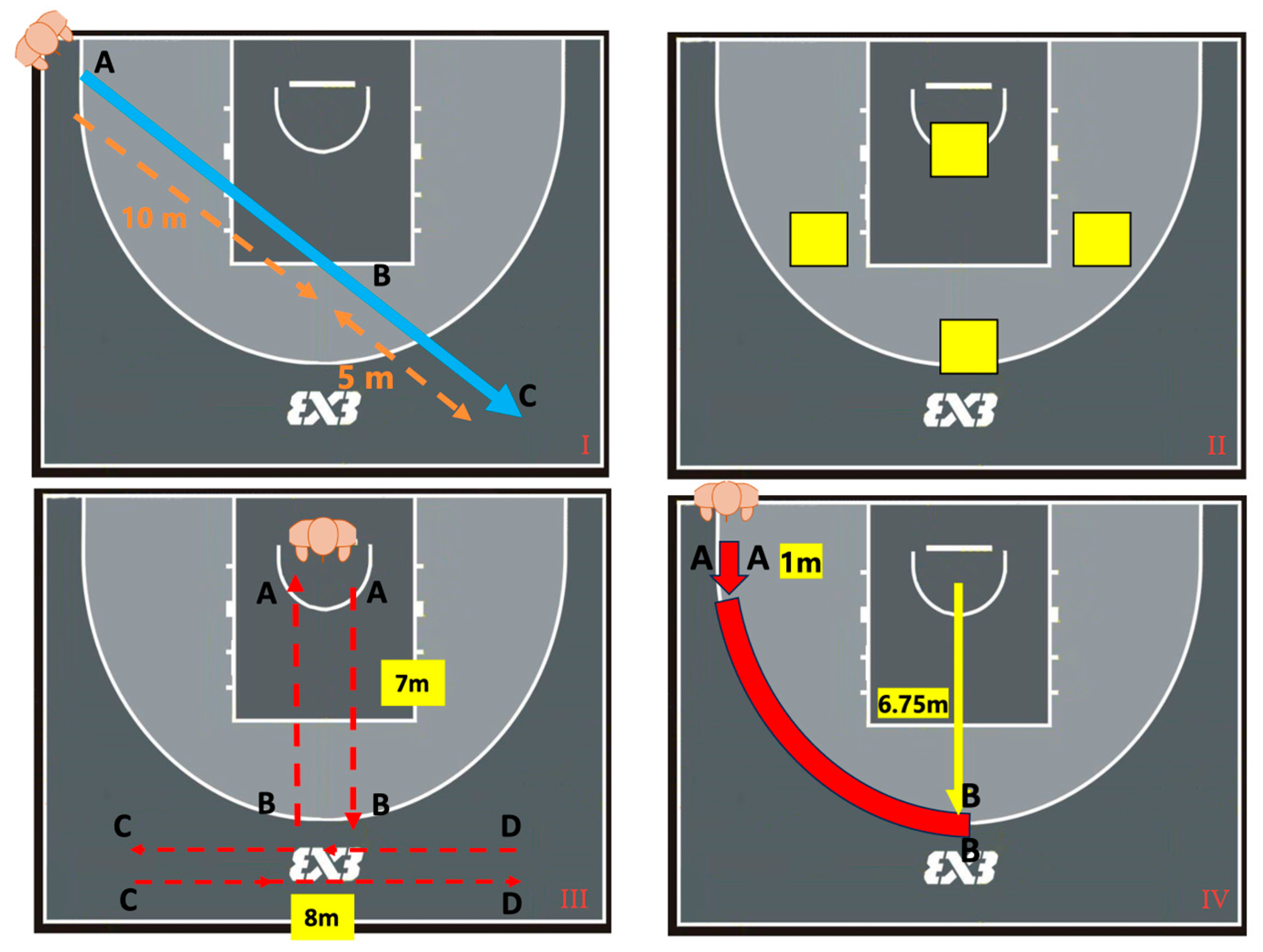
2.4. Experiment Procedures
2.5. Data Collection
2.6. Statistical Analysis
3. Results
3.1. Horizontal-Displacement Validity
3.2. Average Speed Measurement Consistency
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Willberg, C.; Wieland, B.; Rettenmaier, L.; Behringer, M.; Zentgraf, K. The Relationship between External and Internal Load Parameters in 3x3 Basketball Tournaments. BMC Sports Sci. Med. Rehabil. 2022, 14, 152. [Google Scholar] [CrossRef] [PubMed]
- FIBA Paris Olympics: Games. Available online: https://fiba3x3.com/2024/olympics/games (accessed on 11 June 2025).
- Svilar, L.; Jukić, I. Load Monitoring System in Top-Level Basketball Team. Kinesiology 2018, 50, 25–33. [Google Scholar] [CrossRef]
- Towner, R.; Larson, A.; Gao, Y.; Ransdell, L.B. Longitudinal Monitoring of Workloads in Women’s Division I (DI) Collegiate Basketball across Four Training Periods. Front. Sports Act. Living 2023, 5, 1108965. [Google Scholar] [CrossRef] [PubMed]
- Russell, J.L.; McLean, B.D.; Impellizzeri, F.M.; Strack, D.S.; Coutts, A.J. Measuring Physical Demands in Basketball: An Explorative Systematic Review of Practices. Sports Med. 2021, 51, 81–112. [Google Scholar] [CrossRef] [PubMed]
- Sampaio, J.; McGarry, T.; Calleja-González, J.; Jiménez Sáiz, S.; Schelling I Del Alcázar, X.; Balciunas, M. Exploring Game Performance in the National Basketball Association Using Player Tracking Data. PLoS ONE 2015, 10, e0132894. [Google Scholar] [CrossRef]
- Ben Abdelkrim, N.; El Fazaa, S.; El Ati, J. Time–Motion Analysis and Physiological Data of Elite under-19-Year-Old Basketball Players during Competition. Br. J. Sports Med. 2007, 41, 69–75. [Google Scholar] [CrossRef]
- Colyer, S.L.; Evans, M.; Cosker, D.P.; Salo, A.I.T. A Review of the Evolution of Vision-Based Motion Analysis and the Integration of Advanced Computer Vision Methods Towards Developing a Markerless System. Sports Med.-Open 2018, 4, 24. [Google Scholar] [CrossRef]
- Tang, J.; Kim, K.; Wang, K. From Screen to Reality: Exploring the Evolution and Integration of Motion Capture Technology for Virtual Digital Humans. Asia-Pac. J. Converg. Res. Interchange 2024, 10, 153–168. [Google Scholar] [CrossRef]
- Scataglini, S.; Abts, E.; Van Bocxlaer, C.; Van den Bussche, M.; Meletani, S.; Truijen, S. Accuracy, Validity, and Reliability of Markerless Camera-Based 3D Motion Capture Systems versus Marker-Based 3D Motion Capture Systems in Gait Analysis: A Systematic Review and Meta-Analysis. Sensors 2024, 24, 3686. [Google Scholar] [CrossRef]
- Needham, L.; Evans, M.; Wade, L.; Cosker, D.P.; McGuigan, M.P.; Bilzon, J.L.; Colyer, S.L. The Development and Evaluation of a Fully Automated Markerless Motion Capture Workflow. J. Biomech. 2022, 144, 111338. [Google Scholar] [CrossRef]
- D’Haene, M.; Chorin, F.; Colson, S.S.; Guérin, O.; Zory, R.; Piche, E. Validation of a 3D Markerless Motion Capture Tool Using Multiple Pose and Depth Estimations for Quantitative Gait Analysis. Sensors 2024, 24, 7105. [Google Scholar] [CrossRef] [PubMed]
- Corazza, S.; Mündermann, L.; Chaudhari, A.M.; Demattio, T.; Cobelli, C.; Andriacchi, T.P. A Markerless Motion Capture System to Study Musculoskeletal Biomechanics: Visual Hull and Simulated Annealing Approach. Ann. Biomed. Eng. 2006, 34, 1019–1029. [Google Scholar] [CrossRef]
- Aderinola, T.B.; Younesian, H.; Whelan, D.; Caulfield, B.; Ifrim, G. Quantifying Jump Height Using Markerless Motion Capture with a Single Smartphone. IEEE Open J. Eng. Med. Biol. 2023, 4, 109–115. [Google Scholar] [CrossRef]
- Clark, R.A.; Mentiplay, B.F.; Hough, E.; Pua, Y.H. Three-Dimensional Cameras and Skeleton Pose Tracking for Physical Function Assessment: A Review of Uses, Validity, Current Developments and Kinect Alternatives. Gait Posture 2019, 68, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Zago, M.; Luzzago, M.; Marangoni, T.; De Cecco, M.; Tarabini, M.; Galli, M. 3D Tracking of Human Motion Using Visual Skeletonization and Stereoscopic Vision. Front. Bioeng. Biotechnol. 2020, 8, 181. [Google Scholar] [CrossRef] [PubMed]
- Nakano, N.; Sakura, T.; Ueda, K.; Omura, L.; Kimura, A.; Iino, Y.; Fukashiro, S.; Yoshioka, S.; Nakano, N.; Sakura, T.; et al. Evaluation of 3D Markerless Motion Capture Accuracy Using OpenPose with Multiple Video Cameras. Front. Sports Act. Living 2020, 2, 50. [Google Scholar] [CrossRef]
- Cabarkapa, D.; Cabarkapa, D.V.; Miller, J.D.; Templin, T.T.; Frazer, L.L.; Nicolella, D.P.; Fry, A.C. Biomechanical Characteristics of Proficient Free-Throw Shooters—Markerless Motion Capture Analysis. Front. Sports Act. Living 2023, 5, 1208915. [Google Scholar] [CrossRef]
- Blythman, R.; Saxena, M.; Tierney, G.J.; Richter, C.; Smolic, A.; Simms, C. Assessment of Deep Learning Pose Estimates for Sports Collision Tracking. J. Sports Sci. 2022, 40, 1885–1900. [Google Scholar] [CrossRef]
- Giulietti, N.; Caputo, A.; Chiariotti, P.; Castellini, P. SwimmerNET: Underwater 2D Swimmer Pose Estimation Exploiting Fully Convolutional Neural Networks. Sensors 2023, 23, 2364. [Google Scholar] [CrossRef]
- Jiang, T.; Lu, P.; Zhang, L.; Ma, N.; Han, R.; Lyu, C.; Li, Y.; Chen, K. RTMPose: Real-Time Multi-Person Pose Estimation Based on MMPose. arXiv 2023, arXiv:2303.07399. [Google Scholar]
- Yamada, K.; Yin, L.; Hu, Q.; Ding, N.; Iwashita, S.; Ichikawa, J.; Kotani, K.; Yeung, C.; Fujii, K. TrackID3x3: A Dataset and Algorithm for Multi-Player Tracking with Identification and Pose Estimation in 3x3 Basketball Full-Court Videos. arXiv 2025, arXiv:2503.18282. [Google Scholar]
- Armitano-Lago, C.; Willoughby, D.; Kiefer, A.W. A SWOT Analysis of Portable and Low-Cost Markerless Motion Capture Systems to Assess Lower-Limb Musculoskeletal Kinematics in Sport. Front. Sports Act. Living 2022, 3, 809898. [Google Scholar] [CrossRef] [PubMed]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice Recognition Algorithms Using Mel Frequency Cepstral Coefficient (MFCC) and Dynamic Time Warping (DTW) Techniques. arXiv 2010, arXiv:1003.4083. [Google Scholar]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Ellrich, N.; Niermeyer, K.; Peto, D.; Decker, J.; Fietzek, U.M.; Katzdobler, S.; Höglinger, G.U.; Jahn, K.; Zwergal, A.; Wuehr, M. Precision Balance Assessment in Parkinson’s Disease: Utilizing Vision-Based 3D Pose Tracking for Pull Test Analysis. Sensors 2024, 24, 3673. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision—ECCV 2014 Part V; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 8693, pp. 740–755. ISBN 978-3-319-10601-4. [Google Scholar] [CrossRef]
- Abdel-Aziz, Y.I.; Karara, H.M. Direct Linear Transformation from Comparator Coordinates into Object Space Coordinates in Close-Range Photogrammetry. Photogramm. Eng. Remote Sens. 2015, 81, 103–107. [Google Scholar] [CrossRef]
- Dong, J.; Fang, Q.; Jiang, W.; Yang, Y.; Huang, Q.; Bao, H.; Zhou, X. Fast and Robust Multi-Person 3D Pose Estimation and Tracking From Multiple Views. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 6981–6992. [Google Scholar] [CrossRef]
- Bermuth, D.; Poeppel, A.; Reif, W. RapidPoseTriangulation: Multi-View Multi-Person Whole-Body Human Pose Triangulation in a Millisecond. arXiv 2025, arXiv:2503.21692. [Google Scholar]
- Hodder, R.W.; Ball, K.A.; Serpiello, F.R. Criterion Validity of Catapult ClearSky T6 Local Positioning System for Measuring Inter-Unit Distance. Sensors 2020, 20, 3693. [Google Scholar] [CrossRef]
- Huggins, R.A.; Giersch, G.E.W.; Belval, L.N.; Benjamin, C.L.; Curtis, R.M.; Sekiguchi, Y.; Peltonen, J.; Casa, D.J. The Validity and Reliability of Global Positioning System Units for Measuring Distance and Velocity During Linear and Team Sport Simulated Movements. J. Strength Cond. Res. 2020, 34, 3070–3077. [Google Scholar] [CrossRef]
- Jennings, D.; Cormack, S.; Coutts, A.J.; Boyd, L.; Aughey, R.J. The Validity and Reliability of GPS Units for Measuring Distance in Team Sport Specific Running Patterns. Int. J. Sports Physiol. Perform. 2010, 5, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Portas, M.D.; Harley, J.A.; Barnes, C.A.; Rush, C.J. The Validity and Reliability of 1-Hz and 5-Hz Global Positioning Systems for Linear, Multidirectional, and Soccer-Specific Activities. Int. J. Sports Physiol. Perform. 2010, 5, 448–458. [Google Scholar] [CrossRef]
- Varley, M.C.; Fairweather, I.H.; Aughey, R.J. Validity and Reliability of GPS for Measuring Instantaneous Velocity during Acceleration, Deceleration, and Constant Motion. J. Sports Sci. 2012, 30, 121–127. [Google Scholar] [CrossRef]
- Roberts, S.; Trewartha, G.; Stokes, K.; Roberts, S.; Trewartha, G.; Stokes, K. A Comparison of Time–Motion Analysis Methods for Field-Based Sports. Int. J. Sports Physiol. Perform. 2006, 1, 388–399. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, G.; Nevill, A.M. Statistical Methods For Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sports Med. 1998, 26, 217–238. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G.; Schabort, E.J.; Hawley, J.A. Reliability of Power in Physical Performance Tests. Sports Med. 2001, 31, 211–234. [Google Scholar] [CrossRef]
- Hopkins, W. Spreadsheets for Analysis of Validity and Reliability. Available online: http://sportsci.org/2015/ValidRely.htm (accessed on 15 June 2025).
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Hopkins, W.G. Measures of Reliability in Sports Medicine and Science. Sports Med. 2000, 30, 1–15. [Google Scholar] [CrossRef]
- Liu, H.; Hopkins, W.; Gómez, A.M.; Molinuevo, S.J. Inter-Operator Reliability of Live Football Match Statistics from OPTA Sportsdata. Int. J. Perform. Anal. Sport 2013, 13, 803–821. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Gray, A.J.; Jenkins, D.; Andrews, M.H.; Taaffe, D.R.; Glover, M.L. Validity and Reliability of GPS for Measuring Distance Travelled in Field-Based Team Sports. J. Sports Sci. 2010, 28, 1319–1325. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.T.U.; Scott, T.J.; Kelly, V.G. The Validity and Reliability of Global Positioning Systems in Team Sport. J. Strength Cond. Res. 2016, 30, 1470–1490. [Google Scholar] [CrossRef]
- Tang, H.; Munkasy, B.; Li, L. Differences between Lower Extremity Joint Running Kinetics Captured by Marker-Based and Markerless Systems Were Speed Dependent. J. Sport Health Sci. 2024, 13, 569–578. [Google Scholar] [CrossRef]
- Van Hooren, B.; Pecasse, N.; Meijer, K.; Essers, J.M.N. The Accuracy of Markerless Motion Capture Combined with Computer Vision Techniques for Measuring Running Kinematics. Scand. Med. Sci. Sports 2023, 33, 966–978. [Google Scholar] [CrossRef]
- Bright, J.; Chen, Y.; Zelek, J. Mitigating Motion Blur for Robust 3D Baseball Player Pose Modeling for Pitch Analysis. arXiv 2023, arXiv:2309.01010. [Google Scholar]
- Parada, L.A.; Bona, R.L.; Biancardi, C.M. Biomechanics of Lateral Movements. Sci. J. Sport Perform. 2024, 3, 443–456. [Google Scholar] [CrossRef]
- Noorbhai, H.; Moon, S.; Fukushima, T. A Conceptual Framework and Review of Multi-Method Approaches for 3D Markerless Motion Capture in Sports and Exercise. J. Sports Sci. 2025, 43, 1167–1174. [Google Scholar] [CrossRef]


| Task | N | Condition | Reference Distance (m) | Measured Distance (Mean ± SD, m) | CV (%) | Bias (%) | SEE (%) |
|---|---|---|---|---|---|---|---|
| Straight-Line Running | |||||||
| 10 m Acceleration | 50 | Without Ball | 10 | 10.045 ± 0.062 | 0.62% | 0.60% | 0.48% |
| 10 m Acceleration | 50 | With Ball | 10 | 10.052 ± 0.137 | 1.36% | 0.96% | 0.26% |
| Average | 100 | - | 10 | 10.049 ± 0.106 | 1.06% | 0.63% | 0.66% |
| 5 m Deceleration | 50 | Without Ball | 5 | 4.994 ± 0.088 | 1.76% | 1.10% | 1.36% |
| 5 m Deceleration | 50 | With Ball | 5 | 4.957 ± 0.148 | 2.99% | 1.76% | 0.31% |
| Average | 100 | - | 5 | 4.975 ± 0.123 | 2.46% | 0.92% | 1.37% |
| T-Test | |||||||
| Linear 7 m | 30 | Without Ball | 7 | 7.017 ± 0.084 | 1.20% | 0.66% | 1.03% |
| Lateral Shuffle 8 m | 30 | Without Ball | 8 | 8.296 ± 0.28 | 3.38% | 4.61% | 2.11% |
| Backpedal 7 m | 30 | Without Ball | 7 | 7.068 ± 0.092 | 1.30% | 1.15% | 1.16% |
| Average | - | - | - | - | - | - | - |
| Curved Running | |||||||
| Curved Running, 11.6 m | 24 | Without Ball | 11.6 | 11.665 ± 0.523 | 4.48% | 3.42% | 2.90% |
| Curved Running, 11.6 m | 24 | With Ball | 11.6 | 11.533 ± 0.527 | 4.57% | 3.32% | 3.09% |
| Average | 48 | - | 11.6 | 11.599 ± 0.518 | 4.47% | 3.37% | 2.38% |
| Task | N | MMC (M ± SD, m/s) | TMA (M ± SD, m/s) | SCM (95%CI) | STE (95%CI) | ICC (95%CI) |
|---|---|---|---|---|---|---|
| Straight-Line Running | ||||||
| 10 m Acceleration (No Ball) | 50 | 4.56 ± 0.47 | 4.59 ± 0.47 | 0.05 (0.00~0.10) | 0.04 (0.03~0.09) | 1.00 (0.99~1.00) |
| 10 m Acceleration (With Ball) | 50 | 3.97 ± 0.31 | 3.97 ± 0.28 | 0.05 (−0.06~0.17) | 0.10 (0.06~0.20) | 0.99 (0.97~1.00) |
| 5 m Deceleration (No Ball) | 50 | 4.33 ± 0.80 | 4.34 ± 0.79 | 0.01 (−0.05~0.06) | 0.05 (0.03~0.10) | 1.00 (0.99~1.00) |
| 5 m Deceleration (With Ball) | 50 | 3.48 ± 0.43 | 3.48 ± 0.43 | −0.02 (−0.14~0.10) | 0.10 (0.07~0.21) | 0.99 (0.96~1.00) |
| T-Test | ||||||
| Linear 7 m | 30 | 3.15 ± 0.16 | 3.12 ± 0.17 | −0.13 (−0.34~0.08) | 0.18 (0.12~0.37) | 0.98 (0.89~0.99) |
| Lateral Shuffle 8 m | 30 | 2.39 ± 0.17 | 2.36 ± 0.16 | −0.29 (−0.53~0.04) | 0.21 (0.14~0.42) | 0.97 (0.86~0.99) |
| Backpedal 7 m | 30 | 2.51 ± 0.25 | 2.50 ± 0.28 | −0.02 (−0.17~0.12) | 0.12 (0.08~0.25) | 0.99 (0.95~1.00) |
| Curved Running | ||||||
| Curved Running, 11.6 m (No Ball) | 24 | 2.77 ± 0.25 | 2.77 ± 0.22 | 0.01 (−0.19~0.20) | 0.16 (0.11~0.33) | 0.98 (0.92~1.00) |
| Curved Running, 11.6 m (With Ball) | 24 | 2.81 ± 0.28 | 2.82 ± 0.28 | 0.04 (−0.12~0.19) | 0.13 (0.09~0.26) | 0.99 (0.95~1.00) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Zhang, M.; Dong, R.; Qiu, M.; Wang, W. Feasibility and Accuracy of an RTMPose-Based Markerless Motion Capture System for Single-Player Tasks in 3x3 Basketball. Sensors 2025, 25, 4003. https://doi.org/10.3390/s25134003
Zheng W, Zhang M, Dong R, Qiu M, Wang W. Feasibility and Accuracy of an RTMPose-Based Markerless Motion Capture System for Single-Player Tasks in 3x3 Basketball. Sensors. 2025; 25(13):4003. https://doi.org/10.3390/s25134003
Chicago/Turabian StyleZheng, Wen, Mingxin Zhang, Rui Dong, Mingjia Qiu, and Wei Wang. 2025. "Feasibility and Accuracy of an RTMPose-Based Markerless Motion Capture System for Single-Player Tasks in 3x3 Basketball" Sensors 25, no. 13: 4003. https://doi.org/10.3390/s25134003
APA StyleZheng, W., Zhang, M., Dong, R., Qiu, M., & Wang, W. (2025). Feasibility and Accuracy of an RTMPose-Based Markerless Motion Capture System for Single-Player Tasks in 3x3 Basketball. Sensors, 25(13), 4003. https://doi.org/10.3390/s25134003







