A Two-Branch ResNet-BiLSTM Deep Learning Framework for Extracting Multimodal Features Applied to PPG-Based Cuffless Blood Pressure Estimation
Abstract
1. Introduction
- We propose seven novel groups of trend features designed to capture the signal trend over time. These features have not been previously utilized in the extraction of PPG signal features, but they are instrumental in PPG-based models that aim to predict blood pressure. Given the established correlation between the PPG waveform and the cardiac cycle, as well as blood pressure fluctuations, it is imperative to effectively capture the signal’s volatility and instantaneous frequency changes. These characteristics indirectly reflect the closely related relationship between the cardiac activity cycle and blood pressure fluctuations, thereby enhancing the time-dependent modeling capability of the model.
- We implement a feature selection method using Support Vector Machine-Recursive Feature Elimination (SVM-RFE), which eliminates the features that are least correlated with blood pressure levels in each round of training, retaining only the features that are most critical for prediction.
- We propose a two-branch deep learning framework combining ResNet and BiLSTM that simultaneously processes manually extracted features and raw PPG waveforms. This framework achieves both high accuracy and interpretability, with performance exceeding AAMI, IEEE 1708 standards and achieving BHS Level A standards, particularly for systolic blood pressure (SBP) prediction.
2. Related Work
2.1. Feature-Based Methods
2.2. End-to-End Deep Learning Methods
2.3. Hybrid Approaches
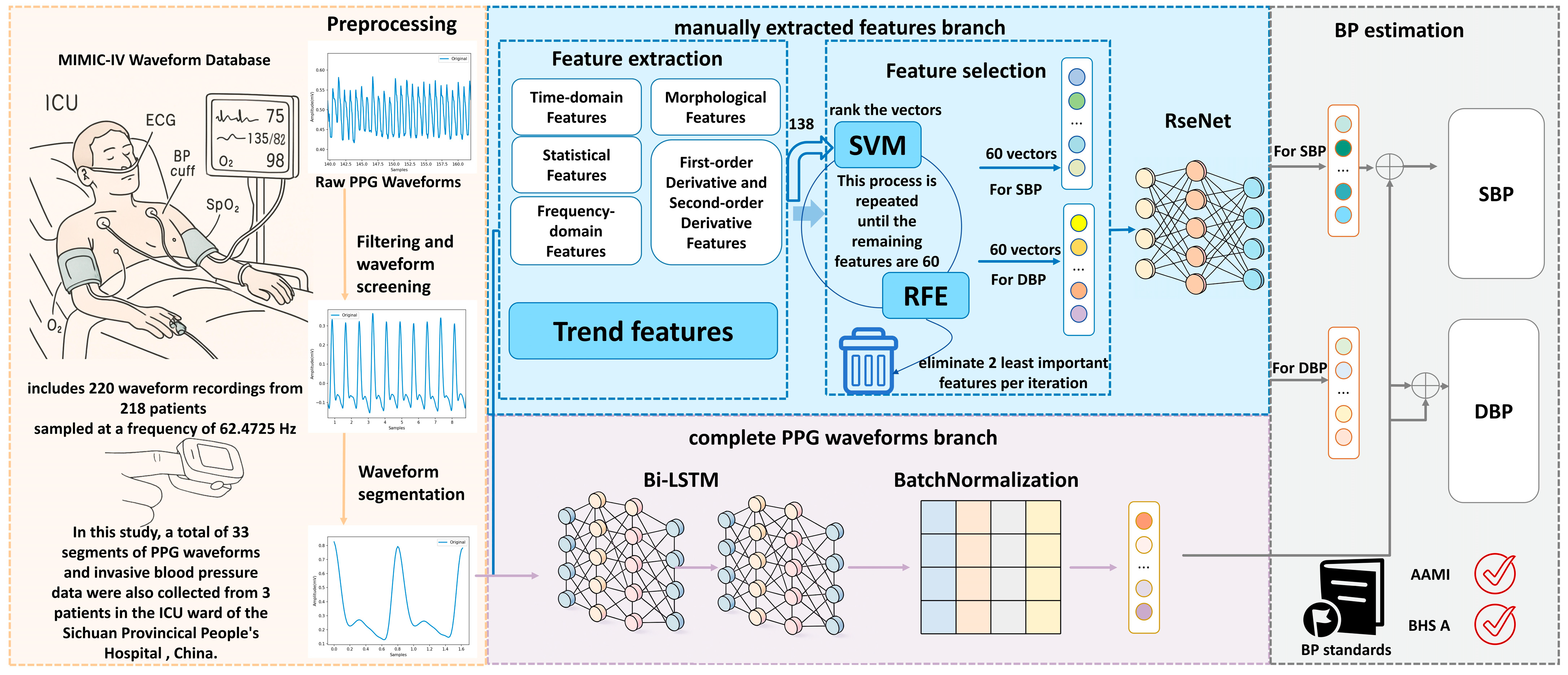
3. Materials and Methods
3.1. Problem Statement
3.2. Overview
3.3. PPG Signal Preprocessing Based on Systolic Peak Detection
3.4. Manually Extracted Features Branch
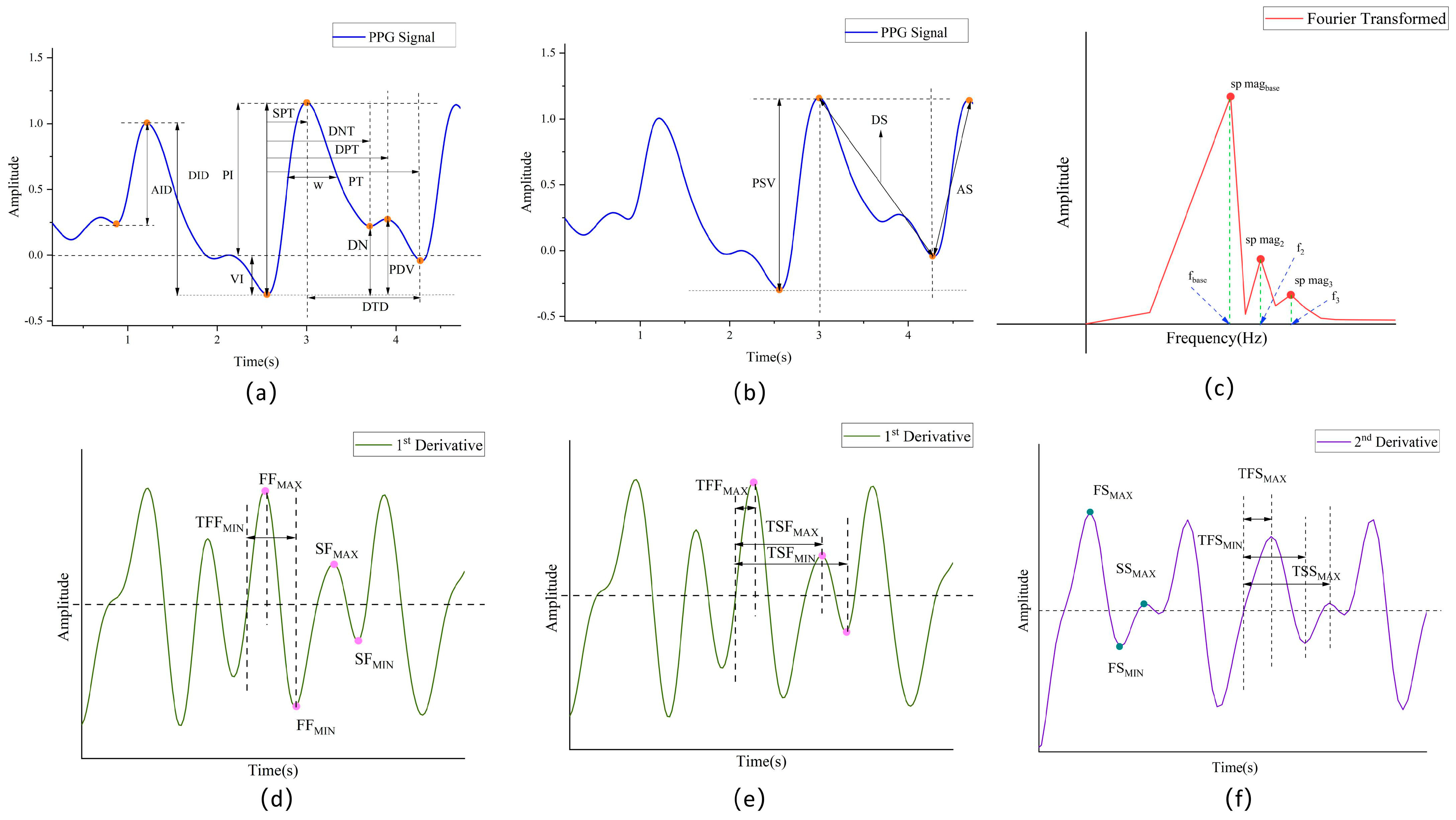
3.4.1. Feature Extraction
Time-Domain Features
Morphological Features
Statistical Features
Frequency-Domain Features
First-Order Derivative and Second-Order Derivative Features
Trend Features
- Short-Time Spectral Subband Energy Rate (STSSE)
- 2.
- Root Mean Square Energy (RMSE)
- 3.
- Spectral Center of Mass
- 4.
- Spectral Bandwidth
- 5.
- Overall Trend: In order to capture the overall trend change in the PPG signal, reflecting the change in vascular elasticity and thus the overall trend in blood pressure, the following three features were utilized: calculated amplitude, mean, and variance features.
- 6.
- Short-Time Energy (STE)
- 7.
- Short-Time Zero Crossing Rate (STZCR).
3.4.2. Feature Selection
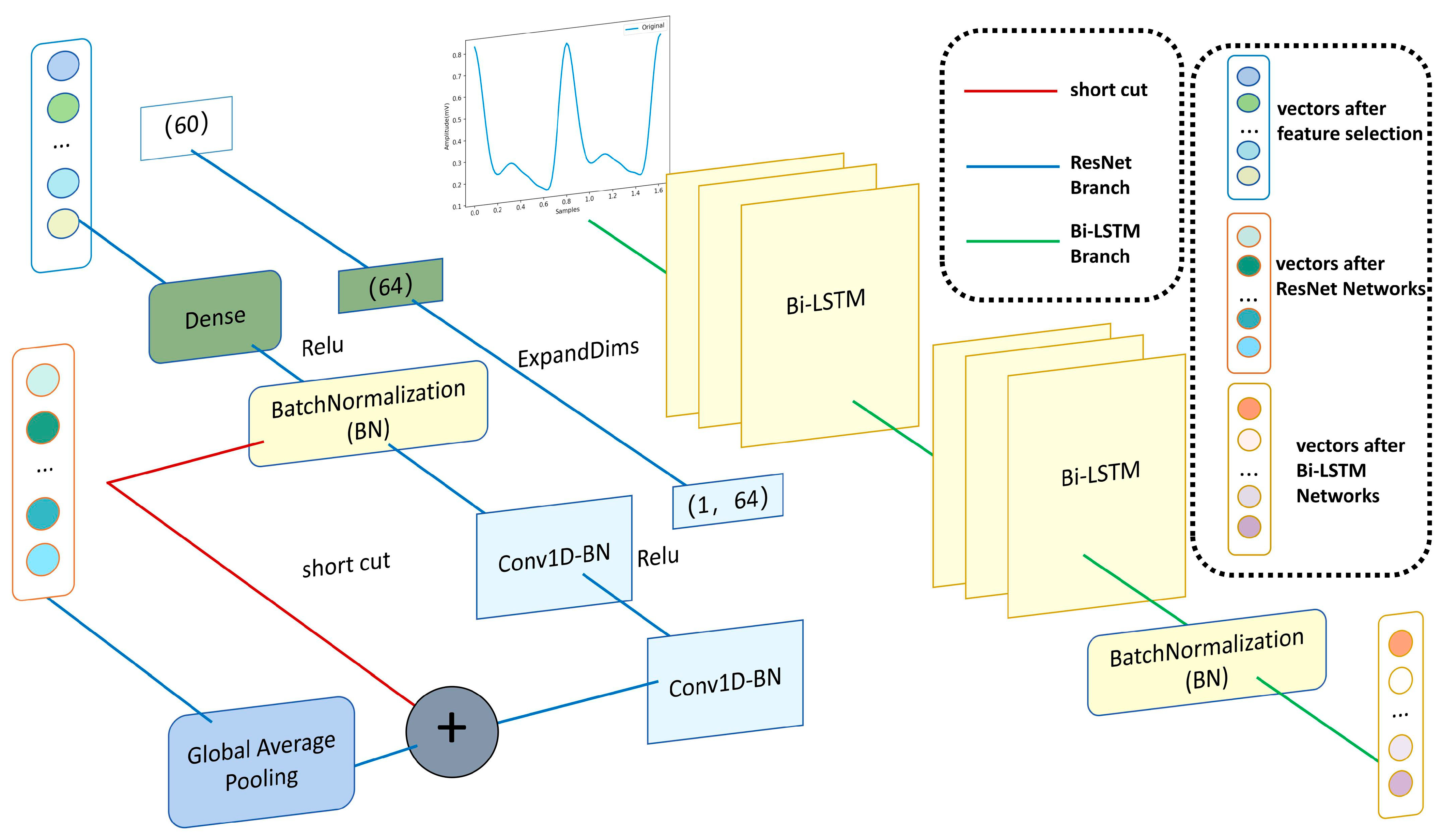
3.4.3. ResNet Neural Networks
3.5. Complete the PPG Waveforms Branch
4. Experiment Setup
4.1. Dataset
4.2. Training and Testing the Algorithms
4.3. Evaluation Metrics
5. Results
5.1. BP Estimation on Our Method Compared to the AAMI Standard and BHS Standard
5.2. Bland–Altman Analysis of BP Estimation on Our Method
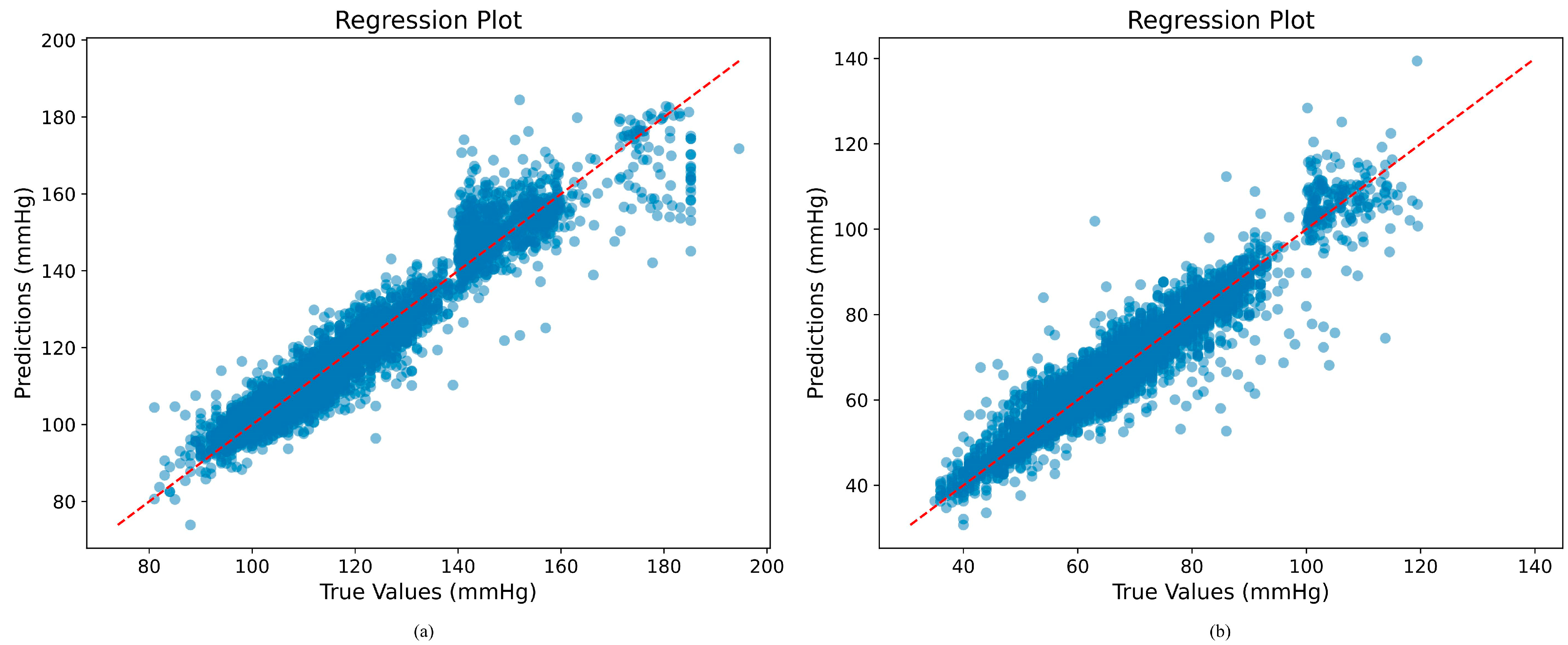
5.3. Regression Plot Analysis of BP Estimation on Our Method
5.4. Comparison with Other Works
5.5. Ablation Experiment
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- WHO. Global Status Report on Noncommunicable Diseases 2010; WHO: Geneva, Switzerland, 2014.
- Kjeldsen, S.E. Hypertension and cardiovascular risk: General aspects. Pharmacol. Res. 2018, 129, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Leong, D.P.; Joseph, P.G.; McKee, M.; Anand, S.S.; Teo, K.K.; Schwalm, J.D.; Yusuf, S. Reducing the Global Burden of Cardiovascular Disease, Part 2 Prevention and Treatment of Cardiovascular Disease. Circ. Res. 2017, 121, 695–710. [Google Scholar] [CrossRef]
- Darbhasayanam, S.H.; Mohammad, H.A.A.; Komalla, A.R. Photoplethysmogram (PPG)-Based Blood Pressure Estimation using Vision Transformer Networks: A Deep Learning Approach. In Proceedings of the 2024 3rd International Conference on Artificial Intelligence for Internet of Things (AIIoT), Vellore, India, 3–4 May 2024; pp. 1–6. [Google Scholar]
- Lim, S.; Kim, T.; Lee, H.; Kim, Y.; Park, M.; Kim, K.-Y.; Kim, M.; Kim, K.H.; Jung, J.; Song, K. Robust optimization for PPG-based blood pressure estimation. Biomed. Signal Process. Control. 2025, 105, 107585. [Google Scholar] [CrossRef]
- Tian, Z.H.; Liu, A.P.; Zhu, G.K.; Chen, X. A paralleled CNN and Transformer network for PPG-based cuff-less blood pressure estimation. Biomed. Signal Process. Control. 2025, 99, 10. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, C.; Ren, X.; Wang, Q.; Wang, H.; Xiang, T.; Qiu, S.; Zhang, Y.-T.; Ye, X. Personalized Continuous Blood Pressure Tracking through Single channel PPG in Wearable Scenarios. IEEE J. Biomed. Health Inform. 2025, 29, 4109–4120. [Google Scholar] [CrossRef]
- Duan, K.; Qian, Z.; Atef, M.; Wang, G. A feature exploration methodology for learning based cuffless blood pressure measurement using photoplethysmography. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6385–6388. [Google Scholar]
- Lin, W.-H.; Wang, H.; Samuel, O.W.; Liu, G.; Huang, Z.; Li, G. New photoplethysmogram indicators for improving cuffless and continuous blood pressure estimation accuracy. Physiol. Meas. 2018, 39, 025005. [Google Scholar] [CrossRef]
- Liu, M.; Po, L.-M.; Fu, H. Cuffless blood pressure estimation based on photoplethysmography signal and its second derivative. Int. J. Comput. Theory Eng. 2017, 9, 202. [Google Scholar] [CrossRef]
- Slapničar, G.; Luštrek, M.; Marinko, M. Continuous blood pressure estimation from PPG signal. Informatica 2018, 42, 33–42. [Google Scholar]
- Zhang, Y.; Feng, Z. A SVM method for continuous blood pressure estimation from a PPG signal. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; pp. 128–132. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Baek, S.; Jang, J.; Yoon, S. End-to-end blood pressure prediction via fully convolutional networks. IEEE Access 2019, 7, 185458–185468. [Google Scholar] [CrossRef]
- Panwar, M.; Gautam, A.; Biswas, D.; Acharyya, A. PP-Net: A deep learning framework for PPG-based blood pressure and heart rate estimation. IEEE Sens. J. 2020, 20, 10000–10011. [Google Scholar] [CrossRef]
- Yan, C.; Li, Z.; Zhao, W.; Hu, J.; Jia, D.; Wang, H.; You, T. Novel deep convolutional neural network for cuff-less blood pressure measurement using ECG and PPG signals. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 1917–1920. [Google Scholar]
- Chao, P.C.P.; Wu, C.C.; Nguyen, D.H.; Nguyen, B.S.; Huang, P.C.; Le, V.H. The Machine Learnings Leading the Cuffless PPG Blood Pressure Sensors Into the Next Stage. IEEE Sens. J. 2021, 21, 12498–12510. [Google Scholar] [CrossRef]
- Kurylyak, Y.; Lamonaca, F.; Grimaldi, D. A Neural Network-based Method for Continuous Blood Pressure Estimation from a PPG Signal. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 280–283. [Google Scholar]
- Khalid, S.G.; Zhang, J.; Chen, F.; Zheng, D. Blood Pressure Estimation Using Photoplethysmography Only: Comparison between Different Machine Learning Approaches. J. Healthc. Eng. 2018, 2018, 1548647. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.-H.; Harfiya, L.N.; Purwandari, K.; Lin, Y.-D. Real-time cuffless continuous blood pressure estimation using deep learning model. Sensors 2020, 20, 5606. [Google Scholar] [CrossRef]
- Chowdhury, M.H.; Shuzan, M.N.I.; Chowdhury, M.E.H.; Mahbub, Z.B.; Uddin, M.M.; Khandakar, A.; Reaz, M.B. Estimating Blood Pressure from the Photoplethysmogram Signal and Demographic Features Using Machine Learning Techniques. Sensors 2020, 20, 3127. [Google Scholar] [CrossRef] [PubMed]
- Nishan, A.; Raju, S.; Hossain, M.I.; Dipto, S.A.; Uddin, S.M.T.; Sijan, A.; Chowdhury, M.A.; Ahmad, A.; Khan, M.M.H. A continuous cuffless blood pressure measurement from optimal PPG characteristic features using machine learning algorithms. Heliyon 2024, 10, e27779. [Google Scholar] [CrossRef]
- Peng, S.; Xiao-Rong, D.; Yuan-Ting, Z.; Jing, L.; Fen, M.; Ni, Z. Long-term blood pressure prediction with deep recurrent neural networks. In Proceedings of the IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 323–328. [Google Scholar] [CrossRef]
- Yen, C.T.; Liao, J.X.; Huang, Y.K. Applying a Deep Learning Network in Continuous Physiological Parameter Estimation Based on Photoplethysmography Sensor Signals. IEEE Sens. J. 2022, 22, 385–392. [Google Scholar] [CrossRef]
- Wang, W.N.; Mohseni, P.; Kilgore, K.L.; Najafizadeh, L. Cuff-Less Blood Pressure Estimation From Photoplethysmography via Visibility Graph and Transfer Learning. IEEE J. Biomed. Health Inform. 2022, 26, 2075–2085. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, Y.T.; Kim, H.; Kim, D.J. DeepCNAP: A Deep Learning Approach for Continuous Noninvasive Arterial Blood Pressure Monitoring Using Photoplethysmography. IEEE J. Biomed. Health Inform. 2022, 26, 3697–3707. [Google Scholar] [CrossRef]
- Tanveer, M.S.; Hasan, M.K. Cuffless blood pressure estimation from electrocardiogram and photoplethysmogram using waveform based ANN-LSTM network. Biomed. Signal Process. Control. 2019, 51, 382–392. [Google Scholar] [CrossRef]
- Aguirre, N.; Grall-Maës, E.; Cymberknop, L.J.; Armentano, R.L. Blood Pressure Morphology Assessment from Photoplethysmogram and Demographic Information Using Deep Learning with Attention Mechanism. Sensors 2021, 21, 2167. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Systolic Peak Detection in Acceleration Photoplethysmograms Measured from Emergency Responders in Tropical Conditions. PLoS ONE 2013, 8, e76585. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, X. Non-invasive blood viscosity detection method based on random forest. In Proceedings of the 4th International Conference on Information Science, Electrical, and Automation Engineering (ISEAE 2022), Guangzhou, China, 25–27 March 2022; Volume 12257, pp. 499–504. [Google Scholar] [CrossRef]
- Opthof, T. The normal range and determinants of the intrinsic heart rate in man. Cardiovasc. Res. 2000, 45, 177–184. [Google Scholar] [CrossRef]
- Rundo, F.; Conoci, S.; Ortis, A.; Battiato, S. An Advanced Bio-Inspired PhotoPlethysmoGraphy (PPG) and ECG Pattern Recognition System for Medical Assessment. Sensors 2018, 18, 405. [Google Scholar] [CrossRef]
- El-Hajj, C.; Kyriacou, P.A. Deep learning models for cuffless blood pressure monitoring from PPG signals using attention mechanism. Biomed. Signal Process. Control 2021, 65, 102301. [Google Scholar] [CrossRef]
- Rong, M.; Li, K.Y. A Blood Pressure Prediction Method Based on Imaging Photoplethysmography in combination with Machine Learning. Biomed. Signal Process. Control 2021, 64, 102328. [Google Scholar] [CrossRef]
- Visvanathan, A.; Sinha, A.; Pal, A. Estimation of Blood Pressure Levels from Reflective Photoplethysmograph using Smart Phones. In Proceedings of the IEEE 13th International Conference on Bioinformatics and Bioengineering (BIBE), Chania, Greece, 10–13 November 2013. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Ali Siddiqui, S.; Kos, A. Non-invasive Blood-Glucose Estimation Using Smartphone PPG Signals and Subspace KNN Classifier. Electrotech. Rev. Elektrotehniski Vestn. 2019, 86, 68–74. [Google Scholar]
- Chan-Dewar, F. The cardiac cycle. Anaesth. Intensive Care Med. 2012, 13, 391–396. [Google Scholar] [CrossRef]
- Mansoor, G.A.; White, W.B.; McCabe, E.J.; Giacco, S. The relationship of electronically monitored physical activity to blood pressure, heart rate, and the circadian blood pressure profile. Am. J. Hypertens. 2000, 13, 262–267. [Google Scholar] [CrossRef][Green Version]
- Awad, A.A.; Haddadin, A.S.; Tantawy, H.; Badr, T.M.; Stout, R.G.; Silverman, D.G.; Shelley, K.H. The relationship between the photoplethysmographic waveform and systemic vascular resistance. J. Clin. Monit. Comput. 2007, 21, 365–372. [Google Scholar] [CrossRef]
- Baek, H.J.; Kim, J.S.; Kim, Y.S.; Lee, H.B.; Park, K.S. Second derivative of photoplethysmography for estimating vascular aging. In Proceedings of the 6th IEEE International Special Topic Conference on Information Technology Applications in Biomedicine, Tokyo, Japan, 8–10 November 2007; pp. 70–72. [Google Scholar]
- Inoue, N.; Kawakami, H.; Yamamoto, H.; Ito, C.; Fujiwara, S.; Sasaki, H.; Kihara, Y. Second derivative of the finger photoplethysmogram and cardiovascular mortality in middle-aged and elderly Japanese women. Hypertens. Res. 2017, 40, 207–211. [Google Scholar] [CrossRef]
- Takazawa, K.; Tanaka, N.; Fujita, M.; Matsuoka, O.; Saiki, T.; Aikawa, M.; Tamura, S.; Ibukiyama, C. Assessment of vasoactive agents and vascular aging by the second derivative of photoplethysmogram waveform. Hypertension 1998, 32, 365–370. [Google Scholar] [CrossRef]
- Jong, G.-J.; Aripriharta; Horng, G.-J. The PPG physiological signal for heart rate variability analysis. Wirel. Pers. Commun. 2017, 97, 5229–5276. [Google Scholar] [CrossRef]
- Islam, M.T.; Zabir, I.; Ahamed, S.T.; Yasar, M.T.; Shahnaz, C.; Fattah, S.A. A time-frequency domain approach of heart rate estimation from photoplethysmographic (PPG) signal. Biomed. Signal Process. Control 2017, 36, 146–154. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J.; IEEE. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hammad, M.; Plawiak, P.; Wang, K.Q.; Acharya, U.R. ResNet-Attention model for human authentication using ECG signals. Expert Syst. 2021, 38, 17. [Google Scholar] [CrossRef]
- Hu, S.G.; Li, R.W.; Hu, Q.; Qiao, G.C. ResNet-TCN: A Joint Model for ECG Heartbeat Classification with High Accuracy. In Proceedings of the 37th International Conference on Information Networking (ICOIN), Bangkok, Thailand, 11–14 January 2023; pp. 467–471. [Google Scholar]
- Wu, C.W.; Ye, N.; Jiang, J.L. Classification and Recognition of Lung Sounds Based on Improved Bi-ResNet Model. IEEE Access 2024, 12, 73079–73094. [Google Scholar] [CrossRef]
- Yang, C.; Gan, X.L.; Peng, A.T.; Yuan, X.Y. ResNet Based on Multi-Feature Attention Mechanism for Sound Classification in Noisy Environments. Sustainability 2023, 15, 10762. [Google Scholar] [CrossRef]
- Sentürk, Ü.; Yücedag, I.; Polat, K. Repetitive neural network (RNN) based blood pressure estimation using PPG and ECG signals. In Proceedings of the 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Kizilcahamam, Turkey, 19–21 October 2018; pp. 188–191. [Google Scholar]
- Zhang, Q.; Ma, P. Classification of pulmonary arterial pressure using photoplethysmography and bi-directional LSTM. Biomed. Signal Process. Control 2023, 86, 105071. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Ren, X.L.; Liang, X.; Ye, X.S.; Zhou, C.C. A Refined Blood Pressure Estimation Model Based on Single Channel Photoplethysmography. IEEE J. Biomed. Health Inform. 2022, 26, 5907–5917. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.; Bulgarelli, L.; Pollard, T.; Gow, B.; Moody, B.; Horng, S.; Celi, L.A.; Mark, R. MIMIC-IV (version 3.0). PhysioNet 2024. [Google Scholar] [CrossRef]
- Johnson, A.E.W.; Bulgarelli, L.; Shen, L.; Gayles, A.; Shammout, A.; Horng, S.; Pollard, T.J.; Hao, S.; Moody, B.; Gow, B.; et al. MIMIC-IV, a freely accessible electronic health record dataset. Sci. Data 2023, 10, 1. [Google Scholar] [CrossRef] [PubMed]
- ANSI/AAMI SP10; American National Standard for Electronic or Automated Sphygmomanometers. Association for the Advancement of Medical Instrumentation (AAMI): Arlington, VA, USA, 2002.
- O’Brien, E.; Petrie, J.; Littler, W.; de Swiet, M.; Padfield, P.L.; O’Malley, K.; Jamieson, M.; Altman, D.; Bland, M.; Atkins, N. The British Hypertension Society protocol for the evaluation of automated and semi-automated blood pressure measuring devices with special reference to ambulatory systems. J. Hypertens. 1990, 8, 607–619. [Google Scholar] [CrossRef]
- Schlesinger, O.; Vigderhouse, N.; Eytan, D.; Moshe, Y. Blood pressure estimation from ppg signals using convolutional neural networks and siamese network. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1135–1139. [Google Scholar]
- Baker, S.; Xiang, W.; Atkinson, I. A computationally efficient CNN-LSTM neural network for estimation of blood pressure from features of electrocardiogram and photoplethysmogram waveforms. Knowl.-Based Syst. 2022, 250, 109151. [Google Scholar] [CrossRef]
- Ibtehaz, N.; Mahmud, S.; Chowdhury, M.E.H.; Khandakar, A.; Khan, M.S.; Ayari, M.A.; Tahir, A.M.; Rahman, M.S. PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms. Bioengineering 2022, 9, 692. [Google Scholar] [CrossRef]
- Qin, C.J.; Li, Y.; Liu, C.B.; Ma, X.B. Cuff-Less Blood Pressure Prediction Based on Photoplethysmography and Modified ResNet. Bioengineering 2023, 10, 400. [Google Scholar] [CrossRef]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuff-Less High-Accuracy Calibration-Free Blood Pressure Estimation Using Pulse Transit Time. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 1006–1009. [Google Scholar]

| Category | The Distribution of Our Dataset | AAMI/ISO Requirements |
|---|---|---|
| SBP ≥ 160 mmHg | 5.02% | ≥5% |
| SBP ≥ 140 mmHg | 21.22% | ≥20% |
| SBP ≤ 100 mmHg | 11.11% | ≥5% |
| DBP ≥ 100 mmHg | 5.13% | ≥5% |
| DBP ≥ 85 mmHg | 22.36% | ≥20% |
| DBP ≤ 60 mmHg | 30.58% | ≥5% |
| Feature | Definition | Feature | Definition |
|---|---|---|---|
| 1. PSV(SBP)(DBP) | Peak systolic value | 38. SK(SBP)(DBP) | Skewness in one cycle |
| 2. PDV(SBP) | Peak diastolic value | 39. KU(SBP)(DBP) | Kurtosis in a cycle |
| 3. DN(SBP)(DBP) | Dicrotic notch | 40. VAR(SBP)(DBP) | Variance over a cycle |
| 4. tPI(SBP)(DBP) | Pulse period | 41. MF(SBP)(DBP) | The ratio of maximum value to mean square value |
| 5. PDV/PSV | 42. fbase | Fundamental frequency | |
| 6. (PSV-PDV)/PSV | 43. sp mag base(SBP) | Spectral magnitude at the fundamental frequency | |
| 7. DN/PSV(SBP)(DBP) | 44. f2 | Frequency of the second-largest spectral component | |
| 8. (PDV-DN)/PSV | 45. sp mag2(SBP)(DBP) | Amplitude of the second-largest spectral component | |
| 9. SPT(SBP)(DBP) | Systolic peak time | 46. f3(SBP)(DBP) | Frequency of the third largest spectral component |
| 10. DNT(SBP)(DBP) | Dicrotic notch time | 47. sp mag3(SBP)(DBP) | Amplitude of the third largest spectral component |
| 11. DPT | Diastolic peak time | 48. TFFMAX(SBP)(DBP) | Time of the first maximum value of the first derivative |
| 12. DPT-SPT(SBP)(DBP) | 49. TFFMIN(DBP) | Time of the first minimum value of the first derivative | |
| 13. width | Bandwidth in hemisystole | 50. TSFMAX(SBP)(DBP) | Time of the second largest value of the first derivative |
| 14. A2/A1(SBP)(DBP) | Area ratio of the ascending and descending branches of a waveform | 51. TSFMIN(SBP)(DBP) | The time to the second minimum of the first-order derivative |
| 15. SPT/PSV | 52. FSMIN/FSMAX | ||
| 16. PDV/(tPI-DPT)(SBP)(DBP) | 53. SSMAX/FSMAX | ||
| 17. SPT/tPI(SBP)(DBP) | 54. (FSMIN+SSMAX)/FSMAX | ||
| 18. DNT/tpi(DBP) | 55. TFSMAX(SBP)(DBP) | ||
| 19. DPT/tpi | 56. TFSMIN(SBP)(DBP) | ||
| 20. (DPT-SPT)/tpi | 57. TFFMAX/tPI(SBP)(DBP) | ||
| 21. VI | Valley depth | 58. TFFMIN/tPI(SBP)(DBP) | |
| 22. PT(SBP) | Cycle duration | 59. TSFMAX/tPI(DBP) | |
| 23. PI | Peak height | 60. TSFMIN/tPI(SBP)(DBP) | |
| 24. DTD(SBP)(DBP) | Decline duration | 61. TFSMAX/tPI(SBP)(DBP) | |
| 25. AID | Wave height | 62. TFSMIN/tPI(SBP)(DBP) | |
| 26. DID | Waveform depth | 63. (TFFMAX-TFSMAX)/tPI(DBP) | |
| 27. AS(SBP)(DBP) | Rising slope | 64. (TFFMIN-TFSMIN)/tPI(SBP) | |
| 28. DS(DBP) | Downward slope | 65. (TSFMAX-DNT)/tPI | |
| 29. K(SBP)(DBP) | The ratio of the mean value to the difference between the minimum and maximum values in a cycle | 66. (TSFMIN-DPT)/tPI(SBP)(DBP) | |
| 30. AA(SBP) | Descending area | 67. STSSE(DBP) | Short-time spectral subband energy rate |
| 31. DA(SBP)(DBP) | Rising area | 68. RMSE(SBP) | Root mean square energy |
| 32. AID[X] | Threshold points divided into 10 equal parts according to AIDs | 69. spectral centroid(SBP DBP) | Spectral center of mass |
| 33. SW[X](SBP)(DBP) | Time from the wave start point to each AID[x] threshold point | 70. spectral_bandwidth(SBP DBP) | Spectral bandwidth |
| 34. DID[X] | Threshold points divided into 10 equal parts according to DID | 71. Overall Trend(SBP) | Calculate amplitude, mean, and variance characteristics |
| 35. DW[X](SBP)(DBP) | Time from wave end point to each DID[x] threshold point | 72. STE(SBP)(DBP) | Short-time energy |
| 36. DAS[X](SBP)(DBP) | Sum of each DW[x] and corresponding SW[x] | 73. STZCR(SBP)(DBP) | Short-time zero crossing rate |
| 37. DDS[X](SBP)(DBP) | The ratio of each DW[x] to the corresponding SW[x] |
| SBP (mmHg) | DBP (mmHg) | ||
|---|---|---|---|
| ME ± SD | MAE | ME ± SD | MAE |
| −0.01 ± 5.06 | 3.47 | 0.34 ± 4.11 | 2.81 |
| Cumulative Error | ≤5 mmHg | ≤10 mmHg | ≤15 mmHg | Grade |
|---|---|---|---|---|
| BHS | 60% | 85% | 95% | A |
| 50% | 75% | 90% | B | |
| 40% | 65% | 85% | C | |
| SBP | 78.24% | 95.02% | 98.19% | A |
| DBP | 85.00% | 97.34% | 99.17% | A |
| Study | Dataset | Subject Sizes | Methods | MAE(mmHg) | SD(mmHg) | ||
|---|---|---|---|---|---|---|---|
| SBP | DBP | SBP | DBP | ||||
| Schlesinger et al. [60] | MIMIC-II | 106,074 30 s windows from 304 different patients | CNN Siamese | 5.95 | 3.41 | 6.69 | 3.97 |
| Aguirre et al. [30] | MIMIC-III | 1131 subjects | seq2seq-attention | 12.08 | 5.56 | 15.67 | 7.32 |
| N. Ibtehaz et al. [27] | MIMIC-II | 11,294 segments from 348 records | CNN | 6.17 | 3.66 | 8.46 | 5.36 |
| Stephanie Baker et al. [61] | MIMIC-III | 222,343 “good” records | CNN-LSTM | 4.57 | 3.36 | 6.34 | 4.96 |
| Ibtehaz et al. [62] | MIMIC-III | 127,260 episodes from 12,000 records | GRU+ Attention | 5.73 | 3.45 | 10.69 | 6.86 |
| C. Qin et al. [63] | MIMIC-II | 47,964 segments | CNN | 5.98 | 3.24 | 7.79 | 4.94 |
| Darbhasayanam et al. [4] | MIMIC-III | 11,787 segments | Vision Transformer | 17.59 | 8.09 | ||
| Tian et al. [6] | MIMIC-III | 808 subjects | PCTN | 4.44 | 2.36 | 5.98 | 3.22 |
| Our Work | MIMIC-IV | 149,403 segments from 220 records of 218 patients | ResNet-BiLSTM | 3.47 | 2.81 | 5.06 | 4.11 |
| Serial Number | Method | MAE(mmHg) | SD(mmHg) | ||
|---|---|---|---|---|---|
| SBP | DBP | SBP | DBP | ||
| 1 | Manually Extracted Features Branch | 4.58 | 3.45 | 6.12 | 4.84 |
| 2 | Manually Extracted Features Branch+ Features Selection (60 feature vectors) | 4.26 | 3.32 | 5.94 | 4.77 |
| 3 | Manually Extracted Features Branch+ Features Selection (50 feature vectors) | 4.50 | 3.38 | 5.99 | 4.79 |
| 4 | Manually Extracted Features Branch+ Features Selection (40 feature vectors) | 4.55 | 3.47 | 6.09 | 4.82 |
| 5 | Manually Extracted Features Branch+ Features Selection (80 feature vectors) | 4.47 | 3.38 | 6.03 | 4.80 |
| 6 | Manually Extracted Features Branch+ Features Selection (60 feature vectors)+ Complete PPG Waveforms Branch | 3.47 | 2.81 | 5.06 | 4.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Qiao, M.; Liu, Y.; Zhang, J.; He, L. A Two-Branch ResNet-BiLSTM Deep Learning Framework for Extracting Multimodal Features Applied to PPG-Based Cuffless Blood Pressure Estimation. Sensors 2025, 25, 3975. https://doi.org/10.3390/s25133975
Liu Z, Qiao M, Liu Y, Zhang J, He L. A Two-Branch ResNet-BiLSTM Deep Learning Framework for Extracting Multimodal Features Applied to PPG-Based Cuffless Blood Pressure Estimation. Sensors. 2025; 25(13):3975. https://doi.org/10.3390/s25133975
Chicago/Turabian StyleLiu, Zenan, Minghong Qiao, Yezi Liu, Jing Zhang, and Ling He. 2025. "A Two-Branch ResNet-BiLSTM Deep Learning Framework for Extracting Multimodal Features Applied to PPG-Based Cuffless Blood Pressure Estimation" Sensors 25, no. 13: 3975. https://doi.org/10.3390/s25133975
APA StyleLiu, Z., Qiao, M., Liu, Y., Zhang, J., & He, L. (2025). A Two-Branch ResNet-BiLSTM Deep Learning Framework for Extracting Multimodal Features Applied to PPG-Based Cuffless Blood Pressure Estimation. Sensors, 25(13), 3975. https://doi.org/10.3390/s25133975






