Non-Destructive Thickness Measurement of Energy Storage Electrodes via Terahertz Technology
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
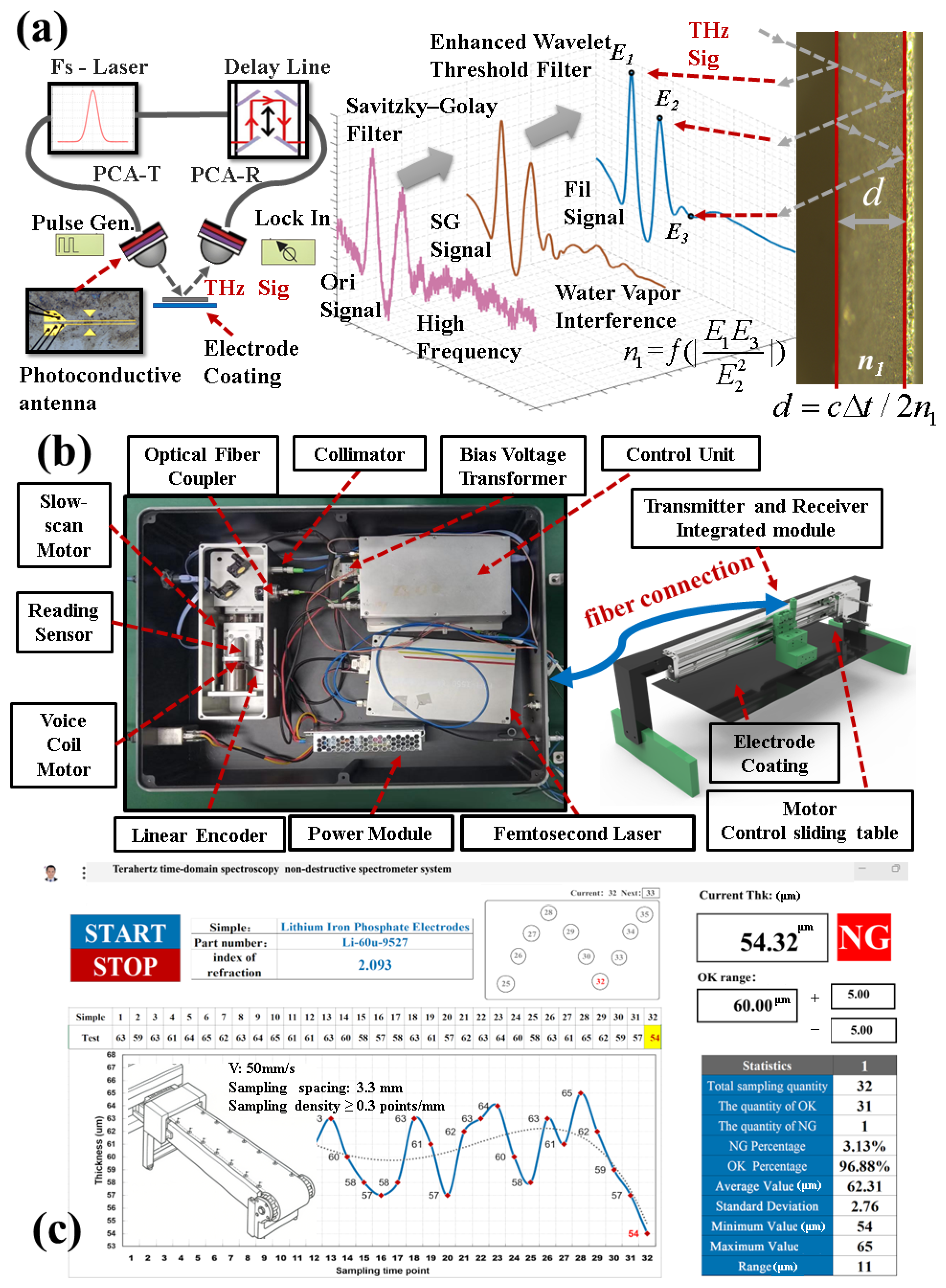
3.1. Combined SG and Enhanced Wavelet Thresholding Algorithms
3.2. Software Calculation of Refractive Index at Specific Thickness Amplitudes
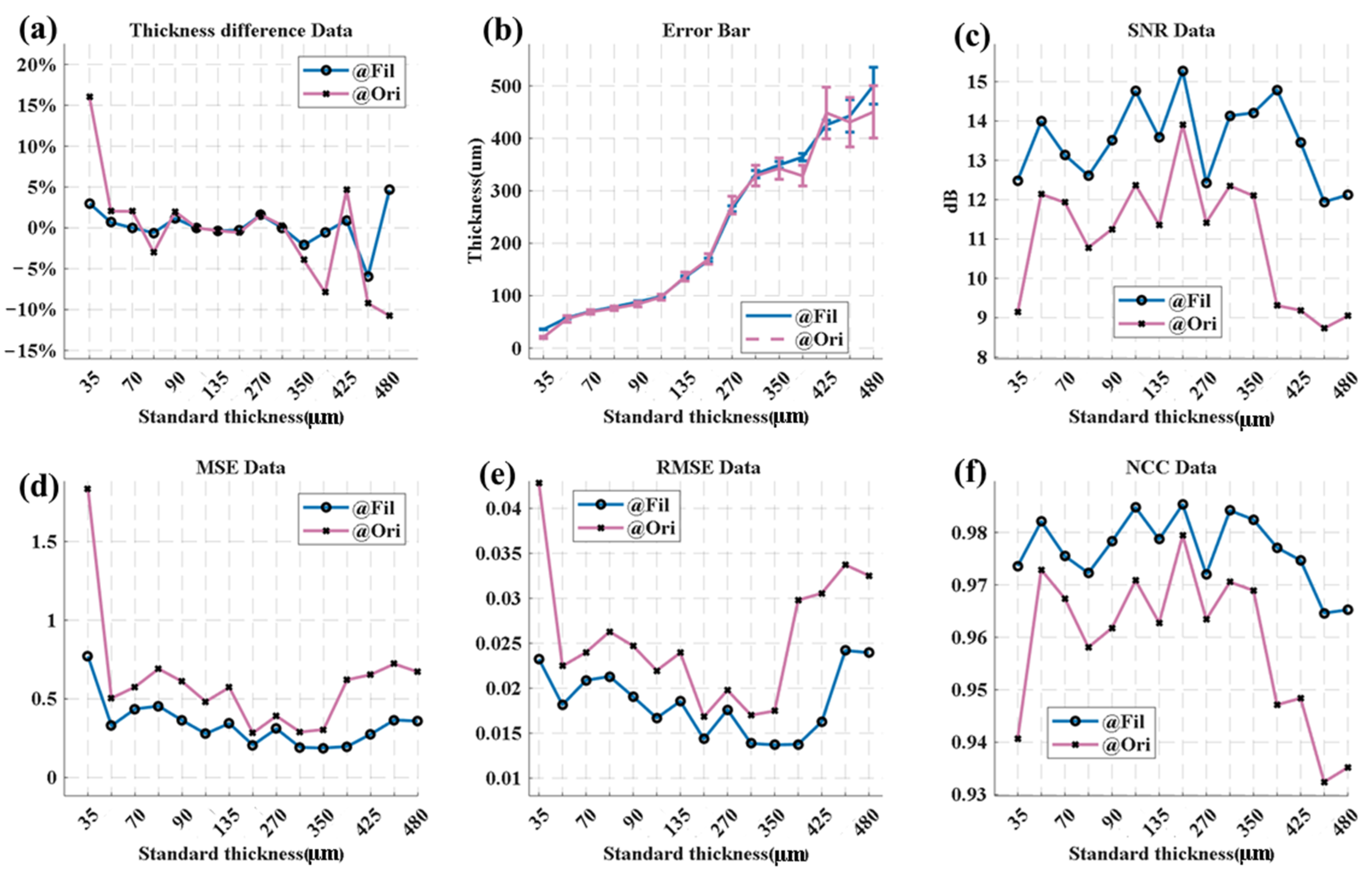
3.3. Spectra and Analysis of LFP Coating Materials with Different Thicknesses
4. Conclusions
5. Patents
- Zhengxian Gao, Xiaoqing Jia, Xuecou Tu, Peiheng Wu, and Jin Wang applied for a Chinese patent (No. CN202411485728.8) [39].
- Zhengxian Gao, Xiaoqing Jia, Peiheng Wu, Jin Wang, Jianyong Wang, and Dongshan Wei applied for a Chinese patent (No. CN202411485764.4) [40].
- Zhengxian Gao, Xiaoqing Jia, Xuecou Tu, Peiheng Wu, Zhijun Zhou, and Jin Wang applied for a Chinese patent (No. CN202411485766.3) [41].
- Zhengxian Gao, Xiaoqing Jia, Xuecou Tu, Lin Kang, Jian Chen, Peiheng Wu, Zhijun Zhou, Jin Wang, and Jianyong Wang applied for a Chinese patent (No. CN202410415816.4). The remaining authors declare that they have no conflict of interest [42].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grant, A.; O’DWyer, C. Real-time nondestructive methods for examining battery electrode materials. Appl. Phys. Rev. 2023, 10, 011312. [Google Scholar] [CrossRef]
- Gold, L.; Herzog, T.; Schubert, F.; Heuer, H.; Giffin, G.A. Ultrasound Propagation in Lithium-Ion Battery Cell Materials: Basis for Developing Monitoring and Imaging Methods. Energy Technol. 2023, 11, 2200861. [Google Scholar] [CrossRef]
- Schewe, M.; Rembe, C. Signal Diversity for Laser-Doppler Vibrometers with Raw-Signal Combination. Sensors 2021, 21, 998. [Google Scholar] [CrossRef]
- Goodman, A.M. Optical Interference Method for the Approximate Determination of Refractive Index and Thickness of a Transparent Layer. Appl. Opt. 1978, 17, 2779–2784. [Google Scholar] [CrossRef]
- USC Environmental Health & Safety. X-Ray Safety Manual; University of Southern California: Los Angeles, CA, USA, 2023. [Google Scholar]
- Jackson, J.B.; Labaune, J.; Bailleul-Lesuer, R.; D’aLessandro, L.; Whyte, A.; Bowen, J.W.; Menu, M.; Mourou, G. Terahertz pulse imaging in archaeology. Front. Optoelectron. 2015, 8, 81–92. [Google Scholar] [CrossRef]
- van Mechelen, J.L.M.; Kuzmenko, A.B.; Merbold, H. Stratified dispersive model for material characterization using terahertz time-domain spectroscopy. Opt. Lett. 2014, 39, 3853–3856. [Google Scholar] [CrossRef]
- Zeitler, J.; Shen, Y.; Baker, C.; Taday, P.F.; Pepper, M.; Rades, T. Analysis of Coating Structures and Interfaces in Solid Oral Dosage Forms by Three Dimensional Terahertz Pulsed Imaging. J. Pharm. Sci. 2007, 96, 330–340. [Google Scholar] [CrossRef]
- White, J.; Fichter, G.; Chernovsky, A.; Whitaker, J.F.; Das, D.; Pollock, T.M.; Zimdars, D. Time Domain Terahertz Non-Destructive Evaluation of Aeroturbine Blade Thermal Barrier Coatings. AIP Conf. Proc. 2009, 1096, 434–439. [Google Scholar]
- Hussain, B.; Nawaz, M.; Ahmed, M.; Raja, M.Y.A. Measurement of thickness and refractive index using femtosecond and terahertz pulses. Laser Phys. Lett. 2013, 10, 055301. [Google Scholar] [CrossRef]
- May, R.K.; Evans, M.J.; Zhong, S.; Warr, I.; Gladden, L.F.; Shen, Y.; Zeitler, J.A. Terahertz In-Line Sensor for Direct Coating Thickness Measurement of Individual Tablets During Film Coating in Real-Time. J. Pharm. Sci. 2011, 100, 1535–1544. [Google Scholar] [CrossRef]
- Krimi, S.; Klier, J.; Jonuscheit, J.; von Freymann, G.; Urbansky, R.; Beigang, R. Highly accurate thickness measurement of multi-layered automotive paints using terahertz technology. Appl. Phys. Lett. 2016, 109, 7518–7526. [Google Scholar] [CrossRef]
- Tu, W.; Zhong, S.; Shen, Y.; Incecik, A.; Fu, X. Neural network-based hybrid signal processing approach for resolving thin marine protective coating by terahertz pulsed imaging. Ocean Eng. 2019, 173, 58–67. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, L.; He, M. Extension of terahertz time-domain spectroscopy: A micron-level thickness gauging technology. Opt. Commun. 2022, 506, 127597. [Google Scholar] [CrossRef]
- Sun, F.; Fan, M.; Cao, B.; Zheng, D.; Liu, H.; Liu, L. Terahertz based thickness measurement of thermal barrier coatings using long short-term memory networks and local extrema. IEEE Trans. Ind. Inform. 2021, 18, 2508–2517. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, C.; Zheng, X.; Li, C.; Jia, X.; Tu, X.; Kang, L.; Chen, J.; Wu, P. Real-time on-line thickness measurement of supercapacitor electrode coating using terahertz technology. In Proceedings of the 2023 48th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Montreal, QC, Canada, 17–22 September 2023. [Google Scholar]
- Cao, B.; Shang, H.; Fan, M.; Sun, F. CNN-GRU based method for peak location of reflected Terahertz signals from thermal barrier coatings. Nondestruct. Test. Eval. 2023, 39, 2132–2149. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, Y.; Hu, H. Thickness Characterization of Steel Plate Coating Materials with Terahertz Time-Domain Reflection Spectroscopy Based on BP Neural Network. Sensors 2024, 24, 4992. [Google Scholar] [CrossRef]
- Waddie, A.J.; Schemmel, P.J.; Chalk, C.; Isern, L.; Nicholls, J.R.; Moore, A.J. Terahertz optical thickness and birefringence measurement for thermal barrier coating defect location. Opt. Express 2020, 28, 31535–31552. [Google Scholar] [CrossRef]
- Park, D.-W.; Oh, G.-H.; Kim, D.-J.; Kim, H.-S. In-Situ thickness measurement of epoxy molding compound in semiconductor package products using a Terahertz-Time of Flight System. NDT E Int. 2019, 105, 11–18. [Google Scholar] [CrossRef]
- Ellrich, F.; Weinland, T.; Molter, D.; Jonuscheit, J.; Beigang, R. Compact fiber-coupled terahertz spectroscopy system pumped at 800 nm wavelength. Rev. Sci. Instrum. 2011, 82, 053102. [Google Scholar] [CrossRef]
- Cui, S.; Chen, J.; Yuan, Y.; Sun, F. Femtosecond Fiber Laser Developed for Real-time Terahertz Spectrometer. In Proceedings of the 9th International Symposium on Ultrafast Phenomena and Terahertz Waves, Changsha, China, 23–26 April 2018. [Google Scholar]
- Minamide, H.; Nawata, K.; Takida, Y. Leading-Edge terahertz-wave parametric sources and their applications. In Proceedings of the Terahertz Emitters, Receivers, and Applications XI, Online, 20 August 2020. [Google Scholar]
- Gao, W.; Wang, Y.; Zhao, Z. Development of the data acquisition and control system for a portable THz time-domain spectrometer. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Terahertz Technologies and Applications, Beijing, China, 23 August 2013. [Google Scholar]
- Liu, H.; Zhang, Z.; Yang, Y.; Chen, T.; Zhang, C. Identification terahertz spectra for the dyestuffs based on principal component analysis and Savitzky-Golay filter. Optik 2018, 172, 668–673. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, P.; Zhang, Z.; Jin, C. Numerical method based on transfer function for eliminating water vapor noise from terahertz spectra. Appl. Opt. 2017, 56, 5698–5704. [Google Scholar] [CrossRef]
- Liu, H.; Fan, Y.-X.; Li, L.; Chen, H.-G.; Wang, P.-F.; Tao, Z.-Y. Self-adaptive terahertz spectroscopy from atmospheric vapor based on Hilbert-Huang transform. Opt. Express 2018, 26, 27279–27293. [Google Scholar] [CrossRef]
- Karan, V. Wavelet Transform-Based Classification of Electromyogram Signals Using an Anova Technique. Neurophysiology 2015, 47, 302–309. [Google Scholar] [CrossRef]
- Saeedi, J.; Moradi, M.H.; Faez, K. A new wavelet-based fuzzy single and multi-channel image denoising. Image Vis. Comput. 2010, 28, 1611–1623. [Google Scholar] [CrossRef]
- Dixit, A.; Sharma, P. A Comparative Study of Wavelet Thresholding for Image Denoising. Int. J. Image Graph. Signal Process. (IJIGSP) 2014, 6, 39–46. [Google Scholar] [CrossRef][Green Version]
- Gao, H.Y. Wavelet Shrinkage Denoising Using the Non-Negative Garrote. J. Comput. Graph. Stat. 2012, 7, 469–488. [Google Scholar] [CrossRef]
- Cassar, Q.; Chopard, A.; Fauquet, F.; Guillet, J.-P.; Pan, M.; Perraud, J.-B.; Mounaix, P. Iterative Tree Algorithm to Evaluate Terahertz Signal Contribution of Specific Optical Paths Within Multilayered Materials. Terahertz Sci. Technol. IEEE Trans. (T-THZ) 2019, 9, 11. [Google Scholar] [CrossRef]
- Ramachandran, S.; Nicholson, J.W.; Ghalmi, S.; Yan, M.F.; Wisk, P.; Monberg, E.; Dimarcello, F.V. Light propagation with ultralarge modal areas in optical fibers. Opt. Lett. 2006, 31, 1797–1799. [Google Scholar] [CrossRef]
- Lecaruyer, P.; Maillart, E.; Canva, M.; Rolland, J. Generalization of the Rouard method to an absorbing thin-film stack and application to surface plasmon resonance. Appl. Opt. 2006, 45, 8419–8423. [Google Scholar] [CrossRef]
- Jagannathan, A.; Gatesman, A.J.; Giles, R.H. Characterization of roughness parameters of metallic surfaces using terahertz reflection spectra. Opt. Lett. 2009, 34, 1927–1929. [Google Scholar] [CrossRef]
- Geng, J.; Zhang, S.; Hu, X.; Ling, W.; Peng, X.; Zhong, S.; Liang, F.; Zou, Z. A review of graphene-decorated LiFePO4 cathode materials for lithium-ion batteries. Ionics 2022, 28, 4899–4922. [Google Scholar] [CrossRef]
- Adityarini, A.R.; Ramadhan, E.Y.; Dyartanti, E.R.; Purwanto, A. Effect of LiFePO4 Cathode Thickness on Lithium Battery Performance. Mater. Sci. Forum 2015, 827, 146–150. [Google Scholar] [CrossRef]
- Safety Requirements and Test Methods for Power Batteries of Electric Vehicles; China Standard Press: Beijing, China, 2015.
- Gao, Z.; Jia, X.; Tu, X.; Wu, P.; Wang, J.; Long, J. A Pair of Terahertz Photoconductive Antenna Transmitters and Detectors Based on Frequency Doubling. Patent No. CN202411485728.8, 10 January 2025. [Google Scholar]
- Gao, Z.; Jia, X.; Wu, P.; Wang, J.; Wang, J.; Wei, D. A Terahertz Thickness Measurement Method and Device Based on Lithium—Ion Electrode Multi—Coatings. Patent No. CN202411485764.4, 18 February 2025. [Google Scholar]
- Gao, Z.; Jia, X.; Tu, X.; Wu, P.; Zhou, Z.; Wang, J. A Terahertz Fiber Laser. Patent No. CN202411485766.3, 24 January 2025. [Google Scholar]
- Gao, Z.; Jia, X.; Tu, X.; Kang, L.; Chen, J.; Wu, P.; Zhou, Z.; Wang, J.; Wang, J.; Yi, H. A Terahertz Nondestructive Testing Device. Patent No. CN202410415816.4, 9 July 2024. [Google Scholar]



| Performance Indicator | Effective Spectral Range | Dynamic Range | Time-Domain Length | Imaging Scanning Speed | Femtosecond Laser |
|---|---|---|---|---|---|
| Specification | 0.1–4.0 THz | ≥70 dB | 53–300 ps | 15 Hz | 1560 nm |
| SNR | MSE | RMSE | NCC | |
|---|---|---|---|---|
| Hard threshold | 16.777 | 0.000148 | 0.012 | 0.989 |
| Soft threshold | 15.190 | 0.000217 | 0.015 | 0.989 |
| Enhance threshold | 18.181 | 0.000107 | 0.010 | 0.992 |
| Sub-Fig | TOF (ps) | n1 (Microscope) | Thickness (μm) (Microscope) | Thickness (μm) (n1 = 2.025) | Thickness Deviation Rate |
|---|---|---|---|---|---|
| 135 μm thick | 1.847 | 2.042 | 135.531 | 136.721 | 0.88% |
| 70 μm thick | 0.987 | 2.171 | 68.125 | 71.350 | 4.73% |
| 330 μm thick | 0.746 | 2.110 | 332.981 | 338.922 | 1.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Jia, X.; Wang, J.; Zhou, Z.; Wang, J.; Wei, D.; Tu, X.; Kang, L.; Chen, J.; Chen, D.; et al. Non-Destructive Thickness Measurement of Energy Storage Electrodes via Terahertz Technology. Sensors 2025, 25, 3917. https://doi.org/10.3390/s25133917
Gao Z, Jia X, Wang J, Zhou Z, Wang J, Wei D, Tu X, Kang L, Chen J, Chen D, et al. Non-Destructive Thickness Measurement of Energy Storage Electrodes via Terahertz Technology. Sensors. 2025; 25(13):3917. https://doi.org/10.3390/s25133917
Chicago/Turabian StyleGao, Zhengxian, Xiaoqing Jia, Jin Wang, Zhijun Zhou, Jianyong Wang, Dongshan Wei, Xuecou Tu, Lin Kang, Jian Chen, Dengzhi Chen, and et al. 2025. "Non-Destructive Thickness Measurement of Energy Storage Electrodes via Terahertz Technology" Sensors 25, no. 13: 3917. https://doi.org/10.3390/s25133917
APA StyleGao, Z., Jia, X., Wang, J., Zhou, Z., Wang, J., Wei, D., Tu, X., Kang, L., Chen, J., Chen, D., & Wu, P. (2025). Non-Destructive Thickness Measurement of Energy Storage Electrodes via Terahertz Technology. Sensors, 25(13), 3917. https://doi.org/10.3390/s25133917









