An Image-Free Single-Pixel Detection System for Adaptive Multi-Target Tracking
Abstract
1. Introduction
2. Principle and Method
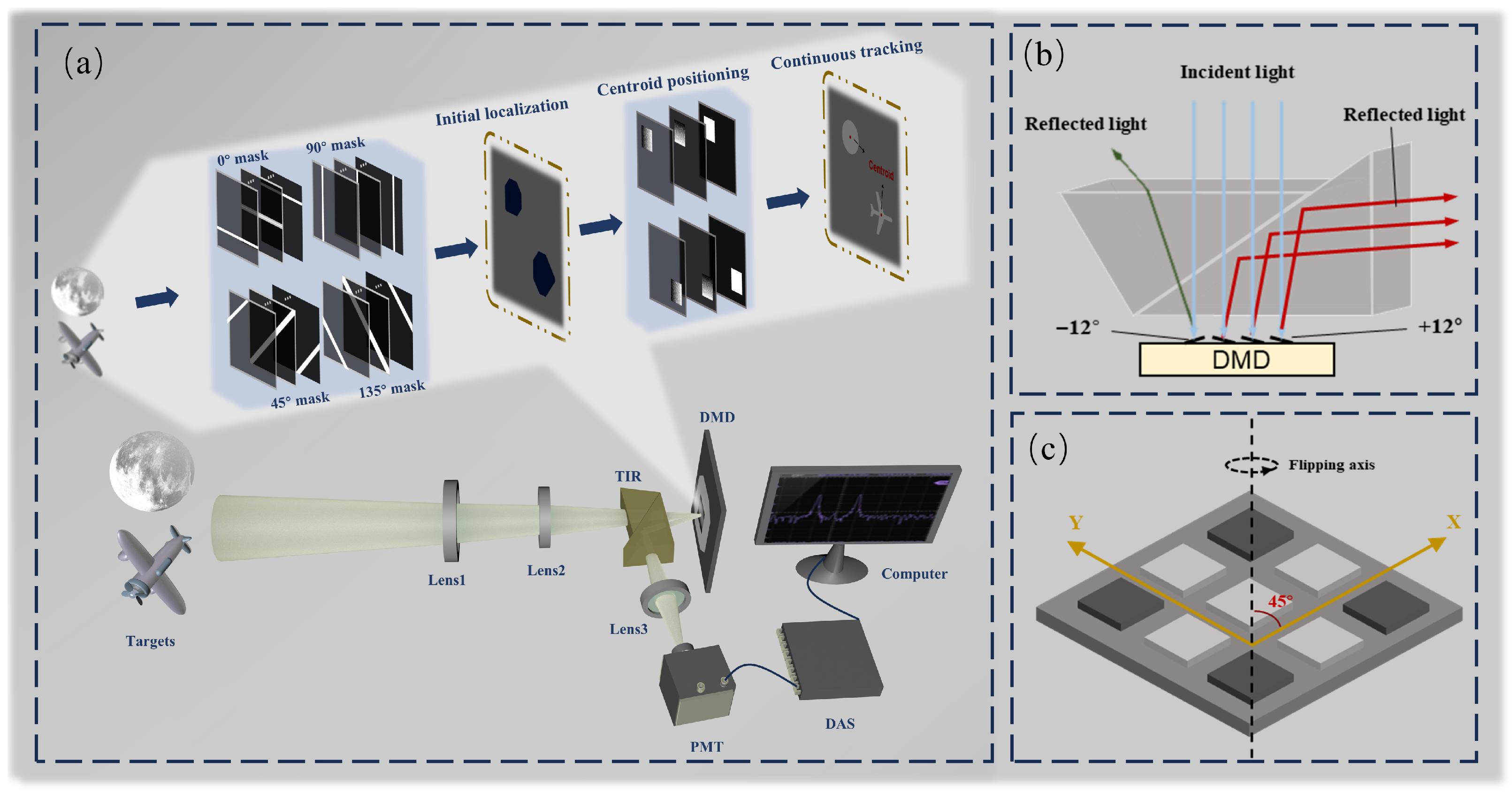
2.1. Single-Pixel System Design for Multi-Target Tracking
2.2. DMD-Based Multi-Target Localization
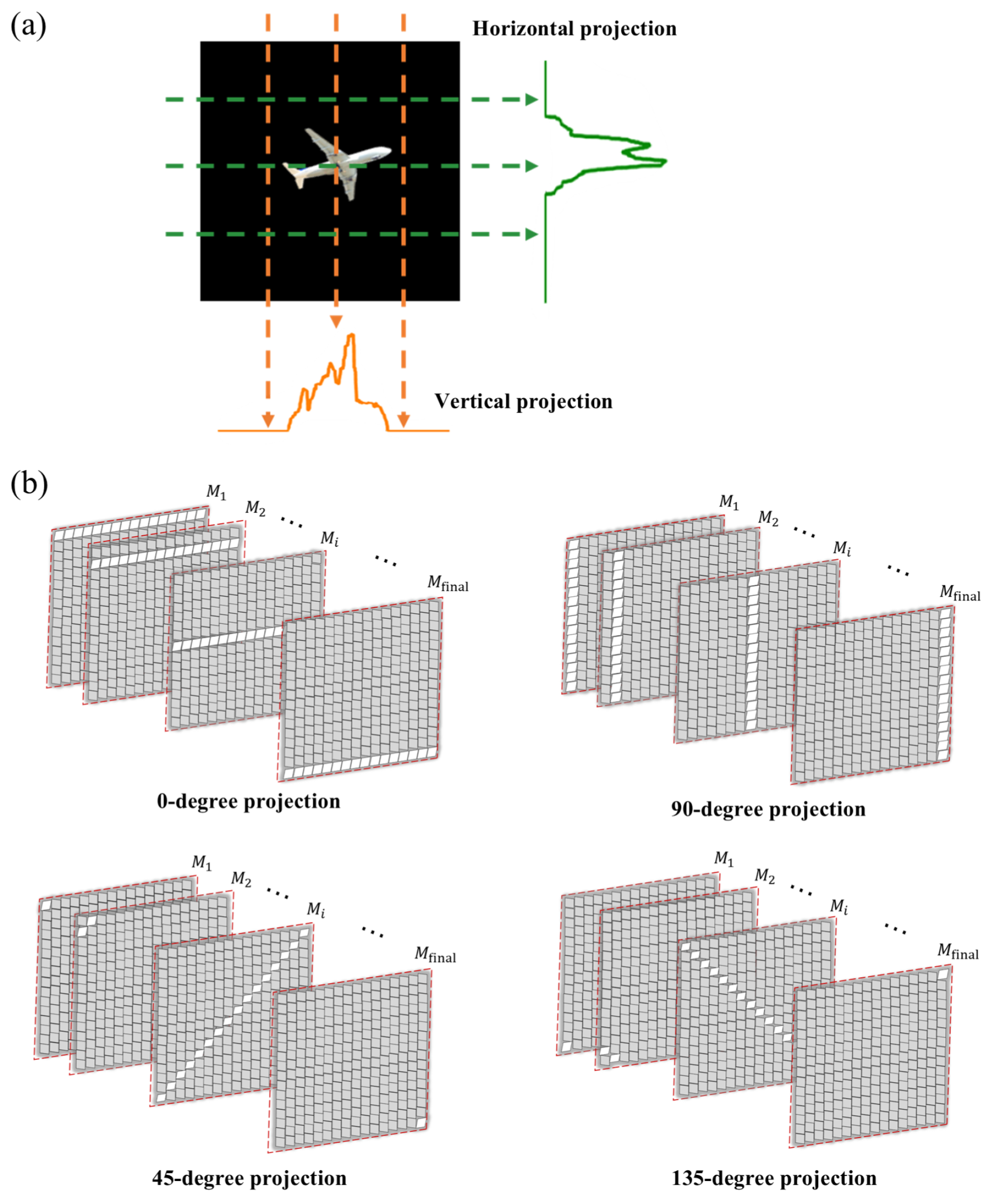
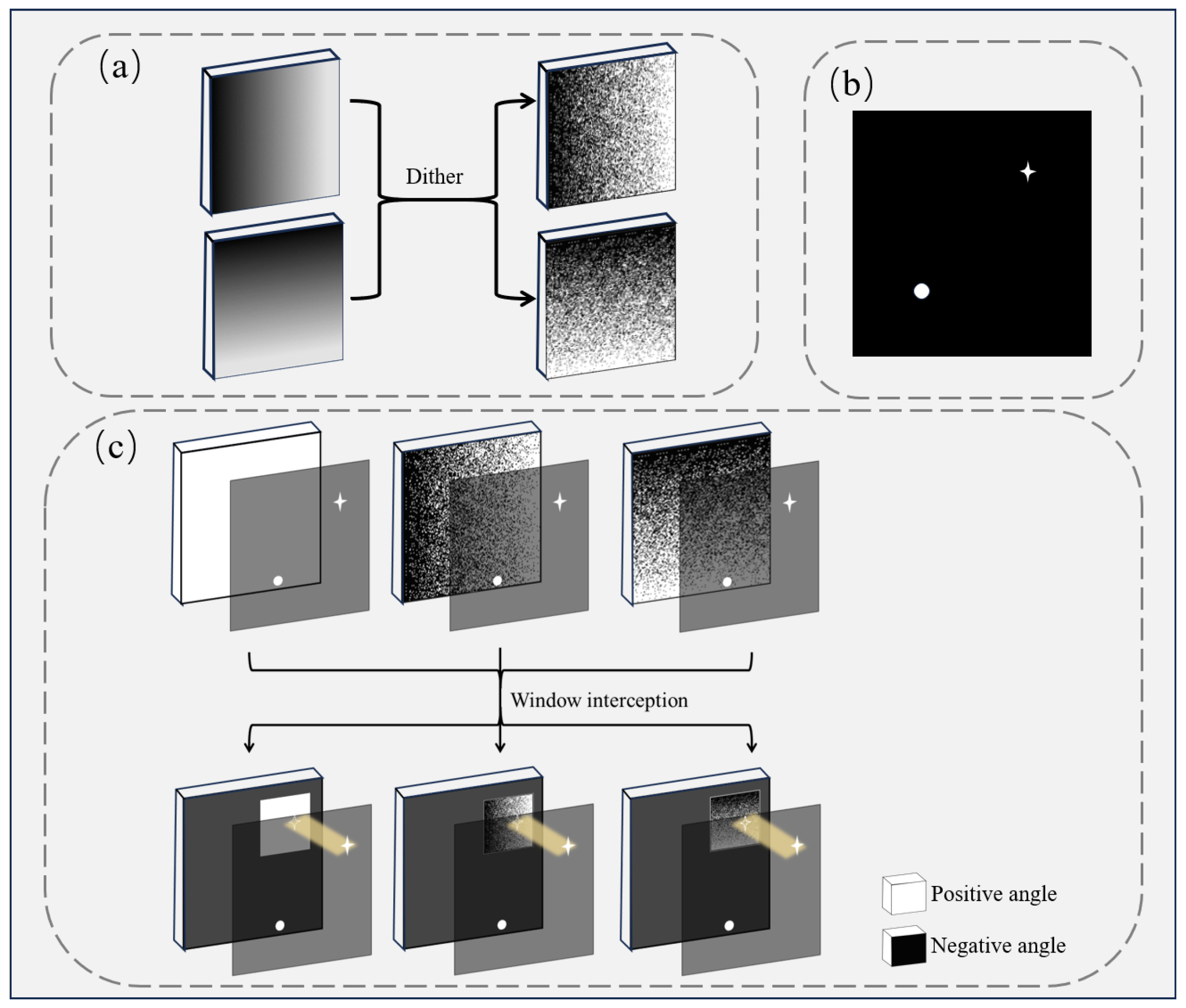
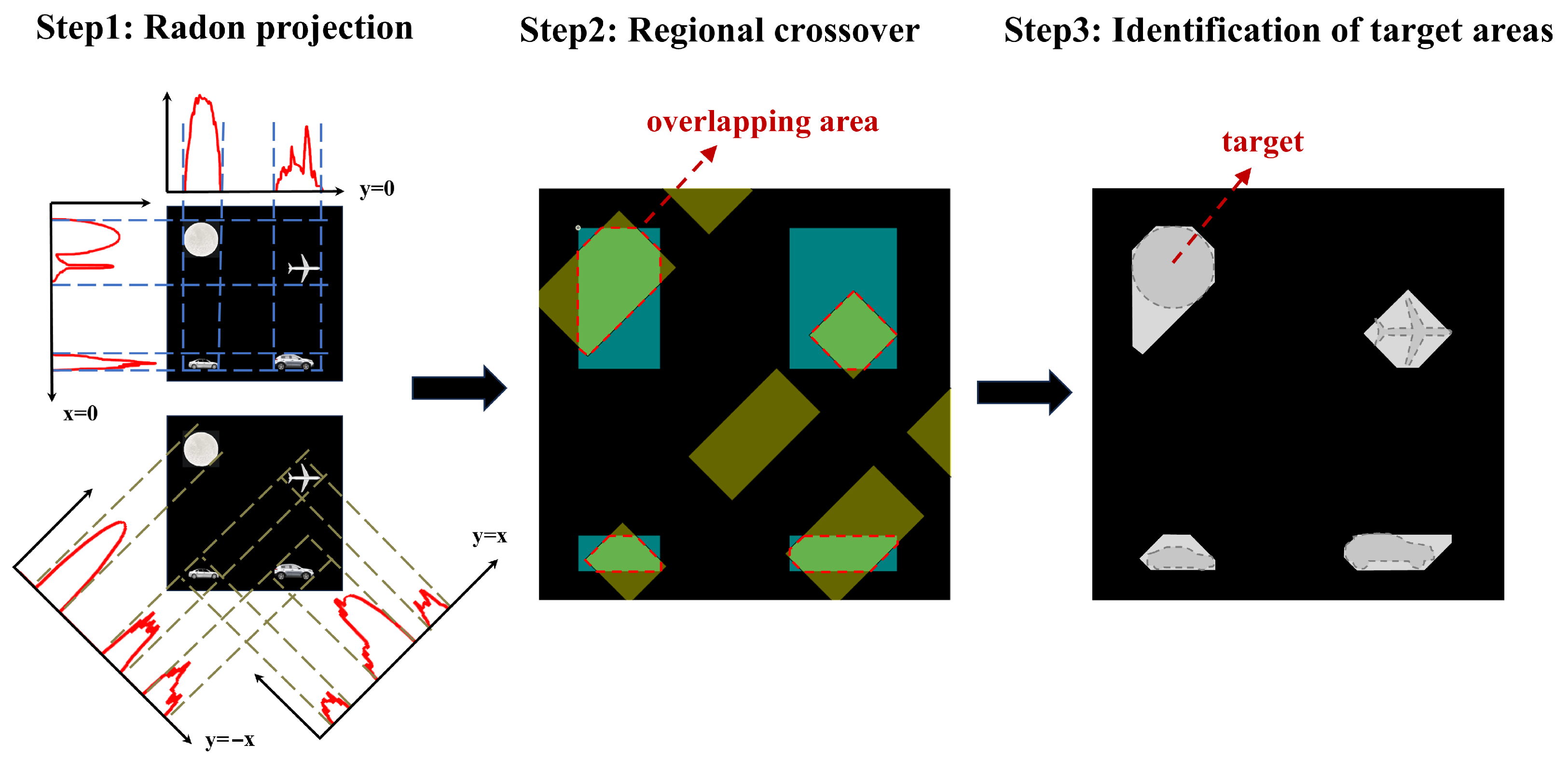
2.2.1. Initial Multi-Target Localization Based on Radon Projection
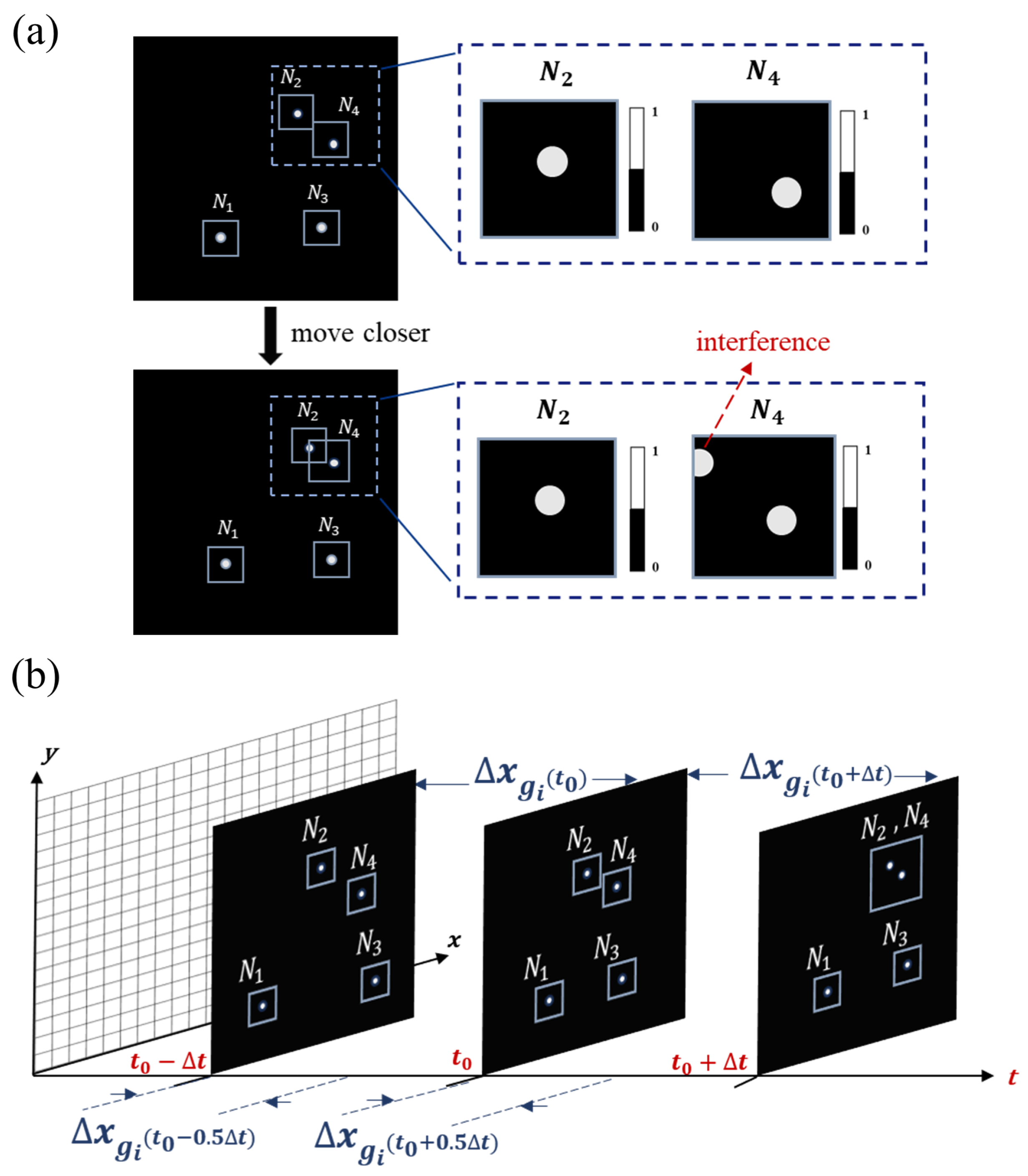
2.2.2. Continuous Tracking via Geometric Moments
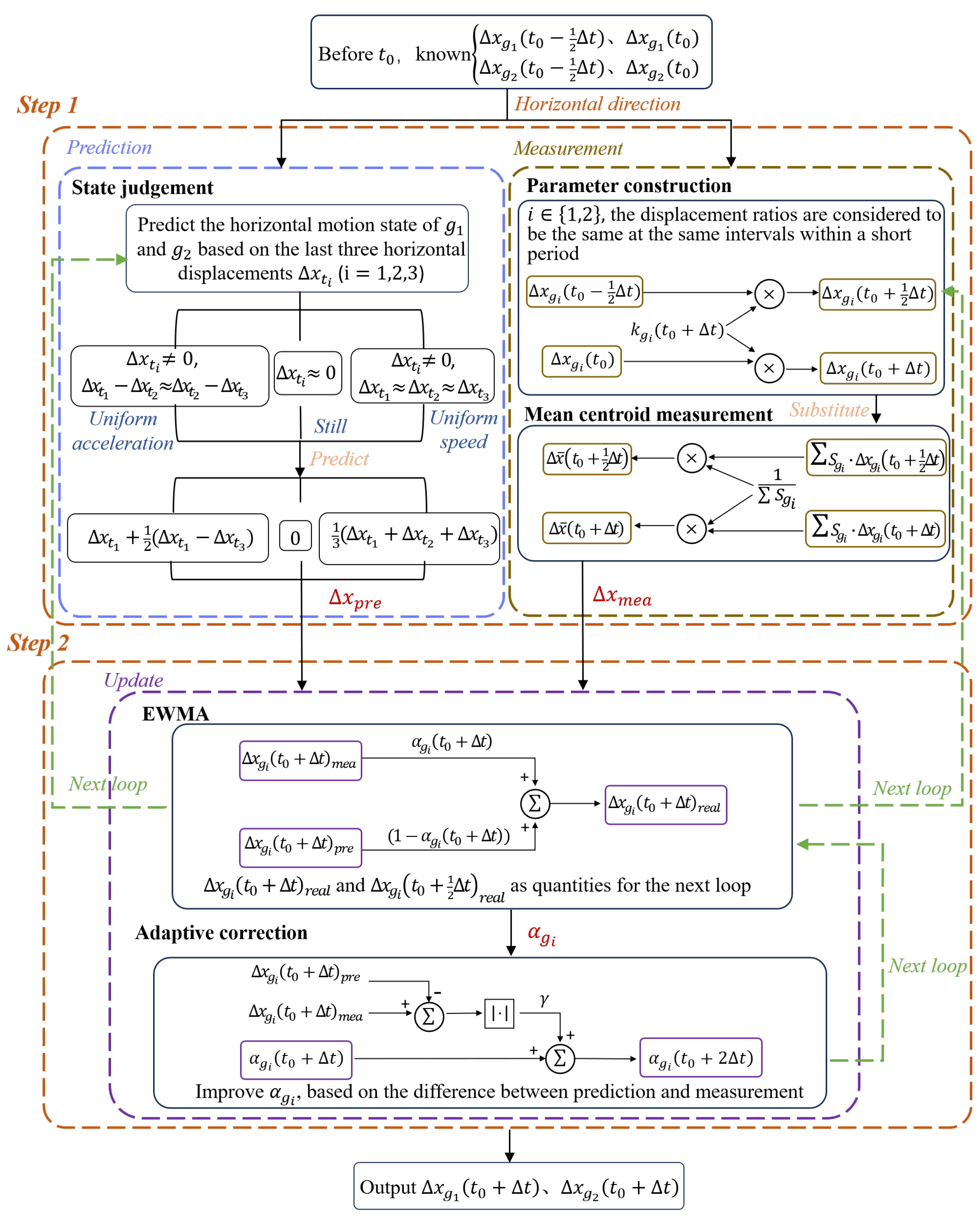
2.3. Multi-Target Window Tracking Method Based on Adaptive EWMA
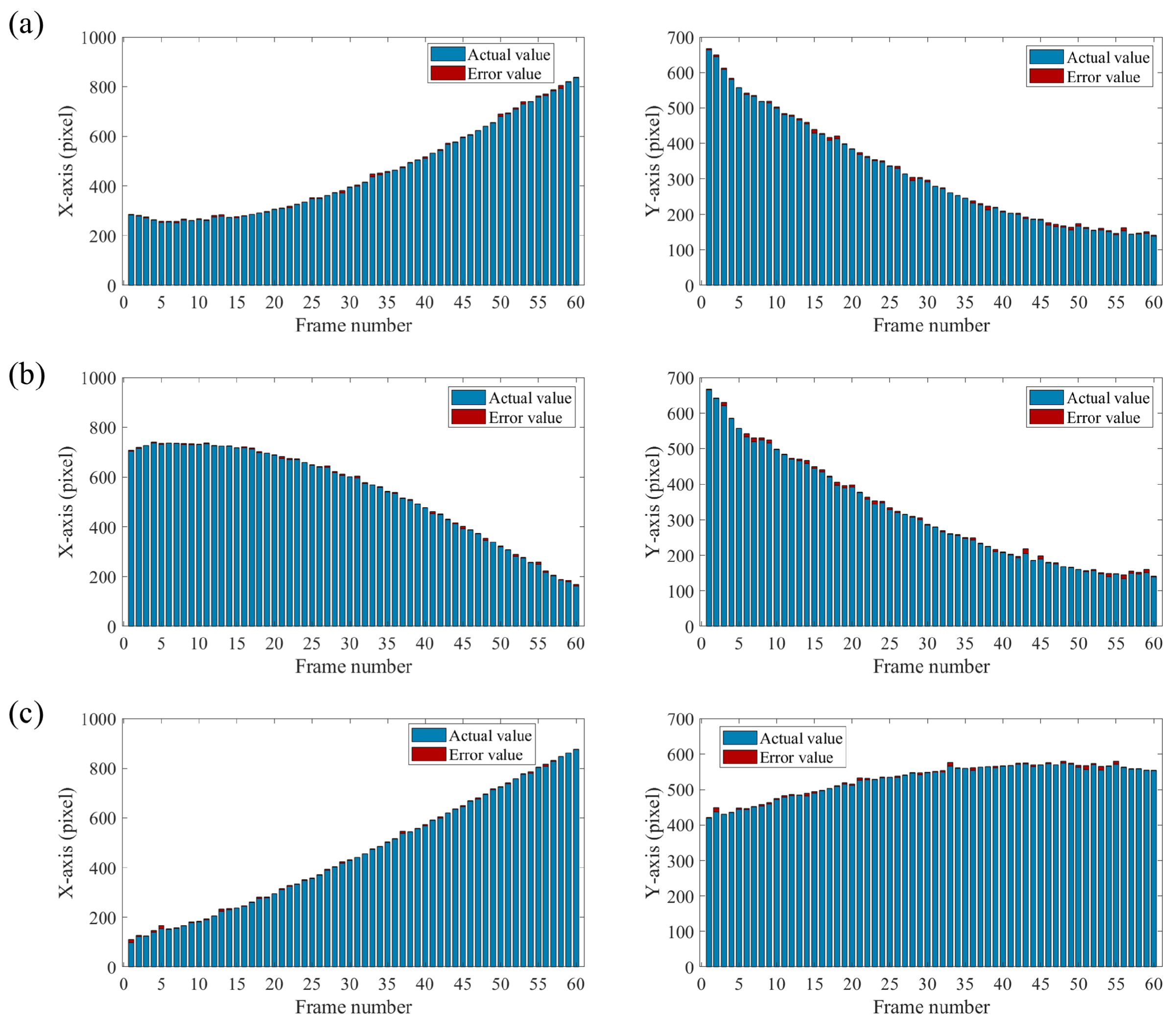
3. Simulation and Experiment
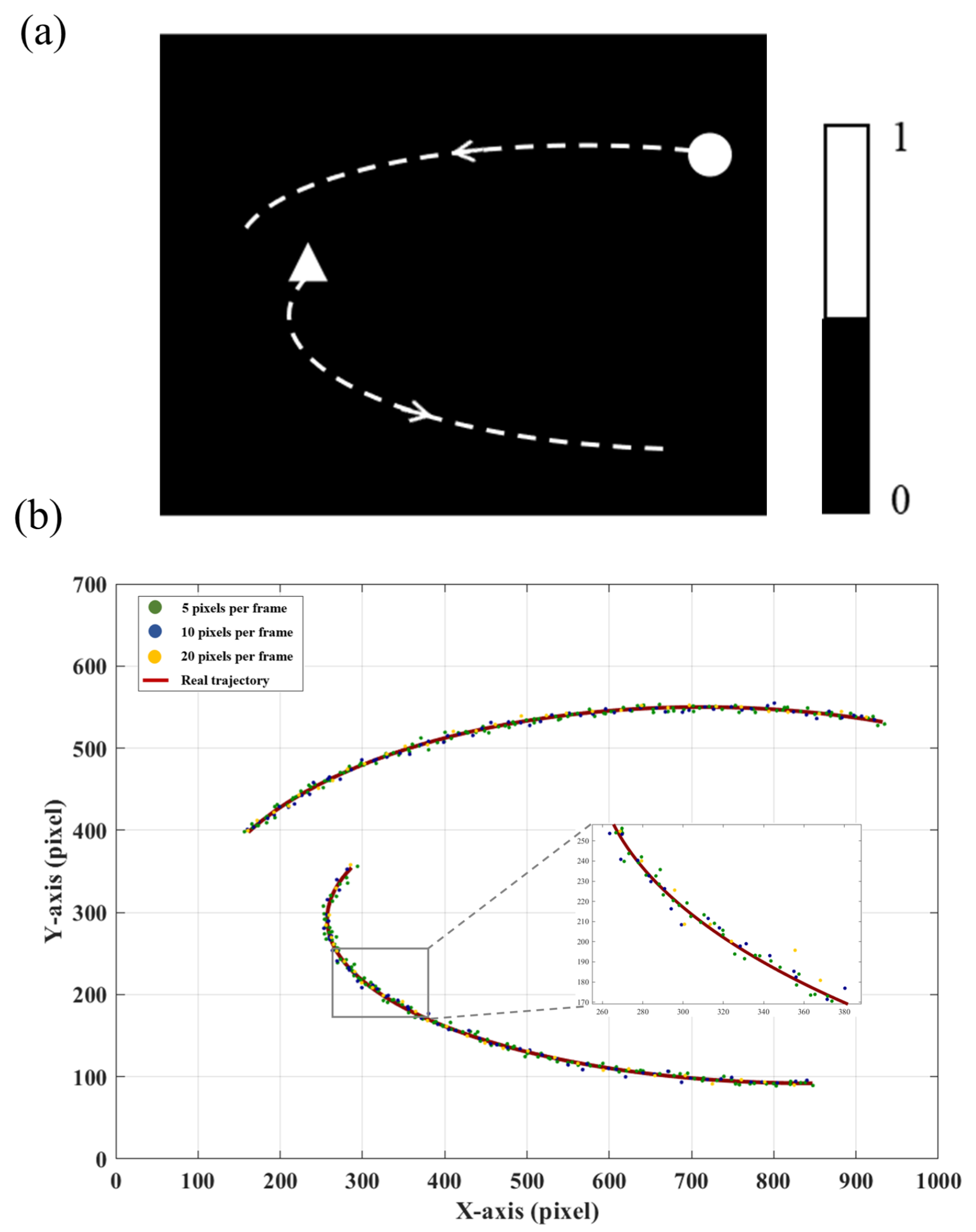
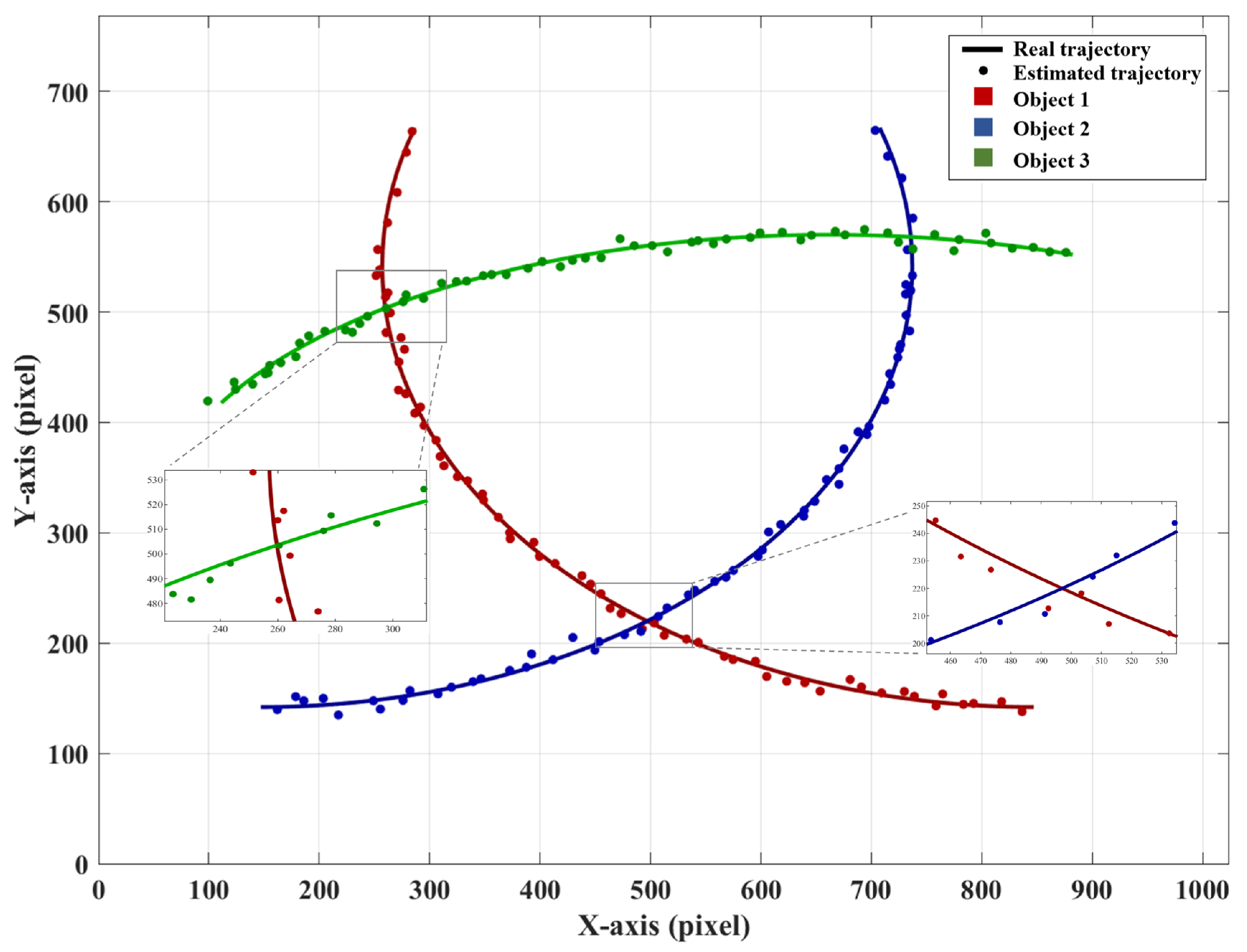
3.1. Simulation
3.1.1. Radon Projection
3.1.2. Multi-Target Window Tracking Method Based on Adaptive EWMA
3.2. Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EWMA | Exponentially weighted moving average |
| WGM | Window-based geometric moment |
| NRMSE | Normalized root mean square error |
| DMD | Digital micromirror device |
| PMT | Photomultiplier tube |
| TIR | Total internal reflection |
References
- Masmitja, I.; Martin, M.; O’Reilly, T.; Kieft, B.; Palomeras, N.; Navarro, J.; Katija, K. Dynamic robotic tracking of underwater targets using reinforcement learning. Sci. Robot. 2023, 8, eade7811. [Google Scholar] [CrossRef]
- Verma, V.; Maimone, M.W.; Gaines, D.M.; Francis, R.; Estlin, T.A.; Kuhn, S.R.; Rabideau, G.R.; Chien, S.A.; McHenry, M.M.; Graser, E.J.; et al. Autonomous robotics is driving Perseverance rover’s progress on Mars. Sci. Robot. 2023, 8, eadi3099. [Google Scholar] [CrossRef]
- Pardhasaradhi, B.; Cenkeramaddi, L.R. GPS spoofing detection and mitigation for drones using distributed radar tracking and fusion. IEEE Sens. J. 2022, 22, 11122–11134. [Google Scholar] [CrossRef]
- Gabr, K.; Abdelkader, M.; Jarraya, I.; AlMusalami, A.; Koubaa, A. SMART-TRACK: A Novel Kalman Filter-Guided Sensor Fusion For Robust UAV Object Tracking in Dynamic Environments. IEEE Sens. J. 2024, 25, 3086–3097. [Google Scholar]
- Vo-Doan, T.T.; Titov, V.V.; Harrap, M.J.; Lochner, S.; Straw, A.D. High-resolution outdoor videography of insects using Fast Lock-On tracking. Sci. Robot. 2024, 9, eadm7689. [Google Scholar] [CrossRef]
- Xiao, D.; Kedem Orange, R.; Opatovski, N.; Parizat, A.; Nehme, E.; Alalouf, O.; Shechtman, Y. Large-FOV 3D localization microscopy by spatially variant point spread function generation. Sci. Adv. 2024, 10, eadj3656. [Google Scholar] [CrossRef] [PubMed]
- Jiao, L.; Zhang, X.; Liu, X.; Liu, F.; Yang, S.; Ma, W.; Li, L.; Chen, P.; Feng, Z.; Guo, Y.; et al. Transformer meets remote sensing video detection and tracking: A comprehensive survey. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1–45. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, X.; Li, C.; Tang, J.; Huang, Z. Long-term Motion Assisted Remote Sensing Object Tracking. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5407514. [Google Scholar] [CrossRef]
- Kondo, Y.; Takubo, K.; Tominaga, H.; Hirose, R.; Tokuoka, N.; Kawaguchi, Y.; Takaie, Y.; Ozaki, A.; Nakaya, S.; Yano, F.; et al. Development of ‘HyperVision HPV-X’ high-speed video camera. Shimadzu Rev. 2012, 69, 285–291. [Google Scholar]
- Fuller, P. An introduction to high speed photography and photonics. Imaging Sci. J. 2009, 57, 293–302. [Google Scholar] [CrossRef]
- Wei, M.; Xing, F.; You, Z. An implementation method based on ERS imaging mode for sun sensor with 1 kHz update rate and 1 precision level. Opt. Express 2013, 21, 32524–32533. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.S.; Xing, F.; You, Z. A real-time detection and positioning method for small and weak targets using a 1D morphology-based approach in 2D images. Light. Sci. Appl. 2018, 7, 18006. [Google Scholar] [CrossRef] [PubMed]
- Teman, A.; Fisher, S.; Sudakov, L.; Fish, A.; Yadid-Pecht, O. Autonomous CMOS image sensor for real time target detection and tracking. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems (ISCAS), Seattle, WA, USA, 18–21 May 2008; pp. 2138–2141. [Google Scholar]
- Deng, Q.; Zhang, Z.; Zhong, J. Image-free real-time 3-D tracking of a fast-moving object using dual-pixel detection. Opt. Lett. 2020, 45, 4734–4737. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Z.; Zhou, M.; Zhang, Z.; Chen, M.; Geng, Z. Prior-free 3D tracking of a fast-moving object at 6667 frames per second with single-pixel detectors. Opt. Lett. 2024, 49, 3628–3631. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Yang, J.; Liu, C.; Wang, C.; Zhang, G.; Ding, Y. Study on Exposure Time Difference Compensation Method for DMD-Based Dual-Path Multi-Target Imaging Spectrometer. Remote Sens. 2025, 17, 2021. [Google Scholar] [CrossRef]
- Zheng, J.L.; Xu, D.S.; Yang, Z.H.; Yu, Y.J. Fast Image-free high precision target tracking using single pixel detection. In Proceedings of the 2023 38th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2023; pp. 1131–1136. [Google Scholar]
- Yu, Y.; Yang, Z.; Li, W.; Shao, H. Image-Free Positioning Tracking Scheme via Single Pixel Detection. In Proceedings of the Advances in Guidance, Navigation and Control: Proceedings of 2020 International Conference on Guidance, Navigation and Control, ICGNC 2020, Tianjin, China, 23–25 October 2020; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1349–1357. [Google Scholar]
- Peng, Y.; Sun, T.; Yang, J.; Yu, S.; Feng, Y.; Liu, H. Research on Enhancing the Precision of Real-Time Target Centroid Localization Based on Digital Micromirror Device. In Proceedings of the 2024 Academic Conference of China Instrument and Control Society (ACCIS), Chengdu, China, 28–31 July 2024; pp. 335–339. [Google Scholar]
- Shi, D.; Yin, K.; Huang, J.; Yuan, K.; Zhu, W.; Xie, C.; Liu, D.; Wang, Y. Fast tracking of moving objects using single-pixel imaging. Opt. Commun. 2019, 440, 155–162. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, J.; Deng, Q.; Zhong, J. Image-free real-time detection and tracking of fast moving object using a single-pixel detector. Opt. Express 2019, 27, 35394–35401. [Google Scholar] [CrossRef]
- Yang, Z.H.; Chen, X.; Zhao, Z.H.; Song, M.Y.; Liu, Y.; Zhao, Z.D.; Lei, H.D.; Yu, Y.J.; Wu, L.A. Image-free real-time target tracking by single-pixel detection. Opt. Express 2022, 30, 864–873. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X.; Zhang, L.; Zhang, L.; Yan, T.; Fu, S.; Sun, T.; Zhan, H.; Xing, F.; You, Z. Real-time localization and classification of the fast-moving target based on complementary single-pixel detection. Opt. Express 2025, 33, 11301–11316. [Google Scholar] [CrossRef]
- Zha, L.; Meng, W.; Shi, D.; Huang, J.; Yuan, K.; Yang, W.; Chen, Y.; Wang, Y. Complementary moment detection for tracking a fast-moving object using dual single-pixel detectors. Opt. Lett. 2022, 47, 870–873. [Google Scholar] [CrossRef]
- Fu, S.; Xing, F.; You, Z. Dual-pixel tracking of the fast-moving target based on window complementary modulation. Opt. Express 2022, 30, 39747–39761. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, H.; Yin, Y.; Jiang, W.; Sun, B. Mask-based single-pixel tracking and imaging for moving objects. Opt. Express 2023, 31, 32554–32564. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.F.; Yu, Y.J.; Ji, P.C.; Zhou, S.J.; Zhang, H.J. Image-free single-pixel fast localization of multi-target using small window projection. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 4036–4041. [Google Scholar]
- Zhang, J.; Hu, T.; Shao, X.; Xiao, M.; Rong, Y.; Xiao, Z. Multi-target tracking using windowed Fourier single-pixel imaging. Sensors 2021, 21, 7934. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, Z.H.; Liu, Y.X.; Li, M.F.; Wu, F.L.; Yu, Y.J. Long-Range Fast Single-Pixel Localization of Multiple Moving Targets. IEEE Sens. J. 2024, 24, 24699–24707. [Google Scholar] [CrossRef]
- Meng, W.; Shi, D.; Yang, W.; Zha, L.; Zhao, Y.; Wang, Y. Multi-object positioning and imaging based on single-pixel imaging using binary patterns. Sensors 2022, 22, 3211. [Google Scholar] [CrossRef]
- Zheng, J.; Yu, Y.; Chen, S.; Yang, Z.; Li, G. Image-free localization and tracking of multi-targets based on single pixel detection. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 3814–3819. [Google Scholar]
- Bowron, J.W.; Jonas, R.P. Off-axis illumination design for DMD systems. In Design of Efficient Illumination Systems; SPIE: Bellingham, WA, USA, 2003; Volume 5186, pp. 72–82. [Google Scholar]
- Ostromoukhov, V. A simple and efficient error-diffusion algorithm. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 567–572. [Google Scholar]
- Crowder, S.V.; Hamilton, M.D. An EWMA for monitoring a process standard deviation. J. Qual. Technol. 1992, 24, 12–21. [Google Scholar] [CrossRef]



| Objects | Object Centroid Value (pixel) | Window Function Center Value (pixel) |
|---|---|---|
| Moon | (200, 212) | (200.50, 258.00) |
| Plane | (794, 366) | (783.25, 358.50) |
| Car 1 | (212, 925) | (209.25, 918.50) |
| Car 2 | (730, 903) | (742.50, 908.00) |
| Objects | WGM Method Without EWMA RMSE (pixel) | EWMA-Based WGM Method RMSE (pixel) |
|---|---|---|
| 1.21 | 0.73 | |
| 16.29 | 1.17 | |
| 1.47 | 1.16 | |
| N.A. | 1.57 |
| Objects | NRMSE at Motion Speed of S Pixels per Frame | ||
|---|---|---|---|
| S = 5 | S = 10 | S = 20 | |
| Object 1 | 0.00618 | 0.00694 | 0.00722 |
| Object 2 | 0.00783 | 0.00814 | 0.00903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Yang, J.; Feng, Y.; Yu, S.; Xing, F.; Sun, T. An Image-Free Single-Pixel Detection System for Adaptive Multi-Target Tracking. Sensors 2025, 25, 3879. https://doi.org/10.3390/s25133879
Peng Y, Yang J, Feng Y, Yu S, Xing F, Sun T. An Image-Free Single-Pixel Detection System for Adaptive Multi-Target Tracking. Sensors. 2025; 25(13):3879. https://doi.org/10.3390/s25133879
Chicago/Turabian StylePeng, Yicheng, Jianing Yang, Yuhao Feng, Shijie Yu, Fei Xing, and Ting Sun. 2025. "An Image-Free Single-Pixel Detection System for Adaptive Multi-Target Tracking" Sensors 25, no. 13: 3879. https://doi.org/10.3390/s25133879
APA StylePeng, Y., Yang, J., Feng, Y., Yu, S., Xing, F., & Sun, T. (2025). An Image-Free Single-Pixel Detection System for Adaptive Multi-Target Tracking. Sensors, 25(13), 3879. https://doi.org/10.3390/s25133879








