Multi-Modal Joint Pulsed Eddy Current Sensor Signal Denoising Method Integrating Inductive Disturbance Mechanism
Abstract
1. Introduction
2. Using Improved Whale Optimization to Construct Variational Mode Decomposition Parameter Selection
2.1. Improved Whale Optimization (IWOA)
2.2. Whale Optimization Improvement Method
2.2.1. Inductive Disturbance Mechanism
2.2.2. Search Path Changes
2.3. Improved Whale Optimization Implementation Steps
2.3.1. Prey Hunting
2.3.2. Bubble Net Attack Phase
2.3.3. Searching for Prey
3. Variational Mode Decomposition-Singular Value Decomposition-Wavelet Threshold Denoising Combined Pulsed Eddy Current Noise Reduction Method Based on Improved Whale Optimization
3.1. Construction of Variational Mode Decomposition-Singular Value Decomposition-Wavelet Threshold Denoising Denoising Method
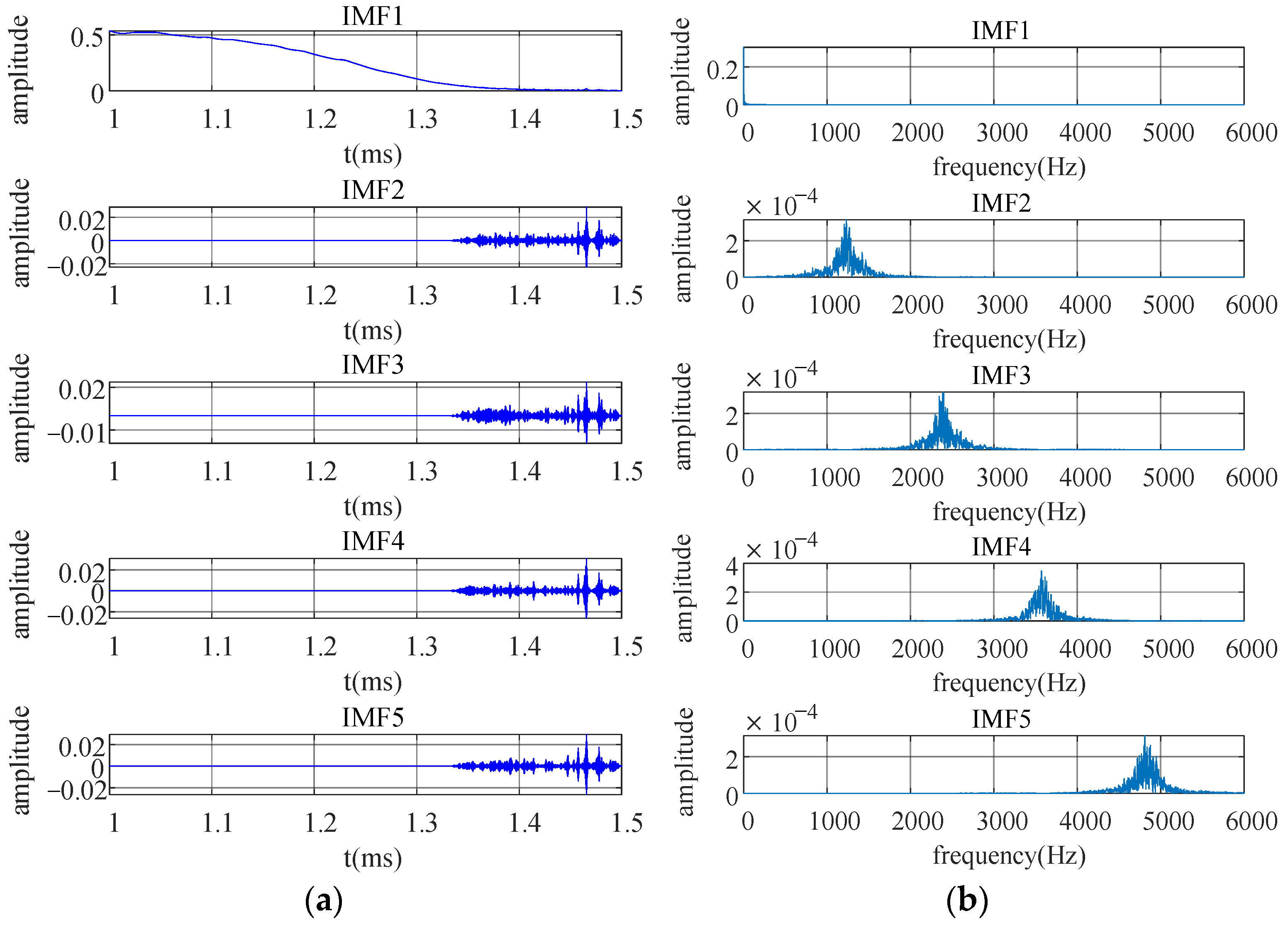
3.1.1. VMD Decomposition Structure
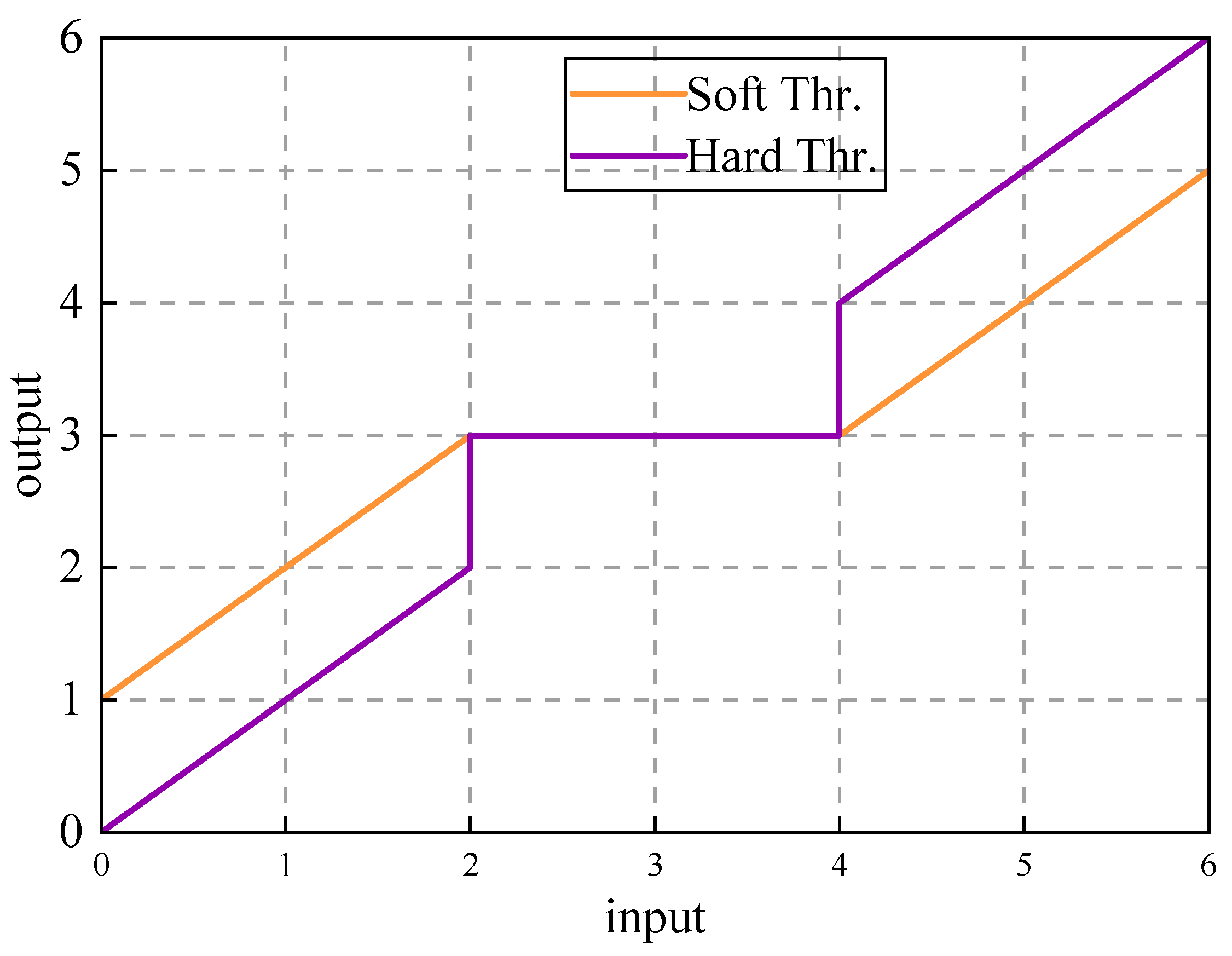
3.1.2. Singular Value Decomposition and Wavelet Threshold Denoising Construction
3.2. Denoising Performance Indicators
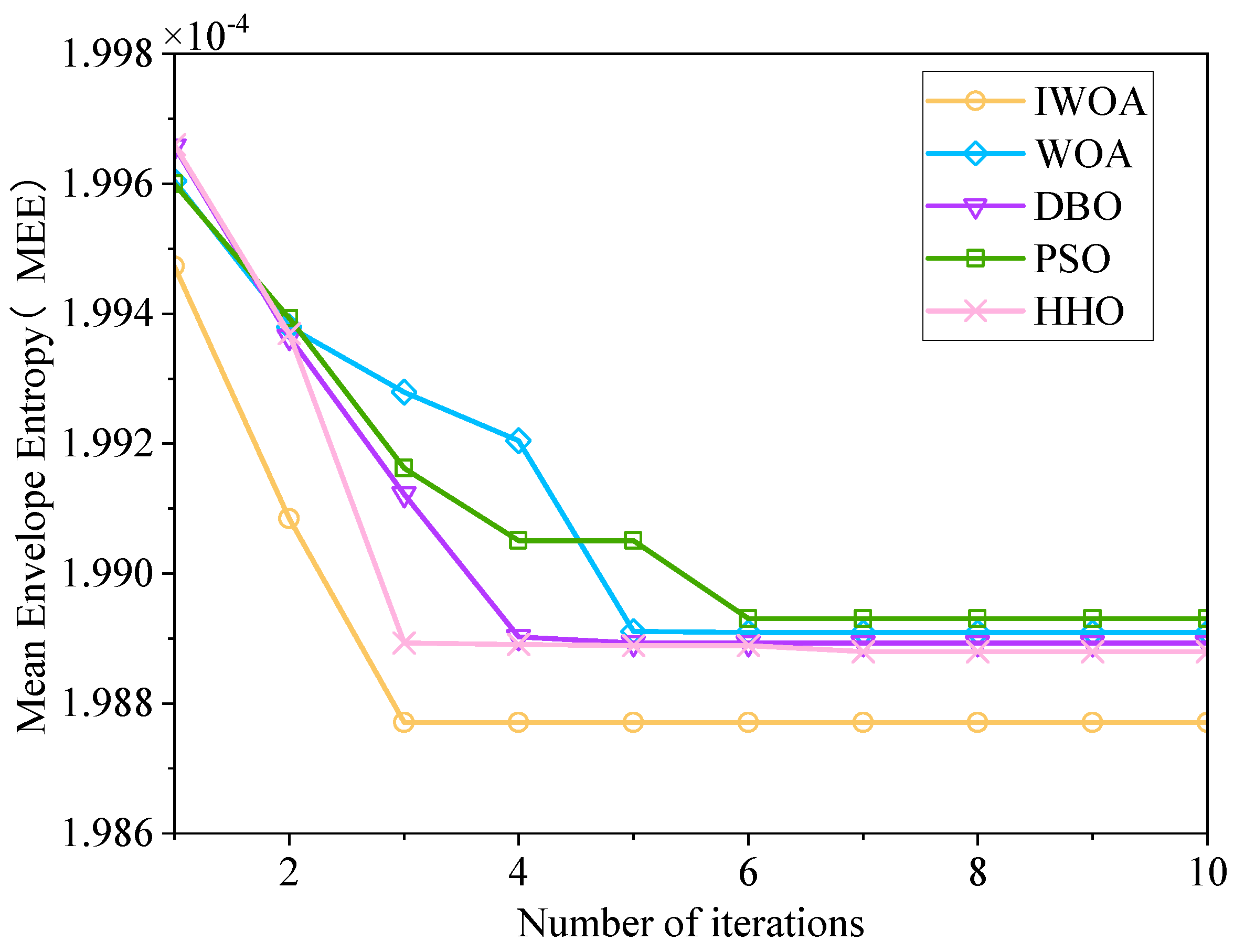
4. IWOA-VMD-SVD-WTD Model Test
4.1. Device Structure and Parameter Settings
4.2. Random Noise Test
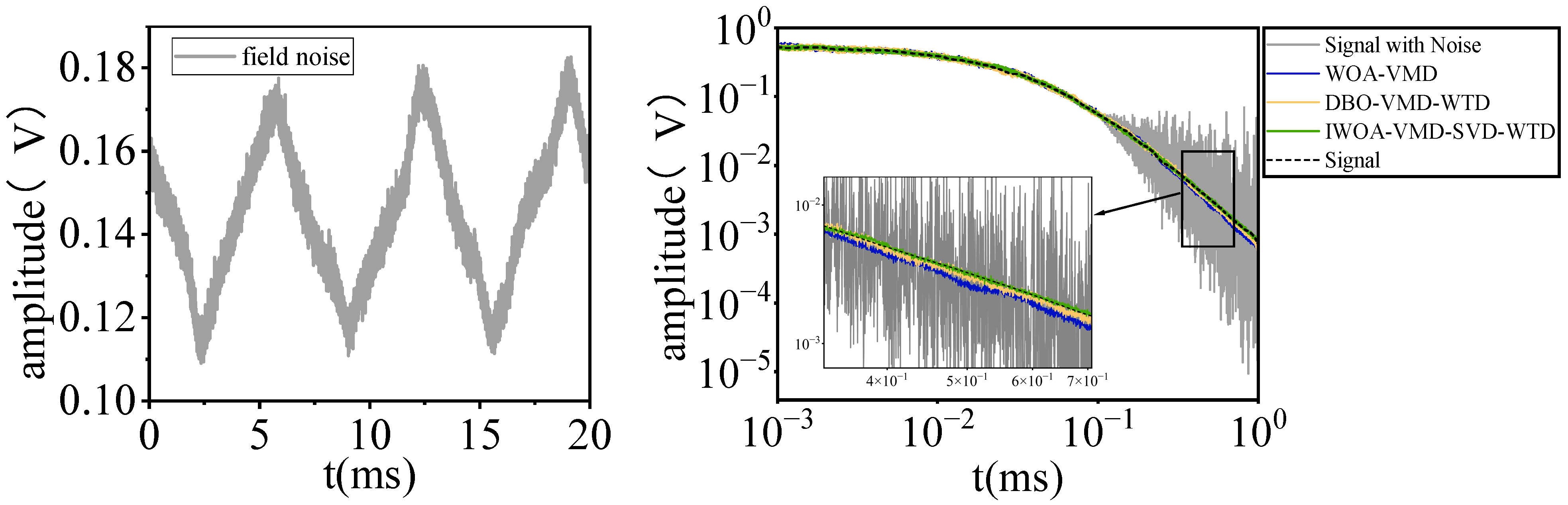
4.3. On-Site Noise Test
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, B.; Luo, F. Study of Pulsed Eddy Current Nondestructive Testing Technology. Instrum. Technol. Sens. 2004, 45–46. [Google Scholar]
- Zhou, D.; Tian, G.; Wang, H.; Wang, P. Evaluation of applied stress using pulsed eddy current technology. Chin. J. Sci. Instrum. 2010, 31, 1588–1593. [Google Scholar]
- Wu, X.; Zhang, Q.; Shen, G. Review on advances in pulsed eddy current nondestructive testing technology. Chin. J. Sci. Instrum. 2016, 37, 1698–1712. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Nai-Chyuan, Y.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data. Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data. Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Duan, X.; Li, X.; Chen, W. Improved particles swarm optimization algorithm-based VMD-GRU methodfor short-term load forecasting. New Technol. Electr. Eng. Energy 2022, 41, 8–17. [Google Scholar]
- Liu, D.; Zhang, Q.; Zhu, G. Bearing Fault Diagnosis Based on Optimized VMD Parameters and VGG Models. Mach. Tools Hydraul. 2024, 52, 195–202. [Google Scholar]
- Zhang, Y.; Wu, Y.; Li, L.; Liu, Z. A Hybrid Energy Storage System Strategy for Smoothing Photovoltaic Power Fluctuation Based on Improved HHO-VMD. Int. J. Photoenergy 2023, 2023, 9633843. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Long, Q. Indoor visible light positioning method using ISSA-ELM neural network based on circle chaotic mapping. Acta Opt. Sin. 2023, 43, 33–42. [Google Scholar]
- Nguyen, H.; Bui, X.N.; Drebenstedt, C.; Choi, Y. Enhanced Prediction Model for Blast-Induced Air Over-Pressure in Open-Pit Mines Using Data Enrichment and Random Walk-Based Grey Wolf Optimization–Two-Layer ANN Model. Nat. Resour. Res. 2024, 33, 943–972. [Google Scholar] [CrossRef]
- Qian, Z.; Cheng, L.; Li, Y. Noise reduction method based on singular value decomposition. J. Vib. Meas. Diagn. 2011, 31, 459–463. [Google Scholar]
- Jing-Yi, L.; Hong, L.; Dong, Y.; Yan-Sheng, Z. A new wavelet threshold function and denoising application. Math. Probl. Eng. 2016, 2016, 3195492. [Google Scholar] [CrossRef]
- Qi, T.Y.; Wei, H.R.; Feng, G.R.; Zhang, X.; Yu, C.; Zhao, D.; Sun, D. Denoising method of transient electromagnetic detection signalbased on WOA-VMD algorithm. J. Cent. South Univ. Sci. Technol. 2021, 52, 3885–3898. [Google Scholar]
- Qi, T.; Wei, X.; Feng, G.; Zhang, F.; Zhao, D.; Guo, J. A method for reducing transient electromagnetic noise: Combination of variational mode decomposition and wavelet denoising algorithm. Measurement 2022, 198, 111420. [Google Scholar] [CrossRef]
- Lv, P.; Wu, X.; Zhao, Y.; Chang, J. Noise removal for semi-airborne data using wavelet threshold and singular value decomposition. J. Appl. Geophys. 2022, 201, 104622. [Google Scholar] [CrossRef]
- Song, D.; Feng, G.; Qi, T.; Wang, H.; Pan, D.; Zhang, L. A new combined transient electromagnetic noise reduction method of VMD-SVD-WTD based on improved dung beetle optimization algorithm with multi-strategy fusion. Meas. Sci. Technol. 2024, 36, 016105. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Wei, X. An improved whale optimization algorithm based on different searching paths and perceptual disturbance. Symmetry 2018, 10, 210. [Google Scholar] [CrossRef]
- Lei, Z.; Wang, F.; Li, C. A denoising method of partial discharge signal based on improved SVD-VMD. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 2107–2116. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]






| Parameter Name | Parameter Value | Unit |
|---|---|---|
| Transmitter coil radius | 0.2 | m |
| Receiving coil radius | 0.6 | m |
| Transmitting coil turns | 10 | turn |
| Receiving coil turns | 1700 | turn |
| Sampling frequency | 25 | MHz |
| Excitation current amplitude | 20 | A |
| Excitation voltage | 12 | V |
| Excitation voltage waveform | Bipolar pulse square wave | / |
| Modal Components | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 |
|---|---|---|---|---|---|
| Correlation coefficient | 0.8463 | 0.4648 | 0.3791 | 0.3119 | 0.1179 |
| SNR | WOA-VMD | DBO-VMD-WTD | IWOA-VMD-SVD-WTD |
|---|---|---|---|
| −25 | 15.48 | 19.32 | 24.31 |
| −10 | 18.87 | 27.13 | 29.72 |
| 5 | 18.46 | 26.78 | 29.64 |
| Indicator Function | WOA-VMD | DBO-VMD-WTD | IWOA-VMD-SVD-WTD |
|---|---|---|---|
| SNR (dB) | 30.21 | 33.47 | 39.78 |
| RMSE | 0.031 | 0.023 | 0.017 |
| AC | 0.79 | 0.0.87 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Y.; Hu, G.; Gan, F.; Zeng, Z.; Lin, Z.; Wang, X.; Xu, R.; Wen, L.; Hu, S.; Le, H.; et al. Multi-Modal Joint Pulsed Eddy Current Sensor Signal Denoising Method Integrating Inductive Disturbance Mechanism. Sensors 2025, 25, 3830. https://doi.org/10.3390/s25123830
Zuo Y, Hu G, Gan F, Zeng Z, Lin Z, Wang X, Xu R, Wen L, Hu S, Le H, et al. Multi-Modal Joint Pulsed Eddy Current Sensor Signal Denoising Method Integrating Inductive Disturbance Mechanism. Sensors. 2025; 25(12):3830. https://doi.org/10.3390/s25123830
Chicago/Turabian StyleZuo, Yun, Gebiao Hu, Fan Gan, Zhiwu Zeng, Zhichi Lin, Xinxun Wang, Ruiqing Xu, Liang Wen, Shubing Hu, Haihong Le, and et al. 2025. "Multi-Modal Joint Pulsed Eddy Current Sensor Signal Denoising Method Integrating Inductive Disturbance Mechanism" Sensors 25, no. 12: 3830. https://doi.org/10.3390/s25123830
APA StyleZuo, Y., Hu, G., Gan, F., Zeng, Z., Lin, Z., Wang, X., Xu, R., Wen, L., Hu, S., Le, H., Wu, R., & Wang, J. (2025). Multi-Modal Joint Pulsed Eddy Current Sensor Signal Denoising Method Integrating Inductive Disturbance Mechanism. Sensors, 25(12), 3830. https://doi.org/10.3390/s25123830






