RFID-Based Real-Time Salt Concentration Monitoring with Adaptive EKF
Abstract
1. Introduction
- Noninvasive Dual-tag RFID Sensing System with Physics-based Modeling: We propose a novel dual-tag RFID wireless sensing system that enables noninvasive concentration detection. Based on the Cole–Cole model, we establish accurate state and observation models that fundamentally characterize the system dynamics, overcoming the limitations of conventional empirical approaches. This physics-based modeling provides a solid foundation for the subsequent algorithmic estimation.
- Forward Estimation Framework based on KF: Conventional concentration estimation methods require computationally intensive inversion of the complex observation model to obtain the state x from observation z, making them impractical for real-time monitoring applications. The proposed KF-based approach fundamentally transforms this inverse problem by utilizing only forward calculations of within its recursive prediction and update mechanism. This avoids the need for iterative equation solving while maintaining estimation accuracy through analytical state updates via the Kalman gain matrix, enabling real-time operation without compromising precision.
- Dynamic Noise Adaptation Using Innovation Sequence: Existing EKF-based approaches often assume fixed noise covariances ( and ), leading to degraded performance in real-world environments. The proposed AEKF iteratively updates and matrices using innovation sequence, enabling automatic adaptation to time-varying noise conditions. This adaptation mechanism significantly improves estimation stability in noisy RFID sensing scenarios without requiring manual parameter tuning.
2. Materials and Methods
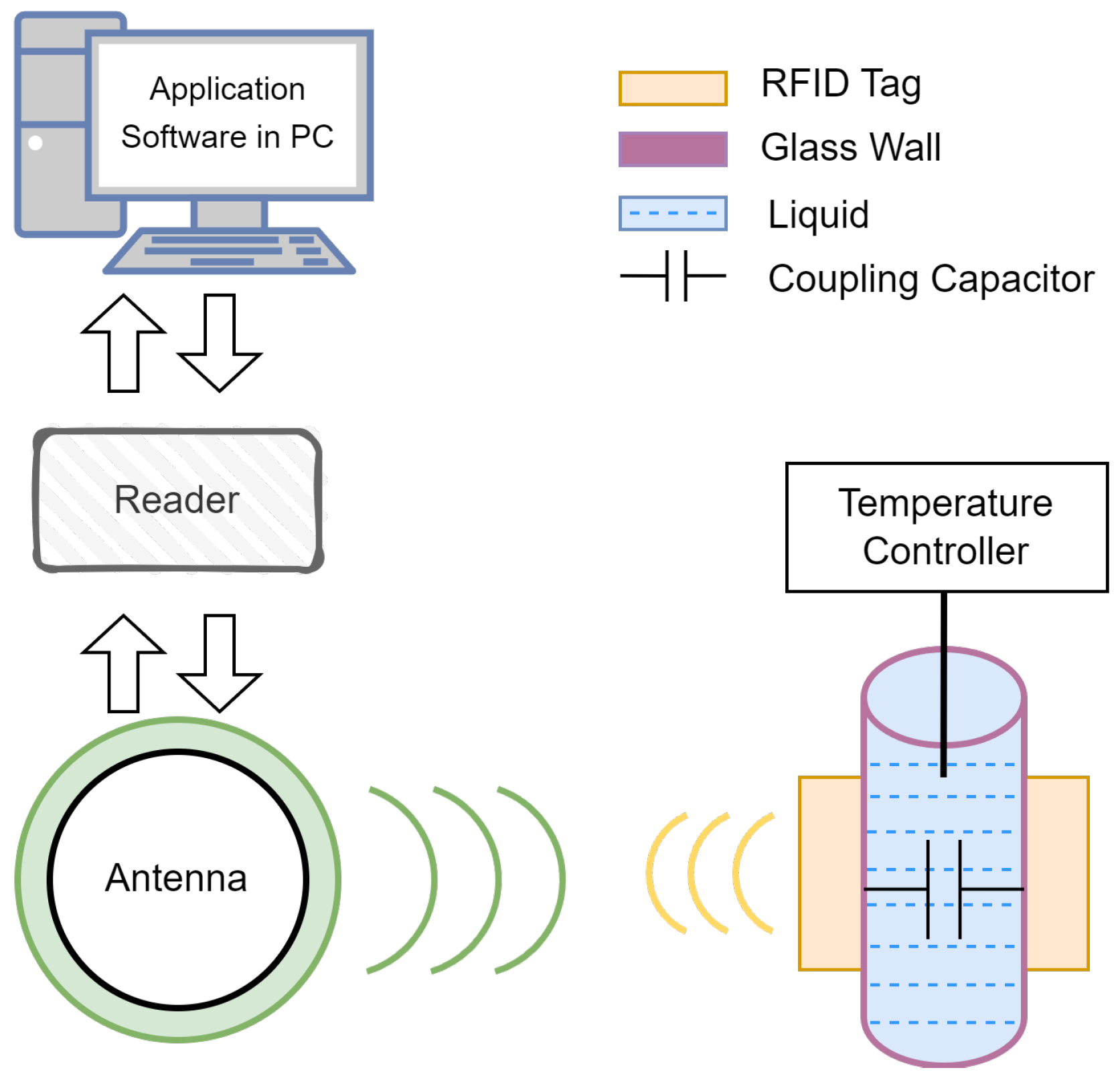
2.1. RFID Sensing System
2.2. System Model
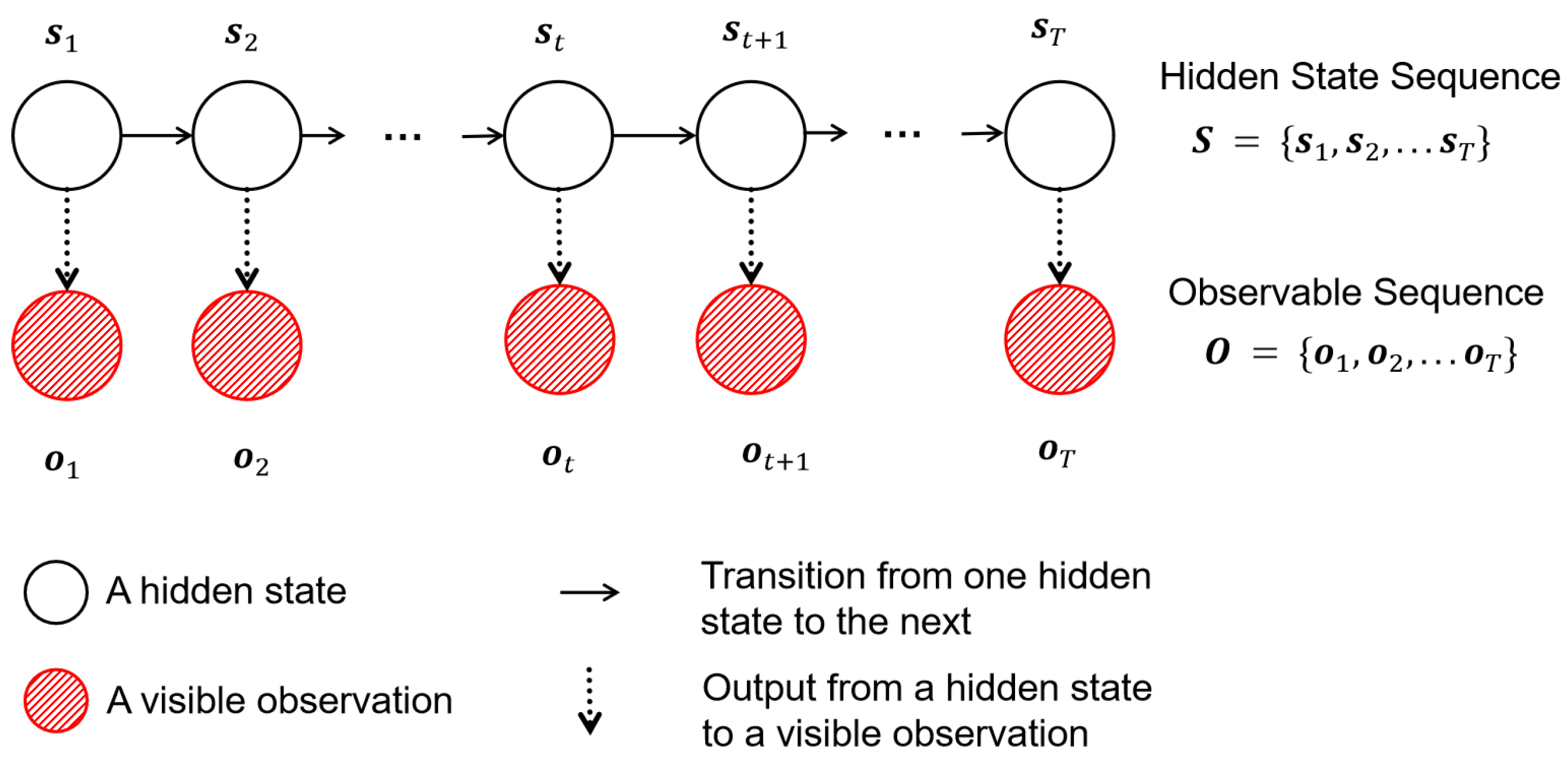
2.2.1. State-Space Model Based on HMM
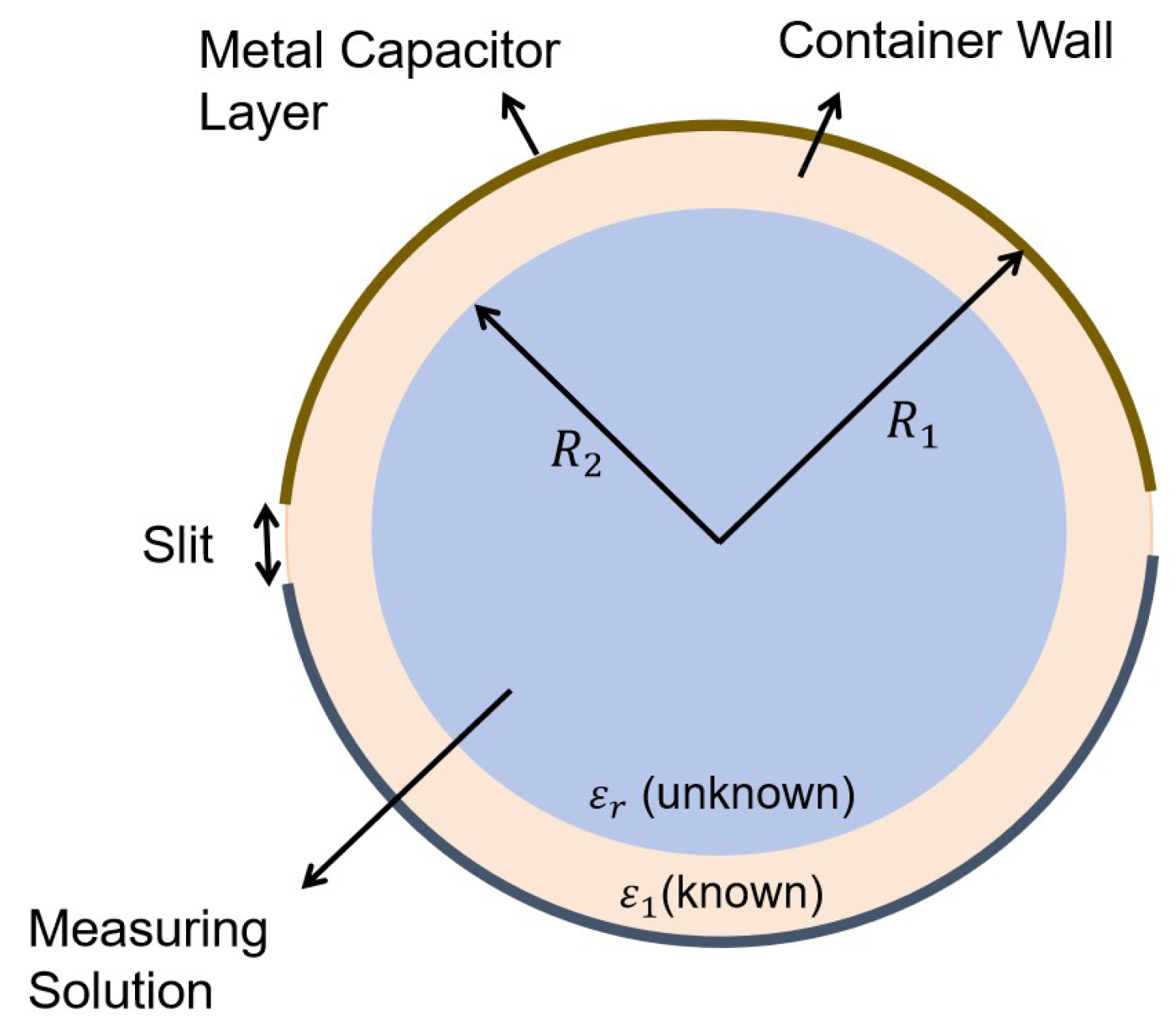
2.2.2. RFID Observation Model
2.3. Algorithm Design for Concentration Tracking
| Algorithm 1 Concentration estimation based on modified AEKF. |
3. Experiments and Results
3.1. Sample Preparation
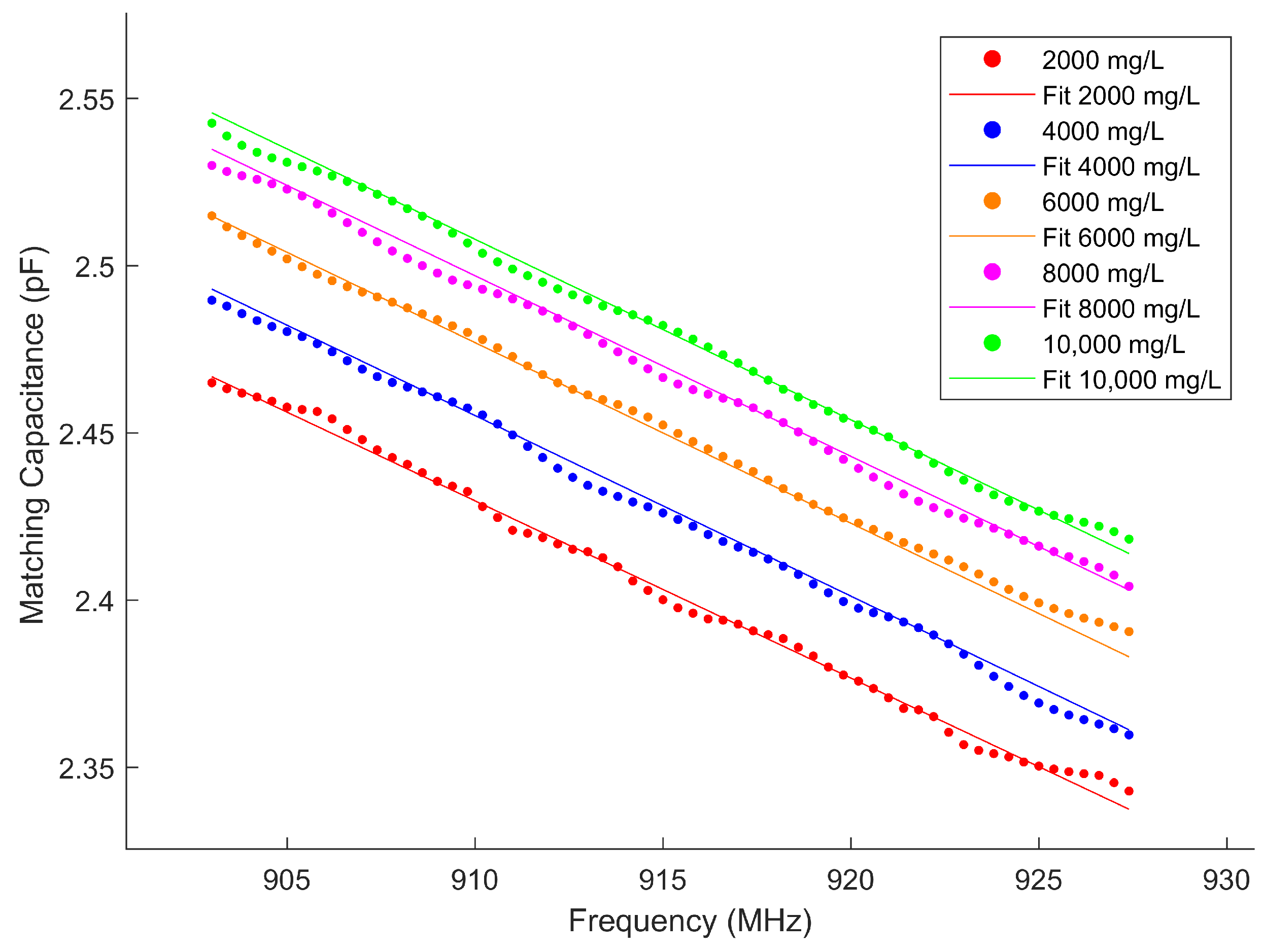
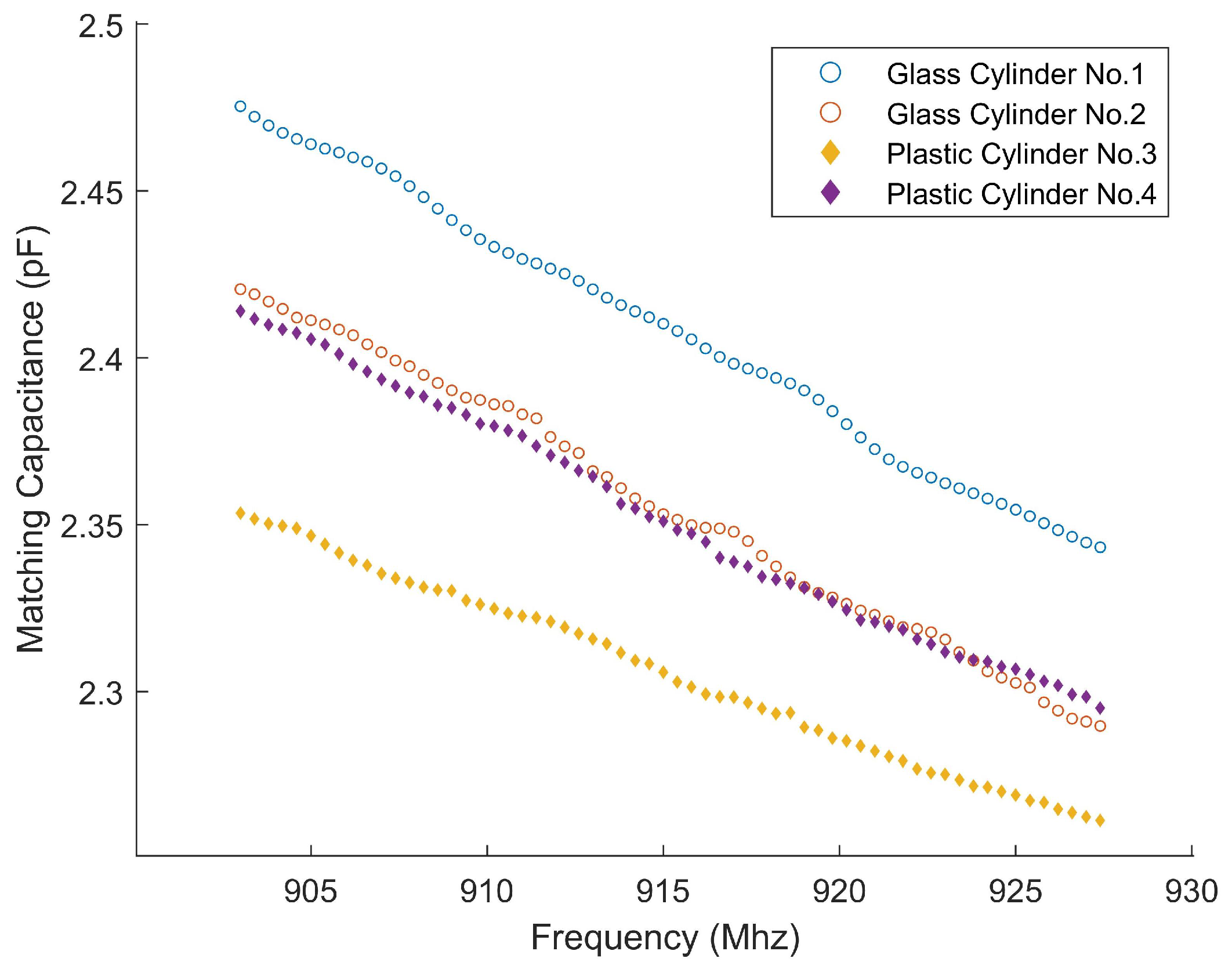
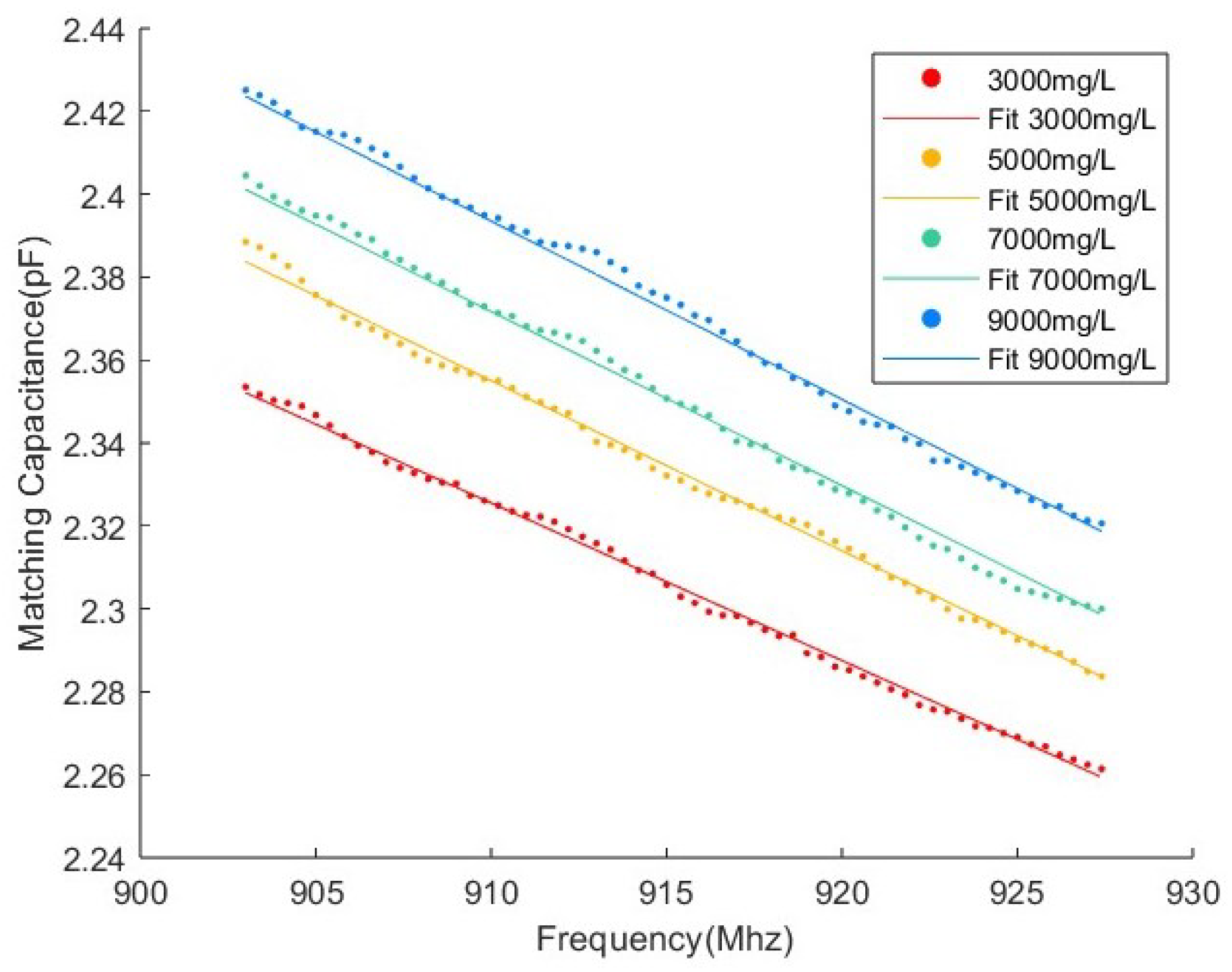
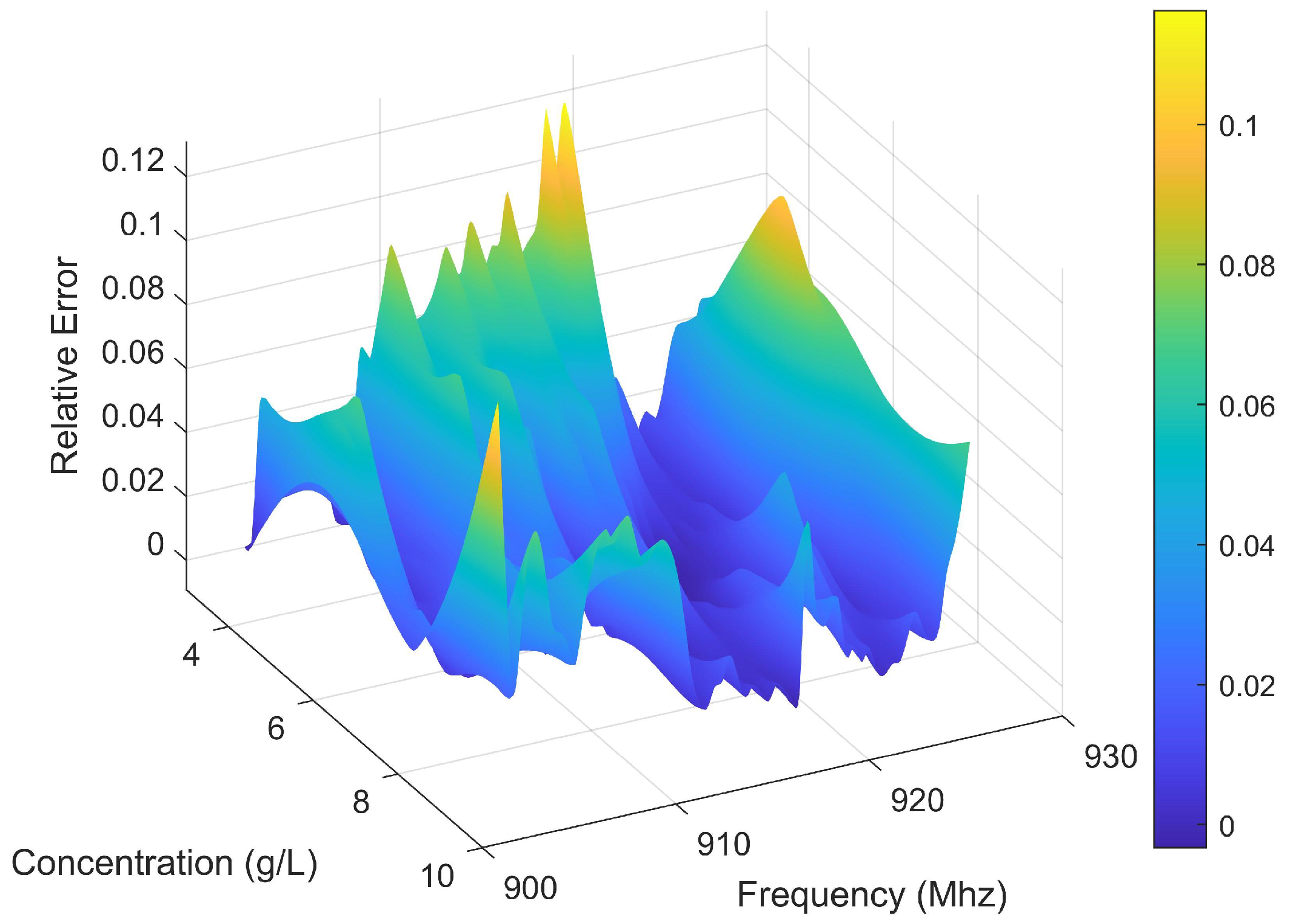
3.2. Parameter Acquirement
3.3. Experimental Methods for Concentration Estimation
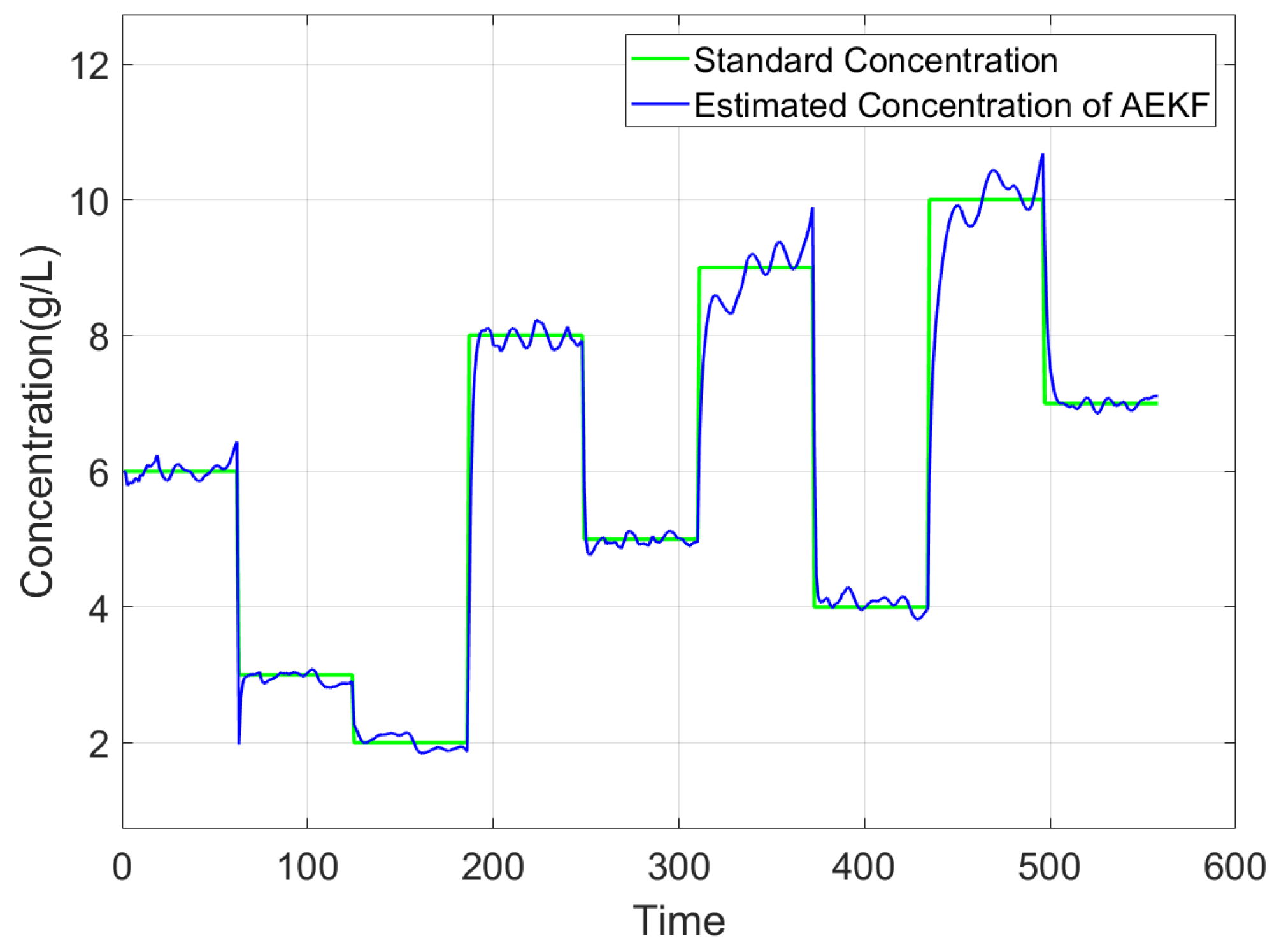
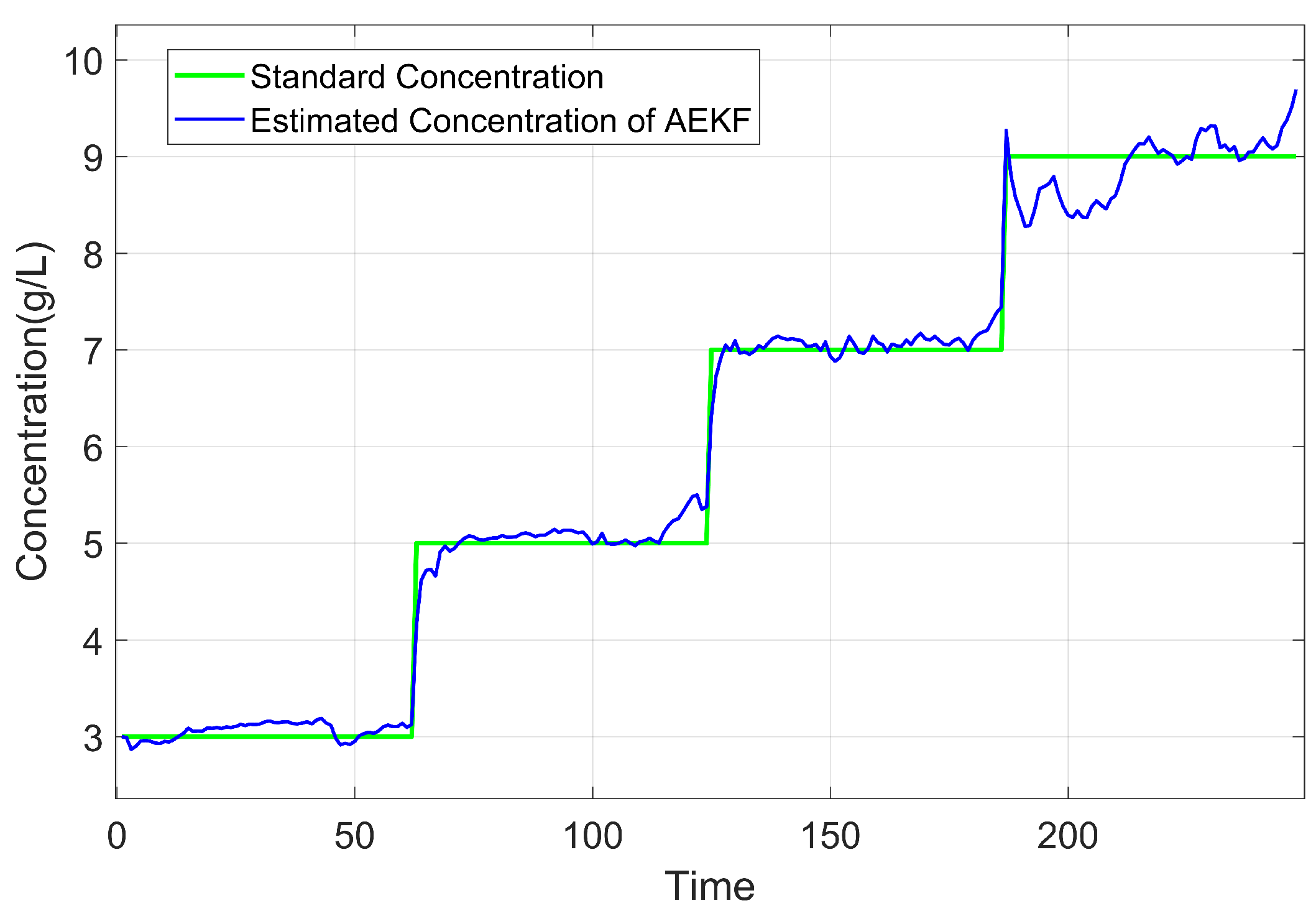
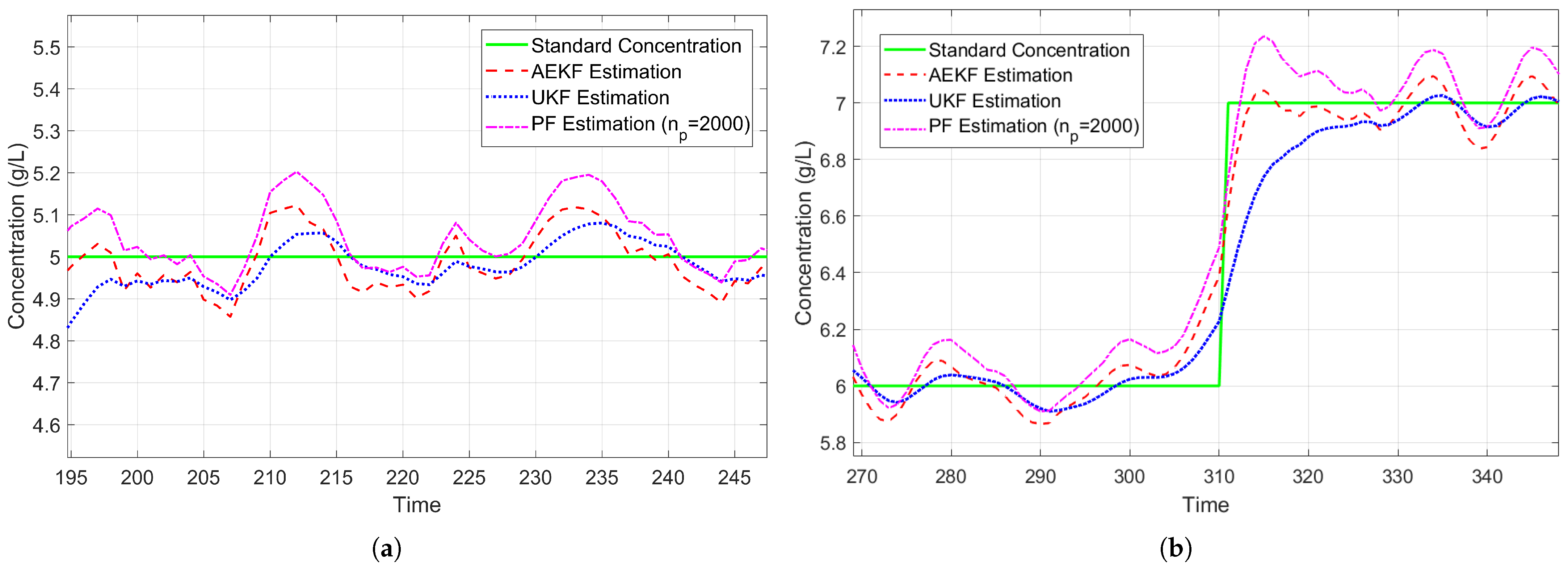
3.4. Experimental Results
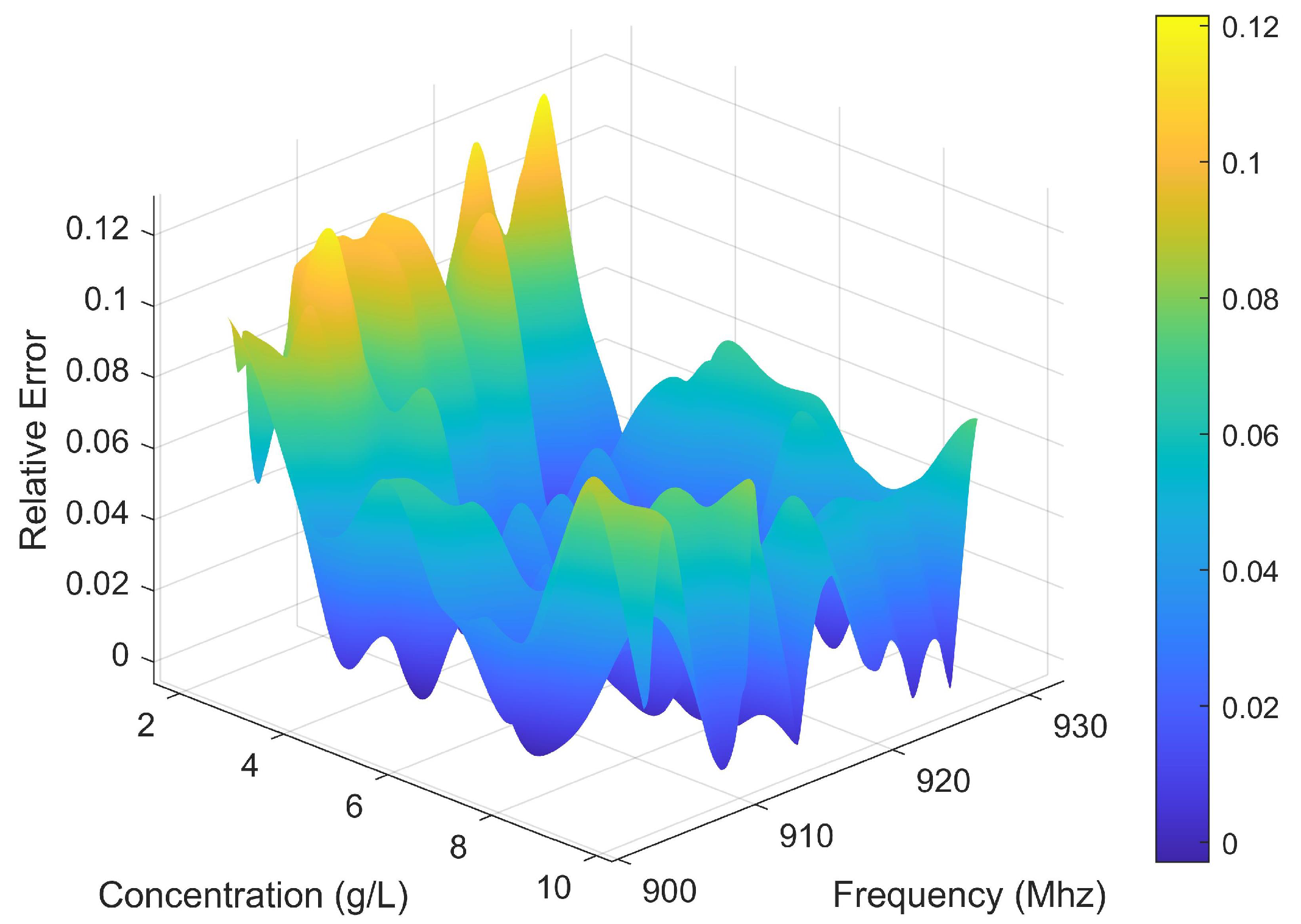
3.5. Performance Evaluation
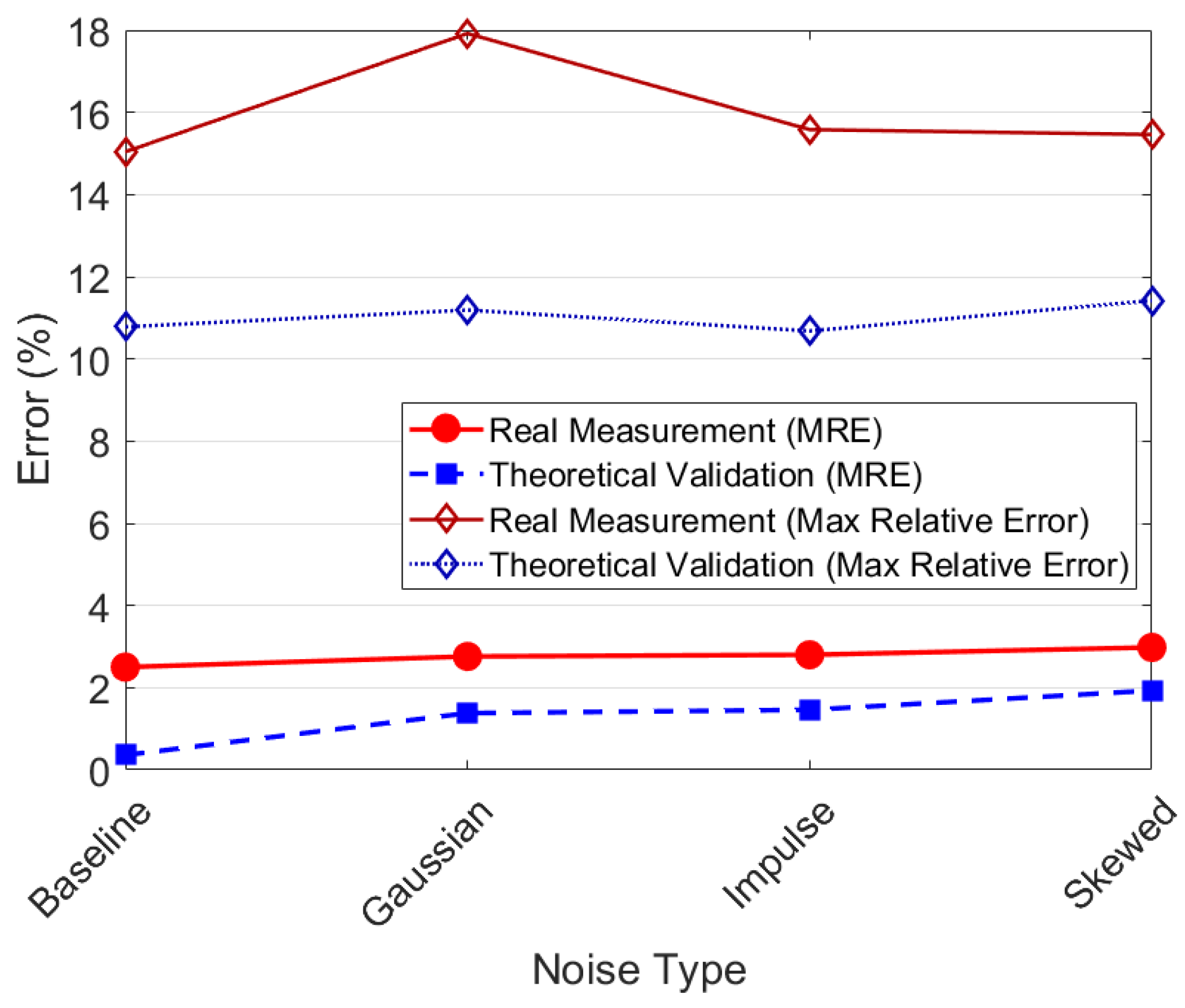
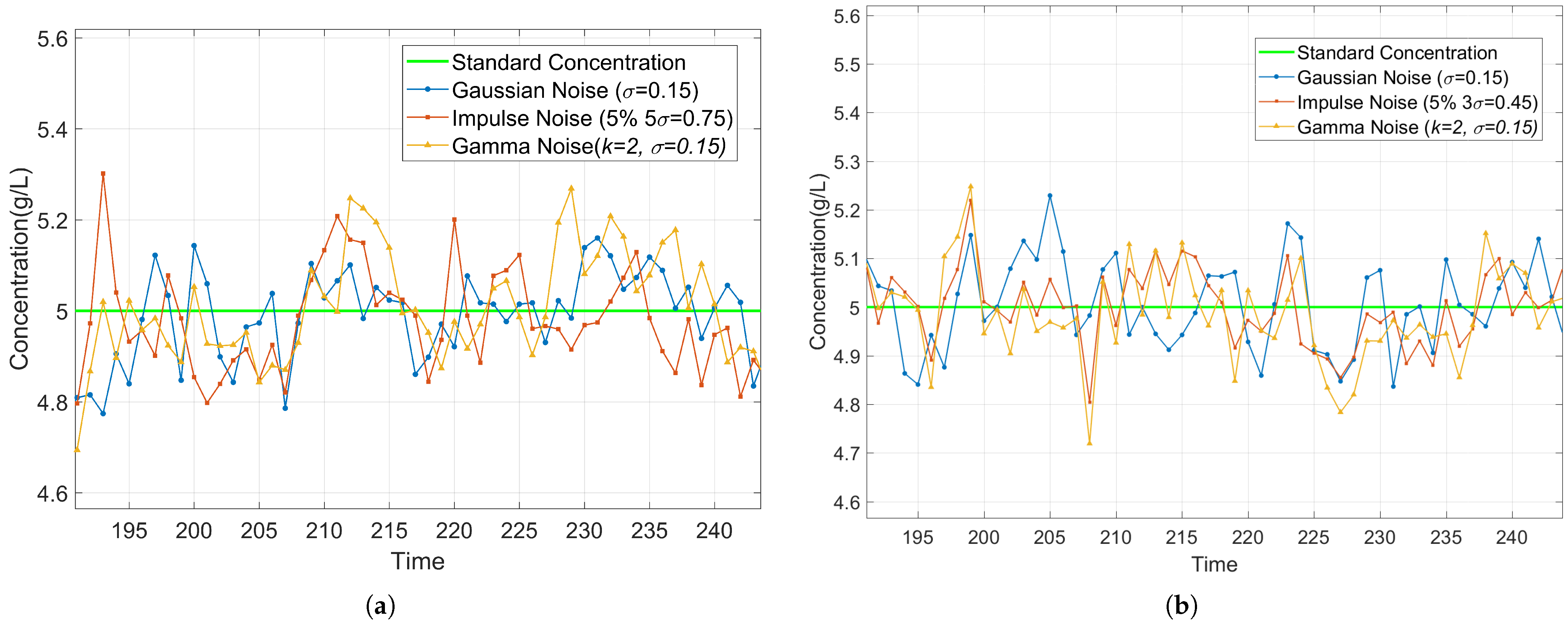
3.5.1. Robustness Analysis Under Noise Conditions
3.5.2. Computational Efficiency Comparison
4. Discussion
4.1. Discussion of Experimental Findings
4.2. Practical Considerations and Future Improvements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woolard, C.; Irvine, R. Treatment of hypersaline wastewater in the sequencing batch reactor. Water Res. 1995, 29, 1159–1168. [Google Scholar] [CrossRef]
- Smythe, G.; Matelli, G.; Bradford, M.; Rocha, C. Biological treatment of salty wastewater. Environ. Prog. 2006, 16, 179–183. [Google Scholar] [CrossRef]
- Wen, Z.; Wolfs, K.; Van Schepdael, A.; Adams, E. Determination of Inorganic Ions in Parenteral Nutrition Solutions by Ion Chromatography. Molecules 2022, 27, 5266. [Google Scholar] [CrossRef] [PubMed]
- Grabarczyk, M.; Wlazlowska, E.; Fialek, M. Electrochemical Methods for the Analysis of Trace Tin Concentrations—Review. Materials 2023, 16, 7545. [Google Scholar] [CrossRef]
- Ma, L.; Xiong, H.; Zhang, F. Prediction of Major Ions in Soil Salinity Based on Field VIS-NIR Spectroscopy. Soil 2020, 52, 188–194. [Google Scholar]
- Mutunga, T.; Sinanovic, S.; Harrison, C. A Wireless Network for Monitoring Pesticides in Groundwater: An Inclusive Approach for a Vulnerable Kenyan Population. Sensors 2024, 24, 4665. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.A.; Jiao, G.; Dang, P.; Nie, G.; Liu, Z.; Sun, J. Review of Wireless RFID Strain Sensing Technology in Structural Health Monitoring. Sensors 2023, 23, 6925. [Google Scholar] [CrossRef]
- Zhou, S.; Sheng, W.; Deng, F.; Wu, X.; Fu, Z. A Novel Passive Wireless Sensing Method for Concrete Chloride Ion Concentration Monitoring. Sensors 2017, 17, 2871. [Google Scholar] [CrossRef]
- Makarovaite, V.; Hillier, A.J.R.; Holder, S.J.; Gourlay, C.W.; Batchelor, J.C. Passive Wireless UHF RFID Antenna Label for Sensing Dielectric Properties of Aqueous and Organic Liquids. IEEE Sens. J. 2019, 19, 4299–4307. [Google Scholar] [CrossRef]
- Qian, X.; Li, Z.; Meng, Z.; Gao, N.; Zhang, Z. Flexible RFID Tag for Sensing the Total Minerals in Drinking Water via Smartphone Tapping. IEEE Sens. J. 2021, 21, 24749–24758. [Google Scholar] [CrossRef]
- Ye, F.; Mao, Y.; Li, Y.; Liu, X. Target threat estimation based on discrete dynamic Bayesian networks with small samples. J. Syst. Eng. Electron. 2022, 33, 1135–1142. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An Adaptive Particle Filter Technique for System State Estimation and Prognosis. IEEE Trans. Instrum. Meas. 2020, 69, 6756–6765. [Google Scholar] [CrossRef]
- Han, J.; Ding, Q.; Xiong, A.; Zhao, X. A State-Space EMG Model for the Estimation of Continuous Joint Movements. IEEE Trans. Ind. Electron. 2015, 62, 4267–4275. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach To Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82D, 35–45. [Google Scholar] [CrossRef]
- Huang, Z.; Gao, F.; Huang, W. Sensitive Probes for Capacitive Sensors. Instrum. Technol. Sens. 1996, 5, 14–16+23. [Google Scholar]
- Xie, S.; Ma, C.; Feng, R.; Xiang, X.; Jiang, P. Wireless Glucose Sensing System Based on Dual-Tag RFID Technology. IEEE Sens. J. 2022, 22, 13632–13639. [Google Scholar] [CrossRef]
- Hench, L.L.; West, J.K. Principles of Electronic Ceramics; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Ting, C.; Glenn, H.; Richard, B. Dielectric Spectroscopy of Aqueous Solutions of KCl and CsCl. ChemInform 2003, 107, 4025–4031. [Google Scholar]
- Buchner, R.; Hefter, G.T.; May, P.M. Dielectric Relaxation of Aqueous NaCl Solutions. J. Phys. Chem. A 1999, 103, 1–9. [Google Scholar] [CrossRef]
- Gulich, R.; Köhler, M.; Lunkenheimer, P.; Loidl, A. Dielectric spectroscopy on aqueous electrolytic solutions. Radiat. Environ. Biophys. 2009, 48, 107–114. [Google Scholar] [CrossRef]
- Zeng, N.; Li, J.; Igbe, T.; Liu, Y.; Yan, C.; Nie, Z. Investigation on Dielectric Properties of Glucose Aqueous Solutions at 500 KHz–5 MHz for Noninvasive Blood Glucose Monitoring. In Proceedings of the 2018 IEEE 20th International Conference on e-Health Networking, Applications and Services (Healthcom), Ostrava, Czech Republic, 17–20 September 2018; pp. 1–5. [Google Scholar]
- Wu, Z.; Zhou, T.; Li, L.; Chen, L.; Ma, Y. A New Modified Efficient Levenberg–Marquardt Method for Solving Systems of Nonlinear Equations. Math. Probl. Eng. 2021, 2021, 5608195. [Google Scholar] [CrossRef]
- Wu, H. High Salt Chemical Wastewater Treatment Process and Parameter Optimization of Research. Master’s Thesis, South China University of Technology, Guangzhou, China, 2010. [Google Scholar]
- Gao, L. The Study on Effects of Salt Content in Aquatic Products Processing Wastewater on the Treatment Efficiency of Contact Oxidation Process. Master’s Thesis, Qingdao Technological University, Qingdao, China, 2013. [Google Scholar]
- Liang, Q.; Jiang, L.; Zheng, J.; Duan, N. Determination of High Concentration Copper Ions Based on Ultraviolet—Visible Spectroscopy Combined with Partial Least Squares Regression Analysis. Processes 2024, 12, 1408. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, F.; Tan, C. Concentration Profile Measurement of Liquid–Solid Two-Phase Horizontal Pipe Flow Using Ultrasound Doppler. IEEE Trans. Instrum. Meas. 2023, 72, 7504109. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. Microwave-Based Microfluidic Sensor for Non-Destructive and Quantitative Glucose Monitoring in Aqueous Solution. Sensors 2016, 16, 1733. [Google Scholar] [CrossRef]


| Parameter | ||||
|---|---|---|---|---|
| 0.9980 | ||||
| 0.9974 | ||||
| (ns) | 0.9982 |
| Container | (mm) | (mm) |
|---|---|---|
| Glass Cylinder No. 1 | 12.45 | 10.9 |
| Glass Cylinder No. 2 | 21 | 19 |
| Plastic Cylinder No. 3 | 28 | 25 |
| Plastic Cylinder No. 4 | 36 | 34 |
| Standard Concentration (mg/L) | Preparation Error (%) | Average Estimated Concentration (mg/L) | Standard Deviation of Estimated Concentration (mg/L) | MRE (%) |
|---|---|---|---|---|
| 2000 | 0.50 | 2015.7 | 193.5 | 6.13 |
| 3000 | 0.33 | 2958.3 | 83.9 | 2.44 |
| 4000 | 0.25 | 4061.7 | 115.3 | 2.71 |
| 5000 | 0.14 | 4966.1 | 94.0 | 1.65 |
| 6000 | 0.12 | 6006.7 | 136.8 | 1.71 |
| 7000 | 0.14 | 6997.6 | 102.4 | 1.19 |
| 8000 | 0.12 | 7968.4 | 161.0 | 1.67 |
| 9000 | 0.11 | 8953.6 | 467.5 | 4.16 |
| 10,000 | 0.10 | 9996.9 | 467.4 | 3.51 |
| Algorithm | MRE (%) | Execution Time (ms) |
|---|---|---|
| AEKF | 2.50 | 151.35 |
| UKF | 2.70 | 293.36 |
| PF | 2.58 | 2018.37 |
| Method | Solutions | Concentration | Performance | Real-Time |
|---|---|---|---|---|
| [26] (UV-Vis) | Water/Cu2+ | 0.1–7.7 g/L | MRE = 0.63% | No |
| [27] (Ultrasound) | Water/Solid | 0.21–1.24% (Volume) | MAE = 2.72–6.85% | Yes |
| [28] (Microwave) | Water/Glucose | 0.3–80 g/L | Resolution = 0.4 g/L | Yes |
| This work (RFID) | Water/CaCl2 | 2–10 g/L | MRE = 2.80% | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, R.; Lin, X. RFID-Based Real-Time Salt Concentration Monitoring with Adaptive EKF. Sensors 2025, 25, 3826. https://doi.org/10.3390/s25123826
Feng R, Lin X. RFID-Based Real-Time Salt Concentration Monitoring with Adaptive EKF. Sensors. 2025; 25(12):3826. https://doi.org/10.3390/s25123826
Chicago/Turabian StyleFeng, Renhai, and Xinyi Lin. 2025. "RFID-Based Real-Time Salt Concentration Monitoring with Adaptive EKF" Sensors 25, no. 12: 3826. https://doi.org/10.3390/s25123826
APA StyleFeng, R., & Lin, X. (2025). RFID-Based Real-Time Salt Concentration Monitoring with Adaptive EKF. Sensors, 25(12), 3826. https://doi.org/10.3390/s25123826






