Autogenetic Gravity Center Placement
Abstract
Highlights
What are the main findings?
- Real-time inertia identification proved very rapid (in fractions of a second).
- Autogenetic mass center location was also rapid, resolving in mere seconds.
- Relatively poor (decimal-degree-to-single-degree accuracy) state estimation was necessary.
What is the implication of the main finding?
- The validated novel method produces larger convergence than the modern comparative benchmark method.
- The modern comparative benchmark method was considerably slower.
- Dynamic space operations, like refueling, repair, grappling, and manipulation, are enhanced.
Abstract
1. Introduction
1.1. How Conventional Methods Measure the Center of Mass Position and Inertia Parameters
1.2. Required Input Conditions
1.3. Specific Implementation Approaches
1.4. Existing Limitations
2. Materials and Methods
2.1. Autonomous Control by Adopting Governing Kinetics as the Control
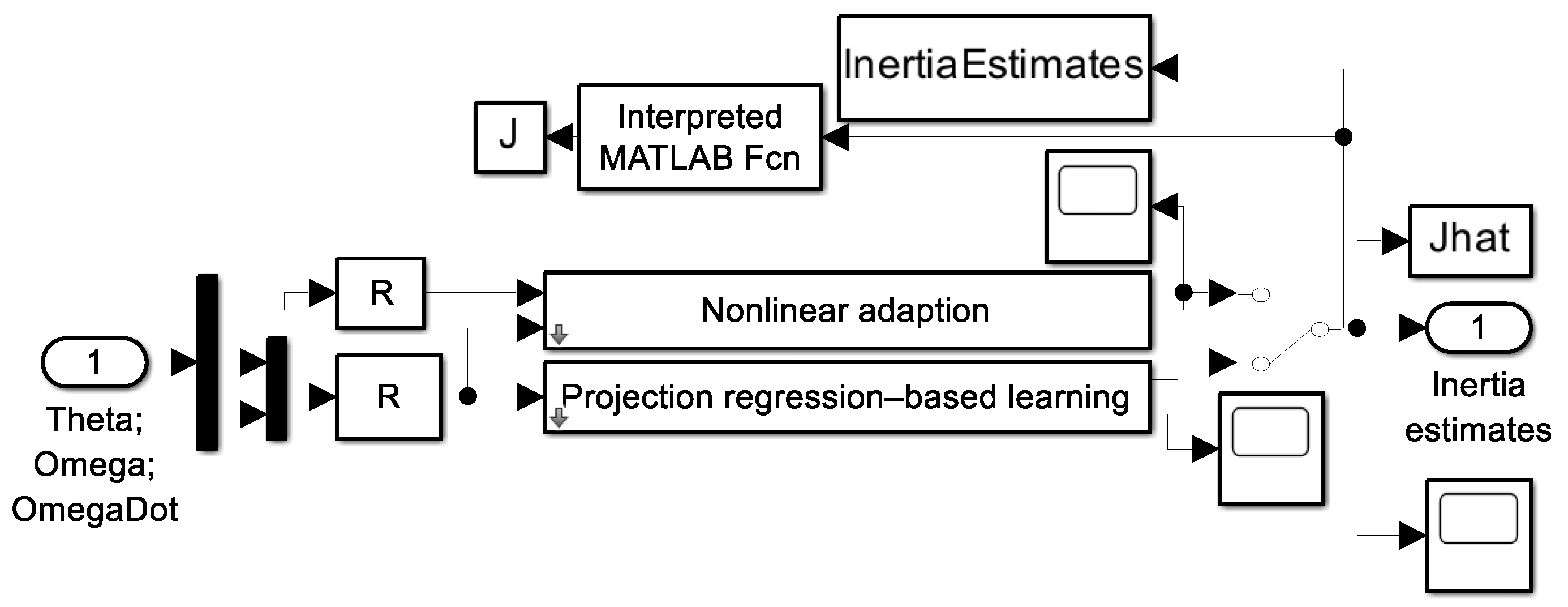
2.2. Autonomous Inertia Identification Using Projection-Based Learning
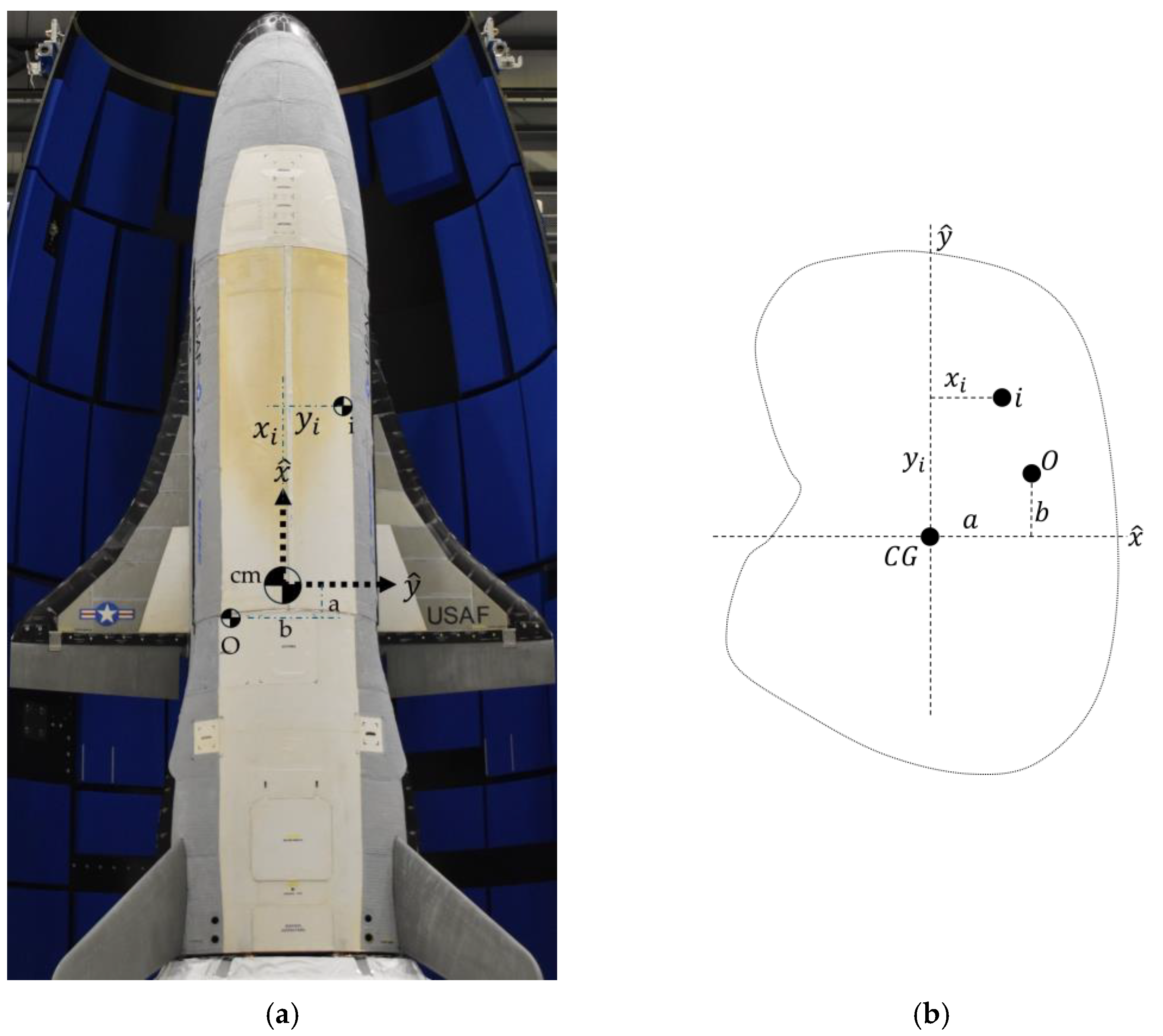
2.3. Center of Gravity Auto-Location Parameterized by the Parallel Axis Theorem
2.4. Pseudocode Summarizing the Auto-Location Algorithm
- Adopt the governing kinetics as the control.
- Formulate the controlled kinetics into exact regression parameterization.
- Invert the control expressed in regression form, isolating the inertia matrix components (both moments and cross-products).
- Use angular velocity and angular acceleration estimates from nonlinear Luenberger observers to solve for the inertia matrix components (both moments and cross-products).
- Expand the parallel axis theorem, solving three equations for three unknown position coordinates of the center of gravity parameterized in the off-diagonal inertia cross products alone.
- Use the off-diagonal inertia cross products alone for the auto-location of the center of gravity at every timestep.
3. Results
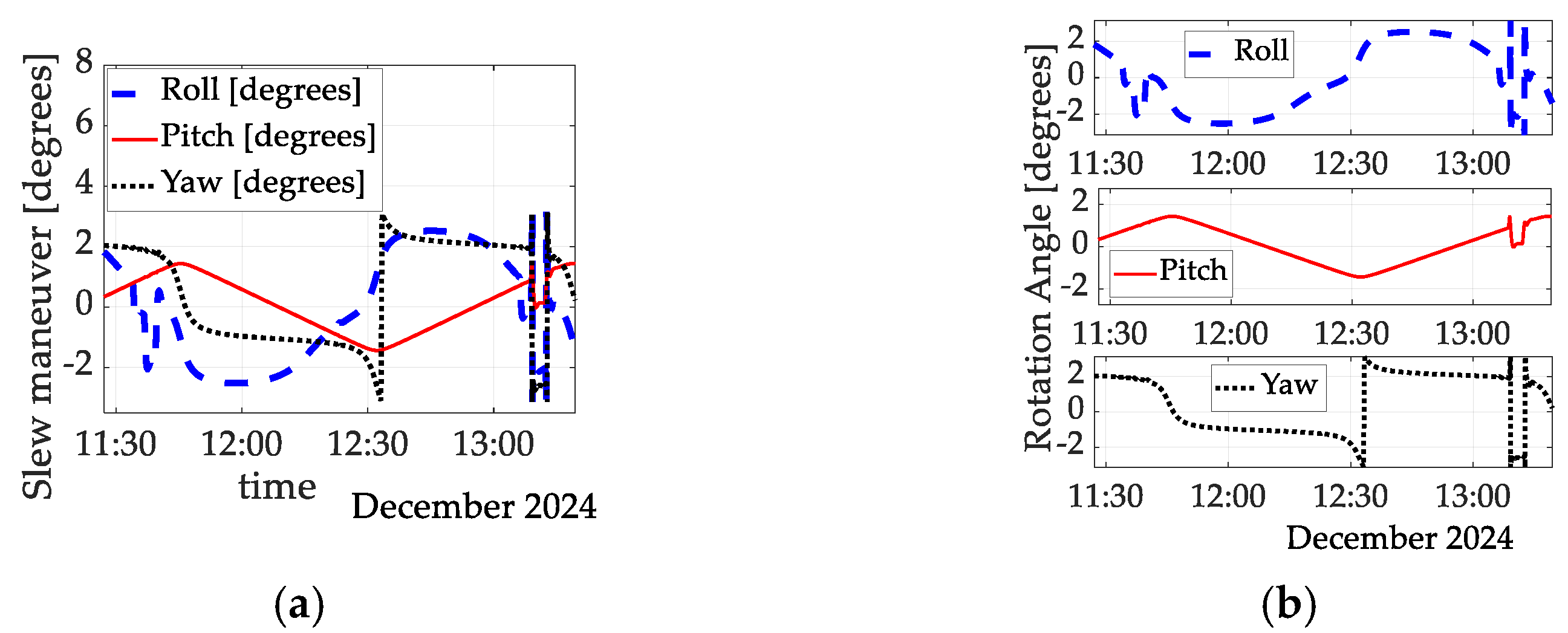
3.1. Spaceflight Test Maneuvers
3.2. Inertia Identification
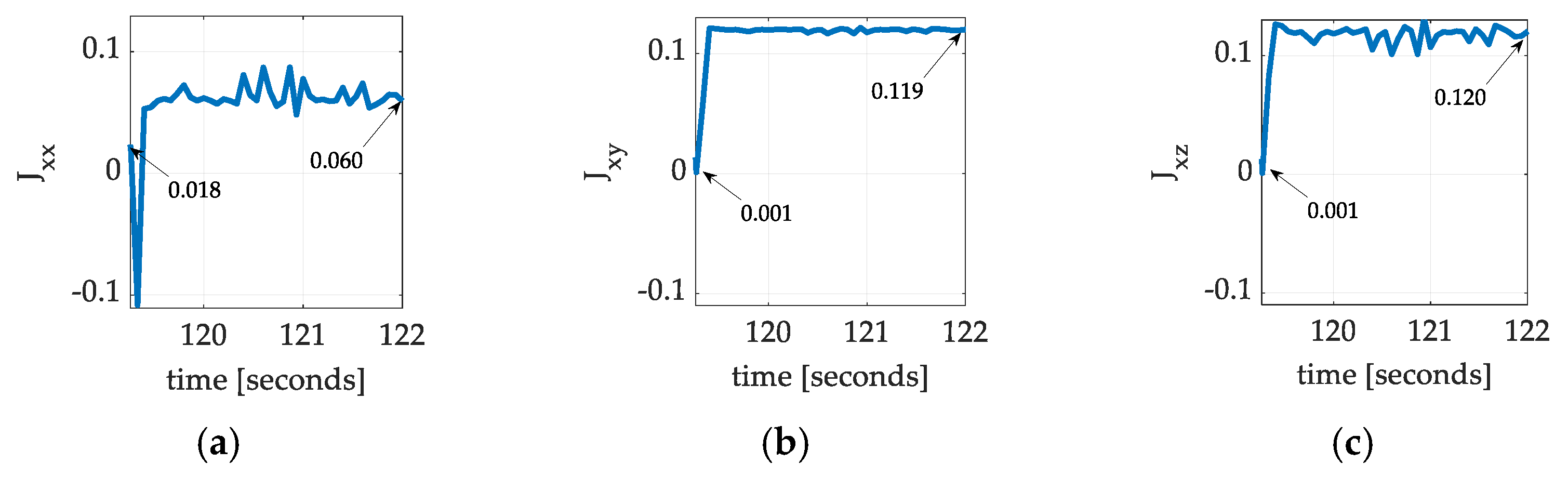
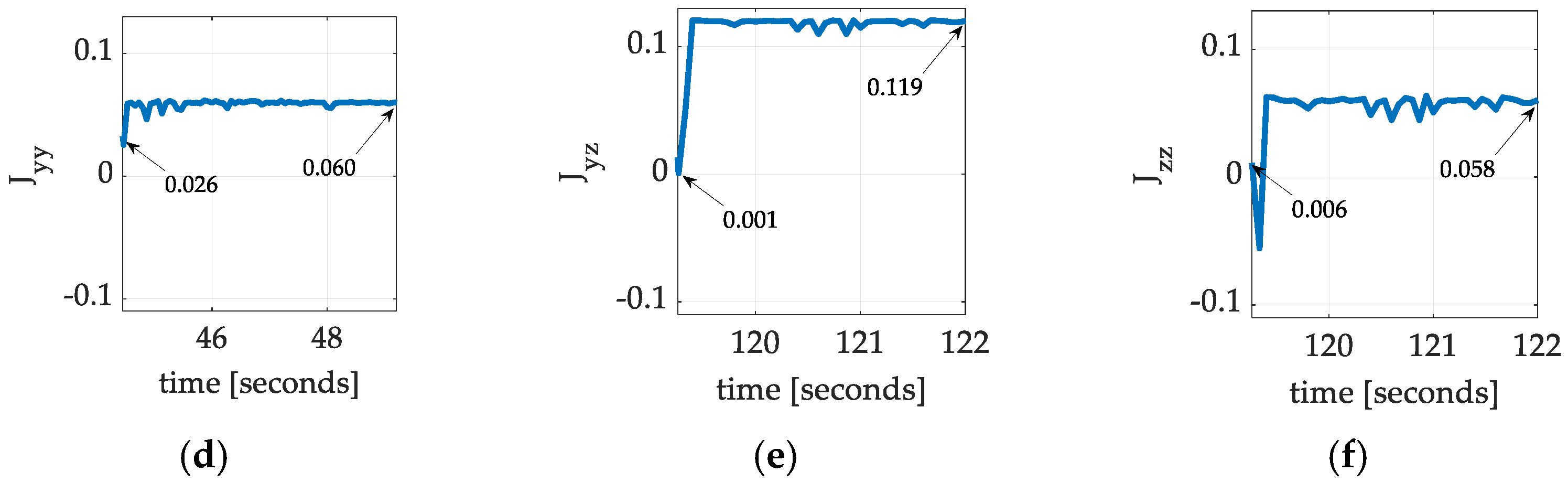
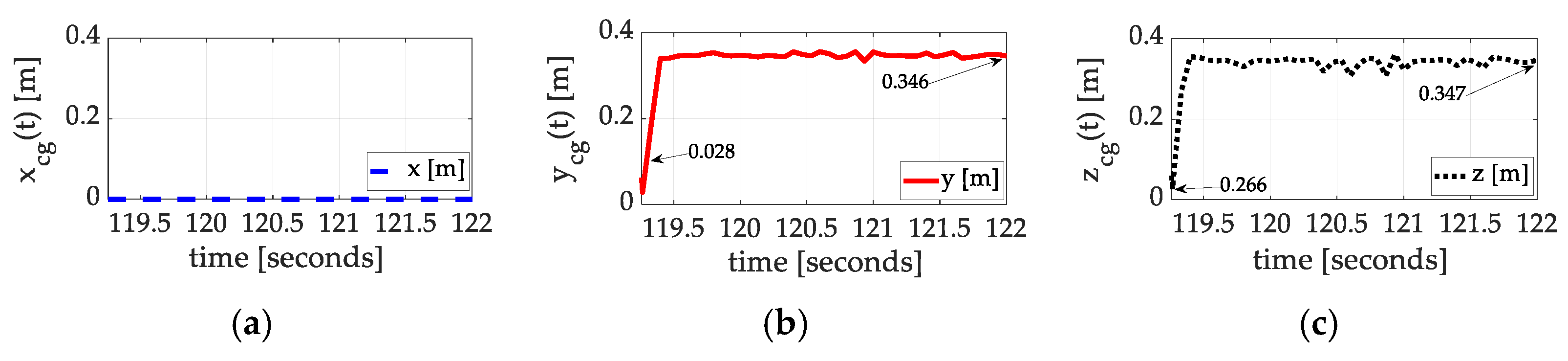
3.3. Center of Gravity Auto-Location
4. Discussion
Recommended Future Research
- Improved nonlinear state estimation (analytic study).
- Performance in response to grappling unknown objects.
- Investigate converged values’ reliability using Monte Carlo analysis and simulations.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NASA | National Aeronautics and Space Administration |
| MATLAB | Matrix Laboratory |
| MOST | Microvariability and Oscillations of Stars/Microvariabilité et Oscillations STellaire |
| LAGEOS | LAser GEOdynamic Satellite |
| RSAT–P | Repair Satellite-Prototype |
| USNA–19 | Nineteenth satellite of United States Naval Academy small satellite program |
| ELaNa XIX | Educational Launch of Nanosatellites 19 |
Appendix A
Appendix A.1
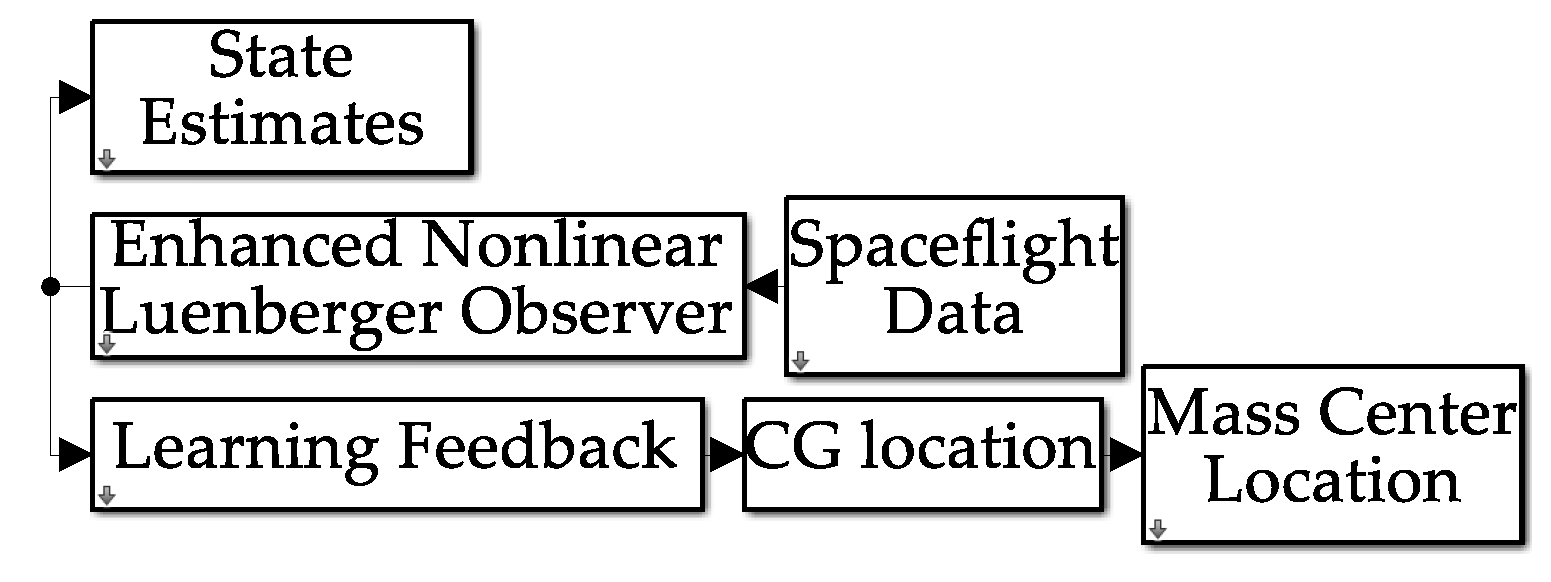

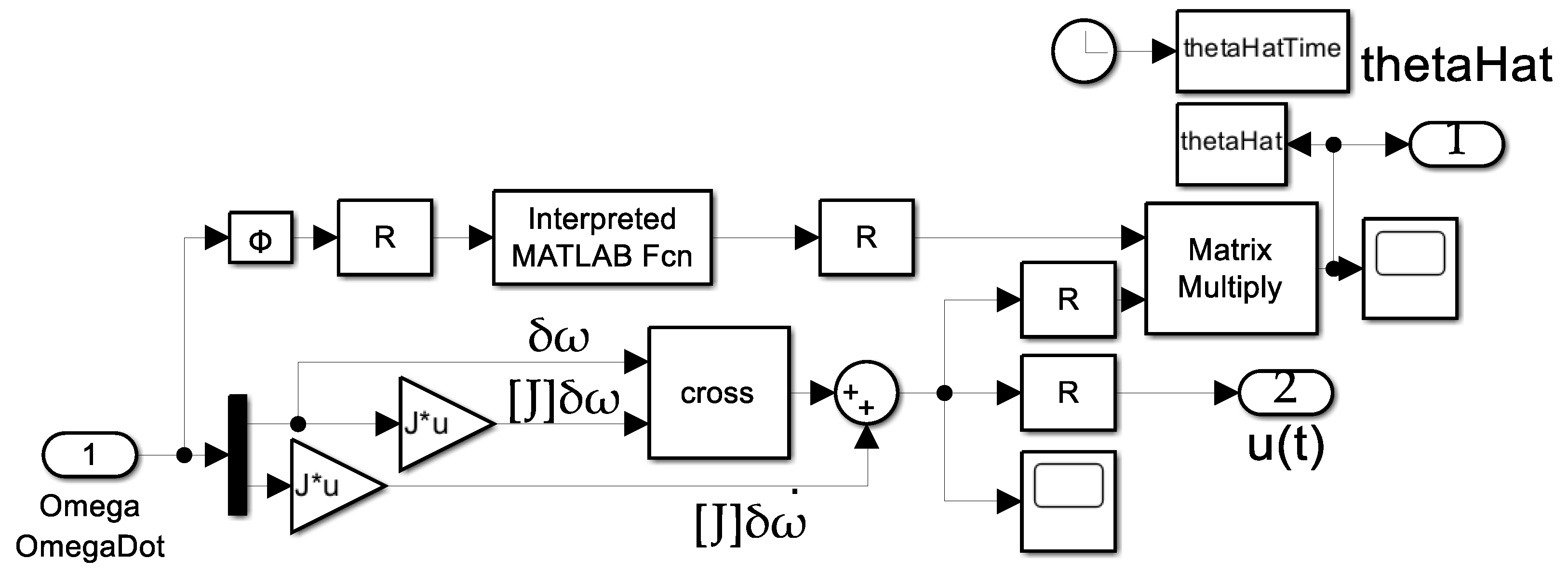
Appendix B
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Angular velocity [radians/second] | Moments of inertia | ||
| Unit vectors | Products of inertia | ||
| Positional coordinates | Moment of inertia matrix |
References
- Herritage, T. (Secretary of the Air Force Public Affairs). X-37B Begins Novel Space Maneuver. Available online: https://www.spaceforce.mil/News/Article-Display/Article/3932137/x-37b-begins-novel-space-maneuver/ (accessed on 6 February 2025).
- Air Force X-37B Space Plane Returns to Earth. Composite Magazine, 15 May 2017. Available online: https://acmanet.org/air-force-x-37b-space-plane-returns-earth/ (accessed on 6 February 2025).
- Goecker, J. Inside Boeing’s X-37B Space Plane Conducting Secret Missions for the U.S. Available online: https://pari.purdue.edu/blog/2024/01/12/inside-boeings-x-37b-space-plane-conducting-secret-missions-for-the-u-s/ (accessed on 6 February 2025).
- Mian, S.; Garrett, T.; Glandon, A.; Manderino, C.; Balachandran, S.; Muñoz, C.; Dolph, C. Autonomous Spacecraft Inspection with Free-Flying Drones. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Available online: https://www.af.mil/News/Article-Display/Article/114795/x-37b-orbital-test-vehicle-lands-at-vandenberg-afb/ (accessed on 6 February 2025).
- Available online: https://www.spaceforce.mil/News/Article/3217077/x-37b-orbital-test-vehicle-concludes-sixth-successful-mission/ (accessed on 6 February 2025).
- Department of Defense Photographs and Imagery, Unless Otherwise Noted, Are in the Public Domain. Use of Department of Defense Imagery. Available online: https://www.defense.gov/Contact/Help-Center/Article/Article/2762906/use-of-department-of-defense-imagery/ (accessed on 12 June 2025).
- Modernized Selected Acquisition Report (MSAR) MQ-25 Stingray (MQ-25), FY 2025 President’s Budget. Department of Defense Document MSAR. 31 December 2023. Available online: https://www.esd.whs.mil/Portals/54/Documents/FOID/Reading%20Room/Selected_Acquisition_Reports/FY_2023_SARS/MQ-25%20MSAR%20Dec%202023.pdf (accessed on 6 February 2025).
- Available online: https://www.nasa.gov/robonaut2/ (accessed on 6 February 2025).
- Available online: https://www.nasa.gov/podcasts/houston-we-have-a-podcast/valkyrie/ (accessed on 6 February 2025).
- NASA Images and Media Usage Guidelines. NASA Content—Images, Audio, Video, and Media Files Used in the Rendition of 3-Dimensional Models, Such as Texture Maps and Polygon Data in Any Format—Generally Are Not Subject to Copyright in the United States. Available online: https://www.nasa.gov/nasa-brand-center/images-and-media/ (accessed on 6 February 2025).
- Available online: https://www.flickr.com/photos/nasa_goddard/8379612361/in/album-72157626998686813 (accessed on 6 February 2025).
- Available online: https://www.flickr.com/photos/nasa_goddard/8380692496/in/album-72157626998686813 (accessed on 6 February 2025).
- Available online: https://svs.gsfc.nasa.gov/10988/ (accessed on 6 February 2025).
- Izzo, D.; Märtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2022, 6, 441–443. [Google Scholar] [CrossRef]
- Kyuroson, A.; Banerjee, A.; Tafanidis, N.; Satpute, S.; Nikolakopoulos, G. Towards fully autonomous orbit management for low-earth orbit satellites based on neuro-evolutionary algorithms and deep reinforcement learning. Eur. J. Con. 2024, 80, 101052. [Google Scholar] [CrossRef]
- Ferguson, P. On-Orbit Spacecraft Inertia and Rate Sensor Scale Factor Estimation for Microsatellites. In Proceedings of the 22nd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 11–14 August 2007. [Google Scholar]
- Rucinski, S.; Carroll, K.; Kuschnig, R.; Matthews, J. MOST (Microvariability & Oscillations of STars) Canadian astronomical micro-satellite. Adv. Space Res. 2003, 31, 371–373. [Google Scholar]
- Gu, Y.; Huang, F.; Huang, J.; Yuan, H.; Yu, B.; Gao, C. Filling the gap between GRACE and GRACE follow-on observations based on principal component analysis. Geo. J. Inter. 2024, 236, 1216–1233. [Google Scholar]
- Visco, M.; Lucchesi, D. Review and critical analysis of mass and moments of inertia of the LAGEOS and LAGEOS II satellites for the LARASE program. Adv. Space Res. 2016, 57, 1928–1938. [Google Scholar] [CrossRef]
- Shao, K.; Zicong, A. Precise multi-satellite orbit and geodetic parameter determination using satellite laser ranging observations from LAGEOS, Etalon and newly launched LARES-2. Meas. Sci. Tech. 2025, 36, 026319. [Google Scholar] [CrossRef]
- Kornfeld, R.; Arnold, B.; Gross, M.; Dahya, N.; Klipstein, W.; Gath, P.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Space. Roc. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Pan, Z.; Xiao, Y. Data Quality Assessment of Gravity Recovery and Climate Experiment Follow-On Accelerometer. Sensors 2024, 24, 4286. [Google Scholar] [CrossRef] [PubMed]
- Bender, P.; Conklin, J.; Wiese, D. Short-period mass variations and the next generation gravity mission. J. Geo. Res. Solid Earth 2025, 130, e2024JB030290. [Google Scholar] [CrossRef]
- Huang, Z.; Li, S.; Cai, L.; Fan, D.; Huang, L. Estimation of the Center of Mass of GRACE-Type Gravity Satellites. Remote Sens. 2022, 14, 4030. [Google Scholar] [CrossRef]
- Available online: https://media.defense.gov/2020/May/06/2002295322/-1/-1/0/200506-F-XX000-0004.JPG (accessed on 11 February 2025).
- Available online: https://www.usna.edu/Users/aero/kang/Research.php#panel3RSatPRoboticArmSatellitePrototype (accessed on 6 February 2025).
- Luenberger Observer. Available online: https://www.mathworks.com/help/sps/ref/luenbergerobserver.html (accessed on 6 February 2025).
- Zhu, Z.; Wang, Y.; Wang, Y.; Jing, X. Nonlinear inertia and its effect within an X-shaped mechanism—Part I: Modelling & nonlinear properties. Mech. Sys. Sig. Proc. 2023, 200, 110590. [Google Scholar]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators With Swift Arm Motions. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025. AIAA 2025-1809. [Google Scholar] [CrossRef]
- Sands, T. Flattening the Curve of Flexible Space Robotics. Appl. Sci. 2022, 12, 2992. [Google Scholar] [CrossRef]
- Sands, T. Bio-Inspired Space Robotic Control Compared to Alternatives. Biomimetics 2024, 9, 108. [Google Scholar] [CrossRef] [PubMed]
- Sands, T. Autonomous Real–Time Mass Center Location and Inertia Identification for Grappling Space Robotics. Technologies 2025, 13, 148. [Google Scholar] [CrossRef]
- Adams, G. Arizona State University Physics Department Proof of the Parallel Axis Theorem. Available online: https://www.public.asu.edu/~gbadams/sum00/parallelaxisT.pdf (accessed on 19 November 2024).







| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Inertia matrix or tensor | Moment of inertia about | ||
| Angular acceleration | inertia product | ||
| Angular velocity | inertia product | ||
| Angular acceleration in the -direction | Moment of inertia about | ||
| Angular acceleration in the -direction | inertia product | ||
| Angular acceleration in the -direction | Moment of inertia about | ||
| Regression matrix of knowns | Unknown, predicted variables |
| Variable/Acronym | Definition | Variable/Acronym | Definition |
|---|---|---|---|
| Desired angular velocity about | Desired angular acceleration about | ||
| Desired angular velocity about | Desired angular acceleration about | ||
| Desired angular velocity about | Desired angular acceleration about | ||
| Regression matrix of sensor data | Regression matrix of desired states | ||
| Unknown, predicted variables | Estimated variables | ||
| Total control signal | Feedforward control signal | ||
| Estimated Moment of inertia about | Estimated inertia product | ||
| Estimated Moment of inertia about | Estimated inertia product | ||
| Estimated Moment of inertia about | Estimated inertia product |
| Inertia Component | Initial Guess | Converged Value | Percent Change |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0.028 | 0.346 | 1136% | |
| 0.266 | 0.347 | 30% |
| Inertia Component | Initial Guess | Converged Value | Percent Change |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0.015 | 0.347 | 2213% | |
| 0.015 | 0.346 | 2207% |
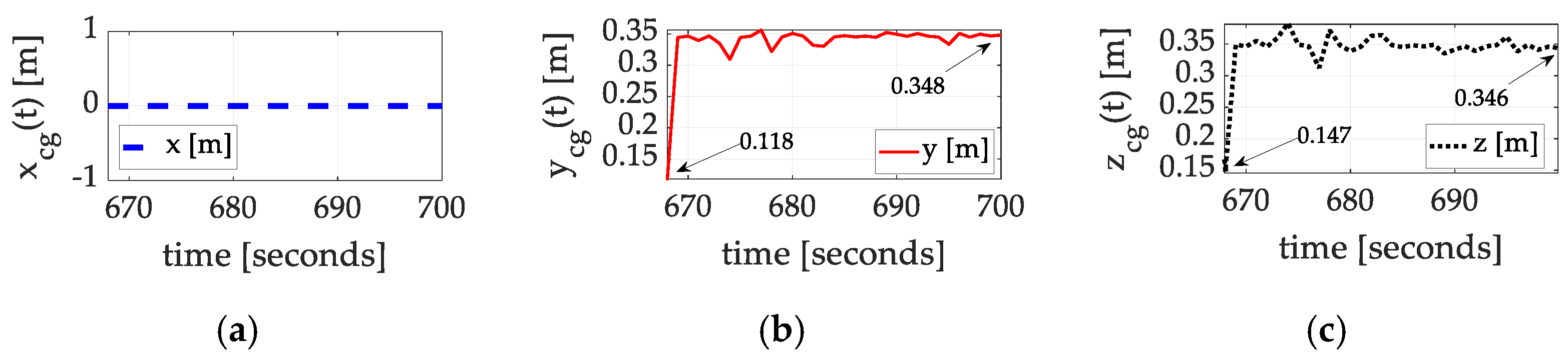
| Inertia Component | Initial Guess | Converged Value | Percent Change |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0.118 | 0.348 | 195% | |
| 0.147 | 0.346 | 135% |
| Parameter | Convergence Percentage | Converged Value | Convergence Time [Seconds] |
|---|---|---|---|
| 233% | 0.060 | 3 | |
| 11,800% | 0.119 | ||
| 11,900% | 0.120 | ||
| 131% | 0.060 | ||
| 11,800% | 0.119 | ||
| 867% | 0.058 | ||
| Space test #1 | 0 | 0 | |
| Space test #1 | 1136% | 0.347 | |
| Space test #1 | 30% | 0.346 | |
| Space test #2 | 0 | 0 | 7 |
| Space test #2 | 2213% | 0.347 | |
| Space test #2 | 2207% | 0.346 | |
| Space test #3 | 0% | 0 | 32 |
| Space test #3 | 2213% | 0.347 | |
| Space test #3 | 2207% | 0.346 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sands, T. Autogenetic Gravity Center Placement. Sensors 2025, 25, 3786. https://doi.org/10.3390/s25123786
Sands T. Autogenetic Gravity Center Placement. Sensors. 2025; 25(12):3786. https://doi.org/10.3390/s25123786
Chicago/Turabian StyleSands, Timothy. 2025. "Autogenetic Gravity Center Placement" Sensors 25, no. 12: 3786. https://doi.org/10.3390/s25123786
APA StyleSands, T. (2025). Autogenetic Gravity Center Placement. Sensors, 25(12), 3786. https://doi.org/10.3390/s25123786







