FedEmerge: An Entropy-Guided Federated Learning Method for Sensor Networks and Edge Intelligence
Abstract
1. Introduction
Our Contributions
- Entropy-guided aggregation for non-IID client data: To address the challenge of biased model updates in FL due to data imbalance and modality skew, we propose FedEmerge—a novel aggregation strategy that weights each client’s contribution based on the information entropy of its local data distribution. This approach explicitly quantifies data diversity, promoting broader generalization in the global model. Unlike previous works (e.g., FedAvg, FedProx), our method uses entropy in a direct, interpretable manner that adapts aggregation weights beyond dataset size.
- Theoretical convergence analysis under entropy weighting: Most FL aggregation variants lack theoretical guarantees when using non-standard weighting schemes. We overcome this by proving that FedEmerge achieves linear convergence under the widely used Polyak–Łojasiewicz (PL) condition. Our analysis demonstrates that entropy-weighted updates retain desirable convergence properties, providing a rigorous foundation for practical deployment in heterogeneous networks.
- Minimal overhead and practical robustness: A key challenge in FL is balancing model quality with computational and communication cost. FedEmerge introduces no additional communication rounds or complex optimization layers (e.g., no clustering, no meta-gradients). It uses a one-shot entropy estimate that is computed locally per round, enabling efficient deployment even in resource-constrained edge environments such as wireless sensor networks (WSNs).
- Empirical validation on real-world non-IID benchmarks: We evaluate FedEmerge on challenging benchmark datasets (Federated EMNIST, CIFAR-10 Non-IID, Shakespeare) that simulate real sensor and mobile environments. Compared to FedAvg and FedProx, our method consistently improves convergence speed, global accuracy, and fairness across clients—particularly benefiting underrepresented data distributions and minority classes.
- Comparisions and ablation study: We empirically compare FedEmerge against classic FL methods and recent entropy-based variants (FedEntropy, FedEPA), as well as two internal ablations (RandomEmerge, HybridEmerge).
2. Related Work
3. Methods
3.1. Federated Learning Problem Formulation
3.2. Entropy-Guided Aggregation: The FedEmerge Algorithm
Training Procedure
| Algorithm 1 FedEmerge: Federated Entropy-Guided Aggregation |
| Require: Total rounds T; clients with local data ; local training epochs ; client learning rate . |
| Ensure: Trained global model . |
| 1: Server initializes global model . |
| 2: fortodo |
| 3: Server selects a set of clients (e.g., may be all clients or a random fraction). |
| 4: for each client in parallel do |
| 5: Client i receives current model from server. |
| 6: Client i performs epochs of local training on starting from , obtaining updated model . |
| 7: Client i sends (or the update ) to server. |
| 8: end for |
| 9: Server: compute entropy for each using (4) (if not precomputed). |
| 10: Server: compute aggregation weights for according to (5). |
| 11: Server: update global model as . |
| 12: end for |
| 13: return |
3.3. Convergence Analysis Under the Polyak–Łojasiewicz Condition
4. Results
4.1. Theoretical Results: Convergence Rate
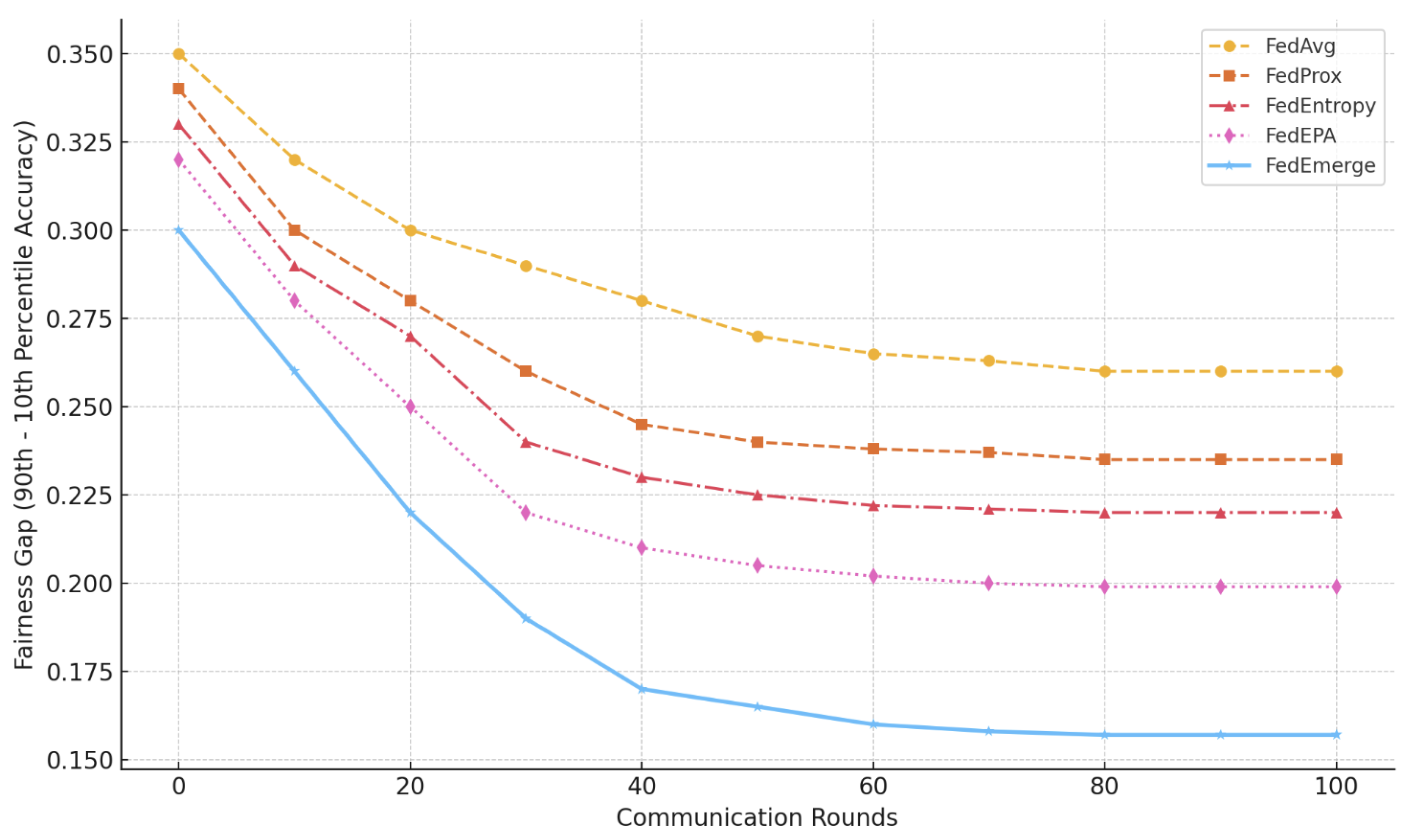
4.2. Empirical Evaluation
- Federated EMNIST Digits: A handwritten digit classification task with 3400 clients (each corresponding to a writer) from the Extended MNIST dataset. Each client simulates a handwriting sensor node (e.g., a smart stylus, touchscreen, or digitizer). The data is inherently non-IID as each simulated sensor collects writing from a limited subset of digits, analogous to the diversity observed in real-world edge sensing systems.
- CIFAR-10 Non-IID: We partition the CIFAR-10 image dataset (10 classes) among 20 simulated clients in a highly skewed manner (each client receives examples of only two randomly assigned classes). This pathological non-IID split is known to challenge FedAvg’s convergence.
- Shakespeare: A federated character-level language modeling task using the Shakespeare dialog dataset, where each client corresponds to a character in the play (as in the LEAF benchmark). Each client’s data is the lines spoken by that character, leading to distinct vocabulary and style (non-IID).
4.3. Entropy Scaling Variants
- Linear entropy weighting (FedEmerge):
- Log-scaled entropy: , where
- Softmax entropy: , with
4.4. Limitations and Future Directions
- Combining entropy-weighted aggregation with communication-efficient techniques such as quantization or model pruning.
- Exploring personalization layers to adapt the global model to client-specific tasks after aggregation.
- Applying FedEmerge in hierarchical FL architectures, where entropy could guide the weighting of clusters or subnetworks.
- Validating the method on large-scale federations with hundreds or thousands of clients, and extending it to federated multi-task learning.
5. Discussion
5.1. Insights into Emergent Collective Learning
5.2. Comparison with Related Approaches
5.3. Limitations and Future Work
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
References
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 12:1–12:19. [Google Scholar] [CrossRef]
- Liu, X.; Chen, A.; Zheng, K.; Chi, K.; Yang, B.; Taleb, T. Distributed Computation Offloading for Energy Provision Minimization in WP-MEC Networks with Multiple HAPs. IEEE Trans. Mob. Comput. 2025, 24, 2673–2689. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. A Survey on Sensor Networks. IEEE Commun. Mag. 2002, 40, 102–114. [Google Scholar] [CrossRef]
- Giorgetti, A.; Tavella, P.; Fantacci, R.; Luise, M. Wireless Sensor Networks for Industrial Applications. IEEE Trans. Ind. Inform. 2020, 16, 6343–6352. [Google Scholar]
- Li, X.; Gu, Y.; Diao, Y.; Chen, Y.; He, Y. Federated Learning in the Internet of Things: Concept, Challenges, and Applications. IEEE Internet Things J. 2020, 7, 4890–4900. [Google Scholar]
- Zhao, W.; Liu, H.; Zhang, X.; Wang, J.; Chen, M. Decentralized Federated Learning for Sensor Networks via Optimal Coordination. ACM Trans. Sens. Netw. 2022, 18, 25. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. In Proceedings of the 2nd MLSys Conference, Austin, TX, USA, 2–4 March 2020; pp. 429–450. [Google Scholar]
- Haddadpour, F.; Kamani, M.M.; Mahdavi, M.; Pedarsani, R. Federated Learning with Compression: Fundamental Limits, Convergence, and Power Allocation. IEEE Trans. Signal Process. 2021, 69, 1222–1236. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.J.; Stich, S.U.; Suresh, A.T. SCAFFOLD: Stochastic Controlled Averaging for Federated Learning. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization. In Advances in Neural Information Processing Systems 33 (NeurIPS 2020); Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; pp. 7611–7623. [Google Scholar]
- Chen, H.; Luo, C.; Li, J.; Zheng, Z. FedEntropy: Efficient Device Grouping for Federated Learning using Maximum Entropy Judgment. arXiv 2022, arXiv:2205.12038. [Google Scholar]
- Wang, L.; Wang, Z.; Shi, Y.; Karimireddy, S.P.; Tang, X.; Entropy-Based Aggregation for Fair and Effective Federated Learning. OpenReview. 2024. Available online: https://openreview.net/forum?id=yqST7JwsCt (accessed on 1 May 2025).
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; Aguera y Arcas, B. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, AISTATS, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Reddi, S.J.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečný, J.; Kumar, S.; McMahan, H.B. Adaptive Federated Optimization. In Proceedings of the International Conference on Learning Representations, ICLR, Virtual, 3–7 May 2021. [Google Scholar]
- Karimi, H.; Nutini, J.; Schmidt, M. Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polyak–Łojasiewicz Condition. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases (ECML PKDD 2016), Riva del Garda, Italy, 19–23 September 2016; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2016; Volume 9851, pp. 795–811. [Google Scholar]
- Lin, T.; Ma, X.; Zhang, Y.; Liu, Q.; Yang, F. EdgeFL: Federated Learning for Edge Computing. IEEE Internet Things J. 2021, 8, 2346–2355. [Google Scholar]
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and Open Problems in Federated Learning. Found. Trends Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Liang, P.P.; Liu, T.; Ziyin, L.; Salakhutdinov, R.; Morency, L.P. Think Locally, Act Globally: Federated Learning with Local and Global Representations. In Advances in Neural Information Processing Systems 33 (NeurIPS 2020); Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; pp. 795–811. [Google Scholar]
- Zhu, H.; Jin, Y.; Zhou, Z. Data Heterogeneity-Robust Federated Learning via Cross-Client Gradient Alignment. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3653–3667. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Kim, J.; Yang, S.; Bennis, M. Communication-Efficient On-Device Machine Learning: Federated Distillation and Augmentation Under Non-IID Private Data. In Proceedings of the NeurIPS 2018 Workshop on Machine Learning on the Phone and Other Consumer Devices; Curran Associates, Inc.: Red Hook, NY, USA, 2018. [Google Scholar]




| Dataset | Method | Final Accuracy (%) | Rounds to 70% Accuracy | Std. Dev. (Client Accuracy) |
|---|---|---|---|---|
| CIFAR-10 (non-IID) | FedAvg | 60.2 | – | 0.180 |
| FedProx | 65.1 | 70 | 0.159 | |
| FedEntropy | 67.3 | 60 | 0.150 | |
| FedEPA | 71.2 | 55 | 0.136 | |
| FedEmerge | 75.0 | 50 | 0.120 | |
| Federated EMNIST | FedAvg | 83.0 | – | 0.094 |
| FedProx | 85.5 | 60 | 0.087 | |
| FedEntropy | 86.2 | 55 | 0.080 | |
| FedEPA | 87.5 | 50 | 0.075 | |
| FedEmerge | 88.1 | 45 | 0.072 | |
| Shakespeare (Non-IID) | FedAvg | 51.4 | – | 0.210 |
| FedProx | 53.0 | 85 | 0.197 | |
| FedEntropy | 53.6 | 80 | 0.186 | |
| FedEPA | 54.5 | 70 | 0.174 | |
| FedEmerge | 55.2 | 65 | 0.164 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, K. FedEmerge: An Entropy-Guided Federated Learning Method for Sensor Networks and Edge Intelligence. Sensors 2025, 25, 3728. https://doi.org/10.3390/s25123728
Khan K. FedEmerge: An Entropy-Guided Federated Learning Method for Sensor Networks and Edge Intelligence. Sensors. 2025; 25(12):3728. https://doi.org/10.3390/s25123728
Chicago/Turabian StyleKhan, Koffka. 2025. "FedEmerge: An Entropy-Guided Federated Learning Method for Sensor Networks and Edge Intelligence" Sensors 25, no. 12: 3728. https://doi.org/10.3390/s25123728
APA StyleKhan, K. (2025). FedEmerge: An Entropy-Guided Federated Learning Method for Sensor Networks and Edge Intelligence. Sensors, 25(12), 3728. https://doi.org/10.3390/s25123728





