Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method
Abstract
1. Introduction
2. Methodology
2.1. ICEEMDAN
- 1.
- Join into to acquire :
- 2.
- and are calculated as follows:
- 3.
- Calculate :
- 4.
- and are acquired by repeating the second step:
- 5.
- Acquire and , for k = 3, …, k, as follows:
- 6.
- The preceding steps are repeated until the computation and decomposition are complete.
2.2. DFA
- 1.
- Obtain by processing as Equation (9). Then, divide it into length segments.
- 2.
- To obtain local trends in each segment , nonlinear fitting between extreme points is accomplished using least squares and kth order polynomials:
- 3.
- In each segment , remove the local trends, then average the squares of the outcome:
- 4.
- Obtain the second-order fluctuation function:
- 5.
- Change the length of the segments , then repeat steps 2, 3, and 4. The curve of the full-sequence fluctuation function can be obtained as follows:
- 6.
- Calculate the scaling exponent by
2.3. Improved Wavelet Threshold Denoising
2.4. The Proposed Method
3. Experiments and Analysis
3.1. The Proposed Method Evaluation
3.2. Stability Experiment
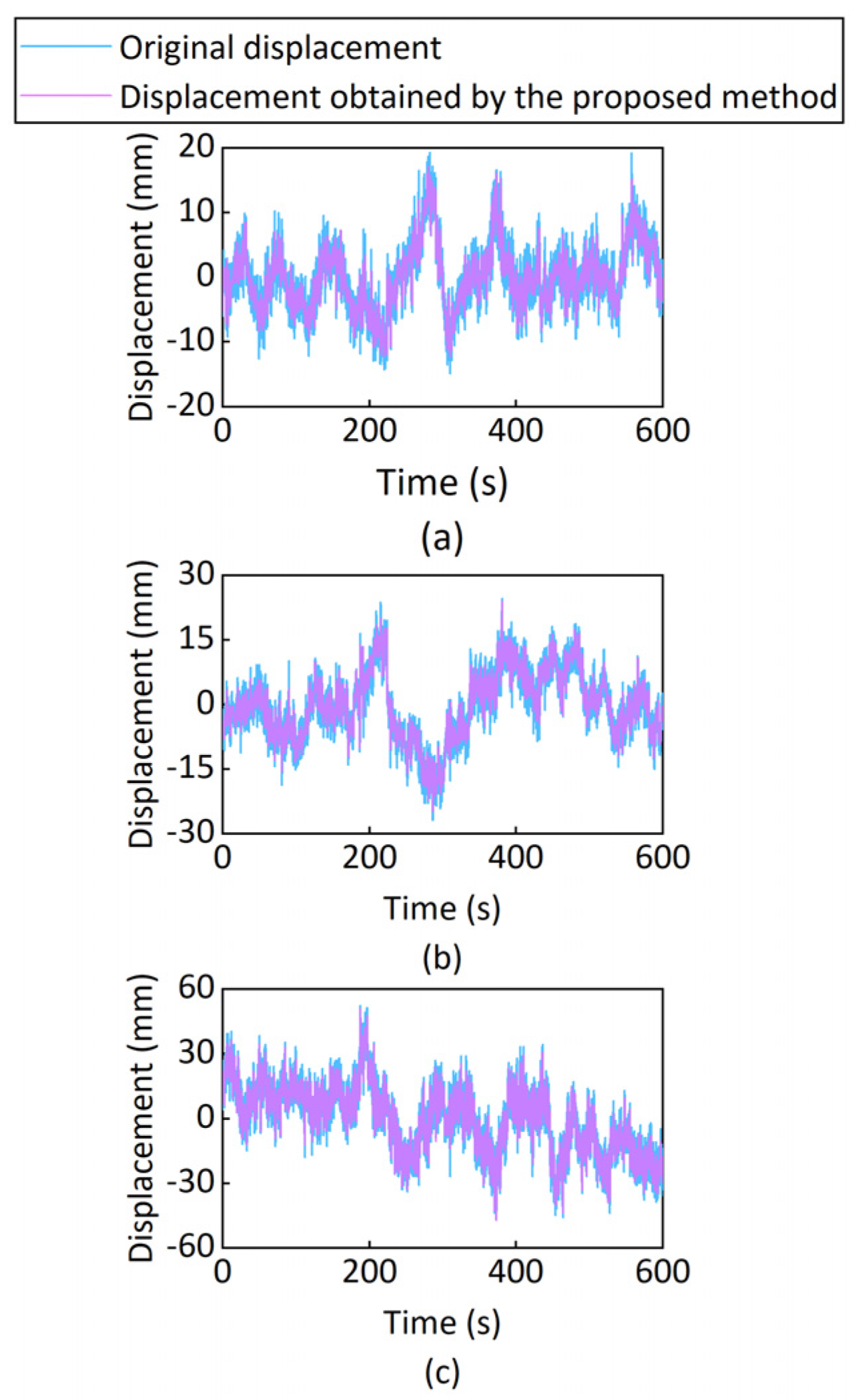
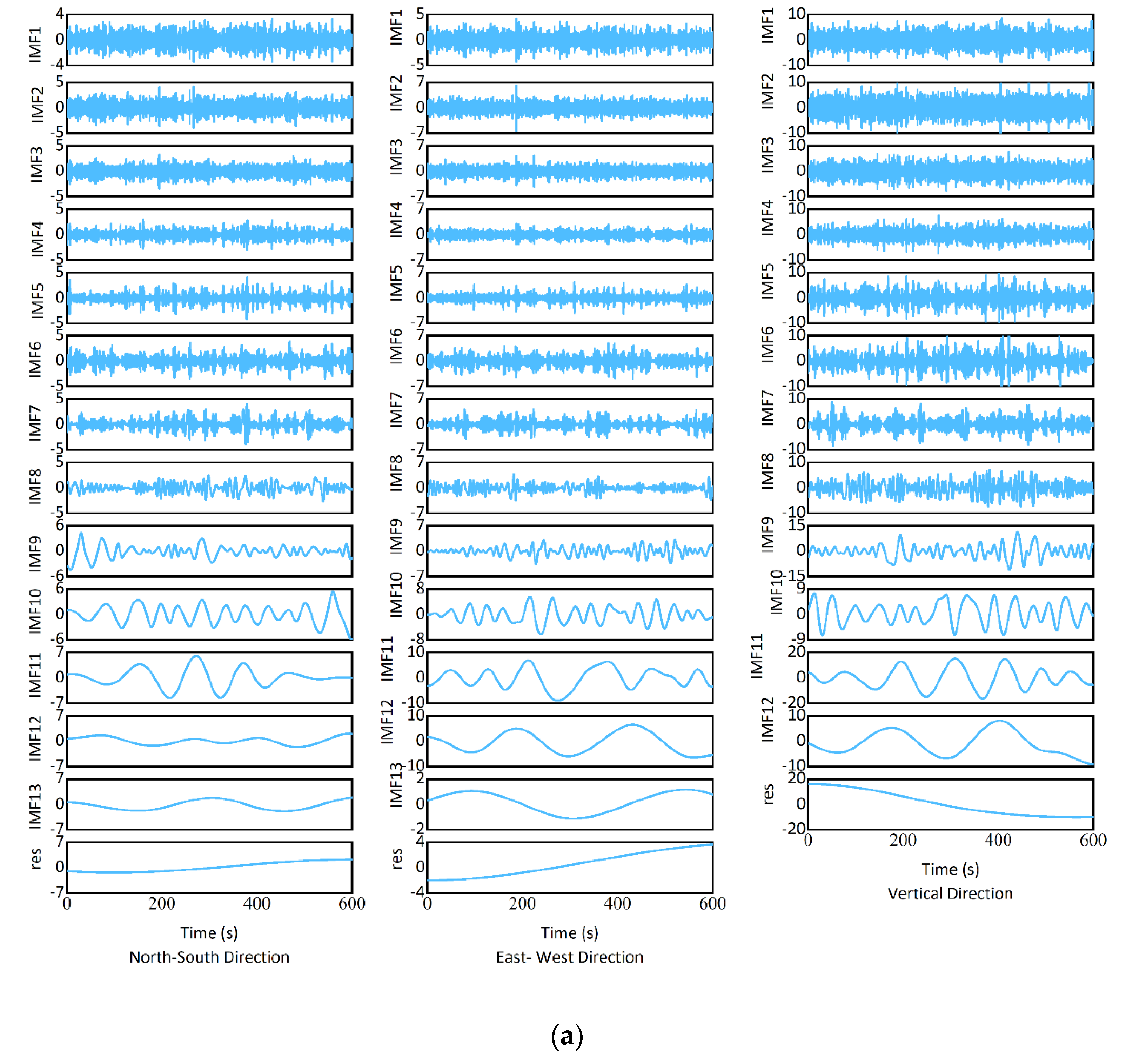
3.3. Engineering Monitoring
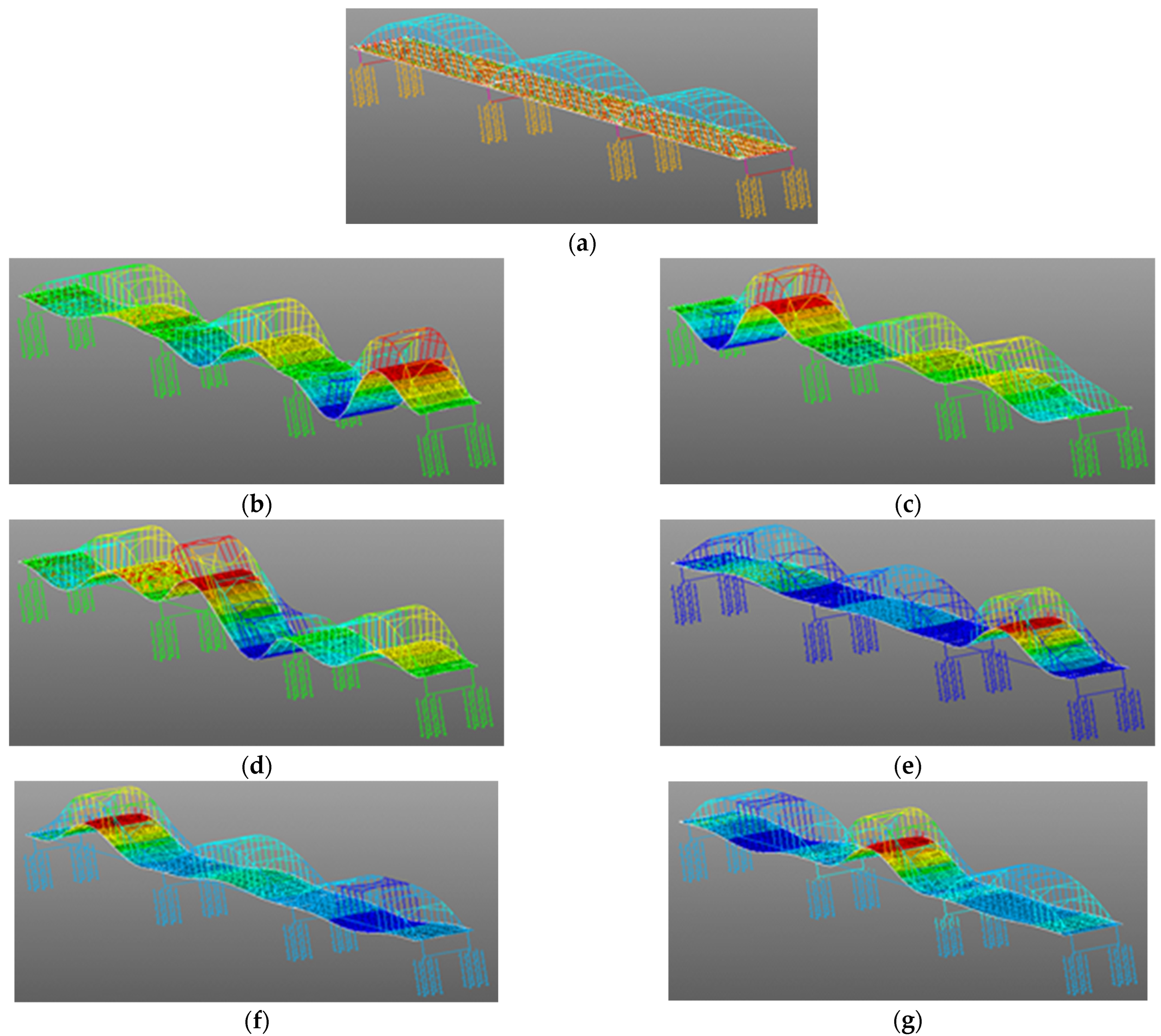
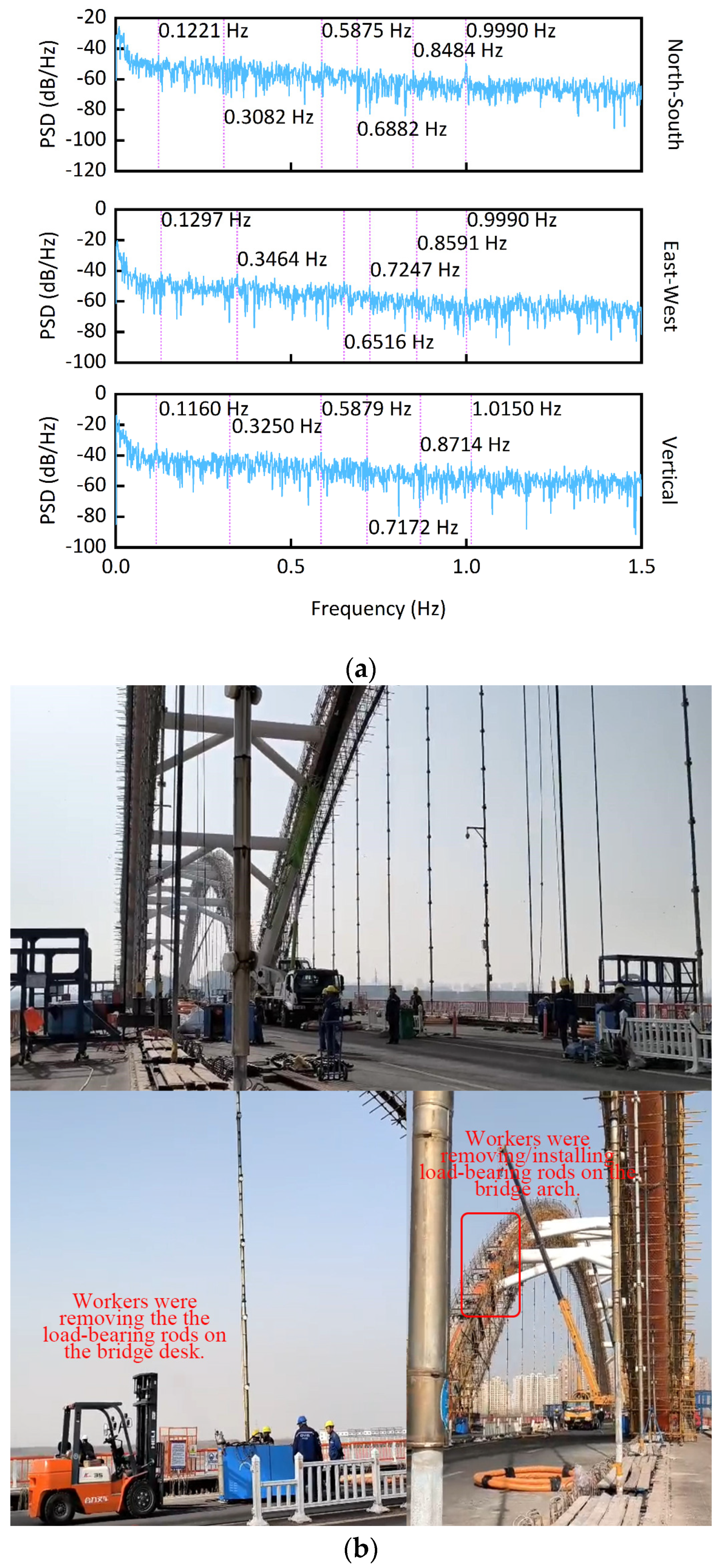
4. Dynamic Characteristics Identification
5. Conclusions
- The improved wavelet threshold denoising method overcomes the drawbacks of the traditional wavelet threshold denoising method. The improved threshold function is continuous at , and rapidly from the soft threshold function tends to the hard threshold function at . The stability experiment also demonstrated that the improved wavelet threshold denoising method was more effective in reducing GNSS-RTK noise.
- The simulation experiment proved that the proposed method is superior to the ICEEMDAN method and the CEEMDAN-WT method. The proposed method acquired lower RMSE and higher SNR compared to the ICEEMDAN. The signal acquired using the proposed method is similar to the original signal.
- The bridge’s vertical dynamic displacements exceeded the planar dynamic displacements. The proposed approach processed fewer displacements than the initial monitoring displacements. It indicates the proposed method reduces noise significantly when monitoring the bridge based on the GNSS-RTK sensor.
- Dynamic characteristics identification revealed the bridge’s features during maintenance and rehabilitation construction. The sixth-order frequency from the PSD is similar to that from the FEA. The lower modes’ natural frequencies from the PSD are smaller than those from the FEA. It illustrates the features of the natural frequencies in the repair of bridges. During the repair process, the missing load-bearing rods made the bridge less stiff and strong, which led to the lower natural frequencies of the bridge being smaller. The bridge still maintains the shape of an arch bridge in construction, so it preserves some mechanical characteristics of its design, that the sixth-order natural frequencies from the PSD and the FEA are similar.
- The external excitation frequency coinciding with the natural frequency of the bridge will cause the bridge to resonate. The resonance effect of the bridge may lead to the collapse of the bridge. The smaller natural frequencies of the bridge, the complex construction environment, the diversity of workers’ operations, and some unforeseen circumstances occurring in the construction all bring risks to the safety of the bridge. We should pay more attention to the dynamic monitoring of the bridge during the construction, in order to understand the structural status in time to prevent accidents.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation List
| the fitting polynomial coefficient | |
| the wavelet coefficient | |
| th-layer IMF components produced by EMD with | |
| th-layer IMF component | |
| the signal operator’s local average | |
| the number of the segment | |
| th-layer residual component | |
| the original signal | |
| the average of | |
| amplitude coefficients of the th time adding white noise | |
| the threshold | |
| white Gaussian noise | |
| the pooled average operator |
References
- Zhi, L.; Yu, P.; Li, Q.-S.; Chen, B.; Fang, M. Identification of wind loads on super-tall buildings by Kalman filter. Comput. Struct. 2018, 208, 105–117. [Google Scholar] [CrossRef]
- Xi, R.J.; He, Q.Y.; Meng, X.L. Bridge monitoring using multi-GNSS observations with high cutoff elevations: A case study. Measurement 2021, 168, 108303. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, P.; Xu, B.; Meng, X. Experimental assessment of high sampling-rate robotic total station for monitoring bridge dynamic responses. Measurement 2017, 104, 60–69. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic Deflections of a Stiff Footbridge Using 100-Hz GNSS and Accelerometer Data. J. Surv. Eng. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K.; Sohn, H. Autonomous dynamic displacement estimation from data fusion of acceleration and intermittent displacement measurements. Mech. Syst. Signal Process. 2014, 42, 194–205. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W.; Hester, D.; Koo, K.Y. Long-span bridges: Enhanced data fusion of GPS displacement and deck accelerations. Eng. Struct. 2017, 147, 639–651. [Google Scholar] [CrossRef]
- Naderi, K.; Kosary, M.; Sharifi, M.A.; Farzaneh, S. A Novel Time–Frequency Approach Based on the Noise Characterization for Structural Health Monitoring (SHM) Using GNSS Observations. J. Surv. Eng. 2023, 149, 04023014. [Google Scholar] [CrossRef]
- Gaxiola-Camacho, J.R.; Vazquez-Ontiveros, J.R.; Guzman-Acevedo, G.M.; Bennett, R.A.; Reyes-Blanco, J.M.; Vazquez-Becerra, G.E. Real-Time Probabilistic Structural Evaluation of Bridges Using Dynamic Displacements Extracted via GPS Technology. J. Surv. Eng. 2021, 147, 04021002. [Google Scholar] [CrossRef]
- Xi, R.J.; Jiang, W.P.; Meng, X.L.; Chen, H.; Chen, Q.S. Bridge monitoring using BDS-RTK and GPS-RTK techniques. Measurement 2018, 120, 128–139. [Google Scholar] [CrossRef]
- Vazquez-Ontiveros, J.R.; Vazquez-Becerra, G.E.; Quintana, J.A.; Carrion, F.J.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, J.R. Implementation of PPP-GNSS measurement technology in the probabilistic SHM of bridge structures. Measurement 2021, 173, 108677. [Google Scholar] [CrossRef]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Qi, W.; Li, F.; Yu, L.; Fan, L.; Zhang, K. Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests. Sensors 2025, 25, 379. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Psimoulis, P.A.; Meng, X. Feasibility analysis of the performance of low-cost GNSS receivers in monitoring dynamic motion. Measurement 2022, 202, 111819. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, C.; Liu, C.; Zhao, X.; Hu, H. Empirical wavelet transform method for GNSS coordinate series denoising. J. Geovisualization Spat. Anal. 2021, 5, 9. [Google Scholar] [CrossRef]
- Li, W.; Guo, J. Extraction of periodic signals in Global Navigation Satellite System (GNSS) vertical coordinate time series using the adaptive ensemble empirical modal decomposition method. Nonlinear Process. Geophys. 2024, 31, 99–113. [Google Scholar] [CrossRef]
- Yu, L.; Cao, H.; Lian, J.; Li, Y.; Fan, L.; Liu, H.; Liu, Y. GNSS-PPP for dynamic deformation monitoring of large-scale engineering structures and a case study. J. Civ. Struct. Health Monit. 2025; in press. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.o.; Patrick, F. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Prague, Czech Republic, 2011; pp. 4144–4147. [Google Scholar]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. A Comparative Analysis of Signal Decomposition Techniques for Structural Health Monitoring on an Experimental Benchmark. Sensors 2021, 21, 1825. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Niu, Y.; Ye, Y.; Zhao, W.; Duan, Y.; Shu, J. Identifying Modal Parameters of a Multispan Bridge Based on High-Rate GNSS–RTK Measurement Using the CEEMD–RDT Approach. J. Bridge Eng. 2021, 26, 04021049. [Google Scholar] [CrossRef]
- Xiong, C.; Shang, Z.; Chen, W.; Wang, M. Bw-ICEEMDAN/NExT-ERA method of data processing for dynamic monitoring of a super high-rise TV tower based on GNSS-RTK technique. GPS Solut. 2024, 28, 1. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; Wang, Y.; Cheng, X. A Comprehensive Diagnosis Method of Rolling Bearing Fault Based on CEEMDAN-DFA-Improved Wavelet Threshold Function and QPSO-MPE-SVM. Entropy 2021, 23, 1142. [Google Scholar] [CrossRef] [PubMed]
- Xiong, C.; Shang, Z.; Wang, M. Improved Hybrid Denoising Method for Dynamic Monitoring of a Super-High-Rise Building Based on a GNSS-RTK Technique. J. Struct. Eng. 2024, 150, 04024116. [Google Scholar] [CrossRef]
- Cui, H.; Zhao, R.; Hou, Y. Improved Threshold Denoising Method Based on Wavelet Transform. Phys. Procedia 2012, 33, 1354–1359. [Google Scholar] [CrossRef]
- Mert, A.; Akan, A. Detrended fluctuation thresholding for empirical mode decomposition based denoising. Digit. Signal Process. 2014, 32, 48–56. [Google Scholar] [CrossRef]
- Xiong, C.; Yu, L.; Niu, Y. Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis. Appl. Sci. 2019, 9, 1301. [Google Scholar] [CrossRef]


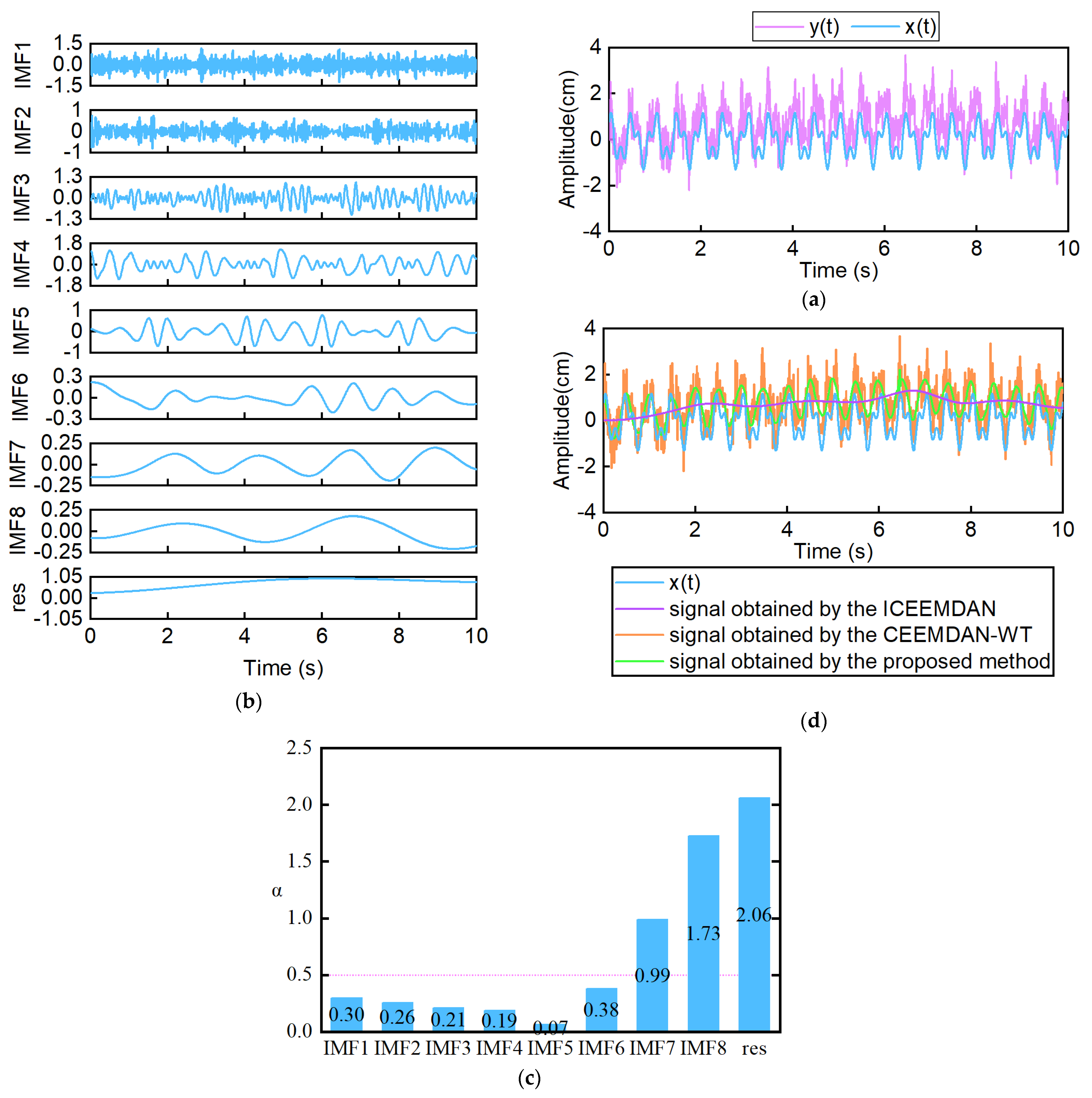




| Evaluating Indicators | ICEEMDAN | CEEMDAN-WT | Proposed Method |
|---|---|---|---|
| SNR (dB) | −3.72 | −3.08 | −2.11 |
| RMSE (mm) | 1.02 | 0.95 | 0.85 |
| Direction | North–South | East–West | Vertical | |
|---|---|---|---|---|
| Original | Displacement (mm) | −14.9–19.3 | −26.9–24.7 | −46.7–52.3 |
| Difference (mm) | 34.2 | 51.6 | 99.0 | |
| obtained by the proposed method | Displacement (mm) | −12.3–17.2 | −24.6–24.1 | −46.7–51.1 |
| Difference (mm) | 29.5 | 48.7 | 97.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, C.; Shang, Z.; Wang, M.; Lian, S. Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method. Sensors 2025, 25, 3723. https://doi.org/10.3390/s25123723
Xiong C, Shang Z, Wang M, Lian S. Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method. Sensors. 2025; 25(12):3723. https://doi.org/10.3390/s25123723
Chicago/Turabian StyleXiong, Chunbao, Zhi Shang, Meng Wang, and Sida Lian. 2025. "Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method" Sensors 25, no. 12: 3723. https://doi.org/10.3390/s25123723
APA StyleXiong, C., Shang, Z., Wang, M., & Lian, S. (2025). Dynamic Monitoring of a Bridge from GNSS-RTK Sensor Using an Improved Hybrid Denoising Method. Sensors, 25(12), 3723. https://doi.org/10.3390/s25123723






