Multiphysics-Coupled Load-Bearing Capacity of Piezoelectric Stacks in Low-Temperature Environments
Abstract
:1. Introduction
2. Methodology for Assessing PSA Load-Bearing Capacity
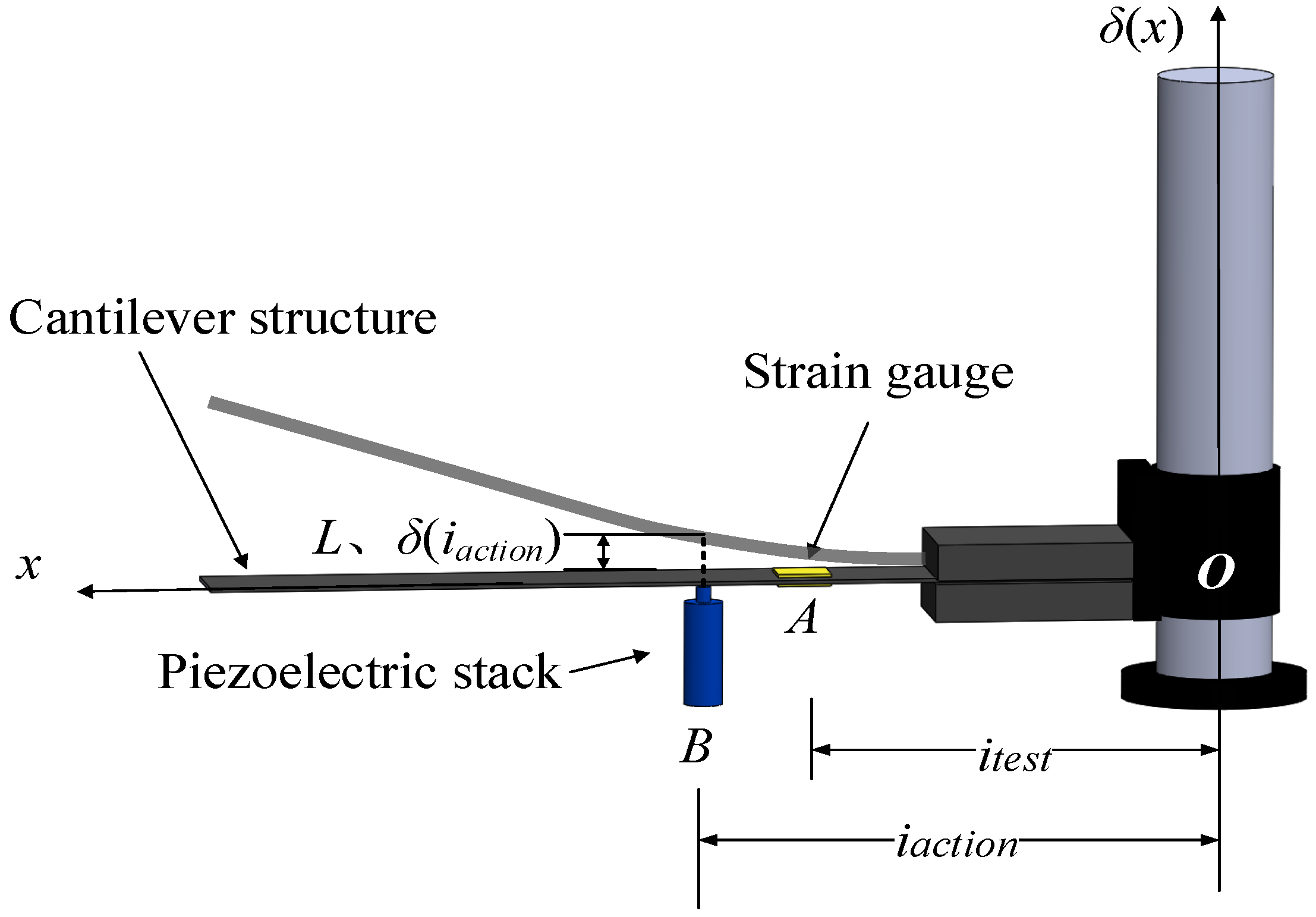
2.1. Analytical Framework for PSA-Driven Cantilever Systems
- 1.
- Actuation interface distance iaction: Separation between the PSA actuation point (Point B) and the anchored end (Point O).
- 2.
- Measurement node distance itest: Span from Point O to the strain sensor location (Point A).
- 1.
- Deflection profile δ(x): Spatial variation of beam deflection along the longitudinal axis (coordinate x).
- 2.
- Flexural moment MA: Bending moment magnitude at the strain sensor location (Point A).
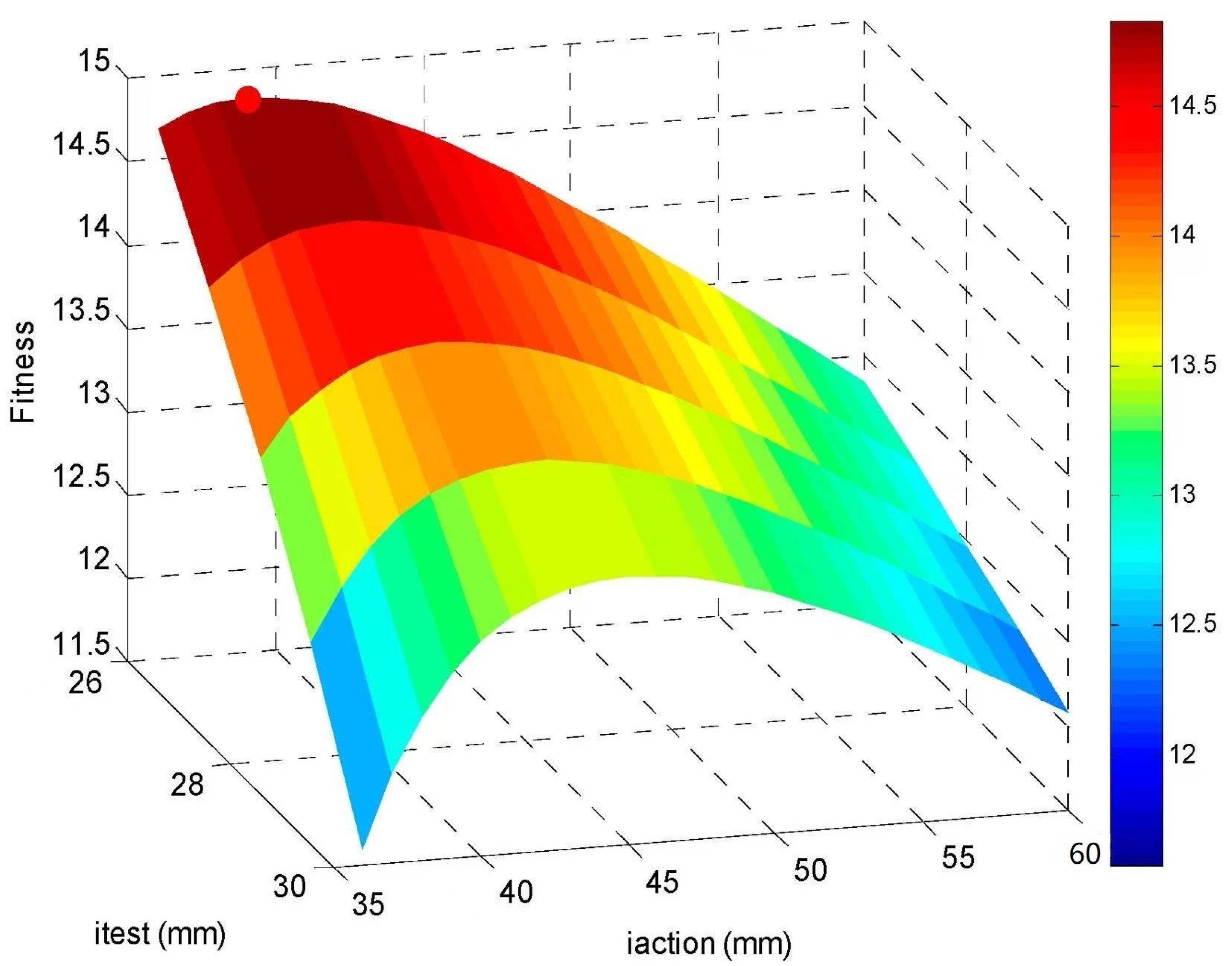
2.2. Optimal Placement of Strain Sensor and Actuation Positions via Particle Swarm Optimization
2.2.1. Formulation of Optimization Objectives and Constraints
2.2.2. Implementation of Particle Swarm Optimization
- (1)
- Particle Definition: Each particle in the swarm represents a candidate solution xi = (itest, iaction), where itest ∈ [20 mm, 50 mm] and iaction ∈ [30 mm, 60 mm]. The velocity vector vi = (vitest, viaction) governs the search direction. A population of N = 30 particles is randomly initialized within the feasible domain.
- (2)
- Fitness Evaluation: The fitness of each particle is quantified by evaluating the objective function f (itest, iaction), which integrates SNR and sensitivity metrics. Solutions violating constraints are subjected to penalty mechanisms: particles exceeding strain limits are reinitialized within feasible regions, while those violating spatial separation are dynamically repositioned.
- (3)
- Iterative Position-Velocity Update: The swarm’s exploration-exploitation balance is maintained through velocity and position updates at each iteration:
- (4)
- Constraint Handling Mechanism: If the PSA actuation interface violates the minimum spatial separation requirement iaction < itest + 10 mm, the particle is dynamically repositioned to iaction = itest + 10 mm + δ, where δ ~ U (1 mm, 5 mm) introduces stochastic displacement compensation; Particles exceeding the strain limit (εA ≥ 500 με) are immediately discarded and regenerated within the feasible domain to prevent non-physical solutions.
- (5)
- Termination Criteria: The algorithm terminates after T = 100 iterations or when the objective function converges (relative change < 0.1% over 10 iterations).
3. Experimental Characterization of PSA Load-Bearing Capacity Under Multi-Physical Coupling
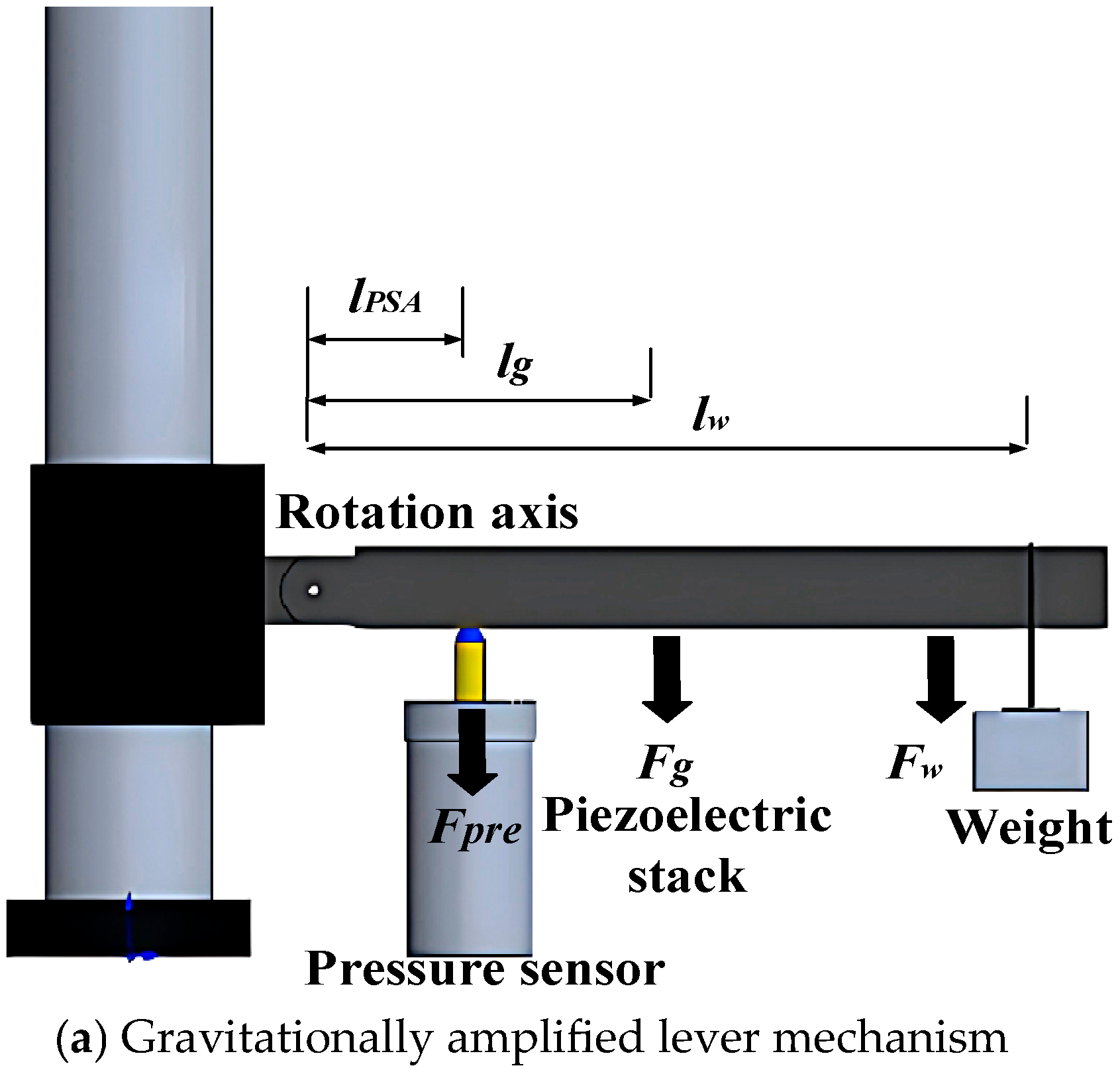
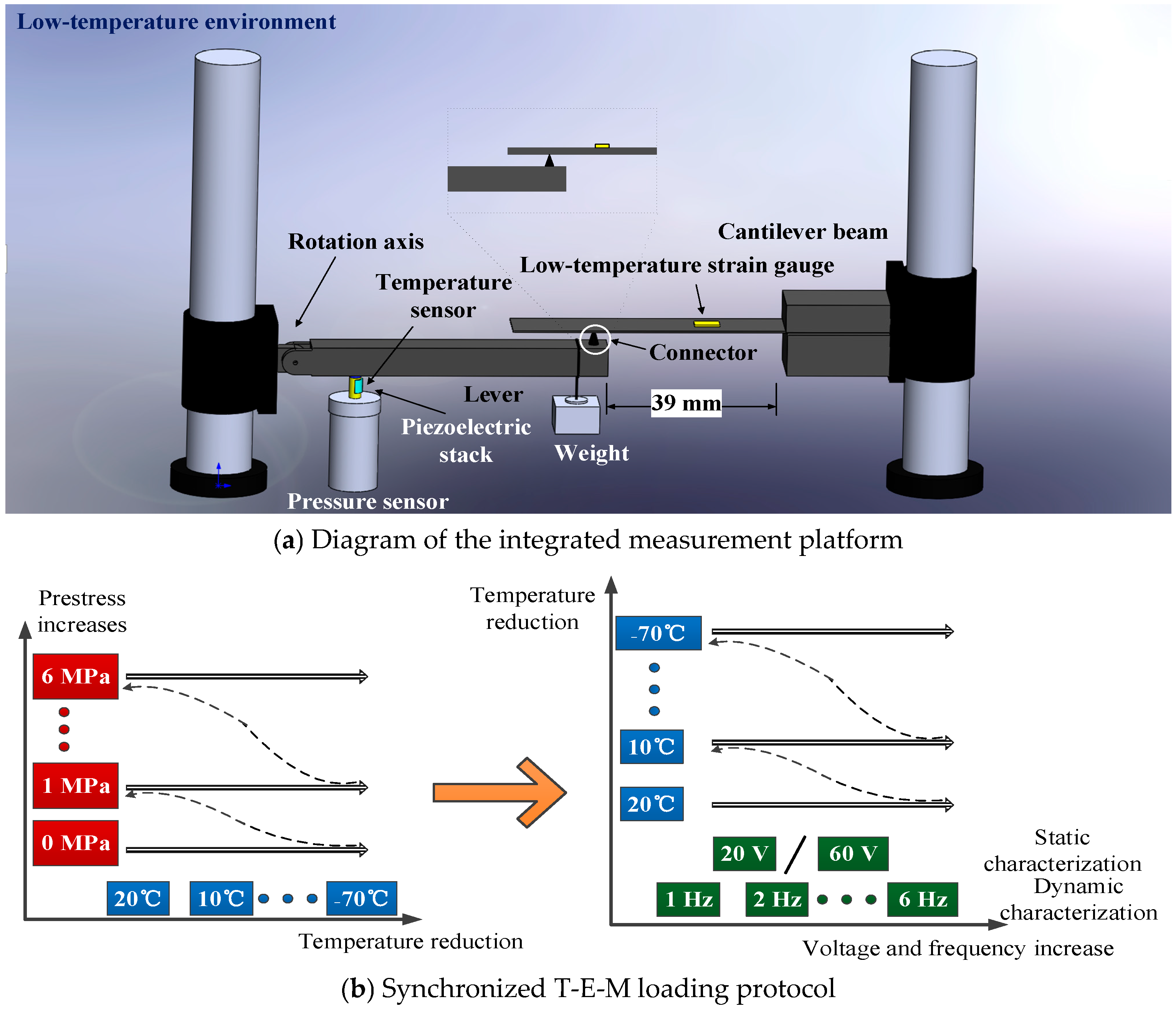
3.1. Low-Temperature Mechanical Instrumentation Design
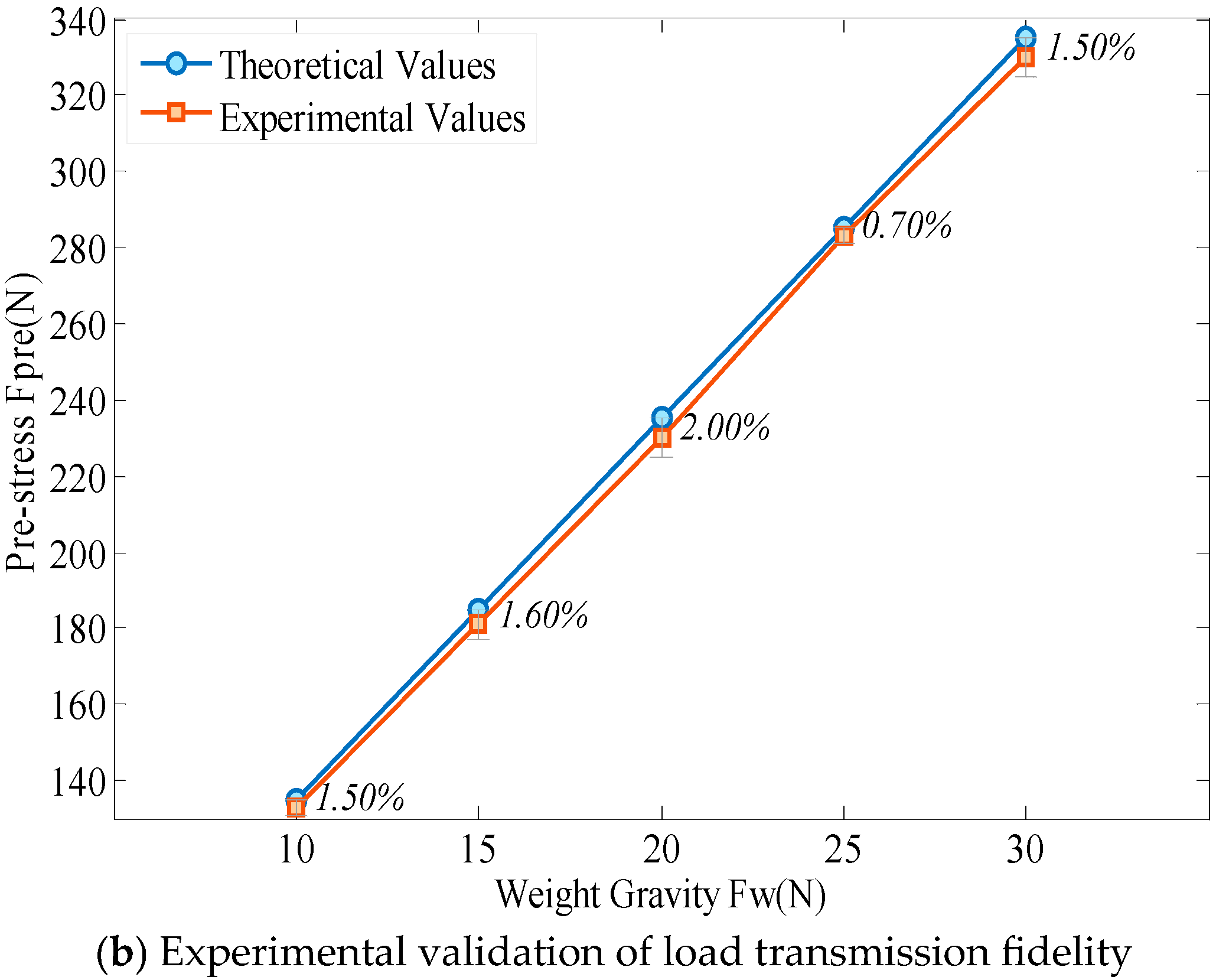
3.2. Characterization of Coupled Thermo-Electro-Mechanical Response
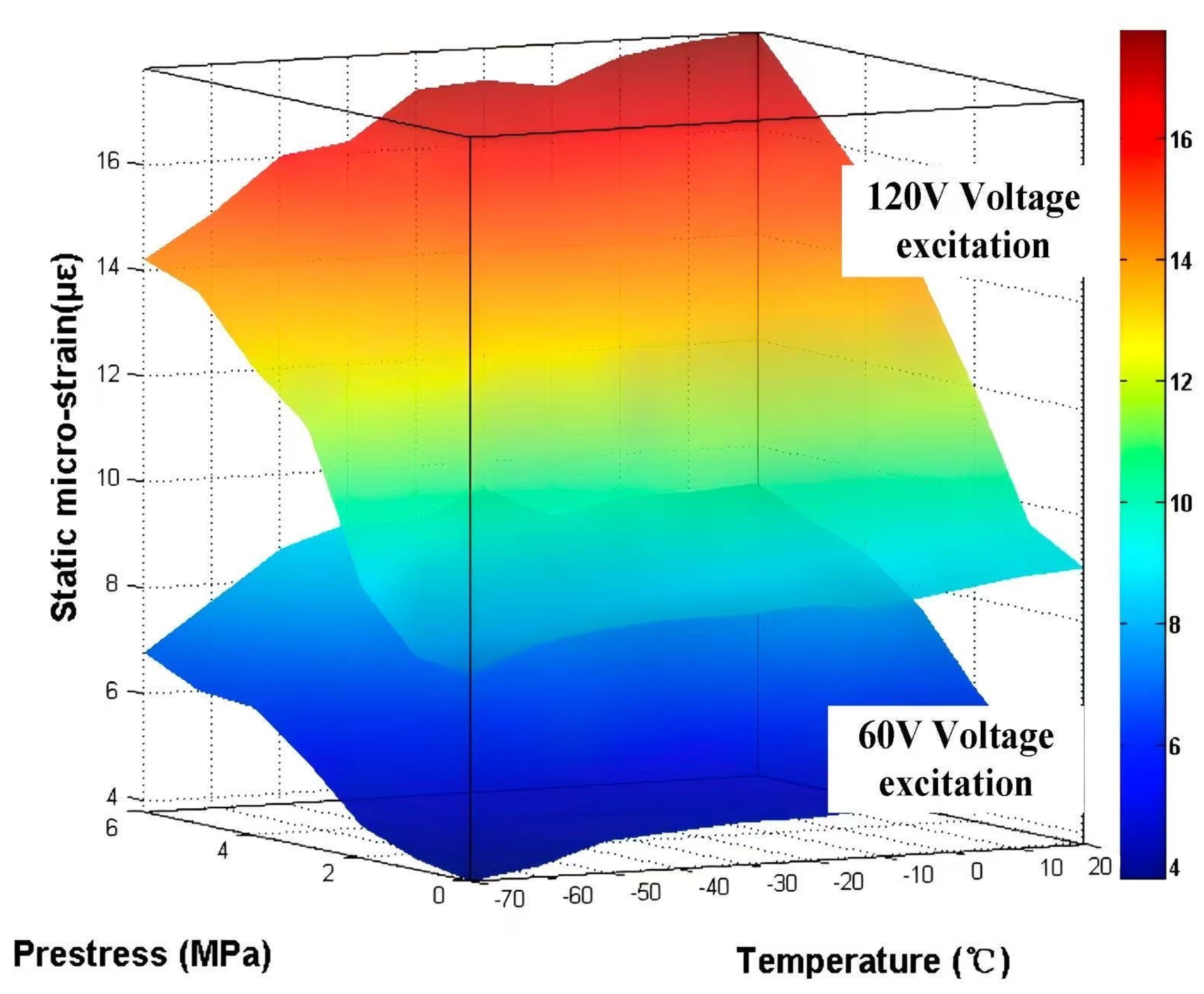
3.2.1. Static Load-Bearing Capacity Analysis
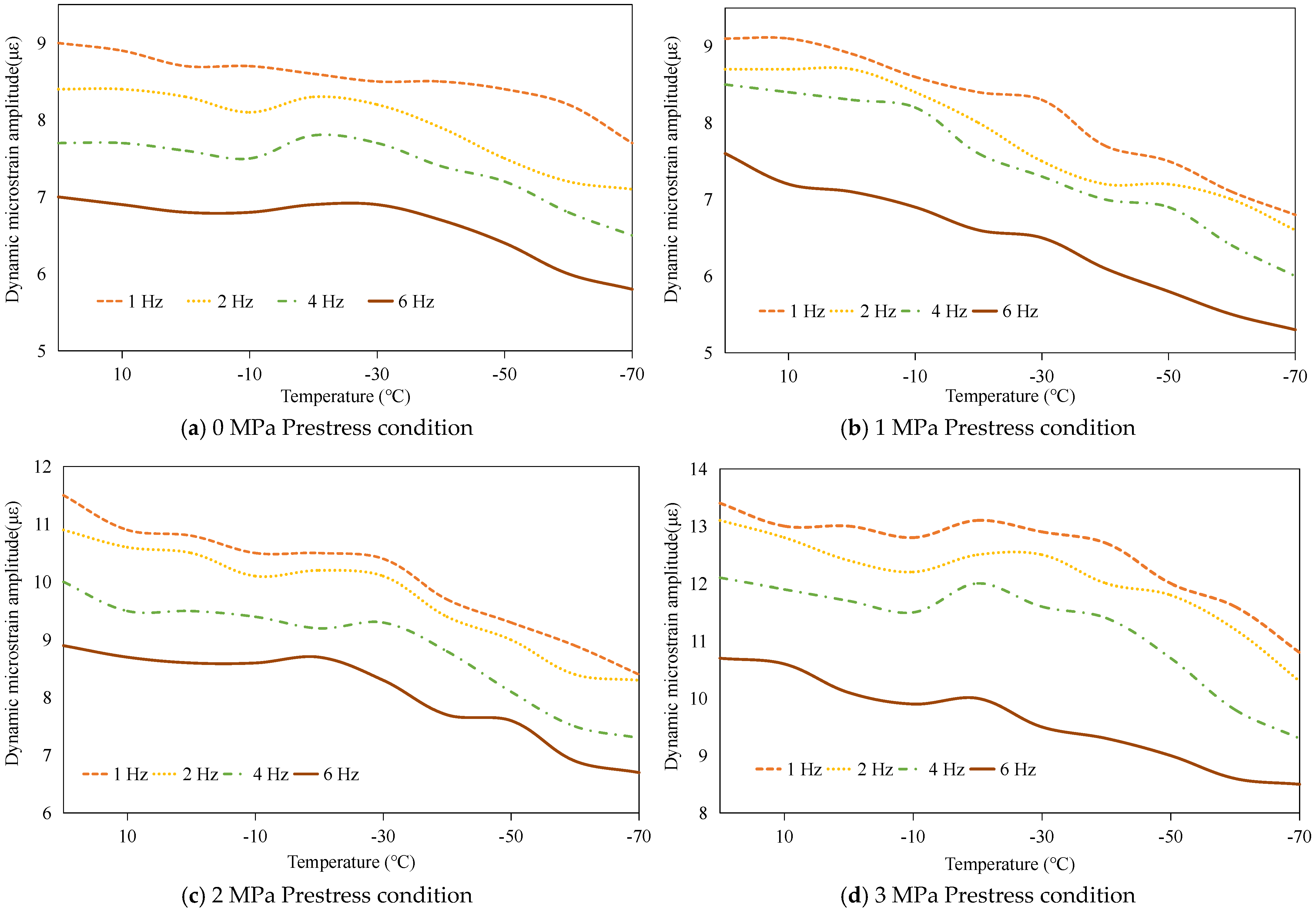
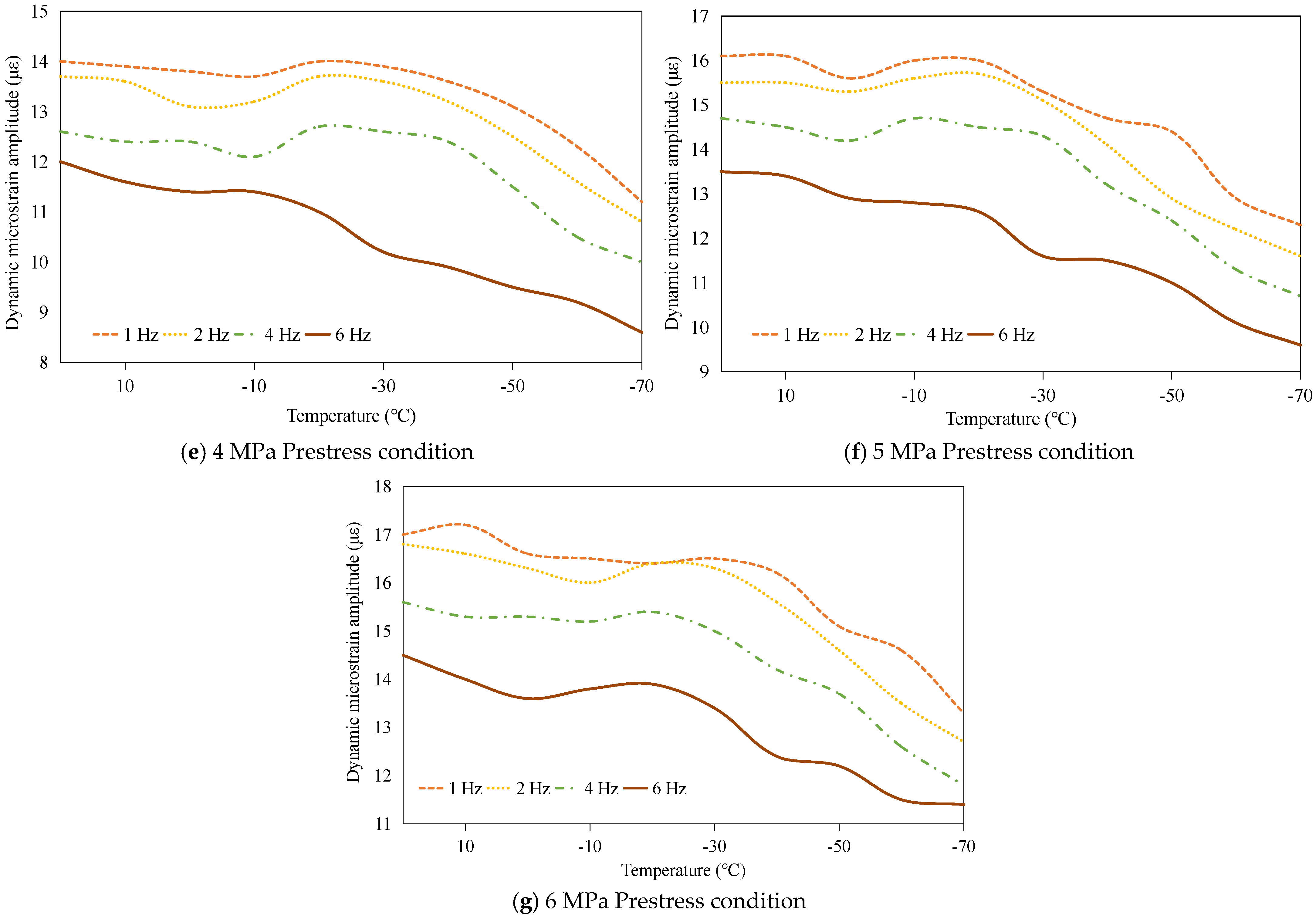
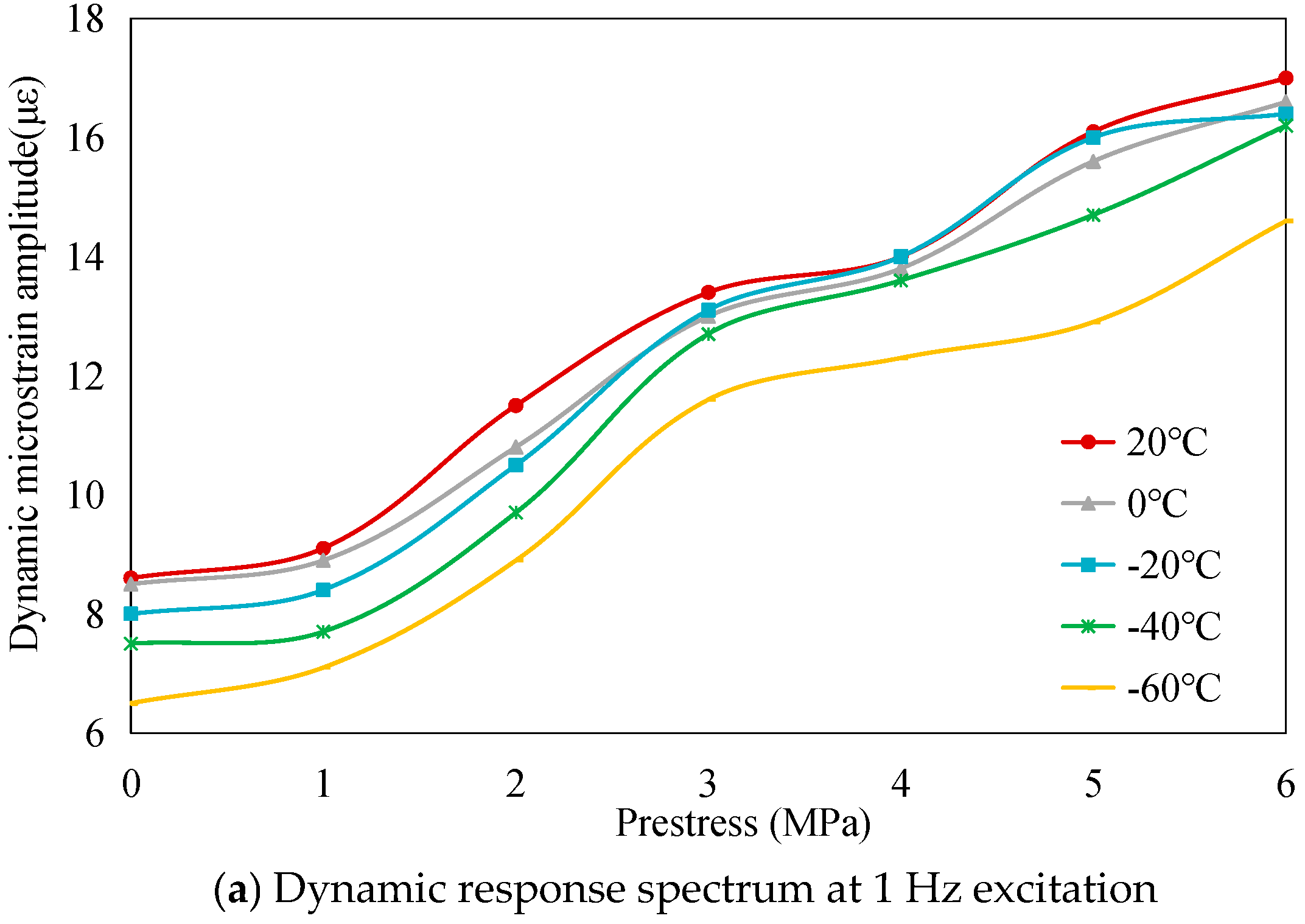
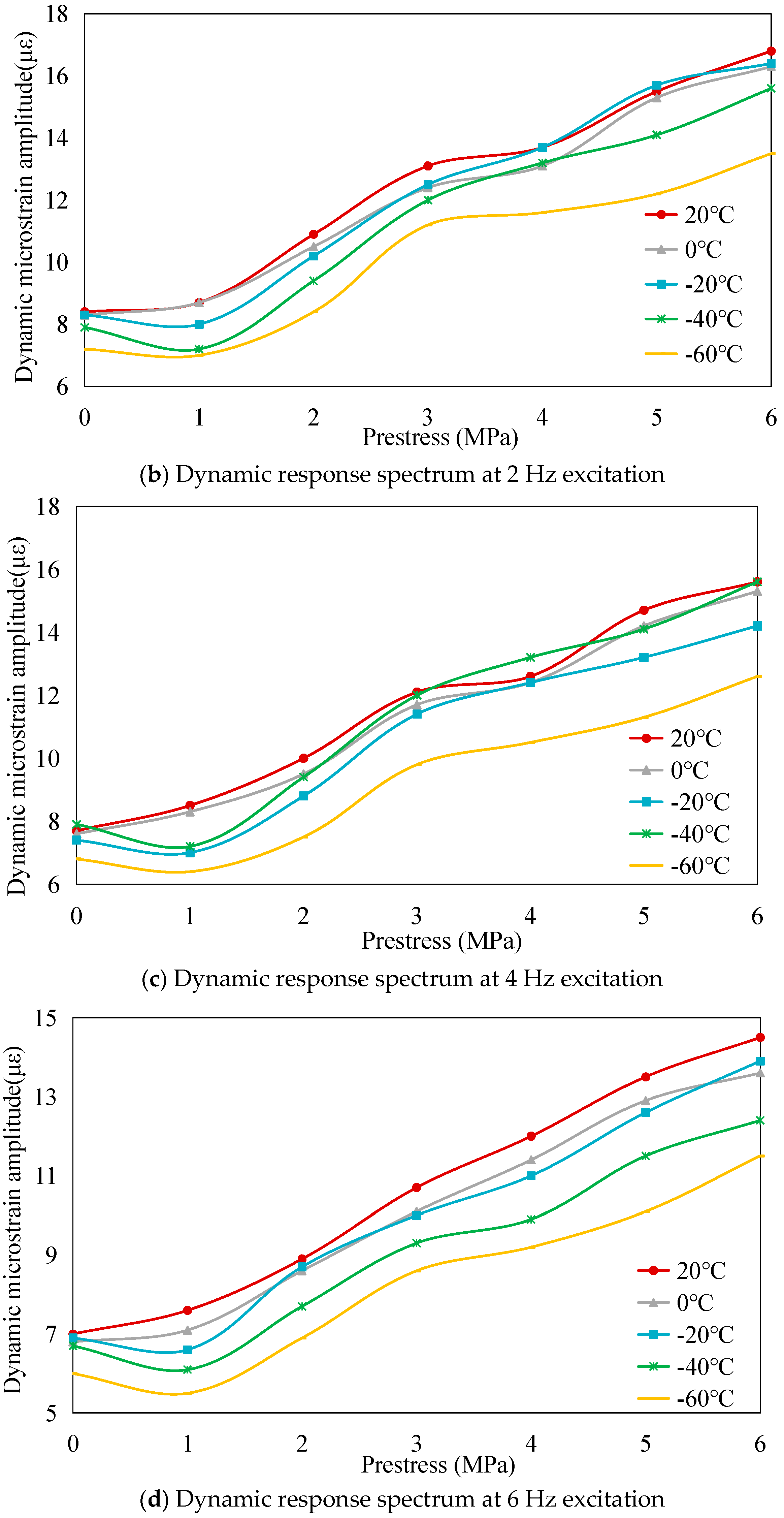
3.2.2. Dynamic Load-Bearing Capacity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Persano, L.; Camposeo, A.; Matino, F.; Wang, R.; Natarajan, T.; Li, Q.; Pan, M.; Su, Y.; Kar-Narayan, S.; Auricchio, F.; et al. Advanced Materials for Energy Harvesting and Soft Robotics: Emerging Frontiers to Enhance Piezoelectric Performance and Functionality. Adv. Mater. 2024, 36, e2405363. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on piezoelectric actuators based on high performance piezoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef] [PubMed]
- Barber, M.E.; Steppke, A.; Mackenzie, A.P.; Hicks, C.W. Piezoelectric-based uniaxial pressSure cell with integrated force and displacement sensors. Rev. Sci. Instrum. 2019, 90, 023904. [Google Scholar] [CrossRef] [PubMed]
- Pratishtha, T.; Kumar, D.A. Role of Piezoelectricity in Disease Diagnosis and Treatment: A Review. Acs. Biomater. Sci. Eng. 2024, 10, 6061–6077. [Google Scholar]
- Xu, L.; Li, H.; Li, P.; Ge, C. A High-voltage and low-noise power amplifier for driving piezoelectric stack actuators. Sensors 2020, 20, 6528. [Google Scholar] [CrossRef]
- Ghosh, B.; Jain, R.K.; Majumder, S.; Roy, S.S.; Mukhopadhyay, S. Experimental performance evaluation of smart bimorph piezoelectric actuator and its application in micro robotics. Microsyst. Technol. 2017, 23, 4619–4635. [Google Scholar] [CrossRef]
- Tian, B.; Lou, J.; Shen, J.; Liu, L. Design, fabrication and realization of a parallel microrobot at the millimeterscale for minimally invasive surgery. J. Mech. Eng. 2024, 60, 147–155. [Google Scholar]
- Zhou, Z.; Wang, D.; Zhang, Z.; Wang, Y.; Wang, L.; Fang, X.; Zou, X. Research on Piezoelectric Actuator Applied to the Smart Wing. Piezoelectrics Acoustooptics 2016, 38, 420–422+426. [Google Scholar]
- Wang, J.; Jing, Z.; Xie, Z.; Ning, Z.; Qi, B. Analysis and Optimization of Dynamic and Static Characteristics of the Compliant-Amplifying Mechanisms. Micromachines 2023, 14, 1502. [Google Scholar] [CrossRef]
- Fehren, H.; Gnauert, U.; Wimmel, R. Validation testing with the active damping system in the European Transonic Wind tunnel. In Proceedings of the 39th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; pp. 1–8. [Google Scholar]
- Balakrishna, S.; Butler, D.H.; White, R. Active damping of sting vibrations in transonic wind tunnel testing. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; pp. 1–15. [Google Scholar]
- Balakrishna, S.; Butler, D.; Acheson, M.; White, E. Design and performance of an active sting damper for the NASA common research model. In Proceedings of the 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; pp. 1–9. [Google Scholar]
- Sekalski, P.; Napieralski, A.; Fouaidy, M.; Bosotti, A.; Paparella, R. Measurement of static force at liquid helium temperature. Meas. Sci. Technol. 2007, 18, 2356–2364. [Google Scholar] [CrossRef]
- Zhao, J.; Du, H.; Qu, S.; Zhang, H.; Xu, Z. Improvement in the piezoelectric temperature stability of (K0.5Na0.5)NbO3 ceramics. Chin. Sci. Bull. 2011, 56, 2389–2393. [Google Scholar] [CrossRef]
- Sabat, R.G.; Mukherjee, B.K.; Ren, W.; Yang, G. Temperature dependence of the complete material coefficients matrix of soft and hard doped piezoelectric lead zirconate titanate ceramics. J. Appl. Phys. 2007, 101, 064111. [Google Scholar]
- Zhao, X.; Fang, B.; Cao, H.; Guo, Y.; Luo, H. Dielectric and piezoelectric performance of PMN-PT single crystals with compositions around the MPB: Influence of composition, poling field and crystal orientation. Mater. Sci. Eng. B 2002, 96, 254–262. [Google Scholar] [CrossRef]
- Senousy, M.; Li, F.; Mumford, D.; Gadala, M.; Rajapakse, R. Thermo-electro-mechanical performance of piezoelectric stack actuators for fuel injector applications. J. Intell. Mater. Syst. Struct. 2009, 20, 387–399. [Google Scholar] [CrossRef]
- Senousy, M.S.; Li, F.X.; Mumford, D.; Gadala, M.; Rajapakse, R.K.N.D. Dynamic thermo-electro-mechanical performance of piezoelectric stack actuators. In Proceedings of the International Symposium On: Smart Structures and Materials and Nondestructive Evaluation and Health Monitoring, Vancouver, BC, Canada, 9 April 2007; p. 652609. [Google Scholar]
- Liao, X.; Qiu, Z.; Jiang, T.; Sadiq, M.R.; Huang, Z.; Demore, C.E.M.; Cochran, S. Functional piezocrystal characterisation under varying conditions. Materials 2015, 8, 8304–8326. [Google Scholar] [CrossRef]
- Qiu, Z.; Sadiq, M.R.; Demore, C.; Parker, M.F.; Marin, P.; Mayne, K.; Cochran, S. Characterization of piezocrystals for practical configurations with temperature- and pressure-dependent electrical impedance spectroscopy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1793–1803. [Google Scholar]
- Mitrovic, M.; Carman, G.P.; Straub, F.K. Response of piezoelectric stack actuators under combined electro-mechanical loading. Int. J. Solids Struct. 2001, 38, 4357–4374. [Google Scholar] [CrossRef]
- Li, F.X.; Rajapakse, R.K.N.D.; Mumford, D.; Gadala, M. Quasi-static thermo-electro-mechanical behaviour of piezoelectric stack actuators. Smart Mater. Struct. 2008, 17, 015049. [Google Scholar] [CrossRef]
- Oliveira, A.N.; Moreira, L.S.; Sacramento, R.L.; Kosulic, L.; Brasil, V.B.; Wolff, W.; Cesar, C.L. Cryogenic mount for mirror and piezoelectric actuator for an optical cavity. Rev. Sci. Instrum. 2017, 88, 063104. [Google Scholar] [CrossRef]
- Islam, M.S.; Beamish, J. Piezoelectric creep in LiNbO3, PMN-PT and PZT-5A at low temperatures. J. Appl. Phys. 2019, 126, 204101. [Google Scholar] [CrossRef]
- Li, Y.; Shen, X.; Kou, X.; Yu, L. Design, experiment, and verification of a heating and insulation structure for the piezoelectric stack. J. Intell. Mater. Syst. Struct. 2020, 31, 719–736. [Google Scholar] [CrossRef]
- Sherrit, S.; Jones, C.M.; Aldrich, J.B.; Blodget, C.; Bao, X.; Badescu, M.; Bar-Cohen, Y. Multilayer piezoelectric stack actuator characterization. In Behavior and Mechanics of Multifunctional and Composite Materials; SPIE: Bellingham, WA, USA, 2008; Volume 6929. [Google Scholar]
- Rupitsch, S.J.; Ilg, J.; Sutor, A.; Lerch, R. Variation of material parameters for the thickness extensional mode of piezoceramic discs in case of mechanical loading. Procedia Eng. 2011, 25, 1441–1444. [Google Scholar] [CrossRef]
- Fouaidy, M.; Hammoudi, N. Characterization of piezoelectric actuators used for SRF cavities active tuning at low temperature. In Proceedings of the 11th Workshop on RF Superconductivity, Orsay, France, 8–12 September 2003; pp. 669–674. [Google Scholar]
- Li, G.; Eugene, F.; Haertling, G.H. Stress-enhanced displacements in PLZT rainbow actuators. J. Am. Ceram. Soc. 2010, 80, 1382–1388. [Google Scholar] [CrossRef]


| Description | Parameter | Value | Unit |
|---|---|---|---|
| Stiffness of the PSA | k | 6 × 107 | N/m |
| Output displacement of the PSA under free state | Lo | 3.5 × 10−5 | m |
| Electrical excitation range | UPSA | 0~120 | V |
| Length of the PSA | LPSA | 4.6 × 10−2 | m |
| Width of the cantilever | b | 3 × 10−2 | m |
| Thickness of the cantilever | d | 2 × 10−3 | m |
| Elastic modulus of the cantilever | E | 2.1 × 1011 | Pa |
| Description | Value | Unit |
|---|---|---|
| Average current | 60 | mA |
| Peak current | 180 | mA |
| Average power | 7 | W |
| Bandwidth | 1 | kHz |
| Voltage gain | 12 | - |
| Input voltage range | 0~10 | V |
| Output voltage range | 0~120 | V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zheng, Y.; Song, L.; Yao, Z.; Zhang, H.; Wang, Y.; Fei, Z.; Xu, X.; Xiang, X. Multiphysics-Coupled Load-Bearing Capacity of Piezoelectric Stacks in Low-Temperature Environments. Sensors 2025, 25, 3642. https://doi.org/10.3390/s25123642
Li Y, Zheng Y, Song L, Yao Z, Zhang H, Wang Y, Fei Z, Xu X, Xiang X. Multiphysics-Coupled Load-Bearing Capacity of Piezoelectric Stacks in Low-Temperature Environments. Sensors. 2025; 25(12):3642. https://doi.org/10.3390/s25123642
Chicago/Turabian StyleLi, Yang, Yongping Zheng, Leipeng Song, Zhefan Yao, Hui Zhang, Yonglin Wang, Zhengshun Fei, Xiaozhou Xu, and Xinjian Xiang. 2025. "Multiphysics-Coupled Load-Bearing Capacity of Piezoelectric Stacks in Low-Temperature Environments" Sensors 25, no. 12: 3642. https://doi.org/10.3390/s25123642
APA StyleLi, Y., Zheng, Y., Song, L., Yao, Z., Zhang, H., Wang, Y., Fei, Z., Xu, X., & Xiang, X. (2025). Multiphysics-Coupled Load-Bearing Capacity of Piezoelectric Stacks in Low-Temperature Environments. Sensors, 25(12), 3642. https://doi.org/10.3390/s25123642






