The Role of Phase-Change Memory in Edge Computing and Analog In-Memory Computing: An Overview of Recent Research Contributions and Future Challenges
Abstract
1. Introduction
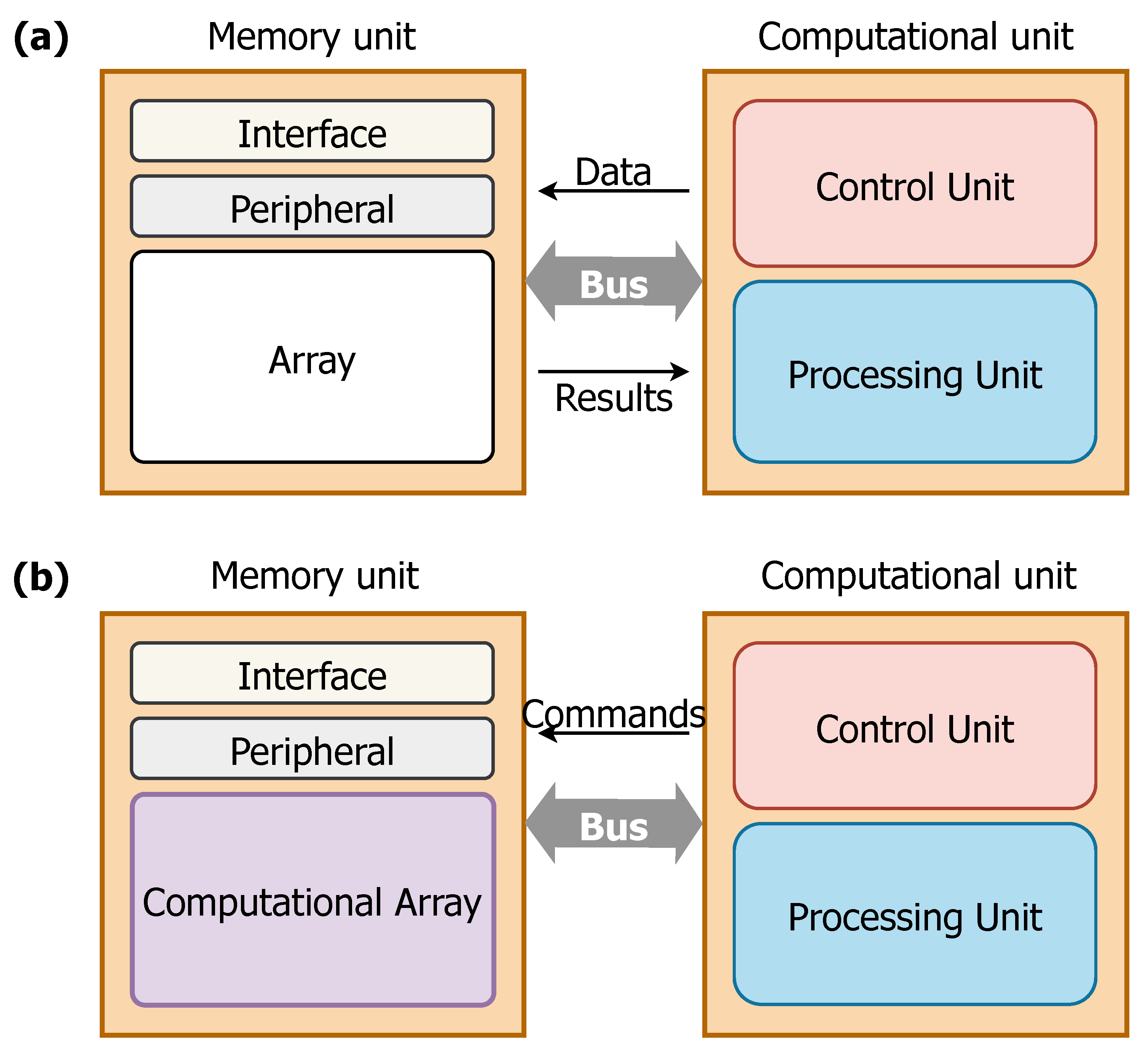
2. Analog In-Memory Computing
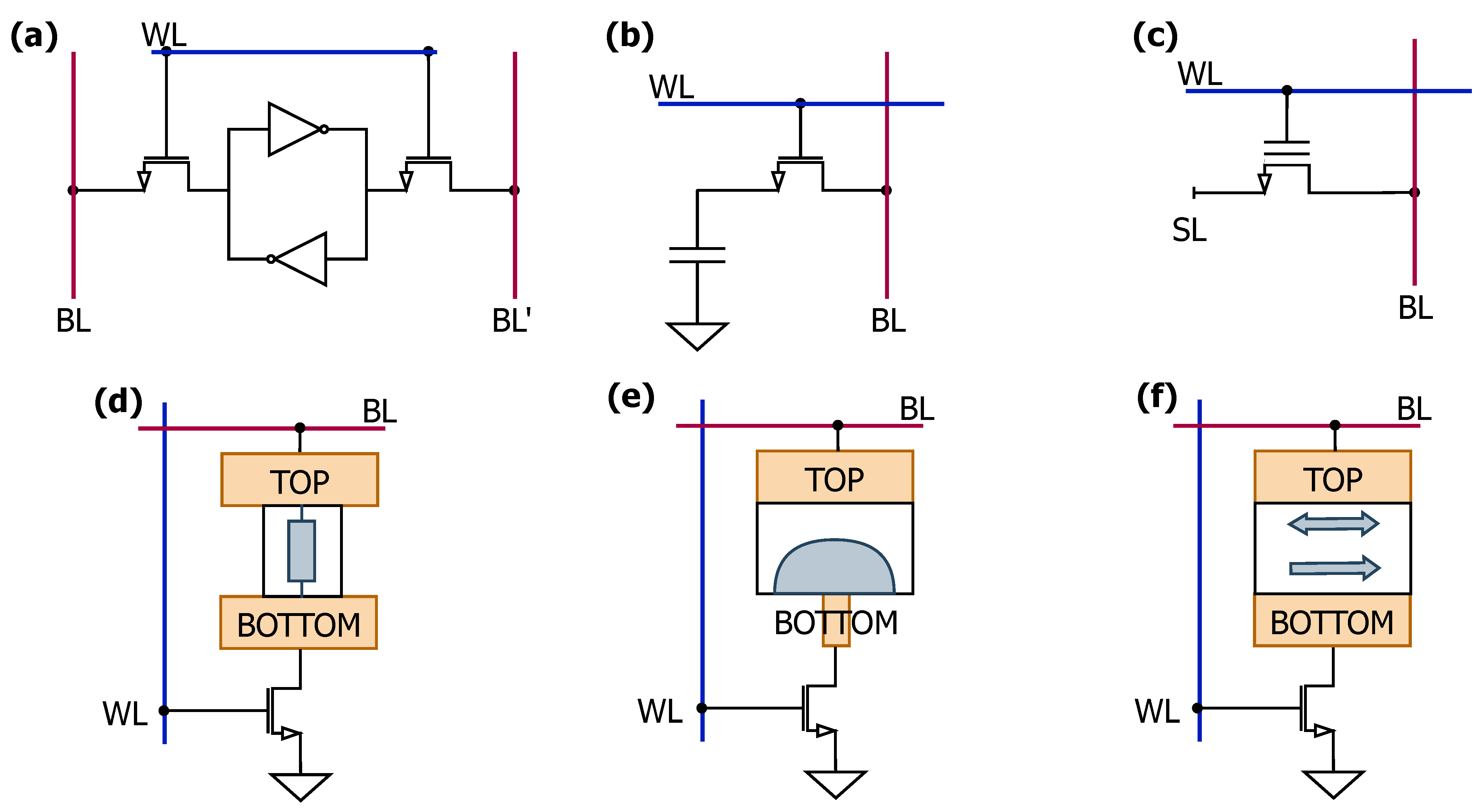
2.1. Memory Devices
2.2. Phase-Change Memory for Analog In-Memory Computing
3. PCM-Based AIMC Protoypes
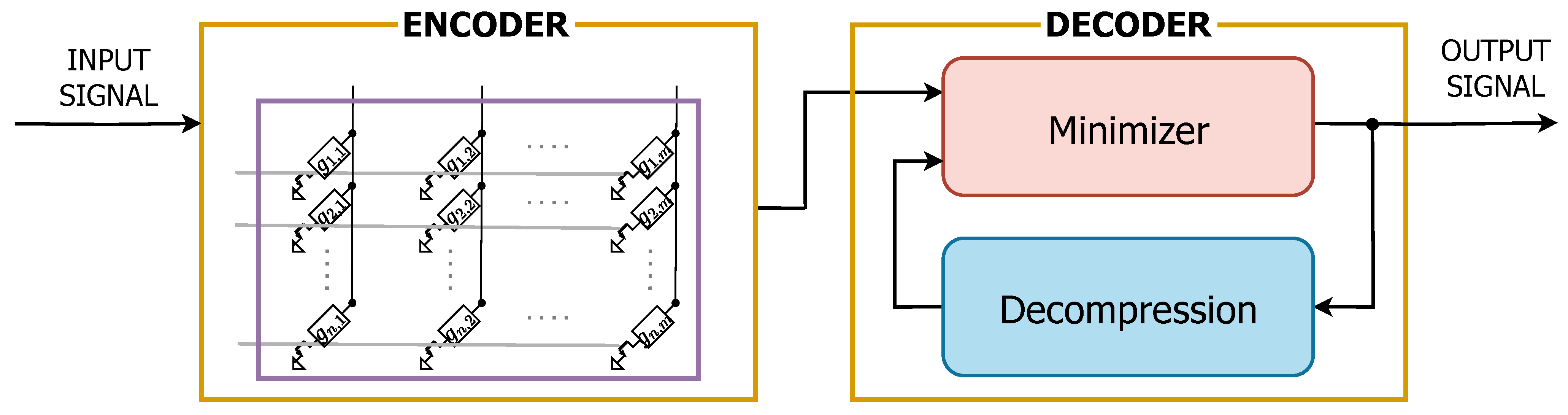
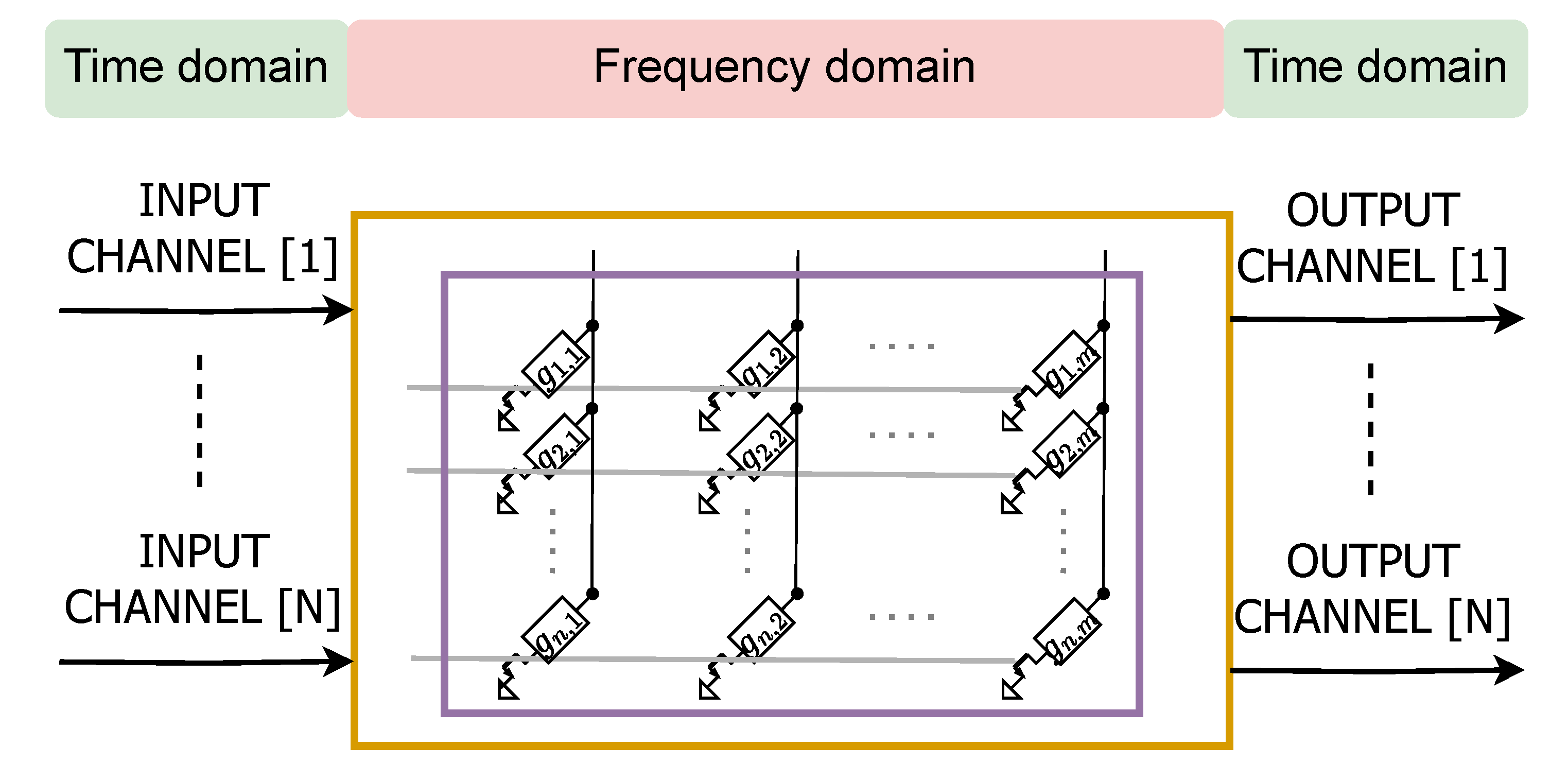
4. Analog PCM-Based Encoder for Compressed Sensing
4.1. AIMC Test Chip and Conductance Models
4.2. Compressed Sensing and Reconstruction Algorithms
4.3. Experimental Evaluations and Key Findings
5. PCM in Smart Sensing and Structural Health Monitoring
5.1. Background
5.2. Experimental Testing on an Italian Viaduct
- Batch filtering, in which signals are processed in a single step using large convolutional filters.
- Recursive filtering, in which data are processed progressively, reducing the number of simultaneous operations.
6. PCM for Motor Control
6.1. Implementation and Methodology
6.2. Experimental Results
7. PCM in Binary Pattern Matching
7.1. Background
7.2. Experimental Testing
8. Using PCM Technology for Human Body Monitoring Applications
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Verma, N.; Jia, H.; Valavi, H.; Tang, Y.; Ozatay, M.; Chen, L.Y.; Zhang, B.; Deaville, P. In-Memory Computing: Advances and Prospects. IEEE Solid-State Circuits Mag. 2019, 11, 43–55. [Google Scholar] [CrossRef]
- Hartmann, J.; Cappelletti, P.; Chawla, N.; Arnaud, F.; Cathelin, A. Artificial Intelligence: Why moving it to the Edge? In Proceedings of the ESSCIRC 2021—IEEE 47th European Solid State Circuits Conference (ESSCIRC), Grenoble, France, 13–22 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mannocci, P.; Ielmini, D. A generalized block-matrix circuit for closed-loop analogue in-memory computing. IEEE J. Explor. Solid-State Comput. Devices Circuits 2023, 9, 47–55. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Ambrosi, E.; Bricalli, A.; Wang, W.; Ielmini, D. Solving matrix equations in one step with cross-point resistive arrays. Proc. Natl. Acad. Sci. USA 2019, 116, 4123–4128. [Google Scholar] [CrossRef]
- Haensch, W.; Gokmen, T.; Puri, R. The Next Generation of Deep Learning Hardware: Analog Computing. Proc. IEEE 2019, 107, 108–122. [Google Scholar] [CrossRef]
- Sebastian, A.; Le Gallo, M.; Khaddam-Aljameh, R.; Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 2020, 15, 529–544. [Google Scholar] [CrossRef]
- Pronold, J.; Jordan, J.; Wylie, B.; Kitayama, I.; Diesmann, M.; Kunkel, S. Routing brain traffic through the von Neumann bottleneck: Efficient cache usage in spiking neural network simulation code on general purpose computers. Parallel Comput. 2022, 113, 102952. [Google Scholar] [CrossRef]
- Kneip, A.; Bol, D. Impact of Analog Non-Idealities on the Design Space of 6T-SRAM Current-Domain Dot-Product Operators for In-Memory Computing. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1931–1944. [Google Scholar] [CrossRef]
- Seshadri, V.; Lee, D.; Mullins, T.; Hassan, H.; Boroumand, A.; Kim, J.; Kozuch, M.A.; Mutlu, O.; Gibbons, P.B.; Mowry, T.C. Ambit: In-Memory Accelerator for Bulk Bitwise Operations Using Commodity DRAM Technology. In Proceedings of the 2017 50th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Cambridge, MA, USA, 14–18 October 2017; pp. 273–287. [Google Scholar] [CrossRef]
- Li, S.; Niu, D.; Malladi, K.T.; Zheng, H.; Brennan, B.; Xie, Y. DRISA: A DRAM-based Reconfigurable In-Situ Accelerator. In Proceedings of the 2017 50th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Cambridge, MA, USA, 14–18 October 2017; pp. 288–301. [Google Scholar] [CrossRef]
- Valavi, H.; Ramadge, P.J.; Nestler, E.; Verma, N. A 64-Tile 2.4-Mb In-Memory-Computing CNN Accelerator Employing Charge-Domain Compute. IEEE J. Solid-State Circuits 2019, 54, 1789–1799. [Google Scholar] [CrossRef]
- Biswas, A.; Chandrakasan, A.P. CONV-SRAM: An Energy-Efficient SRAM With In-Memory Dot-Product Computation for Low-Power Convolutional Neural Networks. IEEE J. Solid-State Circuits 2019, 54, 217–230. [Google Scholar] [CrossRef]
- Burr, G.W.; Kurdi, B.N.; Scott, J.C.; Lam, C.H.; Gopalakrishnan, K.; Shenoy, R.S. Overview of candidate device technologies for storage-class memory. IBM J. Res. Dev. 2008, 52, 449–464. [Google Scholar] [CrossRef]
- Nirschl, T.; Philipp, J.B.; Happ, T.D.; Burr, G.W.; Rajendran, B.; Lee, M.H.; Schrott, A.; Yang, M.; Breitwisch, M.; Chen, C.F.; et al. Write strategies for 2 and 4-bit multi-level phase-change memory. In Proceedings of the Technical Digest—International Electron Devices Meeting, IEDM, Washington, DC, USA, 10–12 December 2007; pp. 461–464. [Google Scholar] [CrossRef]
- Baldo, M.; Petroni, E.; Laurin, L.; Samanni, G.; Melinc, O.; Ielmini, D.; Redaelli, A. Interaction between forming pulse and integration process flow in ePCM. In Proceedings of the 2022 17th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Villasimius, Italy, 12–15 June 2022; pp. 145–148. [Google Scholar] [CrossRef]
- Laurin, L.; Baldo, M.; Petroni, E.; Samanni, G.; Turconi, L.; Motta, A.; Borghi, M.; Serafini, A.; Codegoni, D.; Scuderi, M.; et al. Unveiling Retention Physical Mechanism of Ge-rich GST ePCM Technology. In Proceedings of the 2023 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 26–30 March 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Burr, G.W.; Brightsky, M.J.; Sebastian, A.; Cheng, H.Y.; Wu, J.Y.; Kim, S.; Sosa, N.E.; Papandreou, N.; Lung, H.L.; Pozidis, H.; et al. Recent Progress in Phase-Change Memory Technology. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 146–162. [Google Scholar] [CrossRef]
- Boniardi, M.; Baldo, M.; Allegra, M.; Redaelli, A. Phase Change Memory: A Review on Electrical Behavior and Use in Analog In-Memory-Computing (A-IMC) Applications. Adv. Electron. Mater. 2024, 10, 2400599. [Google Scholar] [CrossRef]
- Close, G.F.; Frey, U.; Morrish, J.; Jordan, R.; Lewis, S.C.; Maffitt, T.; BrightSky, M.J.; Hagleitner, C.; Lam, C.H.; Eleftheriou, E. A 256-Mcell Phase-Change Memory Chip Operating at 2+ Bit/Cell. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1521–1533. [Google Scholar] [CrossRef]
- Mackin, C.; Rasch, M.; Chen, A. Optimised weight programming for analogue memory-based deep neural networks. Nat. Commun. 2022, 13, 3765. [Google Scholar] [CrossRef]
- Antolini, A.; Lico, A.; Scarselli, E.F.; Carissimi, M.; Pasotti, M. Phase-change memory cells characterization in an analog in-memory computing perspective. In Proceedings of the 2022 17th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Villasimius, Italy, 12–15 June 2022; pp. 233–236. [Google Scholar] [CrossRef]
- Joshi, V.; Le Gallo, M.; Haefeli, S.; Boybat, I.; Nandakumar, S.R.; Piveteau, C.; Dazzi, M.; Rajendran, B.; Sebastian, A.; Eleftheriou, E. Accurate deep neural network inference using computational phase-change memory. Nat. Commun. 2020, 11, 2473. [Google Scholar] [CrossRef]
- Paolino, C.; Antolini, A.; Pareschi, F.; Mangia, M.; Rovatti, R.; Scarselli, E.F.; Setti, G.; Canegallo, R.; Carissimi, M.; Pasotti, M. Phase-Change Memory in Neural Network Layers with Measurements-based Device Models. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022; pp. 1536–1540. [Google Scholar] [CrossRef]
- Le Gallo, M.; Sebastian, A.; Cherubini, G.; Giefers, H.; Eleftheriou, E. Compressed Sensing With Approximate Message Passing Using In-Memory Computing. IEEE Trans. Electron Devices 2018, 65, 4304–4312. [Google Scholar] [CrossRef]
- Allstot, D.; Rovatti, R.; Setti, G. Special issue on circuits, systems and algorithms for compressed sensing. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 337–339. [Google Scholar] [CrossRef]
- Antolini, A.; Zavalloni, F.; Lico, A.; Vignali, R.; Iannelli, L.; Zurla, R.; Bertolini, J.; Calvetti, E.; Pasotti, M.; Scarselli, E.F.; et al. Controlled Acceleration of PCM Cells Time Drift Through On-Chip Current-Induced Annealing for AIMC Multilevel MVM Computation. IEEE Trans. Electron Devices 2025, 72, 215–221. [Google Scholar] [CrossRef]
- Antolini, A.; Lico, A.; Zavalloni, F.; Scarselli, E.F.; Gnudi, A.; Torres, M.L.; Canegallo, R.; Pasotti, M. A Readout Scheme for PCM-Based Analog In-Memory Computing with Drift Compensation Through Reference Conductance Tracking. IEEE Open J. Solid-State Circuits Soc. 2024, 4, 69–82. [Google Scholar] [CrossRef]
- Carissimi, M.; Auricchio, C.; Calvetti, E.; Capecchi, L.; Torres, M.; Zanchi, S.; Gupta, P.; Zurla, R.; Cabrini, A.; Gallinari, D.; et al. An Extended Temperature Range ePCM Memory in 90-nm BCD for Smart Power Applications. In Proceedings of the ESSCIRC 2022—IEEE 48th European Solid State Circuits Conference (ESSCIRC), Milan, Italy, 19–22 September 2022; pp. 373–376. [Google Scholar] [CrossRef]
- Khaddam-Aljameh, R.; Stanisavljevic, M.; Fornt Mas, J.; Karunaratne, G.; Brändli, M.; Liu, F.; Singh, A.; Müller, S.M.; Egger, U.; Petropoulos, A.; et al. HERMES-Core—A 1.59-TOPS/mm2 PCM on 14-nm CMOS In-Memory Compute Core Using 300-ps/LSB Linearized CCO-Based ADCs. IEEE J. Solid-State Circuits 2022, 57, 1027–1038. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Nair, V.; Hinton, G. CIFAR-10 Database (Canadian Institute for Advanced Research). Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 22 February 2025).
- Pistolesi, L.; Glukhov, A.; de Gracia Herranz, A.; Lopez-Vallejo, M.; Carissimi, M.; Pasotti, M.; Rolandi, P.; Redaelli, A.; Martín, I.M.; Bianchi, S.; et al. Drift Compensation in Multilevel PCM for in-Memory Computing Accelerators. In Proceedings of the 2024 IEEE International Reliability Physics Symposium (IRPS), Grapevine, TX, USA, 14–18 April 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Khwa, W.S.; Chiu, Y.C.; Jhang, C.J.; Huang, S.P.; Lee, C.Y.; Wen, T.H.; Chang, F.C.; Yu, S.M.; Lee, T.Y.; Chang, M.F. A 40-nm, 2M-Cell, 8b-Precision, Hybrid SLC-MLC PCM Computing-in-Memory Macro with 20.5–65.0 TOPS/W for Tiny-Al Edge Devices. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; Volume 65, pp. 1–3. [Google Scholar] [CrossRef]
- Antolini, A.; Lico, A.; Franchi Scarselli, E.; Gnudi, A.; Perilli, L.; Torres, M.L.; Carissimi, M.; Pasotti, M.; Canegallo, R.A. An embedded PCM Peripheral Unit adding Analog MAC In Memory Computing Feature addressing Non linearity and Time Drift Compensation. In Proceedings of the 2022 IEEE 48th European Solid State Circuit Research (ESSCIRC), Milan, Italy, 19–22 September 2022; pp. 109–112. [Google Scholar] [CrossRef]
- Khaddam-Aljameh, R.; Stanisavljevic, M.; Mas, J.F.; Karunaratne, G.; Braendli, M.; Liu, F.; Singh, A.; Müller, S.M.; Egger, U.; Petropoulos, A.; et al. HERMES Core—A 14 nm CMOS and PCM-based In-Memory Compute Core using an array of 300 ps/LSB Linearized CCO-based ADCs and local digital processing. In Proceedings of the 2021 Symposium on VLSI Technology, Kyoto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Le Gallo, M.; Khaddam-Aljameh, R.; Stanisavljevic, M.; Vasilopoulos, A.; Kersting, B.; Dazzi, M.; Karunaratne, G.; Brändli, M.; Singh, A.; Müller, S.M.; et al. A 64-core mixed-signal in-memory compute chip based on phase-change memory for deep neural network inference. Nat. Electron. 2023, 6, 680–693. [Google Scholar] [CrossRef]
- Paolino, C.; Pareschi, F.; Mangia, M.; Rovatti, R.; Setti, G. A Practical Architecture for SAR-based ADCs with Embedded Compressed Sensing Capabilities. In Proceedings of the 15th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Lausanne, Switzerland, 15–18 July 2019; pp. 133–136. [Google Scholar] [CrossRef]
- Renna, F.; Rodrigues, M.R.; Chen, M.; Calderbank, R.; Carin, L. Compressive sensing for incoherent imaging systems with optical constraints. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 5484–5488. [Google Scholar] [CrossRef]
- Ye, P.; Paredes, J.L.; Arce, G.R.; Wu, Y.; Chen, C.; Prather, D.W. Compressive confocal microscopy. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Taipei, Taiwan, 19–24 April 2009; pp. 429–432. [Google Scholar] [CrossRef]
- Paolino, C.; Antolini, A.; Zavalloni, F.; Lico, A.; Franchi Scarselli, E.; Mangia, M.; Marchioni, A.; Pareschi, F.; Setti, G.; Rovatti, R.; et al. Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing. J. Low Power Electron. Appl. 2023, 13, 17. [Google Scholar] [CrossRef]
- Paolino, C.; Antolini, A.; Pareschi, F.; Mangia, M.; Rovatti, R.; Scarselli, E.F.; Gnudi, A.; Setti, G.; Canegallo, R.; Carissimi, M.; et al. Compressed Sensing by Phase Change Memories: Coping with encoder non-linearities. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Manchanda, R.; Sharma, K. A Review of Reconstruction Algorithms in Compressive Sensing. In Proceedings of the 2020 International Conference on Advances in Computing, Communication and Materials (ICACCM), Dehradun, India, 21–22 August 2020; pp. 322–325. [Google Scholar] [CrossRef]
- Gharehbaghi, V.R.; Farsangi, E.N.; Noori, M.; Yang, T.Y.; Li, S.; Nguyen, A.; Málaga-Chuquitaype, C.; Gardoni, P.; Mirjalili, S. A Critical Review on Structural Health Monitoring: Definitions, Methods, and Perspectives. Arch. Comput. Methods Eng. 2022, 29, 2209–2235. [Google Scholar] [CrossRef]
- Ragusa, E.; Zonzini, F.; De Marchi, L.; Zunino, R. Compression–Accuracy Co-Optimization Through Hardware-Aware Neural Architecture Search for Vibration Damage Detection. IEEE Internet Things J. 2024, 11, 31745–31757. [Google Scholar] [CrossRef]
- Sonbul, O.S.; Rashid, M. Algorithms and Techniques for the Structural Health Monitoring of Bridges: Systematic Literature Review. Sensors 2023, 23, 4230. [Google Scholar] [CrossRef]
- Quqa, S.; Antolini, A.; Scarselli, E.F.; Gnudi, A.; Lico, A.; Carissimi, M.; Pasotti, M.; Canegallo, R.; Landi, L.; Diotallevi, P.P. Phase Change Memories in Smart Sensing Solutions for Structural Health Monitoring. J. Comput. Civ. Eng. 2022, 36, 04022013. [Google Scholar] [CrossRef]
- Quqa, S.; Landi, L.; Paolo Diotallevi, P. Modal assurance distribution of multivariate signals for modal identification of time-varying dynamic systems. Mech. Syst. Signal Process. 2021, 148, 107136. [Google Scholar] [CrossRef]
- Schenke, M.; Kirchgässner, W.; Wallscheid, O. Controller Design for Electrical Drives by Deep Reinforcement Learning: A Proof of Concept. IEEE Trans. Ind. Inform. 2020, 16, 4650–4658. [Google Scholar] [CrossRef]
- Zavalloni, F.; Antolini, A.; Torres, M.L.; Nicolosi, A.; D’Angelo, F.; Lico, A.; Franchi Scarselli, E.; Pasotti, M. Drift-Tolerant Implementation of a Neural Network on a PCM-Based Analog In-Memory Computing Unit for Motor Control Applications. In Proceedings of the 2024 19th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Larnaca, Cyprus, 9–12 June 2024. [Google Scholar] [CrossRef]
- Zavalloni, F.; Antolini, A.; Lico, A.; Franchi Scarselli, E.; Torres, M.L.; Zurla, R.; Pasotti, M. A Binary Pattern Matching Task Performed in an ePCM-Based Analog In-Memory Computing Unit. In Proceedings of the SIE 2023, Noto, Italy, 6–8 September 2023; Ciofi, C., Limiti, E., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 3–11. [Google Scholar] [CrossRef]
- Matsumura, G.; Honda, S.; Kikuchi, T.; Mizuno, Y.; Hara, H.; Kondo, Y.; Nakamura, H.; Watanabe, S.; Hayakawa, K.; Nakajima, K.; et al. Real-time personal healthcare data analysis using edge computing for multimodal wearable sensors. Device 2025, 3, 100597. [Google Scholar] [CrossRef]
- Pereira, C.V.F.; de Oliveira, E.M.; de Souza, A.D. Machine Learning Applied to Edge Computing and Wearable Devices for Healthcare: Systematic Mapping of the Literature. Sensors 2024, 24, 6322. [Google Scholar] [CrossRef] [PubMed]
- Le Gallo, M.; Sebastian, A. An overview of phase-change memory device physics. J. Phys. D Appl. Phys. 2020, 53, 213002. [Google Scholar] [CrossRef]
- Boybat, I.; Le Gallo, M.; Nandakumar, S.R.; Rajendran, B.; Sebastian, A.; Eleftheriou, E. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 2018, 9, 2514. [Google Scholar] [CrossRef] [PubMed]
- Hoffer, B.; Wainstein, N.; Neumann, C.M.; Pop, E.; Yalon, E.; Kvatinsky, S. Stateful logic using phase change memory. arXiv 2023, arXiv:2212.14377. [Google Scholar] [CrossRef]
- Antolini, A.; Paolino, C.; Zavalloni, F.; Lico, A.; Franchi Scarselli, E.; Mangia, M.; Pareschi, F.; Setti, G.; Rovatti, R.; Torres, M.L.; et al. Combined HW/SW Drift and Variability Mitigation for PCM-based Analog In-memory Computing for Neural Network Applications. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 395–407. [Google Scholar] [CrossRef]
- Burr, G.W.; Shelby, R.M.; Sidler, S.; di Nolfo, C.; Jang, J.; Boybat, I.; Le Gallo, M.; Moon, K.; Woo, J.; Hwang, H.; et al. Experimental demonstration and tolerancing of a large-scale neural network (165,000 synapses) using phase-change memory as the synaptic weight element. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 4.4.1–4.4.4. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.P.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef]


| Feature | [34] (90 nm) | [35] (14 nm) | [32] (90 nm) | [33] (40 nm) |
|---|---|---|---|---|
| Focus | AIMC unit for MAC operations | High-speed PCM-based DL inference | PCM drift compensation in MLC | Hybrid SLC-MLC PCM for edge devices |
| Core innovation | Bitline readout + conductance ratio for drift correction | Linearized CCO-based ADCs + local digital processing | Differential conductance representation for drift immunity | Hybrid SLC-MLC storage + VSR-VSA + IN-R scheme |
| Accuracy | 95.56% MAC accuracy | 98.3% (MNIST), 85.6% (CIFAR-10) | 5-bit precision after 1 day at 180 °C | 0.81% degradation (CIFAR-100) |
| Energy efficiency | Not specified | 10.5 TOPS/W | Not specified | 20.5–65.0 TOPS/W |
| Performance under drift | <1% degradation after 24 h at 85 °C | High-speed operation with DL inference | error after extended drift | Enhanced signal margin and throughput |
| Application | Topic | Main Challenges | Proposed Solutions | Key Results |
|---|---|---|---|---|
| Compressed Sensing | Develop an AIMC encoder to reduce data needed for signal reconstruction | Conductance drift, programming variability | Drift compensation techniques and conductance level optimization | Reduced reconstruction error, better balance between energy consumption and accuracy |
| Structural Health Monitoring | Reduce energy consumption in structural health monitoring systems | High energy consumption of traditional systems, PCM memory instability | Convolutional filtering with PCM, reduced data transmission | 90% energy savings, high reliability even after accelerated aging |
| Motor Control | Improve the efficiency of neural networks for embedded applications | Conductance drift, precision loss over time | Periodic calibration of reference conductance | Accuracy above 96% after 5 days of operation |
| Binary Pattern Matching | Develop an efficient AIMC system for binary pattern matching | Conductance drift, programming variability | SSC programming for greater stability | Over 90% accuracy in pattern recognition |
| Category | Model | Parameters (Order of Magnitude) |
|---|---|---|
| Small networks (MNIST) | MLP, CNN | ∼– |
| Image classification | ResNet, VGG, AlexNet | ∼– |
| Natural language processing (NLP) | BERT, GPT | ∼– |
| Advanced generation | GPT-3, Stable Diffusion | ∼– |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antolini, A.; Zavalloni, F.; Lico, A.; Quqa, S.; Greco, L.; Mangia, M.; Pareschi, F.; Pasotti, M.; Franchi Scarselli, E. The Role of Phase-Change Memory in Edge Computing and Analog In-Memory Computing: An Overview of Recent Research Contributions and Future Challenges. Sensors 2025, 25, 3618. https://doi.org/10.3390/s25123618
Antolini A, Zavalloni F, Lico A, Quqa S, Greco L, Mangia M, Pareschi F, Pasotti M, Franchi Scarselli E. The Role of Phase-Change Memory in Edge Computing and Analog In-Memory Computing: An Overview of Recent Research Contributions and Future Challenges. Sensors. 2025; 25(12):3618. https://doi.org/10.3390/s25123618
Chicago/Turabian StyleAntolini, Alessio, Francesco Zavalloni, Andrea Lico, Said Quqa, Lorenzo Greco, Mauro Mangia, Fabio Pareschi, Marco Pasotti, and Eleonora Franchi Scarselli. 2025. "The Role of Phase-Change Memory in Edge Computing and Analog In-Memory Computing: An Overview of Recent Research Contributions and Future Challenges" Sensors 25, no. 12: 3618. https://doi.org/10.3390/s25123618
APA StyleAntolini, A., Zavalloni, F., Lico, A., Quqa, S., Greco, L., Mangia, M., Pareschi, F., Pasotti, M., & Franchi Scarselli, E. (2025). The Role of Phase-Change Memory in Edge Computing and Analog In-Memory Computing: An Overview of Recent Research Contributions and Future Challenges. Sensors, 25(12), 3618. https://doi.org/10.3390/s25123618








