Uncertainty Quantification of First Fix in a Time-Differenced Carrier Phase Observation Model
Abstract
1. Introduction
2. Related Work
2.1. TDCP Models
2.2. Uncertainty Quantification
2.3. Overview of Proposed Method
3. Carrier Phase Observation Model and TDCP
3.1. Carrier Phase Observation Model
3.2. TDCP Observation Model and Corrections
3.3. TDCP Model with True Receiver Position and Receiver Displacement
3.4. TDCP Model with Assumed Receiver Position and Receiver Displacement
3.5. Estimation of a Receiver Displacement and Clock Bias Difference from TDCP Observations
4. Estimation: Computation of Mean Squared Error and Its Lower Bound
4.1. Estimator of a Real Vector
4.2. Properties of the Estimator
- Since , the estimators’s mean vector is ;
- The estimator’s bias is ;
- Since , the estimator’s covariance matrix is .
4.3. Lower Bound of the Mean Squared Error of a Biased Estimator
4.4. Application to the Problem
5. Experiments
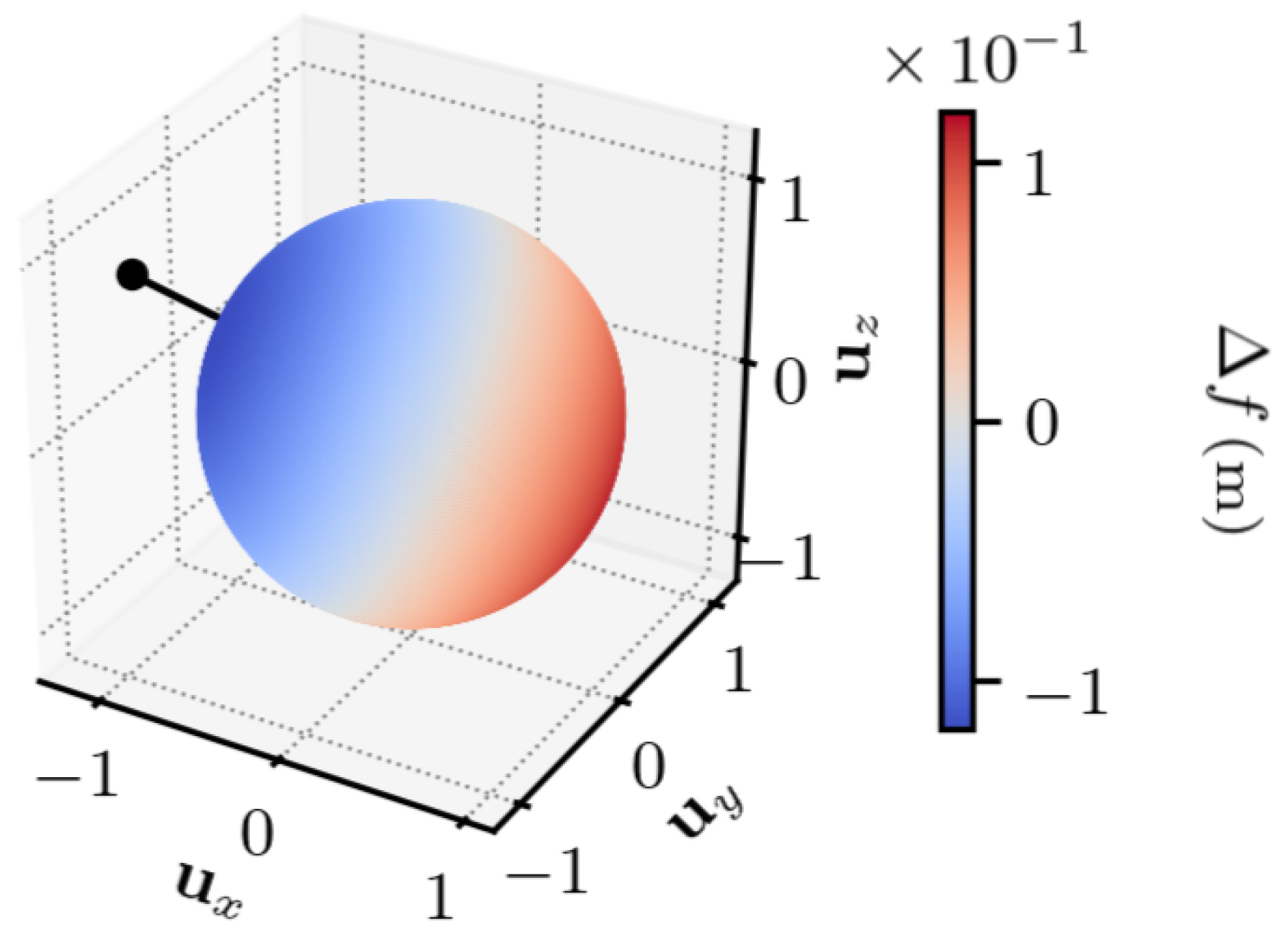
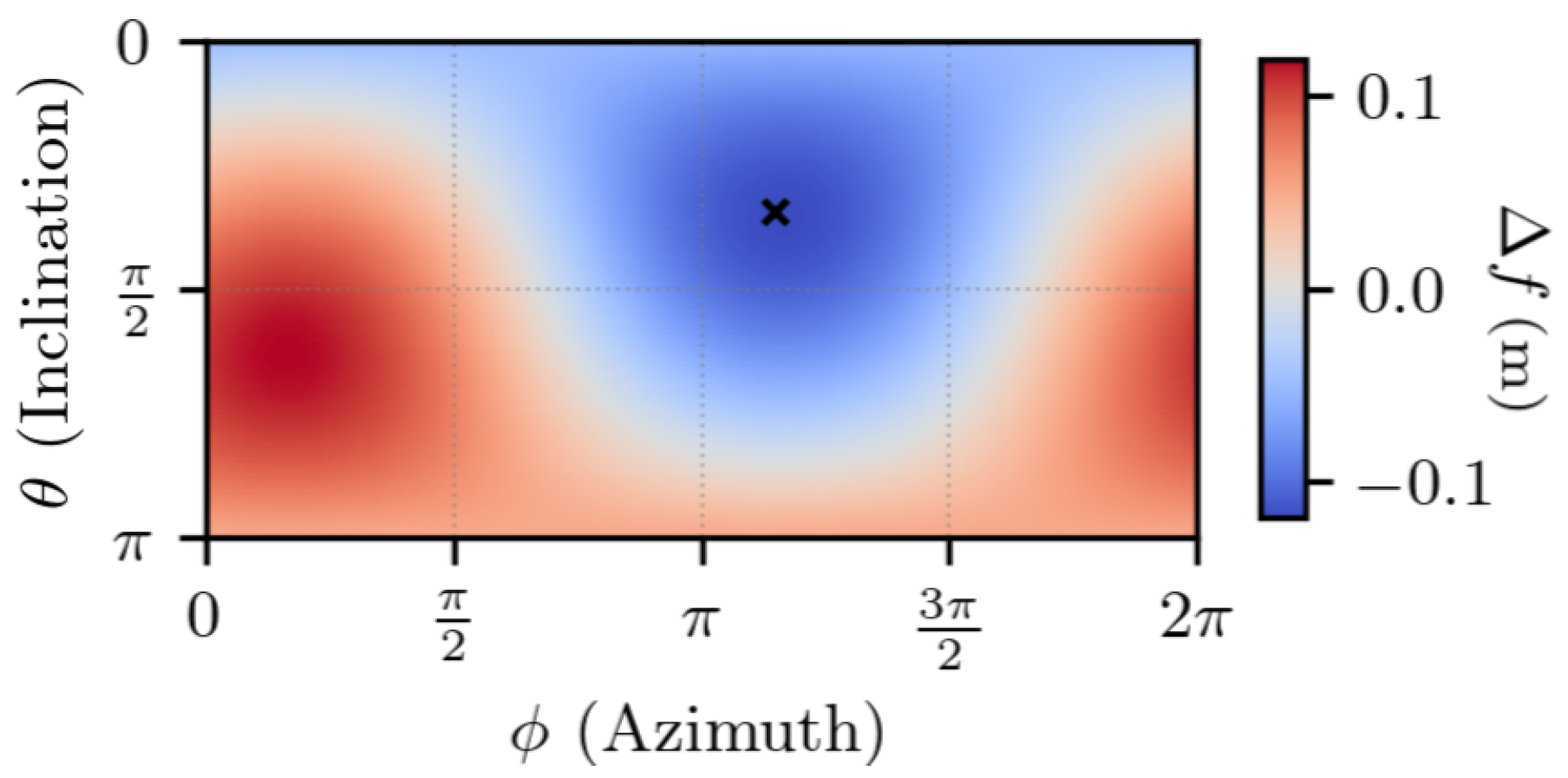
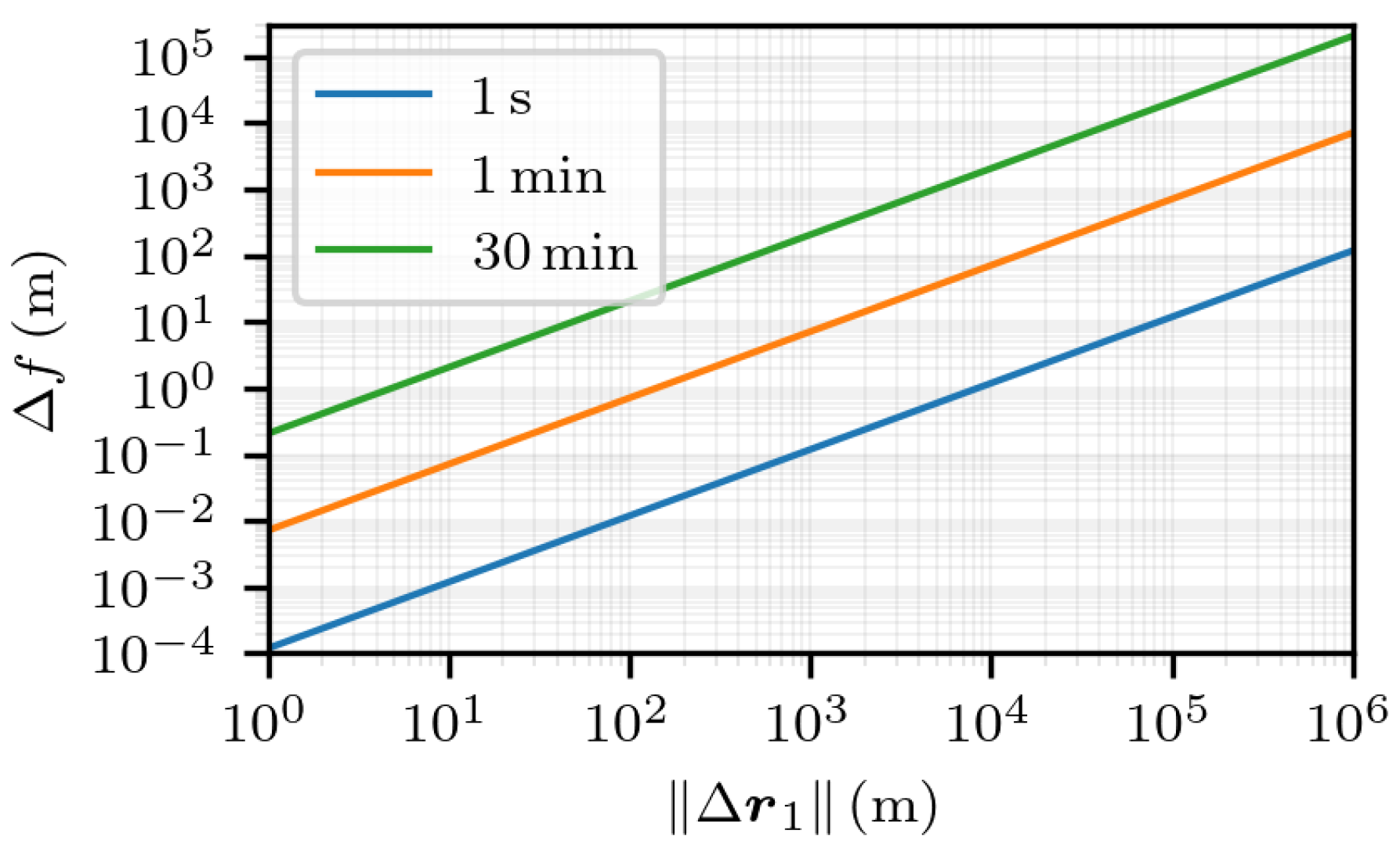
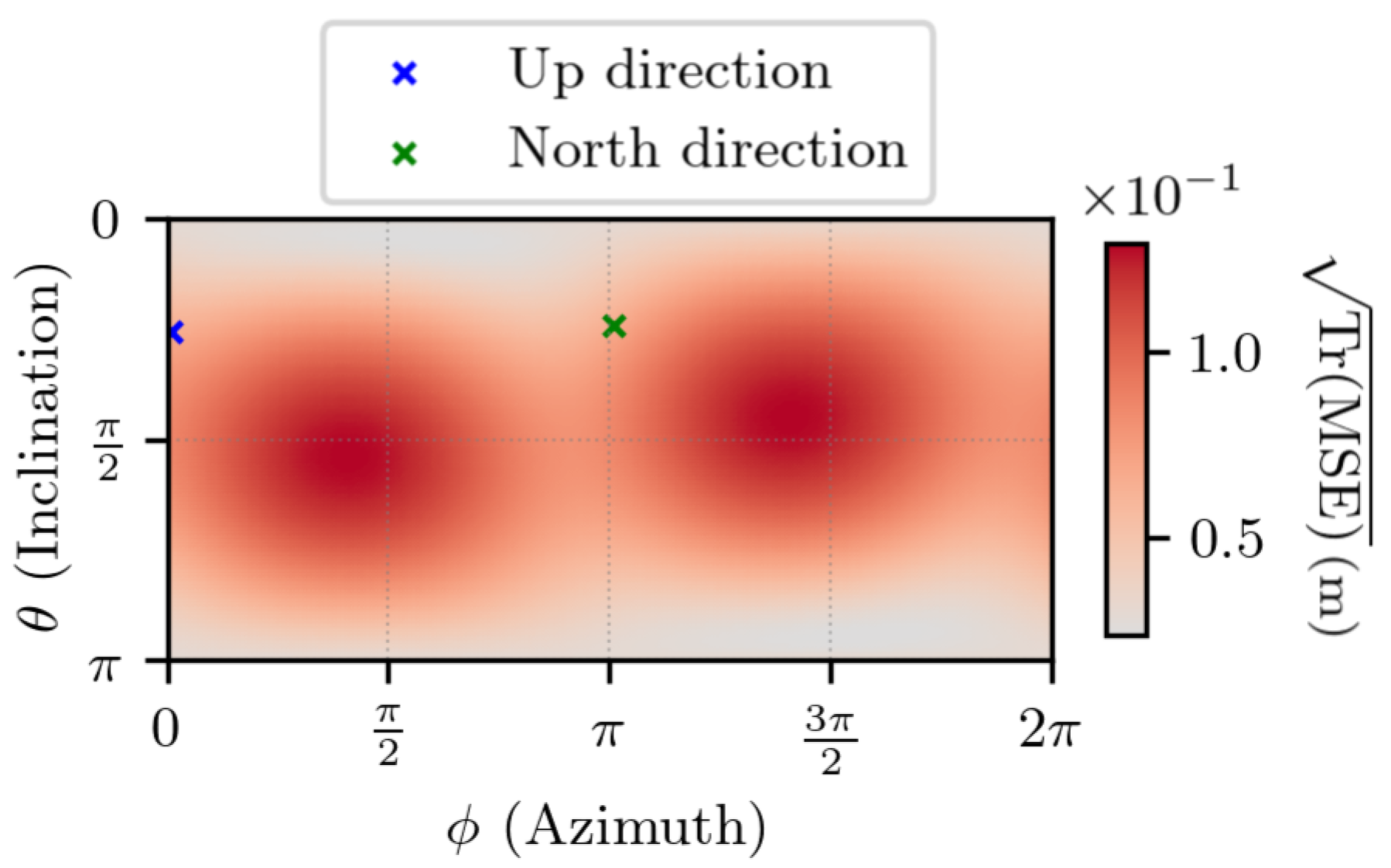
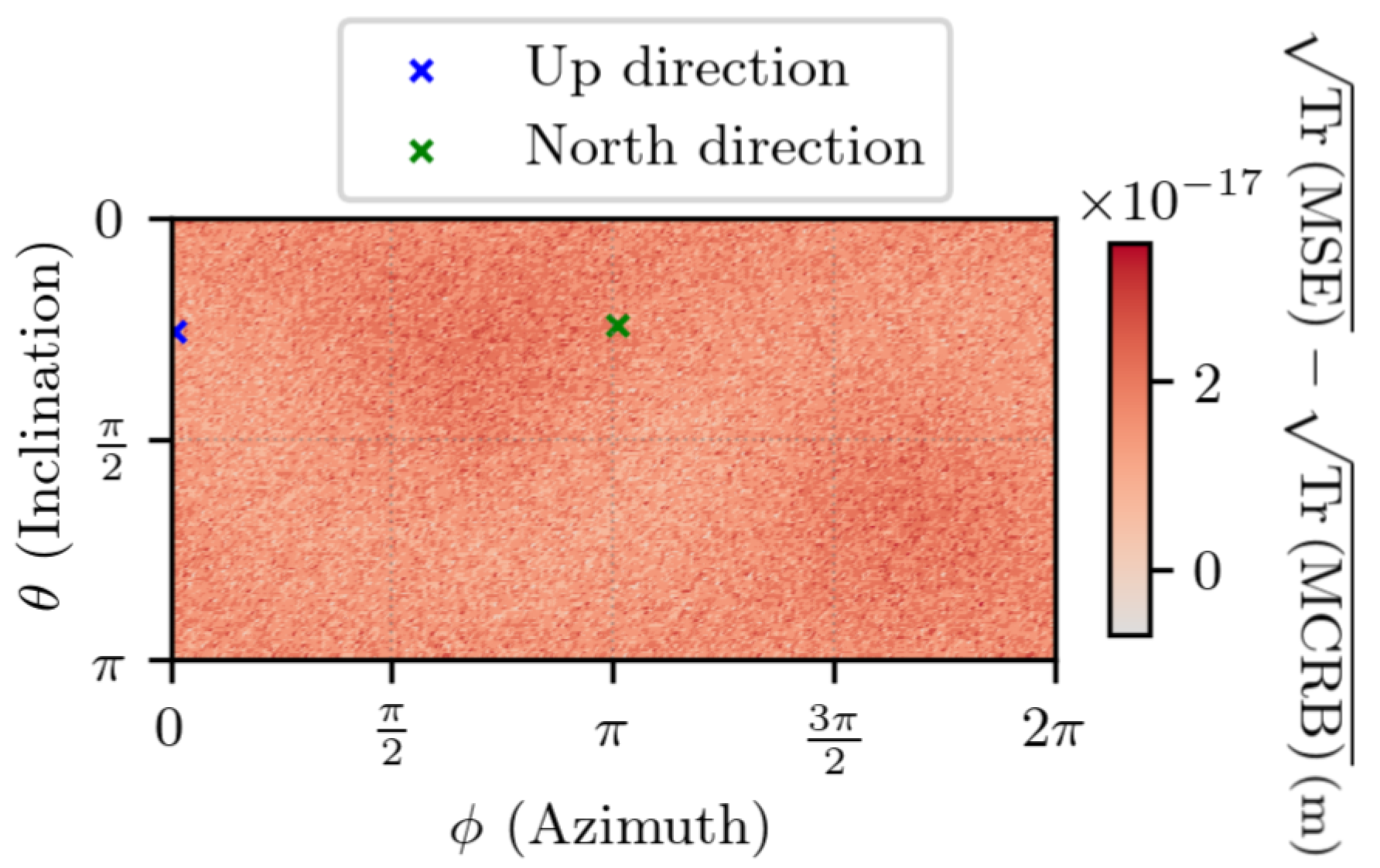
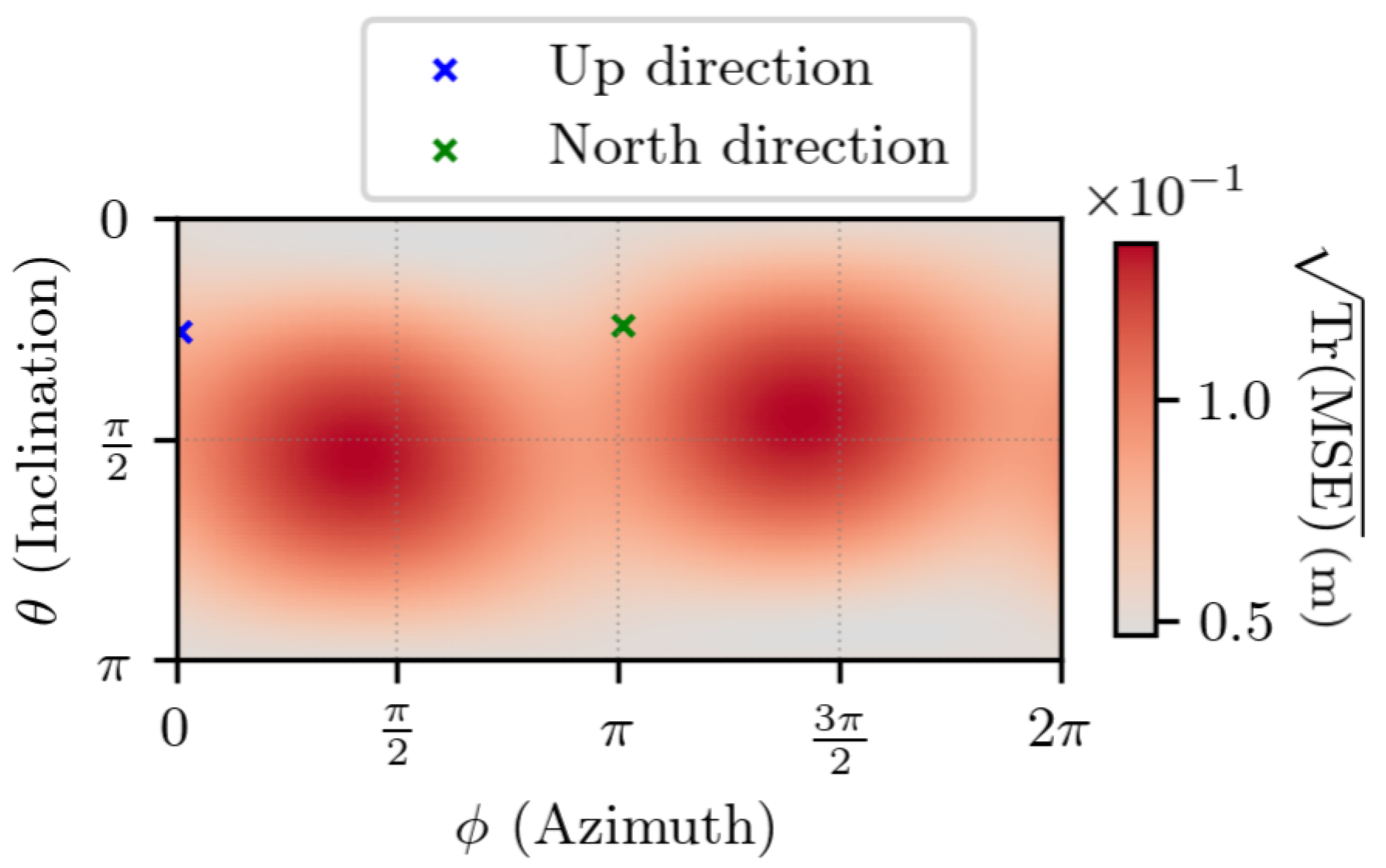
5.1. Experimental Uncertainty Quantification of TDCP Model
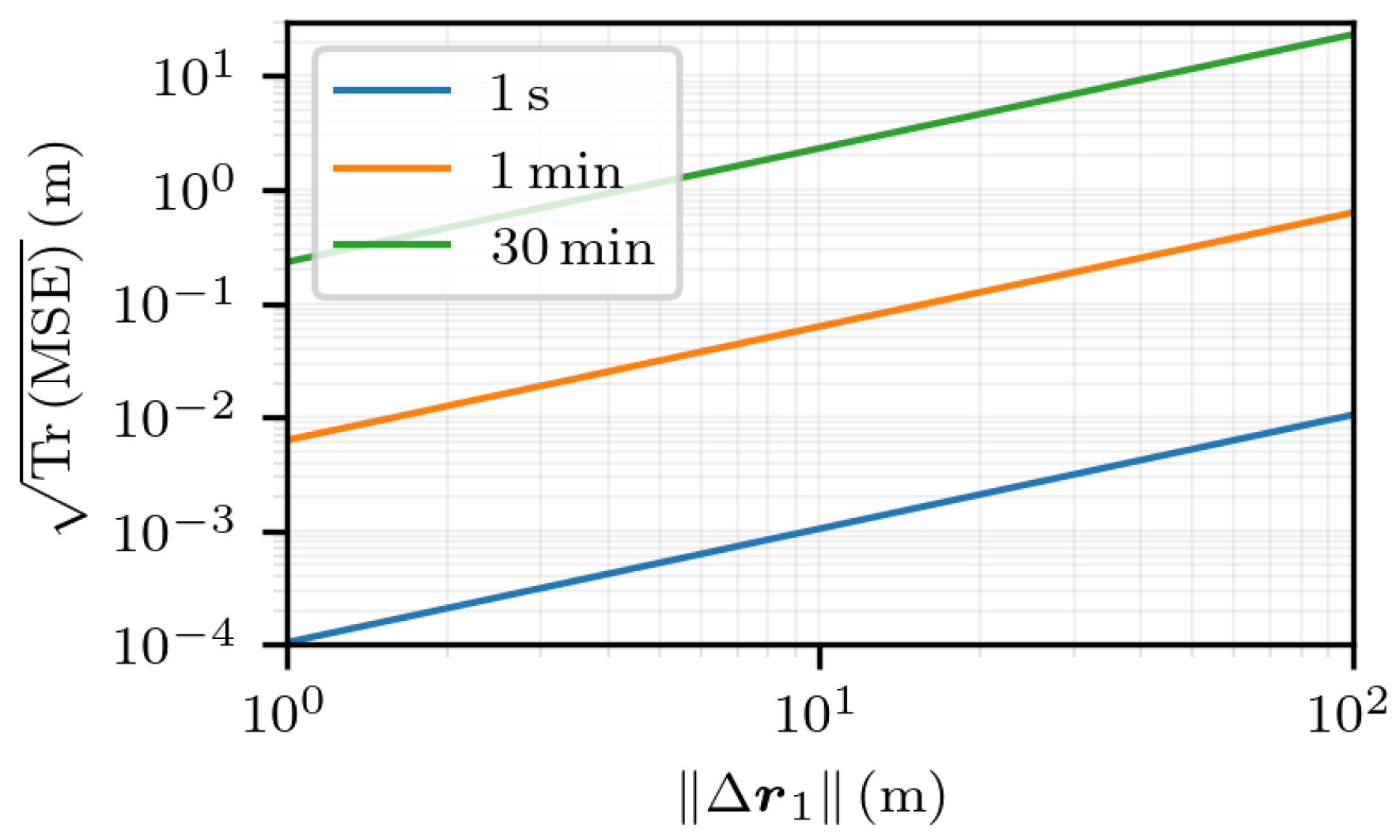
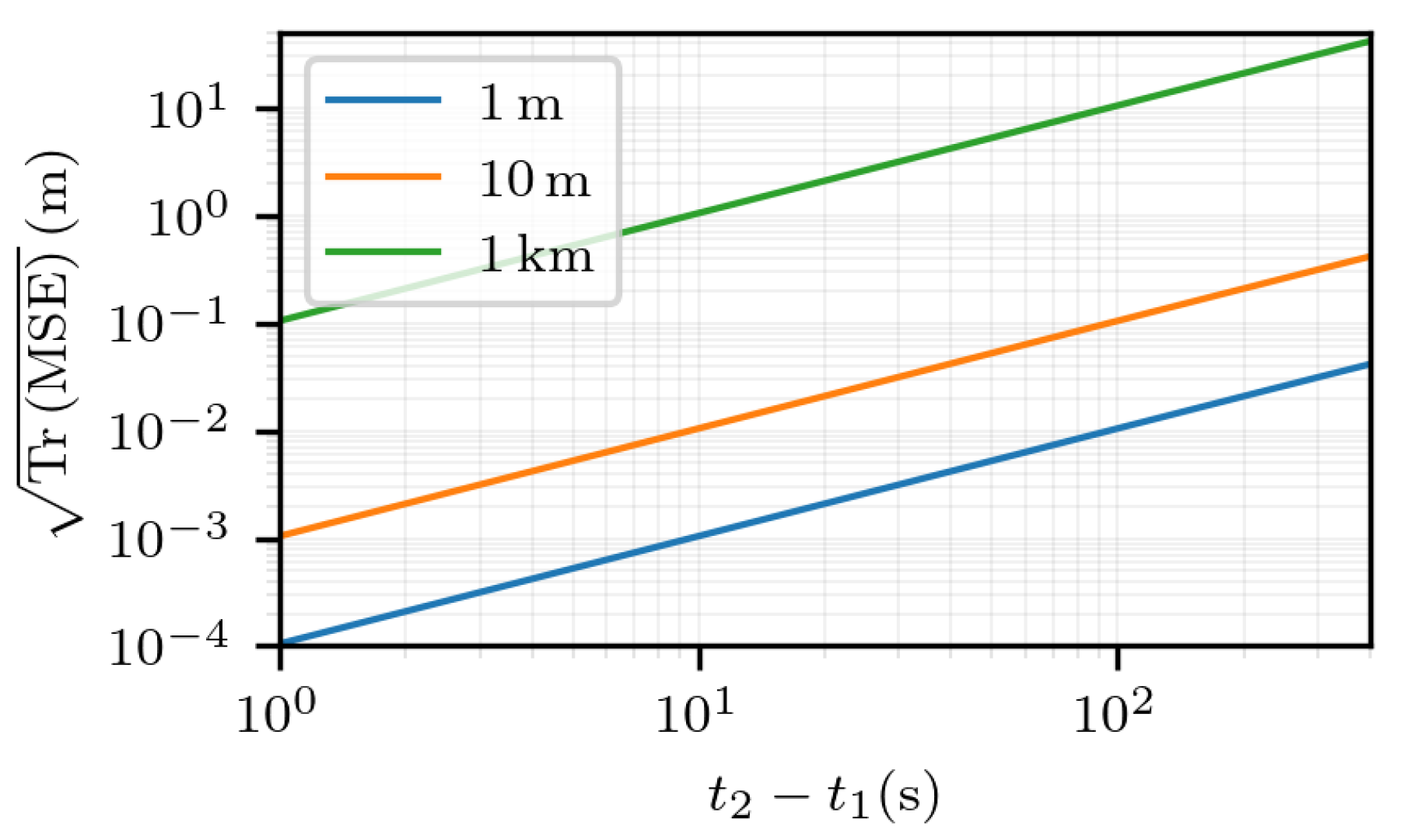
5.2. Experimental Uncertainty Quantification of Estimated Displacement with Noiseless Measurements
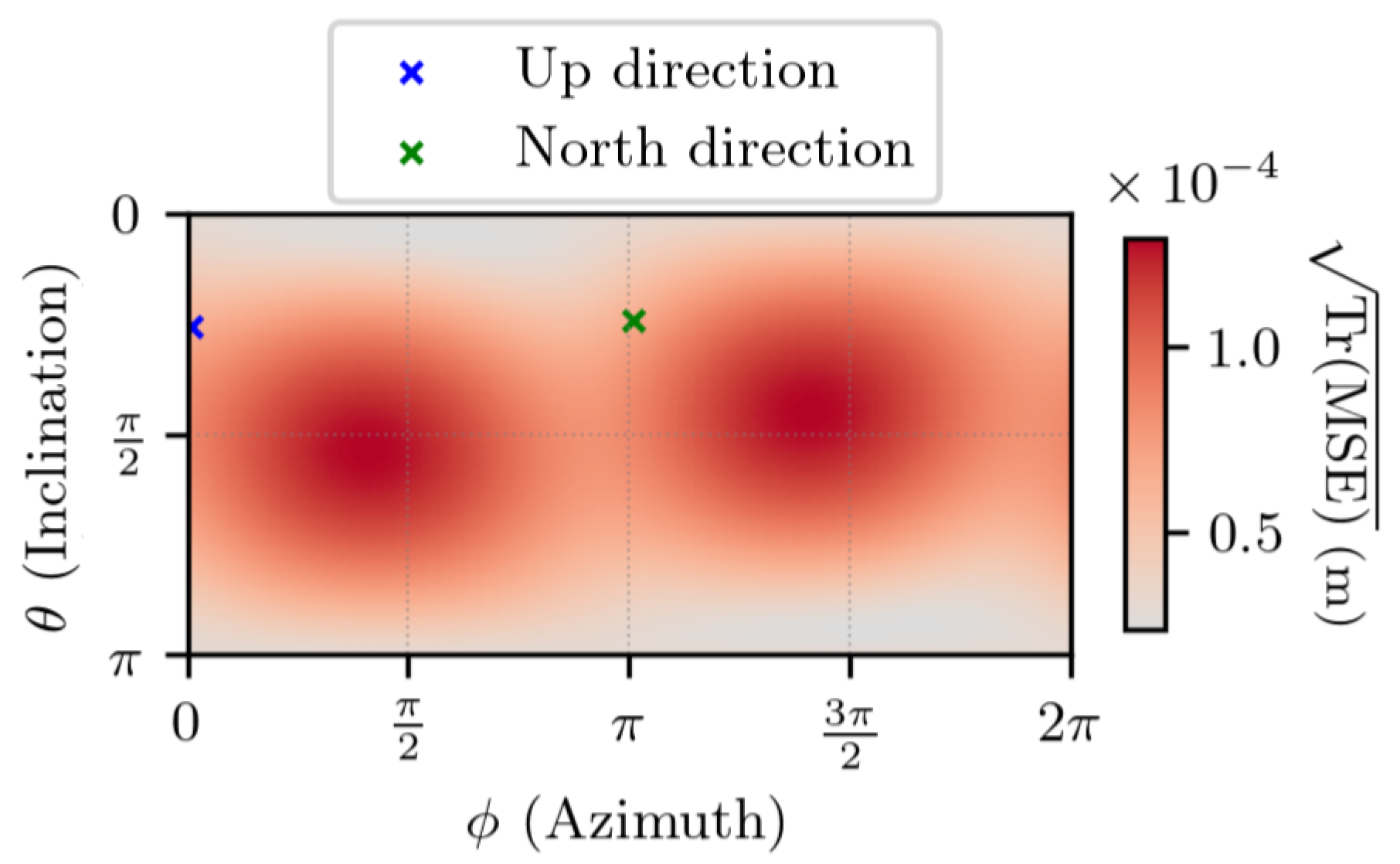
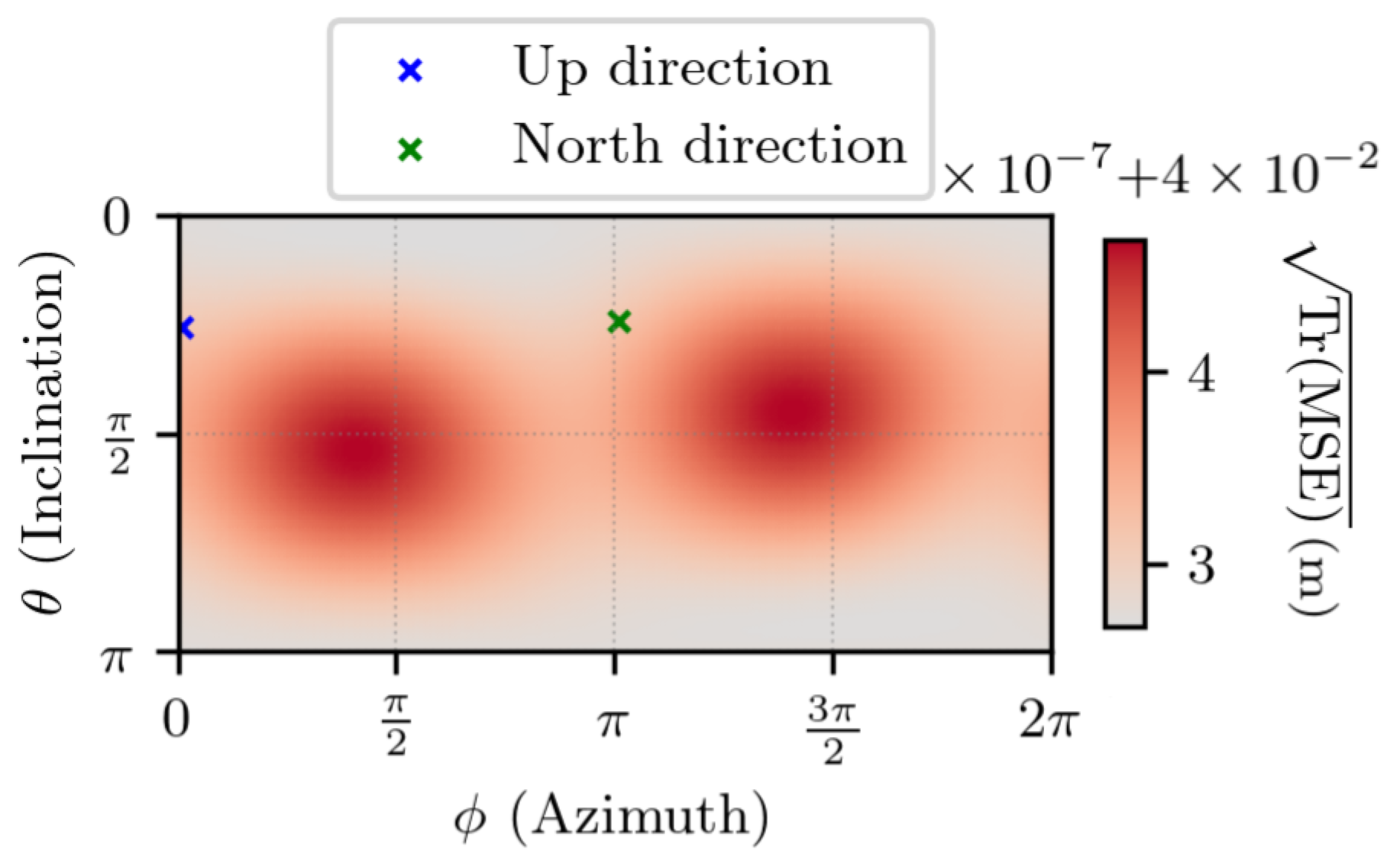
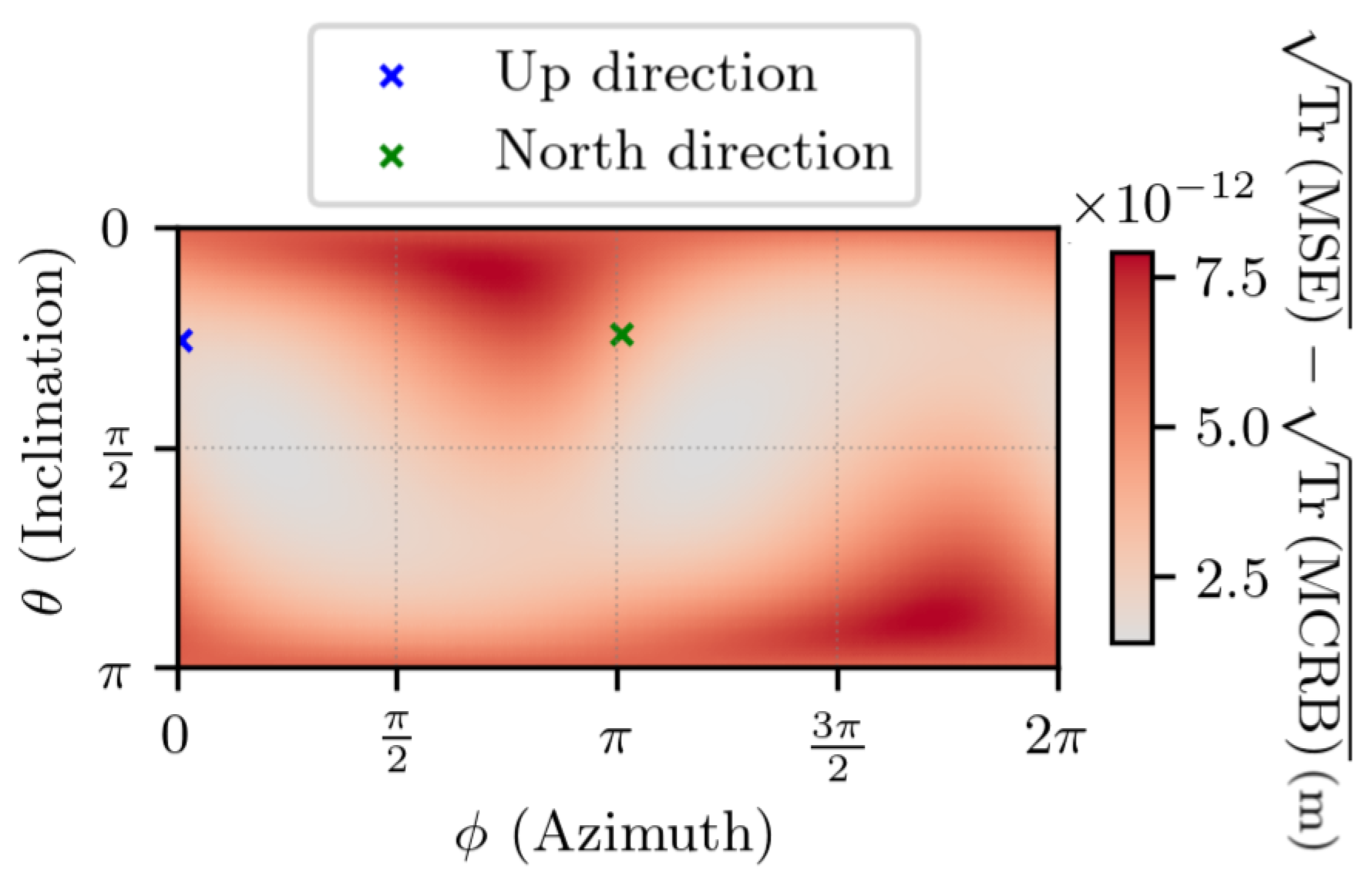
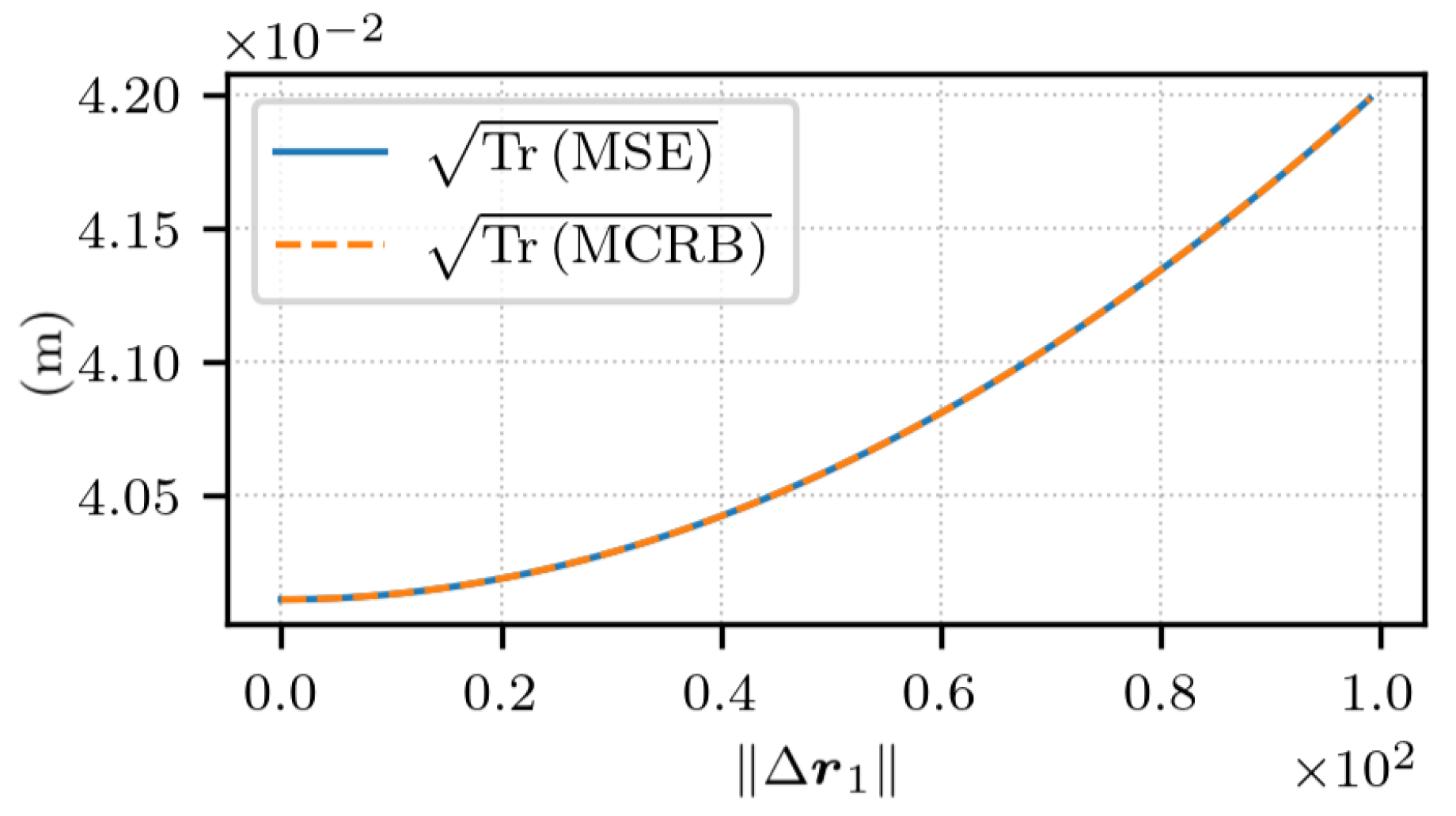
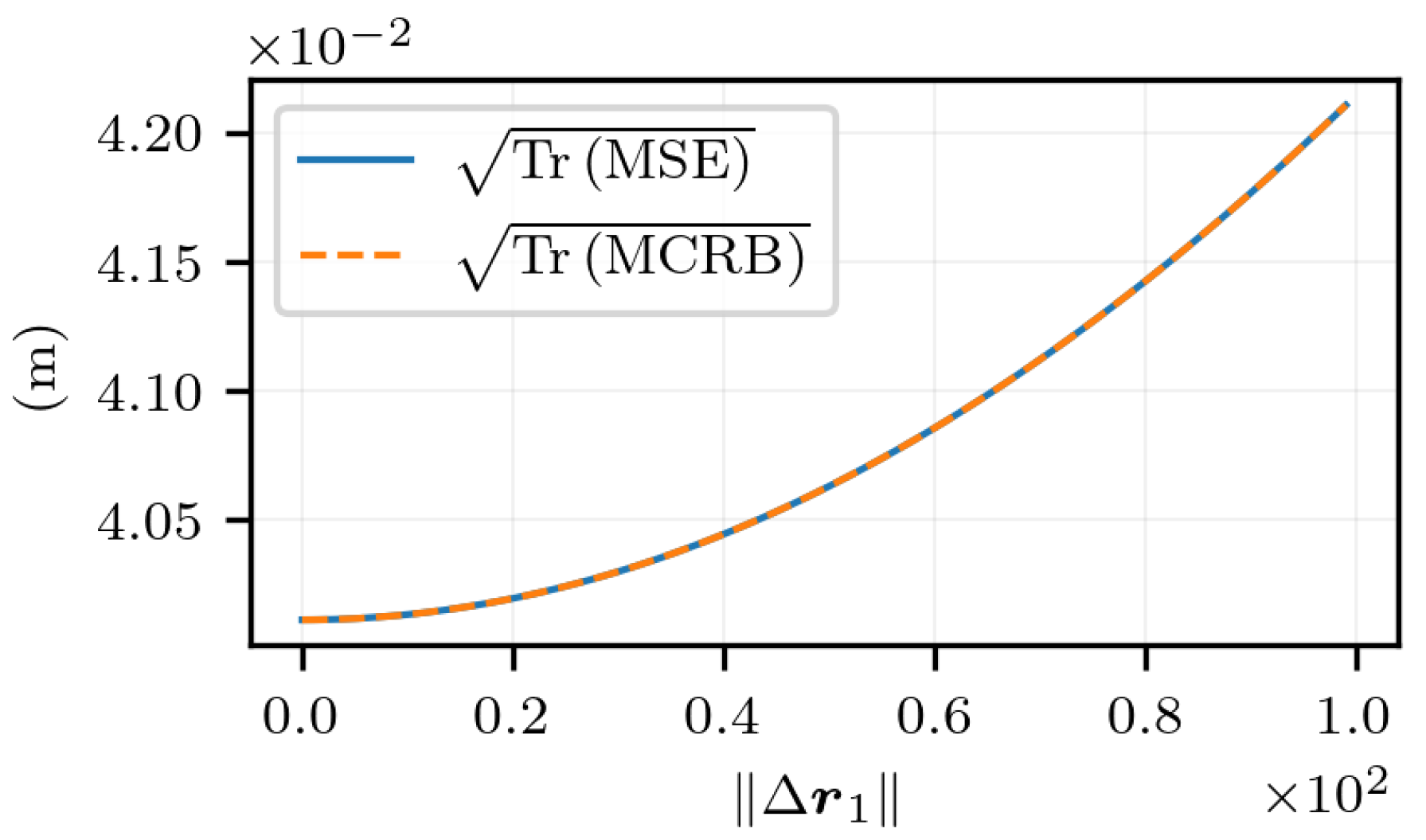
5.3. Experimental Uncertainty Quantification of Estimated Displacement with Noisy Measurements
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Direction of Null and Extremum Model Error
Appendix B. Model Error Along the Worst Direction
References
- Rustamov, R.B.; Hashimov, A.M. Multifunctional Operation and Application of GPS; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar]
- Congram, B.; Barfoot, T.D. Experimental Comparison of Visual and Single-Receiver GPS Odometry. arXiv 2021, arXiv:2106.02122. [Google Scholar]
- Kim, J.; Park, M.; Bae, Y.; Kim, O.J.; Kim, D.; Kim, B.; Kee, C. A Low-Cost, High-Precision Vehicle Navigation System for Deep Urban Multipath Environment Using TDCP Measurements. Sensors 2020, 20, 3254. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Chang, G.; Chen, C.; Zhu, T. An improved TDCP-GNSS/INS integration scheme considering small cycle slip for low-cost land vehicular applications. Meas. Sci. Technol. 2021, 32, 055006. [Google Scholar] [CrossRef]
- Ji, L.; Sun, R.; Cheng, Q.; Wang, J. Evaluation of the performance of GNSS-based velocity estimation algorithms. Satell. Navig. 2022, 3, 18. [Google Scholar] [CrossRef]
- Sun, R.; Cheng, Q.; Wang, J. Precise vehicle dynamic heading and pitch angle estimation using time-differenced measurements from a single GNSS antenna. GPS Solut. 2020, 24, 84. [Google Scholar] [CrossRef]
- Li, Z.; Wang, D.; Dong, Y.; Wu, J. An enhanced tightly-coupled integrated navigation approach using phase-derived position increment (PDPI) measurement. Optik 2018, 156, 135–147. [Google Scholar] [CrossRef]
- Suzuki, T. GNSS Odometry: Precise Trajectory Estimation Based on Carrier Phase Cycle Slip Estimation. IEEE Robot. Autom. Lett. 2022, 7, 7319–7326. [Google Scholar] [CrossRef]
- Freda, P.; Angrisano, A.; Gaglione, S.; Troisi, S. Time-differenced carrier phases technique for precise GNSS velocity estimation. GPS Solut. 2015, 19, 335–341. [Google Scholar] [CrossRef]
- Lyu, P.; Bai, S.; Lai, J.; Wang, B.; Sun, X.; Huang, K. Optimal Time Difference-Based TDCP-GPS/IMU Navigation Using Graph Optimization. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Olivier, A.; Giovanis, D.G.; Aakash, B.; Chauhan, M.; Vandanapu, L.; Shields, M.D. UQpy: A general purpose Python package and development environment for uncertainty quantification. J. Comput. Sci. 2020, 47, 101204. [Google Scholar] [CrossRef]
- Purnell, D.; Gomez, N.; Chan, N.H.; Strandberg, J.; Holland, D.M.; Hobiger, T. Quantifying the Uncertainty in Ground-Based GNSS-Reflectometry Sea Level Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4419–4428. [Google Scholar] [CrossRef]
- Martin, A.; Soundy, A.; Panckhurst, B.; Brown, C.; Schumayer, D.; Molteno, T.; Parry, M. Real-time uncertainty quantification using correlated noise models for GNSS positioning. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Su, J.; Schön, S. Deterministic Approaches for Bounding GNSS Uncertainty: A Comparative Analysis. In Proceedings of the 10th Workshop on Satellite Navigation Technology (NAVITEC), Noordwijk, The Netherlands, 5–7 April 2022; pp. 1–8. [Google Scholar]
- Richmond, C.D.; Horowitz, L.L. Parameter Bounds on Estimation Accuracy Under Model Misspecification. IEEE Trans. Signal Process. 2015, 63, 2263–2278. [Google Scholar] [CrossRef]
- Mennad, A.; Fortunati, S.; El Korso, M.N.; Younsi, A.; Zoubir, A.M.; Renaux, A. Slepian-Bangs-type formulas and the related Misspecified Cramér-Rao Bounds for Complex Elliptically Symmetric distributions. Signal Process. 2018, 142, 320–329. [Google Scholar] [CrossRef]
- Fortunati, S.; Ortega, L. On the efficiency of misspecified Gaussian inference in nonlinear regression: Application to time-delay and Doppler estimation. Signal Process. 2024, 225, 109614. [Google Scholar] [CrossRef]
- Yang, C.; Guo, J.; Geng, T.; Zhao, Q.; Jiang, K.; Xie, X.; Lv, Y. Assessment and Comparison of Broadcast Ionospheric Models: NTCM-BC, BDGIM, and Klobuchar. Remote Sens. 2020, 12, 1215. [Google Scholar] [CrossRef]
- Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Stienne, G.; Reboul, S.; Choquel, J.; Benjelloun, M. Cycle slip detection and repair with a circular on-line change-point detector. Signal Process. 2014, 100, 51–63. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006. [Google Scholar]
- Nielsen, F. Connected at Infinity II: A Selection of Mathematics by Indians; Chapter Cramér-Rao Lower Bound and Information Geometry; Hindustan Book Agency: Delhi, India, 2013; pp. 18–37. [Google Scholar]
- Eldar, Y. Minimum Variance in Biased Estimation: Bounds and Asymptotically Optimal Estimators. Trans. Sig. Proc. 2004, 52, 1915–1930. [Google Scholar] [CrossRef]
- Schöller, C.; Aravantinos, V.; Lay, F.; Knoll, A. What the Constant Velocity Model Can Teach Us About Pedestrian Motion Prediction. IEEE Robot. Autom. Lett. 2020, 5, 1696–1703. [Google Scholar] [CrossRef]
- Pellegrini, S.; Ess, A.; Van Gool, L. Visual Analysis of Humans: Looking at People; Chapter Predicting Pedestrian Trajectories; Springer: London, UK, 2011; pp. 473–491. [Google Scholar]
- Won, D.H.; Ahn, J.; Lee, S.W.; Lee, J.; Sung, S.; Park, H.W.; Park, J.P.; Lee, Y.J. Weighted DOP with Consideration on Elevation-Dependent Range Errors of GNSS Satellites. IEEE Trans. Instrum. Meas. 2012, 61, 3241–3250. [Google Scholar] [CrossRef]
| Estimation | TDCP |
|---|---|
| as in Equation (9) | as in Equation (4) |
| as in Equation (9) | |
| with as in Equation (3) | |
| g as in Equation (9) | , with as in Equation (5) |
| h as in Equation (10) | , with as in Equation (6) |
| as in Equation (9) | |
| where is the variance of Equation (3) |
| 1 s | 1 min | 30 min | ||
|---|---|---|---|---|
| 1.2 × 10−4 m | 7.1 × 10−3 m | 2.1 × 10−1 m | ||
| 1.2 × 10−3 m | 7.1 × 10−2 m | 2.1 m | ||
| 1.2 × 10−1 m | 7.1 m | 2.1 × 101 m | ||
| 1.2 × 102 m | 7.1 × 103 m | 2.1 × 105 m | ||
| 1 s | 1 min | 30 min | ||
|---|---|---|---|---|
| 2.4 × 10−5 m | 1.3 × 10−3 m | 7.7 × 10−2 m | ||
| 2.4 × 10−4 m | 1.3 × 10−2 m | 7.7 × 10−1 m | ||
| 2.4 × 10−2 m | 1.3 m | 7.7 × 101 m | ||
| 2.4 × 101 m | 1.3 × 103 m | 7 × 104 m | ||
| 1 s | 1 min | 30 min | ||
|---|---|---|---|---|
| 1.3 × 10−4 m | 7.7 × 10−3 m | 3.8 × 10−1 m | ||
| 1.3 × 10−3 m | 7.7 × 10−2 m | 3.8 m | ||
| 1.3 × 10−1 m | 7.7 m | 3.8 × 102 m | ||
| 1.3 × 102 m | 7.8 × 103 m | 3.8 × 105 m | ||
| 1 s | 1 min | 30 min | ||
|---|---|---|---|---|
| 8.8 × 10−5 m | 5.3 × 10−3 m | 1.7 × 10−1 m | ||
| 8.8 × 10−4 m | 5.3 × 10−2 m | 1.7 m | ||
| 8.8 × 10−2 m | 5.3 m | 1.7 × 102 m | ||
| 8.9 × 101 m | 5.3 × 103 m | 1.7 × 105 m | ||
| 1 s | 1 min | 30 min | ||
|---|---|---|---|---|
| 1.1 × 10−4 m | 6.7 × 10−3 m | 3.2 × 10−1 m | ||
| 1.1 × 10−3 m | 6.7 × 10−2 m | 3.2 m | ||
| 1.1 × 10−1 m | 6.7 m | 3.2 × 102 m | ||
| 1.2 × 102 m | 6.7 × 103 m | 3.2 × 105 m | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherfi, H.; Lesouple, J.; Solà, J.; Thevenon, P. Uncertainty Quantification of First Fix in a Time-Differenced Carrier Phase Observation Model. Sensors 2025, 25, 3480. https://doi.org/10.3390/s25113480
Cherfi H, Lesouple J, Solà J, Thevenon P. Uncertainty Quantification of First Fix in a Time-Differenced Carrier Phase Observation Model. Sensors. 2025; 25(11):3480. https://doi.org/10.3390/s25113480
Chicago/Turabian StyleCherfi, Hakim, Julien Lesouple, Joan Solà, and Paul Thevenon. 2025. "Uncertainty Quantification of First Fix in a Time-Differenced Carrier Phase Observation Model" Sensors 25, no. 11: 3480. https://doi.org/10.3390/s25113480
APA StyleCherfi, H., Lesouple, J., Solà, J., & Thevenon, P. (2025). Uncertainty Quantification of First Fix in a Time-Differenced Carrier Phase Observation Model. Sensors, 25(11), 3480. https://doi.org/10.3390/s25113480






