Channel Modeling for Multi-Receiver Molecular Communication System by Impulsive Force in Internet of Nano Things
Abstract
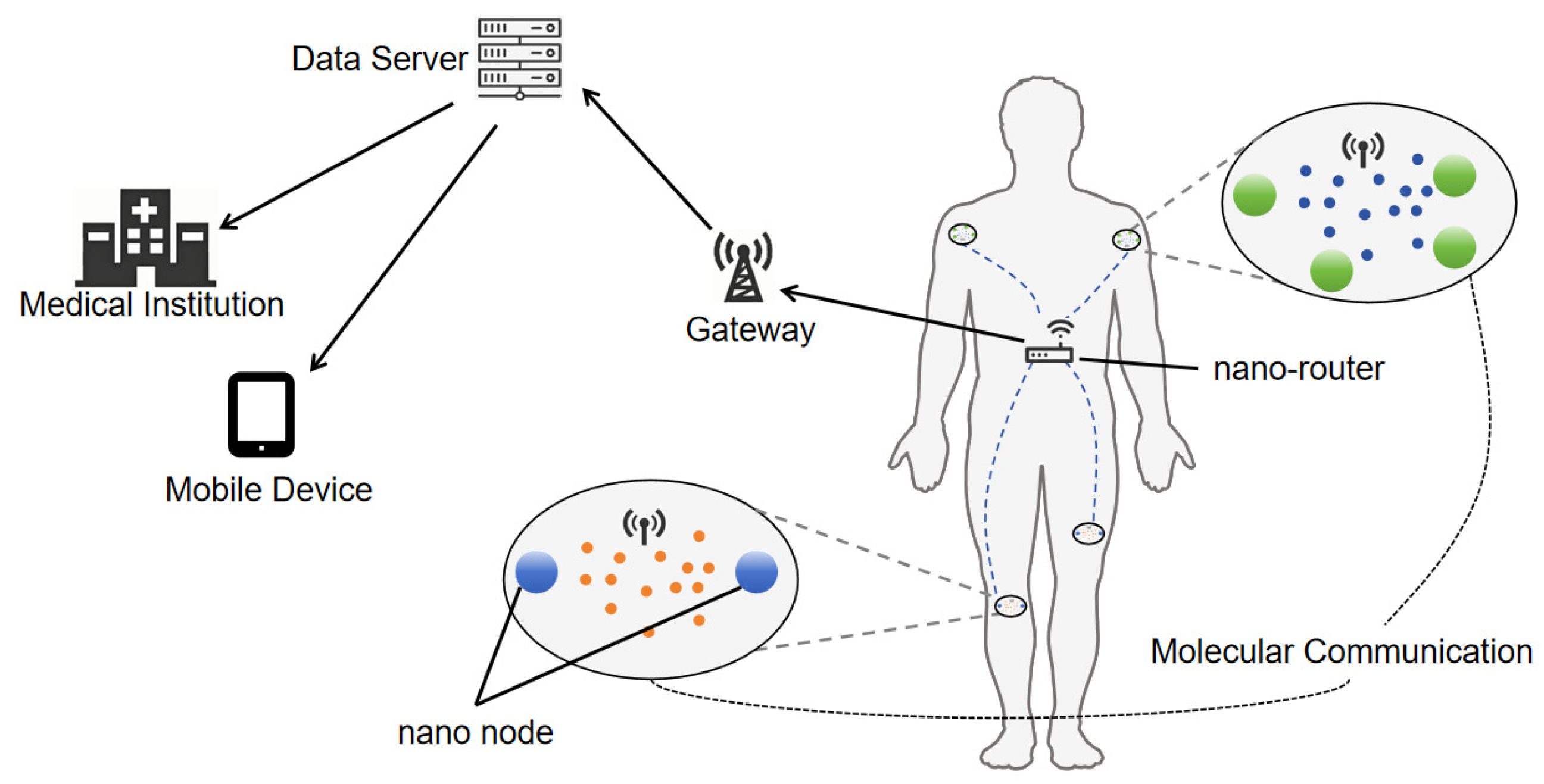
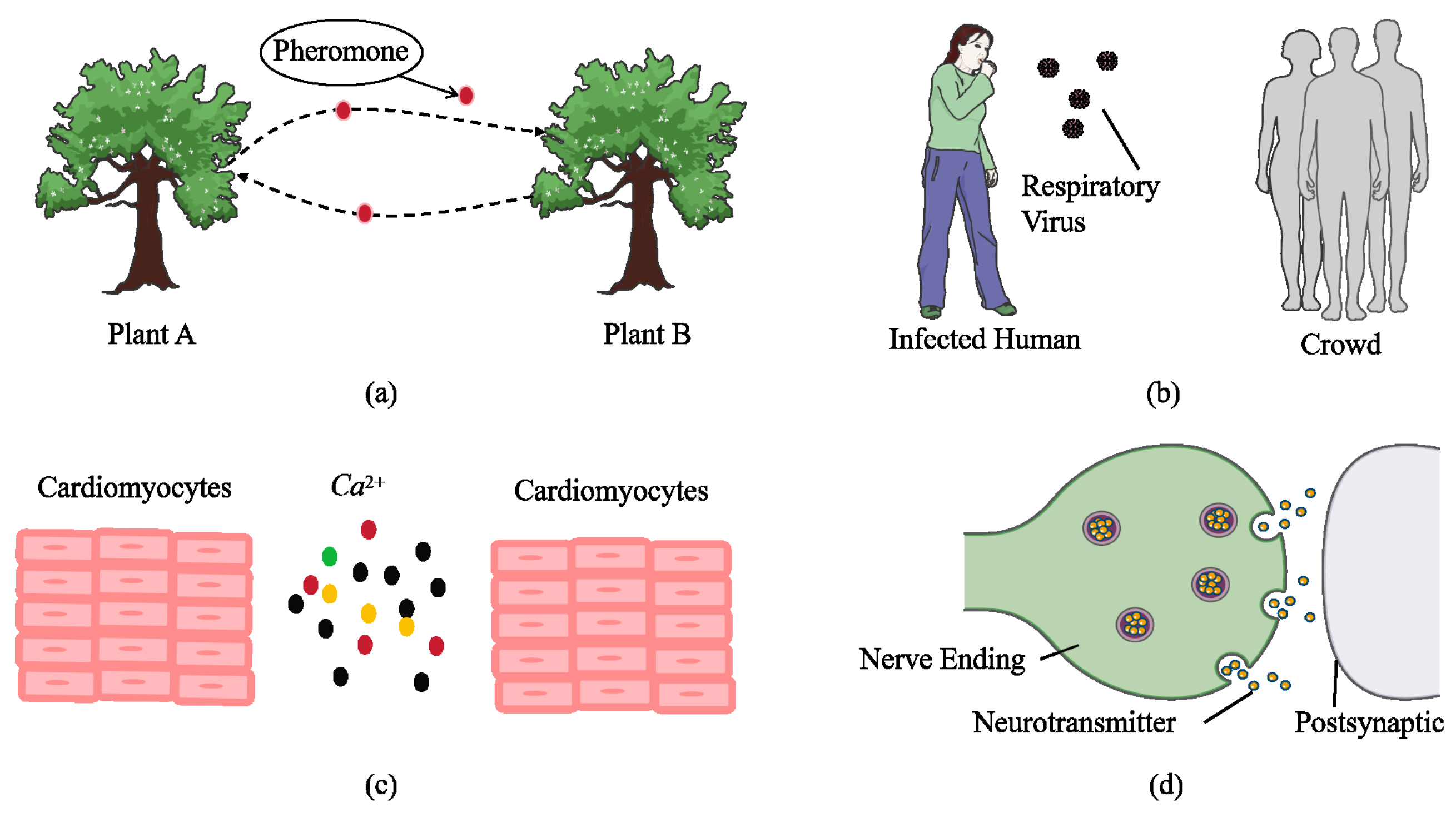
1. Introduction
2. System Model
3. Channel Modeling
3.1. Channel Impulse Response for Pulse-Assisted SISO MC System
3.2. Channel Impulse Response for SIMO MC System
4. Results
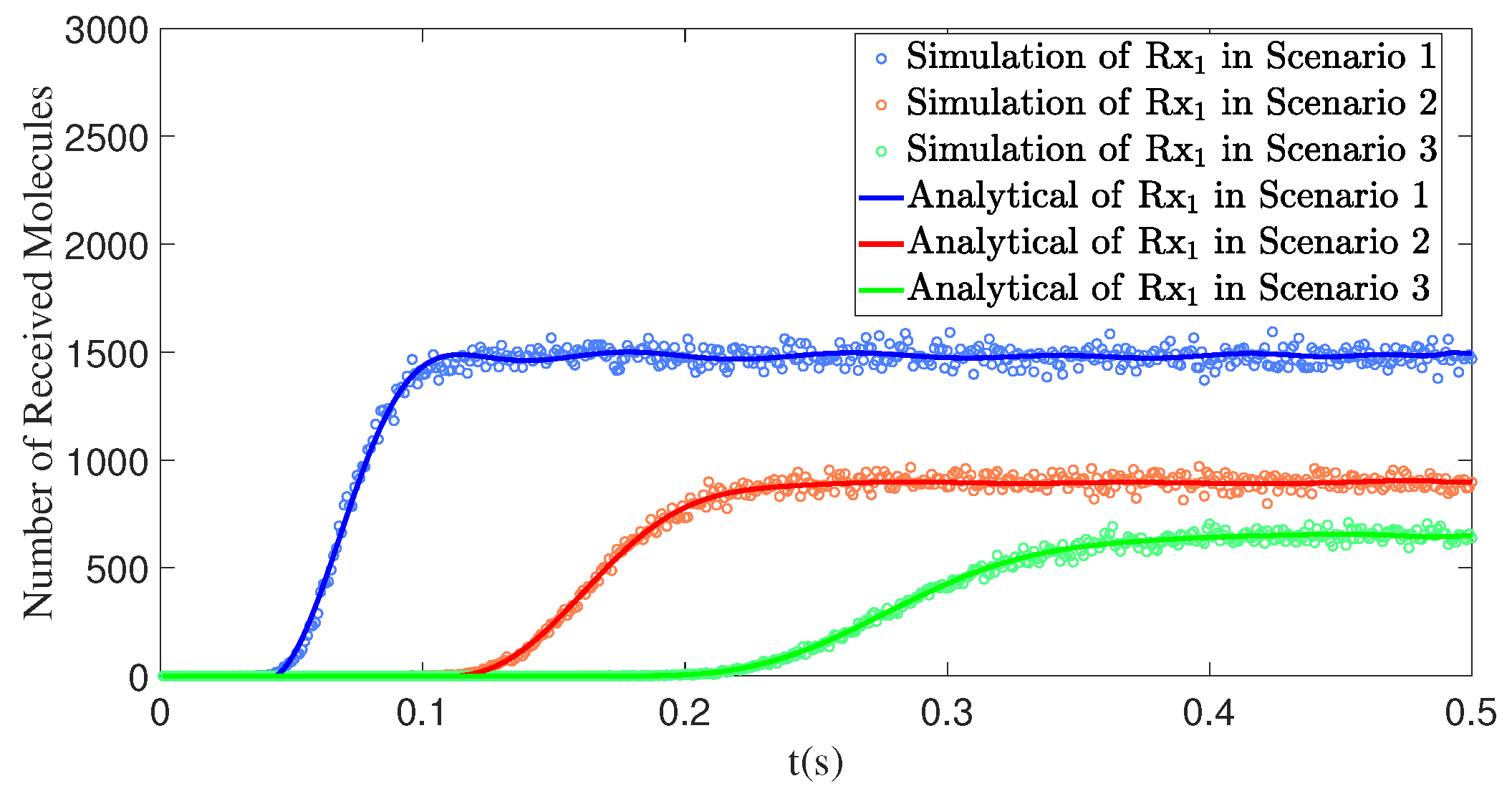
4.1. Simulation Settings
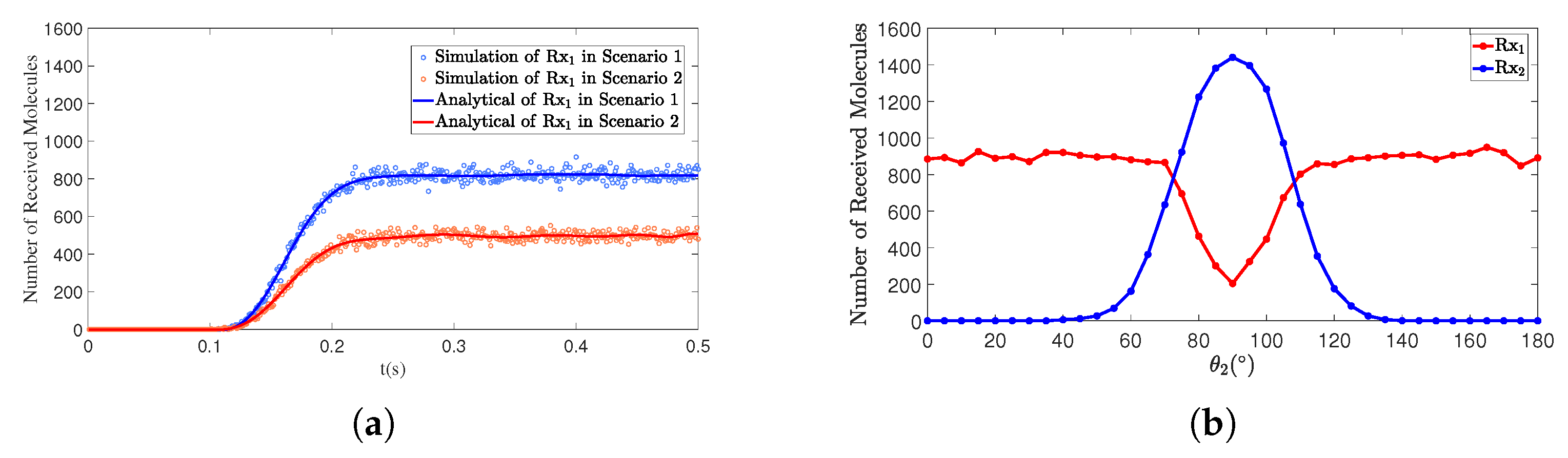
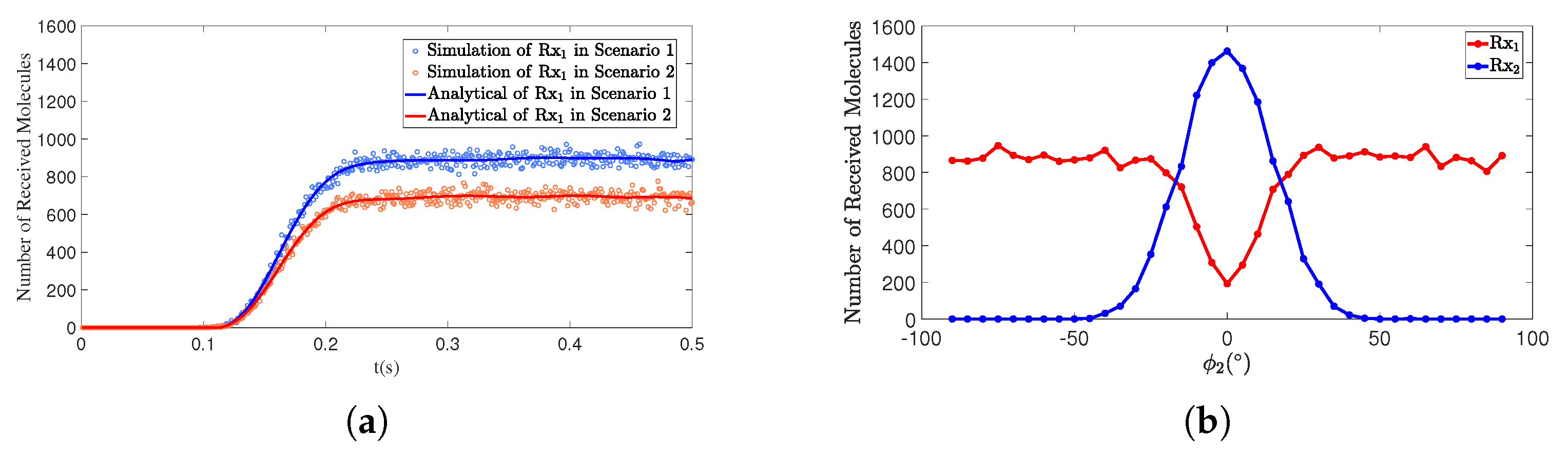
4.2. The Angle Influences the Number of Molecules Received
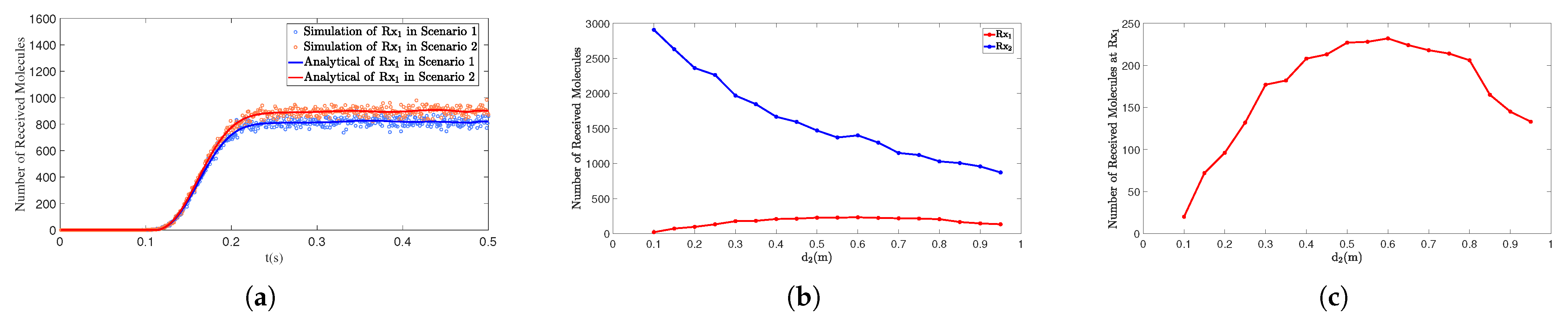
4.3. The Distance Influences the Number of Molecules Received
4.4. The Interfering Receiver Influences the Number of Molecules Received by the Primary Receiver
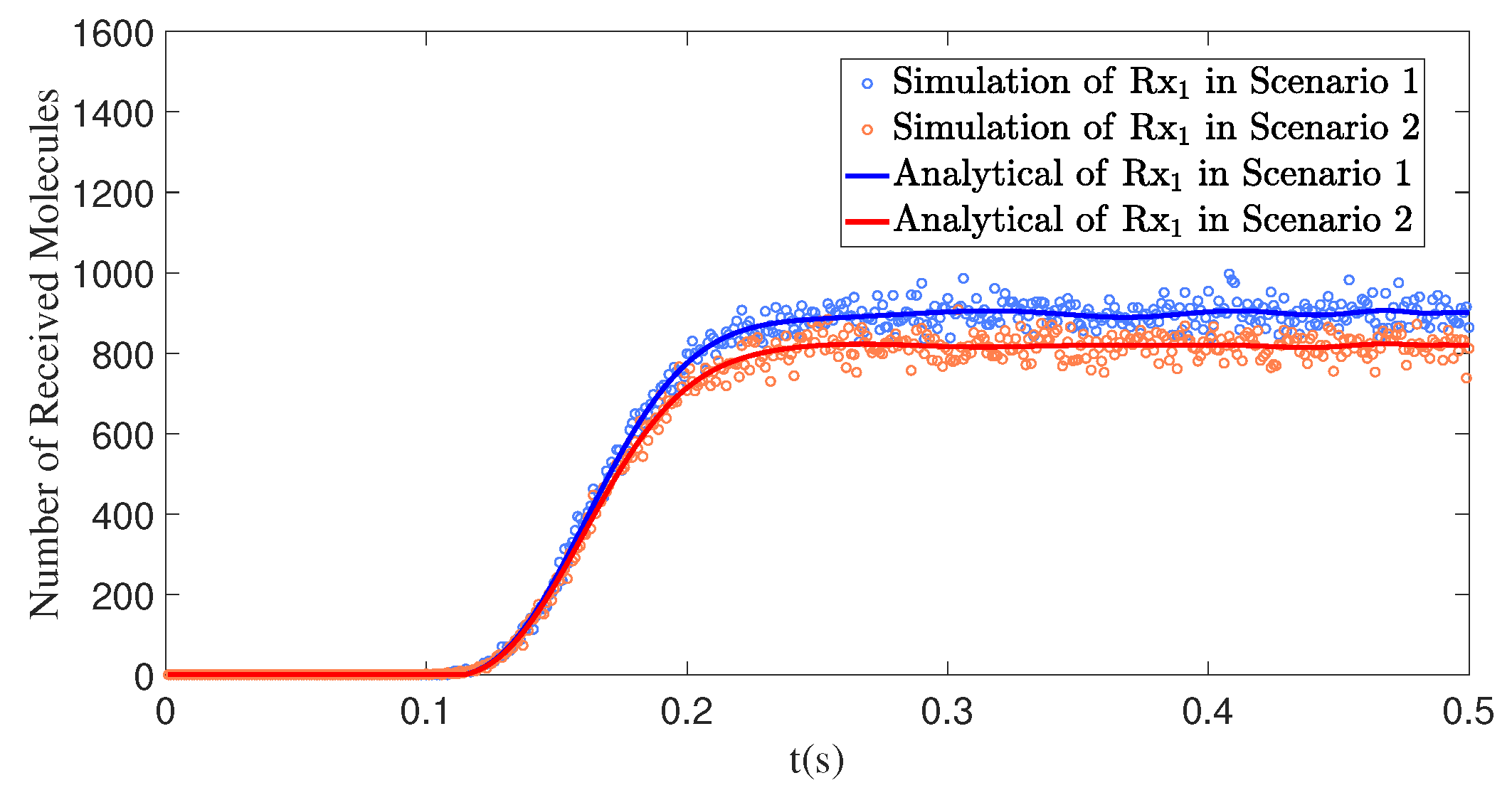
4.4.1. The Distance Between the Interfering Receiver and the Transmitter Affects the Number of Molecules Received by the Primary Receiver
4.4.2. The Angle Between the Interfering Receiver and the Transmitter Affects the Number of Molecules Received by the Primary Receiver
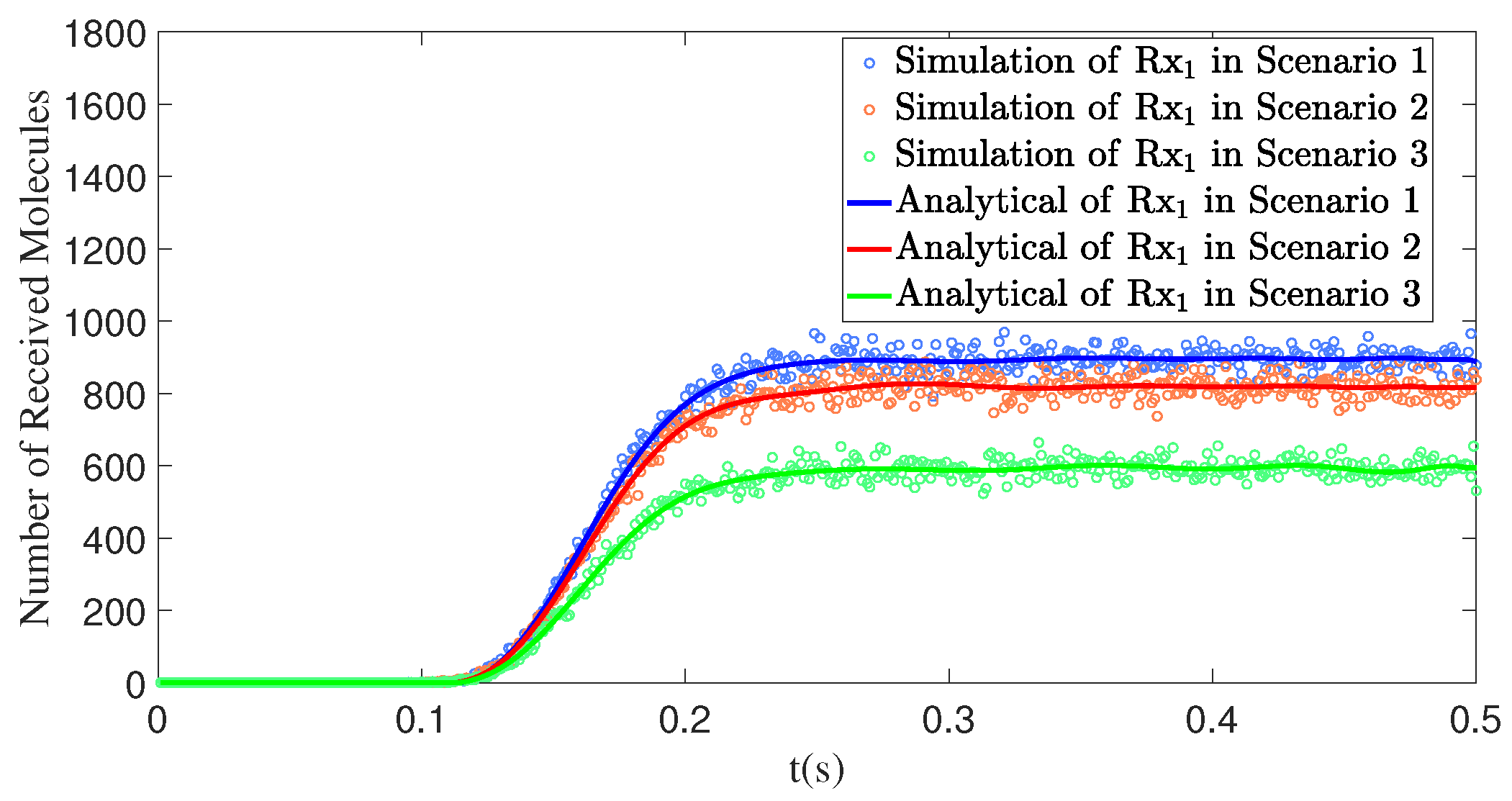
4.4.3. The Number of Interfering Receivers Influences the Number of Molecules Received by the Primary Receiver
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
References
- Asorey-Cacheda, R.; Garcia, L.; Garcia-Sanchez, A.-J.; Garcia-Haro, J. Transmission power allocation in flow-guided nanocommunication networks. Internet Things 2024, 25, 101137. [Google Scholar] [CrossRef]
- Junejo, A.R.; Kaabar, M.K.A.; Li, X. Optimization: Molecular Communication Networks for Viral Disease Analysis Using Deep Leaning Autoencoder. Comput. Math. Methods Med. 2021, 2021, 9949328. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, P.K.D.; Solanki, A.; Debnath, A.; Nayyar, A.; El-Sappagh, S.; Kwak, K.-S. Advancing Modern Healthcare with Nanotechnology, Nanobiosensors, and Internet of Nano Things: Taxonomies, Applications, Architecture, and Challenges. IEEE Access 2020, 8, 65230–65266. [Google Scholar] [CrossRef]
- Nayyar, A.; Puri, V.; Le, D.-N. Internet of Nano Things (IoNT): Next Evolutionary Step in Nanotechnology. J. Nanotechnol. 2017, 7, 4–8. [Google Scholar]
- Zafar, S.; Nazir, M.; Bakhshi, T.; Khattak, H.A.; Khan, S.; Bilal, M.; Choo, K.-K.R.; Kwak, K.-S.; Sabah, A. A Systematic Review of Bio-Cyber Interface Technologies and Security Issues for Internet of Bio-Nano Things. IEEE Access 2021, 9, 93529–93566. [Google Scholar] [CrossRef]
- Duong, T.M.; Hyun, S.-H.; Kwon, S. Channel modeling and achievable data rate for 1-D molecular communication in bounded environments. Comput. Netw. 2023, 232, 109852. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Joint localization and channel estimation in flow-assisted molecular communication systems. Nano Commun. Netw. 2023, 35, 100434. [Google Scholar] [CrossRef]
- Hofmann, P.; Bassoli, R.; Fitzek, F.H.P.; Reisslein, M. MC NFV: Molecular Communication NFV in 6G Networks. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1205–1210. [Google Scholar]
- Aghababaiyan, K.; Kebriaei, H.; Shah-Mansouri, V.; Maham, B.; Niyato, D. Enhanced Modulation for Multiuser Molecular Communication in Internet of Nano Things. IEEE Internet Things J. 2022, 9, 19787–19802. [Google Scholar] [CrossRef]
- Egan, M.; Kuscu, M.; Barros, M.T.; Booth, M.; Llopis-Lorente, A.; Magarini, M.; Martins, D.P.; Schäfer, M.; Stano, P. Toward Interdisciplinary Synergies in Molecular Communications: Perspectives from Synthetic Biology, Nanotechnology, Communications Engineering, and Philosophy of Science. Life 2023, 13, 208. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low-complexity MIMO-FBMC sparse channel parameter estimation for industrial big data communications. IEEE Trans. Ind. Inform. 2020, 17, 3422–3430. [Google Scholar] [CrossRef]
- Fedoreyeva, L.I. Molecular Mechanisms of Regulation of Root Development by Plant Peptides. Plants 2023, 12, 1320. [Google Scholar] [CrossRef] [PubMed]
- Khalid, M.; Amin, O.; Ahmed, S.; Shihada, B.; Alouini, M.-S. Modeling of Viral Aerosol Transmission and Detection. IEEE Trans. Commun. 2020, 68, 4859–4873. [Google Scholar] [CrossRef]
- Yue, G.; Liu, Q.; Yang, K. Bio-Internet of Things Through Micro-Circulation Network: A Molecular Communication Channel Modeling. IEEE Internet Things J. 2024, 11, 36521–36533. [Google Scholar] [CrossRef]
- Chouhan, L.; Alouini, M.-S. Interfacing of Molecular Communication System with Various Communication Systems over Internet of Every Nano Things. IEEE Internet Things J. 2023, 10, 14552–14568. [Google Scholar] [CrossRef]
- Bao, X.; Shen, Q.; Zhu, Y.; Zhang, W. Relative Localization for Silent Absorbing Target in Diffusive Molecular Communication System. IEEE Internet Things J. 2022, 9, 5009–5018. [Google Scholar] [CrossRef]
- Femminella, M.; Reali, G.; Vasilakos, A.V. A Molecular Communications Model for Drug Delivery. IEEE Trans. Nanobiosci. 2015, 14, 935–945. [Google Scholar] [CrossRef]
- Peng, L.; Xiong, W.; Han, C.; Li, Z.; Chen, X. CellDialog: A Computational Framework for Ligand-Receptor-Mediated Cell-Cell Communication Analysis. IEEE J. Biomed. Health Inform. 2024, 28, 580–591. [Google Scholar] [CrossRef]
- Gulec, F.; Atakan, B. A Molecular Communication Perspective on Airborne Pathogen Transmission and Reception via Droplets Generated by Coughing and Sneezing. IEEE Trans. Mol. Biol. -Multi-Scale Commun. 2021, 7, 175–184. [Google Scholar] [CrossRef]
- Christian, N.; Perlin, M.H. Plant-endophyte communication: Scaling from molecular mechanisms to ecological outcomes. Mycologia 2024, 116, 227–250. [Google Scholar] [CrossRef]
- Nakano, T.; Moore, M.J.; Okaie, Y.; Enomoto, A.; Suda, T. Cooperative Drug Delivery through Molecular Communication among Biological Nanomachines. In Proceedings of the 2013 IEEE International Conference on Communications Workshops (ICC), Budapest, Hungary, 9–13 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 809–812. [Google Scholar]
- Zhang, P.; Lu, P.; Wang, X.; Liao, X. Modeling of Respiratory Virus Transmission Using Single-Input-Multiple-Output Molecular Communication Techniques. Electronics 2025, 14, 213. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, M.; Lee, C.; Chae, C.-B.; Ji, F. A Two-Way Molecular Communication Assisted by an Impulsive Force. IEEE Trans. Ind. Inform. 2019, 15, 3048–3057. [Google Scholar] [CrossRef]
- Yaylali, G.; Akdeniz, B.C.; Tugcu, T.; Pusane, A.E. Channel Modeling for Multi-Receiver Molecular Communication Systems. IEEE Trans. Commun. 2023, 71, 4499–4512. [Google Scholar] [CrossRef]
- Petroni, D.; Fabbri, C.; Babboni, S.; Menichetti, L.; Basta, G.; Del Turco, S. Extracellular Vesicles and Intercellular Communication: Challenges for In Vivo Molecular Imaging and Tracking. Pharmaceutics 2023, 15, 1639. [Google Scholar] [CrossRef] [PubMed]
- Kuran, M.S.; Yilmaz, H.B.; Tugcu, T. A Tunnel-Based Approach for Signal Shaping in Molecular Communication. In Proceedings of the 2013 IEEE International Conference on Communications Workshops (ICC), Budapest, Hungary, 9–13 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 776–781. [Google Scholar]
- Wang, L.; Wang, D.; Ye, Z.; Xu, J. Engineering Extracellular Vesicles as Delivery Systems in Therapeutic Applications. Adv. Sci. 2023, 10, 2300552. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N.; Spalding, D.B. Transport Phenomena. J. Appl. Mech. 1961, 28, 317–318. [Google Scholar] [CrossRef][Green Version]
- Nellis, G.; Klein, S. Heat Transfer; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Akdeniz, B.C.; Turgut, N.A.; Yilmaz, H.B.; Chae, C.-B.; Tugcu, T.; Pusane, A.E. Molecular Signal Modeling of a Partially Counting Absorbing Spherical Receiver. IEEE Trans. Commun. 2018, 66, 6237–6246. [Google Scholar] [CrossRef]






| Model | Attribute |
|---|---|
| SISO Model | Fluid Velocity Effects: Partially considered in some studies. Velocity directed toward the receiver. Interference Among Receivers: Not applicable. Application Scenarios: Free-diffusion and fluid-assisted scenarios. Maximum Model Dimension: Three-dimensional. Factors Influencing System Performance: Distance. |
| SIMO Model | Fluid Velocity Effects: Not addressed. Interference Among Receivers: Addressed in limited studies Application Scenarios: Free-diffusion scenario. Maximum Model Dimension: Mostly two-dimensional. Some three-dimensional studies simplified to two-dimensional. Factors Influencing System Performance: Distance. If receiver interference is studied, also consider receiver–receiver and receiver–transmitter angles. |
| Our Fluid-Assisted SIMO Model | Fluid Velocity Effects: Considers fluid resistance and convection velocity. Interference Among Receivers: Quantifies the interference effects among multiple receivers. Application Scenarios: Free-diffusion and fluid-assisted scenarios. Maximum Model Dimension: Three-dimensional. Factors Influencing System Performance: Distance, initial fluid velocity. If receiver interference is studied, also consider the polar and azimuthal angles of receiver–receiver and receiver–transmitter. |
| Parameter | Value |
|---|---|
| Number of transmitting molecules per step (N) | 3000 |
| Dynamic viscosity of fluid () | |
| Radius of molecules (r) | |
| Initial velocity () | |
| Mass of molecules (m) | |
| Diffusion coefficient (D) | |
| Radius of receiver (R) | |
| Simulation step () | |
| Simulation duration | |
| Simulation repetitions | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Lu, P.; Liao, X.; Wang, X.; Zhou, P. Channel Modeling for Multi-Receiver Molecular Communication System by Impulsive Force in Internet of Nano Things. Sensors 2025, 25, 3472. https://doi.org/10.3390/s25113472
Zhang P, Lu P, Liao X, Wang X, Zhou P. Channel Modeling for Multi-Receiver Molecular Communication System by Impulsive Force in Internet of Nano Things. Sensors. 2025; 25(11):3472. https://doi.org/10.3390/s25113472
Chicago/Turabian StyleZhang, Pengfei, Pengfei Lu, Xuening Liao, Xiaofang Wang, and Ping Zhou. 2025. "Channel Modeling for Multi-Receiver Molecular Communication System by Impulsive Force in Internet of Nano Things" Sensors 25, no. 11: 3472. https://doi.org/10.3390/s25113472
APA StyleZhang, P., Lu, P., Liao, X., Wang, X., & Zhou, P. (2025). Channel Modeling for Multi-Receiver Molecular Communication System by Impulsive Force in Internet of Nano Things. Sensors, 25(11), 3472. https://doi.org/10.3390/s25113472







