1. Introduction
In the age of Industry 4.0, the basic processes for monitoring and assuring the quality of fault risk management and reliability assessment are essential in maintaining the stability and intactness of operations for industrial equipment. The model for equipment maintenance is changing from passive maintenance to digital precision forecasting, performed through the detection of any faults with high-grade precision in a complex condition of operations [
1]; this subsequently reduces the impact of equipment failure on the production process. The recent developments in enhancing GPU logic for deeper learning algorithms speed up the study of good artificial-intelligence-based models for fault prediction and health diagnosis. Accurate prediction of RUL and health status prediction of the equipment enhances the long-term stability of the equipment and reduces maintenance costs. Thus, RUL prediction has become one of the most important directions for research in the field of fault diagnosis and health management.
Current research methods for RUL prediction can be classified broadly into two groups: physics-based methods [
2] and data-driven methods [
3,
4,
5,
6]. Physics-based methodologies take into account the physical laws and mathematical structures of equipment that explain the physical processes and mechanisms of failure in a reasonable way. However, complex nonlinear relationships and large uncertainties are very often involved in the failure processes of equipment, meaning that those mechanisms are at least well understood, aiding their explanation. In addition, their accuracy heavily relies on the passable estimates of system parameters; even with minor errors in the true parameters, the predictions could significantly deviate from the optimal outcome [
7]. They also encounter great difficulties in tackling sudden or stochastic failings. On the other hand, data-driven RUL prediction methods automatically identify nonlinear dependencies associated with the equipment defect process, with minimal reliance on physical parameters. These methods can be broadly applied to various types of equipment. In recent years, data-driven RUL prediction methods based on deep learning have proved to be of incredible potential, with studies being published that include the use of CNNs [
8,
9], Long Short-Term Memory (LSTM) networks [
10], Generative Adversarial Networks (GANs) [
11], Graph Neural Networks (GNNs) [
12,
13,
14], attention mechanisms (AMs) [
15,
16], and Transformer models [
17,
18]. Keshun et al. [
19] proposed an RUL prediction model based on a three-dimensional attention mechanism, CNN, and BiLSTM that enhances prediction accuracy while achieving interpretability. Shi et al. [
5] introduced a lightweight novel RUL prediction model integrating exponential smoothing, attention mechanisms, and LSTMs. Such models can be properly exploited in fault diagnosis or health prediction applications which demand quick responses. However, the performance of existing hybrid models using attention mechanisms and classical neural networks typically degrades with longer sequences.
State space models (SSMs) are mathematical representations derived from control systems theory, which describe how states evolve in dynamic systems and define the relationships between inputs and outputs. SSMs rely mainly on their state equations and representation output to use hidden states to preserve historical information [
20]. In addition, by alleviating the vanishing gradient issue typical in traditional recurrent neural networks, this approach enables more effective modeling of long-range dependencies. By integrating recursive inference with convolutional training mechanisms, SSMs effectively balance real-time processing efficiency and parallel computation, significantly improving computational performance. Furthermore, SSMs possess the ability to dynamically adapt their parameters, allowing for flexible alignment with the dynamic properties of diverse systems. SSM is widely applied in time–series analysis, control systems, and signal processing. Regarding RUL prediction models based on SSM, for example, one may refer to [
21,
22]. However, traditional SSMs face challenges with high computational complexity when processing long sequences. Mamba [
23] is an improved state space model that was developed to overcome traditional SSMs’ limitations in modeling long sequences. It has linear complexity, allowing it to efficiently model long sequences while capturing their dynamic changes. It excels in tasks such as language modeling and time–series forecasting, while also offering high computational efficiency. Currently, the application of Mamba in RUL prediction is still relatively limited. For example, Liang and Zhao [
24] proposed a Mamba-based state space model for early RUL prediction of lithium-ion batteries and demonstrated the method’s strengths in terms of prediction performance, robustness, and efficiency. Zhu et al. [
25] integrated attention–Mamba networks with the Physics-Informed Neural Networks (PINNs) framework, incorporating hard-to-detect physical information into the neural network to improve the model’s RUL prediction accuracy.
Feature selection is a crucial step in modern data-driven modeling [
26], focusing on identifying and extracting the most relevant features from the original feature set to reduce redundancy and retain essential information. This process is designed with the aim of enhancing model performance, interpretability, and computational efficiency. Causal discovery algorithms are designed to uncover causal relationships between variables from observational data. Studies on improving feature selection through causal structure learning can be found in works such as [
27]. Transfer entropy (TE) is an information–theoretic metric used to measure the directional flow of information or causal influence between time–series. In the context of equipment life prediction, applying the TE algorithm helps identify and select key causal relationships from large datasets, leading to more accurate prediction models. Causal discovery has been widely applied in time–series forecasting, such as in [
28,
29], which demonstrated the effectiveness of this method in improving model performance.
Although the transfer entropy algorithm demonstrates excellent performance in causality identification, its computational complexity is considerable, particularly when handling high-dimensional time–series data [
30], as the computational burden grows significantly. Additionally, the TE algorithm is sensitive to noise, and the presence of noise in the data may lead to erroneous causality inferences. Inspired by [
5,
31], this paper proposes an RUL prediction model based on Bidirectional Mamba (BiMamba) and causal discovery algorithms. Firstly, the impact of random noise is effectively reduced through exponential smoothing techniques. Subsequently, the maximum information transfer entropy method, as described in [
31], is employed to construct a causal graph of feature variables; based on these, key feature variables are selected. Then, utilizing these key feature variables, a model (namely, Cau–BiMamba–LSTM) combining BiMamba, LSTM, and causality is applied for RUL prediction.
This paper makes the following key contributions:
- (1)
To tackle the noise issue in time–series data, exponential smoothing is employed to weight and average the data points. Furthermore, the maximum information transfer entropy algorithm is utilized to identify more accurate causal relationships. This causality-driven feature selection method enhances the interpretability and prediction accuracy of the model.
- (2)
This paper is the first to apply the BiMamba model to the RUL prediction of aircraft engines. By integrating a hybrid model that combines bidirectional processing mechanisms, Mamba, attention mechanisms, and LSTM, the ability to model long sequences is significantly improved. The approach takes full advantage of Mamba’s low complexity and high computational efficiency, achieving enhanced accuracy while minimizing computational resource usage.
- (3)
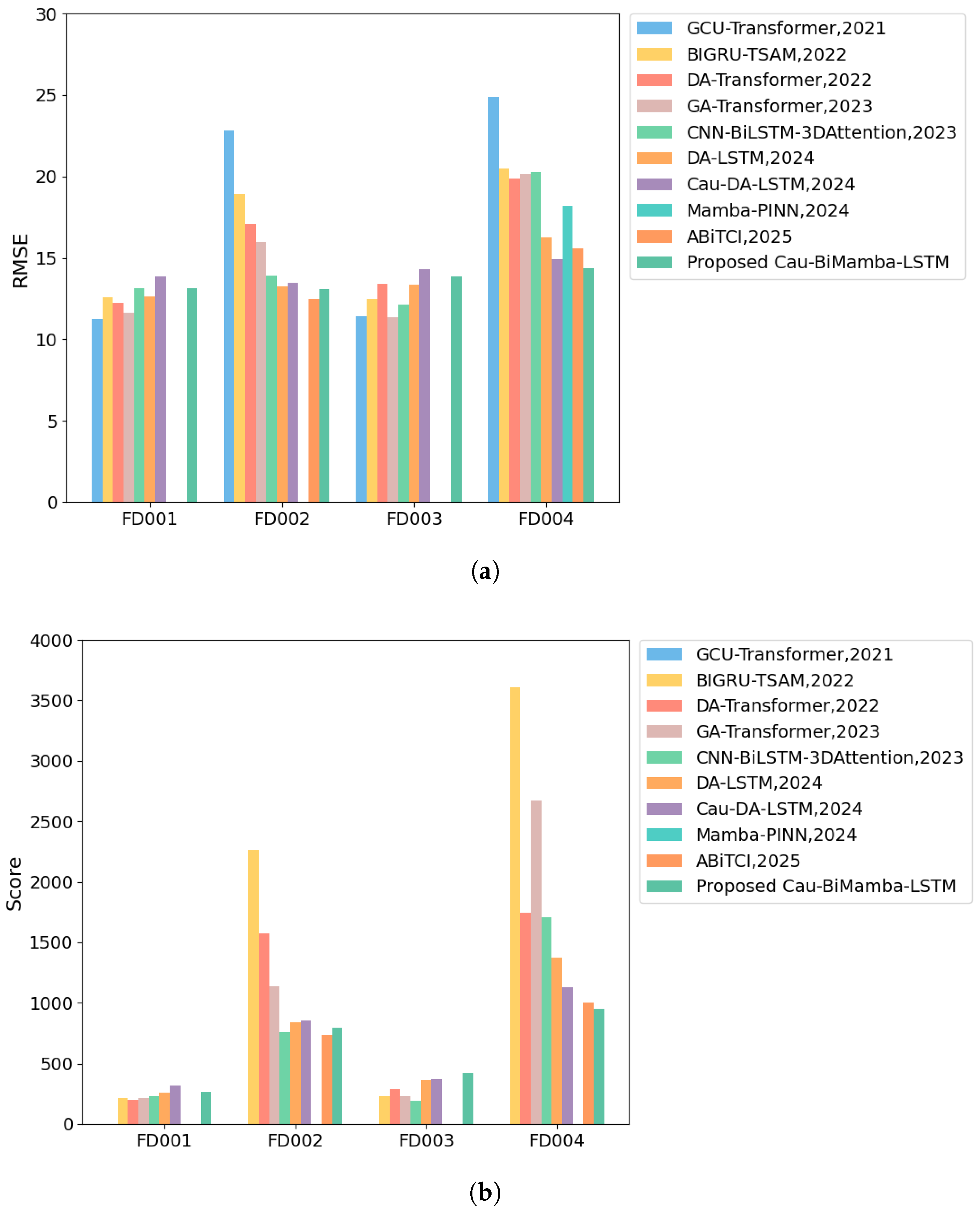
Our model demonstrates superior performance on the C-MAPSS dataset, highlighting its potential as a versatile method for predicting RUL. The Cau–BiMamba–LSTM model achieves optimal performance in terms of RMSE and SCORE on the C-MAPSS dataset, with a parameter count as low as 3323. The prediction accuracy on the FD002 and FD004 datasets outperforms most existing models. Specifically, on the most complex sub-dataset, FD004, the RMSE reaches 14.37 and SCORE reaches 948, making it the best-performing model in terms of prediction accuracy compared to all other models.
The sections of the paper are organized as follows: in
Section 2, preliminaries are discussed; in
Section 3, the proposed Cau–BiMamba–LSTM prediction framework is presented; in
Section 4, the experimental setup and the efficiency of the approach are developed; and finally,
Section 5 concludes the paper and proposes some further research directions.
3. Methodology
The authors of [
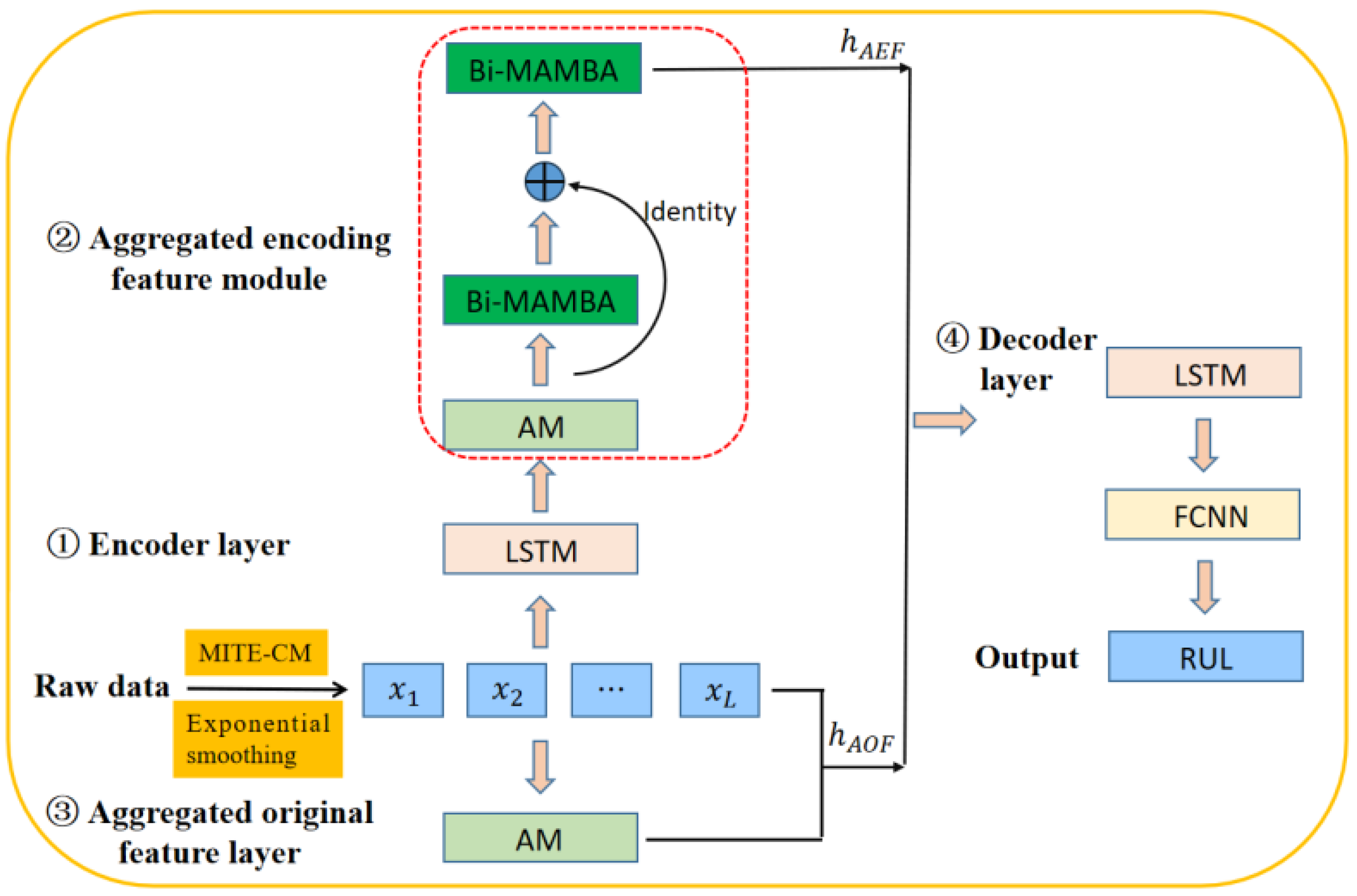
29] employ the MITE-CM algorithm to perform causal analysis on the CMAPSS dataset for aircraft engines, thereby improving the performance of prediction. However, they do not consider the impact of noise in the data on the causal relationships, which leads to inaccurate causal inference. To address this limitation, we utilize an approach that combines exponential smoothing with the MITE-CM algorithm for causal feature selection and introduce a new BiMamba module, integrating models such as LSTM and attention mechanisms for RUL prediction. The network architecture of our proposed Cau–BiMamba–LSTM model is illustrated in
Figure 3.
First, this paper employs the simple exponential smoothing method and the MITE-CM algorithm for causal feature selection. Subsequently, the selected features are processed through an encoder layer, an aggregated encoding feature (AEF) module, an aggregated original feature (AOF) layer, and a decoder layer for RUL prediction. Compared to the methods proposed in [
5,
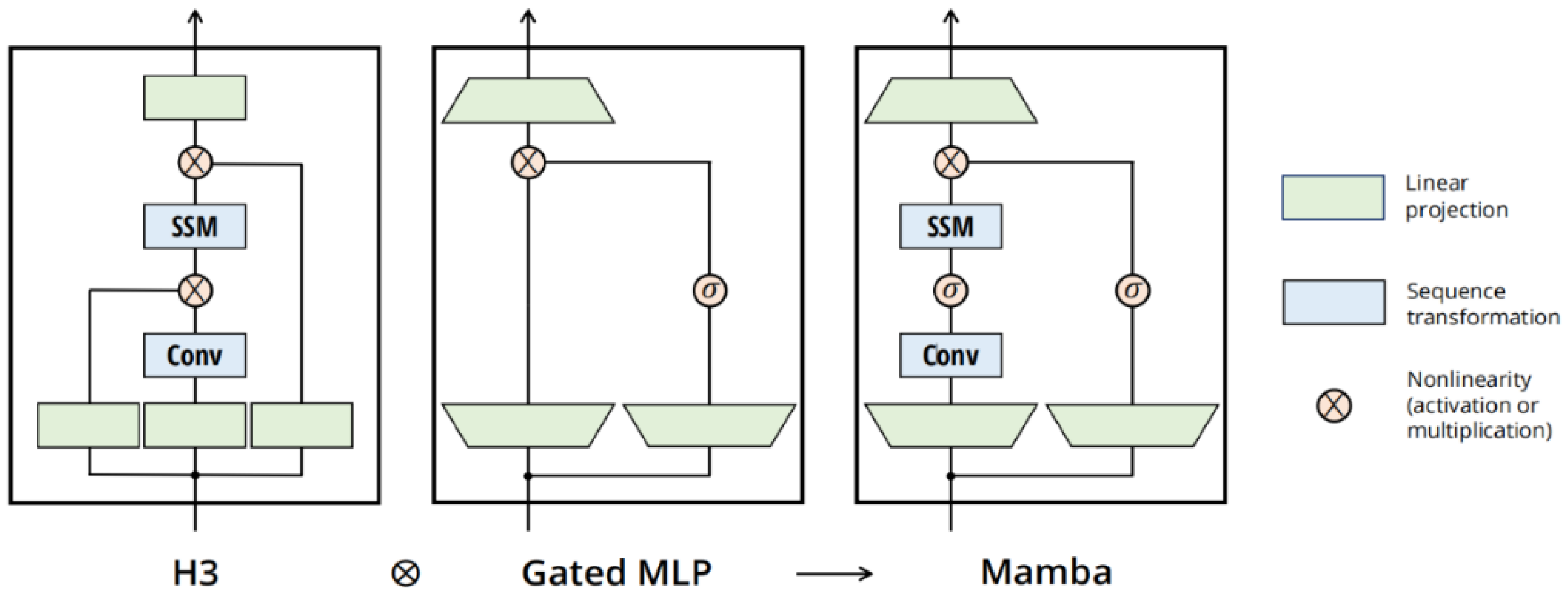
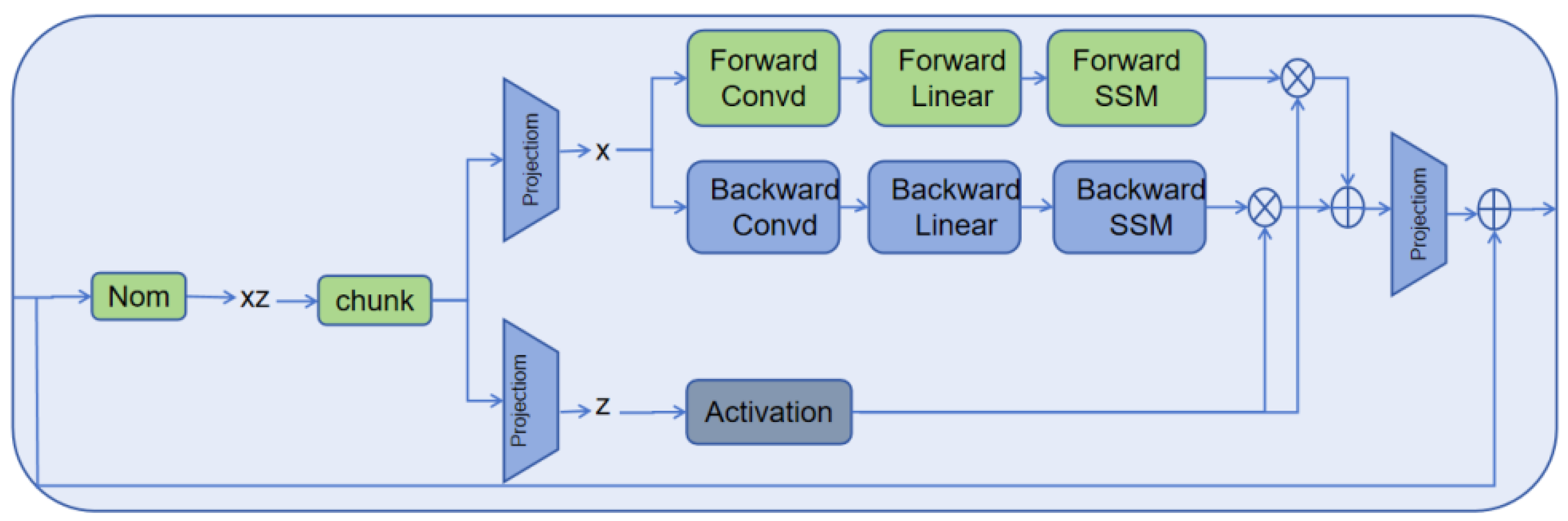
29], our innovation lies in the design of a BiMamba-based aggregated encoding feature layer. By leveraging a BiMamba module combined with residual networks, our approach enables the more precise extraction of data features. The architecture of the BiMamba module, as described in [
32], is depicted in
Figure 2.
We utilize an self-attention mechanism to aggregate the original features of key variables, employ LSTM for encoding, and leverage a combination of BiMamba, residual connection, and additive mechanisms for aggregating the encoded features. The two types of aggregated features are then concatenated and decoded using LSTM. The LSTM output is processed by a fully connected layer to produce the final decoded result, thereby achieving RUL prediction. In the BiMamba-based aggregated encoding feature layer, a self-attention mechanism is initially applied, with its output acting as the input for the initial BiMamba module. The output from this module is then combined with the self-attention mechanism output through a residual connection and passed into the second BiMamba module. This design effectively harnesses the capabilities of BiMamba, allowing it to capture a wide range of features and produce a more detailed representation, which enhances the accuracy of RUL prediction.
The Cau–BiMamba–LSTM model has advantages in the following three aspects:
- (1)
Information flow perspective: BiMamba and LSTM exhibit complementarity. BiMamba excels at capturing long-range dependencies and effectively modeling complex long-term trends in time–series data [
32]. On the other hand, LSTM is better suited for local pattern recognition, as it can remember and forget specific information within shorter time spans. By combining these two models, the hybrid model leverages their respective strengths, capturing both long-term trends and short-term fluctuations. This complementarity enhances the model’s performance when handling complex time–series data.
- (2)
Computational complexity: The computational complexity of the Cau–BiMamba–LSTM model remains linear [
5,
32]. When dealing with large-scale datasets, integrating multiple models can significantly improve performance. However, the addition of models often results in increased computational burden. Through optimized design, the proposed hybrid model maintains high performance without a significant increase in computational cost, ensuring that the complexity grows linearly.
- (3)
Innovative causal feature selection and effective fusion with attention mechanism: The hybrid model innovatively combines causal feature selection with an attention mechanism. It fully leverages the advantages of transfer entropy theory for feature selection. The model uses exponential smoothing to remove noise and employs maximum transfer entropy for causal feature selection to enhance subsequent prediction accuracy. Additionally, the attention mechanism is incorporated to dynamically focus on important features. This allows the model to automatically prioritize features that contribute more significantly to the prediction, achieving effective fusion of information. By combining transfer entropy for causal feature selection with attention mechanisms for feature weighting, the hybrid model efficiently utilizes input features and improves overall prediction performance.
In summary, the Cau–BiMamba–LSTM model integrates various independent yet complementary modules, including exponential smoothing, causal feature selection, BiMamba, LSTM, and attention mechanisms. This combination not only fully leverages the strengths of each module but also overcomes the limitations that individual modules may have. Exponential smoothing reduces the impact of noise, the MITE-CM algorithm enhances causal inference capabilities, and the BiMamba module, through the integration of LSTM and the attention mechanism, improves feature learning and modeling of temporal dependencies. As a result, the model effectively improves the accuracy and reliability of RUL prediction by comprehensively addressing noise suppression, causal relationship discovery, and the learning of both long-term and short-term features in time–series.
6. Conclusions
This study proposes a lightweight Cau–BiMamba–LSTM model, enhancing RUL prediction accuracy and robustness. By integrating causal algorithms for feature selection, the BiMamba module for efficient sequence modeling, and the attention module for feature extraction, the model achieves notable performance improvements on the C-MAPSS dataset. Experimental results demonstrate that the proposed model reduces the RMSE to 14.37 and the SCORE to 948 on the C-MAPSS FD004 dataset, surpassing existing models (based on attention, LSTM, or Mamba) on the FD004 dataset, while also achieving a near-optimal level on the FD002 dataset. This validates the model’s generalization ability across multiple datasets, particularly its excellent performance under complex data distributions and long sequence dependencies. Furthermore, the model’s lightweight design enables deployment on resource-limited edge devices, meeting the demands of real-time prediction. Existing pure-data-driven RUL prediction models often face challenges in balancing prediction accuracy, computational complexity, and interpretability. The proposed model addresses these challenges by incorporating feature selection interpretability, making it both lightweight and highly accurate. It shows enhanced stability and robustness when dealing with diverse operating conditions and complex time–series data.
The model still has some limitations: While the attention mechanism can highlight the importance of different features in the prediction, it does not provide clear physical or system-level explanations, leading to a lack of interpretability in the model’s decision-making process. Additionally, it does not consider physical constraints and lacks effective integration of physical knowledge, which limits the model’s generalization ability to some extent. Future work will focus on integrating multi-source data, including time–series and causal graph data. We aim to combine Mamba with physics-informed networks to build an interpretable prediction framework. Additionally, we plan to consider integrating data-driven models with physical models to construct a hybrid prediction framework, further enhancing prediction performance and interpretability.