Measuring the Impact of Limb Asymmetry on Movement Irregularity and Complexity Changes During an Incremental Step Test in Para-Swimmers Using Inertial Measurement Units
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Instrumentation
2.3. Protocol
2.4. Data Processing
2.4.1. Anthropometric Data
2.4.2. Swimming Data
2.5. Statistical Analyses
3. Results
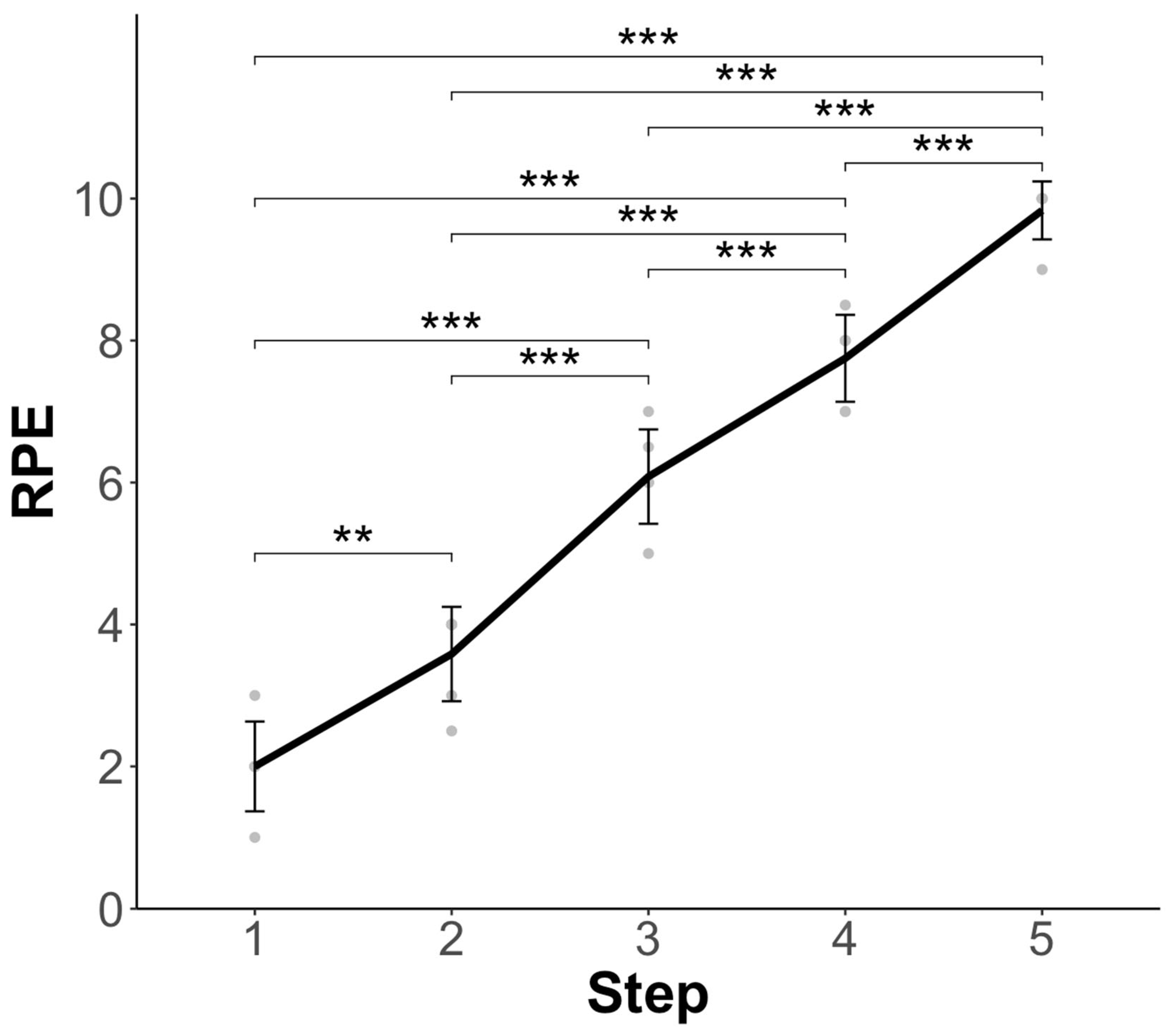
3.1. Rate of Perceived Exertion (RPE)
3.2. Limb Asymmetry
3.3. Motor Variability
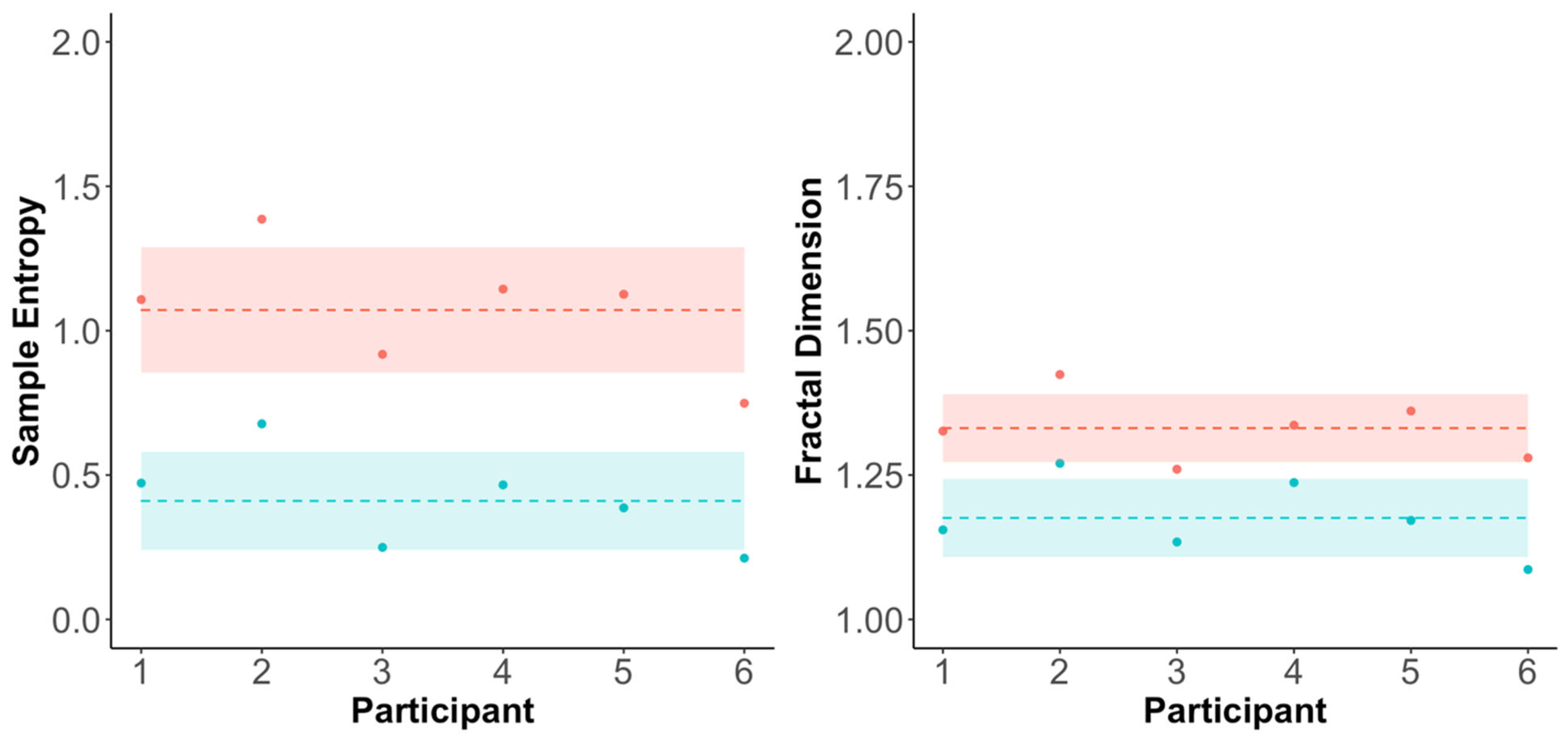
3.3.1. Baseline (Step 1) Values
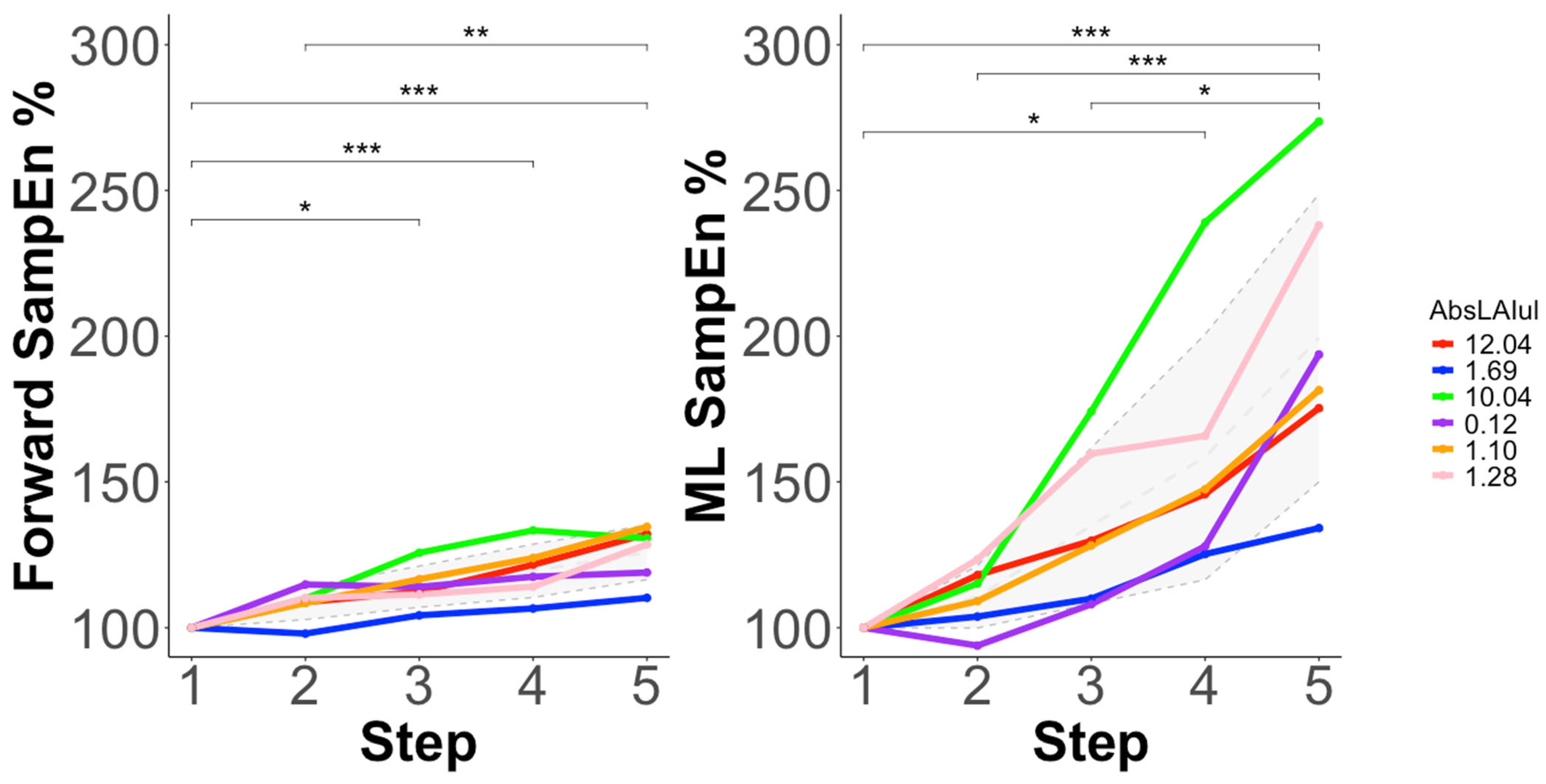
3.3.2. Sample Entropy (SampEn)
3.3.3. Fractal Dimension (FD)
4. Discussion
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stergiou, N.; Harbourne, R.T.; Cavanaugh, J.T. Optimal Movement Variability. J. Neurol. Phys. Ther. 2006, 30, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Slopecki, M.; Hasanbarani, F.; Yang, C.; Bailey, C.A.; Côté, J.N. Uncontrolled Manifold Analysis of the Effects of Different Fatigue Locations on Kinematic Coordination During a Repetitive Upper-Limb Task. Mot. Control 2022, 26, 713–728. [Google Scholar] [CrossRef]
- Cowin, J.; Nimphius, S.; Fell, J.; Culhane, P.; Schmidt, M. A Proposed Framework to Describe Movement Variability within Sporting Tasks: A Scoping Review. Sports Med.—Open 2022, 8, 85. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, R.J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. -Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Barbosa, T.M.; Morais, J.E.; Marques, M.C.; Silva, A.J.; Marinho, D.A.; Kee, Y.H. Hydrodynamic profile of young swimmers: Changes over a competitive season. Scand. J. Med. Sci. Sports 2015, 25, e184–e196. [Google Scholar] [CrossRef]
- Barbosa, T.M.; Goh, W.X.; Morais, J.E.; Costa, M.J.; Pendergast, D. Comparison of Classical Kinematics, Entropy, and Fractal Properties As Measures of Complexity of the Motor System in Swimming. Front. Psychol. 2016, 7, 1566. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, T.M.; Simin, C.; Forte, P.; Morais, J.E. The changes in fractal dimension after a maximal exertion in swimming. In Proceedings of the 1st International Conference on Technology and Innovation in Sports, Health and Wellbeing (TISHW), Vila Real, Portugal, 1–3 December 2016; pp. 1–6. [Google Scholar]
- Stergiou, N.; Decker, L.M. Human movement variability, nonlinear dynamics, and pathology: Is there a connection? Hum. Mov. Sci. 2011, 30, 869–888. [Google Scholar] [CrossRef]
- Latash, M.L. The bliss (not the problem) of motor abundance (not redundancy). Exp. Brain Res. 2012, 217, 1–5. [Google Scholar] [CrossRef]
- Möhler, F.; Fadillioglu, C.; Stein, T. Changes in spatiotemporal parameters, joint and CoM kinematics and leg stiffness in novice runners during a high-intensity fatigue protocol. PLoS ONE 2022, 17, e0265550. [Google Scholar] [CrossRef]
- Möhler, F.; Fadillioglu, C.; Scheffler, L.; Müller, H.; Stein, T. Running-Induced Fatigue Changes the Structure of Motor Variability in Novice Runners. Biology 2022, 11, 942. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, T.M.; Goh, W.X.; Morais, J.E.; Costa, M.J. Variation of Linear and Nonlinear Parameters in the Swim Strokes According to the Level of Expertise. Mot. Control 2017, 21, 312–326. [Google Scholar] [CrossRef] [PubMed]
- De Magalhaes, F.A.; Vannozzi, G.; Gatta, G.; Fantozzi, S. Wearable inertial sensors in swimming motion analysis: A systematic review. J. Sports Sci. 2015, 33, 732–745. [Google Scholar] [CrossRef]
- Mooney, R.; Corley, G.; Godfrey, A.; Quinlan, L.; Ólaighin, G. Inertial Sensor Technology for Elite Swimming Performance Analysis: A Systematic Review. Sensors 2015, 16, 18. [Google Scholar] [CrossRef]
- Slopecki, M.; Charbonneau, M.; Lavallière, J.-M.; Côté, J.N.; Clément, J. Validation of Automatically Quantified Swim Stroke Mechanics Using an Inertial Measurement Unit in Paralympic Athletes. Bioengineering 2024, 11, 15. [Google Scholar] [CrossRef]
- Clément, J.; Charbonneau, M.; Thompson, M. Instantaneous velocity estimation for the four swimming strokes using a 3-axis accelerometer: Validation on paralympic athletes. J. Biomech. 2021, 117, 110261. [Google Scholar] [CrossRef]
- Stamm, A.; Shlyonsky, I. Freestyle Swimming Analysis of Symmetry and Velocities using a MEMS based IMU: Introducing a Symmetry Score. In Proceedings of the 8th International Conference on Sport Sciences Research and Technology Support, Budapest, Hungary, 19 May 2020. [Google Scholar]
- Bouvet, A.; Delhaye, E.; Nicolas, G.; Bideau, N. IMU-based clustering of intra and inter-cyclic variability to extract technical abilities during front crawl sprint. In Proceedings of the XIVth International Symposium for Biomechanics and Medecine in Swimming (BMS), Leipzig, Germany, 6–9 September 2023; pp. 1–6. [Google Scholar]
- Bouvet, A.; Pla, R.; Delhaye, E.; Nicolas, G.; Bideau, N. Profiling biomechanical abilities during sprint front-crawl swimming using IMU and functional clustering of variabilities. Sports Biomech. 2024, 1–21. [Google Scholar] [CrossRef]
- Slopecki, M.; Clément, J.; Charbonneau, M.; Côté, J.N. The Impact of Limb Symmetry on Stroke-to-Stroke Movement Variability in Para-Swimmers during an Adapted Aerobic Step Test. ISBS Proc. Arch. 2024, 42, 862–865. [Google Scholar]
- Stamm, A.; Thiel, D.V.; Burkett, B.; James, D.A. Towards determining absolute velocity of freestyle swimming using 3-axis accelerometers. Procedia Eng. 2011, 13, 120–125. [Google Scholar] [CrossRef]
- Stamm, A.; Thiel, D. Investigating Forward Velocity and Symmetry in Freestyle Swimming Using Inertial Sensors. Procedia Eng. 2015, 112, 522–527. [Google Scholar] [CrossRef]
- Stamm, A. Investigating Stroke Length and Symmetry in Freestyle Swimming Using Inertial Sensors. In Proceedings of the International Sports Engineering Association—The Engineering of Sport, Brisbane, Australia, 26–29 March 2018. [Google Scholar]
- Stamm, A.; James, D.; Hagem, R.; Thiel, D. Investigating arm symmetry in swimming using inertial sensors. In Proceedings of the Proceedings of IEEE Sensors, Taipei, Taiwan, 28–31 October 2012; pp. 1–4. [Google Scholar]
- Slopecki, M.; Charbonneau, M.; Deguire, S.; Côté, J.N.; Clément, J. Technical performance analyses in elite Paralympic swimming using wearable technology: Two case studies. Sports Biomech. 2025. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.; Hopkins, W.; Roberts, A.; Pyne, D. Ability of test measures to predict competitive performance in elite swimmers. J. Sports Sci. 2008, 26, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Borg, G.A. Psychophysical bases of perceived exertion. Med. Sci. Sports Exerc. 1982, 14, 377–381. [Google Scholar] [CrossRef] [PubMed]
- Wojdala, G.; Trybulski, R.; Bichowska, M.; Krzysztofik, M. A Comparison of Electromyographic Inter-Limb Asymmetry during a Standard versus a Sling Shot Assisted Bench Press Exercise. J. Hum. Kinet. 2022, 83, 223–234. [Google Scholar] [CrossRef]
- Kennel, M.B.; Abarbanel, H.D.I. False neighbors and false strands: A reliable minimum embedding dimension algorithm. Phys. Rev. E 2002, 66, 026209. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Lamoth, C.J.C.; Ainsworth, E.; Polomski, W.; Houdijk, H. Variability and stability analysis of walking of transfemoral amputees. Med. Eng. Phys. 2010, 32, 1009–1014. [Google Scholar] [CrossRef]
- Sharma, N.; Bhusal, C.K.; Pandit, R. Prevalence of Upper Limb Length Discrepancy among Asymptomatic Population of Medical Students in Nepal: A Descriptive Cross Sectional Study. J. Univers. Coll. Med. Sci. 2024, 12, 21–24. [Google Scholar] [CrossRef]
- Kharbat, A.F.; Cox, C.T.; Martinez, J.M.; Mackay, B.J. Radiographic Assessment of Bilateral Asymmetry in the Upper Extremities of Living Humans. Cureus 2023, 15, e35957. [Google Scholar] [CrossRef]

| Swimmer ID | Impairment | Class |
|---|---|---|
| 1 | Right femoral–fibula–ulnar syndrome; Dysmeliac right upper limb | S8 |
| 2 | Intellectual Impairment | S14 |
| 3 | Dysmelia, congenital left-hand amputee | S10 |
| 4 | Cerebral palsy | S9 |
| 5 | Pseudoachondroplasia | S5 |
| 6 | Achondroplasia dwarfism | S6 |
| Swimmer ID | Left Arm Length (cm) | Right Arm Length (cm) | |
|---|---|---|---|
| 1 | 79.90 | 62.73 | 12.04 |
| 2 | 88.10 | 91.13 | 1.69 |
| 3 | 66.43 | 81.27 | 10.04 |
| 4 | 80.17 | 80.37 | 0.12 |
| 5 | 45.77 | 44.77 | 1.10 |
| 6 | 51.40 | 50.00 | 1.28 |
| Direction | Covariate | Step | |
|---|---|---|---|
| Forward | With | F(4,24) = 13.11, p < 0.001 *** | F(1,24) = 3.64, p = 0.07 |
| Without | F(4,25) = 11.86, p < 0.001 *** | ||
| ML | With | F(4,24) = 10.28, p < 0.001 *** | F(1,24) = 3.16, p = 0.09 |
| Without | F(4,25) = 9.46, p < 0.001 *** |
| Direction | Covariate | Step | |
|---|---|---|---|
| Forward | With | F(4,24) = 6.17, p = 0.001 ** | F(1,24) = 9.68, p = 0.005 ** |
| Without | F(4,25) = 4.58, p = 0.009 ** | ||
| ML | With | F(4,24) = 27.64, p < 0.001 *** | F(1,24) = 8.57, p = 0.021 * |
| Without | F(4,25) = 21.21, p < 0.001 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slopecki, M.; Clément, J.; Charbonneau, M.; Côté, J.N. Measuring the Impact of Limb Asymmetry on Movement Irregularity and Complexity Changes During an Incremental Step Test in Para-Swimmers Using Inertial Measurement Units. Sensors 2025, 25, 3297. https://doi.org/10.3390/s25113297
Slopecki M, Clément J, Charbonneau M, Côté JN. Measuring the Impact of Limb Asymmetry on Movement Irregularity and Complexity Changes During an Incremental Step Test in Para-Swimmers Using Inertial Measurement Units. Sensors. 2025; 25(11):3297. https://doi.org/10.3390/s25113297
Chicago/Turabian StyleSlopecki, Matthew, Julien Clément, Mathieu Charbonneau, and Julie N. Côté. 2025. "Measuring the Impact of Limb Asymmetry on Movement Irregularity and Complexity Changes During an Incremental Step Test in Para-Swimmers Using Inertial Measurement Units" Sensors 25, no. 11: 3297. https://doi.org/10.3390/s25113297
APA StyleSlopecki, M., Clément, J., Charbonneau, M., & Côté, J. N. (2025). Measuring the Impact of Limb Asymmetry on Movement Irregularity and Complexity Changes During an Incremental Step Test in Para-Swimmers Using Inertial Measurement Units. Sensors, 25(11), 3297. https://doi.org/10.3390/s25113297






