Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement
Abstract
1. Introduction
2. Spectral Snapshot Imaging Model
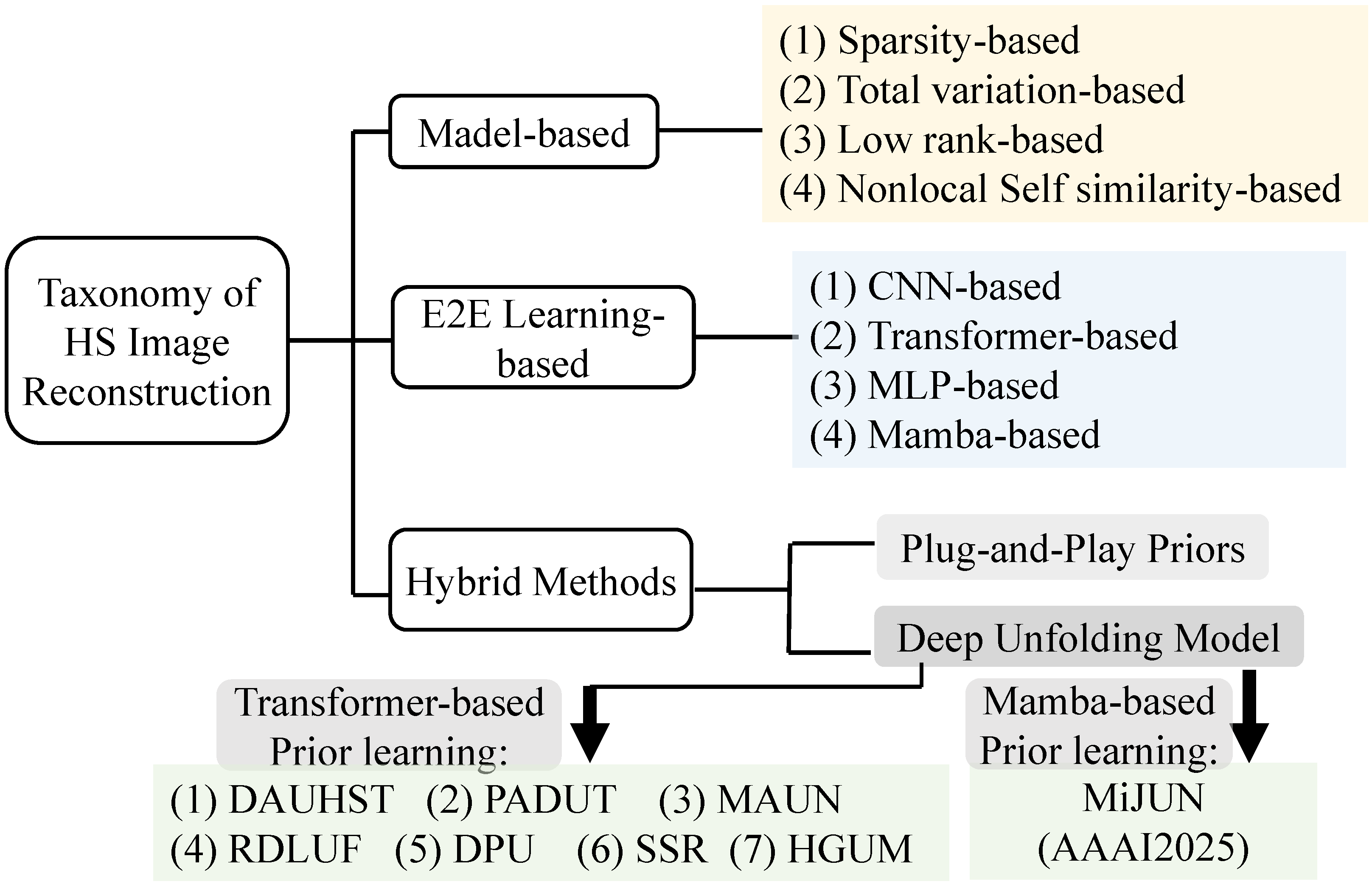
3. Computational Reconstruction Methods
3.1. Model-Based Computational Reconstruction Methods
3.2. Deep Learning-Based Reconstruction Methods
3.3. Deep Unfolding Model (DUM)
4. Hypespectral Image Datasets
5. Result Comparison and Analysis
6. Challenges and Trends
7. Practical Implementations of HS Imaging Techniques
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maggiori, E.; Charpiat, G.; Tarabalka, Y.; Alliez, P. Recurrent neural networks to correct satellite image classification maps. IEEE Trans. Geosci. Remote Sens. 2016, 55, 4962–4971. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Hanachi, R.; Sellami, A.; Farah, I.R.; Mura, M.D. Multi-view graph representation learning for hyperspectral image classification with spectral–spatial graph neural networks. Neural Comput. Appl. 2024, 36, 3737–3759. [Google Scholar] [CrossRef]
- Borengasser, M.; Hungate, W.S.; Watkins, R. Hyperspectral Remote Sensing: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Solomon, J.; Rock, B. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar]
- Ding, C.; Zheng, M.; Zheng, S.; Xu, Y.; Zhang, L.; Wei, W. Integrating prototype learning with graph convolution network for effective active hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Zhi, L.; Zhang, D.; Qi Yan, J.; Li, Q.L.; Lin Tang, Q. Classification of hyperspectral medical tongue images for tongue diagnosis. Comput. Med. Imaging Graph. 2007, 31, 672–678. [Google Scholar] [CrossRef]
- Fei, B. Hyperspectral imaging in medical applications. Data Handl. Sci. Technol. 2019, 32, 523–565. [Google Scholar]
- Llull, P.; Liao, X.; Yuan, X.; Yang, J.; Kittle, D.; Carin, L.; Sapiro, G.; Brady, D.J. Coded Aperture Compressive Temporal Imaging; Optics Express: Washington, DC, USA, 2013. [Google Scholar]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar] [CrossRef]
- Wagadarikar, A.A.; Pitsianis, N.P.; Sun, X.; Brady, D.J. Video Rate Spectral Imaging Using a Coded Aperture Snapshot Spectral Imager; Optics Express: Washington, DC, USA, 2009. [Google Scholar]
- Cao, X.; Yue, T.; Lin, X.; Lin, S.; Yuan, X.; Dai, Q.; Carin, L.; Brady, D.J. Computational snapshot multispectral cameras: Toward dynamic capture of the spectral world. IEEE Signal Process. Mag. 2016, 33, 95–108. [Google Scholar] [CrossRef]
- Gehm, M.E.; John, R.; Brady, D.J.; Willett, R.M.; Schulz, T.J. Single-Shot Compressive Spectral Imaging with a Dual-Disperser Architecture; Optics Express: Washington, DC, USA, 2007. [Google Scholar]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive coded aperture spectral imaging: An introduction. IEEE Signal Process. Mag. 2013, 31, 105–115. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, Z.; Gao, D.; Shi, G.; Zeng, W.; Wu, F. High-speed hyperspectral video acquisition with a dual-camera architectur. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4942–4950. [Google Scholar]
- Motoki, Y.; Yoshikazu, Y.; Takayuki, K. Video-rate hyperspectral camera based on a cmoscompatible random array of fabry–pérot filters. Nat. Photonics 2023, 17, 218–223. [Google Scholar]
- Liu, Y.; Yuan, X.; Suo, J.; Brady, D.J.; Dai, Q. Rank minimization for snapshot compressive imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2990–3006. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xiong, Z.; Shi, G.; Wu, F.; Zeng, W. Adaptive nonlocal sparse representation for dual-camera compressive hyperspectral imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 2104–2111. [Google Scholar] [CrossRef]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q.; Zhang, H.; Zhang, L. Non-local meets global: An iterative paradigm for hyperspectral image restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2089–2107. [Google Scholar] [CrossRef]
- Yuan, X. Generalized alternating projection based total variation minimization for compressive sensing. In Proceedings of the 2016 IEEE International conference on image processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2539–2543. [Google Scholar]
- Figueiredo, M.A.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2017, 1, 586–597. [Google Scholar] [CrossRef]
- Meng, Z.; Ma, J.; Yuan, X. End-to-end low cost compressive spectral imaging with spatial-spectral self attention. In European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2020; pp. 187–204. [Google Scholar]
- Hu, X.; Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L.V. Hdnet: High-resolution dual-domain learning for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Miao, X.; Yuan, X.; Pu, Y.; Athitsos, V. λ-net: Reconstruct hyperspectral images from a snapshot measurement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Wang, L.; Sun, C.; Fu, Y.; Kim, M.H.; Huang, H. Hyperspectral image reconstruction using a deep spatial-spectral prior. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Yorimoto, K.; Han, X.H. HyperMixNet: Hyperspectral Image Reconstruction with Deep Mixed Network From a Snapshot Measurement. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1184–1193. [Google Scholar]
- Zhang, X.; Zhang, Y.; Xiong, R.; Sun, Q.; Zhang, J. Herosnet: Hyperspectral explicable reconstruction and optimal sampling deep network for snapshot compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17532–17541. [Google Scholar]
- Takabe, T.; Han, X.; Chen, Y. Deep Versatile Hyperspectral Reconstruction Model from A Snapshot Measurement with Arbitrary Masks. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 2390–2394. [Google Scholar]
- Han, X.; Wang, J.; Chen, Y. Hyperspectral Image Reconstruction Using Hierarchical Neural Architecture Search from A Snapshot Image. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 2500–2504. [Google Scholar]
- Wang, L.; Sun, C.; Zhang, M.; Fu, Y.; Huang, H. Dnu: Deep non-local unrolling for computational spectral imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1661–1671. [Google Scholar]
- Huang, T.; Dong, W.; Yuan, X.; Wu, J.; Shi, G. Deep gaussian scale mixture prior for spectral compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 16216–16225. [Google Scholar]
- Cai, Y.; Lin, J.; Wang, H.; Yuan, X.; Ding, H.; Zhang, Y.; Timofte, R.; Gool, L.V. Degradation-aware unfolding half-shuffle transformer for spectral compressive imaging. Adv. Neural Inf. Process. Syst. 2022, 35, 37749–37761. [Google Scholar]
- Li, M.; Fu, Y.; Liu, J.; Zhang, Y. Pixel adaptive deep unfolding transformer for hyperspectral image reconstruction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023. [Google Scholar]
- Zhang, J.; Su, R.; Fu, Q.; Ren, W.; Heide, F.; Nie, Y. A survey on computational spectral reconstruction methods from RGB to hyperspectral imaging. Sci. Rep. 2022, 12, 11905. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Monjur, O.; Khaliduzzaman, A.; Khaliduzzaman, M. A comprehensive review of deep learning-based hyperspectral image reconstruction for agri-food quality appraisal. Artif. Intell. Rev. 2025, 58, 73–81. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Descour, M.; Volin, C.; Ford, B.; Dereniak, E.; Maker, P.; Wilson, D. Snapshot hyperspectral imaging. In Integrated Computational Imaging Systems; Optica Publishing Group: Washington, DC, USA, 2001. [Google Scholar]
- Han, W.; Wang, Q.; Cai, W. Computed tomography imaging spectrometry based on superiorization and guided image filtering. Opt. Lett. 2021, 46, 2208–2211. [Google Scholar] [CrossRef] [PubMed]
- Bian, L.; Wang, Z.; Zhang, Y.; Li, L.; Zhang, Y.; Yang, C.; Fang, W.; Zhao, J.; Zhu, C.; Meng, Q.; et al. A broadband hyperspectral image sensor with high spatio-temporal resolution. Nature 2024, 635, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wang, L.; Fu, Y.; Zhong, X.; Huang, H. Computational hyperspectral imaging based on dimension-discriminative low-rank tensor recovery. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L.V. Mask-guided spectral-wise transformer for efficient hyperspectral image reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17502–17511. [Google Scholar]
- Cai, Y.; Lin, J.; Hu, X.; Wang, H.; Yuan, X.; Zhang, Y.; Timofte, R.; Gool, L.V. Coarse-to-fine sparse transformer for hyperspectral image reconstruction. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Yuan, X.; Liu, Y.; Suo, J.; Dai, Q. Plug-and-play algorithms for large-scale snapshot compressive imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Zheng, S.; Liu, Y.; Meng, Z.; Qiao, M.; Tong, Z.; Yang, X.; Han, S.; Yuan, X. Deep plug-and-play priors for spectral snapshot compressive imaging. Photonics Res. 2021, 9, B18–B29. [Google Scholar] [CrossRef]
- Hu, Q.; Ma, J.; Gao, Y.; Jiang, J.; Yuan, Y. MAUN: Memory-Augmented Deep Unfolding Network for Hyperspectral Image Reconstruction. IEEE/CAA J. Autom. Sin. 2024, 11, 1139–1150. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, H.; Cao, J.; Chen, Y.; Yu, D.; Zhao, Y.P. Dual Prior Unfolding for Snapshot Compressive Imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 25742–25752. [Google Scholar]
- Zhang, J.; Zeng, H.; Chen, Y.; Yu, D.; Zhao, Y.P. Improving Spectral Snapshot Reconstruction with Spectral-Spatial Rectification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 25817–25826. [Google Scholar]
- Zhang, S.; Dong, Y.; Fu, H.; Huang, S.L.; Zhan, L. A spectral reconstruction algorithm of miniature spectrometer based on sparse optimization and dictionary learning. Sensors 2018, 18, 644. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new twist: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef]
- Eason, D.T.; Andrews, M. Total variation regularization via continuation to recover compressed hyperspectral images. IEEE Trans. Image Process. 2014, 24, 284–293. [Google Scholar] [CrossRef]
- Fu, Y.; Zheng, Y.; Sato, I.; Sato, Y. Exploiting spectral-spatial correlation for coded hyperspectral image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3727–3766. [Google Scholar]
- Ma, J.; Liu, X.; Shou, Z.; Yuan, X. Deep tensor admm-net for snapshot compressive imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Meng, Z.; Jalali, S.; Yuan, X. Gap-net for snapshot compressive imaging. arXiv 2020, arXiv:2012.08364. [Google Scholar]
- Yao, Z.; Liu, S.; Yuan, X.; Fang, L. SPECAT: SPatial-spEctral Cumulative-Attention Transformer for High-Resolution Hyperspectral Image Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Han, X.H.; Wang, J.; Chen, Y.W. Mask-Guided Spatial–Spectral MLP Network for High-Resolution Hyperspectral Image Reconstruction. Sensors 2024, 24, 7362. [Google Scholar] [CrossRef]
- Meng, G.; Tu, J.; Huang, J.; Lin, Y.; Wang, Y.; Tu, X.; Huang, Y.; Ding, X. Sp3ctralMamba: Physics-Driven Joint State Space Model for Hyperspectral Image Reconstruction. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence (AAAI-25), Philadelphia, PA, USA, 25 February–4 March 2025; pp. 6108–6116. [Google Scholar]
- Cai, Y.; Zheng, Y.; Lin, J.; Yuan, X.; Zhang, Y.; Wang, H. Binarized Spectral Compressive Imaging. In Proceedings of the 37th International Conference on Neural Information Processing System, New Orleans LA USA, 10–16 December 2023; pp. 38335–38346. [Google Scholar]
- Wang, J.; Li, K.; Zhang, Y.; Yuan, X. S2-Transformer for Mask-Aware Hyperspectral Image Reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 99, 1–18. [Google Scholar] [CrossRef]
- Luo, F.; Chen, X.; Gong, X.; Wu, W.; Guo, T. Dual-window multiscale transformer for hyperspectral snapshot compressive imaging. Proc. Aaai Conf. Artif. Intell. 2024, 38, 3972–3980. [Google Scholar] [CrossRef]
- Huang, J.; Sun, Y.; Wen, J.; Liu, Q. Transformer-Based Residual Network for Hyperspectral Snapshot Compressive Reconstruction. In Proceedings of the 2022 26th International Conference on Pattern Recognition, Montreal, QC, Canada, 21–25 August 2022. [Google Scholar]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; A. Steiner, D.K.; Uszkoreit, J. Mlp-mixer: An all-mlp architecture for vision. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Liu, H.; Dai, Z.; So, D.; Le, Q.V. Pay attention to mlps. Adv. Neural Inf. Process. Syst. 2021, 34, 9204–9215. [Google Scholar]
- Touvron, H.; Bojanowski, P.; Caron, M.; Cord, M.; ElNouby, A.; Grave, E.; Izacard, G.; Joulin, A.; Synnaeve, G.; Verbeek, J. Resmlp: Feedforward networks for image classification with data-efficient training. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5314–5321. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xie, E.; GE, C.; Chen, R.; Liang, D.; Luo, P. CycleMLP: A MLP-like Architecture for Dense Prediction. arXiv 2021, arXiv:2107.10224. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Hong, R.; Lin, X.; Yang, J.; Ni, Y.; Liu, Z.; Jin, C.; Da, F. A MLP Architecture Fusing RGB and CASSI for Computational Spectral Imaging. Comput. Vis. Image Underst. 2024, 249, 104214. [Google Scholar] [CrossRef]
- Cai, Z.; Zhang, C.; Chen, Y.; Chen, X.; Yang, J.; Shi, W.; Da, F.; Jin, C. MLP-AMDC: A MLP Architecture for Adaptive-Mask-Based Dual-Camera Snapshot Hyperspectral Imaging. In International Conference on Multimedia Modeling; Springer Nature: Singapore, 2024. [Google Scholar]
- Dong, Y.; Gao, D.; Qiu, T.; Li, Y.; Yang, M.; Shi, G. Residual Degradation Learning Unfolding Framework with Mixing Priors across Spectral and Spatial for Compressive Spectral Imaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Han, X.; Wang, J. Multi-Degradation Oriented Deep Unfolding Model for Hyperspectral Image Reconstruction. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025. [Google Scholar]
- Han, X.H. High-generalized Unfolding Model with Coupled Spatial-Spectral Transformer for Hyperspectral Image Reconstruction. IEEE Trans. Comput. Imaging 2025, 11, 625–637. [Google Scholar] [CrossRef]
- Qin, M.; Feng, Y.; Wu, Z.; Zhang, Y.; Yuan, X. Detail Matters: Mamba-Inspired Joint Unfolding Network for Snapshot Spectral Compressive Imaging. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence (AAAI-25), Philadelphia, PA, USA, 25 February–4 March 2025; pp. 6594–6602. [Google Scholar]
- Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: Postcapture control of resolution, dynamic range, and spectrum. IEEE Trans. Image Process. 2010, 19, 2241–2253. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Zickler, T.E. Statistics of real-world hyperspectral images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 193–200. [Google Scholar]
- Arad, B.; Ben-Shahar, O. Sparse recovery of hyperspectral signal from natural RGB images. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 19–34. [Google Scholar]
- Choi, I.; Jeon, D.S.; Nam, G.; Gutierrez, D.; Kim, M.H. High-quality hyperspectral reconstruction using a spectral prior. ACM Trans. Graph. 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Lim, O.; Mancini, S.; Mura, M.D. Feasibility of a Real-Time Embedded Hyperspectral Compressive Sensing Imaging System. Sensors 2022, 22, 9793. [Google Scholar] [CrossRef]
- Lin, Y.; Zhou, S.; Wan, Z.; Qiu, Z.; Zhao, L.; Pang, K.; Li, C.; Yin, Z. A Self-Supervised Anomaly Detector of Fruits Based on Hyperspectral Imaging. Foods 2023, 12, 2669. [Google Scholar] [CrossRef]
- Jia, Y.; Xue, L.; Xu, P.; Luo, B.; Chen, K.; Zhu, L.; Liu, Y.; Yan, M. A novel hyperspectral compressive sensing framework of plant leaves based on multiple arbitrary-shape regions of interest. PeerJ Comput Sci. 2021, 7, e802. [Google Scholar] [CrossRef]
- Ma, L.; Pruitt, K.; Fei, B. Dual-camera laparoscopic imaging with super-resolution reconstruction for intraoperative hyperspectral image guidance. Proc. SPIE Int. Soc. Opt. Eng. 2024, 129280, 97–104. [Google Scholar]
- Lee, L.; Chen, S. Assessment of Hyperspectral Imaging in Pressure Injury Healing. Adv. Skin Wound Care 2022, 35, 429–434. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Nguyen, H.; Lin, T.; Saenprasarn, P.; Liu, P.; Wang, H. Identification of Skin Lesions by Snapshot Hyperspectral Imaging. Cancers 2024, 16, 429–434. [Google Scholar] [CrossRef] [PubMed]


| Aspect | CASSI | FPFA |
|---|---|---|
| Encoding method | Coded aperture + dispersion | Fabry–Pérot filter array |
| Spectral Resolution | 10–20 nm | 10 nm (visible range) |
| Light Throughput | Lower (50% loss at aperture) | High (45% average transmission) |
| Key Advantage | Flexibility in spectral range | Compact, high sensitivity, real-time |
| Prior Type | Underlying Principle | Advantages | Limitations/Challenges | Representative Works/References |
|---|---|---|---|---|
| Sparsity-based | Assumes that the HS data (or its transform coefficients) have a sparse representation. |
|
| Figueiredo et al. (GPSR) [22]; Bioucas-Dias et al. (TwIST) [50]. |
| TV-based | Utilizes total variation regularization to enforce local smoothness while preserving sharp edges by penalizing the image gradient. |
|
| Yuan et al. (GAP-TV) [21] |
| Low-Rank-based | Exploits the observation that HS images lie in a low-dimensional spectral subspace due to the high correlation among spectral bands. |
|
| Zhang et al. (Low-Rank Matrix Recovery) [41] |
| NSS-based | Leverages the phenomenon that similar image patches appear at different, non-adjacent locations within the image to enforce a low-rank structure on groups of similar patches. |
|
| He et al. (Non-local meets global) [20] |
| Architecture Type | Representative Models/Examples | Key Architectural Components | Design Considerations and Strengths |
|---|---|---|---|
| CNN-based | TSA-Net [23], -Net [25], HDNet [24], NAS [30] |
|
|
| Transformer-based | MST [42], CST [43], S2-Tran [59], DWMT [60], SPECAT [55] |
|
|
| MLP-based | MG-S2MLP [56], SSMLP [66], MLP-AMDC [67] |
|
|
| State Space (Mamba-based) | Sp3ctralMamba [57] |
|
|
| Dataset | # of Images | Spatial Resolution | Spectral Channels | Acquisition Conditions |
|---|---|---|---|---|
| CAVE | 32 | 512 × 512 | ∼31 (400–700 nm) | Controlled laboratory environment |
| Harvard | ∼50 | High resolution (varies) | ∼31 (420–720 nm) | Uniform, controlled illumination |
| ICVL | 201 | ∼1392 × 1040 | 31 (approx.) | Natural scenes with diverse content |
| KAIST | ∼30 (approx.) | 2704 × 3376 (approx.) | 28 (approx.) | Outdoor/real-world settings |
| (a) For the captured measurements in CASSI setting | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | Params | GFLOPs | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 | Avg |
| TwIST [50] | - | - | 25.16 | 23.02 | 21.40 | 30.19 | 21.41 | 20.95 | 22.20 | 21.82 | 22.42 | 22.67 | 23.12 |
| 0.700 | 0.604 | 0.711 | 0.851 | 0.635 | 0.644 | 0.643 | 0.650 | 0.690 | 0.569 | 0.669 | |||
| GAP-TV [21] | - | - | 26.82 | 22.89 | 26.31 | 30.65 | 23.64 | 21.85 | 23.76 | 21.98 | 22.63 | 23.1 | 24.36 |
| 0.754 | 0.610 | 0.802 | 0.852 | 0.703 | 0.663 | 0.688 | 0.655 | 0.682 | 0.584 | 0.669 | |||
| DeSCI [18] | - | - | 27.13 | 23.04 | 26.62 | 34.96 | 23.94 | 22.38 | 24.45 | 22.03 | 24.56 | 23.59 | 25.27 |
| 0.748 | 0.620 | 0.818 | 0.897 | 0.706 | 0.683 | 0.743 | 0.673 | 0.732 | 0.587 | 0.721 | |||
| -Net [25] | 62.64M | 117.98 | 30.10 | 28.49 | 27.73 | 37.01 | 26.19 | 28.64 | 26.47 | 26.09 | 27.50 | 27.13 | 28.53 |
| 0.849 | 0.805 | 0.870 | 0.934 | 0.817 | 0.853 | 0.806 | 0.831 | 0.826 | 0.816 | 0.841 | |||
| DSSP [26] | 33.85M | 64.42 | 31.48 | 31.09 | 28.96 | 35.56 | 28.53 | 30.83 | 28.71 | 30.09 | 30.43 | 28.78 | 30.35 |
| 0.856 | 0.842 | 0.823 | 0.902 | 0.808 | 0.877 | 0.824 | 0.881 | 0.868 | 0.842 | 0.852 | |||
| TSA-Net [23] | 44.25M | 110.06 | 32.03 | 31.00 | 32.25 | 39.19 | 29.39 | 31.44 | 30.32 | 29.35 | 30.01 | 29.59 | 31.46 |
| 0.892 | 0.858 | 0.915 | 0.953 | 0.884 | 0.908 | 0.878 | 0.888 | 0.890 | 0.874 | 0.894 | |||
| HDNet [24] | 2.37M | 154.76 | 35.14 | 35.67 | 36.03 | 42.30 | 32.69 | 34.46 | 33.67 | 32.48 | 34.89 | 32.38 | 34.97 |
| 0.935 | 0.940 | 0.943 | 0.969 | 0.946 | 0.952 | 0.926 | 0.941 | 0.942 | 0.937 | 0.943 | |||
| MST-L [42] | 2.03M | 28.15 | 35.40 | 35.87 | 36.51 | 42.27 | 32.77 | 34.80 | 33.66 | 32.67 | 35.39 | 32.50 | 35.18 |
| 0.941 | 0.944 | 0.953 | 0.973 | 0.947 | 0.955 | 0.925 | 0.948 | 0.949 | 0.941 | 0.948 | |||
| CST-L [43] | 3.00M | 40.01 | 35.96 | 36.84 | 38.16 | 42.44 | 33.25 | 35.72 | 34.86 | 34.34 | 36.51 | 33.09 | 36.12 |
| 0.949 | 0.955 | 0.962 | 0.975 | 0.955 | 0.963 | 0.944 | 0.961 | 0.957 | 0.945 | 0.957 | |||
| DWMT [60] | 14.48M | 46.71 | 36.46 | 37.75 | 38.47 | 44.23 | 33.99 | 36.17 | 35.22 | 34.56 | 37.41 | 34.99 | 36.82 |
| 0.957 | 0.963 | 0.965 | 0.984 | 0.963 | 0.970 | 0.949 | 0.968 | 0.965 | 0.959 | 0.964 | |||
| DGSMP [32] | 3.76M | 84.77 | 33.26 | 32.09 | 33.06 | 40.54 | 28.86 | 33.08 | 30.74 | 31.55 | 31.66 | 31.44 | 32.63 |
| 0.915 | 0.898 | 0.925 | 0.964 | 0.882 | 0.937 | 0.886 | 0.923 | 0.911 | 0.925 | 0.917 | |||
| GAP-Net [54] | 4.27M | 78.58 | 33.74 | 33.26 | 34.28 | 41.03 | 31.44 | 32.40 | 32.27 | 30.46 | 33.51 | 30.24 | 33.26 |
| 0.911 | 0.900 | 0.929 | 0.967 | 0.919 | 0.925 | 0.902 | 0.905 | 0.915 | 0.895 | 0.917 | |||
| ADMM-Net [53] | 4.27M | 78.58 | 34.12 | 33.62 | 35.04 | 41.15 | 31.82 | 32.54 | 32.42 | 30.74 | 33.75 | 30.68 | 33.58 |
| 0.918 | 0.902 | 0.931 | 0.966 | 0.922 | 0.924 | 0.896 | 0.907 | 0.915 | 0.895 | 0.918 | |||
| DAUHST-L [33] | 6.15M | 79.50 | 37.25 | 39.02 | 41.05 | 46.15 | 35.80 | 37.08 | 37.57 | 35.10 | 40.02 | 34.59 | 38.36 |
| 0.958 | 0.967 | 0.971 | 0.983 | 0.969 | 0.970 | 0.963 | 0.966 | 0.970 | 0.956 | 0.967 | |||
| PADUT-L [34] | 5.38M | 90.46 | 37.36 | 40.43 | 42.38 | 46.62 | 36.26 | 37.27 | 37.83 | 35.33 | 40.86 | 34.55 | 38.89 |
| 0.962 | 0.978 | 0.979 | 0.990 | 0.974 | 0.974 | 0.966 | 0.974 | 0.978 | 0.963 | 0.974 | |||
| MAUN-L [46] | 3.77M | 143.83 | 37.78 | 40.53 | 41.88 | 46.85 | 36.74 | 37.78 | 37.44 | 36.05 | 40.54 | 34.90 | 39.05 |
| 0.963 | 0.976 | 0.973 | 0.986 | 0.973 | 0.974 | 0.961 | 0.971 | 0.973 | 0.962 | 0.971 | |||
| RDLUF [68] | 1.81M | 115.16 | 37.94 | 40.95 | 43.25 | 47.83 | 37.11 | 37.47 | 38.58 | 35.50 | 41.83 | 35.23 | 39.57 |
| 0.966 | 0.977 | 0.979 | 0.990 | 0.976 | 0.975 | 0.969 | 0.970 | 0.978 | 0.962 | 0.974 | |||
| DPU [47] | 2.85M | 49.26 | 38.79 | 41.78 | 43.80 | 47.69 | 37.96 | 38.48 | 39.00 | 36.81 | 42.65 | 36.28 | 40.33 |
| 0.971 | 0.983 | 0.983 | 0.993 | 0.981 | 0.981 | 0.973 | 0.979 | 0.984 | 0.974 | 0.980 | |||
| SSR [48] | 5.18M | 78.93 | 38.95 | 41.83 | 44.16 | 48.09 | 38.53 | 38.40 | 39.03 | 38.88 | 42.88 | 36.00 | 40.47 |
| 0.973 | 0.984 | 0.983 | 0.994 | 0.983 | 0.981 | 0.974 | 0.980 | 0.985 | 0.973 | 0.981 | |||
| MiJUN [71] | 0.56 | 73.67 | 39.26 | 41.78 | 44.31 | 48.53 | 39.30 | 38.22 | 41.00 | 36.72 | 43.84 | 35.56 | 40.86 |
| 0.973 | 0.983 | 0.983 | 0.994 | 0.985 | 0.979 | 0.983 | 0.978 | 0.985 | 0.967 | 0.982 | |||
| (b) For the captured measurements in FPFA setting | |||||||||||||
| Methods | Params | GFLOPs | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 | Avg |
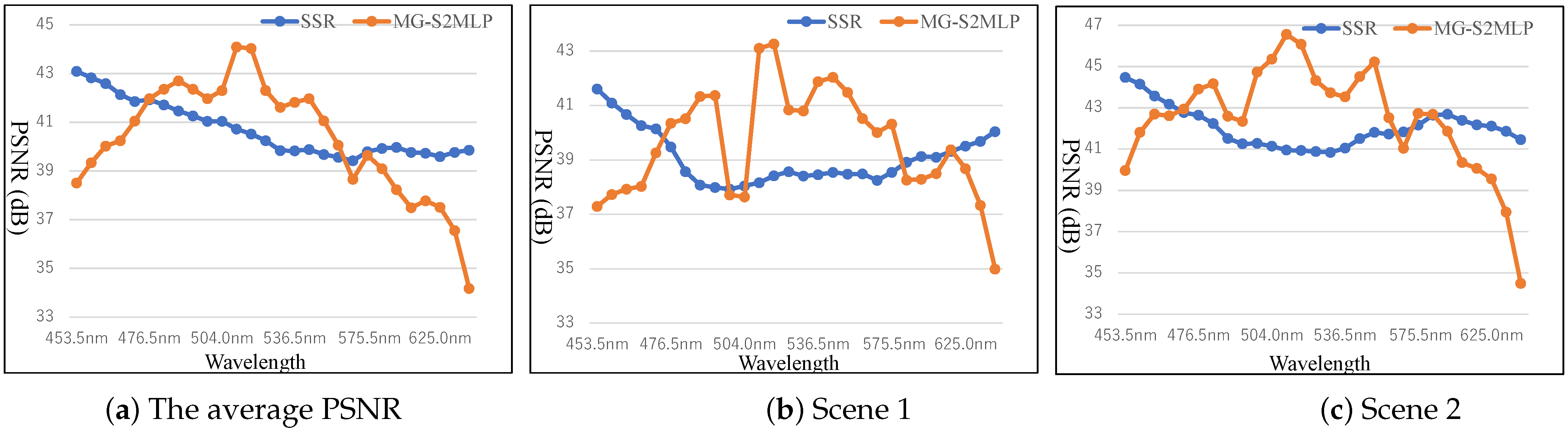
| MG-S2MLP [56] | 0.31 | 15.2 | 39.47 | 42.26 | 41.39 | 45.08 | 39.15 | 39.86 | 38.97 | 37.05 | 40.93 | 37.05 | 40.12 |
| 0.982 | 0.989 | 0.982 | 0.990 | 0.988 | 0.988 | 0.976 | 0.980 | 0.987 | 0.988 | 0.985 | |||
| SPECAT [55] | 0.29 | 12.4 | 40.24 | 42.40 | 41.43 | 44.90 | 39.62 | 39.90 | 39.41 | 37.49 | 40.45 | 37.90 | 40.39 |
| 0.982 | 0.986 | 0.978 | 0.982 | 0.987 | 0.984 | 0.977 | 0.977 | 0.982 | 0.983 | 0.982 | |||
| Sp3ctralMamba [57] | 0.45 | 64.65 | 40.66 | 43.22 | 42.17 | 45.64 | 40.75 | 41.70 | 39.88 | 37.94 | 41.43 | 38.71 | 41.21 |
| 0.989 | 0.992 | 0.988 | 0.990 | 0.993 | 0.991 | 0.986 | 0.988 | 0.986 | 0.989 | 0.989 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.-H.; Wang, J.; Jiang, H. Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement. Sensors 2025, 25, 3286. https://doi.org/10.3390/s25113286
Han X-H, Wang J, Jiang H. Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement. Sensors. 2025; 25(11):3286. https://doi.org/10.3390/s25113286
Chicago/Turabian StyleHan, Xian-Hua, Jian Wang, and Huiyan Jiang. 2025. "Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement" Sensors 25, no. 11: 3286. https://doi.org/10.3390/s25113286
APA StyleHan, X.-H., Wang, J., & Jiang, H. (2025). Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement. Sensors, 25(11), 3286. https://doi.org/10.3390/s25113286







