Multi-Source Causal Invariance for Cuffless Blood Pressure Estimation Based on Photoplethysmography Signal Features
Abstract
1. Introduction
- We propose a novel causal invariance-based feature selection framework for multi-source PPG data, ensuring the identification of stable and domain-invariant features;
- MDSFS-EMB significantly reduces feature redundancy while retaining key causal features and enhanced robustness to device variations and population heterogeneity through nonlinear relationship modeling;
- The MDSFS-EMB algorithm outperforms in feature selection efficiency, prediction accuracy, and generalization capability. External validation also further confirms that the causal feature set selected by the algorithm remains stable and reliable, even when applied to data with unknown distributions.
2. Materials and Methods
2.1. Datasets
2.2. Data Processing and Feature Extraction
2.3. Feature Selection
2.3.1. Causal Model
2.3.2. MDSFS-EMB Algorithm
- PPFS: Cross-validation based aggregation method to find MB for small samples and for datasets that do not follow the fidelity assumption;
- HITON-MB: MB-based local causal structure learning approach focusing on direct cause/effect identification and MB discovery. It is suitable for large-scale datasets, but may face challenges with small sample sizes.
| Algorithm 1. The MDSFS-EMB Algorithm |
| Input: D = {}, M: BP, : significance level, n: feature subset size |
| Output: Best_feature |
|
|
|
2.4. BP Estimation
3. Results
3.1. Model Evaluation
3.2. Splitting Strategy
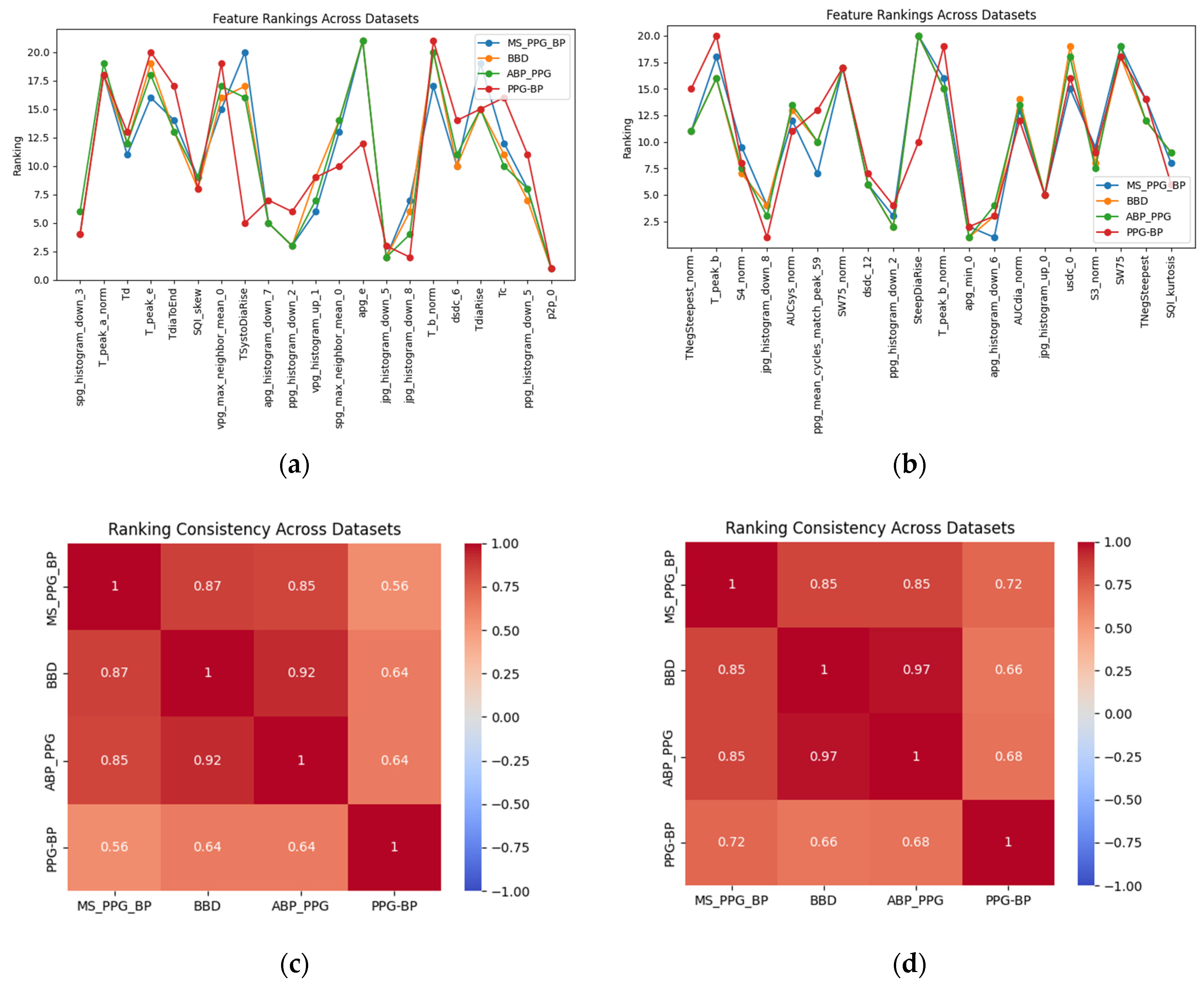
3.3. Feature Selection Results
| Algorithm 2. Baseline Algorithm |
| Input: D = {},M: SBP or DBP Output: MB(M), MB(M)
|
3.4. Performance Comparison of Various Machine Learning Models
4. Discussion
4.1. Advantages of the MDSFS-EMB Algorithm
- By integrating the small-sample adaptability of PPFS with the large-scale structure discovery capability of HITON-MB, the algorithm overcomes sensitivity to dataset size while leveraging MB theory to comprehensively identify causal features of the target variable;
- By transforming marginal distributions into Gaussian form, GCMI preserves rank relationships between variables, effectively capturing the nonlinear and non-monotonic associations between PPG signals and BP parameters. This approach not only enhances robustness to outliers but also eliminates distributional assumptions, making it highly adaptable to heterogeneous multi-source data;
- GCMI- and AMI-based assessment mechanisms mitigate the impact of dataset heterogeneity on feature stability, ensuring consistent and reliable causal feature selection across different data sources.
4.2. Data Heterogeneity Versus Model Generalization
4.3. Limitation
- The MDSFS-EMB feature selection algorithm screened features common to all datasets, which may result in the omission of features unique to some datasets, and reduce the personalized prediction ability of the model;
- The study only focused on BP values without incorporating demographic data (age, gender) and physiological state parameters (exercise/resting state), which may overlook covariates of BP fluctuations, and future multimodal feature fusion models need to be constructed to improve interpretability;
- The study did not explicitly investigate the interpretability of the model, especially its implications for real-world clinical applications, which represents a potential limitation for practical medical deployment.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAMI | Association for the Advancement of Medical Instrumentation |
| ABP | Arterial blood pressure |
| AMI | Average Mutual Information |
| APG | Acceleration Photoplethysmography |
| BP | Blood Pressure |
| CVD | Cardiovascular diseases |
| DBP | Diastolic Blood Pressure |
| GCMI | Gaussian Copula Mutual Information |
| JPG | Jerk Photoplethysmography |
| MAD | Mean Absolute Difference |
| MASE | Mean Absolute Scaled Error |
| MB | Markov Blanket |
| ME | Mean Error |
| MDSFS-EMB | Multi-Dataset Stable Feature Selection via Ensemble MB |
| MS_PPG_BP | Multi-state PPG Blood Pressure Dataset |
| PPG | Photoplethysmography |
| RF | Random Forest |
| SBP | Systolic Blood Pressure |
| SDE | Standard Deviation of Error |
| SPG | Snap Photoplethysmography |
| SQI | Signal Quality Index |
| SVR | Support Vector Regression |
| SW and DW | Widths of the systolic and diastolic phases |
| VPG | Velocity photoplethysmography |
References
- World Health Organization. World Health Statistics 2023: Monitoring Health for the SDGs, Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2023; ISBN 978-92-4-007432-3. [Google Scholar]
- Pattanaik, S. Biomarkers in Essential Hypertension. In Kidney Biomarkers; Elsevier: Amsterdam, The Netherlands, 2020; pp. 247–288. ISBN 978-0-12-815923-1. [Google Scholar]
- Stevens, S.L.; Wood, S.; Koshiaris, C.; Law, K.; Glasziou, P.; Stevens, R.J.; McManus, R.J. Blood Pressure Variability and Cardiovascular Disease: Systematic Review and Meta-Analysis. BMJ 2016, 354, i4098. [Google Scholar] [CrossRef] [PubMed]
- Saugel, B.; Kouz, K.; Meidert, A.S.; Schulte-Uentrop, L.; Romagnoli, S. How to Measure Blood Pressure Using an Arterial Catheter: A Systematic 5-Step Approach. Crit. Care 2020, 24, 172. [Google Scholar] [CrossRef]
- Barvik, D.; Cerny, M.; Penhaker, M.; Noury, N. Noninvasive Continuous Blood Pressure Estimation from Pulse Transit Time: A Review of the Calibration Models. IEEE Rev. Biomed. Eng. 2022, 15, 138–151. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Landaeta, R.; Ramirez, B.; Mejia, J. Estimation of Systolic Blood Pressure by Random Forest Using Heart Sounds and a Ballistocardiogram. Sci. Rep. 2022, 12, 17196. [Google Scholar] [CrossRef] [PubMed]
- Mukkamala, R.; Stergiou, G.S.; Avolio, A.P. Cuffless Blood Pressure Measurement. Annu. Rev. Biomed. Eng. 2022, 24, 203–230. [Google Scholar] [CrossRef]
- Samartkit, P.; Pullteap, S. Non-Invasive Continuous Blood Pressure Sensors in Biomedical Engineering Research: A Review. Sens. Actuators A Phys. 2024, 367, 115084. [Google Scholar] [CrossRef]
- El Hajj, C.; Kyriacou, P.A. Cuffless and Continuous Blood Pressure Estimation from PPG Signals Using Recurrent Neural Networks. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Online, 20–24 July 2020; pp. 4269–4272. [Google Scholar]
- González, S.; Hsieh, W.T.; Chen, T.P.C. A Benchmark for Machine-Learning Based Non-Invasive Blood Pressure Estimation Using Photoplethysmogram. Sci. Data 2023, 10, 149. [Google Scholar] [CrossRef]
- Di Nisio, A.; De Palma, L.; Ragolia, M.A.; Lanzolla, A.M.L.; Attivissimo, F. Performance Comparison of Machine Learning Algorithms for the Estimation of Blood Pressure Using Photoplethysmography. Biomed. Signal Process. Control 2025, 99, 106838. [Google Scholar] [CrossRef]
- Yu, K.; Guo, X.; Liu, L.; Li, J.; Wang, H.; Ling, Z.; Wu, X. Causality-Based Feature Selection: Methods and Evaluations. ACM Comput. Surv. 2020, 53, 1–36. [Google Scholar] [CrossRef]
- Yu, K.; Liu, L.; Li, J. A Unified View of Causal and Non-Causal Feature Selection. arXiv 2018, arXiv:1802.05844. [Google Scholar] [CrossRef]
- Cisnal, A.; Li, Y.; Fuchs, B.; Ejtehadi, M.; Riener, R.; Paez-Granados, D. Robust Feature Selection for BP Estimation in Multiple Populations: Towards Cuffless Ambulatory BP Monitoring. IEEE J. Biomed. Health Inform. 2024, 28, 5768–5779. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, Y.-T.; Wang, W.; Chen, Y.; Ding, X. Causal Inference Based Cuffless Blood Pressure Estimation: A Pilot Study. Comput. Biol. Med. 2023, 159, 106900. [Google Scholar] [CrossRef]
- Liu, L.; Lu, H.; Whelan, M.; Chen, Y.; Ding, X. CiGNN: A Causality-Informed and Graph Neural Network Based Framework for Cuffless Continuous Blood Pressure Estimation. IEEE J. Biomed. Health Inform. 2024, 28, 2674–2686. [Google Scholar] [CrossRef]
- Qiu, P.; Niu, Z.; Zhang, C. Research on the Multi-Source Causal Feature Selection Method Based on Multiple Causal Relevance. Knowl. Based Syst. 2023, 265, 110334. [Google Scholar] [CrossRef]
- Aguirre, N.; Grall-Maës, E.; Cymberknop, L.J.; Armentano, R.L. Blood Pressure Morphology Assessment from Photoplethysmogram and Demographic Information Using Deep Learning with Attention Mechanism. Sensors 2021, 21, 2167. [Google Scholar] [CrossRef]
- Carlson, C.; Turpin, V.-R.; Suliman, A.; Ade, C.; Warren, S.; Thompson, D.E. Bed-Based Ballistocardiography: Dataset and Ability to Track Cardiovascular Parameters. Sensors 2021, 21, 156. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, Z.; Liu, G.; Elgendi, M. A New, Short-Recorded Photoplethysmogram Dataset for Blood Pressure Monitoring in China. Sci. Data 2018, 5, 180020. [Google Scholar] [CrossRef]
- Dey, J.; Gaurav, A.; Tiwari, V.N. InstaBP: Cuff-Less Blood Pressure Monitoring on Smartphone Using Single PPG Sensor. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 17–21 July 2018; pp. 5002–5005. [Google Scholar]
- Hassan, A.; Paik, J.H.; Khare, S.R.; Hassan, S.A. A Wrapper Feature Selection Approach Using Markov Blankets. Pattern Recognit. 2025, 158, 111069. [Google Scholar] [CrossRef]
- Aliferis, C.F.; Tsamardinos, I.; Statnikov, A. HITON: A Novel Markov Blanket Algorithm for Optimal Variable Selection. AMIA Annu. Symp. Proc. 2003, 2003, 21–25. [Google Scholar]
- Yu, K.; Liu, L.; Li, J.; Ding, W.; Le, T.D. Multi-Source Causal Feature Selection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2240–2256. [Google Scholar] [CrossRef]
- Ince, R.A.A.; Giordano, B.L.; Kayser, C.; Rousselet, G.A.; Gross, J.; Schyns, P.G. A Statistical Framework for Neuroimaging Data Analysis Based on Mutual Information Estimated via a Gaussian Copula. Hum. Brain Mapp. 2017, 38, 1541–1573. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.; Kwatra, N.; Jain, M.; McDuff, D. Examining the Challenges of Blood Pressure Estimation via Photoplethysmogram. Sci. Rep. 2024, 14, 18318. [Google Scholar] [CrossRef]
- Qin, K.; Huang, W.; Zhang, T.; Tang, S. Machine Learning and Deep Learning for Blood Pressure Prediction: A Methodological Review from Multiple Perspectives. Artif. Intell. Rev. 2023, 56, 8095–8196. [Google Scholar] [CrossRef]
- White, W.B.; Berson, A.S.; Robbins, C.; Jamieson, M.J.; Prisant, L.M.; Roccella, E.; Sheps, S.G. National Standard for Measurement of Resting and Ambulatory Blood Pressures with Automated Sphygmomanometers. Hypertension 1993, 21, 504–509. [Google Scholar] [CrossRef]
- 1708a-2019; IEEE Standard for Wearable, Cuffless Blood Pressure Measuring Devices—Amendment 1. IEEE Standards Association: New York, NY, USA, 2019.
- Franklin, D.; Tzavelis, A.; Lee, J.Y.; Chung, H.U.; Trueb, J.; Arafa, H.; Kwak, S.S.; Huang, I.; Liu, Y.; Rathod, M.; et al. Synchronized Wearables for the Detection of Haemodynamic States via Electrocardiography and Multispectral Photoplethysmography. Nat. Biomed. Eng. 2023, 7, 1229–1241. [Google Scholar] [CrossRef]
- Asayama, K.; Satoh, M.; Kikuya, M. Diurnal Blood Pressure Changes. Hypertens. Res. 2018, 41, 669–678. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Garudadri, H. Noninvasive Cuffless Estimation of Blood Pressure from Pulse Arrival Time and Heart Rate with Adaptive Calibration. In Proceedings of the 2009 Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 114–119. [Google Scholar]

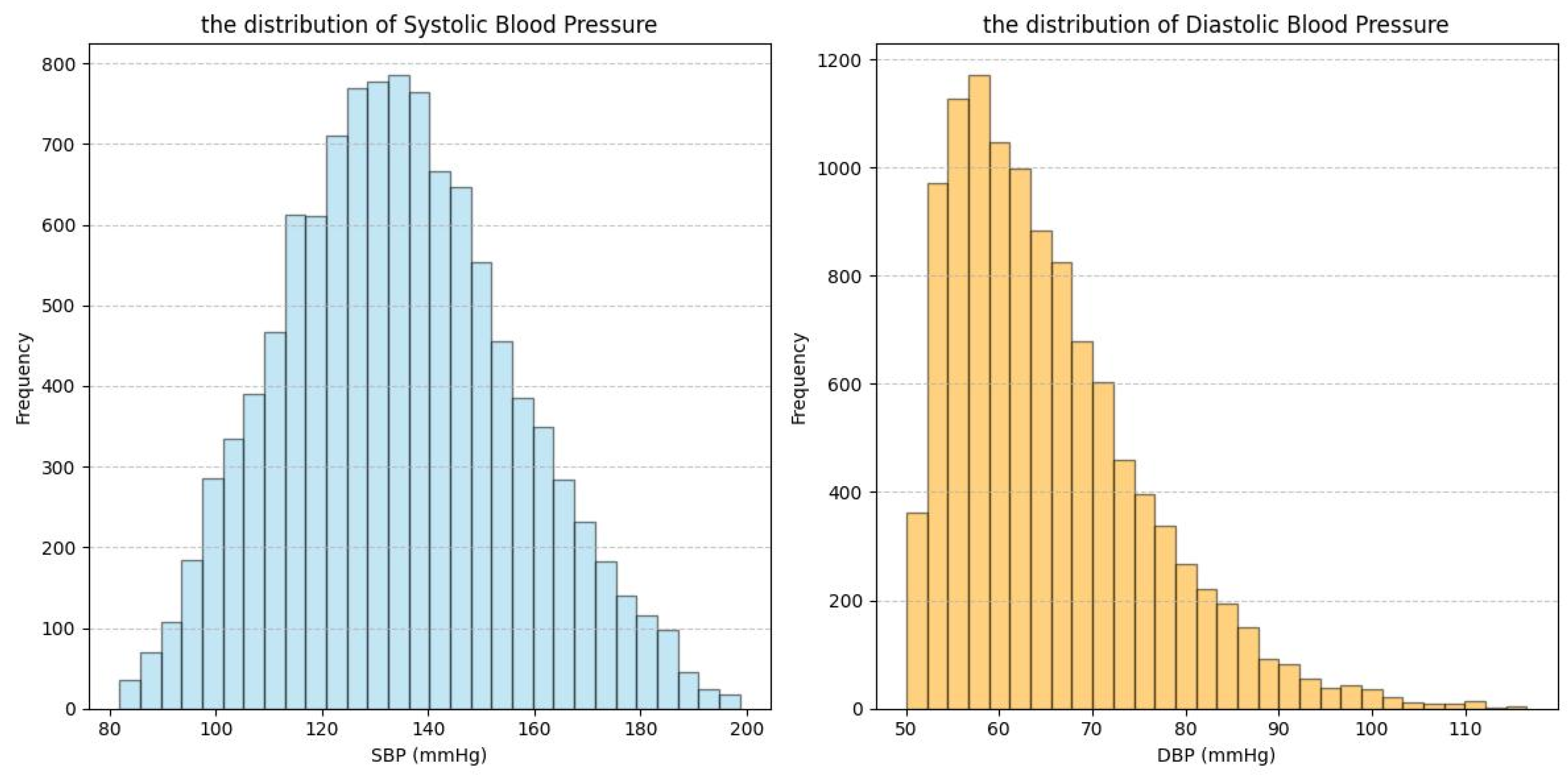
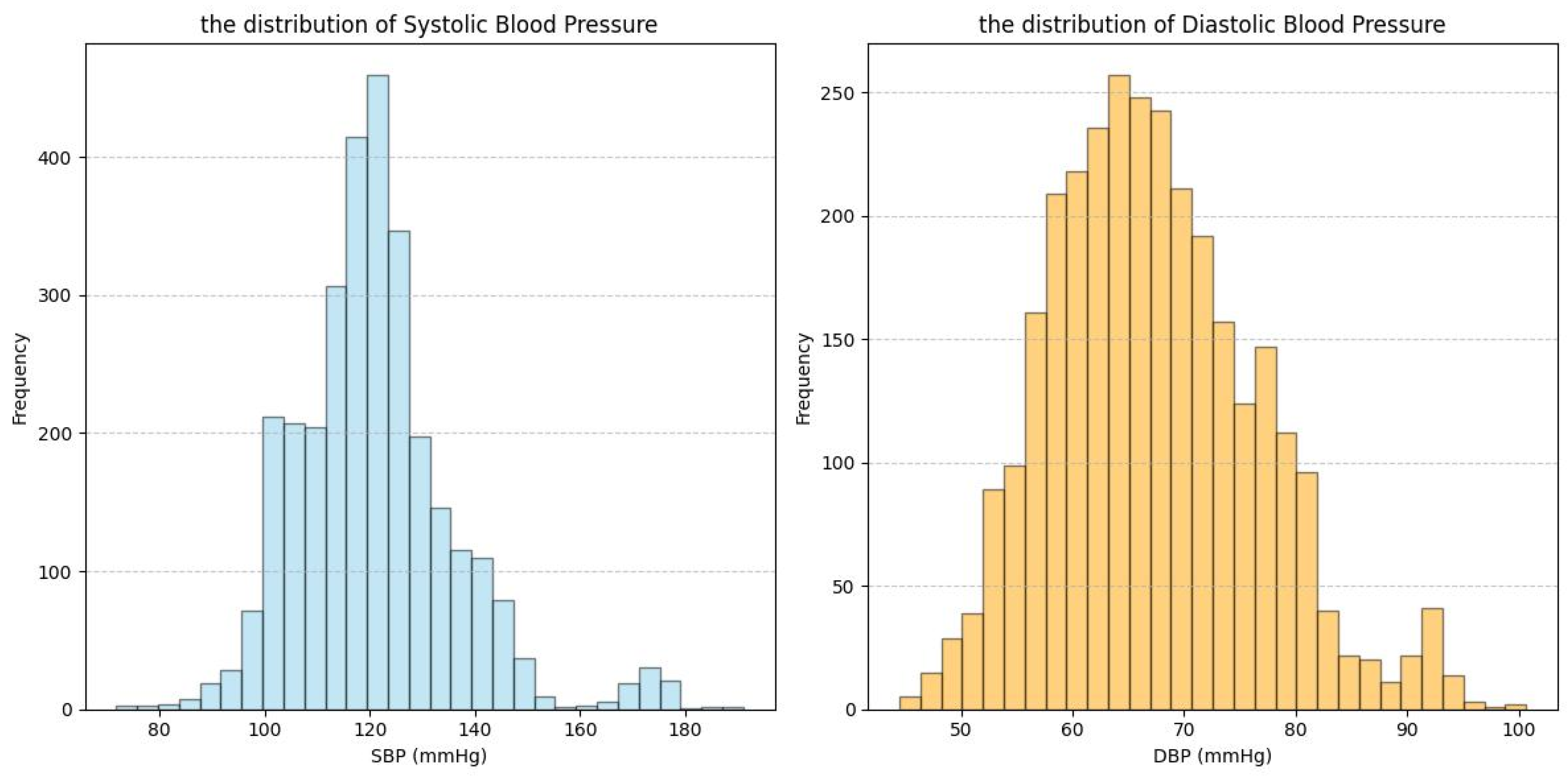
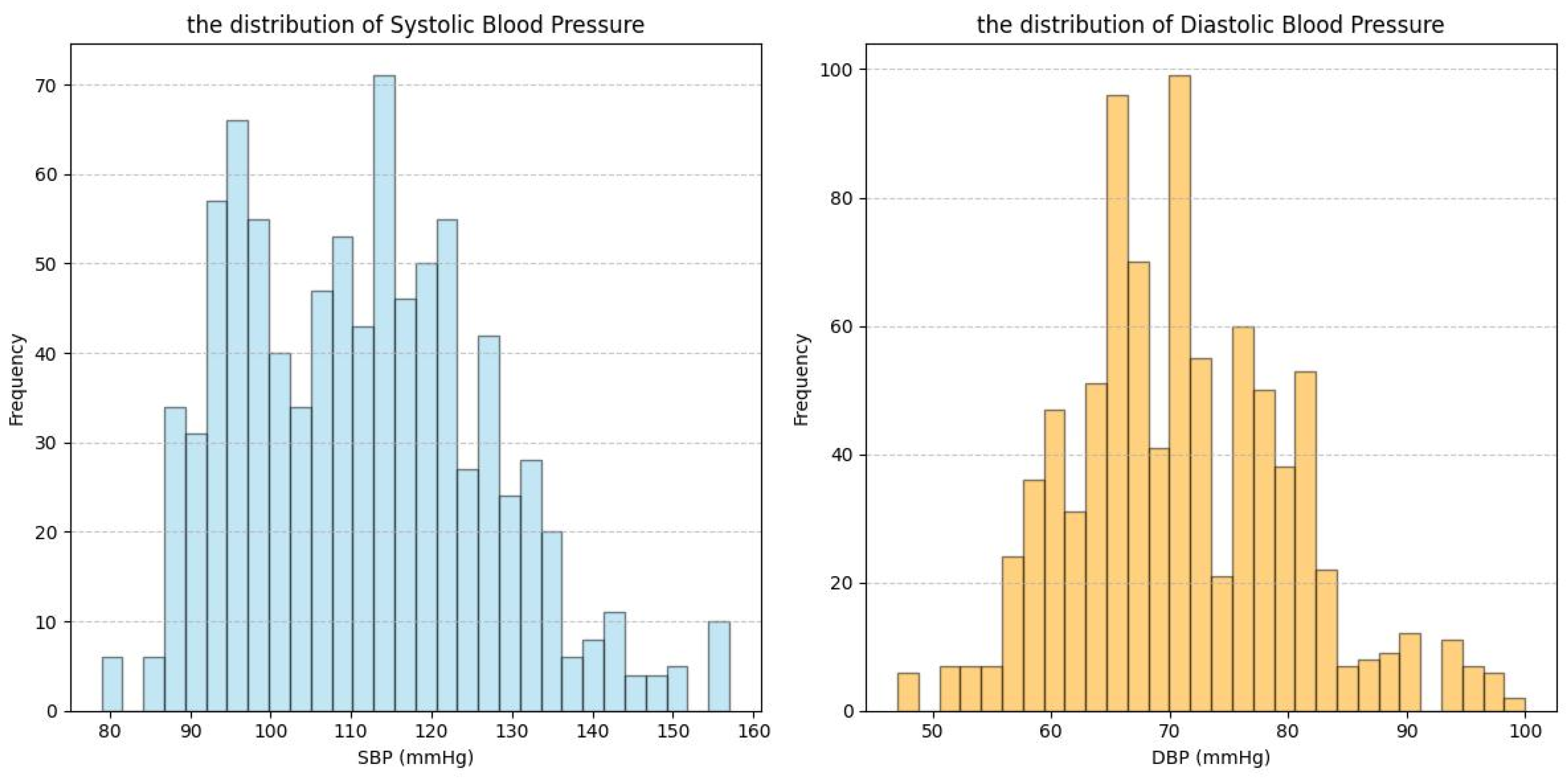
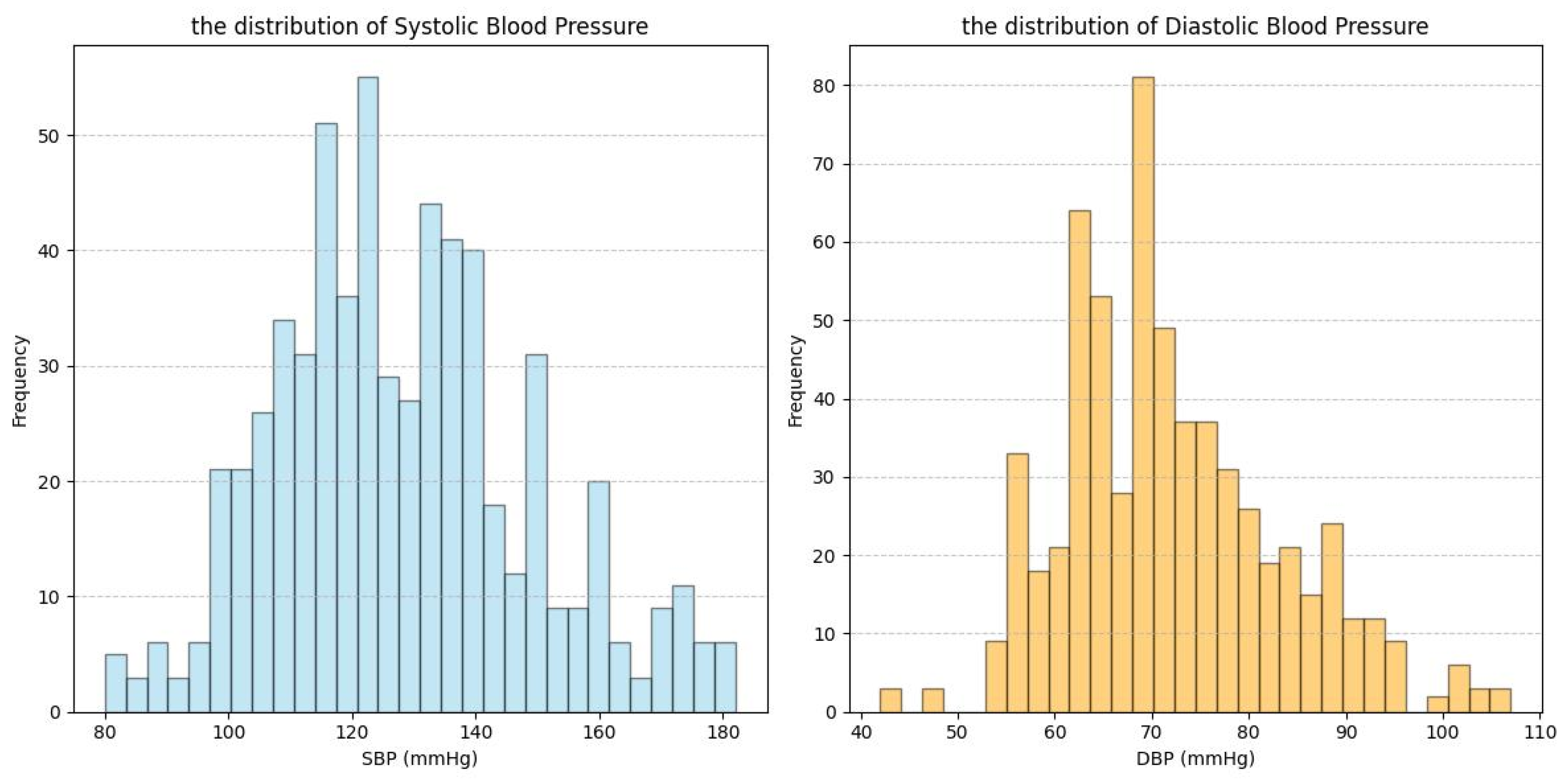

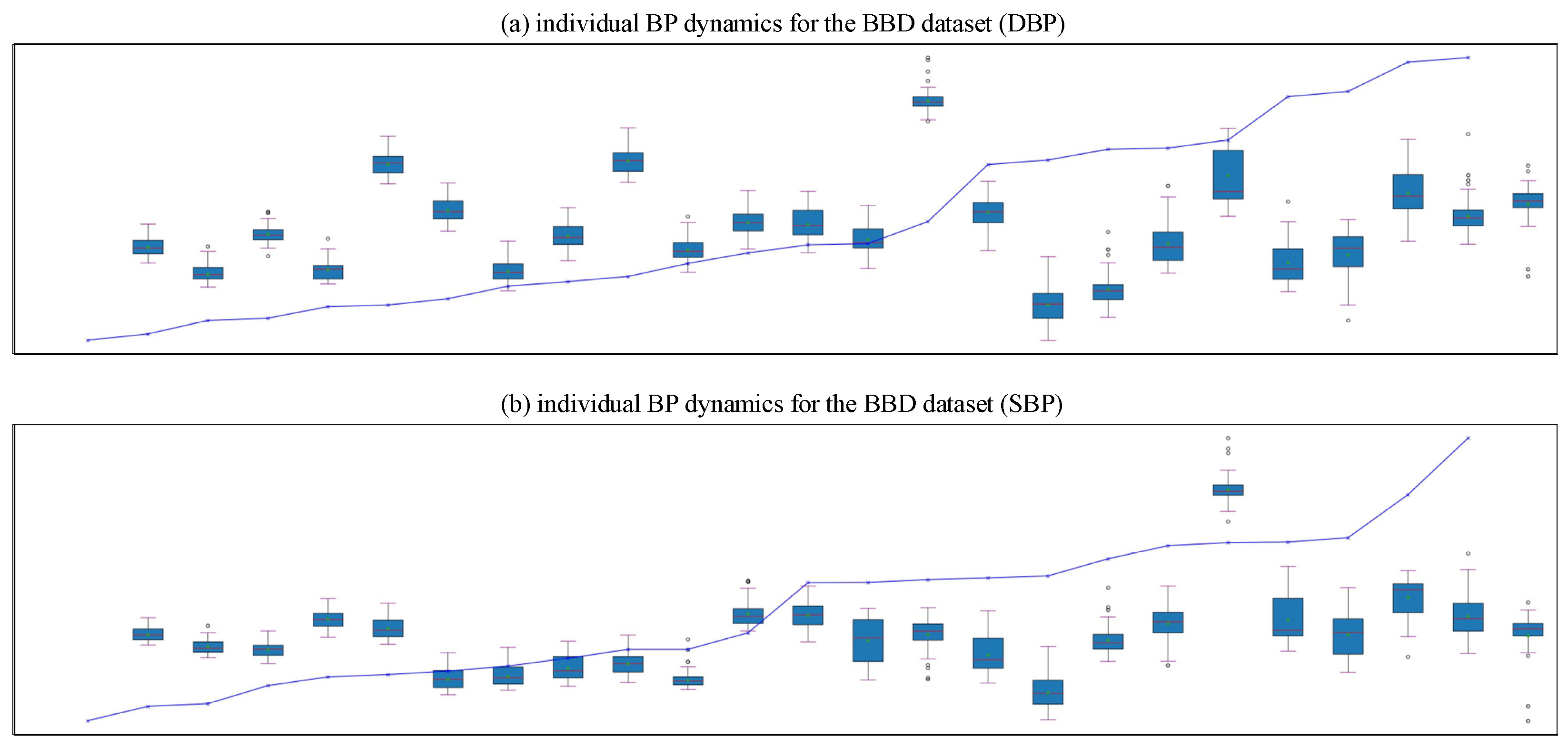
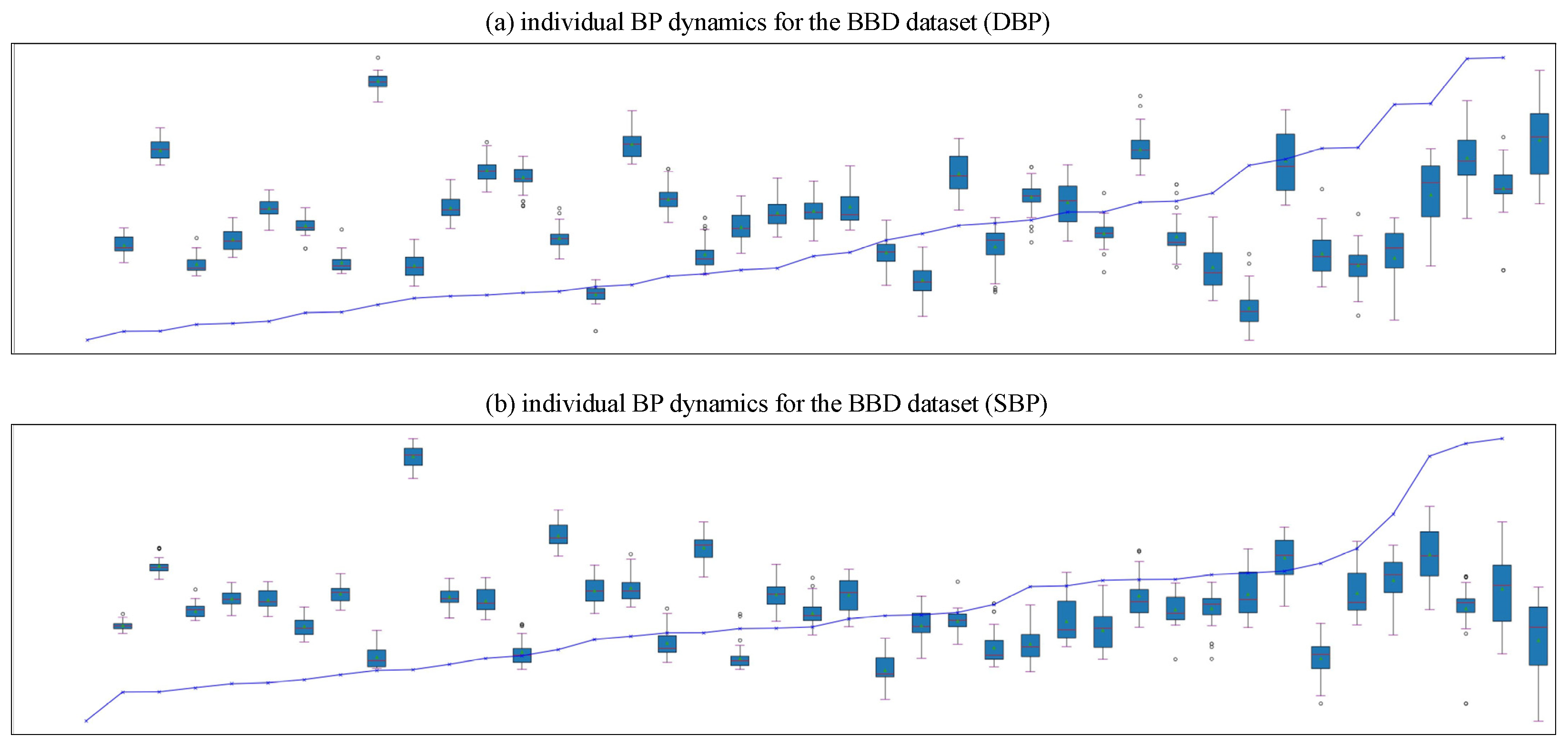
| Dataset | Signal | Subject Number | Age Range | Subject’s Health Status |
|---|---|---|---|---|
| ABP_PPG | PPG | 1195 | 57.1 ± 14.2 | The subjects presented with a diverse array of medical conditions and were all intensive care unit patients. |
| ABP | ||||
| BBD | PPG | 40 | 34.2 ± 14.5 | Four participants were diagnosed with cardiovascular-related diseases. |
| ABP | ||||
| PPG-BP | PPG | 219 | 56.9 ± 15.8 | The subjects exhibited a diverse range of cardiovascular and related disorders. |
| BP | ||||
| MS_PPG_BP | PPG | 30 | 25 ± 1 | Subjects were all healthy youths. |
| BP |
| No. | Feature | Definition |
|---|---|---|
| 1 | Frequency Domain Features | FFT peak of the signal |
| 2 | Height of FFT peak | |
| 3 | Mean value near the peak of the FFT | |
| 4–30 | Time Domain Features | Point-of-interest and their features of PPG, VPG, APG, JPG, SPG |
| 31–58 | Time intervals | |
| 59–70 | Areas under the PPG curve | |
| 71–91 | Cyclicality | |
| 92–112 | SW and DW at 25%, 50%, and 75% of the systolic peak amplitude 25%, 50%, and 75% of the systolic peak amplitude | |
| 113–114 | Statistical Features | SQI: SQI-skew, SQI_kurtosis |
| 115–118 | Indices features | |
| 119–143 | The extraction of Deviation Curve-based features | |
| 144–218 | Histogram features of PPG, APG, VPG, JPG, SPG |
| Splitting Strategy | BP | MAD (mmHg) | STD (mmHg) | ME (mmHg) |
|---|---|---|---|---|
| sample-level splitting | DBP | 2.91 | 4.16 | −0.03 |
| SBP | 4.70 | 6.67 | −0.23 | |
| record-level splitting | DBP | 5.42 | 6.11 | −0.16 |
| SBP | 8.34 | 10.56 | −0.11 |
| Algorithm | BP | Number of Features | ABP_PPG | BBD | MS_PPG_BP | PPG-BP | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAD | MASE | MAD | MASE | MAD | MASE | MAD | MASE | |||
| ∪PPFS | DBP | 105 | 8.63 | 1.044 | 6.60 | 0.834 | 4.89 | 0.653 | 7.85 | 0.887 |
| SBP | 103 | 12.08 | 0.686 | 9.68 | 0.787 | 5.73 | 0.450 | 11.96 | 0.730 | |
| ∪HITON-MB | DBP | 33 | 8.21 | 0.993 | 6.61 | 0.835 | 4.72 | 0.631 | 7.62 | 0.861 |
| SBP | 35 | 11.33 | 0.643 | 9.82 | 0.798 | 6.36 | 0.499 | 9.57 | 0.584 | |
| ∪TREE | DBP | 120 | 8.67 | 1.048 | 6.60 | 0.834 | 4.88 | 0.652 | 7.03 | 0.794 |
| SBP | 98 | 11.76 | 0.668 | 9.60 | 0.780 | 5.52 | 0.4336 | 10.58 | 0.650 | |
| ∩PPFS | DBP | 7 | 8.1 | 0.979 | 7.78 | 0.983 | 4.89 | 0.653 | 5.49 | 0.620 |
| SBP | 2 | 11.66 | 0.6621 | 11.40 | 0.927 | 5.87 | 0.461 | 9.36 | 0.571 | |
| ∩HITON-MB | DBP | 1 | 7.74 | 0.936 | 5.99 | 0.757 | 4.41 | 0.589 | 7.30 | 0.825 |
| SBP | / | / | / | / | / | / | / | / | / | |
| ∩TREE | DBP | 2 | 7.78 | 0.940 | 6.84 | 0.864 | 5.06 | 0.676 | 7.34 | 0.829 |
| SBP | 1 | 11.88 | 0.675 | 10.79 | 0.877 | 6.60 | 0.476 | 9.33 | 0.600 | |
| MDSFS-EMB | DBP | 21 | 6.32 | 0.764 | 5.69 | 0.719 | 3.71 | 0.495 | 5.58 | 0.630 |
| SBP | 20 | 9.87 | 0.560 | 8.10 | 0.658 | 4.47 | 0.351 | 8.56 | 0.523 | |
| Datasets | Models | DBP | SBP | ||||
|---|---|---|---|---|---|---|---|
| MAD | STD | ME | MAD | STD | ME | ||
| ABP_PPG | SVR | 6.59 | 7.59 | 0.4 | 9.35 | 11.45 | 0.12 |
| RF | 7.29 | 8.54 | 0.32 | 10.01 | 11.85 | −1.51 | |
| LightGBM | 6.32 | 7.64 | 0.55 | 9.87 | 10.56 | −1.05 | |
| XGBoost | 7.09 | 8.96 | 0.28 | 9.66 | 10.99 | −0.74 | |
| BBD | SVR | 5.57 | 6.88 | −1.49 | 8.11 | 10.19 | −0.1 |
| RF | 5.75 | 6.60 | −0.02 | 8.36 | 10.46 | −0.06 | |
| LightGBM | 5.69 | 6.99 | 0.0 | 8.10 | 10.23 | −0.07 | |
| XGBoost | 5.42 | 6.11 | −0.16 | 8.34 | 10.56 | −0.11 | |
| MS_PPG_BP | SVR | 3.61 | 5.32 | 0.02 | 5.54 | 8.48 | −0.86 |
| RF | 3.76 | 5.50 | 0.09 | 4.76 | 7.43 | −0.22 | |
| LightGBM | 3.71 | 5.48 | 0.06 | 4.47 | 7.24 | −0.20 | |
| XGBoost | 3.19 | 4.43 | 0.07 | 4.75 | 7.05 | −0.40 | |
| PPG | SVR | 6.34 | 8.63 | −0.32 | 8.98 | 11.49 | −1.16 |
| RF | 5.49 | 8.38 | 0.13 | 8.82 | 11.66 | −0.23 | |
| LightGBM | 5.58 | 8.86 | 0.20 | 8.56 | 11.42 | 0.04 | |
| XGBoost | 5.58 | 8.89 | 0.06 | 8.04 | 11.98 | −0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; He, Z.; Wang, H. Multi-Source Causal Invariance for Cuffless Blood Pressure Estimation Based on Photoplethysmography Signal Features. Sensors 2025, 25, 3254. https://doi.org/10.3390/s25113254
Xu Y, He Z, Wang H. Multi-Source Causal Invariance for Cuffless Blood Pressure Estimation Based on Photoplethysmography Signal Features. Sensors. 2025; 25(11):3254. https://doi.org/10.3390/s25113254
Chicago/Turabian StyleXu, Yiliu, Zhaoming He, and Hao Wang. 2025. "Multi-Source Causal Invariance for Cuffless Blood Pressure Estimation Based on Photoplethysmography Signal Features" Sensors 25, no. 11: 3254. https://doi.org/10.3390/s25113254
APA StyleXu, Y., He, Z., & Wang, H. (2025). Multi-Source Causal Invariance for Cuffless Blood Pressure Estimation Based on Photoplethysmography Signal Features. Sensors, 25(11), 3254. https://doi.org/10.3390/s25113254





