Author Contributions
Conceptualization, S.D. and L.L.; methodology, S.D.; software, S.D.; validation, C.G., Y.D. and S.W.; formal analysis, T.C.; investigation, C.G.; resources, T.C. and L.L.; data curation, S.D.; writing—original draft preparation, S.D.; writing—review and editing, T.C. and C.G.; visualization, S.D.; supervision, L.L.; project administration, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Optical setup of our targeted heterodyne -OTDR system. AOM: acousto-optic modulator; EDFA: erbium-doped optical fiber amplifiers; FUT: fiber under test; IOBUF: I/O buffer; RFADC: radio frequency analog-to-digital converter. Optical circulator: port 1 is input, port 2 is intermediate, port 3 is output.
Figure 1.
Optical setup of our targeted heterodyne -OTDR system. AOM: acousto-optic modulator; EDFA: erbium-doped optical fiber amplifiers; FUT: fiber under test; IOBUF: I/O buffer; RFADC: radio frequency analog-to-digital converter. Optical circulator: port 1 is input, port 2 is intermediate, port 3 is output.
Figure 2.
A simplified view of the -OTDR digital receiver structure. Parts that are less relevant to this study, such as the flash memory interface, analog front-end protection and debugging components, are not drawn in the figure. BPD: balance photodiode; RFADC: radio frequency analog-to-digital converter; FIFO: first-in first-out; DMA: direct memory access; JTAG: Joint Test Action Group; UART: universal asynchronous receiver/transmitter.
Figure 2.
A simplified view of the -OTDR digital receiver structure. Parts that are less relevant to this study, such as the flash memory interface, analog front-end protection and debugging components, are not drawn in the figure. BPD: balance photodiode; RFADC: radio frequency analog-to-digital converter; FIFO: first-in first-out; DMA: direct memory access; JTAG: Joint Test Action Group; UART: universal asynchronous receiver/transmitter.
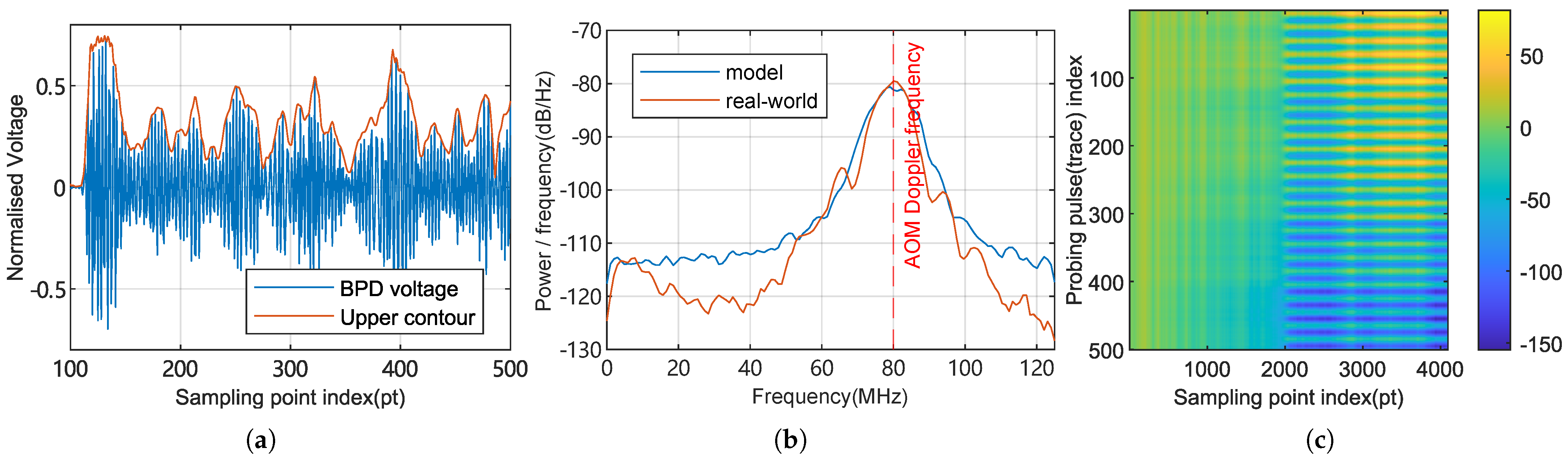
Figure 3.
A simulated output of the signal model, with parameters set to typical values. (a) The first -OTDR trace as seen by BPD (fiber response after transmitting the probe pulse). Spatial distance corresponding to each sampling point is roughly 0.8 m. The contour is computed using the Hilbert transform. (b) The power spectral density estimation of a simulated and real-world measured -OTDR trace, computed using Welch’s method. (c) The absolute phase matrix visualized as an image.
Figure 3.
A simulated output of the signal model, with parameters set to typical values. (a) The first -OTDR trace as seen by BPD (fiber response after transmitting the probe pulse). Spatial distance corresponding to each sampling point is roughly 0.8 m. The contour is computed using the Hilbert transform. (b) The power spectral density estimation of a simulated and real-world measured -OTDR trace, computed using Welch’s method. (c) The absolute phase matrix visualized as an image.
Figure 4.
Block diagram for the quadrature heterodyning phase extraction method. LPF: low-pass filter; IF: intermediate frequency; ZIF: zero intermediate frequency; I: in-phase channel; Q: quadrature channel.
Figure 4.
Block diagram for the quadrature heterodyning phase extraction method. LPF: low-pass filter; IF: intermediate frequency; ZIF: zero intermediate frequency; I: in-phase channel; Q: quadrature channel.
Figure 5.
Block diagram for the Hilbert transform phase extraction method.
Figure 5.
Block diagram for the Hilbert transform phase extraction method.
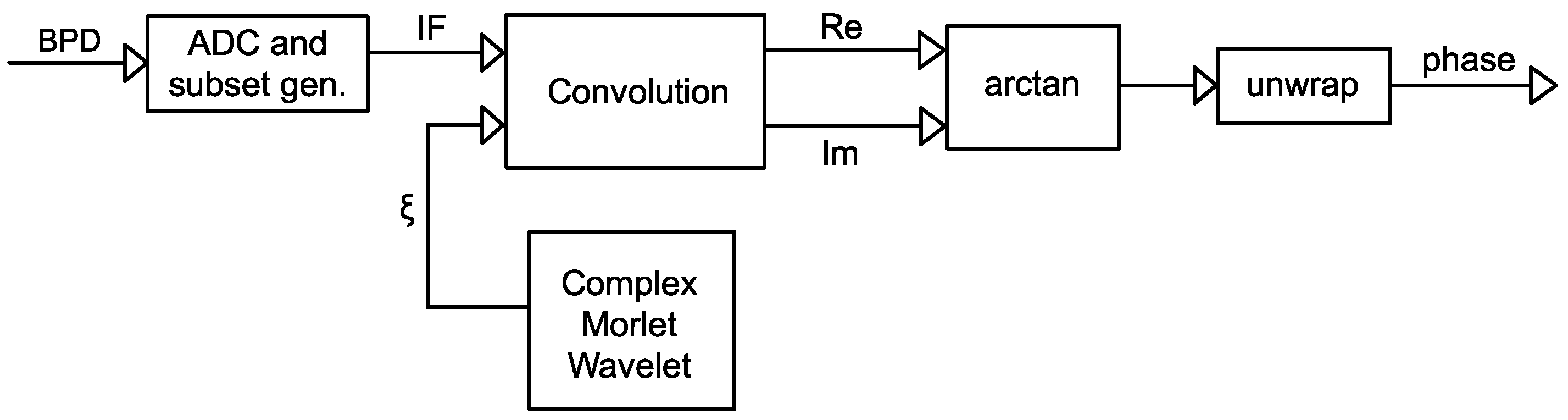
Figure 6.
Block diagram for the complex Morlet wavelet transform phase extraction method. : the wavelet; Re: real part of complex numbers; Im: imaginary part of complex numbers.
Figure 6.
Block diagram for the complex Morlet wavelet transform phase extraction method. : the wavelet; Re: real part of complex numbers; Im: imaginary part of complex numbers.
Figure 7.
Computed complex Morlet wavelet (continuous time) plotted on complex axes, with four typical settings for the number of periods: (a) . (b) . (c) . (d) .
Figure 7.
Computed complex Morlet wavelet (continuous time) plotted on complex axes, with four typical settings for the number of periods: (a) . (b) . (c) . (d) .
Figure 8.
Block diagram for the incremental DC-rejected phase unwrapper (IDRPU) method. Unwrapping and filtering are combined in a single pass and numerical overflow is prevented.
Figure 8.
Block diagram for the incremental DC-rejected phase unwrapper (IDRPU) method. Unwrapping and filtering are combined in a single pass and numerical overflow is prevented.
Figure 9.
Experimental setup for acquiring -OTDR trace data. Two configurations are used to separately evaluate the positioning capability and noise characteristics. (a) Photograph of the setup. (b) Block diagrams illustrating the two configurations designed for capturing uniform acoustic fields and localized events.
Figure 9.
Experimental setup for acquiring -OTDR trace data. Two configurations are used to separately evaluate the positioning capability and noise characteristics. (a) Photograph of the setup. (b) Block diagrams illustrating the two configurations designed for capturing uniform acoustic fields and localized events.
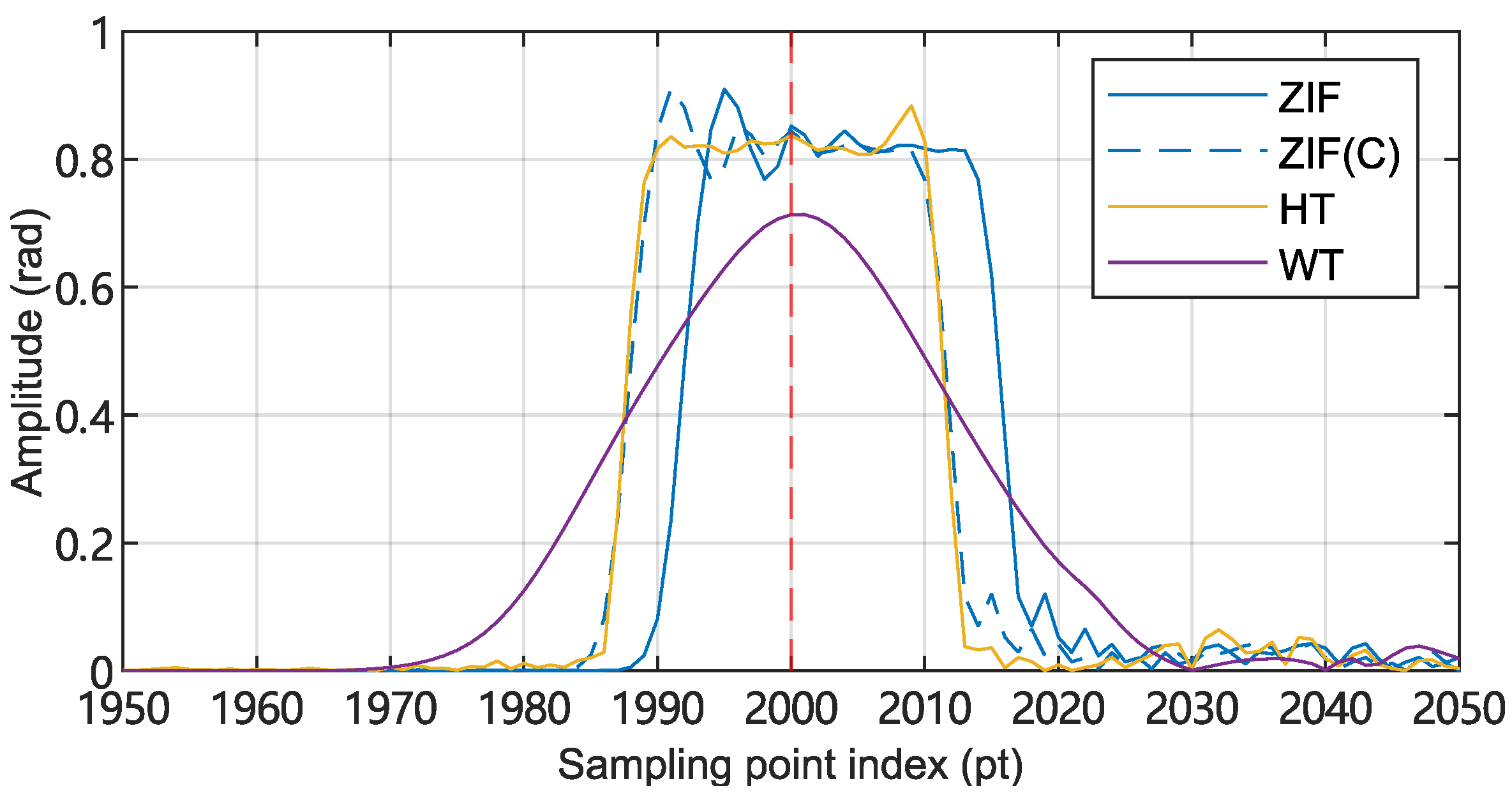
Figure 10.
Positioning characteristics of the three phase extraction methods. A virtual 1 kHz point source is placed at position (indicated by the red dashed line). The figure plots the relationship between the demodulated signal’s amplitude and position (i.e., sampling point index n). ZIF: quadrature heterodyning zero intermediate frequency (ZIF(C) for the shift-compensated result); HT: Hilbert transform; WT: wavelet transform.
Figure 10.
Positioning characteristics of the three phase extraction methods. A virtual 1 kHz point source is placed at position (indicated by the red dashed line). The figure plots the relationship between the demodulated signal’s amplitude and position (i.e., sampling point index n). ZIF: quadrature heterodyning zero intermediate frequency (ZIF(C) for the shift-compensated result); HT: Hilbert transform; WT: wavelet transform.
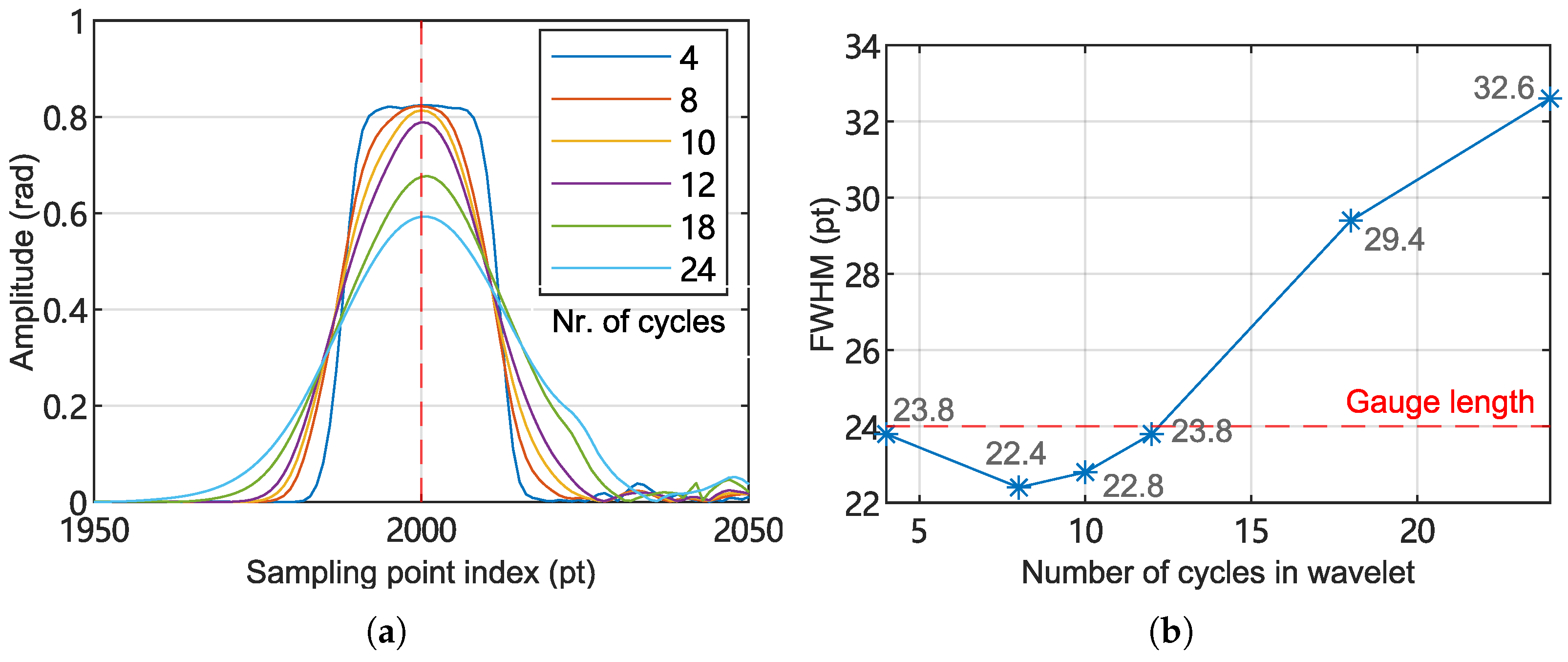
Figure 11.
Positioning performance of WT method tested under varying wavelet cycle numbers. (a) Acoustic signal amplitude as a function of position (sampling point index). (b) FWHM of signal intensity curves as a function of wavelet cycle numbers.
Figure 11.
Positioning performance of WT method tested under varying wavelet cycle numbers. (a) Acoustic signal amplitude as a function of position (sampling point index). (b) FWHM of signal intensity curves as a function of wavelet cycle numbers.
Figure 12.
Phase timeseries “waterfall” diagrams of real-world piezoelectric vibration measurement, using all demodulation schemes. (a) Quadrature heterodyning ZIF method. (b) HT method. (c) WT method with . (d) WT method with .
Figure 12.
Phase timeseries “waterfall” diagrams of real-world piezoelectric vibration measurement, using all demodulation schemes. (a) Quadrature heterodyning ZIF method. (b) HT method. (c) WT method with . (d) WT method with .
Figure 13.
A real-world measured RBS intensity trace showing the fading effect. The trace is obtained by computing the envelope of the beat frequency signal using the Hilbert transform method. (a) RBS intensity as a function of the sample point index (i.e., position along the fiber). (b) A local view of the waveform in (a). (c) Statistical distribution of light intensity. The first bin (−40 dBFS) indicates positions outside the measured fiber, which can be excluded from the statistics.
Figure 13.
A real-world measured RBS intensity trace showing the fading effect. The trace is obtained by computing the envelope of the beat frequency signal using the Hilbert transform method. (a) RBS intensity as a function of the sample point index (i.e., position along the fiber). (b) A local view of the waveform in (a). (c) Statistical distribution of light intensity. The first bin (−40 dBFS) indicates positions outside the measured fiber, which can be excluded from the statistics.
Figure 14.
(a) Three demodulation schemes’ output audio signal SNR as functions of -OTDR trace SNR, computed using simulated controlled conditions, where the fading effect is uniform and has no fluctuations. (b) Scatter plot of the relationship between the short-term sound signal SNR and the instantaneous light beat SNR, using real-world sampled data and 3 studied demodulation schemes. The interferometric fading suppression effect of the WT method can be observed.
Figure 14.
(a) Three demodulation schemes’ output audio signal SNR as functions of -OTDR trace SNR, computed using simulated controlled conditions, where the fading effect is uniform and has no fluctuations. (b) Scatter plot of the relationship between the short-term sound signal SNR and the instantaneous light beat SNR, using real-world sampled data and 3 studied demodulation schemes. The interferometric fading suppression effect of the WT method can be observed.
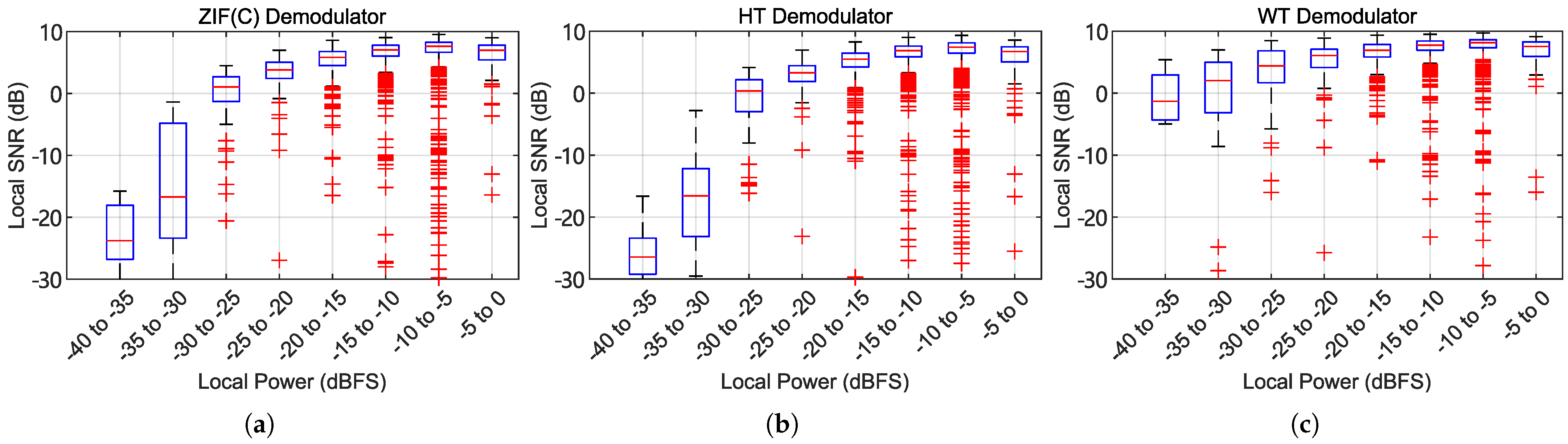
Figure 15.
Box plot of the relationship between the short-term sound signal SNR and the instantaneous light beat SNR, using real-world sampled data and all 3 demodulation schemes. (a) The quadrature heterodyning ZIF method with group delay compensated. (b) The Hilbert transform method. (c) The wavelet transform method.
Figure 15.
Box plot of the relationship between the short-term sound signal SNR and the instantaneous light beat SNR, using real-world sampled data and all 3 demodulation schemes. (a) The quadrature heterodyning ZIF method with group delay compensated. (b) The Hilbert transform method. (c) The wavelet transform method.
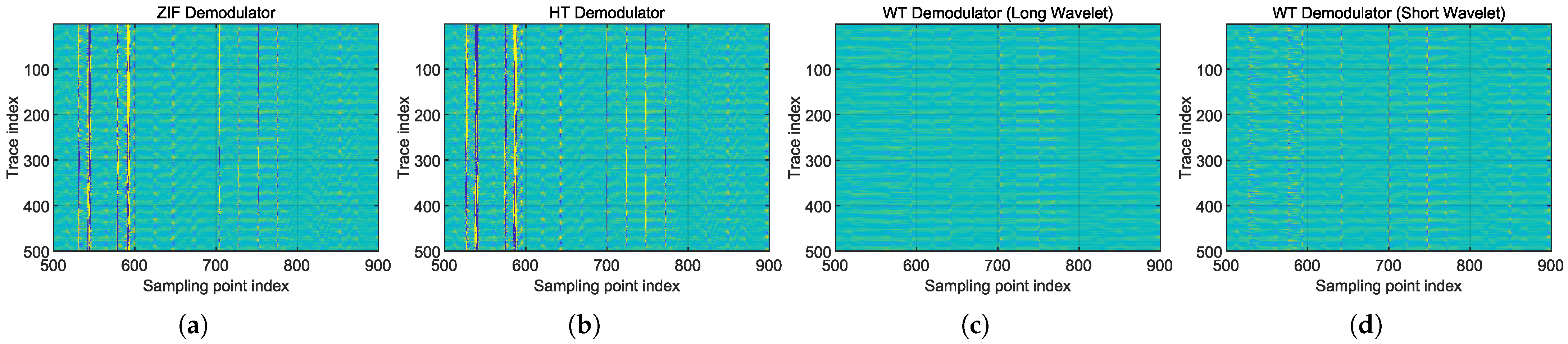
Figure 16.
Phase timeseries “waterfall” diagrams of real-world weak acoustic field measurement, using all demodulation schemes. The random stripes running vertically are the SNR drops caused by interferometric fading. The diagrams were cropped so that local areas with strong and concentrated noise are shown. (a) Quadrature heterodyning ZIF method. (b) HT method. (c) WT method with . (d) WT method with .
Figure 16.
Phase timeseries “waterfall” diagrams of real-world weak acoustic field measurement, using all demodulation schemes. The random stripes running vertically are the SNR drops caused by interferometric fading. The diagrams were cropped so that local areas with strong and concentrated noise are shown. (a) Quadrature heterodyning ZIF method. (b) HT method. (c) WT method with . (d) WT method with .
Table 1.
Estimation of hardware utilization for a quadrature heterodyning ZIF demodulator.
Table 1.
Estimation of hardware utilization for a quadrature heterodyning ZIF demodulator.
| Stage | Components | Resources |
|---|
| Digital mixers 1 | 2 DDS cores for sine and cosine | 2 Block RAMs |
| Mixers for I/Q channels | 2 DSP slices |
| ZIF filters | 2 FIR cores | 18 DSP slices |
| Coefficient storage | ~0.3 kbits Distributed RAM |
| Control logic | ~200 LUTs and FFs |
| Phase angle | Pipelined CORDIC core (16 iterations) | ~1000 LUTs and FFs |
| Pipelined unwrapper | ~300 LUTs and ~400 FFs |
Table 2.
Estimation of hardware utilization for an HT demodulator.
Table 2.
Estimation of hardware utilization for an HT demodulator.
| Stage | Components | Resources |
|---|
| Hilbert transformer | Antisymmetric FIR core | 15 DSP slices |
| Coefficient storage | ~0.2 kbits Distributed RAM |
| Control logic | ~200 LUTs and FFs |
| Delay line for real part | 256 FFs |
| Phase angle | Pipelined CORDIC core (16 iterations) | ~1000 LUTs and FFs |
| Pipelined unwrapper | ~300 LUTs and ~400 FFs |
Table 3.
Estimation of hardware utilization for a complex wavelet transform demodulator.
Table 3.
Estimation of hardware utilization for a complex wavelet transform demodulator.
| Stage | Components | Resources |
|---|
| Wavelet convolution | 2 FIR cores | Up to 104 DSP slices |
| Coefficient storage | ~1.6 kbits Distributed RAM |
| Control logic | ~200 LUTs and FFs |
| Phase angle | Pipelined CORDIC core (16 iterations) | ~1000 LUTs and FFs |
| Pipelined unwrapper | ~300 LUTs and ~400 FFs |
Table 4.
Parameters for phase extractors performance evaluation.
Table 4.
Parameters for phase extractors performance evaluation.
| Type | Parameter | Value |
|---|
| Receiver configurations | ADC sampling clock speed | 250 MSa/s |
| Probe rate | 20 kPulse/s |
| Probe pulse width | 100 ns (25 Sa) |
| Intrinsic fluctuations | bandwidth 1 | 40 MHz |
| bandwidth 2 | 5 Hz |
Table 5.
Additional parameters for positioning accuracy measurement.
Table 5.
Additional parameters for positioning accuracy measurement.
| Type | Parameter | Value |
|---|
| Receiver configurations | Gauge length | 24 Sa |
| of wavelet 1 | 16 |
| Intrinsic fluctuations | gain 2 | 0.5 |
| gain 3 | 0.1 |
| BPD noise gain | |
| Acoustic source | FWHM () | 2 Sa |
| Peak amplitude | 10 rad |
| Interferometric fading | No fading effects |
Table 6.
Parameters for constant trace SNR special case.
Table 6.
Parameters for constant trace SNR special case.
| Type | Parameter | Value |
|---|
| Receiver configurations | Gauge length | 24 Sa |
| of wavelet | 8 |
| Intrinsic fluctuations | | 0 |
| 0 |
| BPD noise gain | |
| Acoustic source | FWHM () | ∞ |
| Peak amplitude | rad |
Table 7.
Median SNRs of demodulators with all local power.
Table 7.
Median SNRs of demodulators with all local power.
| Range of local power (dBFS) | −40–−35 | −35–−30 | −30–−25 | −25–−20 | −20–−15 | −15–−10 | −10–−5 |
| ZIF method’s median SNR (dB) | −23.78 | −16.7 | 1.06 | 3.79 | 5.82 | 7.04 | 7.6 |
| HT method’s median SNR (dB) | −26.44 | −16.55 | 0.37 | 3.29 | 5.48 | 6.88 | 7.41 |
| SNR gain of HT over ZIF (dB) | −2.66 | +0.15 | −0.69 | −0.5 | −0.34 | −0.16 | −0.19 |
| WT method’s median SNR (dB) | −1.31 | 2.03 | 4.41 | 6.07 | 6.91 | 7.74 | 8.13 |
| SNR gain of WT over ZIF (dB) | +22.47 | +18.73 | +3.35 | +2.28 | +1.09 | +0.7 | +0.53 |