NeuroDetect: Deep Learning-Based Signal Detection in Phase-Modulated Systems with Low-Resolution Quantization
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Main Contributions
- Model-Free Detection: We introduce a deep neural network architecture that learns to detect symbols under phase quantization without requiring explicit CSI. The proposed solution complements existing model-based signal detection approaches by offering a robust alternative for scenarios where CSI is unavailable at the receiver with low-resolution quantization.
- Near-Optimum Performance: We demonstrate that NeuroDetect achieves symbol error rates within of the ML detector, which assumes perfect CSI. This is the worst-case performance gap, and we show that the gap is much smaller in almost all scenarios we studied. This result is significant as it shows that near-optimum detection is attainable without the overhead of channel estimation. A key merit of NeuroDetect is to show that a lightweight and fully-connected architecture, if trained model-free, can close the gap to optimal ML detection under severe quantization errors, without the need for custom layers or specialized activation functions.
- Asymptotic Optimality: We show that the proposed DL-based detector achieves the optimum asymptotic error decay rate for different quantization levels, revealing a characteristic ternary behavior in diversity order.
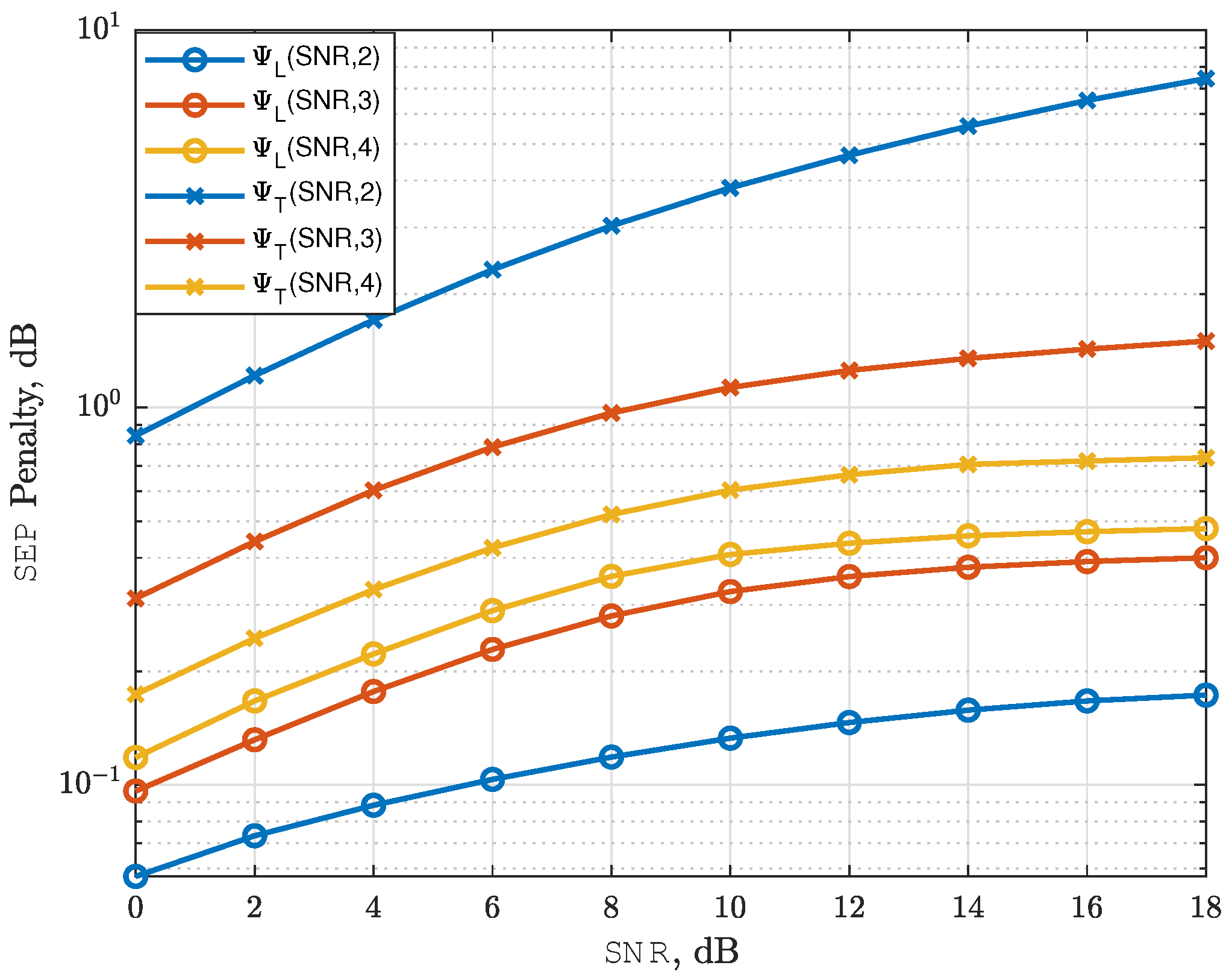
- Penalty Metrics: We develop new metrics to quantify the learning and quantization penalties, offering insights into how the number of bits affects detection accuracy and power requirements.
1.3. Related Work
1.3.1. Classical Approaches
1.3.2. DL-Based Approaches
2. System Setup
2.1. Channel Model and Signal Modulation
2.2. Receiver Architecture
3. Deep Learning-Based Signal Detection
3.1. Deep Learning for Signal Detection with Low-Resolution Quantization
3.2. Deep Learning-Based Signal Detector
3.3. NeuroDetect Architecture
- Input Layer: Receives the quantized received signal , which is the output of the low-resolution ADC.
- Hidden Layers: Four fully connected layers, configured as follows:
- -
- Layer 1: Consists of neurons with a tanh activation function.
- -
- Layer 2: Consists of neurons with a linear activation function.
- -
- Layers 3 and 4: Consist of neurons with ReLU activation function.
- Output Layer: Consists of neurons with a function that outputswhere .
- Inference: To estimate the transmitted symbol , we first take the most probable category , using the optimum parameters . Then, we set the predicted symbol to .
3.3.1. Hidden Layers of NeuroDetect
3.3.2. Training Dataset Generation
3.3.3. One-Hot Encoding of Labels
3.3.4. Parameter Optimization
3.3.5. Hyperparameters
3.4. NeuroDetect Algorithm
| Algorithm 1 Proposed NeuroDetect Algorithm for Signal Detection |
Require: I training samples , number of iterations T. Ensure: in (4). |
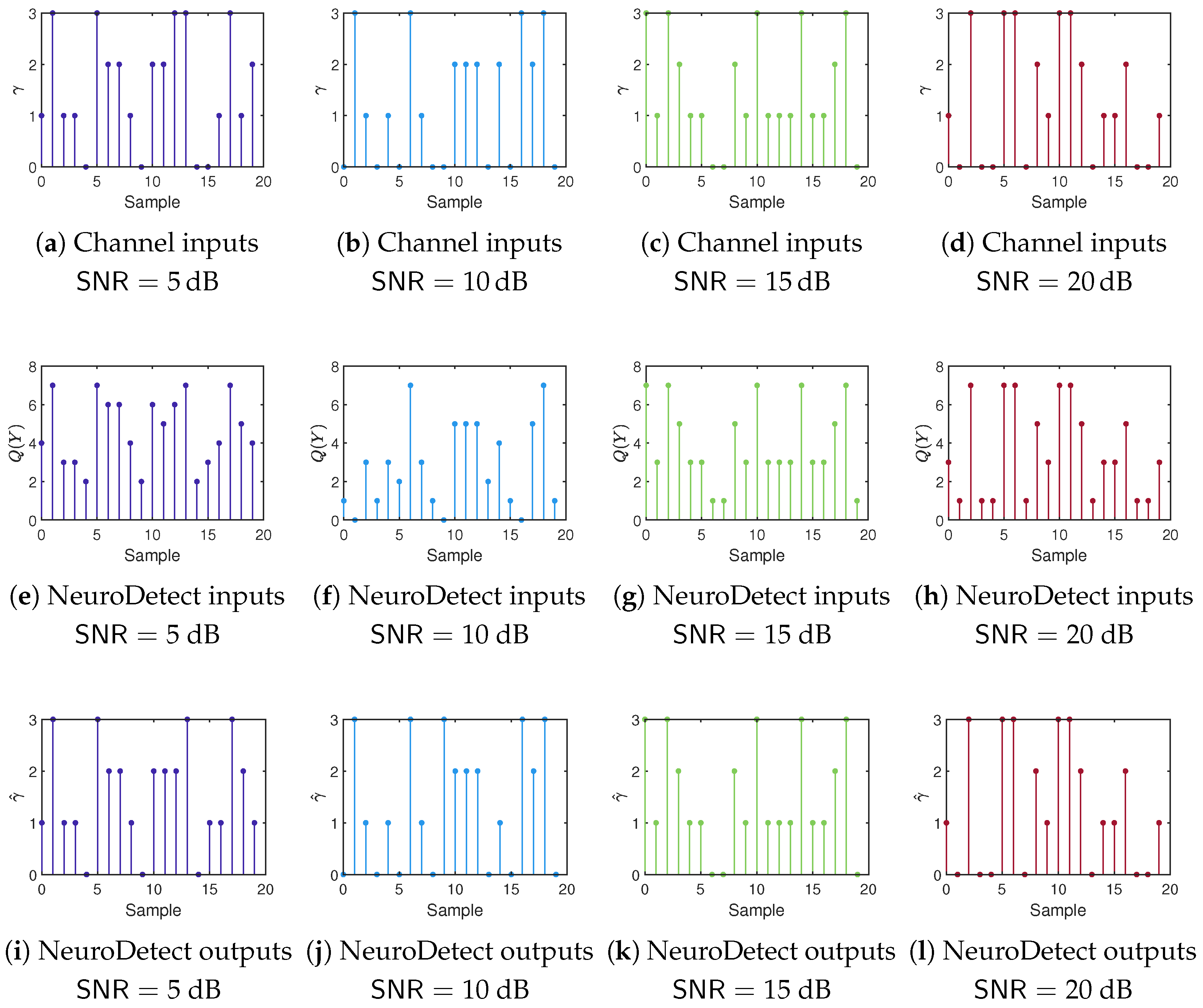
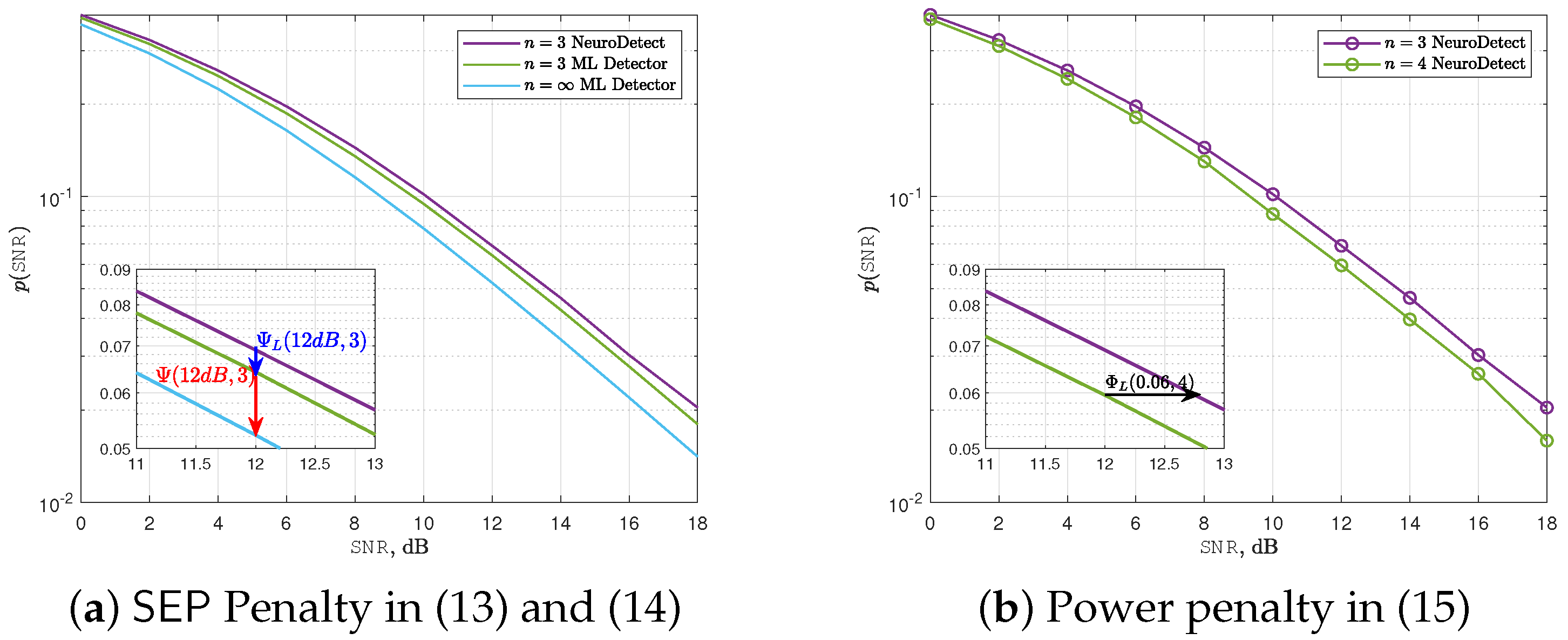
4. Numerical Results
4.1. Performance Comparison with the ML Detector
4.2. Effect of Quantization Bits on System Performance
4.3. Deep Learning Penalty Metrics
4.4. Impact of Channel Mismatch Between Training and Data Detection Phases
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | Analog-to-Digital Converter |
| DAC | Digital-to-Analog Converter |
| AWGN | Additive White Gaussian Noise |
| CSI | Channel State Information |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| ML | Maximum Likelihood |
| MIMO | Multiple-Input Multiple-Output |
| PSK | Phase Shift Keying |
| QPSK | Quadrature Phase Shift Keying |
| Signal-to-Noise Ratio | |
| LMMSE | Linear Minimum-Mean-Square-Error |
| BLMMSE | Bussgang LMMSE |
| MRC | Maximum Ratio Combining |
| ZF | Zero-Forcing |
| OSD | One-bit Sphere Decoding |
| e-MLD | Empirical Maximum Likelihood Detection |
| MMD | Minimum Mean-Distance |
| MCD | Minimum Center Detection |
| FBMCENet | Few-Bit Massive MIMO Channel Estimation Network |
| FBM-DetNet | Few-Bit Massive MIMO Data Detection Network |
| OBMNet | One-Bit Massive MIMO Data Detection Network |
| LoRD-Net | Low Resolution Detection Network |
| BiLSTM | Bidirectional Long Short-Term Memory |
| Rectified Linear Unit | |
| ADAM | Adaptive Moment Estimation |
| TP | Training Phase |
| DP | Data Transmission Phase |
| Symbol Error Probability | |
| Diversity Order |
References
- Lin, X.; Li, J.; Baldemair, R.; Cheng, J.F.T.; Parkvall, S.; Larsson, D.C.; Koorapaty, H.; Frenne, M.; Falahati, S.; Grovlen, A.; et al. 5G new radio: Unveiling the essentials of the next generation wireless access technology. IEEE Commun. Stand. Mag. 2019, 3, 30–37. [Google Scholar] [CrossRef]
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the road to 6G: Visions, requirements, key technologies, and testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Ning, B.; Tian, Z.; Mei, W.; Chen, Z.; Han, C.; Li, S.; Yuan, J.; Zhang, R. Beamforming technologies for ultra-massive MIMO in terahertz communications. IEEE Open J. Commun. Soc. 2023, 4, 614–658. [Google Scholar] [CrossRef]
- Bai, Q.; Nossek, J.A. Energy efficiency maximization for 5G multi-antenna receivers. Trans. Emerg. Telecommun. Technol. 2015, 26, 3–14. [Google Scholar] [CrossRef]
- Gayan, S.; Senanayake, R.; Inaltekin, H.; Evans, J. Reliability Characterization for SIMO Communication Systems with Low-Resolution Phase Quantization Under Rayleigh Fading. IEEE Open J. Commun. Soc. 2021, 2, 2660–2679. [Google Scholar] [CrossRef]
- Walden, R.H. Performance trends for analog to digital converters. IEEE Commun. Mag. 1999, 37, 96–101. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; Li, X.; Liu, Y.; Hanzo, L. On low-resolution ADCs in practical 5G millimeter-wave massive MIMO systems. IEEE Commun. Mag. 2018, 56, 205–211. [Google Scholar] [CrossRef]
- Ivrlac, M.T.; Nossek, J.A. On MIMO channel estimation with single-bit signal-quantization. In Proceedings of the ITG Smart Antenna Workshop, Vienna, Austria, 26–27 February 2007. [Google Scholar]
- Mo, J.; Alkhateeb, A.; Abu-Surra, S.; Heath, R.W. Hybrid architectures with few-bit ADC receivers: Achievable rates and energy-rate tradeoffs. IEEE Trans. Wirel. Commun. 2017, 16, 2274–2287. [Google Scholar] [CrossRef]
- Gayan, S.; Inaltekin, H.; Senanayake, R.; Evans, J. The Cost of Noncoherence: Avoiding Channel Estimation Through Differential Encoding in Phase Quantized Systems. IEEE Open J. Commun. Soc. 2023, 4, 2578–2595. [Google Scholar] [CrossRef]
- Gayan, S.; Senanayake, R.; Inaltekin, H.; Evans, J. Selection Combining for Multi-Antenna Communication with Low-Resolution ADCs. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021; pp. 3343–3348. [Google Scholar]
- Gayan, S.; Senanayake, R.; Inaltekin, H.; Evans, J. Low-resolution quantization in phase modulated systems: Optimum detectors and error rate analysis. IEEE Open J. Commun. Soc. 2020, 1, 1000–1021. [Google Scholar] [CrossRef]
- Jeon, Y.S.; Kim, D.; Hong, S.N.; Lee, N.; Heath, R.W. Artificial intelligence for physical-layer design of MIMO communications with one-bit ADCs. IEEE Commun. Mag. 2022, 60, 76–81. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Lee, K. Deep learning-aided tabu search detection for large MIMO systems. IEEE Trans. Wirel. Commun. 2020, 19, 4262–4275. [Google Scholar] [CrossRef]
- Mezghani, A.; Koufi, M.; Nossek, J.A. A modified MMSE receiver for quantized MIMO systems. In Proceedings of the ITG/IEEE Workshop on Smart Antennas, Vienna, Austria, 26–27 February 2007. [Google Scholar]
- Li, Y.; Tao, C.; Seco-Granados, G.; Mezghani, A.; Swindlehurst, A.L.; Liu, L. Channel estimation and performance analysis of one-bit massive MIMO systems. IEEE Trans. Signal Process. 2017, 65, 4075–4089. [Google Scholar] [CrossRef]
- Jacobsson, S.; Durisi, G.; Coldrey, M.; Gustavsson, U.; Studer, C. Throughput analysis of massive MIMO uplink with low-resolution ADCs. IEEE Trans. Wirel. Commun. 2017, 16, 4038–4051. [Google Scholar] [CrossRef]
- Choi, J.; Love, D.J.; Brown, D.R.; Boutin, M. Quantized distributed reception for MIMO wireless systems using spatial multiplexing. IEEE Trans. Signal Process. 2015, 63, 3537–3548. [Google Scholar] [CrossRef]
- Yu, C.Y.; Shao, M.; Chen, W.K.; Liu, Y.F.; Ma, W.K. An Efficient Global Algorithm for One-Bit Maximum-Likelihood MIMO Detection. In Proceedings of the 2023 IEEE 24th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Shanghai, China, 25–28 September 2023; pp. 231–235. [Google Scholar]
- Shao, M.; Ma, W.K. Divide and Conquer: One-bit MIMO-OFDM Detection by Inexact Expectation Maximization. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4890–4894. [Google Scholar]
- Choi, J.; Mo, J.; Heath, R.W. Near maximum-likelihood detector and channel estimator for uplink multiuser massive MIMO systems with one-bit ADCs. IEEE Trans. Commun. 2016, 64, 2005–2018. [Google Scholar] [CrossRef]
- Jeon, Y.S.; Lee, N.; Hong, S.N.; Heath, R.W. One-bit sphere decoding for uplink massive MIMO systems with one-bit ADCs. IEEE Trans. Wirel. Commun. 2018, 17, 4509–4521. [Google Scholar] [CrossRef]
- Safa, K.; Combes, R.; De Lacerda, R.; Yang, S. Data detection in 1-bit quantized MIMO systems. IEEE Trans. Commun. 2024, 72, 5396–5410. [Google Scholar] [CrossRef]
- Combes, R.; Yang, S. An approximate ML detector for MIMO channels corrupted by phase noise. IEEE Trans. Commun. 2017, 66, 1176–1189. [Google Scholar] [CrossRef]
- Gayan, S.; Inaltekin, H.; Senanayake, R.; Evans, J. Phase modulated communication with low-resolution ADCs. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Singh, J.; Madhow, U. Phase-quantized block noncoherent communication. IEEE Trans. Commun. 2013, 61, 2828–2839. [Google Scholar] [CrossRef]
- Bernardo, N.I.; Zhu, J.; Evans, J. On the Capacity-Achieving Input of Channels With Phase Quantization. IEEE Trans. Inf. Theory 2022, 68, 5866–5888. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B.H. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wirel. Commun. Lett. 2017, 7, 114–117. [Google Scholar] [CrossRef]
- O’shea, T.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Gruber, T.; Cammerer, S.; Hoydis, J.; Ten Brink, S. On deep learning-based channel decoding. In Proceedings of the 2017 51st annual conference on information sciences and systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.H.F. Deep learning in physical layer communications. IEEE Wirel. Commun. 2019, 26, 93–99. [Google Scholar] [CrossRef]
- Ye, H.; Liang, L.; Li, G.Y.; Juang, B.H. Deep learning-based end-to-end wireless communication systems with conditional GANs as unknown channels. IEEE Trans. Wirel. Commun. 2020, 19, 3133–3143. [Google Scholar] [CrossRef]
- Jeon, Y.S.; Hong, S.N.; Lee, N. Blind detection for MIMO systems with low-resolution ADCs using supervised learning. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Jeon, Y.S.; Hong, S.N.; Lee, N. Supervised-learning-aided communication framework for MIMO systems with low-resolution ADCs. IEEE Trans. Veh. Technol. 2018, 67, 7299–7313. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Ngo, D.T.; Tran, N.H.; Swindlehurst, A.L.; Nguyen, D.H. Supervised and semi-supervised learning for MIMO blind detection with low-resolution ADCs. IEEE Trans. Wirel. Commun. 2020, 19, 2427–2442. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Nguyen, D.H.; Swindlehurst, A.L. DNN-based detectors for massive MIMO systems with low-resolution ADCs. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Nguyen, L.V.; Swindlehurst, A.L.; Nguyen, D.H. Linear and deep neural network-based receivers for massive MIMO systems with one-bit ADCs. IEEE Trans. Wirel. Commun. 2021, 20, 7333–7345. [Google Scholar] [CrossRef]
- Khobahi, S.; Shlezinger, N.; Soltanalian, M.; Eldar, Y.C. LoRD-Net: Unfolded deep detection network with low-resolution receivers. IEEE Trans. Signal Process. 2021, 69, 5651–5664. [Google Scholar] [CrossRef]
- Doshi, A.; Andrews, J.G. One-bit mmWave MIMO channel estimation using deep generative networks. IEEE Wirel. Commun. Lett. 2023, 12, 1593–1597. [Google Scholar] [CrossRef]
- Rahman, M.H.; Sejan, M.A.S.; Aziz, M.A.; Tabassum, R.; Baik, J.I.; Song, H.K. Deep learning based one bit-ADCs efficient channel estimation using fewer pilots overhead for massive MIMO system. IEEE Access 2024, 12, 64823–64836. [Google Scholar] [CrossRef]
- Le, H.A.; Van Chien, T.; Nguyen, T.H.; Choo, H.; Nguyen, V.D. Machine learning-based 5G-and-beyond channel estimation for MIMO-OFDM communication systems. Sensors 2021, 21, 4861. [Google Scholar] [CrossRef]
- Helmy, I.; Tarafder, P.; Choi, W. LSTM-GRU model-based channel prediction for one-bit massive MIMO system. IEEE Trans. Veh. Technol. 2023, 72, 11053–11057. [Google Scholar] [CrossRef]
- Kim, S.; Chae, J.; Hong, S.N. Machine learning detectors for MU-MIMO systems with one-bit ADCs. IEEE Access 2020, 8, 86608–86616. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
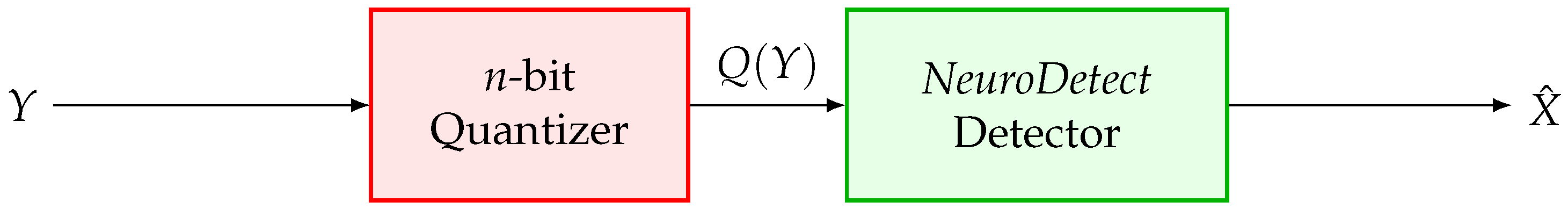







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luckshan, C.; Gayan, S.; Inaltekin, H.; Zhang, R.; Akman, D. NeuroDetect: Deep Learning-Based Signal Detection in Phase-Modulated Systems with Low-Resolution Quantization. Sensors 2025, 25, 3192. https://doi.org/10.3390/s25103192
Luckshan C, Gayan S, Inaltekin H, Zhang R, Akman D. NeuroDetect: Deep Learning-Based Signal Detection in Phase-Modulated Systems with Low-Resolution Quantization. Sensors. 2025; 25(10):3192. https://doi.org/10.3390/s25103192
Chicago/Turabian StyleLuckshan, Chanula, Samiru Gayan, Hazer Inaltekin, Ruhui Zhang, and David Akman. 2025. "NeuroDetect: Deep Learning-Based Signal Detection in Phase-Modulated Systems with Low-Resolution Quantization" Sensors 25, no. 10: 3192. https://doi.org/10.3390/s25103192
APA StyleLuckshan, C., Gayan, S., Inaltekin, H., Zhang, R., & Akman, D. (2025). NeuroDetect: Deep Learning-Based Signal Detection in Phase-Modulated Systems with Low-Resolution Quantization. Sensors, 25(10), 3192. https://doi.org/10.3390/s25103192






