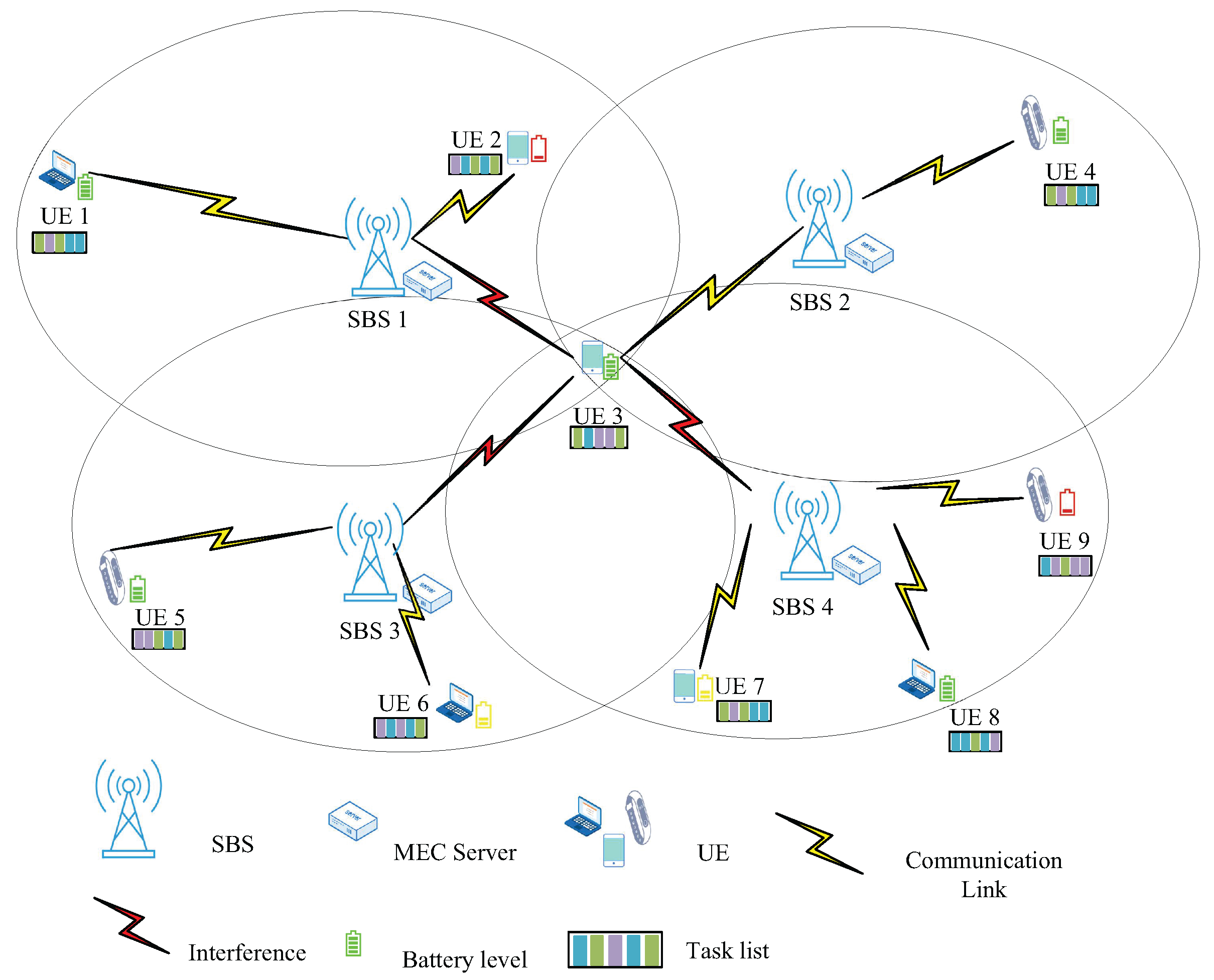
1. Introduction
In recent years, the rapid advancement of wireless communications and internet of things (IoT) technologies has driven a surge in mobile user equipment (UE) and IoT devices. Concurrently, 5G mobile communication technology has reached full-scale commercialization, spurring the emergence of computation-intensive and latency-sensitive applications such as biometric recognition (face/fingerprint/iris), natural language processing, and interactive gaming [
1]. These applications require significant amounts of both energy and computing power from UE. However, the constrained computing and battery capacities of UE often hinder efficient operation, adversely affecting the quality of experience (QoE) of UE. Moreover, reliable communication quality and low network latency are essential for these applications. Proposed by the European Telecommunications Standards Institute (ETSI), mobile edge computing (MEC) has emerged as an effective extension of traditional mobile cloud computing (MCC) [
2]. In technical specification [
3], support for edge computing by the 3rd Generation Partnership Project (3GPP) is described. MEC enables operator and third-party services to be hosted close to the UE’s access point so as to reduce end-to-end latency and transport network load. The fundamental principle of MEC involves processing data at the network edge through MEC servers deployed in proximity to UE. This architecture allows MEC servers to handle latency-sensitive and computation-intensive tasks locally, enabling elastic utilization of computational and storage resources. Consequently, MEC effectively addresses traditional cloud computing challenges including high latency, excessive energy consumption, and data security risks associated with long-distance data transmission.
In dense edge computing systems (DECS), which integrate ultra-dense network (UDN) and MEC, the growing UE population necessitates the adoption of loosely coupled reusable task design as a critical architectural solution. This design paradigm enables applications to be composed of modular tasks where input parameters and output results are decoupled from task code implementation, allowing different input combinations with the same task code to generate corresponding outputs [
4]. For example, virtual reality (VR) and augmented reality (AR) applications require a large amount of real-time rendering and data processing, and multiple pieces of UE may need to handle the same rendering and data processing tasks at the same time within the same region, with only the UE’s own data being different. These tasks can be regarded as reusable tasks, and multiple pieces of UE can share the same rendering resources and processing results through cooperation. Moreover, there are three characteristic scenarios that demonstrate the potential of reusable tasks: (1) For connected vehicle ecosystems, traffic incidents during peak hours often trigger simultaneous requests from numerous UE items for identical real-time navigation data and updated traffic conditions [
4]. (2) In a component-based multiplayer gaming environment, multiple players may frequently reuse the same game components [
5]. (3) In industrial IoT deployments, massive IoT devices often generate reusable task requests in the same scenarios [
6].
In this paper, taking the task similarity into consideration, we want to connect multiple pieces of UE with numerous identical reusable tasks to the same MEC server. In this way, during the processing phase of each task, only one UE device is required to offload the task code to the MEC server for computation. The remaining UE devices merely need to send the task input parameters and can share the corresponding task output results, aiming to reduce energy consumption. In addition, in order to improve the QoE of UE, our goal is to minimize the energy consumption of UE by jointly optimizing the task offloading decisions, subchannel and computing resource allocation, and transmission power allocation while considering the remaining energy of UE. Therefore, we propose a similarity-based cooperative offloading and resource allocation (SCORA) algorithm to achieve our objectives. The main contributions of this paper are as follows:
To address the cooperative offloading problem posed by reusable tasks in DECS, we formulate a joint optimization problem involving offloading decisions, subchannel assignments, computing resource allocation, and transmission power optimization to minimize the energy consumption of UE;
Since the formulated problem is a mixed-integer nonlinear programming problem (MINLP), to facilitate the solution of this problem, we decompose the problem into three subproblems and solve them separately. For the offloading subproblem, considering the task similarity between UE devices, a similarity-based matching offloading strategy is developed to solve it; then, a cooperative-based subchannel allocation strategy is proposed to solve the subchannel allocation subproblem, and finally, the UE devices’ transmission power is optimized using the concave–convex procedure (CCCP) method;
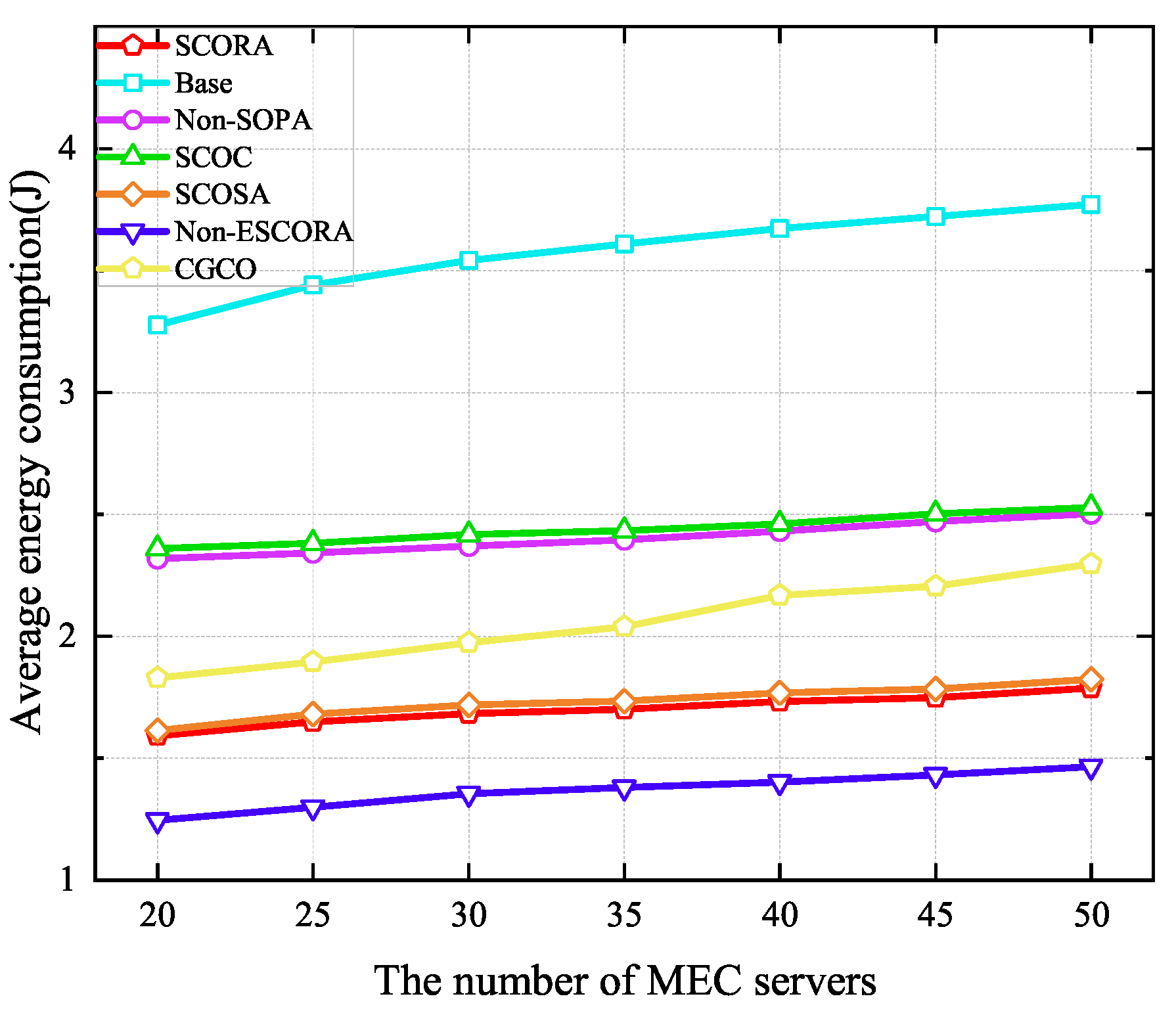
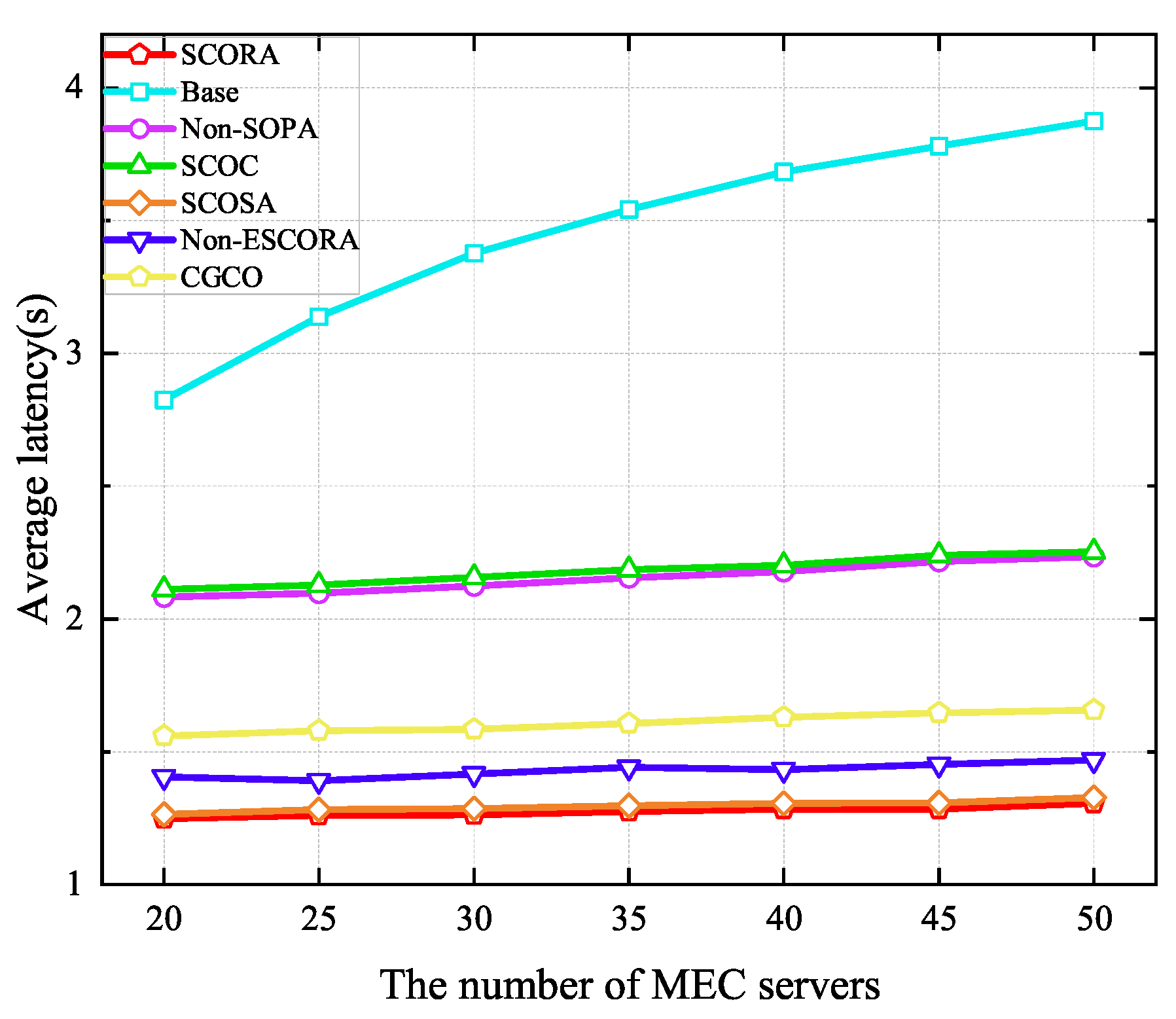
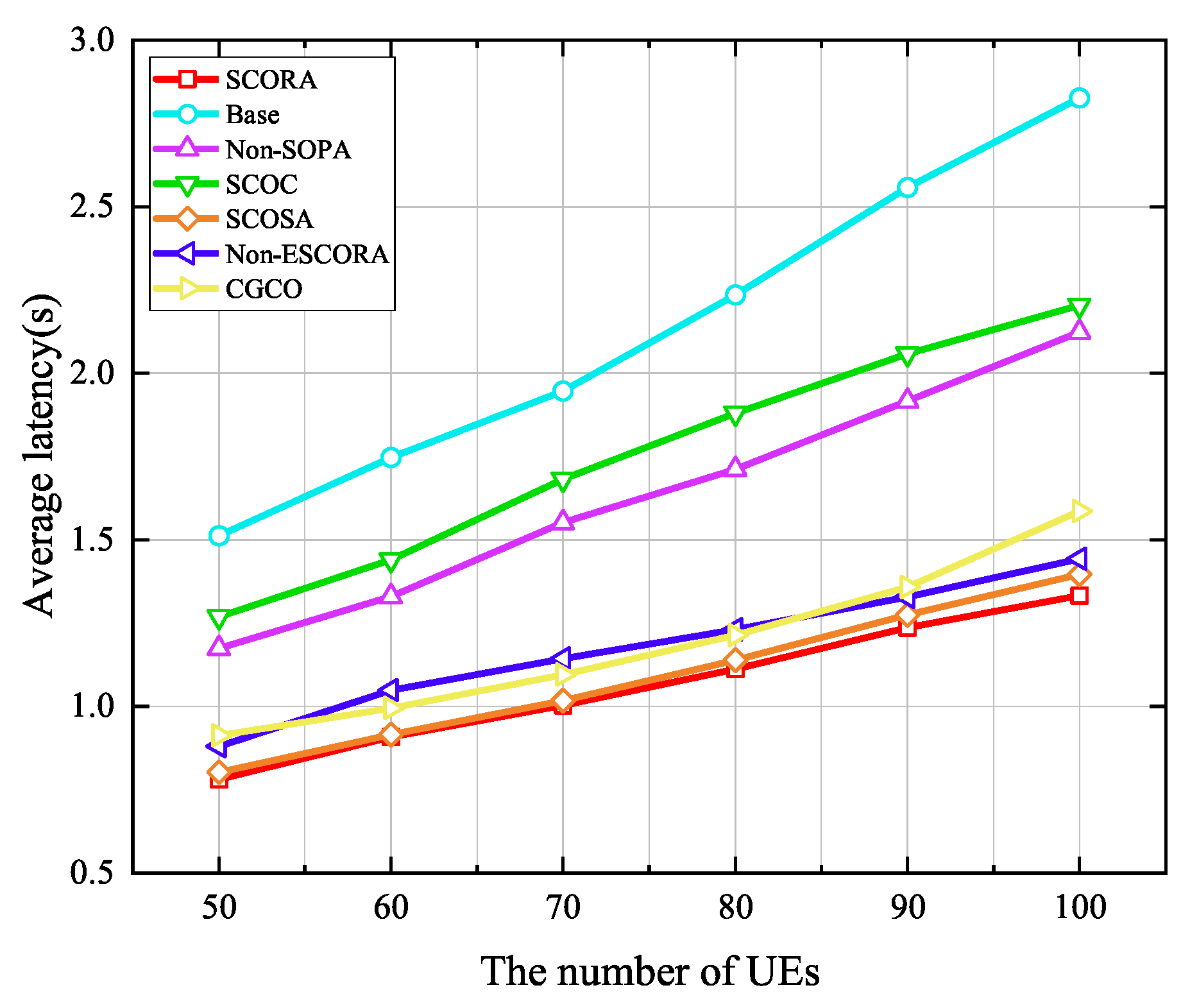
Simulation results show that our scheme performs better than existing ones. It can effectively reduce the average energy consumption and latency of user equipment. Moreover, it can save power for UE with low remaining energy levels, and it adapts well to different numbers of MEC servers and UE devices, providing a reliable solution for reusable task offloading and resource allocation in DECS.
The organization of this article is as follows.
Section 2 describes the related work.
Section 3 introduces the system model, including the network model, the task model, the communication model, the latency model and the energy consumption model, and then formulates the problem. In
Section 4, we decompose the proposed problem into three sub-problems and solve these three sub-problems, respectively.
Section 5 provides the related simulations. Finally, we conclude this article in
Section 6.
2. Related Work
Contemporary academic studies have systematically addressed crucial technical aspects including offloading policy formulation and heterogeneous resource orchestration in the MEC system. In [
7], the authors proposed a collaborative offloading scheme between MEC servers in order to alleviate network congestion and then used the deep Q-network approach to minimize the total execution time concerning deadline constraints. In [
8], the authors added energy consumption constraints while constructing the goal of minimizing system latency. There are many studies aiming to minimize energy consumption [
9,
10,
11]. In [
9], the authors proposed an offloading strategy for the joint optimization of computing and communication resources to minimize energy consumption within the maximum tolerance time. In [
10], the authors considered minimizing energy consumption while maximizing the number of tasks completed in a dynamical system, and they proposed a deep reinforcement learning scheme to jointly optimize the offloading decisions and the computational frequency allocation. In [
11], the authors added service migration cost and task discarding penalties to the proposed objective of minimizing energy consumption in mobile IoT networks using energy harvesting, and they optimized the harvested energy, task allocation factor, central processing unit (CPU) frequency, transmission power, and association vector. In order to obtain a balance of latency and energy consumption, many studies focus on multi-objective optimization frameworks with approaches such as game theory and machine learning algorithms [
12,
13,
14,
15]. In [
12], the authors proposed an improved quantum particle swarm algorithm to optimize task offloading decisions. In [
13], considering the download delay of tasks, the authors proposed a three-stage multi-round combined offload scheduling mechanism and a joint resource allocation policy to solve the joint optimization problem of task offloading and heterogeneous resource allocation. In [
14], the authors considered idle offsite servers and UE mobility, and they proposed a multilateral collaborative computation offloading model and an improved genetic algorithm. In [
15], the authors formulated the system utility as an integrated function of computing service costs, task execution time, and energy consumption and then optimized the joint optimization of offloading decisions, transmission power, computing resource allocation, and computational service costs through a two-tier bargaining-based task offloading and a collaborative computing incentive mechanism.
In the aforementioned studies, although the increased number of MEC servers has proven to be effective in assisting task processing, the quantity of MEC servers typically remains limited. In DECS, the proliferation of MEC servers enhances opportunities for task offloading and collaborative processing among UE devices with rapidly increasing density. However, it also brings some challenges, such as the complexity of task offloading decisions, multidimensional resource allocation, and intricate service migration and caching placement issues. Many studies have endeavored to address the task offloading problems [
16,
17,
18]. In [
16], in order to minimize the long-term average task latency of all UE, the authors developed a novel calibrated contextual bandit learning algorithm to enable UE devices to predict the task offloading decisions of the rest of the UE in order to independently decide their own offloading decisions. In [
17], the authors designed an online task offloading deep reinforcement learning algorithm: the asynchronous advantage actor–critic. This framework operates independently of real-time channel state information and BS computational power, achieving the dual objectives of strict adherence to energy budget constraints and systematic minimization of task completion latency. In [
18], the authors proposed a contextual sleeping bandit learning algorithm (CSBL) with Lyapunov optimization to minimize long-term task delay under price constraints, and they extended it to multi-server scenarios as CSBL-M to address exponential action space growth in task offloading.
In DECS, the proliferation of UE has given rise to pressing resource allocation challenges. Therefore, many of recent studies have focused on addressing computational offloading and resource allocation problems [
19,
20,
21,
22]. In [
19], the authors proposed a deep reinforcement learning-based scheduling algorithm that utilizes deep deterministic policy gradient and behavioral critique networks to solve the task scheduling and resource scheduling problems, aiming to minimize the task latency for all UE devices. In [
20], in order to minimize the system energy consumption, the authors used the improved artificial fish swarm algorithm and the improved particle swarm optimization (PSO) algorithm to jointly optimize the computation offloading decision, the task offloading ratio, and the allocation of communication and computation resources. In [
21], the authors jointly optimized the problems of task offloading, BS selection, and resource scheduling, which is addressed by a Newton-interior point method-based resource allocation algorithm and a genetic algorithm-based scheduling method, achieving the minimization of the weighted sum of system delay and energy consumption. In [
22], taking the uncertainties in UE mobility and resource constraints into consideration, the authors proposed a distributed delay-constrained computation offloading framework that incorporates Lyapunov-based game-theoretic optimization and multi-stage stochastic programming to achieve adaptive task offloading and computational capacity management. In addition, extensive studies exist on dynamic service migration and caching placement mechanisms [
23,
24]. An energy-efficient online algorithm based on Lyapunov and PSO was developed to solve the task migration problem in order to reduce energy consumption while considering the interference and mobility of UE in [
23]. In [
24], the authors proposed a two-timescale hierarchical multi-agent deep reinforcement learning (HMDRL)-based scheme for the joint optimization of cooperative service caching, computation offloading, and resource allocation to minimize weighted energy consumption across energy-harvesting (EH)-powered mobile UE devices and small base stations (SBSs). Although these studies addressed many problems in DECS, they failed to consider the homogeneity of tasks between UE devices and ignored cooperation opportunities brought about by the dense deployment of UE devices and MEC servers.
In the processing of reusable tasks, cooperative offloading realizes resource sharing via task decomposition, resource allocation, and UE cooperation to boost efficiency and reduce energy consumption. To fully exploit the computing capacity of a multi-server system, collaborative offloading among multiple edge servers is necessary [
25]. Scenarios involving reusable tasks are considered in [
4,
5,
6,
26]. In [
4], by applying coalitional game theory, the authors formulated a cooperative offloading process for reusable tasks as a coalitional game to maximize cost savings. In [
5], the authors developed a 0–1 integer nonlinear programming problem to minimize the total energy cost on the player’s side under a delay constraint in a component-based multiplayer game scenario. In [
6], the authors incorporated drones to assist with the offloading of reusable tasks in an MEC environment. By jointly optimizing the UE offloading policy, UE transmission power, server allocation on the unmanned aerial vehicle (UAV), the computation frequency of the UE and the UAV server, and the UAV flight trajectory, a system model was constructed to minimize the system average total energy consumption under time delay constraints. In [
26], the authors formulated the joint offload optimization problem with the aim of minimizing the long-term average task execution cost, taking into account transmission collaboration, shared wireless bandwidth, and varying task queues in UE devices and MEC servers. The above research on cooperative task offloading does not take into account the types of tasks in the scenario, which is important for the completion of cooperative offloading.
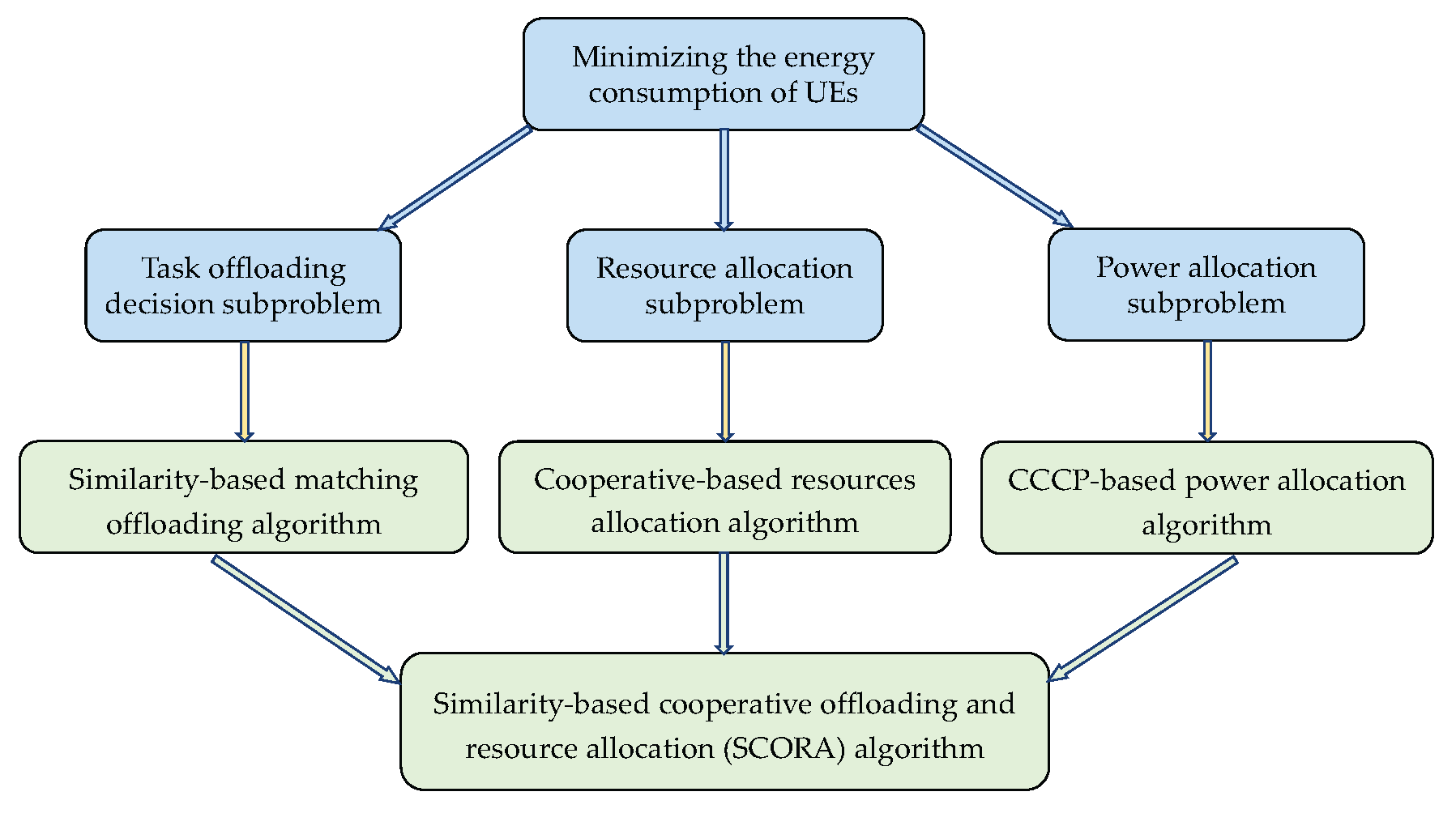
4. Similarity-Based Cooperative Offloading and Resource Allocation Algorithm
In this section, we propose the SCORA algorithm to solve the formulated problem (
11). We divide it into three interdependent subproblems: (1) a task offloading decision subproblem, (2) a resource allocation subproblem, and (3) a power allocation subproblem. In the SCORA algorithm, the similarity-based matching offloading algorithm is proposed to solve the task offloading decision subproblem, and the cooperation-based resource allocation algorithm is designed to tackle the resource allocation problem, leveraging task similarity among UE devices. Finally, the non-convex power allocation optimization is systematically addressed through the CCCP-based power allocation algorithm, enabling efficient energy consumption minimization.
Figure 3 illustrates the original problem and the decomposed subproblems and corresponding algorithms.
4.1. Similarity-Based Matching Offloading Algorithm
Given that each UE offloads its task to exactly one MEC server, while each MEC server is capable of serving multiple UE devices, it is suitable for this problem to be solved by applying many-to-one matching theory. Initially, the matching multinomial group is defined as follows:
are two sets of unrelated collections. In this paper, is the set of MEC servers that executes tasks, and is the set of UE devices that offloads tasks to MEC servers.
represents a list of preferences for MEC servers and UE. Each MEC server maintains a preference list in which the preferences for UE devices are sorted in descending order, that is, , which means that the MEC server m prefers UE n to . Each UE device maintains a preference list for MEC servers in descending order as well.
represents the matching between MEC servers and UE. Each UE device can be matched with at most one MEC server, that is, and , where is the cardinality of the matching result . In addition, each MEC server can be matched with multiple UE devices, that is, and , where is maximum number of access UE devices for the MEC server m.
Subsequently, the definition of the considered many-to-one matching can be described as follows:
Definition 1. Given the UE set and the MEC server set , the matching game for computation offloading is defined as a many-to-one function, such that
and ;
and ;
.
During the computation offloading process, each UE device is willing to associate with the MEC server that has the best channel conditions to obtain a high offloading rate. Therefore, a preference function of UE
n for each MEC server is established:
Each UE device can calculate preferences for the MEC servers and generate a preference list based on the above equation.
In an effort to effectively pair more UE devices that have identical reusable tasks with the same MEC server, the similarity score is introduced as a metric. For example, the similarity score
between UE
i and UE
n can be calculated in the following way: First, the number of similar tasks in the task lists of UE
i and UE
n is counted, and then
can be calculated as a ratio of the number of similar tasks to the total number of tasks of UE
i. Before starting the matching algorithm, we calculate the similarity scores among UE devices. These scores are incorporated into the preference function of MEC servers for UE. In this way, they influence the preferences of UE when choosing the same MEC server, thereby enabling the pairing of more UE devices with identical reusable tasks to the same MEC server. The preference function of the MEC server
m for each UE device can reflect that the MEC server has a higher preference for UE with good channel conditions and low energy consumption, which can prioritize the tasks of UE devices with low remaining energy levels to save the energy, and the addition of similarity scoring can match more UE devices with the same tasks to the same MEC server to achieve more energy savings for UE. The preference function of MEC server
m for each UE device can be calculated as
where
is the remaining energy level of UE
n.
Algorithm 1 summarizes the steps of similarity-based matching offloading strategy. First, all UE devices and MEC servers are not matched. Therefore, the unmatched UE set
and the unmatched MEC server set
are initialized as all UE and all MEC servers, respectively. Calculate the similarity score
between UE
i and UE
n. In the matching process, every unmatched UE device builds its preference list based on (
12) and sends an offloading request to the first MEC server on the preference list. Subsequently, each unmatched MEC server calculates
, which is the number of offloading requests received, and marks UE devices that sent the offloading requests by the set
. If
is not more than the maximum number of access UE devices for MEC server
m , then all UE in
is allowed to communicate with the MEC server
m for task offloading. Otherwise, the unmatched MEC server
m establishes its preference list based on (
13). The first
UE devices in
are allowed to offload their tasks, and the offloading requests of the other UE in
are rejected. Then, the unmatched UE set
and the unmatched MEC server set
are updated. The matching process is not finished until all UE devices and MEC servers are matched. Finally, the offloading indicator can be obtained from the matching result
. Following the same method as in [
31,
35], we can prove that the proposed matching algorithm is stable.
| Algorithm 1 Similarity-based matching offloading algorithm. |
| Input: The maximum latency requirement for all UE to complete the task. |
| Output: Stable matching result . |
- 1:
Initialize the unmatched MEC server set , and the unmatched UE set . Calculate the similarity score between UE and UE . - 2:
while
do - 3:
for all unmatched UE do - 4:
UE n builds its preference list based on ( 12) in a descending order; - 5:
UE n sends an offloading request to the first MEC server in ; - 6:
end for - 7:
while do - 8:
for all unmatched MEC server do - 9:
Count the number of requests received by MEC server m as and denote the set of these UE devices as ; - 10:
if then - 11:
MEC server m allows these UE devices to offload their tasks; - 12:
Remove MEC server m from and , and remove these UE devices from ; - 13:
end if - 14:
if then - 15:
MEC server m updates its preference list in a descending order according to ( 13) and allows the first K UE devices in to offload their tasks; - 16:
Remove MEC server m from and , and remove these UE devices from ; - 17:
end if - 18:
end for - 19:
end while - 20:
For all UE devices matched with MEC server m, ; - 21:
end while
|
4.2. Cooperation-Based Resource Allocation Algorithm
To better achieve the purpose of cooperative offloading, we adopt the agglomerative clustering algorithm in the hierarchical clustering algorithm to form clusters of UE devices with the same type of reusable tasks in the current time slot. The agglomerative hierarchical clustering algorithm divides data points into clusters by calculating the distance between each cluster. In this paper, data points are defined as clusters formed by UE, and the total number of clusters is
.
denotes the set of
UE devices connected to MEC server
m.
represents the cluster formed by UE
. The distance is defined as the task similarity between UE devices. We adopt the merging rule based on the shortest distance and use the task types
and
of the current time of UE
i and UE
n to calculate the distance
. The shortest distance among all clusters is set as
, and the stopping condition is
. If the task types
and
of UE
i and UE
n are the same, then
. When
, the clusters
and
where UE
i and UE
n are located will be merged into
. Here, we introduce the cooperation-based resource allocation algorithm, as shown in Algorithm 2.
| Algorithm 2 Cooperation-based resource allocation algorithm. |
| Input: The Stable matching result . |
| Output: The subchannel allocation result and computing resources allocation result . |
- 1:
for all MEC servers do - 2:
for all UE devices do - 3:
If the task types and of UE i and UE n are the same, then ; - 4:
while do - 5:
The clusters and where UE i and UE n are located will merge into ; - 6:
Compare the task types of the with task types of all remaining clusters ; - 7:
Remove UE n from ; - 8:
end while - 9:
end for - 10:
for all clusters do - 11:
Allocate resources to cluster according to ( 14) and ( 18); - 12:
Select the cluster head according to ( 15); - 13:
Allocate resources to cluster head according to ( 16) and ( 19); - 14:
Allocate resources to cluster member according to ( 17) and ( 20); - 15:
end for - 16:
end for
|
Each MEC server allocates the subchannels to each cluster according to the ratio of the number of UE devices. The number of subchannels allocated to cluster
can be calculated by
where
K is the number of subchannels in the system, and
is the number of UE devices in cluster
.
All of the UE devices
are sorted based on the product of channel gain and residual energy, and the first piece of UE is selected as the cluster head
. The sorting formula is as follows:
In this way, the selected cluster head a the piece of UE with both high channel gain and remaining energy, which is beneficial to reducing the total energy consumption and delaying and reducing the energy consumption for UE with low remaining energy levels.
This strategy allocates subchannels to the cluster head and the remaining UE according to the ratio of the total task size sent by the cluster head and the total task size sent by other UE in the cluster. The number of subchannels allocated to the cluster head
of cluster
can be calculated by
where
is the main code of the task to be sent by all UE in cluster
,
is the task input parameter of the cluster head
, and
is the task input parameter of all UE in cluster
.
The number of subchannels
allocated to the cluster member UE
in cluster
can be expressed as
where
is the task input parameter of the cluster member UE
in cluster
.
The number of computing resources allocated to cluster
can be calculated by
The number of computing resources allocated to the cluster head
of cluster
can be calculated by
The number of computing resources allocated to the cluster member UE
in cluster
can be expressed as
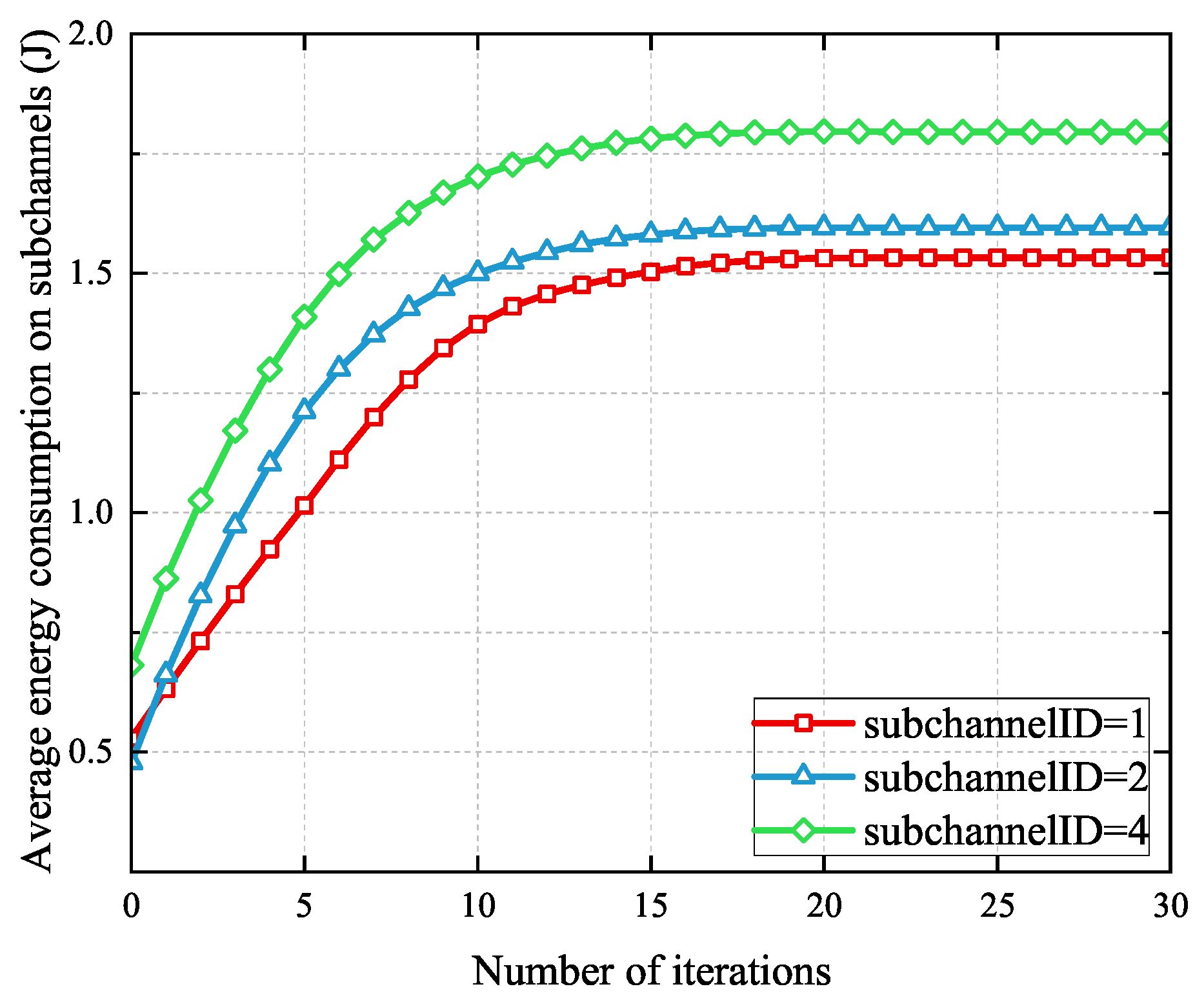
4.3. CCCP-Based Power Allocation Algorithm
After completing the computation offloading and resource allocation, the problem becomes
To better accomplish the power optimization, the problem is rewritten as follows:
Theorem 1 is introduced to make the above equation tractable.
Theorem 1. If is the optimal solution of the problem, then there exist , , when and , such that is a solution to the following problem:and when and , also satisfies the following equations: According to Theorem 1, the optimal solution of problem (
21) can be obtained by solving (
23). If the solution of (
23) is unique, then the solution of (
23) is the optimal solution of problem (
22). Next, we will solve (
23).
After rearranging the objective function in (
24), we obtain
where the functions on the right side of the equation are
and
.
In addition, the non-convex constraint condition
can be transformed into its equivalent convex linear form
through mathematical operations:
Therefore, problem (
23) is equivalent to
The solution of problem (
21) can be obtained by solving (
27). Since
and
are both concave functions with respect to
, problem (
24) has a difference-of-convex structure. Moreover, since
is differentiable, the CCCP algorithm can be used to solve problem (
27). The main idea of the CCCP algorithm is to transform the convex part of
, that is,
, into a linear form through iteration. By introducing Theorem 2, the above problem can be solved.
Theorem 2. Problem (27) can be solved by solving the following sequential convex programming problem:where is the transpose of . represents the gradient of at and . Since (
28) is a convex optimization problem, classical convex optimization algorithms can be used to solve the problem. The Lagrangian function corresponding to the construction of (
28) is
where
and
are Lagrange multipliers. Let
denote the Lagrange function, that is,
The optimum power is obtained as
where
.
The
and
updated by subgradient methods:
where
and
represent the step sizes of
and
at the
iteration step, respectively, and
is the maximum number of iterations.
The
and
should satisfy the following conditions:
It can be proven that (
31) is standard. Therefore, for any value of initial power, the algorithm converges to a unique value. A unique solution can be obtained for (
30), so the solution of problem (
17) is equivalent to the solution of (
30). Algorithm 3 shows the steps of the proposed power allocation algorithm. Correspondingly, the total procedure of the SCORA algorithm is demonstrated in Algorithm 4.
| Algorithm 3 CCCP-based power allocation algorithm. |
| Input: The maximum time delay requirement for UE n to complete the task. |
| Output: The optimal power . |
- 1:
Initialize and . Set and calculate and for all UE devices and MEC servers; - 2:
while or do - 3:
Use CCCP to solve problem ( 27), and the optimal power is obtained according to ( 31); - 4:
Update and according to ( 24); - 5:
Update ; - 6:
end while
|
| Algorithm 4 SCORA algorithm. |
| Input: The maximum time delay requirement for UE n to complete the task. |
| Output: Stable matching result , the subchannel allocation result , the computing resources allocation result and the optimal power . |
- 1:
Initialize the UE device set , the MEC servers set , the subchannel set and maximum time delay requirement for UE device . - 2:
Obtain the stable UE device and MEC server matching according to Algorithm 1. - 3:
Use Algorithm 2 to attain the subchannel allocation result and the computing resources allocation result . - 4:
Use Algorithm 3 to calculate the optimal power .
|
4.4. Complexity Analysis
Here, we will analyze the complexity of Algorithm 4, which mainly consists of the following complexities of Algorithms 1–3. In Algorithm 1, the complexity of computing the similarity scores of UE devices is . The complexity of each UE device sorting M MEC servers in its preference list is . Therefore, the sorting complexity for N UE devices is . Considering the worst case, each MEC server will receive N requests from UE, and the sorting complexity for M MEC servers is . Thus, the complexity of Algorithm 1 in the worst case is . In Algorithm 2, for each MEC server, the complexity of comparing task types between UE devices and performing the merge operation in the worst case is . Since the above steps need to be performed for all MEC servers, the complexity of Algorithm 2 is . In Algorithm 3, updating and requires and iterations in the worst case, respectively. Hence, the complexity of Algorithm 3 is denoted as . Therefore, the complexity of the proposed SCORA algorithm can be calculated as .
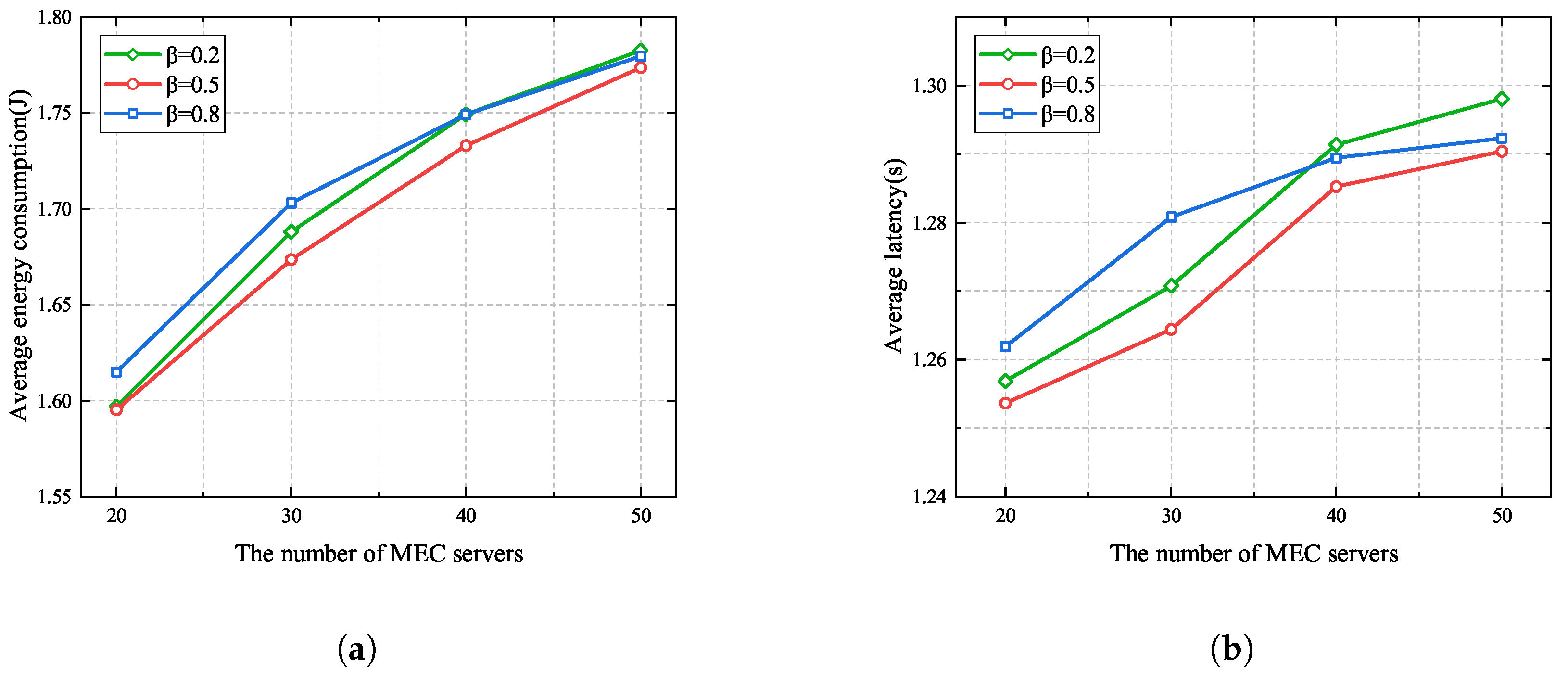
6. Conclusions
In this study, we focus on addressing the energy consumption challenge in DECS with reusable tasks while considering the task similarity between UE devices. By jointly optimizing task offloading, resource allocation, and power allocation, the problem is formulated as an MINLP problem, and the SCORA scheme is proposed to solve it. This strategy aims to minimize the total energy consumption of all UE while considering the remaining energy levels of UE. In the SCORA scheme, the similarity-based matching offloading strategy is developed to solve the task offloading subproblem, the cooperation-based resource allocation strategy is proposed to solve the subchannel and computing resource allocation subproblem, and the CCCP-based power allocation strategy is proposed to solve the UE transmission power optimization subproblem. Through extensive simulation experiments, the SCORA scheme was compared to six benchmark approaches. The results demonstrate that the SCORA scheme can significantly outperform existing schemes in terms of reducing the energy consumption of UE. Notably, compared to the scheme neglecting UE’s remaining energy levels, the SCORA scheme exhibits remarkable advantages in terms of energy conservation for UE with low remaining energy levels, highlighting its adaptability to UE heterogeneity. These findings indicate that the proposed SCORA scheme can provide an efficient and practical solution for joint task offloading and resource allocation in DECS. Since the task offloading in a dynamic environment is more complicated, we consider the computation offloading in a static environment and assume that the user’s task is indivisible. In the future, with the help of the deep reinforcement learning method, our work will expand to intelligent task offloading and resource allocation problems in a dynamic MEC network environment where UE mobility will be taken into account.