Performance Optimization of a High-Speed Permanent Magnet Synchronous Motor Drive System for Formula Electric Vehicle Application
Abstract
1. Introduction
2. Formula EV PMSM Basic Principles
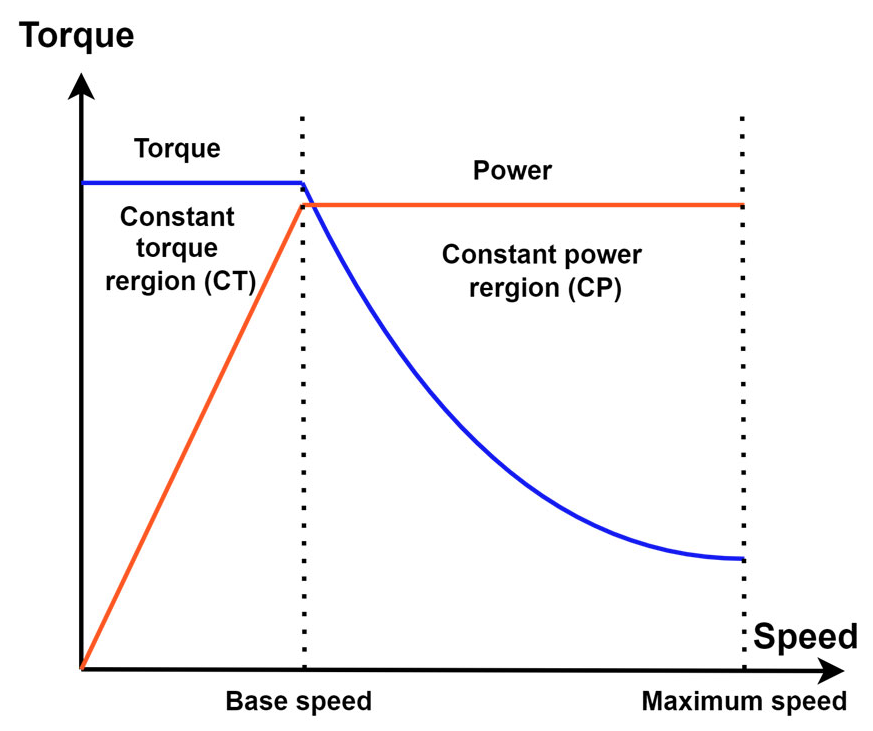
2.1. FEV PMSM Ideal Torque Speed Profile
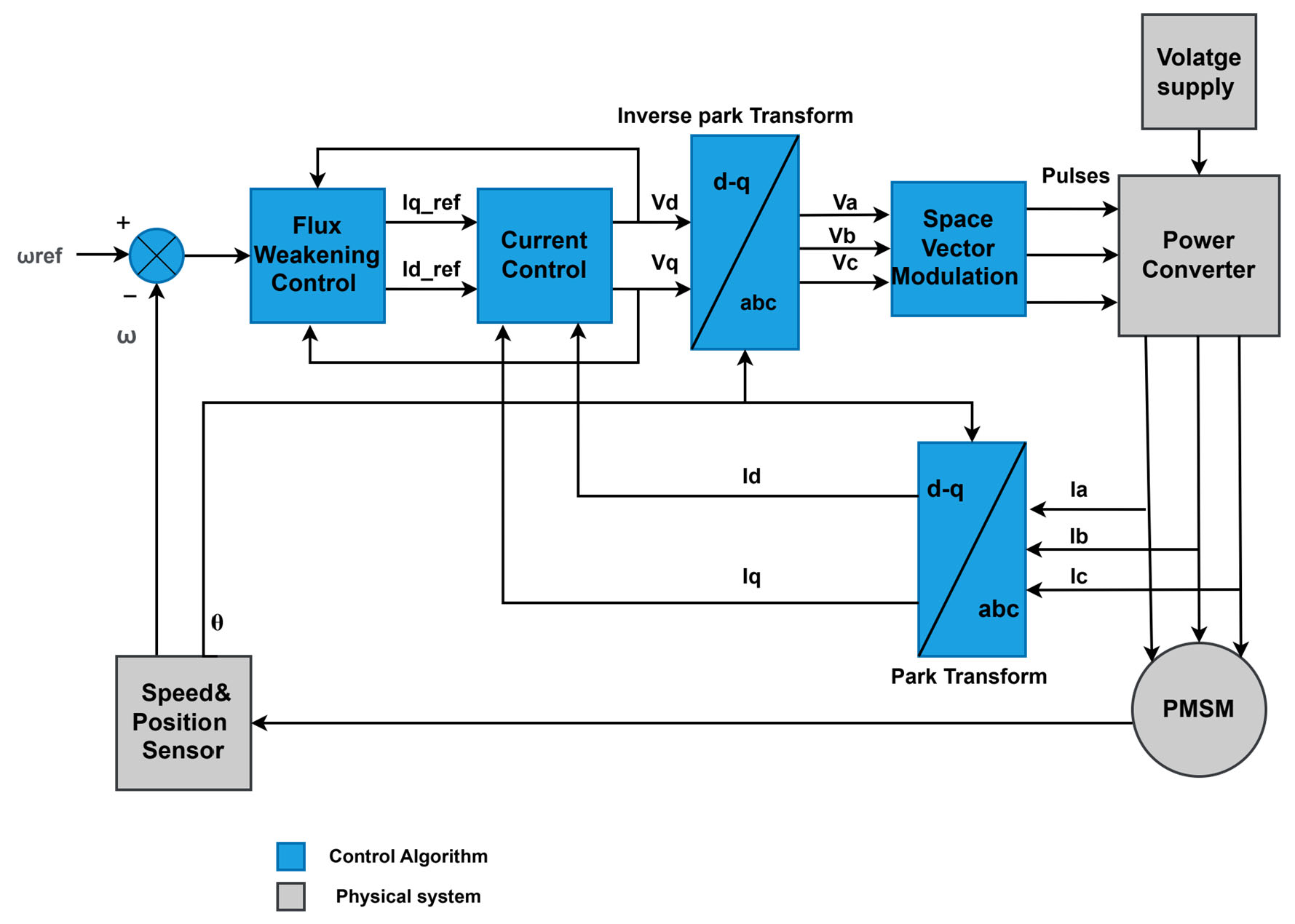
2.2. FEV PMSM Drive System
3. FEV Motor Drive System Modeling and Simulation
3.1. PMSM Mathematical Model
3.2. FEV Motor Drive System Simulation Model
4. FEV Motor Drive System Performance Optimization
4.1. Control Strategy Optimization
4.2. Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
- -
- Initialize: set initial mean vector (m), step size (σ), and covariance matrix (C);
- -
- Sampling: generate a population of candidate solutions (xK) using the multivariate normal distribution;
- -
- Evaluation: Evaluate the fitness of each candidate solution using the objectiv function;
- -
- Selection: Select the top-performing candidates based on their fitness values;
- -
- Update: Adapt the mean vector (m), step size (σ), and covariance matrix (C) based on the selected candidates as follows,
- -
- Iteration: Repeat the sampling, evaluation, selection, and update steps until convergence or a stopping criterion is met, such as a maximum number of iterations or sufficient convergence of the mean vector.
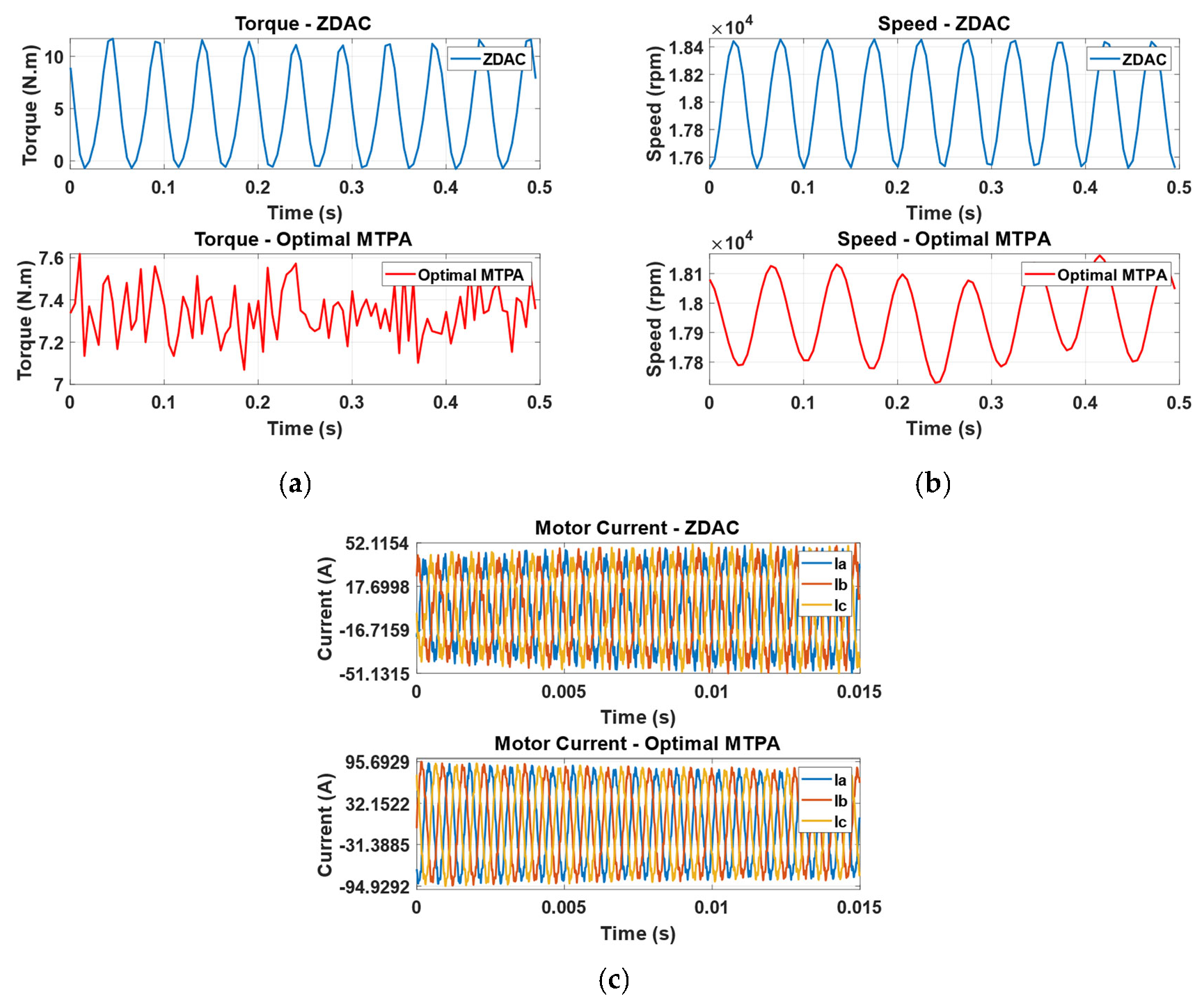
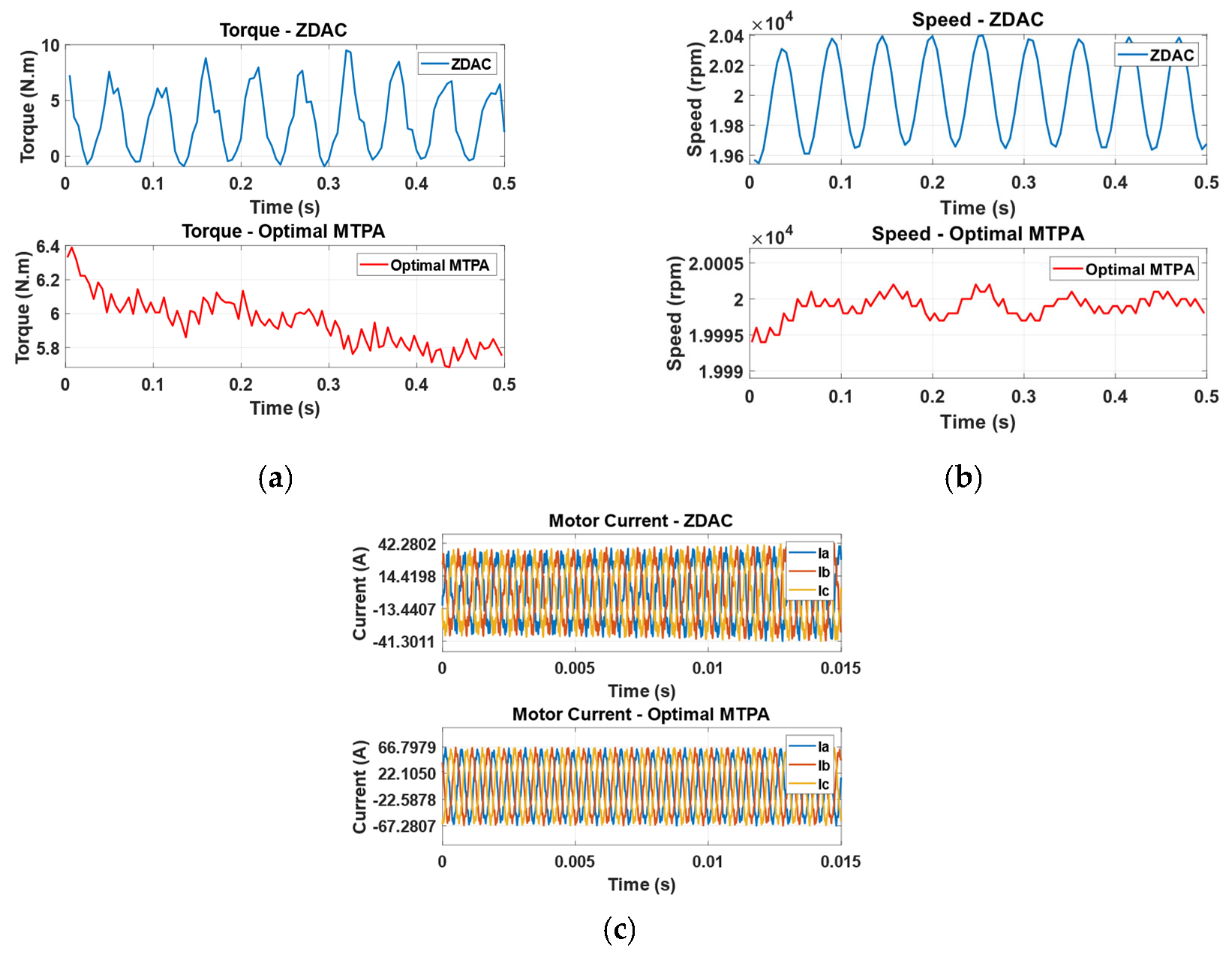
5. Experimental Validation
5.1. Testbench
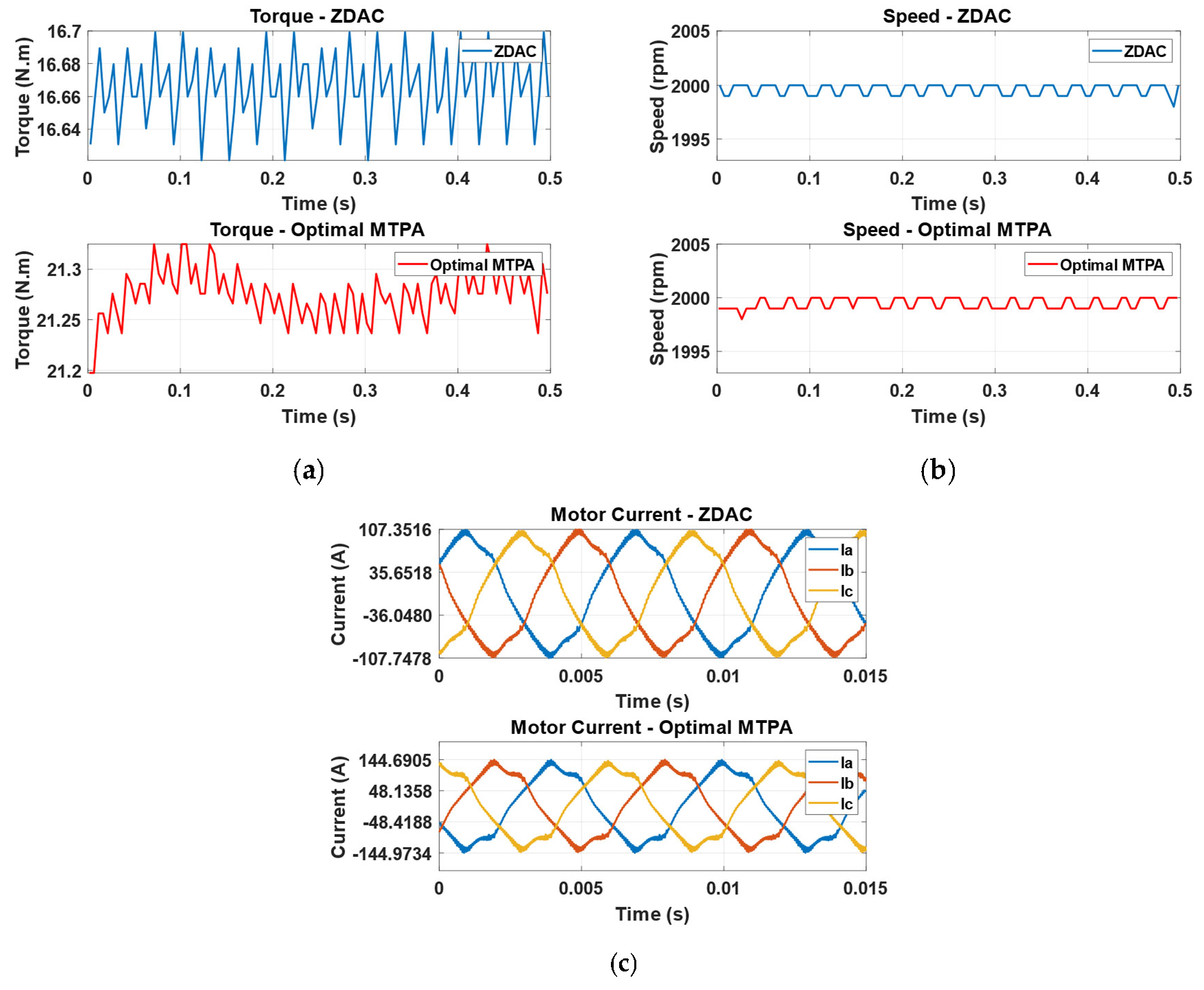
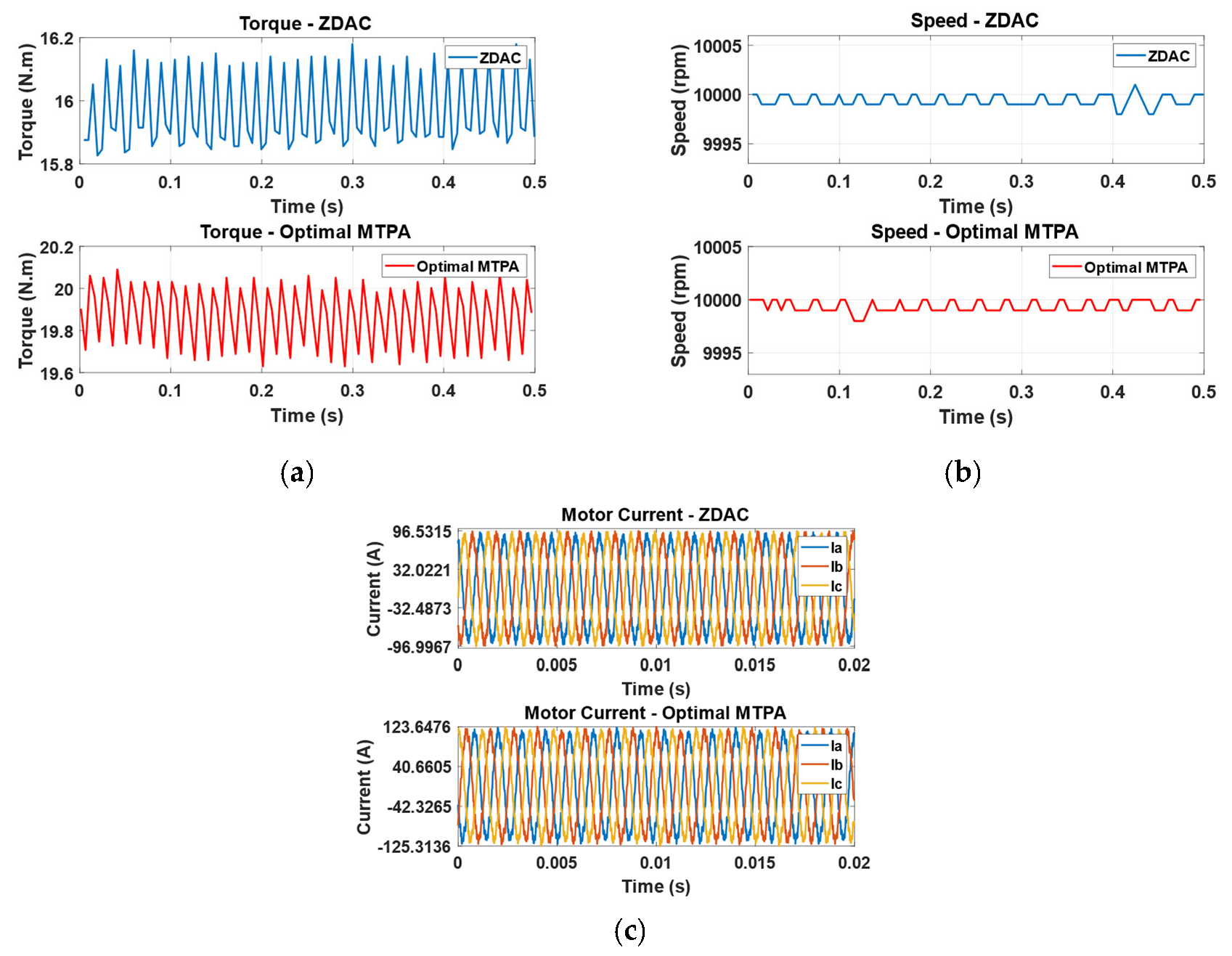
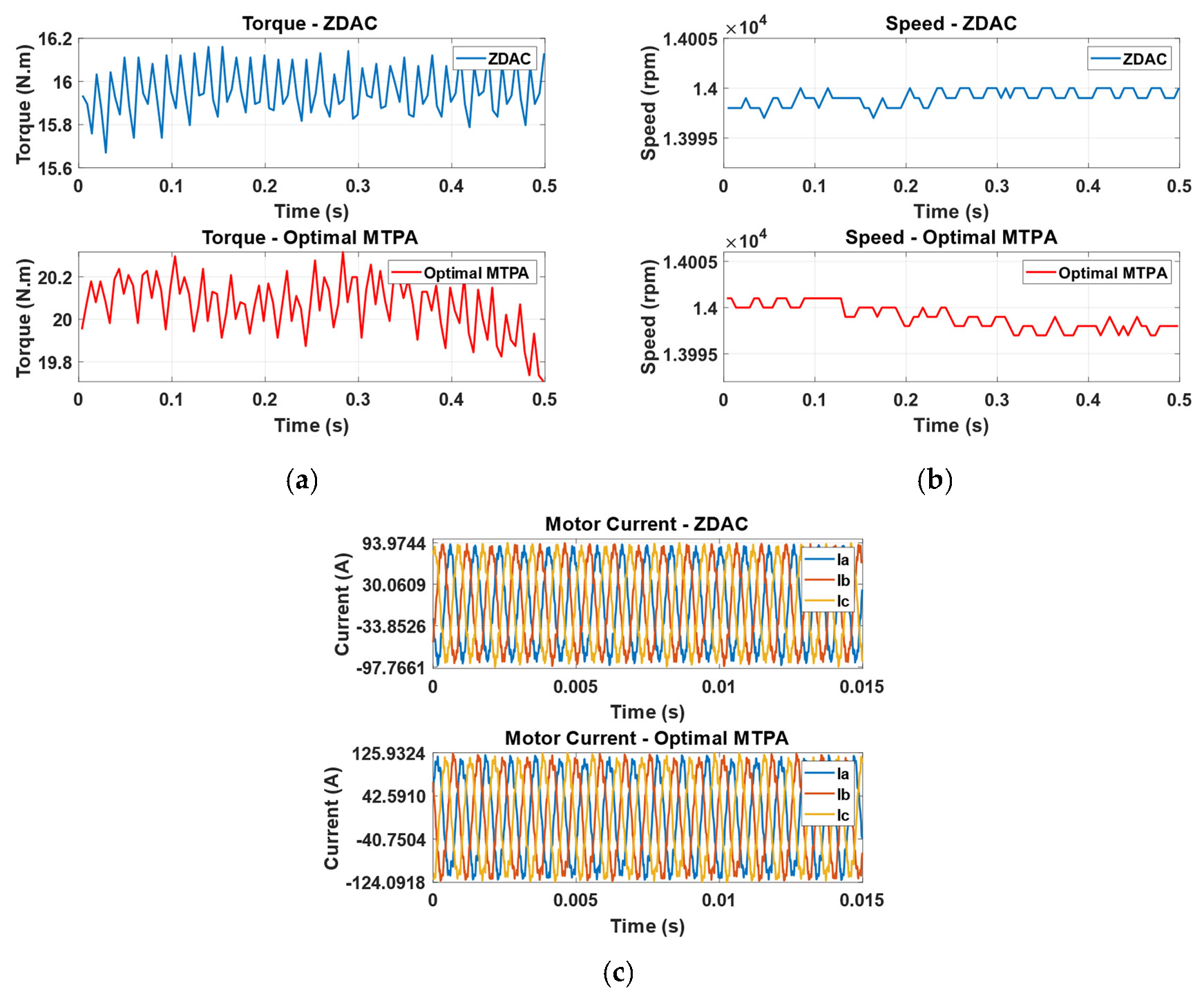
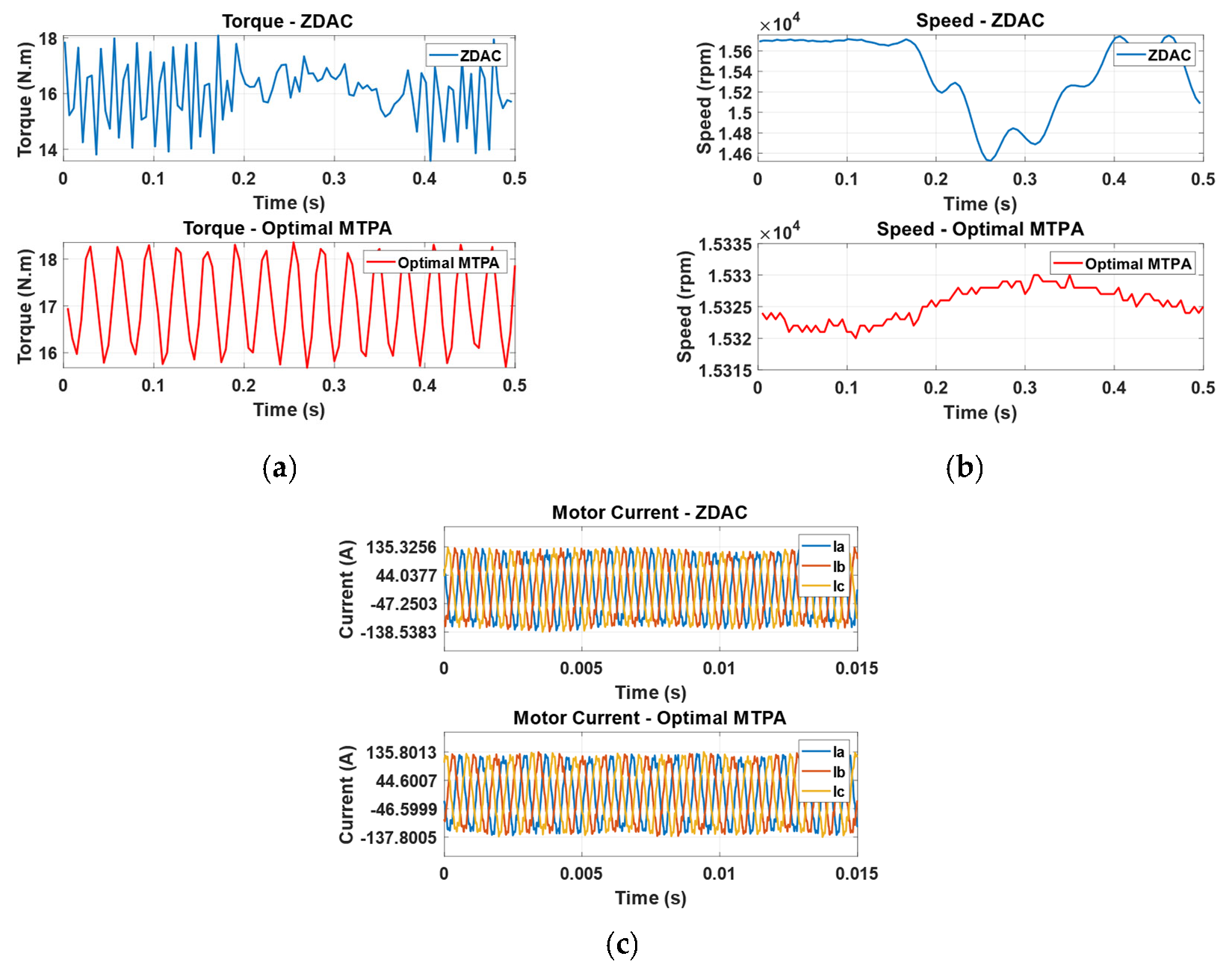
5.2. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Taticchi, P.; Demartini, M.; Corvaglia-Charrey, M. Formula E. In Sustainable Transformation Strategy; Springer: Cham, Switzerland, 2023; pp. 71–83. [Google Scholar] [CrossRef]
- Rossi, N.; Matteazzi, N.; Petti, G.L.; Fazzini, L.; Nuzzo, S.; Barater, D.; Franceschini, G. Design and thermal assessment of a high-performance electric motor for racing applications. In Proceedings of the 2021 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Modena, Italy, 8–9 April 2021; pp. 52–57. [Google Scholar] [CrossRef]
- Özçiflikçi, O.E.; Koç, M.; Bahçeci, S.; Emiroğlu, S. Overview of PMSM control strategies in electric vehicles: A review. Int. J. Dyn. Control. 2024, 12, 2093–2107. [Google Scholar] [CrossRef]
- Arias, A.; Ibarra, E.; Trancho, E.; Griñó, R.; Kortabarria, I.; Caum, J. Comprehensive high speed automotive SM-PMSM torque control stability analysis including novel control approach. Int. J. Electr. Power Energy Syst. 2019, 109, 423–433. [Google Scholar] [CrossRef]
- Elsonbaty, N.A.; Enany, M.A.; Hassanin, M.I. An Efficient Vector Control Policy for EV-Hybrid Excited Permanent-Magnet Synchronous Motor. World Electr. Veh. J. 2020, 11, 42. [Google Scholar] [CrossRef]
- Wei, H.; Yu, J.; Zhang, Y.; Ai, Q. High-speed control strategy for permanent magnet synchronous machines in electric vehicles drives: Analysis of dynamic torque response and instantaneous current compensation. Energy Rep. 2020, 6, 2324–2335. [Google Scholar] [CrossRef]
- Zhao, J.; Hua, M.; Liu, T. Research on a Sliding Mode Vector Control System Based on Collaborative Optimization of an Axial Flux Permanent Magnet Synchronous Motor for an Electric Vehicle. Energies 2018, 11, 3116. [Google Scholar] [CrossRef]
- Murali, A.; Wahab, R.S.; Gade, C.S.R.; Annamalai, C.; Subramaniam, U. Assessing Finite Control Set Model Predictive Speed Controlled PMSM Performance for Deployment in Electric Vehicles. World Electr. Veh. J. 2021, 12, 41. [Google Scholar] [CrossRef]
- Li, X.; Song, W. Research on Control Strategy of PMSM for Electric Vehicles Based on Nonlinear Model. In Proceedings of the IMCEC 2022—IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference, Chongqing, China, 16–18 December 2022; pp. 170–174. [Google Scholar] [CrossRef]
- Da Silva, L.P.; Waltrich, G. Driving Technological Advancements in Formula Student: Developing a Field-Oriented Control Voltage Source Inverter for Enhanced Motor Control. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference, Florianopolis, Brazil, 26–29 November 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Jujjuvarapu, R.K.; Rajulapati, A. Machine Learning-Driven Optimization of MTPA in IPMSM Drives for Electric Vehicles. In Proceedings of the 2024 International Conference of Adisutjipto on Aerospace Electrical Engineering and Informatics (ICAAEEI), Yogyakarta, Indonesia, 11–12 December 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Wu, Z.; Tian, D.; Liu, H. Research on MTPA Control of IPMSM for Electric Vehicle. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024; pp. 837–842. [Google Scholar] [CrossRef]
- Shen, Y.; Zhou, B.; Yuan, X.; Zhang, X. Efficiency Optimization Control of PMSM in Electric Vehicle-A Comparative Study. In Proceedings of the 2023 7th CAA International Conference on Vehicular Control and Intelligence (CVCI), Changsha, China, 27–29 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Dianov, A.; Anuchin, A. Adaptive Maximum Torque per Ampere Control of Sensorless Permanent Magnet Motor Drives. Energies 2020, 13, 5071. [Google Scholar] [CrossRef]
- Mondal, S.; Ghosh, S.; Kumar, R.R.; Chanda, S. Exploring MTPA Technique in Field-Oriented Control of IPMSM Drive for Enhancing Efficiency of Electric Vehicles. In Proceedings of the 2024 IEEE 1st International Conference on Green Industrial Electronics and Sustainable Technologies (GIEST), Imphal, India, 25–26 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, J.; Shen, Y.; Lu, X. IPMSM model free maximum torque per ampere predictive control based on formula calculation. J. Control. Decis. 2025, 1–18. [Google Scholar] [CrossRef]
- Ibrahim, M.; Rjabtsikov, V. EV-Permanent Magnet Synchronous Motor Control Strategy Evaluation Based on Digital Twin Concept. In Proceedings of the CPE-POWERENG 2023—17th IEEE International Conference on compatibility, Power Electronics and Power Engineering, Tallinn, Estonia, 14–16 June 2023. [Google Scholar] [CrossRef]


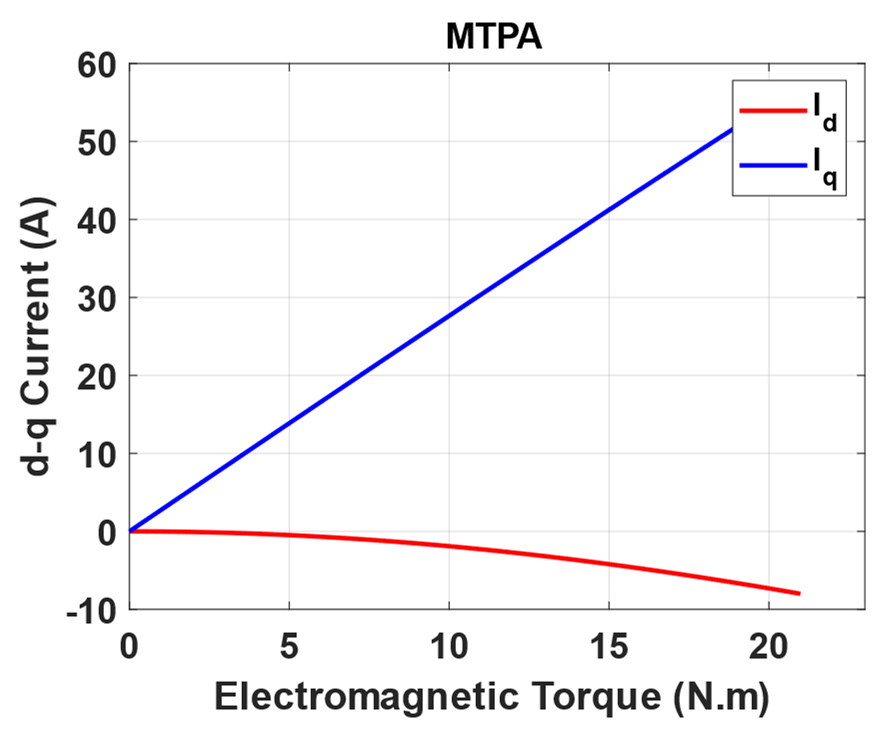

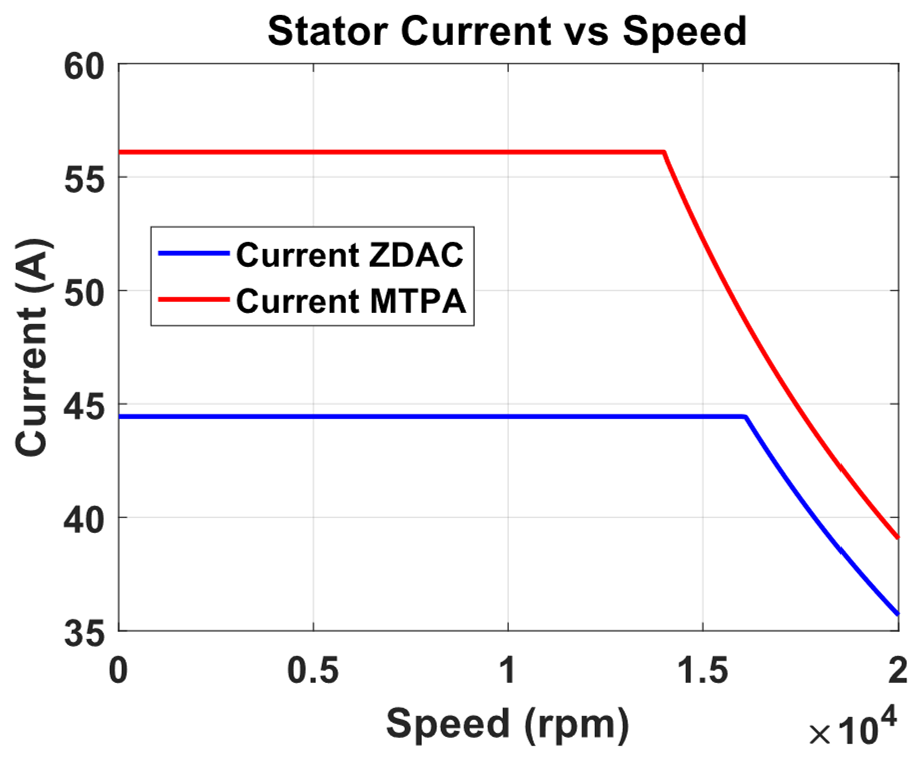



| Parameter | Description | Value | Unit |
|---|---|---|---|
| p | Number of pole pairs | 5 | - |
| Rs | Stator resistance | 0.10087 | Ω |
| Rc | Core resistance | 27 | Ω |
| Lq | q-axis inductance | 2.4 × 10−4 | H |
| Ld | d-axis inductance | 1.2 × 10−4 | H |
| Pmax | Maximum output power | 35 | kW |
| λpm | Permanent magnet linkage flux | 0.048 | Wb |
| Nmax | Maximum speed | 20,000 | rpm |
| Tr | Rated torque | 16 | N.m |
| Tmax | Max torque | 21 | N.m |
| Test Case | Reference Speed (rpm) |
|---|---|
| A | 2000 |
| B | 6000 |
| C | 10,000 |
| D | 14,000 |
| E | 16,000 |
| F | 18,000 |
| G | 20,000 |
| Test Case | Average Torque (N·m) ZDAC Strategy | Average Torque (N·m) Optimal Control Strategy | Improvement (%) |
|---|---|---|---|
| A | 16.66 | 21.25 | 27.53 |
| B | 15.7 | 18.55 | 18.21 |
| C | 16 | 19.89 | 24.31 |
| D | 15.9 | 20.2 | 27.04 |
| E | 16 | 17.3 | 8.13 |
| F | 5.7 | 7.3 | 28.07 |
| G | 4.9 | 5.9 | 20.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, M.; Järg, O.; Seppago, R.; Rassõlkin, A. Performance Optimization of a High-Speed Permanent Magnet Synchronous Motor Drive System for Formula Electric Vehicle Application. Sensors 2025, 25, 3156. https://doi.org/10.3390/s25103156
Ibrahim M, Järg O, Seppago R, Rassõlkin A. Performance Optimization of a High-Speed Permanent Magnet Synchronous Motor Drive System for Formula Electric Vehicle Application. Sensors. 2025; 25(10):3156. https://doi.org/10.3390/s25103156
Chicago/Turabian StyleIbrahim, Mahmoud, Oskar Järg, Raigo Seppago, and Anton Rassõlkin. 2025. "Performance Optimization of a High-Speed Permanent Magnet Synchronous Motor Drive System for Formula Electric Vehicle Application" Sensors 25, no. 10: 3156. https://doi.org/10.3390/s25103156
APA StyleIbrahim, M., Järg, O., Seppago, R., & Rassõlkin, A. (2025). Performance Optimization of a High-Speed Permanent Magnet Synchronous Motor Drive System for Formula Electric Vehicle Application. Sensors, 25(10), 3156. https://doi.org/10.3390/s25103156







