AdapTree: Data-Driven Approach to Assessing Plant Stress Through the AI-Sensor Synergy
Abstract
1. Introduction
- To collect and analyze multimodal sensor data (temperature, humidity, and EIS) under various environmental stress conditions.
- To identify and predict stress-induced physiological responses in plants using machine learning.
- To propose a novel ensemble learning model for enhanced prediction accuracy.
- To evaluate the efficacy of the proposed model against conventional regression techniques for plant stress prediction.
2. Materials and Methods
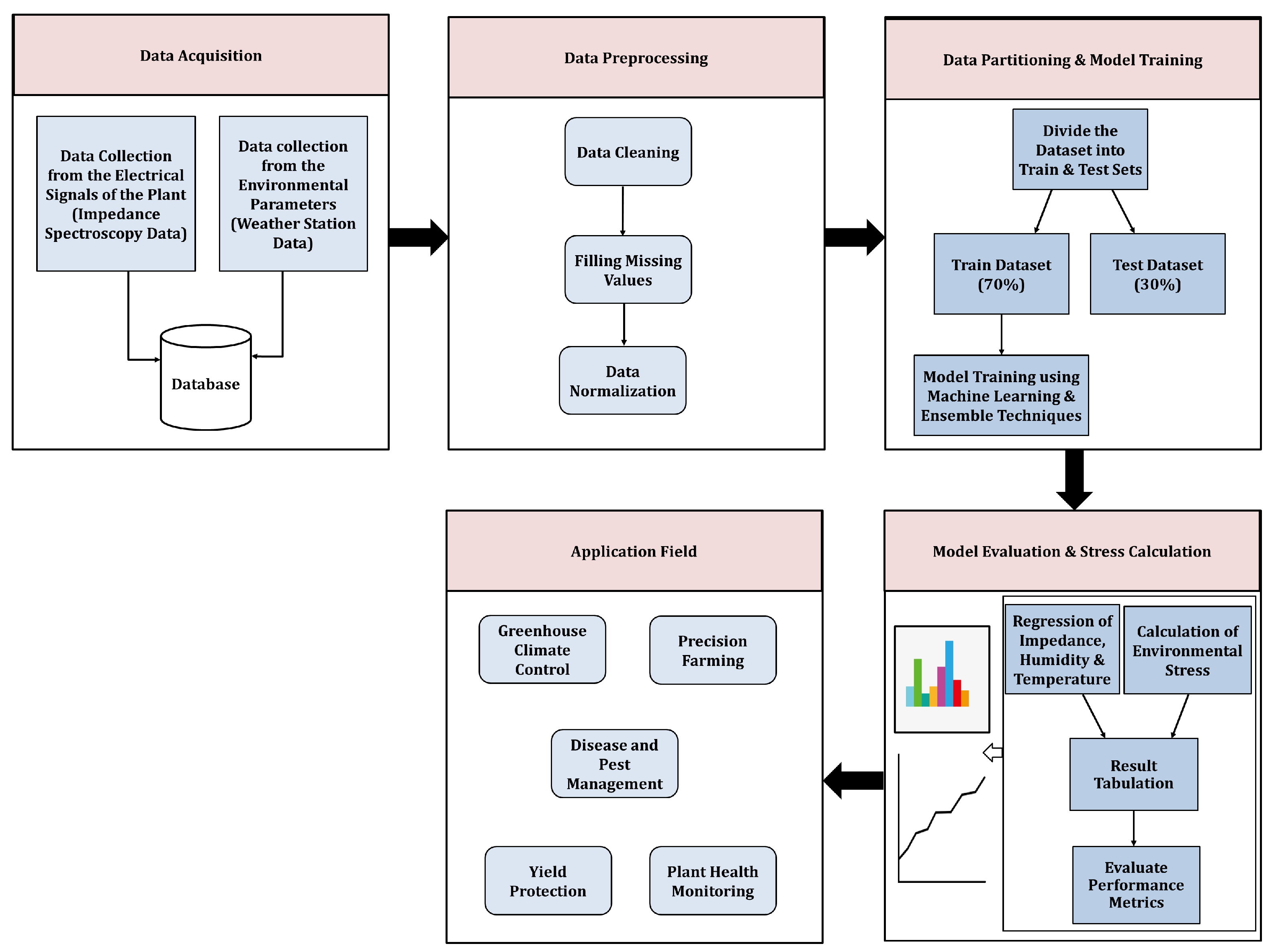
2.1. Experimental Setup and Data Acquisition
- Gravimetric System:An advanced gravimetric plant monitoring system was employed as the primary setup for automated whole-plant phenotyping. This system captured data related to plant weight and water use efficiency, leveraging the gravimetric method, which is widely recognized for its ability to reflect plant health and growth patterns [18,19]. Monitoring water usage further enabled insights into the physiological status and development of the plant.
- Four-Point-Probe Electrical Impedance Spectroscopy System:Alongside the gravimetric system, novel four-point probe impedance spectroscopy measurements were conducted. These measurements continuously gathered data directly from the plant stem over periods ranging from weeks to two months. The setup, detailed and modeled in [16], used a four-point probe configuration to ensure accuracy and reliability. Impedance magnitude and phase values were collected spanning the frequency range of 50 Hz to 2 MHz, with samples taken every 9 min.
- Environmental Monitoring in Greenhouse:The experimental work took place in a controlled greenhouse facility at Tel Aviv University, Israel. This environment, although located outdoors and naturally lit, was systematically regulated for temperature and humidity. The tobacco plant used in the study was connected to the impedance system and monitored throughout the experiment. Around 15 young tobacco plants, cultivated for 3–4 months, were used in the study. These plants had stem diameters ranging from 0.7 to 1.1 cm and an overall height of approximately 0.7 to 1 m. They were cultivated in 3.9 L pots containing coarse sand. The Vapor Pressure Deficit (VPD) within the greenhouse was continuously monitored and exhibited consistent patterns over multiple days. Each pot was irrigated daily during the nighttime hours (around 9PM) with 2 L of water to ensure saturation and promote healthy plant development. A centrally located weather station within the greenhouse continuously recorded vital environmental parameters such as plant weight, Relative Humidity (RH), temperature, Volumetric Water Content (VWC), and Vapor Pressure Deficit (VPD). These readings supported the identification of plant stress and optimization of growing conditions.
2.2. Data Pre-Processing and Model Training
2.2.1. Data Analysis
2.2.2. Data Preparation
- Handling Missing Values:Missing entries were imputed using hot-deck imputation, which involves substituting null values with data from a similar entry within the dataset [20].
- Data Standardization:Each data sample was individually normalized to the unit norm, rescaling values to a common range, usually between 0 and 1.
- Dividing the Dataset into Train and Test Units:The dataset was split into 70% for training (557,781 instances) and 30% for testing (239,049 instances) to develop and assess the machine learning models.
2.3. Model Training
- Decision Tree (DT):The Decision Tree (DT) regressor operates by iteratively dividing the input data into increasingly smaller subsets based on a set of splitting criteria until each subset consists of data points that share similar values of the target variable. The splitting criteria are chosen based on a measure of impurity or error, such as mean absolute or squared error. Once built, predictions for new data points are generated by navigating the tree from the root to the leaf node, where predicted output is the mean or median of training examples in that leaf node. Decision tree regressors can be prone to overfitting [21].
- K-Nearest Neighbors (KNN):KNN regression is a non-parametric algorithm in machine learning. It forecasts a new instance by considering k close neighbors and averaging their target values. The k parameter requires fine-tuning to avoid overfitting [22].
- Multivariate Linear Regression (MLR):In MLR, the model can be represented by a set of linear equations, one for each dependent variable. Multivariate linear regression aims to estimate the coefficients that reduce the difference between observed values and the model’s predicted values across all dependent variables. This is typically achieved using techniques such as least squares regression, which reduces the total sum of squared errors across all dependent variables [23]. The equation for MLR is:where: denote the dependent variables and represent independent variables. are the coefficients for the independent variables, in the equation for dependent variable , are the intercepts for each dependent variable and represents the error terms for each dependent variable.
- AdaBoost:The AdaBoost regressor is an adaptive method that adjusts the weights of individual models to enhance overall system performance. It combines several weak learning models to construct a robust and precise model. In every iteration, a weak learning model is trained using a subset of the training data, and its efficacy is assessed. Instances misclassified by the weak model are assigned higher weights, and this process repeats until the desired level of accuracy is obtained. The final prediction is the weighted mean of all weak model predictions [24].
- Multi-Layer Perceptron (MLP):An MLP regressor comprises several layers of nodes (neurons) connected by weighted edges, where every node in one layer is connected to each node in adjacent layers. It processes input values through a series of hidden layers, each applying an activation function to the weighted sum of its inputs [21].
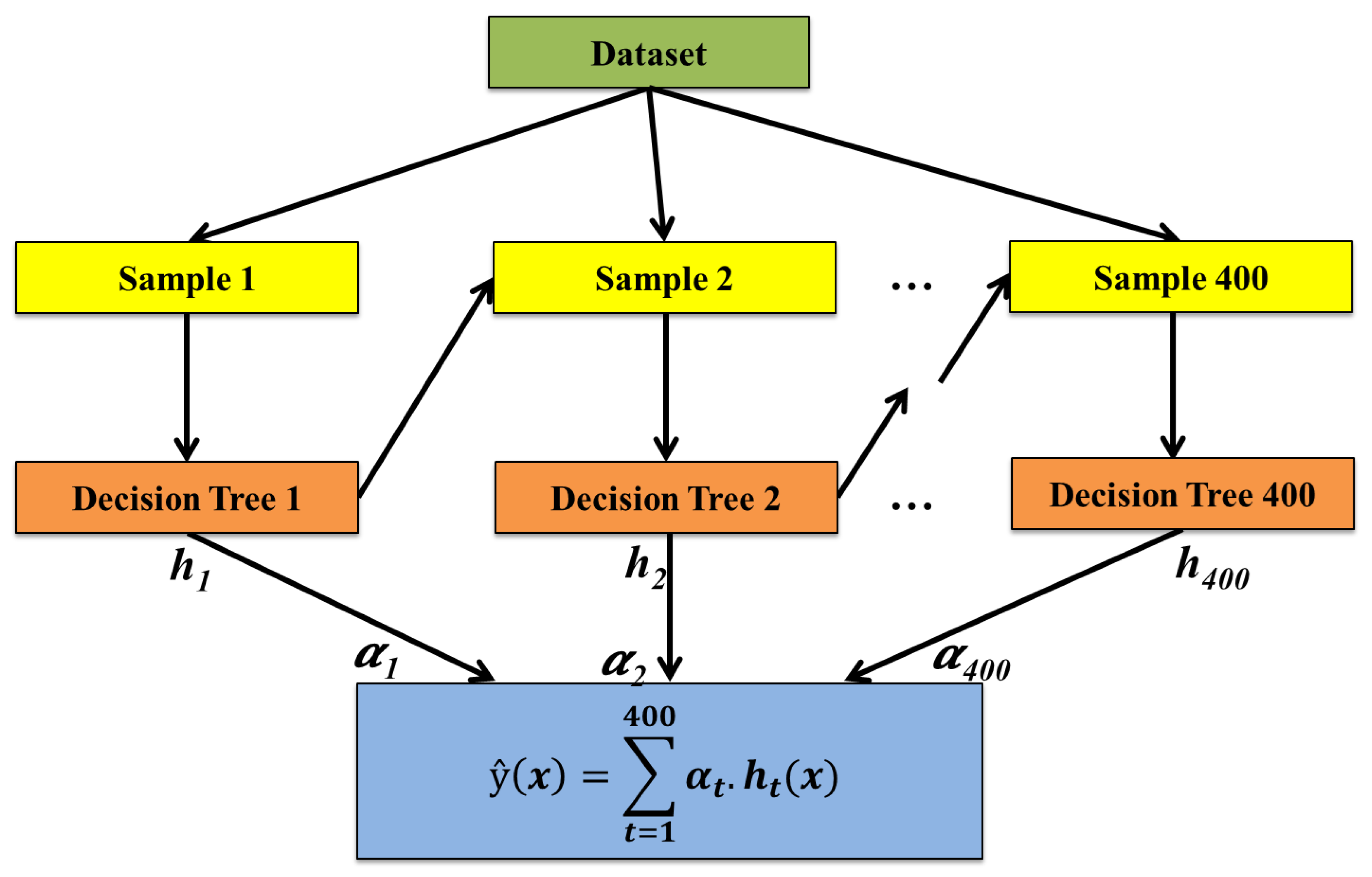
2.3.1. Proposed Boosting-Based Ensemble Approach: AdapTree (Adaptive Boosted Tree for Plant Stress Analysis)
- Step 1: Create the base model. The first step is to define the base model. The base model serves as the weak learner in the ensemble. The choice of the base learner allows for capturing non-linear relationships and interactions between variables.
- Step 2: Initialize weights and train the first model. Initialize weights for all training samples equally. Train the base model on the weighted training dataset. The initial model will be focused on minimizing errors across the dataset.
- Step 3: Compute model errors and update weights. After training the first base model, compute the errors for each training instance. Increase the weights of incorrectly predicted samples so that the next model focuses more on these challenging cases. Update the weights accordingly to reflect the importance of each sample.
- Step 4: Train subsequent models. Train additional base models in sequence, where every model focuses on the errors of the predecessor model. Each new model is trained on a modified dataset with updated weights to emphasize the mistakes made by earlier models.
- Step 5: Aggregate models using boosting algorithm. Combine the predictions from all trained base models using the boosting algorithm. The boosting algorithm assigns a weight to each model based on its accuracy, and the final prediction is computed as a weighted sum of individual model predictions from all models.
- Step 6: Make the final prediction. Use the aggregated predictions to make the final prediction. The combined output from the boosting algorithm will result from the weighted majority vote or the weighted sum of the predictions made by all the base learners.
2.3.2. Plant Stress Calculation
3. Results and Discussion
- Mean Absolute Error (MAE):The MAE represents average absolute differences between predicted and actual values.where n stands for the total number of observations, denotes the actual value of the output variable, and denotes the predicted value of the output variable.
- Mean Squared Error (MSE):The MSE computes the average of squared differences between predicted and actual values.
- Root Mean Squared Error (RMSE):The RMSE represents the square root of the MSE and quantifies the standard deviation of the differences between predicted and actual values.
- Pearson Correlation Coefficient (PCC):The PCC calculates the covariance between two variables, measuring how much the variables vary together. The value of the PCC ranges between −1 and +1. It is calculated using the formula:where: X and Y represent the two variables being analyzed, and denote their respective means, n represents the total number of observations, and and represent the standard deviations of X and Y, respectively. When the PCC approaches 1, it signifies a strong positive linear correlation between the variables, suggesting that as one variable rises, the other typically increases too. Conversely, a PCC close to –1 represents a strong negative relationship, meaning that as one variable increases, other typically decreases.
- R-Square ():The R-squared measures the proportion of variability in the output variable explained by the input variables in the model.where: represents the sum of squared residuals, representing the sum of squared differences between actual and predicted values, and represents the total sum of squares, representing the sum of squared differences between actual values and mean of the output variable. A higher R-squared indicates better model performance.
Comparison with the Baseline Studies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ML | Machine Learning |
| EIS | Electrical Impedance Spectroscopy |
| UAV | Unmanned Aerial Vehicle |
| CWSI | Crop Water Stress Index |
| SVM | Support Vector Machines |
| VPD | Vapor Pressure Deficit |
| RH | Relative Humidity |
| VWC | Volumetric Water Content |
| AC | Alternating Current |
| KNN | K-Nearest Neighbors |
| DT | Decision Tree |
| MLR | Multivariate Linear Regression |
| MLP | Multi-Layer Perceptron |
| AdapTree | Adaptive Boosted Tree for Plant Stress Analysis |
| ESI | Environmental Stress Index |
| T | Temperature |
| PI | Plant Impedance |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| PCC | Pearson Correlation Coefficient |
| R2 | R-Squared |
References
- Mathur, S.; Agrawal, D.; Jajoo, A. Photosynthesis: Response to high temperature stress. J. Photochem. Photobiol. B Biol. 2014, 137, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Szymańska, R.; Ślesak, I.; Orzechowska, A.; Kruk, J. Physiological and biochemical responses to high light and temperature stress in plants. Environ. Exp. Bot. 2017, 139, 165–177. [Google Scholar] [CrossRef]
- Fanourakis, D.; Aliniaeifard, S.; Sellin, A.; Giday, H.; Körner, O.; Nejad, A.R.; Delis, C.; Bouranis, D.; Koubouris, G.; Kambourakis, E.; et al. Stomatal behavior following mid-or long-term exposure to high relative air humidity: A review. Plant Physiol. Biochem. 2020, 153, 92–105. [Google Scholar] [CrossRef]
- Neethirajan, S. Transforming the adaptation physiology of farm animals through sensors. Animals 2020, 10, 1512. [Google Scholar] [CrossRef]
- Anwer, S. Evaluation of Wearable Sensors for Noninvasive Real-Time Assessment of Physical Fatigue Using Physiological and Biomechanical Parameters Among Construction Workers. 2022. Available online: https://theses.lib.polyu.edu.hk/handle/200/11587 (accessed on 31 March 2025).
- Zhang, L.; Zhang, H.; Niu, Y.; Han, W. Mapping maize water stress based on UAV multispectral remote sensing. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Lee, G.; Wei, Q.; Zhu, Y. Emerging wearable sensors for plant health monitoring. Adv. Funct. Mater. 2021, 31, 2106475. [Google Scholar] [CrossRef]
- Singh, A.K.; Dhanapal, S.; Yadav, B.S. The dynamic responses of plant physiology and metabolism during environmental stress progression. Mol. Biol. Rep. 2020, 47, 1459–1470. [Google Scholar] [CrossRef]
- Patel, A.; Machal, M. Chapter-3 Use of High Throughput Phenotyping Techniques for Crop Production under Different Abiotic Stresses. In Plant Physiology Unraveling the Science of Plant Life; Elite: New Delhi, India; p. 35.
- Hamed, K.B.; Zorrig, W.; Hamzaoui, A.H. Electrical impedance spectroscopy: A tool to investigate the responses of one halophyte to different growth and stress conditions. Comput. Electron. Agric. 2016, 123, 376–383. [Google Scholar] [CrossRef]
- Kashyap, B.; Kumar, R. Sensing methodologies in agriculture for monitoring biotic stress in plants due to pathogens and pests. Inventions 2021, 6, 29. [Google Scholar] [CrossRef]
- Liew, O.W.; Chong, P.C.J.; Li, B.; Asundi, A.K. Signature optical cues: Emerging technologies for monitoring plant health. Sensors 2008, 8, 3205–3239. [Google Scholar] [CrossRef]
- Wang, M.; Wang, R.; Mur, L.A.J.; Ruan, J.; Shen, Q.; Guo, S. Functions of silicon in plant drought stress responses. Hortic. Res. 2021, 8, 254. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, U.K.; Meher, P.K.; Naha, S.; Rao, A.R.; Kumar, U.; Pal, S.; Gupta, A. ASmiR: A machine learning framework for prediction of abiotic stress–specific miRNAs in plants. Funct. Integr. Genom. 2023, 23, 92. [Google Scholar] [CrossRef]
- Akbari, M.; Sabouri, H.; Sajadi, S.J.; Yarahmadi, S.; Ahangar, L. Classification and prediction of drought and salinity stress tolerance in barley using GenPhenML. Sci. Rep. 2024, 14, 17420. [Google Scholar] [CrossRef]
- Bar-On, L.; Garlando, U.; Sophocleous, M.; Jog, A.; Motto Ros, P.; Sade, N.; Avni, A.; Shacham-Diamand, Y.; Demarchi, D. Electrical modelling of in-vivo impedance spectroscopy of nicotiana tabacum plants. Front. Electron. 2021, 2, 753145. [Google Scholar] [CrossRef]
- Bar-On, L. Plant Electrical Study for Biosensing and Communication. Ph.D. Thesis, Tel-Aviv University, Tel Aviv, Israel, 2024. [Google Scholar]
- PlantArray, DiTech Ltd. Available online: https://www.plant-ditech.com/products/plantarray (accessed on 31 March 2025).
- Dalal, A.; Shenhar, I.; Bourstein, R.; Mayo, A.; Grunwald, Y.; Averbuch, N. A High-Throughput Gravimetric Phenotyping Platform for Real-Time Physiological Screening of Plant–Environment Dynamic Responses. bioRxiv 2020. [Google Scholar] [CrossRef]
- Andridge, R.R.; Little, R.J. A review of hot deck imputation for survey non-response. Int. Stat. Rev. 2010, 78, 40–64. [Google Scholar] [CrossRef]
- Kruse, R.; Mostaghim, S.; Borgelt, C.; Braune, C.; Steinbrecher, M. Multi-layer perceptrons. In Computational Intelligence: A Methodological Introduction; Springer: Berlin/Heidelberg, Germany, 2022; pp. 53–124. [Google Scholar]
- Parker, W.S. Ensemble modeling, uncertainty and robust predictions. Wiley Interdiscip. Rev. Clim. Change 2013, 4, 213–223. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Schapire, R.E. Explaining adaboost. In Empirical Inference: Festschrift in Honor of Vladimir N. Vapnik; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–52. [Google Scholar]
- Stack Exchange, Cross Validated. Available online: https://stats.stackexchange.com/questions/545979/why-getting-very-high-values-for-mse-mae-mape-when-r2-score-is-verygood (accessed on 31 March 2025).
- Azrai, M.; Aqil, M.; Andayani, N.; Efendi, R.; Suarni; Suwardi; Jihad, M.; Zainuddin, B.; Salim; Bahtiar; et al. Optimizing ensembles machine learning, genetic algorithms, and multivariate modeling for enhanced prediction of maize yield and stress tolerance index. Front. Sustain. Food Syst. 2024, 8, 1334421. [Google Scholar] [CrossRef]
- Chandel, N.S.; Chakraborty, S.K.; Chandel, A.K.; Dubey, K.; Jat, D.; Rajwade, Y.A. State-of-the-art AI-enabled mobile device for real-time water stress detection of field crops. Eng. Appl. Artif. Intell. 2024, 131, 107863. [Google Scholar] [CrossRef]
- Sharma, V.; Honkavaara, E.; Hayden, M.; Kant, S. UAV remote sensing phenotyping of wheat collection for response to water stress and yield prediction using machine learning. Plant Stress 2024, 12, 100464. [Google Scholar] [CrossRef]
- Singh, R.; Krishnan, P.; Bharadwaj, C.; Sah, S.; Das, B. Optimizing chickpea yield prediction under wilt disease through synergistic integration of biophysical and image parameters using machine learning models. Sci. Rep. 2025, 15, 4417. [Google Scholar] [CrossRef] [PubMed]

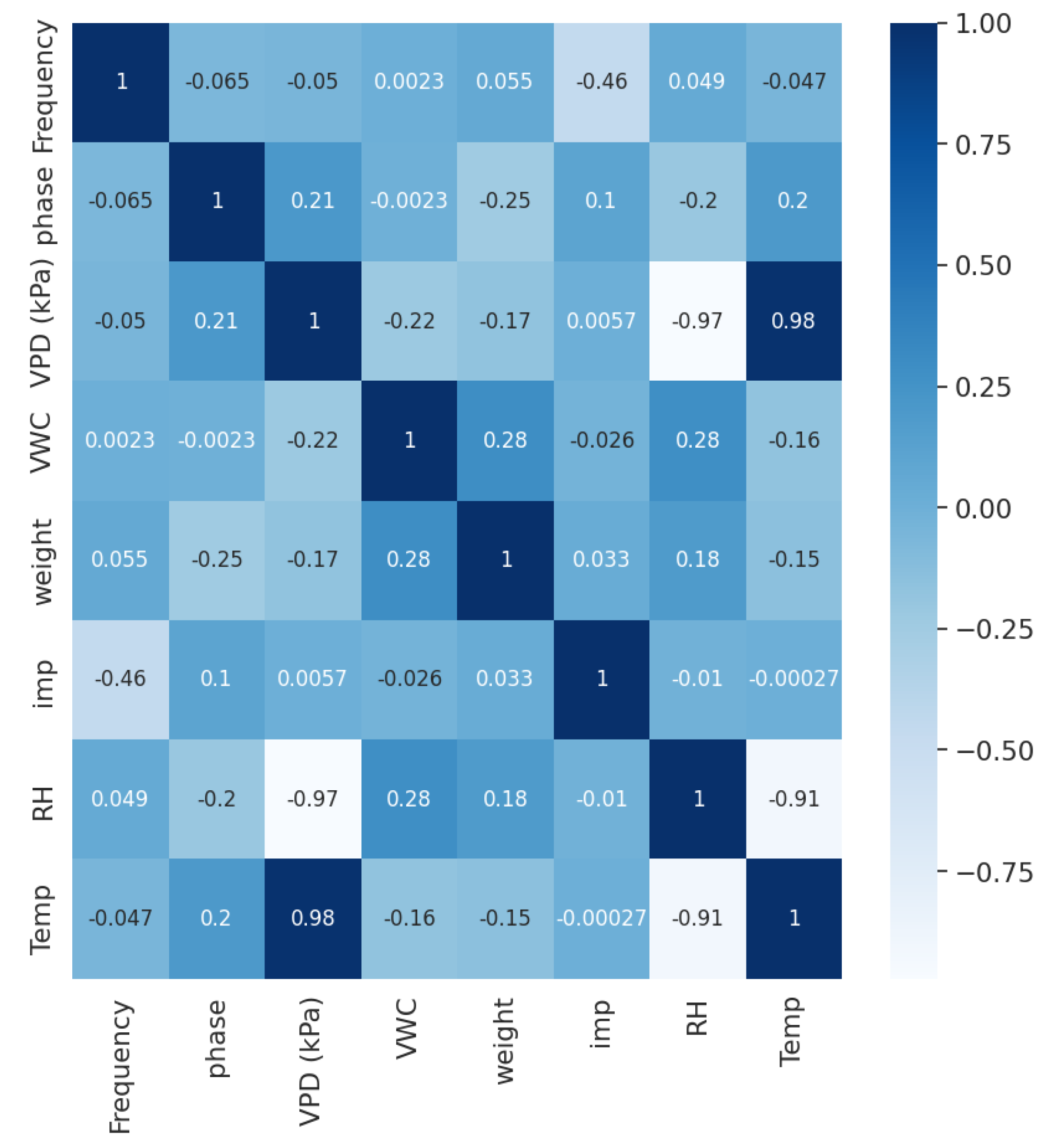
| Experimental Systems | Gathered Parameter | Description | Units | Range |
|---|---|---|---|---|
| Impedance Spectroscopy Setup | Frequency | The frequency value at which measurements were collected. | Hertz (Hz) | 50 to 3,940,000 |
| Impedance Magnitude (Impedance) | Ratio between the Alternating Current (AC) voltage to the AC phasors. | Ohm () | 282.3103 to 7958.325 | |
| Impedance Phase (Phase) | The delay of the angular component of a periodic wave vs. that of the excitation. | Degree (°) | −40.232 to −3.127 | |
| Gravimetric Plant Array System | Plant Weight | The weight of the plant. | Kilograms (kg) | 0.54347 to 1.14102 |
| Volumetric Water Content (VWC) | The amount of water present in a given volume of soil. | Percentage (%) | 0.02961 to 0.18781 | |
| Environmental Parameters | Relative Humidity (RH) | The proportion of water vapor present in air to the maximum amount the air can hold. | Percentage (%) | 27.5 to 91.8 |
| Temperature | The temperature at which the plant is maintained. | Degree Celsius (°C) | 19 to 30 | |
| Vapor Pressure Deficit (VPD) | The difference between the moisture content in the air and the maximum amount of moisture the air can hold. | Kilopascal (kPa) | 0.19159 to 3.07549 |
| Explanatory Variables | Outcome Variables | ||||||
|---|---|---|---|---|---|---|---|
| Frequency | Phase | VPD | VWC | Weight | Impedance | RH | Temperature |
| 1,000,000 | −20.541 | 0.44159 | 0.18251 | 1.01719 | 327 | 81.1 | 20 |
| 101 | −3.563 | 0.29206 | 0.18429 | 1.01821 | 4529.482 | 87.5 | 20 |
| 1010 | −16.043 | 0.28972 | 0.1835 | 1.0172 | 3892.253 | 87.6 | 20 |
| 10,100 | −32.47 | 0.32935 | 0.18468 | 1.01668 | 1869.21 | 85 | 19 |
| 101,000 | −34.239 | 0.54206 | 0.18291 | 1.01812 | 785.5841 | 76.8 | 20 |
| 1020 | −15.933 | 0.34252 | 0.18311 | 1.01747 | 3821.377 | 84.4 | 19 |
| 10,200 | −32.441 | 0.25234 | 0.18291 | 1.01771 | 1846.688 | 89.2 | 20 |
| 102,000 | −34.205 | 0.24767 | 0.18311 | 1.01713 | 775.136 | 89.4 | 20 |
| S.No. | Model | Tuning Parameters |
|---|---|---|
| 1 | DT | criterion = ‘gini’ |
| 2 | KNN | n_neighbors = 2 |
| 3 | MLR | fit_intercept = True; n_jobs = −1; max_iter = 1000; tol = 0.0001 |
| 4 | AdaBoost | n_estimators = 100 |
| 5 | MLP | hidden_layer_sizes = (20, 30); max_iter = 200; alpha = 0.001; solver = ‘adam’ |
| Regression Models | R-Square | MSE | RMSE | MAE | Pearson Coefficient |
|---|---|---|---|---|---|
| MLP | 0.957907 | 161,561.5 | 401.9472 | 288.1211 | 0.978876 |
| MLR | 0.224172 | 2,977,801 | 1725.631 | 1523.617 | 0.473478 |
| DT | 0.981457 | 26,471.97 | 162.7021 | 33.40362 | 0.992099 |
| AdaBoost | 0.936375 | 245,359.1 | 495.3374 | 347.8731 | 0.96841 |
| KNN | 0.982715 | 66,658.18 | 258.1824 | 114.5485 | 0.991329 |
| Proposed | 0.993125 | 19,812.34 | 134.565 | 22.789 | 0.996564 |
| Regression Models | R-Square | MSE | RMSE | MAE | Pearson Coefficient |
|---|---|---|---|---|---|
| MLP | 0.629311 | 179.5437 | 13.39939 | 8.703461 | 0.79441 |
| MLR | 0.948011 | 25.18098 | 5.018066 | 4.064481 | 0.973659 |
| DT | 0.996941 | 0.00031 | 0.017612 | 8.24 × 10−5 | 0.998189 |
| AdaBoost | 0.995829 | 2.020256 | 1.421357 | 1.13163 | 0.997971 |
| KNN | 0.993734 | 3.035085 | 1.74215 | 1.221362 | 0.996878 |
| Proposed | 0.999999 | 4.85 × 10−5 | 0.006966 | 1.51 × 10−5 | 0.999999 |
| Regression Models | R-Square | MSE | RMSE | MAE | Pearson Coefficient |
|---|---|---|---|---|---|
| MLP | 0.505675 | 7.939475 | 2.817707 | 2.044328 | 0.711635 |
| MLR | 0.965393 | 0.555825 | 0.745537 | 0.62162 | 0.982544 |
| DT | 0.999998 | 3.76 × 10−5 | 0.006136 | 3.76 × 10−5 | 0.99999 |
| AdaBoost | 0.989251 | 0.172641 | 0.415501 | 0.382264 | 0.994867 |
| KNN | 0.987155 | 0.206302 | 0.454205 | 0.26097 | 0.993566 |
| Proposed | 0.999998 | 2.51 × 10−5 | 0.0050099 | 2.51 × 10−5 | 0.9999992 |
| Author Name (Year) | Stress Parameter | Plant Type | Models Employed | Results Achieved |
|---|---|---|---|---|
| Pradhan et al. (2023) [14] | Cold Drought Heat Salt | - | SVM | Cold Accuracy: 84.57% Drought Accuracy: 80.62% Heat Accuracy: 80.38% Salt Accuracy: 82.78% |
| Akbari et al. (2024) [15] | Drought | Barley | Neural Network | MAE: 0.0727 RMSE: 0.0105 R2: 0.9999 |
| Akbari et al. (2024) [15] | Salinity | Barley | GenPhenML | MAE: 0.1206 RMSE: 0.0308 R2: 0.9995 |
| Azrai et al. (2024) [26] | Drought | Maize | Ensemble KNN | Stress Tolerance Index: 0.82 |
| Chandel et al. (2024) [27] | Water | Maize Wheat | GoogLeNet | Maize Accuracy: 97.9% Wheat Accuracy: 92.9% |
| Sharma et al. (2024) [28] | Water | Wheat | H2O-3 Deep Learning Model | R2: 0.80 |
| Singh et al. (2025) [29] | Biotic (Wilt Disease) | Chickpea | Extreme Gradient Boosting | R2: 0.99 RMSE: 0.72 |
| Proposed | Impedance | Tobacco | AdapTree | MAE: 22.789 RMSE: 134.565 R2: 0.993125 |
| Humidity | MAE: 1.51 × RMSE: 0.006966 R2: 0.999999 | |||
| Temperature | MAE: 2.51 × RMSE: 0.0050099 R2: 0.999998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, D.; Singh, H.; Shacham-Diamand, Y. AdapTree: Data-Driven Approach to Assessing Plant Stress Through the AI-Sensor Synergy. Sensors 2025, 25, 3149. https://doi.org/10.3390/s25103149
Garg D, Singh H, Shacham-Diamand Y. AdapTree: Data-Driven Approach to Assessing Plant Stress Through the AI-Sensor Synergy. Sensors. 2025; 25(10):3149. https://doi.org/10.3390/s25103149
Chicago/Turabian StyleGarg, Divisha, Harpreet Singh, and Yosi Shacham-Diamand. 2025. "AdapTree: Data-Driven Approach to Assessing Plant Stress Through the AI-Sensor Synergy" Sensors 25, no. 10: 3149. https://doi.org/10.3390/s25103149
APA StyleGarg, D., Singh, H., & Shacham-Diamand, Y. (2025). AdapTree: Data-Driven Approach to Assessing Plant Stress Through the AI-Sensor Synergy. Sensors, 25(10), 3149. https://doi.org/10.3390/s25103149








