Exploitation of Modal Superposition Toward Forced Vibration Localization in a Coupled Symmetric Oscillator Array
Abstract
1. Introduction
2. Methods and Model
2.1. Perturbation Theory
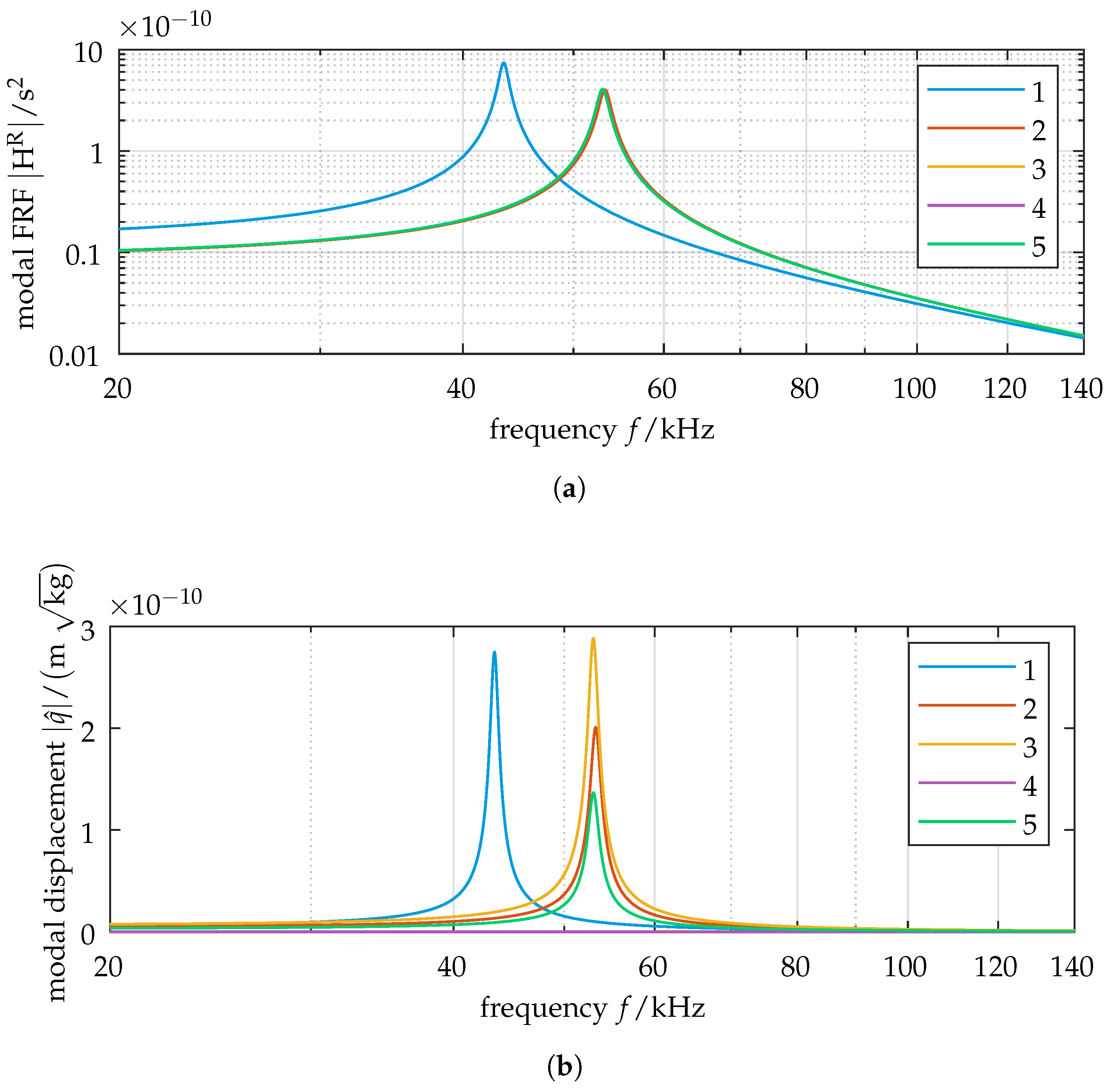
2.2. Frequency Response in Modal Context
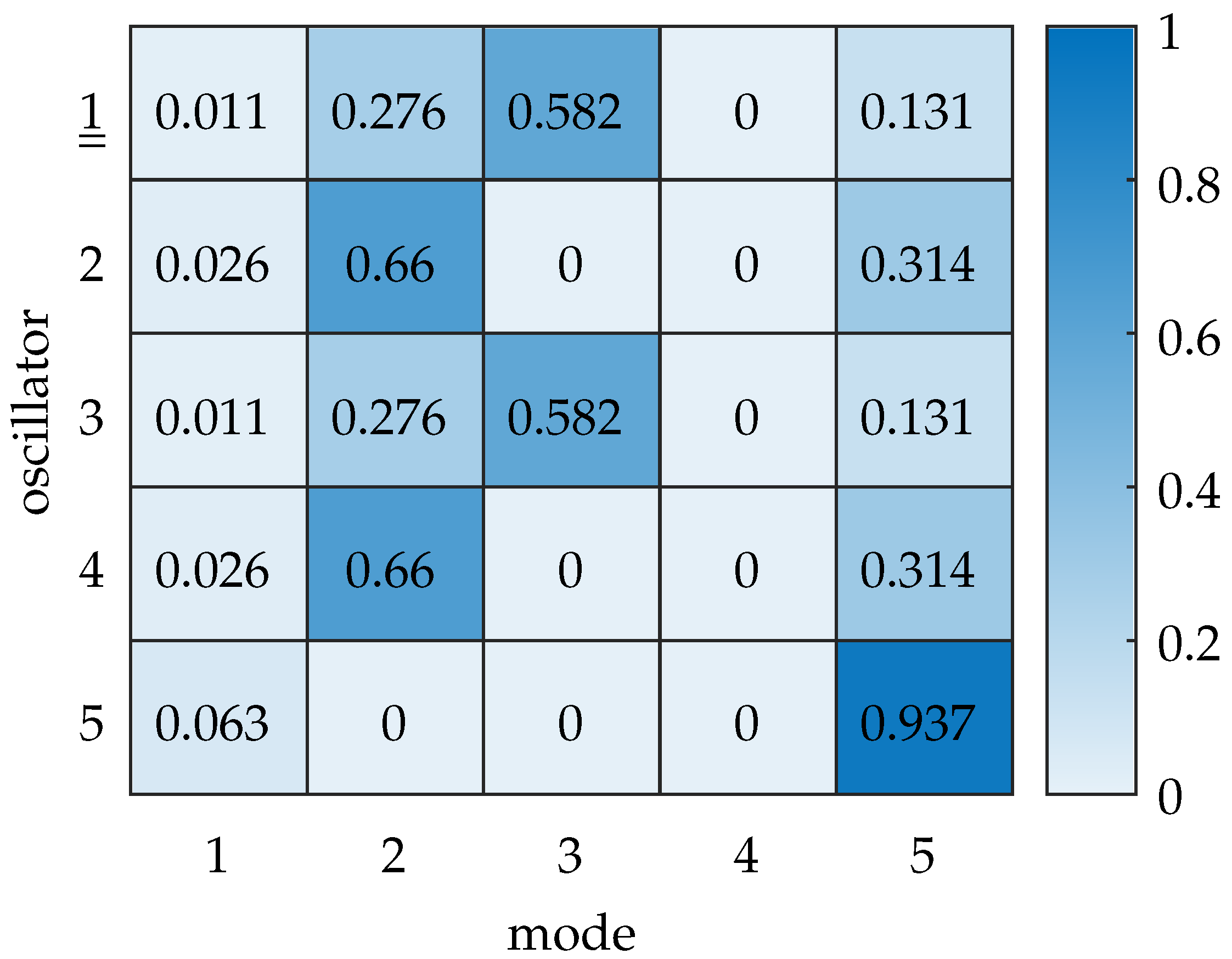
2.3. Modal Contribution Matrix
2.4. Lumped-Parameter Model: A Highly Coupled System
2.4.1. Symmetric Setup
2.4.2. Disordered Model
3. Investigation of the Symmetric System: Results
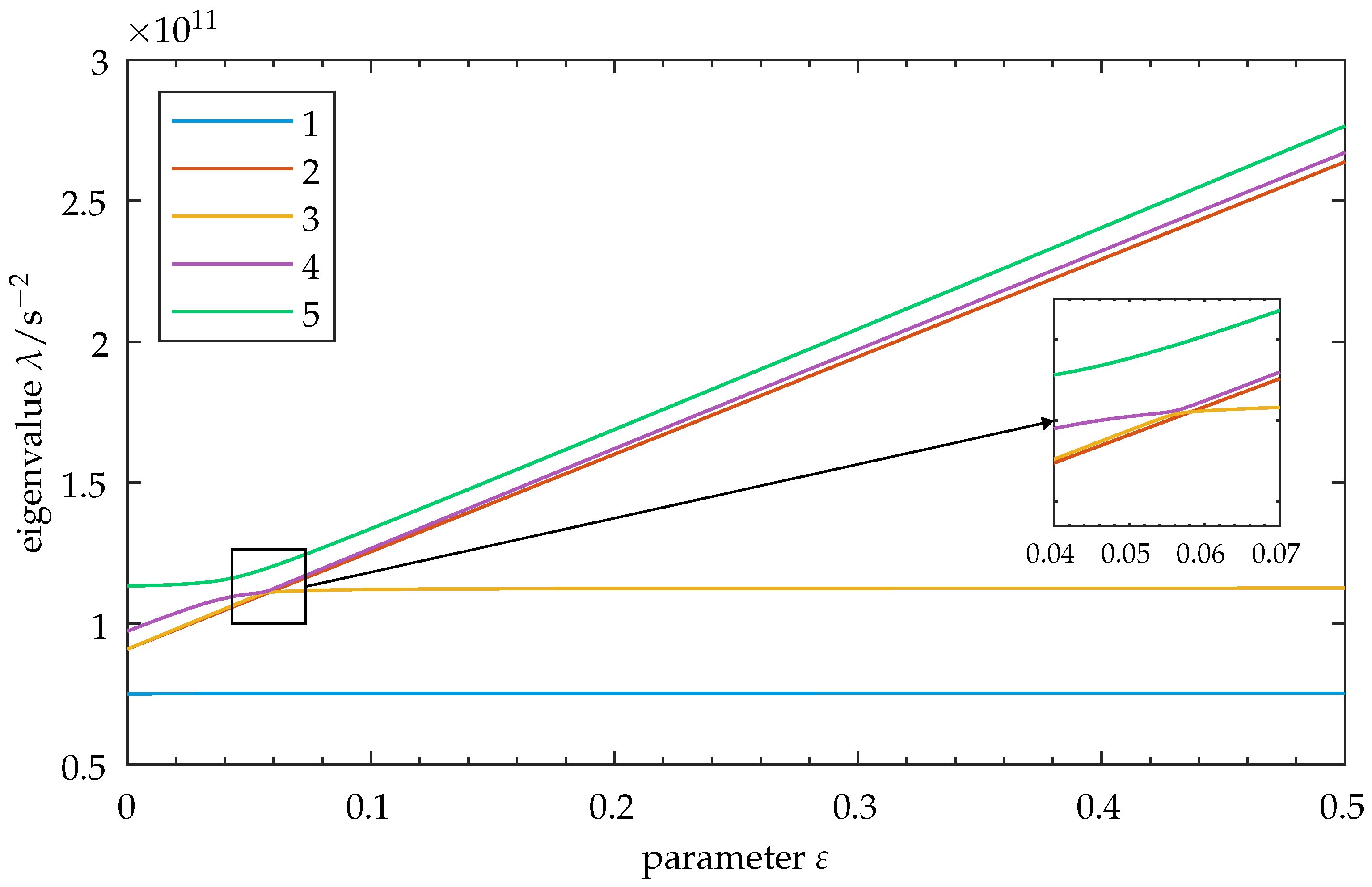
3.1. Parameter Variation: Increase in Coupling Stiffness
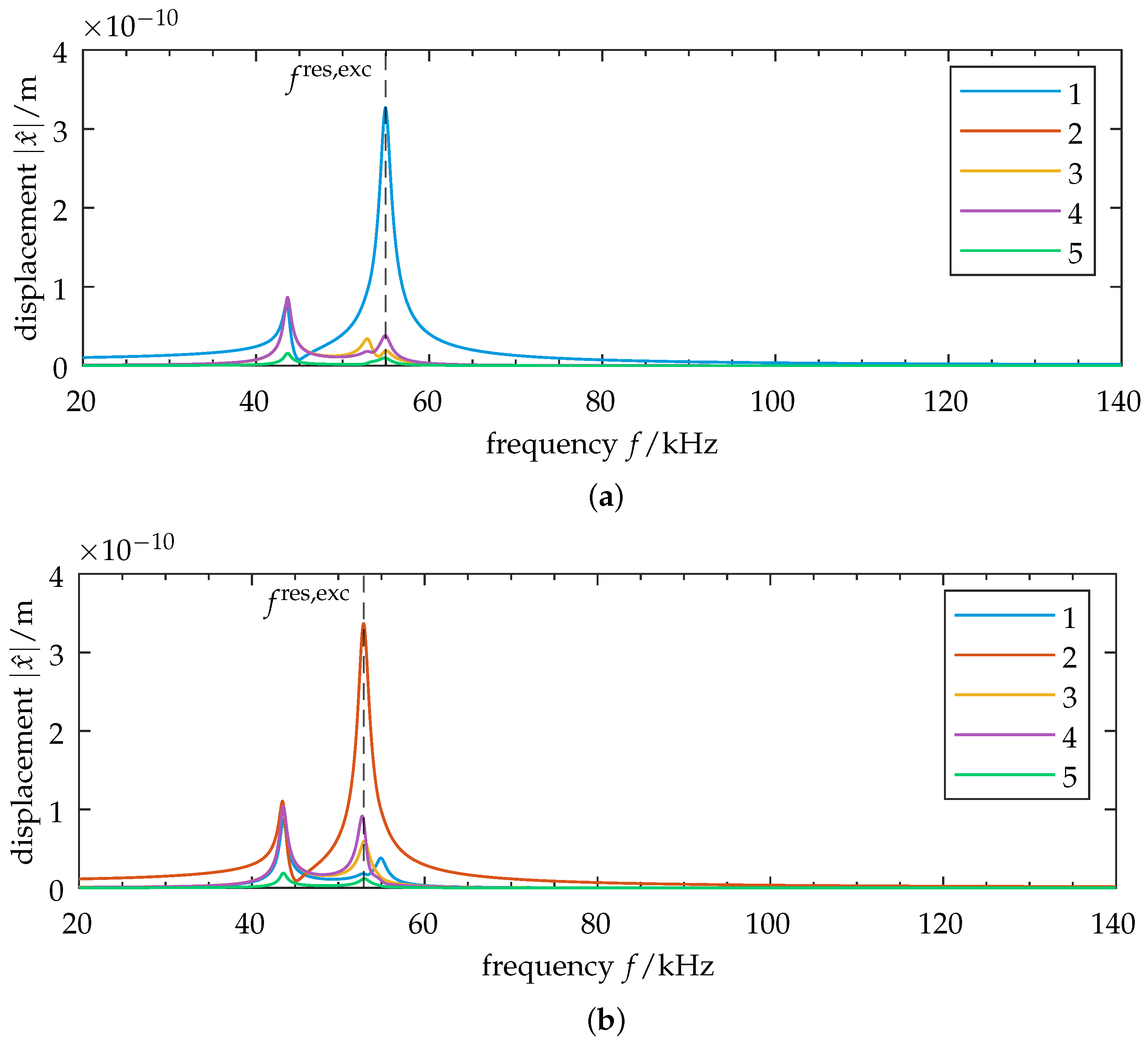
3.2. Effects of Coupling on the Forced Response
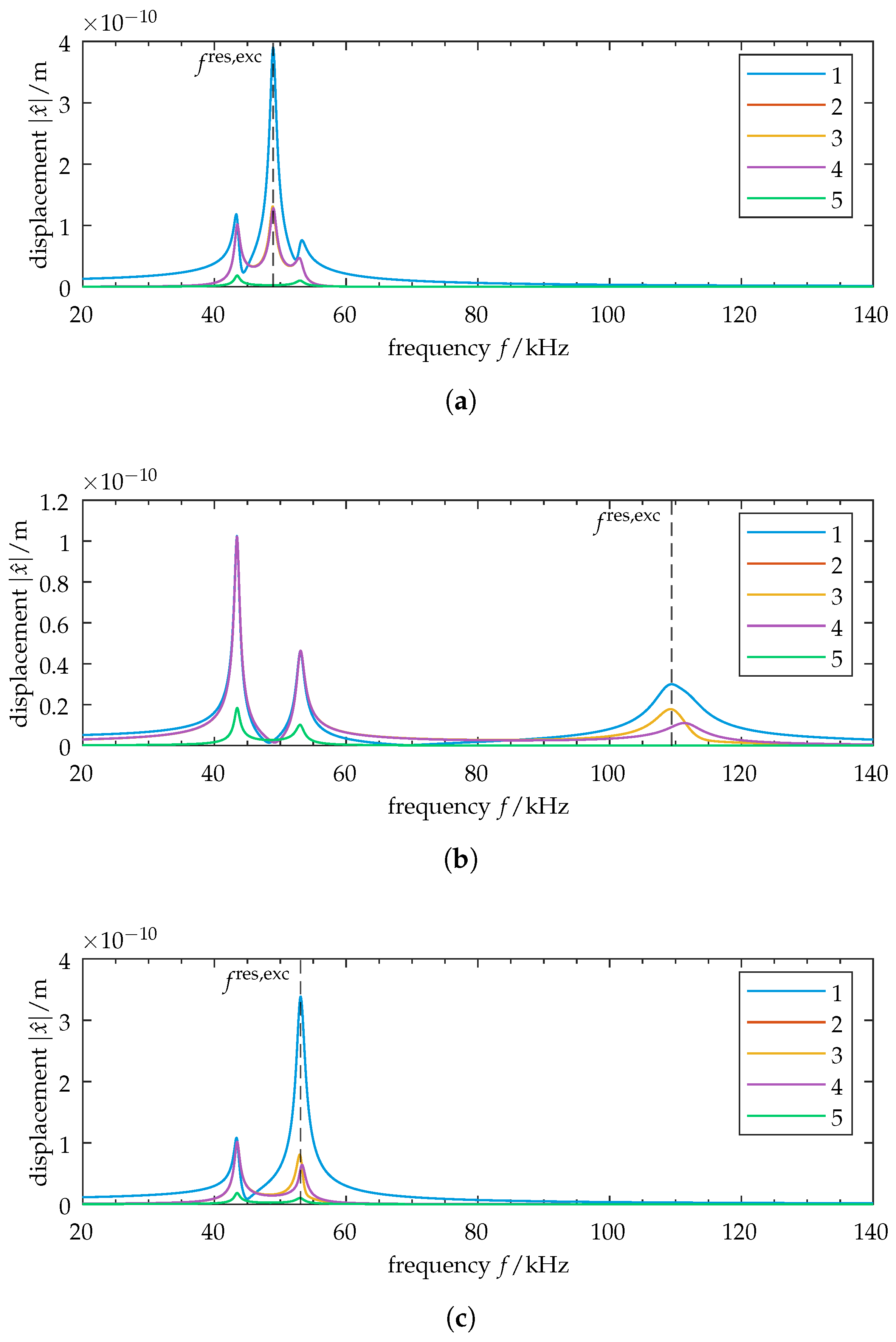
3.2.1. Case 1: Weak Coupling
3.2.2. Case 2: Strong Coupling
3.2.3. Case 3: Eigenvalue Crossing
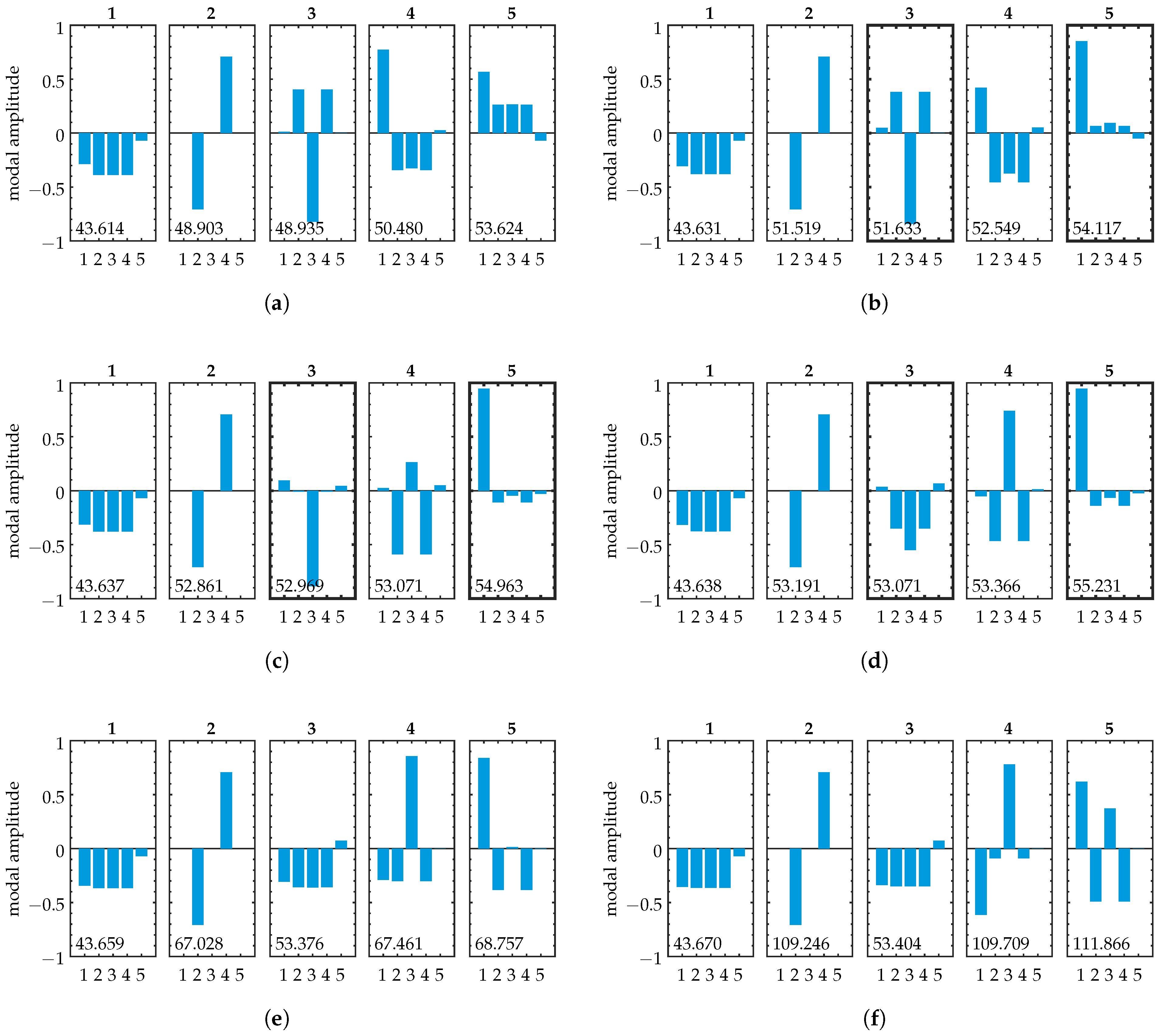
3.3. Relationship of Forced Vibration Localization to Modal Composition
- A note on dampingPreviously, it was determined that modal contributions are influenced by two factors: modal weighting due to the agreement between the mode shape vector and the excitation vector, and modal weighting due to the agreement between a mode’s damped natural frequency and the excitation frequency. Increasing modal damping yields well-known effects: the damped natural frequency of the system is lowered, and the displacement amplitude is reduced, increasing displacement bandwidth. In the context of modal superposition, these effects may cause a more equal contribution of modes with close (but not necessarily equal) frequencies. In other words, as damping increases, a positive effect on vibration localization is expected. This can be demonstrated by increasing the model damping (cf. Table 1), e.g., by a factor of 10. Considering the case of eigenvalue crossing (), a maximum amplitude at the non-excited elements of ≈15% is observed, increasing vibration localization compared to the lower-damped case treated in Section 3.2.3 (cf. Table 2c, where the maximum amplitude at the non-excited elements is ≈23%).
3.4. Interchange of Excitation—Retained Symmetry
3.5. Complete Vibration Localization in a Symmetric System
4. Breaking System Symmetry: Introducing Disorder
4.1. Modal Properties
4.2. Forced Vibration in the Transition Zone
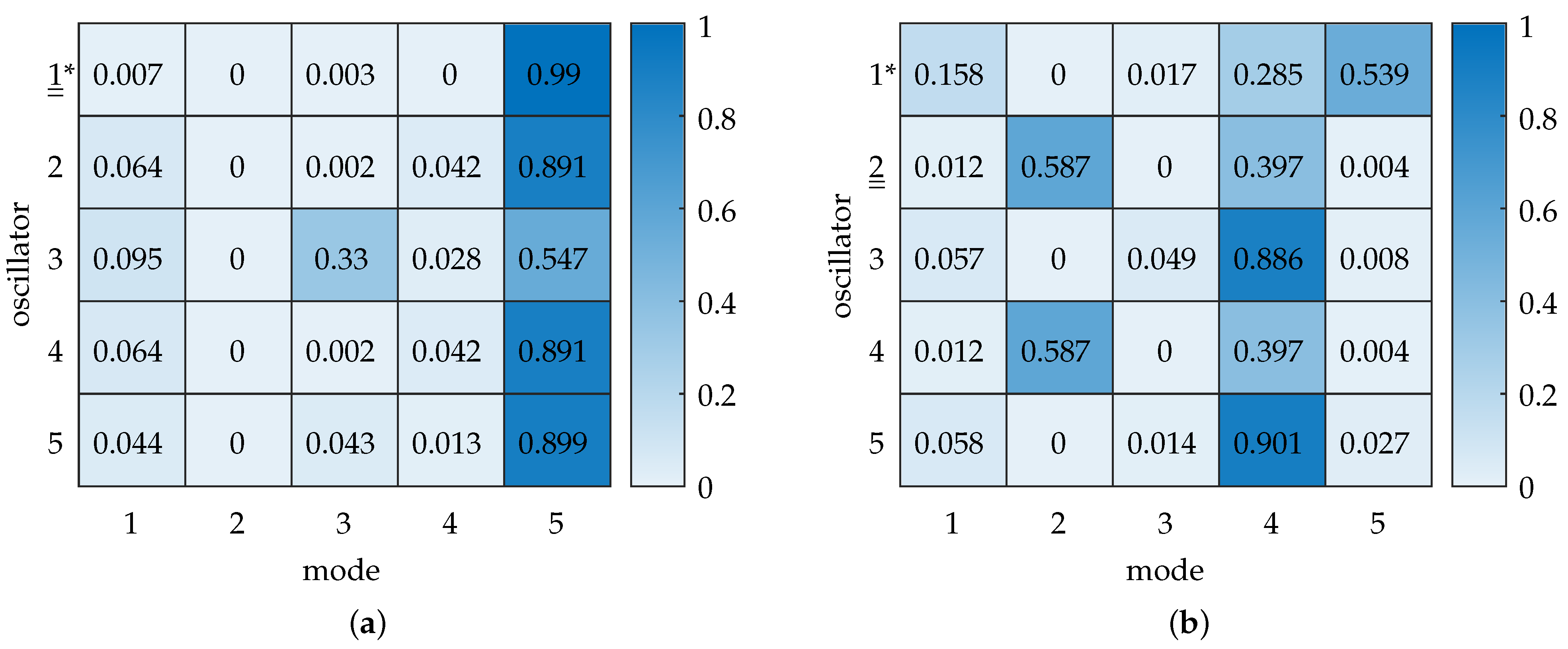
4.3. Modal Composition in the Disordered Model
4.4. Exchange of Excitation
- On resonance frequencyA remark should be made regarding resonance frequency. As we focused our research on the system’s behavior at resonance frequency, the frequency itself was not considered. Table 5 shows the values for resonance frequency as the excitation of the disordered model is exchanged. We can observe a change in resonance frequency that is most significant for the disordered oscillator. This can be attributed to curve veering, where, by definition, the eigenvalues of two modes cannot coincide during interaction. As the excitation of different oscillators mainly involves the corresponding localized normal modes, the resonance frequency changes accordingly. This frequency deviation relates to the amount of localization and curve veering (and, as a consequence, to the chosen parameter point ).
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOF | degree of freedom |
| FRF | frequency-response function |
| MEMS | micro-electromechanical system |
Appendix A. Matrices
Appendix B. Parameter Variation: Full Range Plots
Appendix B.1. Symmetric Model

Appendix B.2. Disordered Model
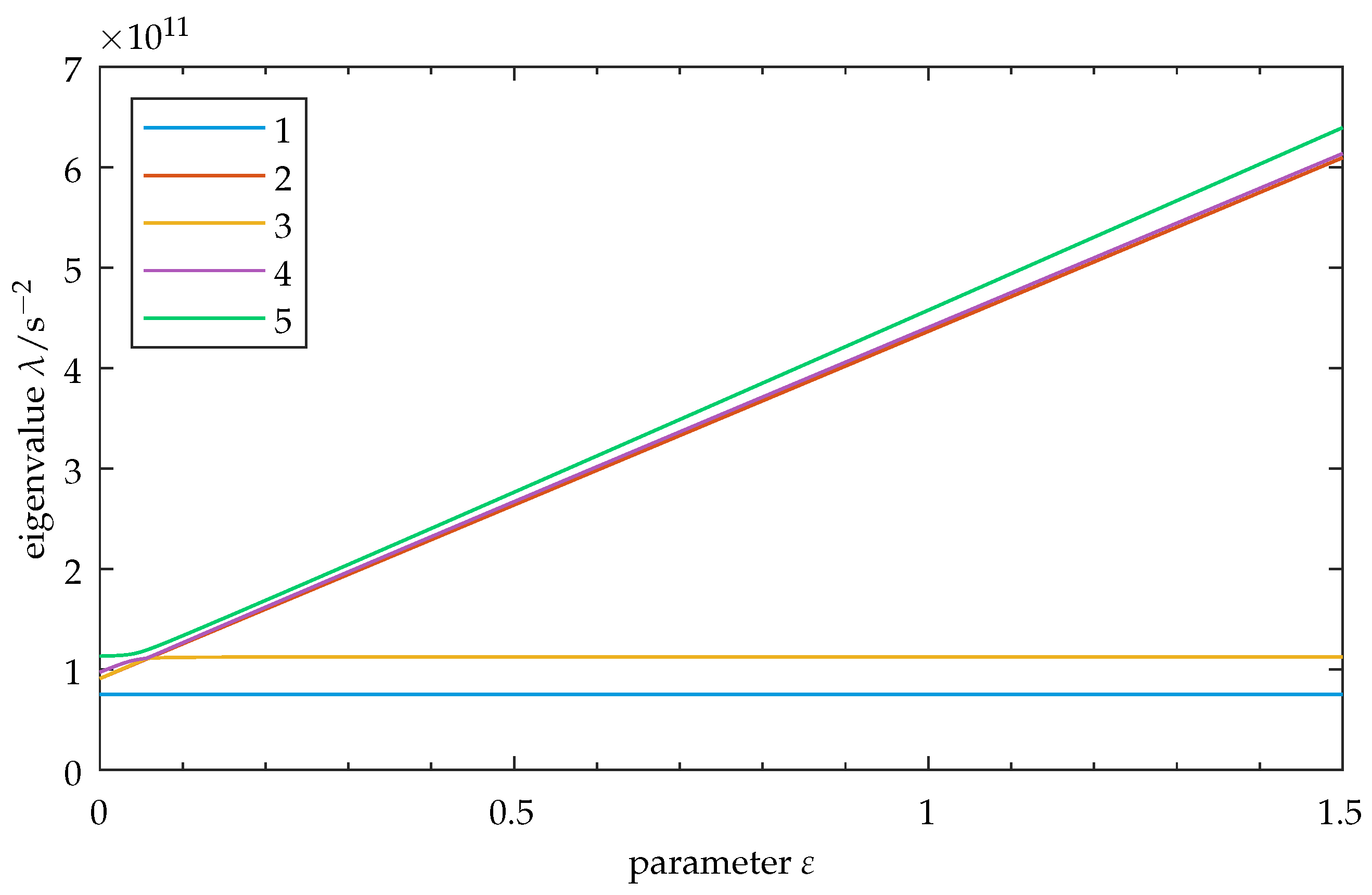
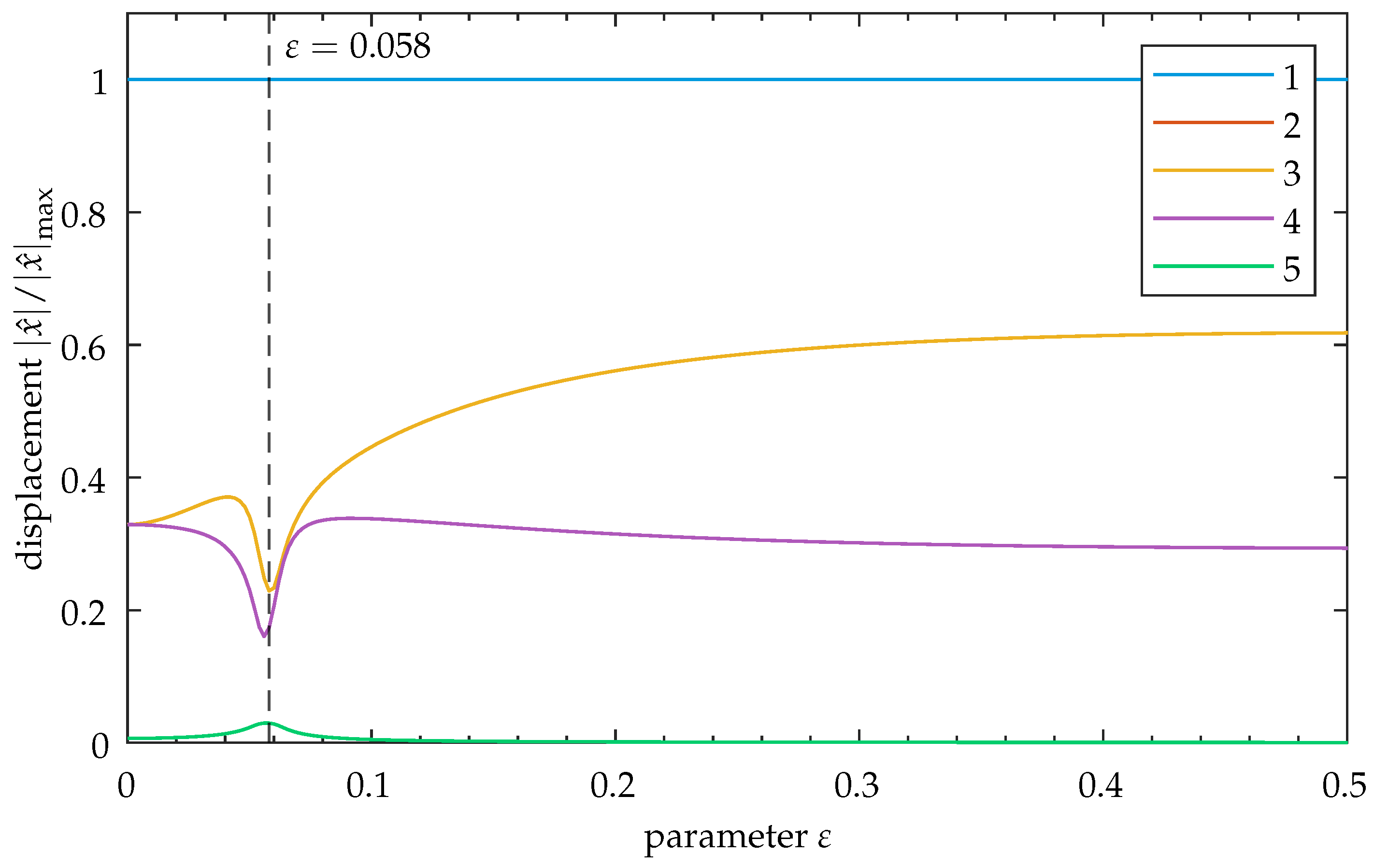
Appendix C. Symmetric Model: Localization Trend
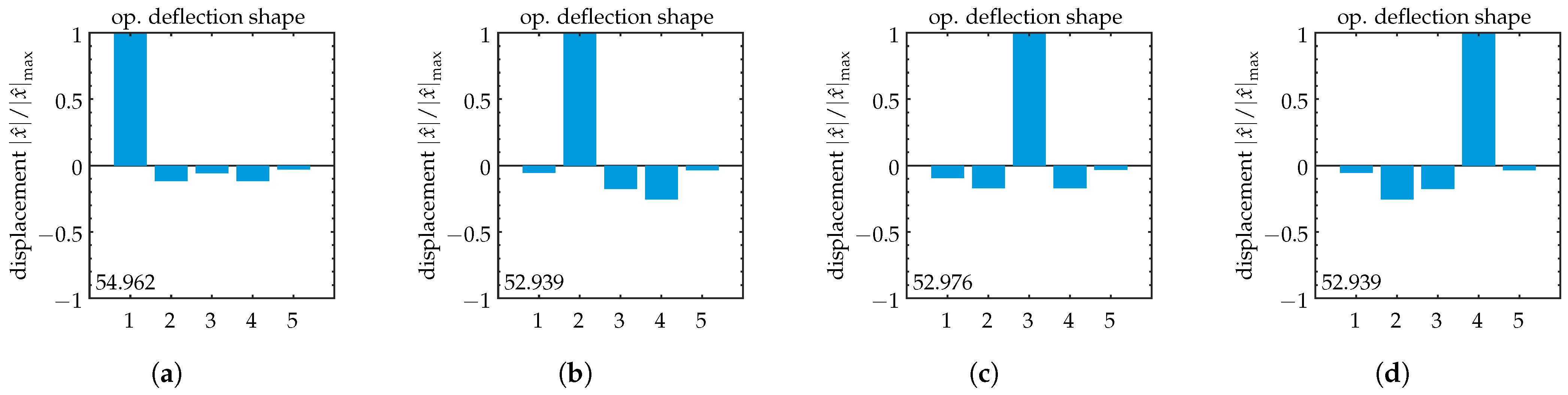
Appendix D. Symmetric Model: Operational Deflection Shapes

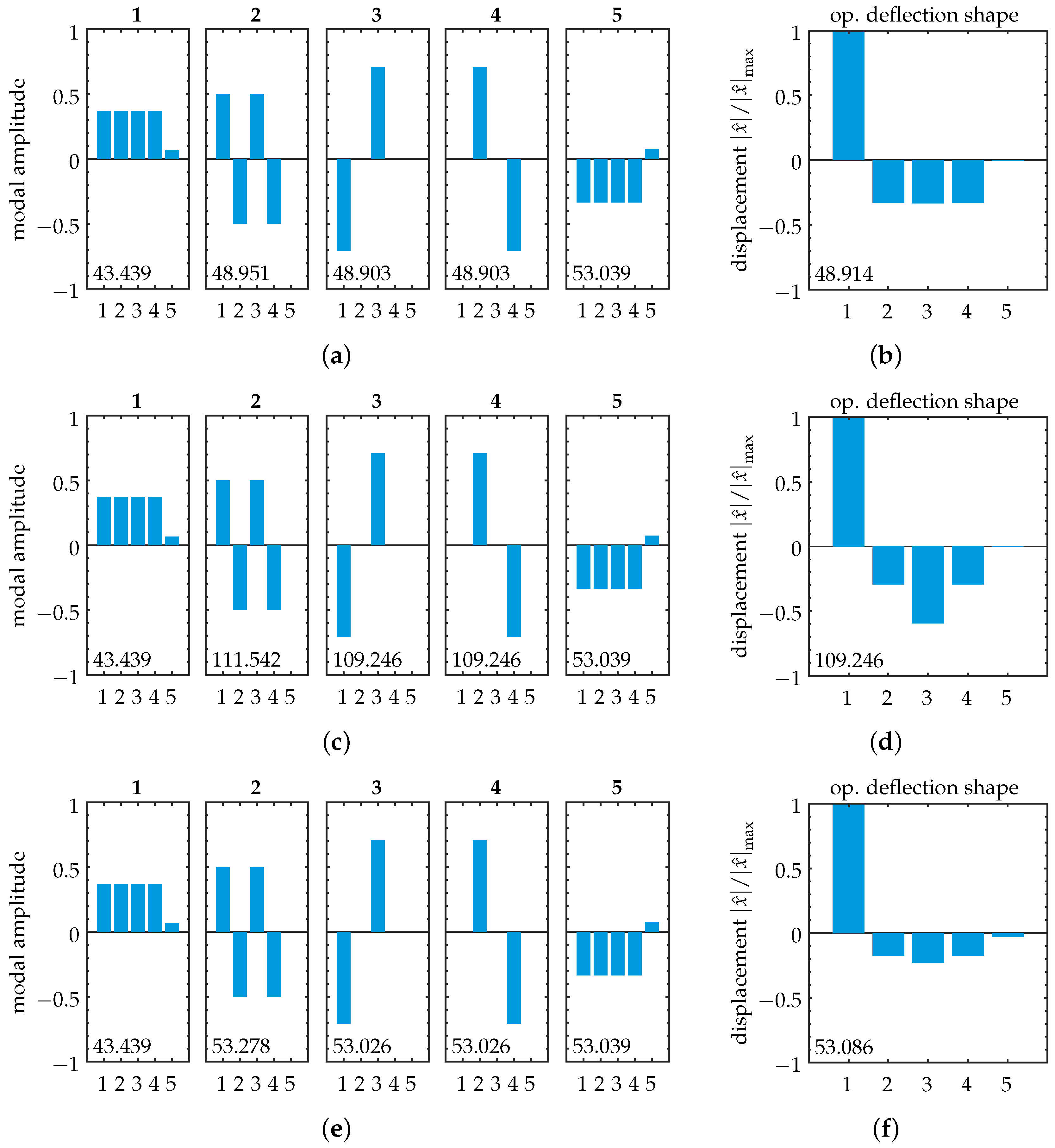
Appendix E. Disordered Model: Operational Deflection Shapes
References
- Schmerr, L.W. Fundamentals of Ultrasonic Phased Arrays; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Balanis, C.A. Antenna Theory: Analysis and Design, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic Arrays for Non-Destructive Evaluation: A Review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Stepanova, G.I. Vibration Spectrum of Disordered Crystal Lattices. Sov. Phys.—JETP [Transl. Zhurnal Eksperimentalnoi Teor. Fiz.] 1956, 3, 656–662. [Google Scholar]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Hodges, C. Confinement of Vibration by Structural Irregularity. J. Sound Vib. 1982, 82, 411–424. [Google Scholar] [CrossRef]
- Hodges, C.H.; Woodhouse, J. Vibration Isolation from Irregularity in a Nearly Periodic Structure: Theory and Measurements. J. Acoust. Soc. Am. 1983, 74, 894–905. [Google Scholar] [CrossRef]
- Pierre, C.; Tang, D.M.; Dowell, E.H. Localized Vibrations of Disordered Multispan Beams—Theory and Experiment. AIAA J. 1987, 25, 1249–1257. [Google Scholar] [CrossRef]
- Pierre, C. Mode Localization and Eigenvalue Loci Veering Phenomena in Disordered Structures. J. Sound Vib. 1988, 126, 485–502. [Google Scholar] [CrossRef]
- Huffington, N.J. On the Occurrence of Nodal Patterns of Nonparallel Form in Rectangular Orthotropic Plates. J. Appl. Mech. 1961, 28, 459–461. [Google Scholar] [CrossRef]
- Webster, J. Free Vibrations of Rectangular Curved Panels. Int. J. Mech. Sci. 1968, 10, 571–582. [Google Scholar] [CrossRef]
- Petyt, M.; Fleischer, C. Free Vibration of a Curved Beam. J. Sound Vib. 1971, 18, 17–30. [Google Scholar] [CrossRef]
- Nair, P.; Durvasula, S. On Quasi-Degeneracies in Plate Vibration Problems. Int. J. Mech. Sci. 1973, 15, 975–986. [Google Scholar] [CrossRef]
- Leissa, A.W. On a Curve Veering Aberration. Z. Angew. Math. Phys. ZAMP 1974, 25, 99–111. [Google Scholar] [CrossRef]
- Kuttler, J.; Sigillito, V. On Curve Veering. J. Sound Vib. 1981, 75, 585–588. [Google Scholar] [CrossRef]
- Balmès, E. High Modal Density, Curve Veering, Localization: A Different Perspective On The Structural Response. J. Sound Vib. 1993, 161, 358–363. [Google Scholar] [CrossRef]
- Bonisoli, E.; Delprete, C.; Esposito, M.; Mottershead, J.E. Structural Dynamics with Coincident Eigenvalues: Modelling and Testing. In Modal Analysis Topics; Springer: New York, NY, USA, 2011; Volume 3, pp. 325–337. [Google Scholar]
- Chen, P.T.; Ginsberg, J.H. On the Relationship Between Veering of Eigenvalue Loci and Parameter Sensitivity of Eigenfunctions. J. Vib. Acoust. 1992, 114, 141–148. [Google Scholar] [CrossRef]
- du Bois, J.L.; Adhikari, S.; Lieven, N.A. Eigenvalue Curve Veering in Stressed Structures: An Experimental Study. J. Sound Vib. 2009, 322, 1117–1124. [Google Scholar] [CrossRef]
- Stephen, N.G. On Veering of Eigenvalue Loci. J. Vib. Acoust. 2009, 131, 054501. [Google Scholar] [CrossRef]
- Chandrashaker, A.; Adhikari, S.; Friswell, M.I. Quantification of Vibration Localization in Periodic Structures. J. Vib. Acoust. 2016, 138, 021002. [Google Scholar] [CrossRef]
- Manconi, E.; Mace, B. Veering and Strong Coupling Effects in Structural Dynamics. J. Vib. Acoust. 2017, 139, 021009. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. Eigenvalue Sensitivity and Veering in Gyroscopic Systems with Application to High-Speed Planetary Gears. Eur. J. Mech.-A/Solids 2018, 67, 123–136. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Structural Dynamics with Parameter Uncertainties. Appl. Mech. Rev. 1987, 40, 309–328. [Google Scholar] [CrossRef]
- Bendiksen, O. Localization Phenomena in Structural Dynamics. Chaos Solitons Fractals 2000, 11, 1621–1660. [Google Scholar] [CrossRef]
- Pierre, C. Localized Free and Forced Vibrations of Nearly Periodic Disordered Structures. In Proceedings of the 28th Structures, Structural Dynamics and Materials Conference, Monterey, CA, USA, 6–8 April 1987. [Google Scholar]
- Glean, A.A.; Judge, J.A.; Vignola, J.F.; Ryan, T.J. Mode-Shape-Based Mass Detection Scheme Using Mechanically Diverse, Indirectly Coupled Microresonator Arrays. J. Appl. Phys. 2015, 117, 054505. [Google Scholar] [CrossRef]
- Erbes, A.; Thiruvenkatanathan, P.; Woodhouse, J.; Seshia, A.A. Numerical Study of the Impact of Vibration Localization on the Motional Resistance of Weakly Coupled MEMS Resonators. J. Microelectromech. Syst. 2015, 24, 997–1005. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ramos, D.; Pini, V.; Calleja, M.; Tamayo, J. Exponential Tuning of the Coupling Constant of Coupled Microcantilevers by Modifying Their Separation. Appl. Phys. Lett. 2011, 98, 123108. [Google Scholar] [CrossRef]
- Ilyas, S.; Younis, M.I. Theoretical and Experimental Investigation of Mode Localization in Electrostatically and Mechanically Coupled Microbeam Resonators. Int. J.-Non-Linear Mech. 2020, 125, 103516. [Google Scholar] [CrossRef]
- Seshia, A.A. Mode-Localized Sensing in Micro- and Nano-Mechanical Resonator Arrays. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Chellasivalingam, M.; Imran, H.; Pandit, M.; Boies, A.M.; Seshia, A.A. Weakly Coupled Piezoelectric MEMS Resonators for Aerosol Sensing. Sensors 2020, 20, 3162. [Google Scholar] [CrossRef]
- Ji, S.M.; Sung, J.H.; Park, C.Y.; Jeong, J.S. Phase-Canceled Backing Structure for Lightweight Ultrasonic Transducer. Sens. Actuators A Phys. 2017, 260, 161–168. [Google Scholar] [CrossRef]
- Celmer, M.; Opieliński, K.; Dopierała, M. Structural Model of Standard Ultrasonic Transducer Array Developed for FEM Analysis of Mechanical Crosstalk. Ultrasonics 2018, 83, 114–119. [Google Scholar] [CrossRef]
- Opielinski, K.J.; Celmer, M.; Bolejko, R. Crosstalk Effect in Medical Ultrasound Tomography Imaging. In Proceedings of the 2018 Joint Conference—Acoustics, Ustka, Poland, 11–14 September 2018; pp. 1–6. [Google Scholar]
- Ramalli, A.; D’hooge, J.; Lovstakken, L.; Tortoli, P. A Direct Measurement of Inter-Element Cross-Talk in Ultrasound Arrays. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; pp. 1301–1303. [Google Scholar]
- Bybi, A.; Khouili, D.; Granger, C.; Garoum, M.; Mzerd, A.; Hladky-Hennion, A.C. Experimental Characterization of A Piezoelectric Transducer Array Taking into Account Crosstalk Phenomenon. Int. J. Eng. Technol. Innov. 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Abdalla, O.M.O.; Massimino, G.; D’Argenzio, C.; Colosio, M.; Soldo, M.; Quaglia, F.; Corigliano, A. An Experimental and Numerical Study of Crosstalk Effects in PMUT Arrays. IEEE Sens. J. 2023, 23, 29029–29041. [Google Scholar] [CrossRef]
- Henneberg, J.; Gerlach, A.; Storck, H.; Cebulla, H.; Marburg, S. Reducing Mechanical Cross-Coupling in Phased Array Transducers Using Stop Band Material as Backing. J. Sound Vib. 2018, 424, 352–364. [Google Scholar] [CrossRef]
- Bybi, A.; Grondel, S.; Assaad, J.; Hladky-Hennion, A.C.; Granger, C.; Rguiti, M. Reducing Crosstalk in Array Structures by Controlling the Excitation Voltage of Individual Elements: A Feasibility Study. Ultrasonics 2013, 53, 1135–1140. [Google Scholar] [CrossRef] [PubMed]
- Bybi, A.; Grondel, S.; Assaad, J.; Hladky-Hennion, A.C. Extension of the Crosstalk Cancellation Method in Ultrasonic Transducer Arrays from the Harmonic Regime to the Transient One. Ultrasonics 2014, 54, 720–724. [Google Scholar] [CrossRef]
- Stytsenko, E.; Meijer, M.; Scott, N.L. Cross-Coupling Control in Linear and 2D Arrays. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–6. [Google Scholar]
- Cheng, D.; Li, J.; Yue, Q.; Liang, R.; Dong, X. Crosstalk Optimization of 5 MHz Linear Array Transducer Based on PZT/Epoxy Piezoelectric Composite. Sens. Actuators A Phys. 2022, 341, 113500. [Google Scholar] [CrossRef]
- Jia, K.; Tong, H.; Hong, F.; Xu, W.; Ma, L. A Method to Address Beam Cross Coupling Errors in Phased Array Doppler Sonar. JASA Express Lett. 2023, 3, 056003. [Google Scholar] [CrossRef]
- Papangelo, A.; Fontanela, F.; Grolet, A.; Ciavarella, M.; Hoffmann, N. Multistability and Localization in Forced Cyclic Symmetric Structures Modelled by Weakly-Coupled Duffing Oscillators. J. Sound Vib. 2019, 440, 202–211. [Google Scholar] [CrossRef]
- Fontanela, F.; Grolet, A.; Salles, L.; Chabchoub, A.; Champneys, A.; Patsias, S.; Hoffmann, N. Dissipative Solitons in Forced Cyclic and Symmetric Structures. Mech. Syst. Signal Process. 2019, 117, 280–292. [Google Scholar] [CrossRef]
- Niedergesäß, B.; Papangelo, A.; Grolet, A.; Vizzaccaro, A.; Fontanela, F.; Salles, L.; Sievers, A.; Hoffmann, N. Experimental Observations of Nonlinear Vibration Localization in a Cyclic Chain of Weakly Coupled Nonlinear Oscillators. J. Sound Vib. 2021, 497, 115952. [Google Scholar] [CrossRef]
- Harata, Y.; Ikeda, T. Modal Analysis for Localization of Harmonic Oscillations in Nonlinear Oscillator Arrays. J. Comput. Nonlinear Dyn. 2022, 17, 121001. [Google Scholar] [CrossRef]
- Nitti, A.; Stender, M.; Hoffmann, N.; Papangelo, A. Spatially Localized Vibrations in a Rotor Subjected to Flutter. Nonlinear Dyn. 2021, 103, 309–325. [Google Scholar] [CrossRef]
- Perkins, N.; Mote, C. Comments on Curve Veering in Eigenvalue Problems. J. Sound Vib. 1986, 106, 451–463. [Google Scholar] [CrossRef]
- Pierre, C.; Dowell, E. Localization of Vibrations by Structural Irregularity. J. Sound Vib. 1987, 114, 549–564. [Google Scholar] [CrossRef]
- du Bois, J.L.; Adhikari, S.; Lieven, N.A.J. On the Quantification of Eigenvalue Curve Veering: A Veering Index. J. Appl. Mech. 2011, 78, 041007. [Google Scholar] [CrossRef]
- du Bois, J.L.; Adhikari, S.; Lieven, N.A.J. Experimental and Numerical Investigation of Mode Veering in a Stressed Structure. In Proceedings of the International Modal Analysis Conference, Copenhagen, Denmark, 30 April–2 May 2007. [Google Scholar]
- du Bois, J.; Adhikari, S.; Lieven, N. Localisation and Curve Veering: A Different Perspective on Modal Interactions. In Proceedings of the 27th Conference and Exposition on Structural Dynamics 2009 (IMAC XXVII), Orlando, FL, USA, 9–12 February 2009. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory, 3rd ed., rev. and enl ed.; Pergamon Press: Oxford, NY, USA, 1977. [Google Scholar]
- Langley, R. On The Forced Response Of One-dimensional Periodic Structures: Vibration Localization By Damping. J. Sound Vib. 1994, 178, 411–428. [Google Scholar] [CrossRef]
- MATLAB Version 23.2.0.2485118 (R2023b) Update 6; The MathWorks: Natick, MA, USA, 2023.
- Winner, H.; Hakuli, S.; Lotz, F.; Singer, C. (Eds.) Handbuch Fahrerassistenzsysteme: Grundlagen, Komponenten und Systeme für Aktive Sicherheit und Komfort; Springer: Wiesbaden, Germany, 2015. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory and Practice, reprint ed.; Research Studies Pr.: Letchworth, UK, 1986. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969. [Google Scholar]


| Measure | Symbol | Unit | Value |
|---|---|---|---|
| Target frequency | Hz | 48,000 | |
| Mass | m | 1 | |
| Stiffness | k | N m−1 | |
| Damping (prop. stiffness) | |||
| Excitation amplitude | N | 1 | |
| Factor mass (base) | a | - | 100 |
| Factor stiffness (base) | b | - | 100 |
| (a) | (b) | (c) | |||||
| Oscillator | |||||||
| 1 | 1 | 1 | −89.4 | 1 | −80.6 | 1 | −89.7 |
| 2 | 0 | 0.328 | 94.3 | 0.293 | 135.1 | 0.173 | 129.1 |
| 3 | 0 | 0.334 | 83.5 | 0.594 | 74.0 | 0.229 | 56.5 |
| 4 | 0 | 0.328 | 94.3 | 0.293 | 135.1 | 0.293 | 135.1 |
| 5 | 0 | 0.007 | 177.8 | 0.000 | 3.9 | 0.030 | 89.3 |
| Required Excitation | |||
| Oscillator | |||
| 1 | 1 | 0.061 | 154.8 |
| 2 | 0 | 0.058 | −178.7 |
| 3 | 0 | 0.052 | −178.7 |
| 4 | 0 | 0.058 | −178.7 |
| 5 | 0 | 1 | −178.7 |
| Reduced Required Excitation | Resulting Displacement | |||||
| Oscillator | ||||||
| 1 | 1 | 1 | 92.5 | 1 | 0 | |
| 2 | 0 | 0.259 | 120.2 | 0 | - | |
| 3 | 0 | 0.231 | 81.2 | 0 | - | |
| 4 | 0 | 0.259 | 120.2 | 0 | - | |
| 5 | - | - | - | 0 | 0.054 | −171.6 |
| Excitation at Oscillator: | ||||||||
| 1 | 2 | 3 | 4 | |||||
| Oscillator | ||||||||
| 1 * | 1 | −90.3 | 0.042 | 164.0 | 0.084 | 105.0 | 0.042 | 164.0 |
| 2 | 0.115 | 94.1 | 1 | −90.1 | 0.177 | 102.7 | 0.239 | 56.1 |
| 3 | 0.056 | 75.6 | 0.177 | 111.7 | 1 | −90.6 | 0.177 | 111.7 |
| 4 | 0.115 | 94.1 | 0.239 | 56.1 | 0.177 | 102.7 | 1 | −90.1 |
| 5 | 0.03 | 95.3 | 0.035 | 100.5 | 0.032 | 87.5 | 0.035 | 100.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manz, Y.; Storck, H.; Gerlach, A.; Hoffmann, N. Exploitation of Modal Superposition Toward Forced Vibration Localization in a Coupled Symmetric Oscillator Array. Sensors 2025, 25, 3106. https://doi.org/10.3390/s25103106
Manz Y, Storck H, Gerlach A, Hoffmann N. Exploitation of Modal Superposition Toward Forced Vibration Localization in a Coupled Symmetric Oscillator Array. Sensors. 2025; 25(10):3106. https://doi.org/10.3390/s25103106
Chicago/Turabian StyleManz, Yannik, Heiner Storck, André Gerlach, and Norbert Hoffmann. 2025. "Exploitation of Modal Superposition Toward Forced Vibration Localization in a Coupled Symmetric Oscillator Array" Sensors 25, no. 10: 3106. https://doi.org/10.3390/s25103106
APA StyleManz, Y., Storck, H., Gerlach, A., & Hoffmann, N. (2025). Exploitation of Modal Superposition Toward Forced Vibration Localization in a Coupled Symmetric Oscillator Array. Sensors, 25(10), 3106. https://doi.org/10.3390/s25103106







