A Novel Loosely Coupled Collaborative Localization Method Utilizing Integrated IMU-Aided Cameras for Multiple Autonomous Robots
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Our Approach
2. Design of the State Vector
2.1. Definition of Variables
2.2. Construction of the SR-CICEKF State Vector
2.2.1. Coupling Process for the SR-CICEKF
2.2.2. Simplification of the SR-CICEKF State Vector
2.2.3. Error of the SR-CICEKF State Vector
2.3. Construction of the MR-CICEKF State Vector
2.3.1. Simplification of the MR-CICEKF State Vector
2.3.2. Error of the MR-CICEKF State Vector
2.4. Relationships Among the Variables in the CICEKF
3. Propagation and Update of the CICEKF
3.1. Propagation and Measurement of the SR-CICEKF
3.1.1. Propagation of the SR-CICEKF
3.1.2. Measurement of the SR-CICEKF
3.2. Propagation and Measurement of the MR-CICEKF
3.3. Entire CICEKF Process
| Algorithm 1: SR-CICEKF | |
| Input: ,,; | |
| 1 | While true do |
| 2 | Update , according to and ; (Propagation process in Section 3.1.1) |
| 3 | Update ; |
| 4 | Update ; |
| 5 | Calculate according to ; (Measurement process in Section 3.1.2) |
| 6 | Update the current state ; |
| 7 | Update ; |
| 8 | ; |
| 9 | Output: . |
| Algorithm 2: MR-CICEKF | |
| Input: ,,,,; | |
| 1 | While true do |
| 2 | Update according to and ; |
| 3 | Update , according to and ; (Propagation process in Section 3.2) |
| 4 | Update ; |
| 5 | Update ; |
| 6 | Calculate according to ; (Measurement process in Section 3.2) |
| 7 | Update the current state ; |
| 8 | Update ; |
| 9 | ; |
| 10 | Output: . |
4. Nonlinear Observability Analysis
4.1. Observability Analysis of the SR-CICEKF
4.2. Observability Analysis of the MR-CICEKF
5. Data Test
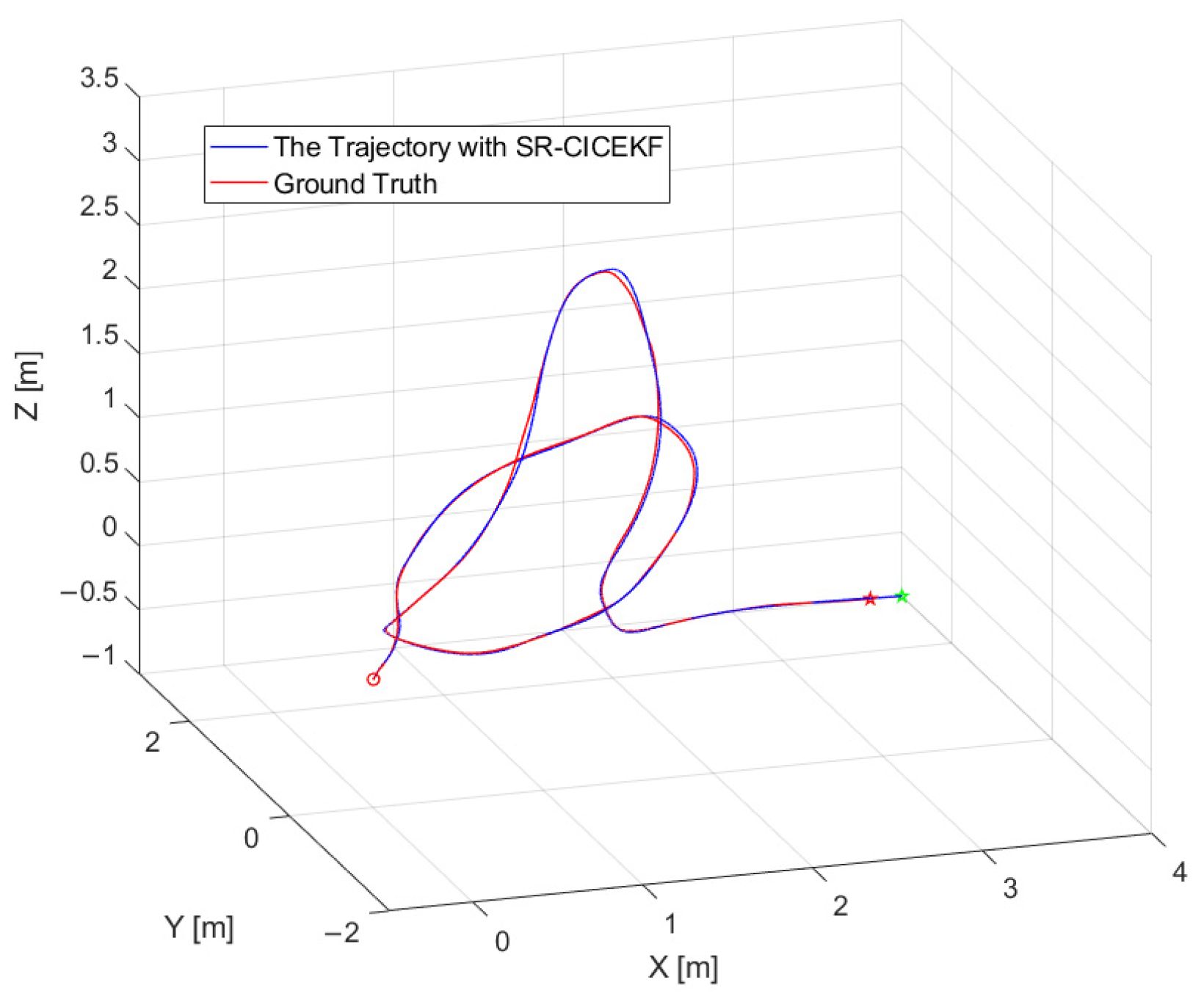
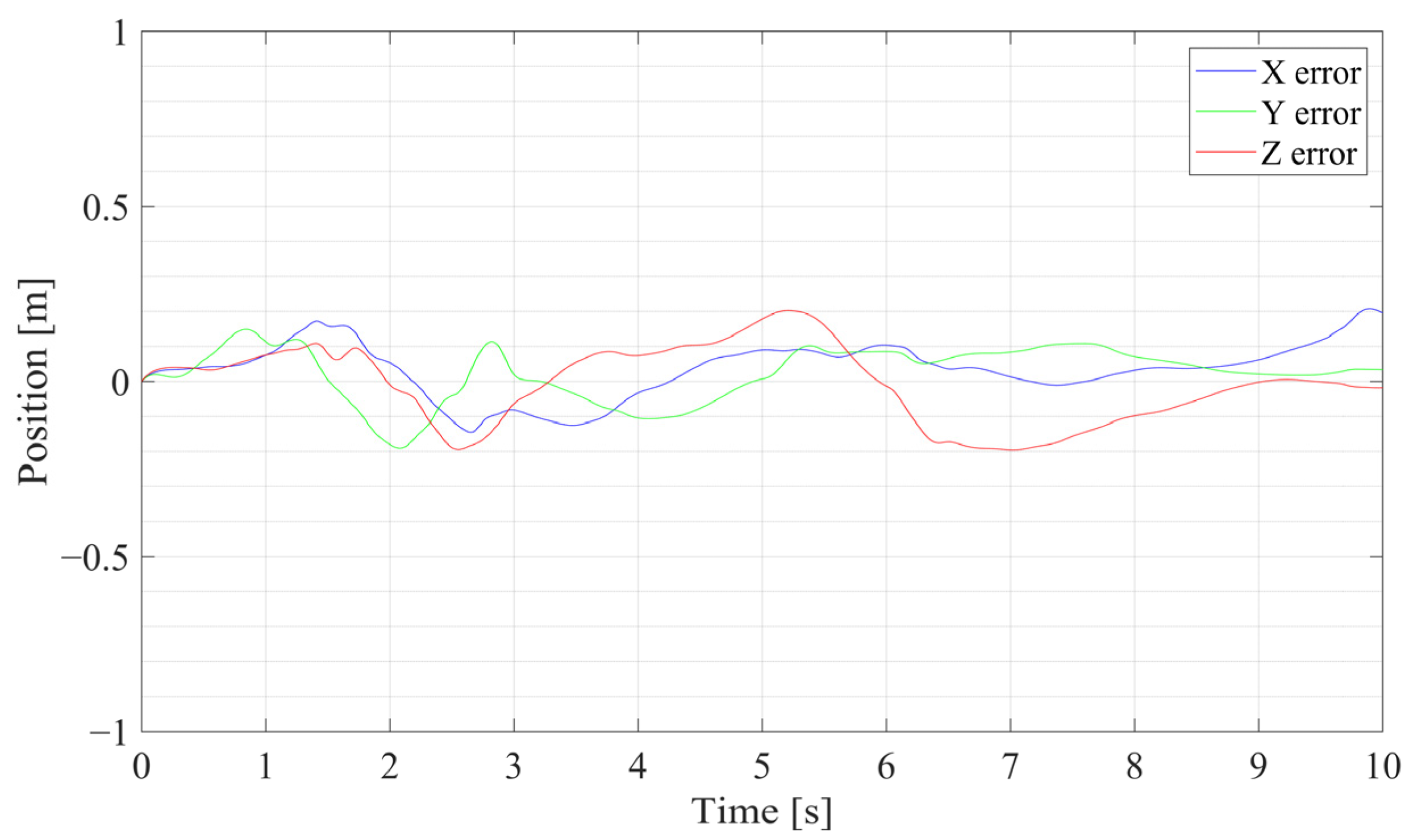
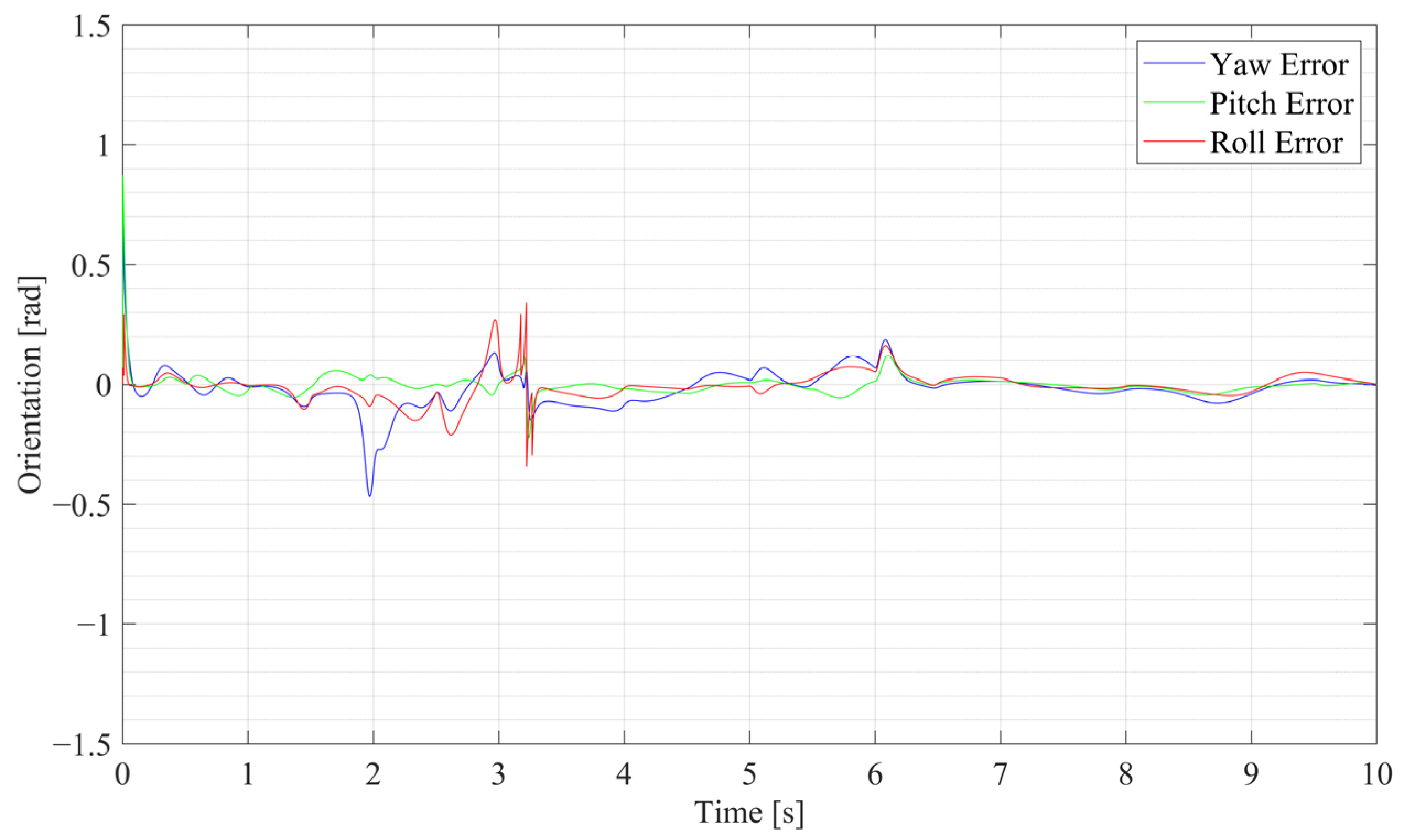
5.1. SR-CICEKF Simulation Test
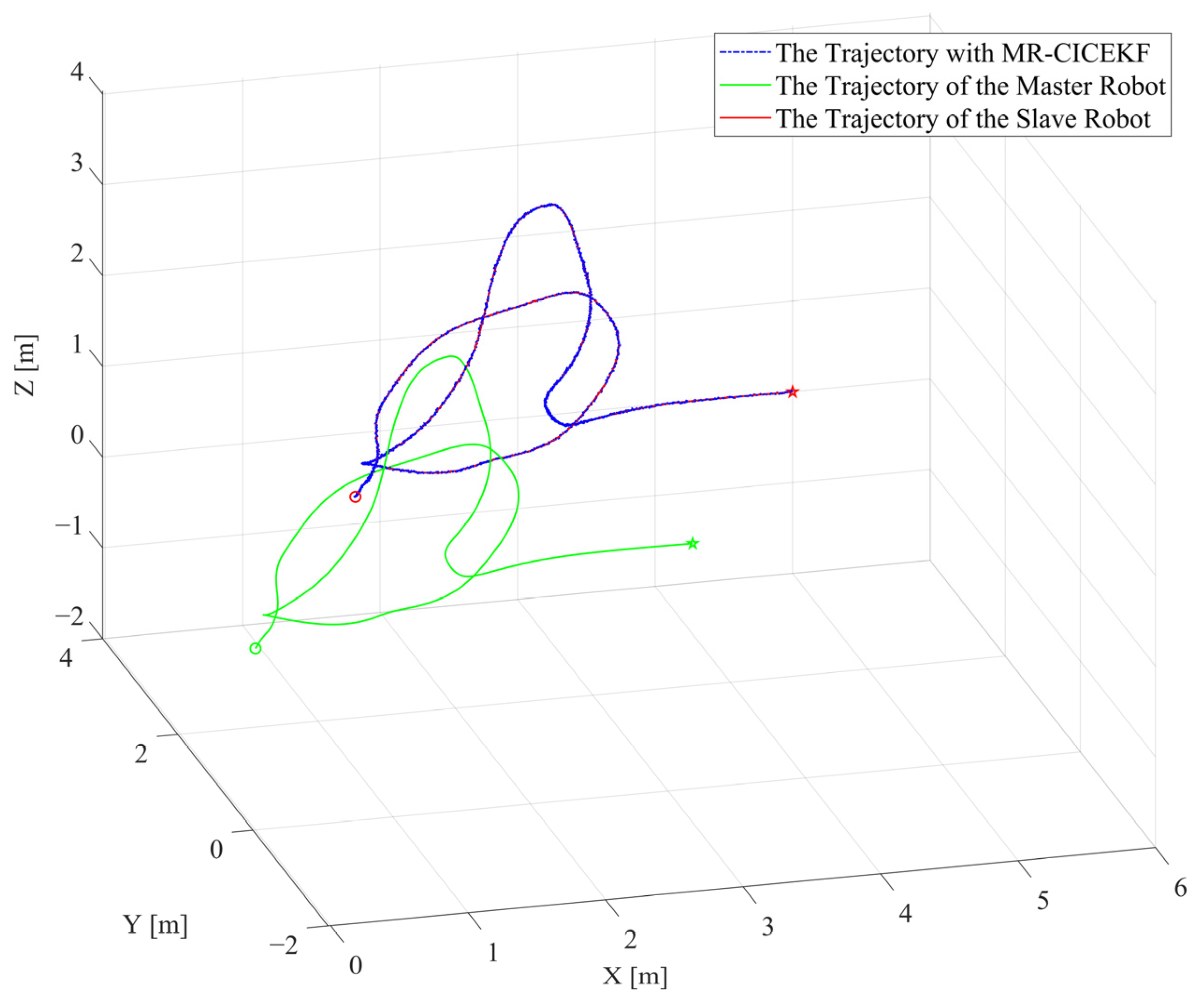
5.2. MR-CICEKF Simulation
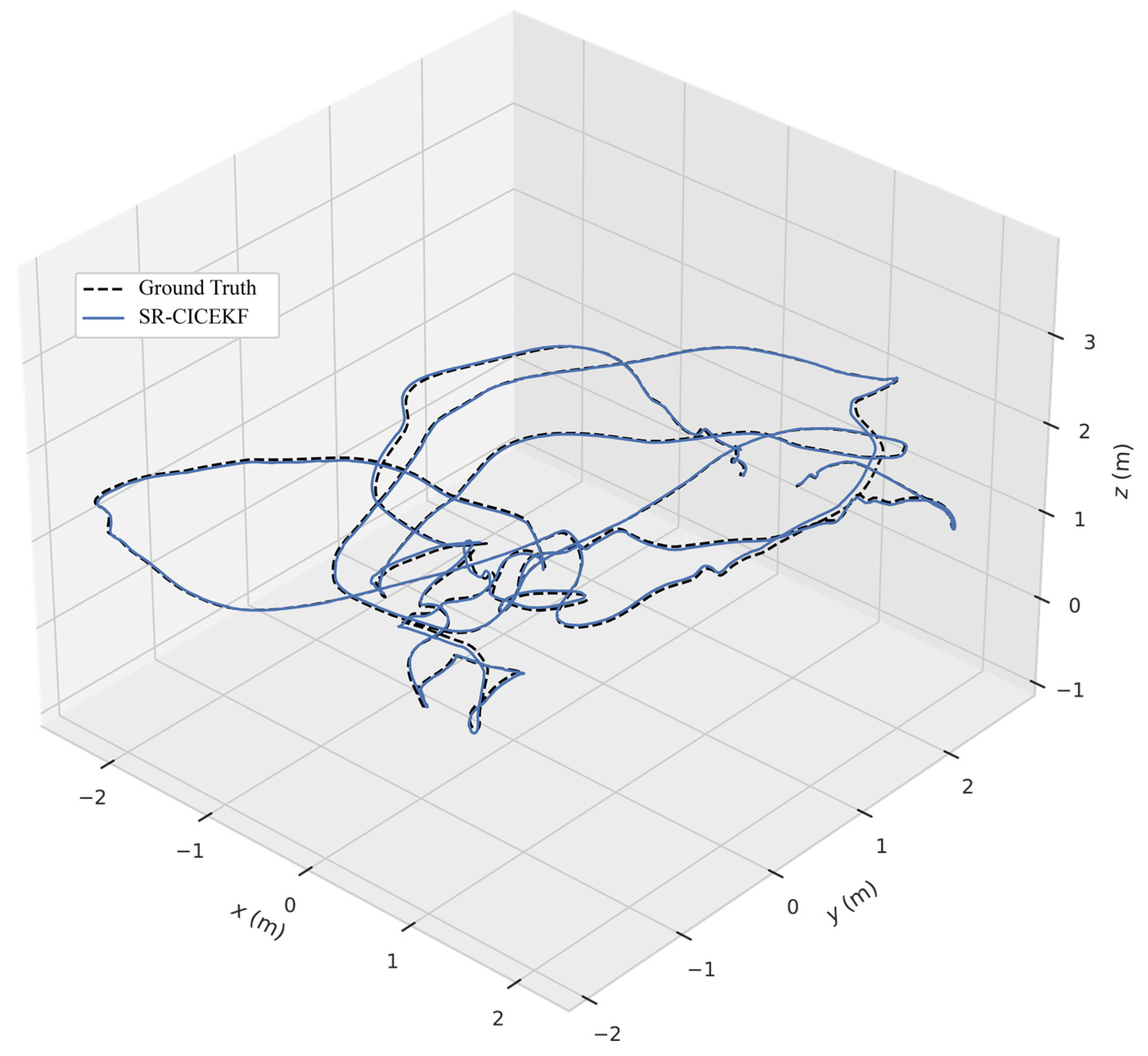
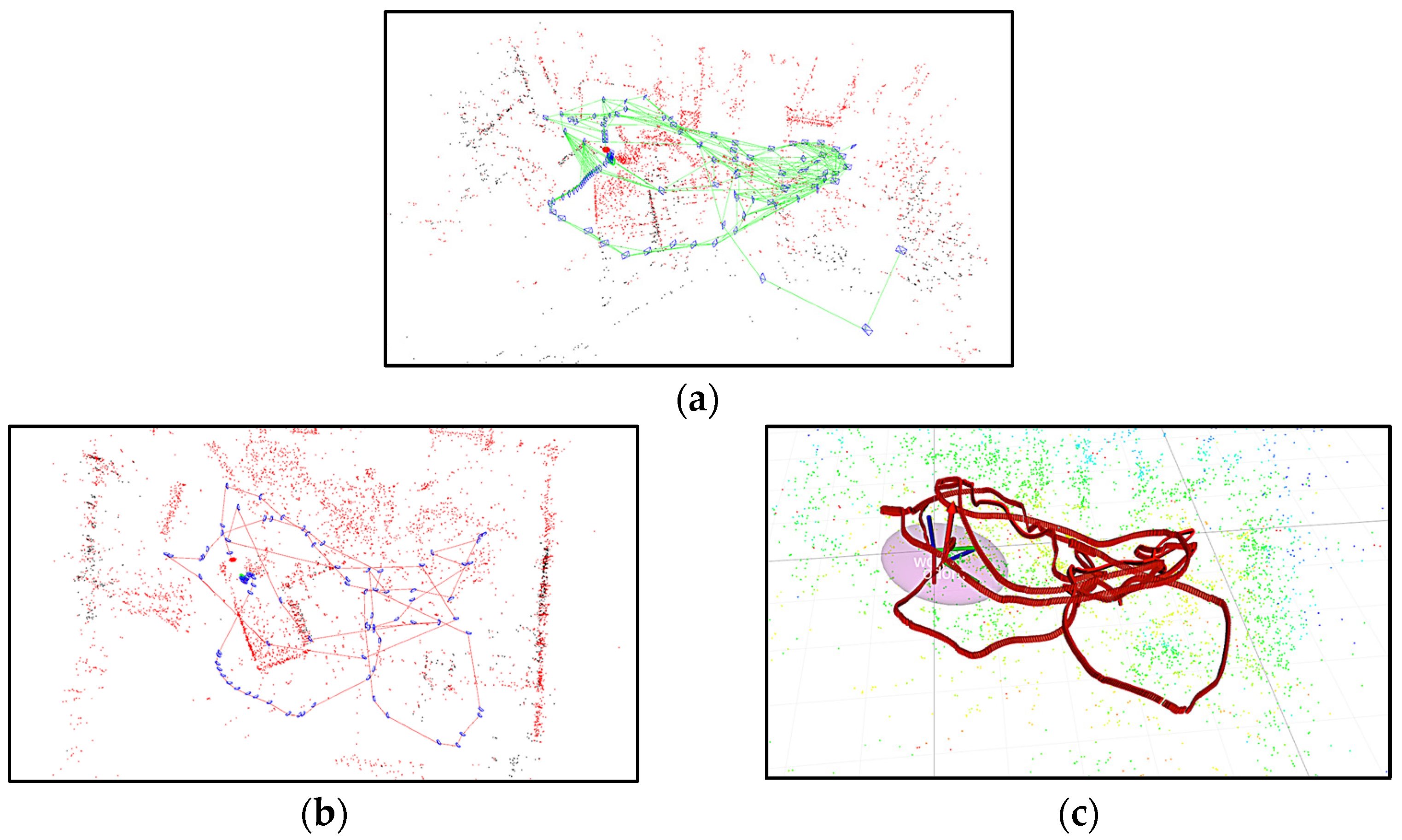
5.3. Dataset Test
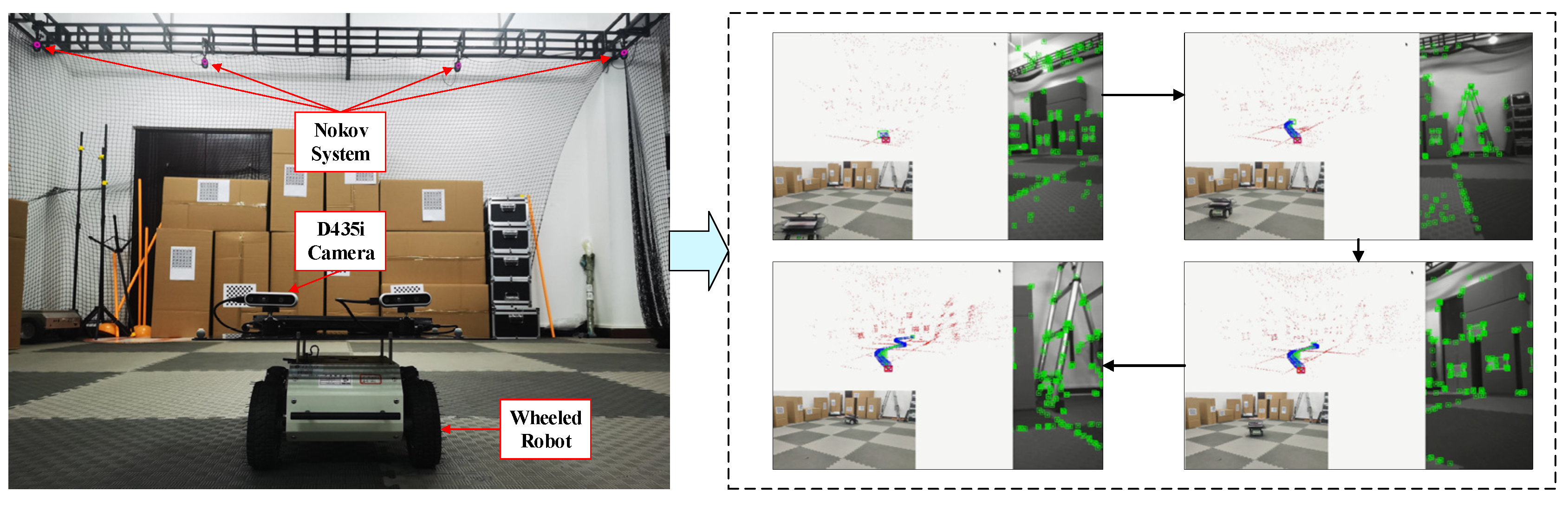
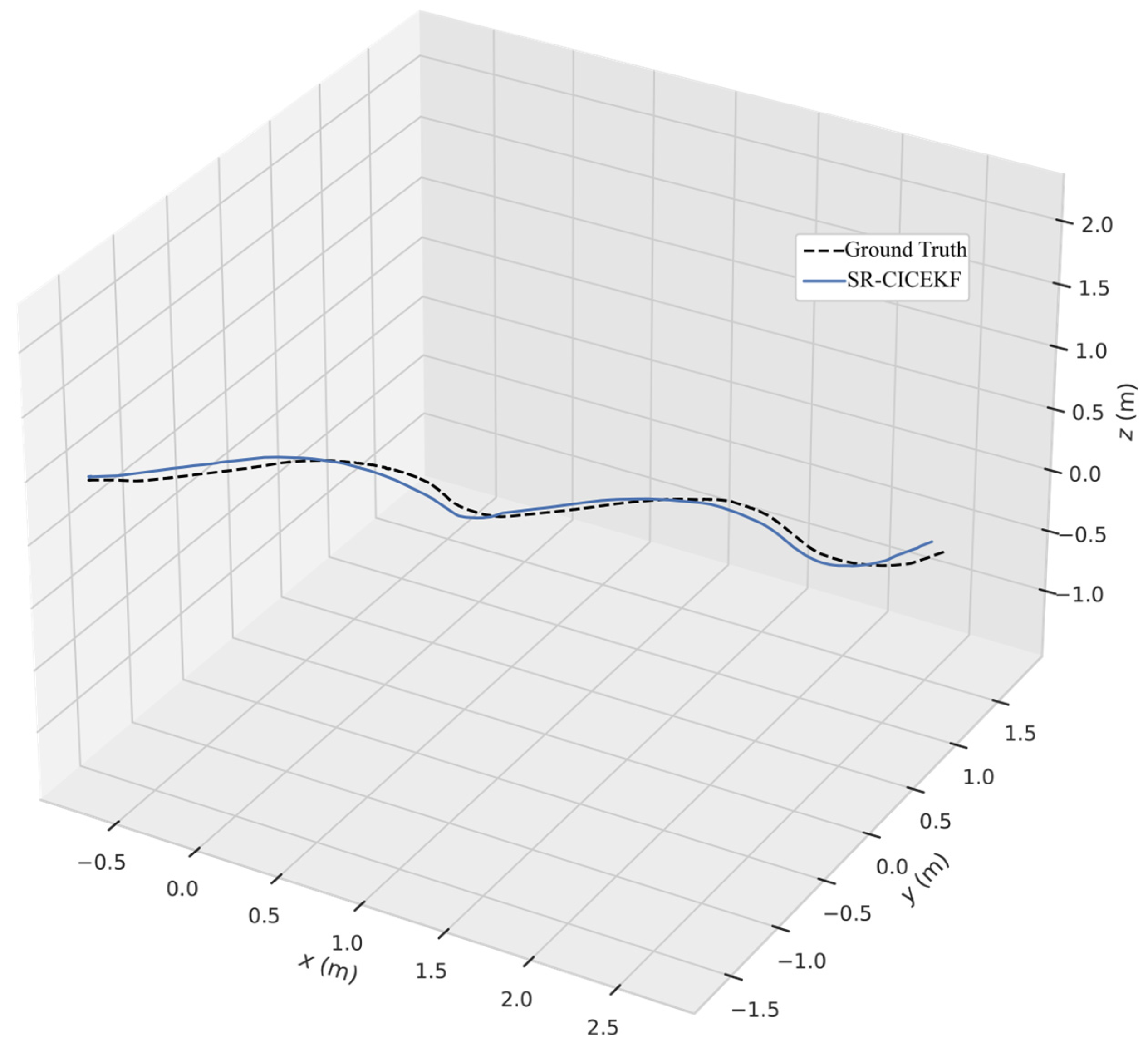
6. Experiments
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Servières, M.; Renaudin, V.; Dupuis, A.; Antigny, N. Visual and Visual-Inertial SLAM: State of the Art, Classification, and Experimental Benchmarking. J. Sens. 2021, 2021, 2054828. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, W.; Tao, X.; Pan, S.; Wu, P.; Huang, H. Semi-tightly coupled robust model for GNSS/UWB/INS integrated positioning in challenging environments. Remote Sens. 2024, 16, 2108. [Google Scholar] [CrossRef]
- He, M.; Zhu, C.; Huang, Q.; Ren, B.; Liu, J. A review of monocular visual odometry. Vis. Comput. 2020, 36, 1053–1065. [Google Scholar] [CrossRef]
- Elamin, A.; El-Rabbany, A.; Jacob, S. Event-Based Visual/Inertial Odometry for UAV Indoor Navigation. Sensors 2024, 25, 61. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Huang, P.; Wang, W. Tightly coupled visual-inertial-UWB indoor localization system with multiple position-unknown anchors. IEEE Robot. Autom. Lett. 2023, 9, 351–358. [Google Scholar] [CrossRef]
- Tonini, A.; Castelli, M.; Bates, J.S.; Lin, N.N.N.; Painho, M. Visual-Inertial Method for Localizing Aerial Vehicles in GNSS-Denied Environments. Appl. Sci. 2024, 14, 9493. [Google Scholar] [CrossRef]
- Nemec, D.; Šimák, V.; Janota, A.; Hruboš, M.; Bubeníková, E. Precise localization of the mobile wheeled robot using sensor fusion of odometry, visual artificial landmarks and inertial sensors. Robot. Auton. Syst. 2019, 112, 168–177. [Google Scholar] [CrossRef]
- Li, Z.; You, B.; Ding, L.; Gao, H.; Huang, F. Trajectory Tracking Control for WMRs with the Time-Varying Longitudinal Slippage Based on a New Adaptive SMC Method. Int. J. Aerosp. Eng. 2019, 2019, 4951538. [Google Scholar] [CrossRef]
- Tschopp, F.; Riner, M.; Fehr, M.; Bernreiter, L.; Furrer, F.; Novkovic, T.; Pfrunder, A.; Cadena, C.; Siegwart, R.; Nieto, J. Versavis—An open versatile multi-camera visual-inertial sensor suite. Sensors 2020, 20, 1439. [Google Scholar] [CrossRef]
- Reginald, N.; Al-Buraiki, O.; Choopojcharoen, T.; Fidan, B.; Hashemi, E. Visual-Inertial-Wheel Odometry with Slip Compensation and Dynamic Feature Elimination. Sensors 2025, 25, 1537. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, C.; Zou, L.; Li, S. Real-Time Optimal States Estimation with Inertial and Delayed Visual Measurements for Unmanned Aerial Vehicles. Sensors 2023, 23, 9074. [Google Scholar] [CrossRef] [PubMed]
- Lajoie, P.-Y.; Beltrame, G. Swarm-slam: Sparse decentralized collaborative simultaneous localization and mapping framework for multi-robot systems. IEEE Robot. Autom. Lett. 2023, 9, 475–482. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Li, D.; Zhao, Q. Distributed relative localization algorithms for multi-robot networks: A survey. Sensors 2023, 23, 2399. [Google Scholar] [CrossRef]
- Cai, Y.; Shen, Y. An integrated localization and control framework for multi-agent formation. IEEE Trans. Signal Process. 2019, 67, 1941–1956. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, B.; Zhou, J.; Zhang, Y.; Liu, X. Real-time localization and mapping utilizing multi-sensor fusion and visual–IMU–wheel odometry for agricultural robots in unstructured, dynamic and GPS-denied greenhouse environments. Agronomy 2022, 12, 1740. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.-M.; Xie, L. Flexible and resource-efficient multi-robot collaborative visual-inertial-range localization. IEEE Robot. Autom. Lett. 2021, 7, 928–935. [Google Scholar] [CrossRef]
- Tian, Y.; Chang, Y.; Arias, F.H.; Nieto-Granda, C.; How, J.P.; Carlone, L. Kimera-multi: Robust, distributed, dense metric-semantic slam for multi-robot systems. IEEE Trans. Robot. 2022, 38, 2022–2038. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, J.; Huang, C.; Li, L. Learning visual semantic map-matching for loosely multi-sensor fusion localization of autonomous vehicles. IEEE Trans. Intell. Veh. 2022, 8, 358–367. [Google Scholar] [CrossRef]
- Kelly, J.; Sukhatme, G.S. Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration. Int. J. Robot. Res. 2011, 30, 56–79. [Google Scholar] [CrossRef]
- Weiss, S.; Siegwart, R. Real-time metric state estimation for modular vision-inertial systems. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4531–4537. [Google Scholar]
- Achtelik, M.W.; Weiss, S.; Chli, M.; Dellaerty, F.; Siegwart, R. Collaborative stereo. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2242–2248. [Google Scholar]
- Brossard, M.; Bonnabel, S.; Barrau, A. Invariant Kalman filtering for visual inertial SLAM. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 2021–2028. [Google Scholar]
- Sun, W.; Li, Y.; Ding, W.; Zhao, J. A novel visual inertial odometry based on interactive multiple model and multistate constrained Kalman filter. IEEE Trans. Instrum. Meas. 2023, 73, 5000110. [Google Scholar] [CrossRef]
- Fornasier, A.; Ng, Y.; Mahony, R.; Weiss, S. Equivariant filter design for inertial navigation systems with input measurement biases. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 4333–4339. [Google Scholar]
- van Goor, P.; Mahony, R. An equivariant filter for visual inertial odometry. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14432–14438. [Google Scholar]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman Filter for 3D Attitude Estimation; University of Minnesota, Department of Computer Science & Engineering, Technical Report: Minneapolis, MN, USA, 2005; Volume 2. [Google Scholar]
- Liu, C.; Wang, T.; Li, Z.; Tian, P. A Novel Real-Time Autonomous Localization Algorithm Based on Weighted Loosely Coupled Visual–Inertial Data of the Velocity Layer. Appl. Sci. 2025, 15, 989. [Google Scholar] [CrossRef]
- Dam, E.B.; Koch, M.; Lillholm, M. Quaternions, Interpolation and Animation; Datalogisk Institut, Københavns Universitet: Copenhagen, Denmark, 1998; Volume 2. [Google Scholar]
- Maybeck, P. Stochastic Models, Estimation, and Control; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Beder, C.; Steffen, R. Determining an initial image pair for fixing the scale of a 3d reconstruction from an image sequence. In Proceedings of the Joint Pattern Recognition Symposium, Hong Kong, China, 17–19 August 2006; pp. 657–666. [Google Scholar]
- Eudes, A.; Lhuillier, M. Error propagations for local bundle adjustment. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2411–2418. [Google Scholar]
- Hermann, R.; Krener, A. Nonlinear controllability and observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. Available online: https://github.com/MichaelGrupp/evo (accessed on 5 April 2025).
- Rehder, J.; Nikolic, J.; Schneider, T.; Hinzmann, T.; Siegwart, R. Extending kalibr: Calibrating the extrinsics of multiple IMUs and of individual axes. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4304–4311. [Google Scholar]
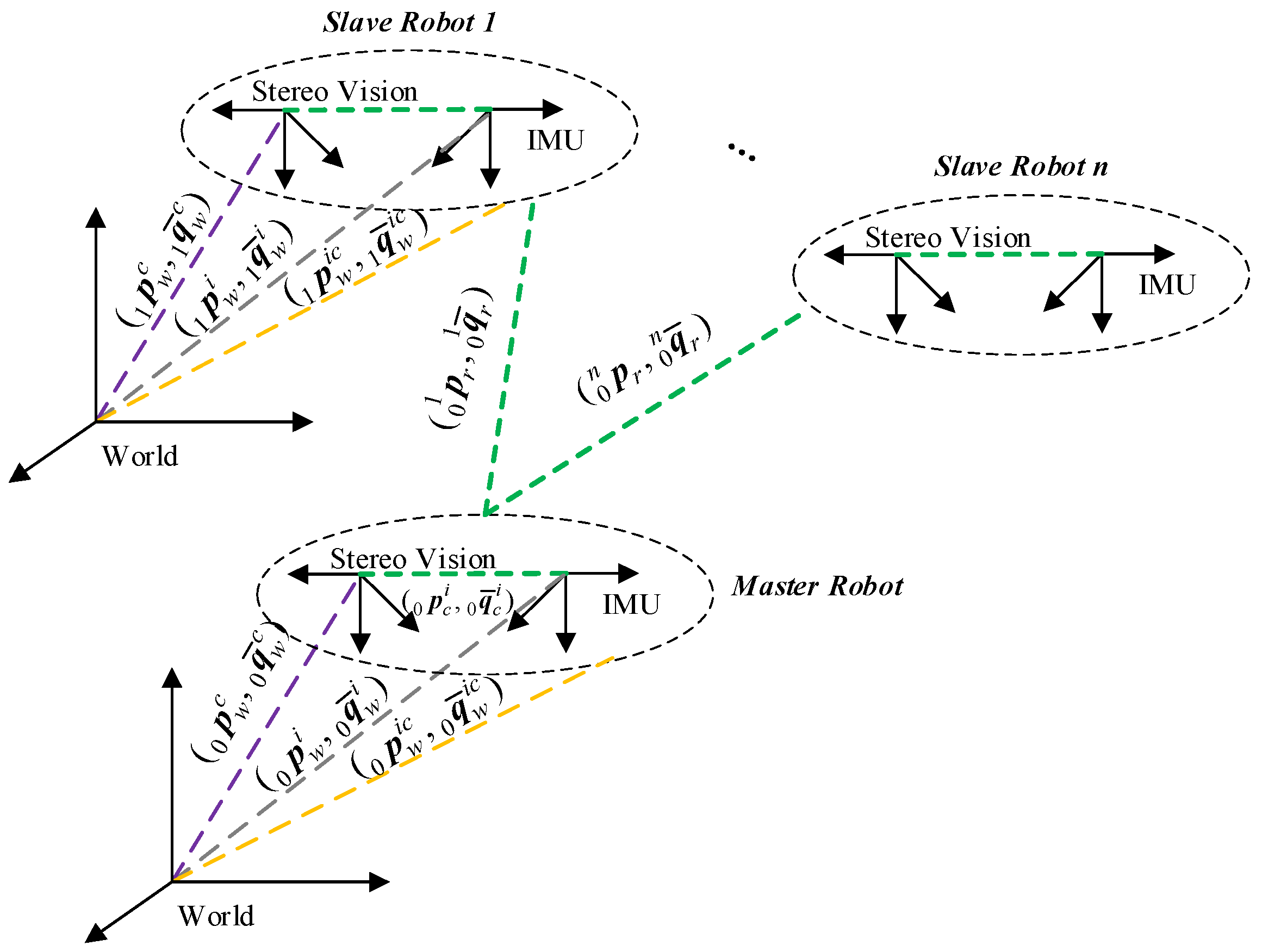
| Symbol | Description |
|---|---|
| w | Coordinate frame of the fixed world |
| i | Coordinate frame attached to the IMU’s rigid body |
| c | Coordinate frame attached to the rigid body of the dual-camera stereo vision |
| ic | Coordinate frame attached to the virtual rigid body of the IMU-aided camera system |
| represents a general viable vector, and are the reference coordinate frames, e.g., denotes the linear translation in the coordinate frame measured with respect to the coordinate frame | |
| represents a general viable vector, and are the robot indexes, e.g., denotes the linear translation of the -th robot measured with respect to the -th robot, particularly, . | |
| Skew-symmetric matrix of , and [28] holds | |
| The linear translation vector of rigid bodies along 3 axes, of which the quasi-quaternion description is | |
| The unit quaternion following the Hamilton notation [21], written as | |
| The conjugate form of , and holds | |
| The uncertain bias of the measurement result | |
| The equivalent rotation matrix of the quaternion , e.g., | |
| White Gaussian noise vector with zero mean and covariance | |
| , | The first-order time derivative form and the estimated form of the vector , respectively |
| The error form of the vector , which is defined as | |
| The error of the quaternion , and holds |
| Translation RMSE | Translation Mean Error | Translation STD | Orientation RMSE | Orientation Mean Error | Orientation STD |
|---|---|---|---|---|---|
| 0.1593 m | 0.0429 m | 0.1535 m | 0.106 rad | 0.0187 rad | 0.1044 rad |
| Translation RMSE | Translation Mean Error | Translation STD | Orientation RMSE | Orientation Mean Error | Orientation STD |
|---|---|---|---|---|---|
| 0.01872 m | 5.286 × 10−6 m | 0.0187 m | 0.0016 rad | 4.95 × 10−7 rad | 0.0016 rad |
| Translation RMSE | Translation Mean Error | Translation STD | |
|---|---|---|---|
| SR-CICEKF | 0.004211 m | 0.003982 m | 0.001371 m |
| Stereo ORB-SLAM V3 | 0.03844 m | 0.03428 m | 0.01739 m |
| Stereo ORB-SLAM V3 with the IMU | 0.003236 m | 0.002785 m | 0.001648 m |
| Stereo MSCKF | 0.0556 m | 0.048994 m | 0.02629 m |
| Translation RMSE | Translation Mean Error | Translation STD | |
|---|---|---|---|
| SR-CICEKF | 0.00459 m | 0.006448 m | 0.004528 m |
| Stereo ORB-SLAM V3 | 0.01723 m | 0.01275 m | 0.01159 m |
| Stereo MSCKF | 0.01745 m | 0.01292 m | 0.01173 m |
| Translation RMSE | Translation Mean Error | Translation STD | Orientation RMSE | Orientation Mean Error | Orientation STD |
|---|---|---|---|---|---|
| 0.009398 m | 0.0001 m | 0.0094 m | 0.032 rad | 0.00602 rad | 0.03145 rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Wang, T.; Li, Z.; Li, S.; Tian, P. A Novel Loosely Coupled Collaborative Localization Method Utilizing Integrated IMU-Aided Cameras for Multiple Autonomous Robots. Sensors 2025, 25, 3086. https://doi.org/10.3390/s25103086
Liu C, Wang T, Li Z, Li S, Tian P. A Novel Loosely Coupled Collaborative Localization Method Utilizing Integrated IMU-Aided Cameras for Multiple Autonomous Robots. Sensors. 2025; 25(10):3086. https://doi.org/10.3390/s25103086
Chicago/Turabian StyleLiu, Cheng, Tao Wang, Zhi Li, Shu Li, and Peng Tian. 2025. "A Novel Loosely Coupled Collaborative Localization Method Utilizing Integrated IMU-Aided Cameras for Multiple Autonomous Robots" Sensors 25, no. 10: 3086. https://doi.org/10.3390/s25103086
APA StyleLiu, C., Wang, T., Li, Z., Li, S., & Tian, P. (2025). A Novel Loosely Coupled Collaborative Localization Method Utilizing Integrated IMU-Aided Cameras for Multiple Autonomous Robots. Sensors, 25(10), 3086. https://doi.org/10.3390/s25103086





