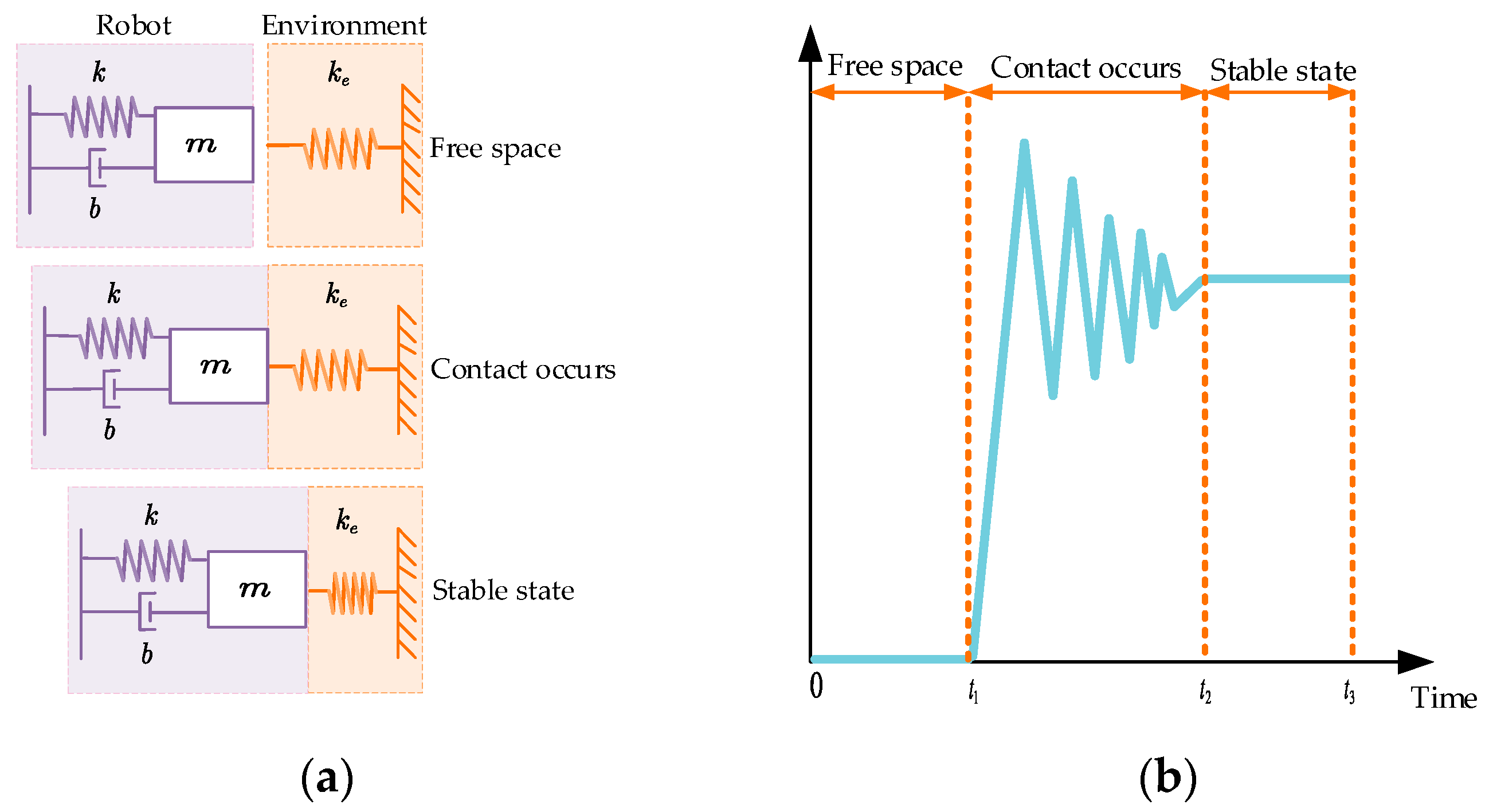
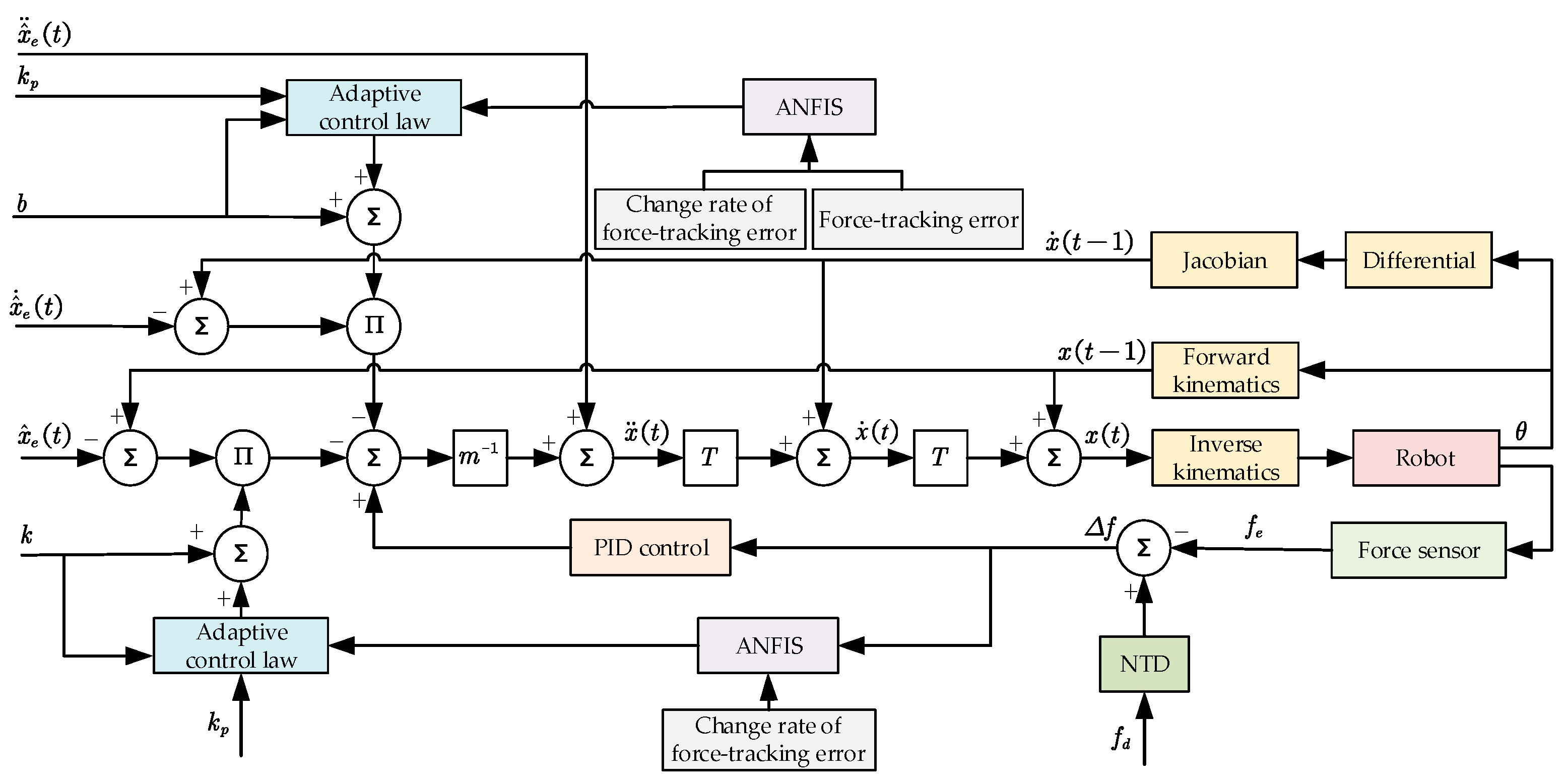
In the process of performing the cleaning task, the cleaning surface may be a more complex curved surface, and the prerequisite of the multi-variable curvature requires that the end-effector of the manipulator maintains a suitable contact force and relative position with the cleaning surface. In accordance with the specific requirements of the mandate, this section investigates the position-based impedance control model and combines it with the adaptive control strategy and ANFIS to design an adaptive variable impedance controller based on ANFIS, which contains the following: (1) an adaptive variable impedance controller is designed, which can adaptively adjust the damping and stiffness coefficients; (2) the stability and convergence of the adaptive variable impedance control algorithm were analyzed, and the stability boundary conditions of the algorithm were obtained; and (3) ANFIS was used to adaptively adjust the update rate instead of the traditional fuzzy controller.
3.1. Design of an Adaptive Variable Impedance Controller
When a manipulator performs a cleaning task, the operating environment usually has non-structural characteristics, such as more complex curved surfaces. In this kind of environment position, the traditional impedance control cannot realize better force tracking due to the dependence on fixed environment parameters, and, thus, cannot complete the work of cleaning tasks, which requires the estimation of the position of the environment. Assuming the environment prediction value , is the environment position perturbation; at this time, the corresponding trajectory error is , which is brought into Equation (1) to obtain the force-tracking error .
To eliminate the steady-state error in force tracking, AVIC can be used to adjust the impedance parameters to adapt to the environmental changes, but, to prevent the system from oscillating, we generally do not modify the mass parameters [
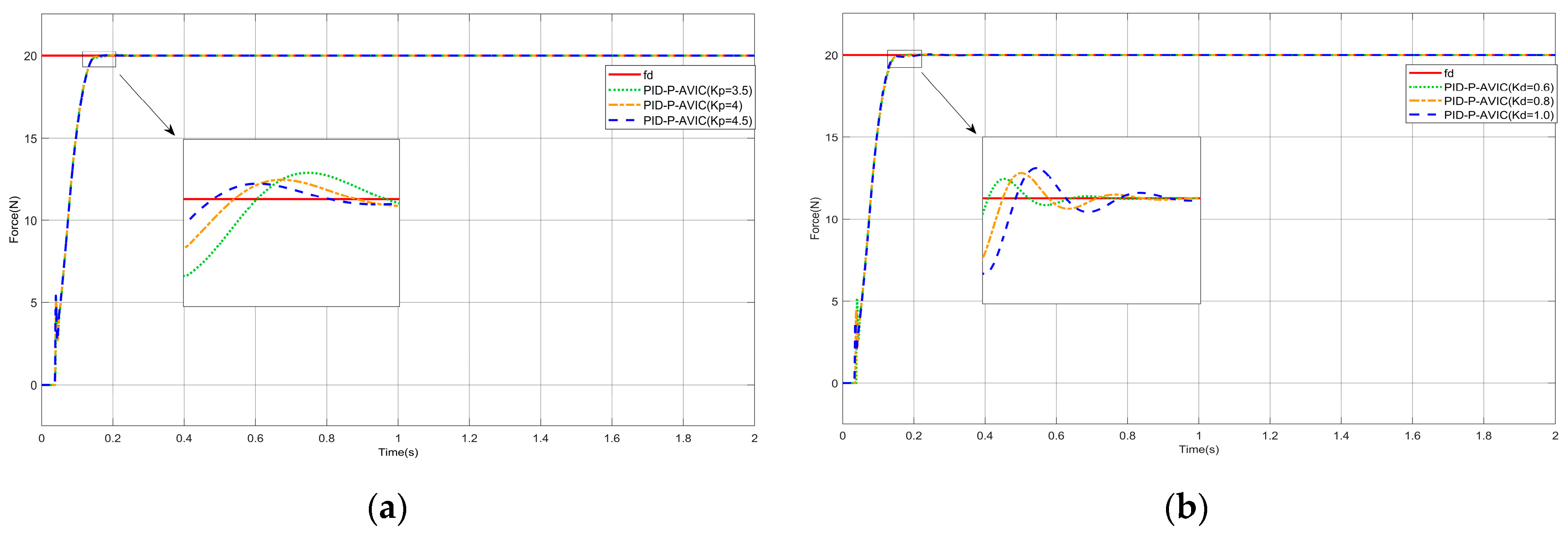
33]. Therefore, in this paper, the damping coefficients and stiffness coefficients are dynamically adapted through the use of adaptive control law. Meanwhile, to improve the response speed of the system and reduce the force overshoot, PID control is introduced based on traditional impedance control, and proportional P control is introduced at the update rate, by which the adaptive variable impedance control (PID-P-AVIC) equation obtained is as follows:
where
are the proportional, integral, and differential coefficients in PID control. The expressions for the damping compensation coefficient
and the stiffness compensation coefficient
are shown in Equation (5):
In the above Equation (5),
is the amount of adaptive compensation at period
.
is the sampling rate.
is the update rate, which is used to represent the adaptive gain of the variable. To prevent the denominator in the above equation from being 0,
is set. The final obtained AVIC principle based on ANFIS is shown in
Figure 3.
3.2. Stability and Convergence Analysis of Adaptive Variable Impedance Controllers
In this section, we will give the constraints when the AVIC of this paper is stabilized and prove that the steady-state error of force tracking is 0, based on the stability and convergence proof methods in the literature [
25,
28]. Firstly, Equation (4) is expanded as follows:
Bringing the trajectory error
into Equation (6) gives the following:
Organizing Equation (7) gives the following:
Since the environment is assumed to be a first-order spring system, the contact force between the robot and the environment can be simplified to
, we obtain
,
,
, which can be obtained by taking it into Equation (8):
Setting the environmental estimated force error
, Equation (9) is expressible in a simplified form:
Equation (10) can be simplified by adding both sides of Equation (10) simultaneously with the equation
, and, in order to simplify the subsequent analysis, new variables
and
are introduced, and Equation (10) can be simplified to:
For the adaptive compensation quantity
in the period
, it satisfies the following:
Similarly, the compensation terms for preceding sampling periods
can be derived as
, as formalized in Equation (13):
The equations in Equation (13) can be obtained by adding up the equations:
Since the initial value of
is generally set to
, i.e.,
, this is obtained by taking it into Equation (14):
Equation (16) can be obtained by the same reasoning:
Equation (11) is organized as follows:
Performing Laplace transformation on Equation (17) yields the following:
The characteristic equation derived from Equation (18) is expressed as follows:
Multiply the left and right sides of Equation (19) by
at the same time to obtain the following:
For sufficiently large
, the following asymptotic relation holds:
The sampling period
is assumed to be small enough to ensure that the discrete-time model closely approximates the continuous-time dynamic properties. At this point, the Taylor expansion equation shows that
. Substituting this approximation into Equation (20) yields the following:
Equation (22) is obtained by organizing the following:
Following the Routh–Hurwitz stability criterion, the Routh array is systematically constructed as presented below:
| | |
| | |
| | 0 |
| | 0 |
To ensure the stability of the control system, the Routh–Hurwitz stability conditions mandate that all first-column elements in the Routh array and all coefficients of the characteristic equation must satisfy strict positivity constraints, i.e., the following:
Solving the aforementioned inequalities yields the stability conditions for the adaptive variable impedance controller as follows:
For a stable system, the force steady-state error
can be derived from its Laplace-domain representation. The error calculation methodology is formalized in Equation (26):
where
denotes the error signal in the Laplace domain. When the system is subjected to a unit step input
, the force steady-state error
is computed as follows:
Thus, the conclusive result is derived as follows:
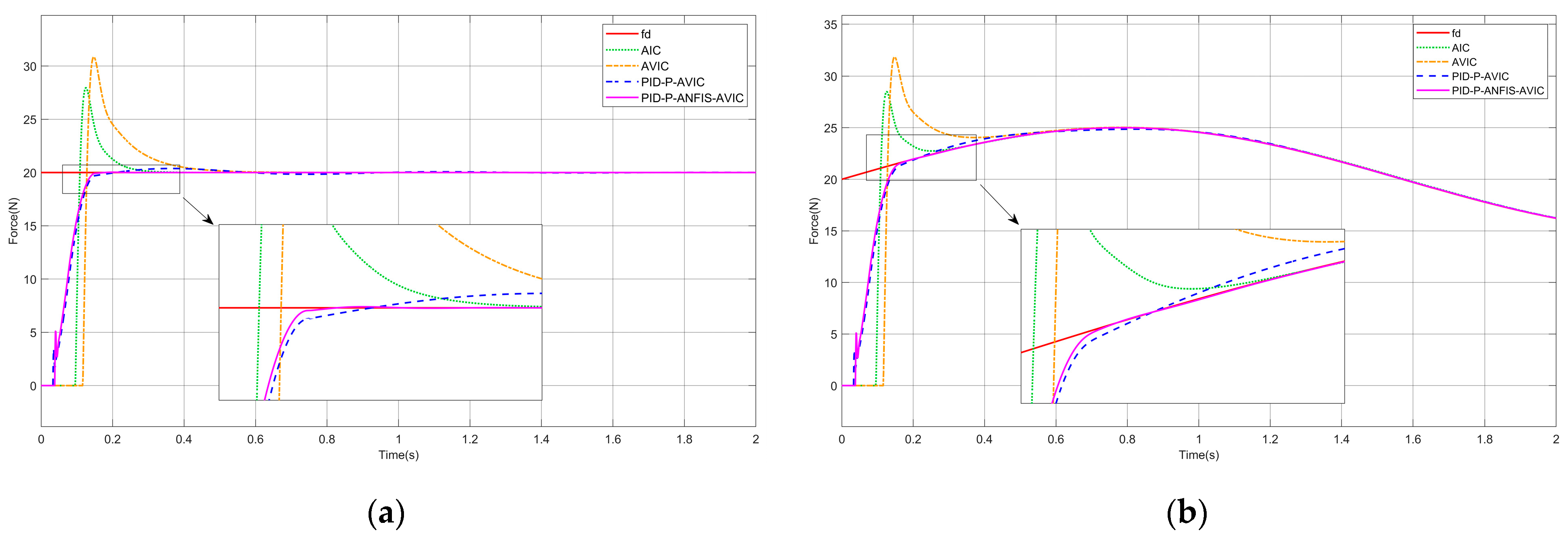
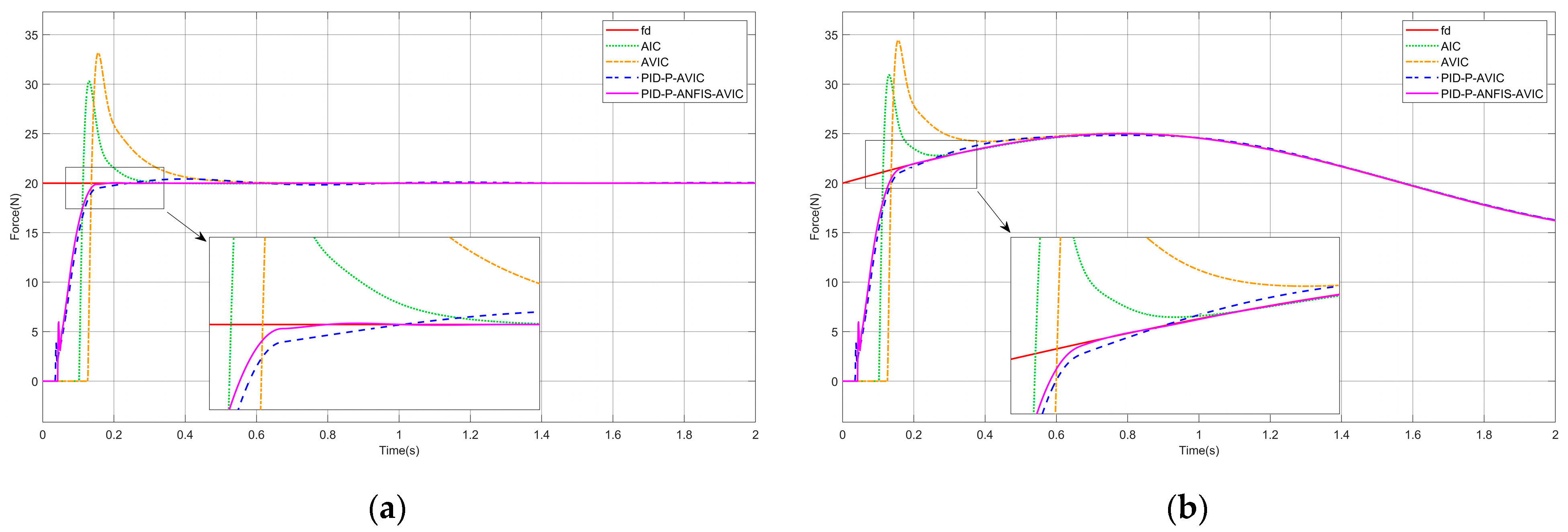
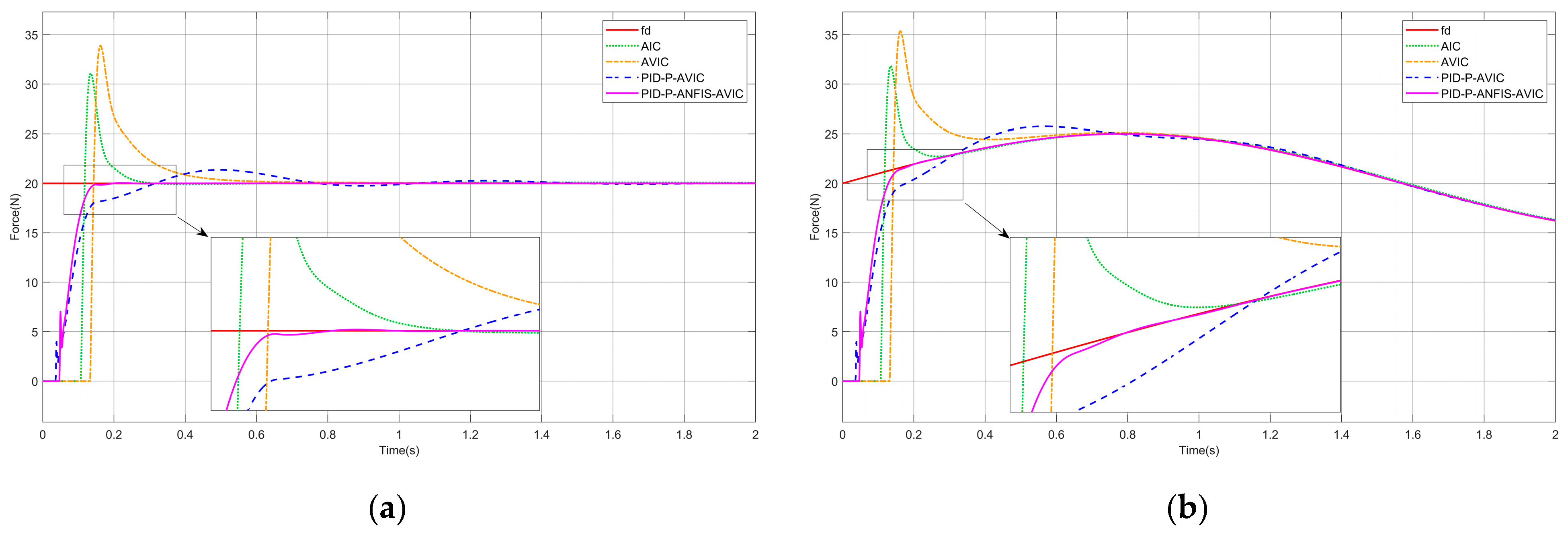
The analytical derivations conclusively demonstrate that the actual contact force asymptotically converges to the desired profile at steady state . Notably, the proposed control architecture maintains robust tracking precision even under time-varying reference signals with complex spectral components.
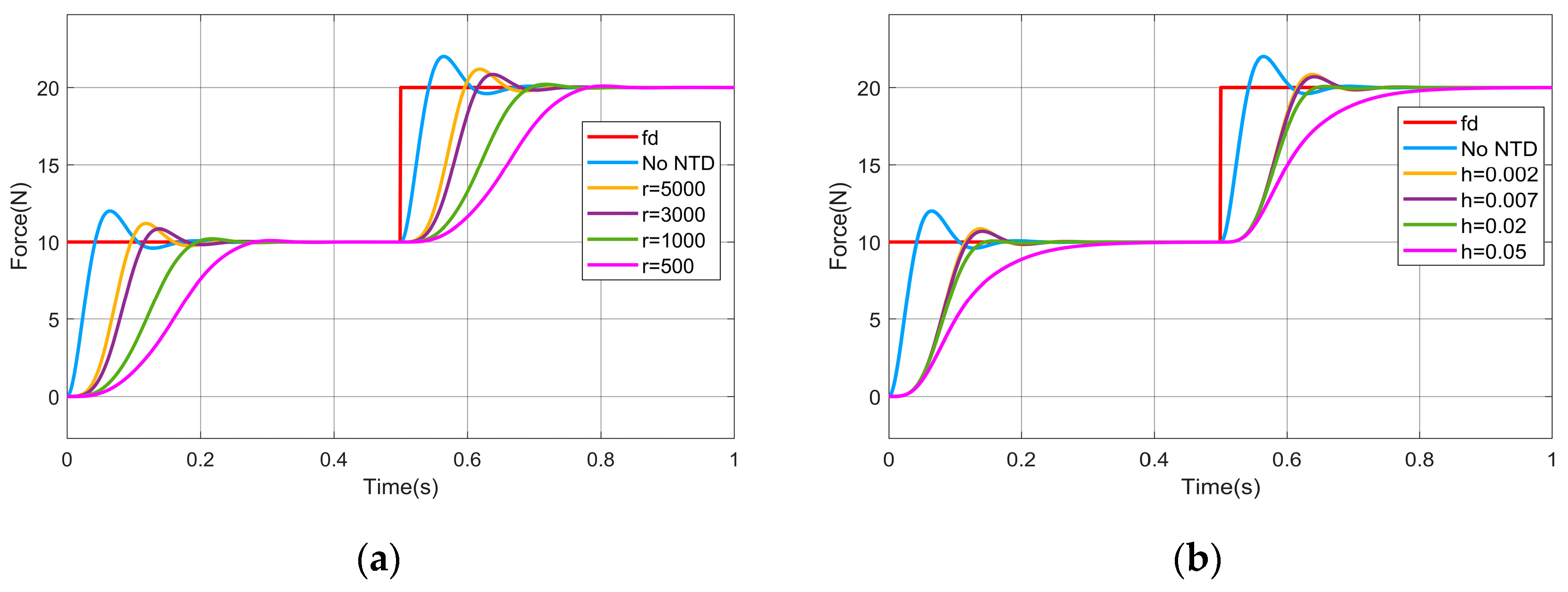
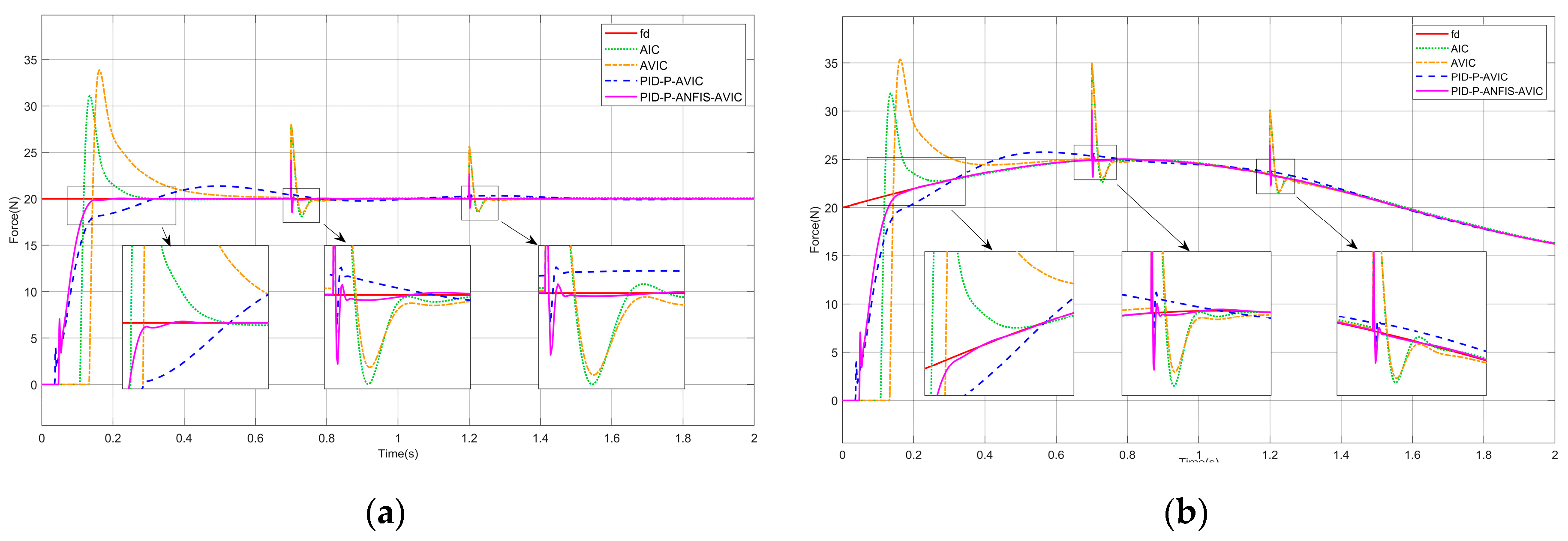
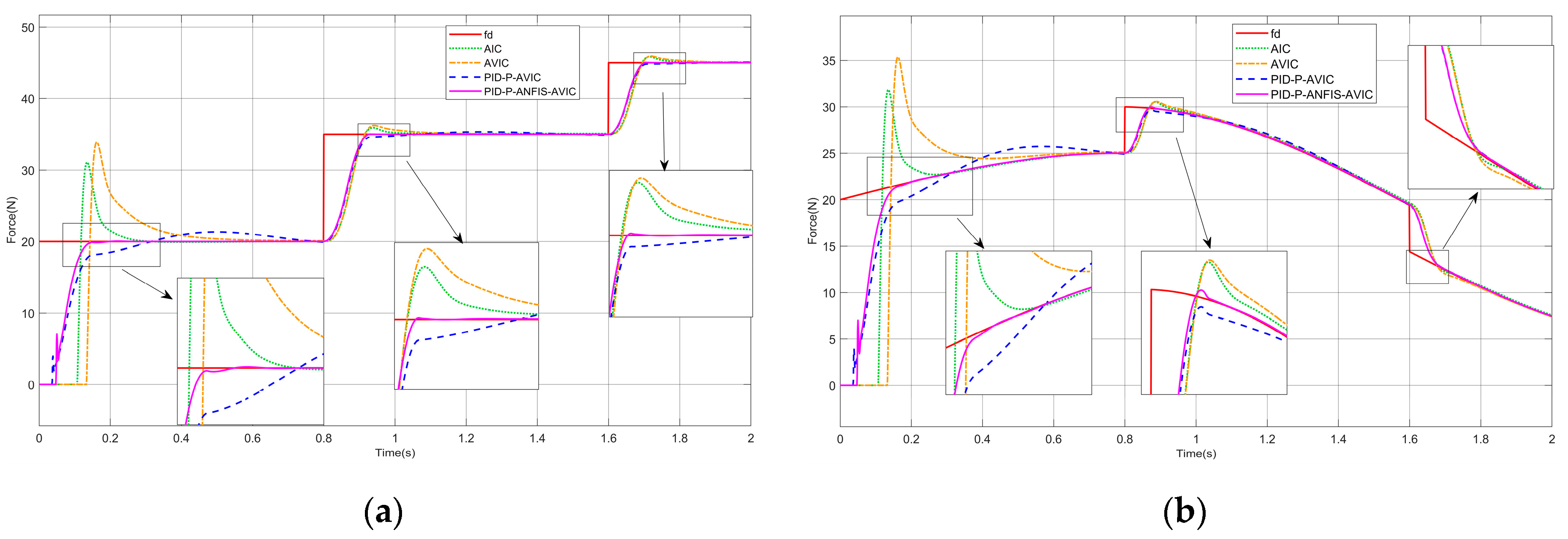
To ensure the successful execution of simulation experiments, systematic parameter selection is conducted under the following principles: The proportional gain is typically set to be greater than 1 to optimize transient response dynamics. For the integral gain , it should be ensured that its effect on the lower limit of the update rate is small; ideally, the lower limit of the update rate should be close to 0, which helps in the subsequent ANFIS design. Therefore, should be selected to be as small as possible while maintaining controller stability. To mitigate the impact of environmental stiffness on the upper bound of the update rate, a larger derivative gain is adopted to satisfy the constraint . Through this parameter configuration, the stability boundary conditions for the update rate are simplified to . This range will serve as the output domain for the ANFIS module.
3.3. Design of ANFIS
As proven in
Section 3.2, the stability boundary conditions of the controller can be derived. However, fixed-update-rate variable impedance controllers exhibit suboptimal control performance [
27], necessitating dynamic update rate adjustments to achieve enhanced control efficacy. To better align with the requirements of cleaning tasks, the dynamic update rate should adhere to the following design principles:
Initial Control Phase: During this stage, both the force-tracking error and manipulator position error of the adaptive variable impedance controller are typically large. A smaller update rate is required to mitigate force overshoot.
Steady-State Control Phase: During this stage, the force-tracking error and manipulator position error diminish significantly. To ensure a sufficient reduction in force steady-state error, a larger update rate must be employed to guarantee precision in force tracking.
Traditional fuzzy controllers can achieve dynamic parameter adjustment but typically rely on expert knowledge to manually define fuzzy rules [
37,
38]. It usually includes the following: setting the fuzzy subsets of the input parameters, determining the range of the domain scopes of individual parameters, designing the affiliation function of the parameters, and, finally, building a fuzzy control rule table based on the experience of experts [
39]. To address the limitations of conventional fuzzy controllers, a fuzzy neural network (FNN) can be employed to automate fuzzy rule learning and enable adaptive parameter tuning. A typical FNN architecture comprises a fuzzification layer, a fuzzy rule layer, a defuzzification layer, and a fuzzy inference engine [
40]. In this study, we adopt the Takagi–Sugeno model-based ANFIS as an advanced alternative. By integrating the semantic reasoning capabilities of fuzzy logic systems (FLSs) with the nonlinear learning abilities of artificial neural networks (ANNs), ANFIS achieves a smooth modulation of the controller’s update rate.
In Takagi–Sugeno fuzzy inference frameworks employing dual inputs and a single output, e.g., two inputs
and
, where
is partitioned into the fuzzy set
and
is partitioned into the fuzzy set
, the
rule can usually be represented as follows [
41]:
If is and is , then .
Here, and represent the fuzzy linguistic sets corresponding to the rule’s input and ; and denotes the output of the rule. These parameters are referred to as the consequent parameters.
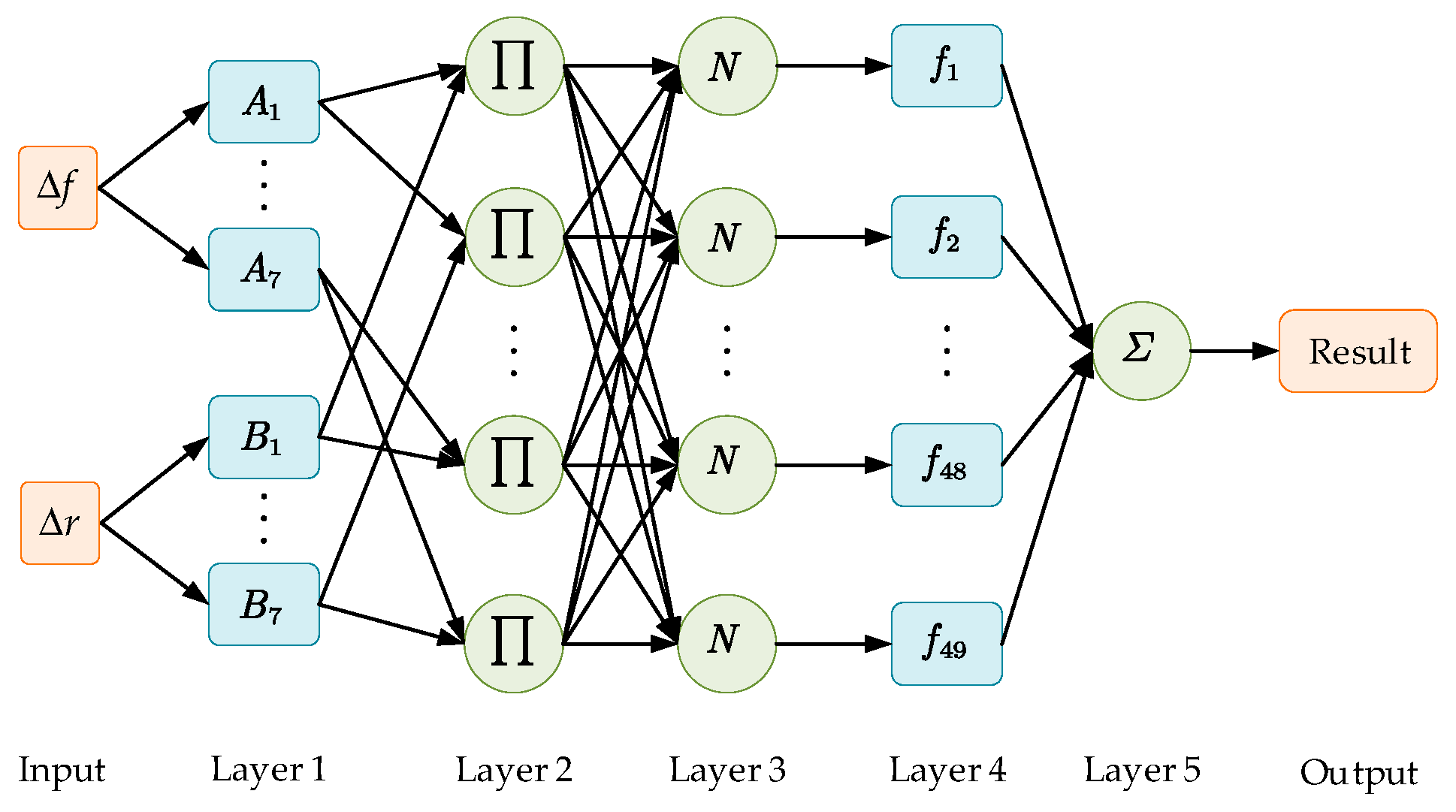
In this paper, we need to dynamically calculate the update rate based on the force-tracking error and the rate of change of the force-tracking error. As described in Reference [
41], the proposed ANFIS adopts a five-layer architecture, as illustrated in
Figure 4. The detailed explanation of each layer is as follows:
Layer 1: This layer computes the membership degree of each input variable to its corresponding fuzzy set. It incorporates two input variables: the force-tracking error
and the rate of force-tracking error change
. The node function for each adaptive node
is defined as follows:
where
and
are the fuzzy linguistic labels assigned to the inputs,
is the output of the
node in Layer 1, and the membership functions employ Gaussian and triangular forms.
Layer 2: The output of each node represents the activation strength of the rule. which is the product of the affiliation of the input variables, as shown in Equation (30):
where
is the rule number and there are 49 rules, and
is the activation strength of each rule.
Layer 3: This layer normalizes the triggering strength of each rule to ensure that the weights sum to 1, avoiding certain rules from over-dominating the output. The function is expressed as follows:
where
is the weight of the normalized rule and the denominator is the sum of the activation strengths of all rules.
Layer 4: This layer calculates the output of each rule, which can be a constant or a linear function. In this work, a linear function is adopted:
where
denotes the consequent parameter set of the fuzzy rules.
Layer 5: This layer aggregates the weighted outputs of all rules to produce the final crisp output:
Regarding the choice of the membership function, common membership functions include the Gaussian membership function, triangular membership function, and trapezoidal membership function. The Gaussian membership function is suitable for continuous and smooth fuzzy sets, suitable for simulating data with a clear central tendency and gradual transition, which helps to improve the smoothness of fuzzy rules; the triangular membership function is suitable for symmetric or single-peaked fuzzy sets, which has high computational efficiency, and only needs three parameters (left boundary, right boundary, and vertex) to divide the input space efficiently, which provides a good balance between the smoothness of the rules and the computational efficiency. The trapezoidal membership function is an extension of the triangular membership function, which is suitable for describing multi-peaks or flat fuzzy sets, and requires more parameters to be defined, and, at the same time, increases the complexity of the model and the computational burden. There are also the Sigmoid membership function (suitable for describing monotonically increasing or decreasing fuzzy sets), Z-shaped membership function (suitable for describing decreasing fuzzy sets), and so on. In summary, this paper chooses a compromise between fuzzy rule smoothness and computational efficiency, i.e., a combination of Gaussian and triangular membership functions.
The ANFIS employs a hybrid-learning algorithm for parameter optimization, which operates in two sequential phases: forward propagation and backward propagation. During the forward phase, the premise parameters maintain static values, whereas the consequent parameters undergo refinement through least squares optimization to minimize the output error. In the backward phase, the consequent parameters are held constant, and the premise parameters are adjusted via gradient descent to further reduce the error. To enhance the model’s generalizability, Gaussian noise with an amplitude equivalent to of the input range is injected into the training data, while boundary constraints are enforced to ensure physical feasibility.
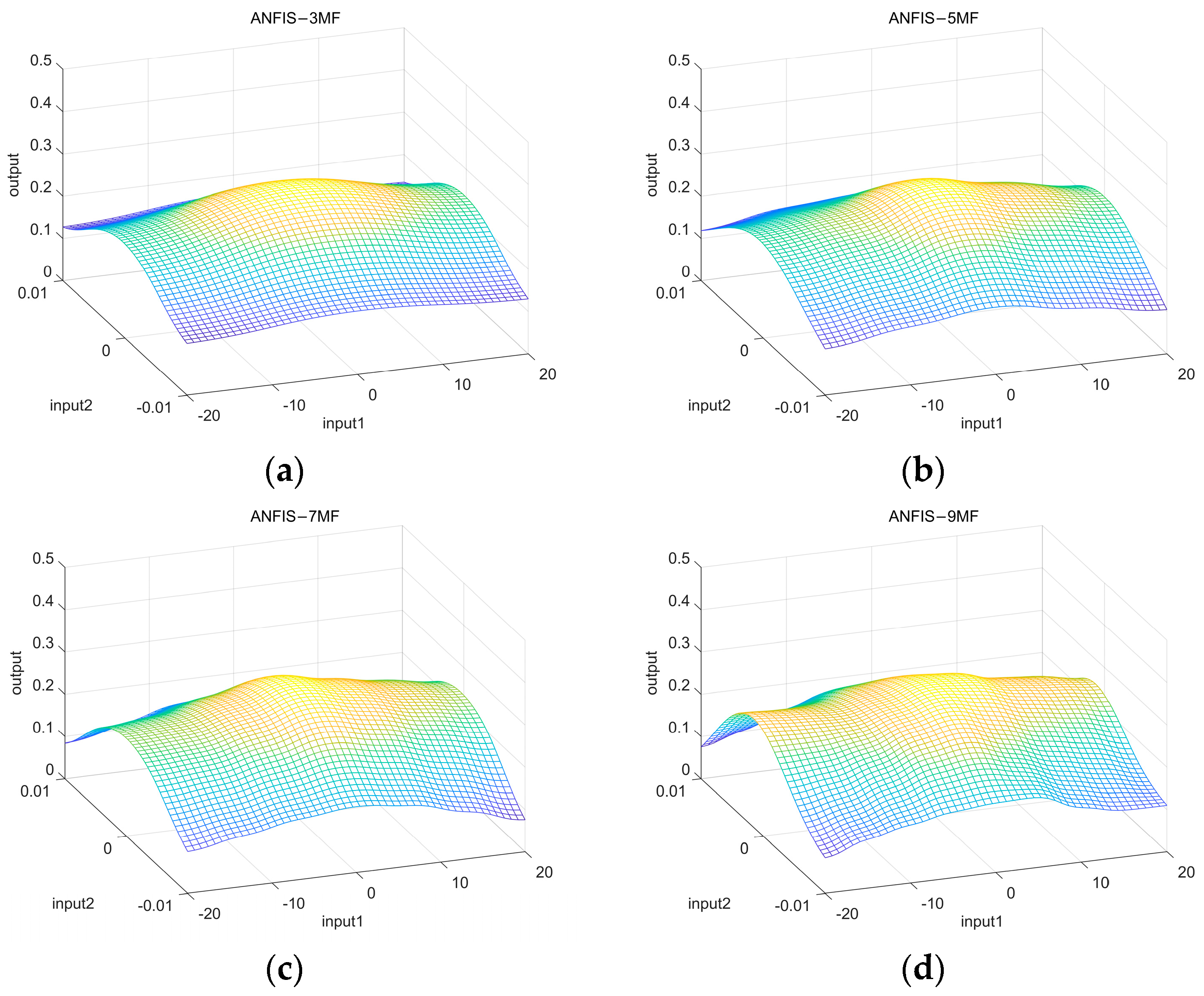
In order to verify the reasonableness of using seven membership functions for the input variables of ANFIS, preliminary experiments are designed in this paper for verification. The experiments were set up with the number of membership functions less than 7 (e.g., 3 and 5) or more than 7 (e.g., 9) and the average absolute error of the model was measured, and the fuzzy rule surfaces with different numbers of membership functions are shown in
Figure 5. The experimental results show that the mean absolute error corresponds to 0.0198, 0.0177, and 0.0156, when the number of membership functions is 3, 5, and 7, respectively. And, when the number of membership functions is 9, the average absolute error is 0.0150; the average absolute error is not significantly reduced, but the computational burden is increased. Therefore, this paper uses seven membership functions for each input variable.