Evaluating PurpleAir Sensors: Do They Accurately Reflect Ambient Air Temperature?
Abstract
Highlights
- PurpleAir sensors exhibit strong temperature overestimations with an MAE of 4.71 °C and RMSE of 6.30 °C.
- Sensor performance demonstrates nonlinear behavior with significant seasonal and diurnal variations.
- Calibrated PurpleAir sensors have the potential to advance hyperlocal heat mapping and multi-hazard vulnerability assessments.
Abstract
1. Introduction
2. Materials and Methods
2.1. Collocated Temperature Sensor Network and Data Preprocessing
2.2. Sensor Data Preprocessing
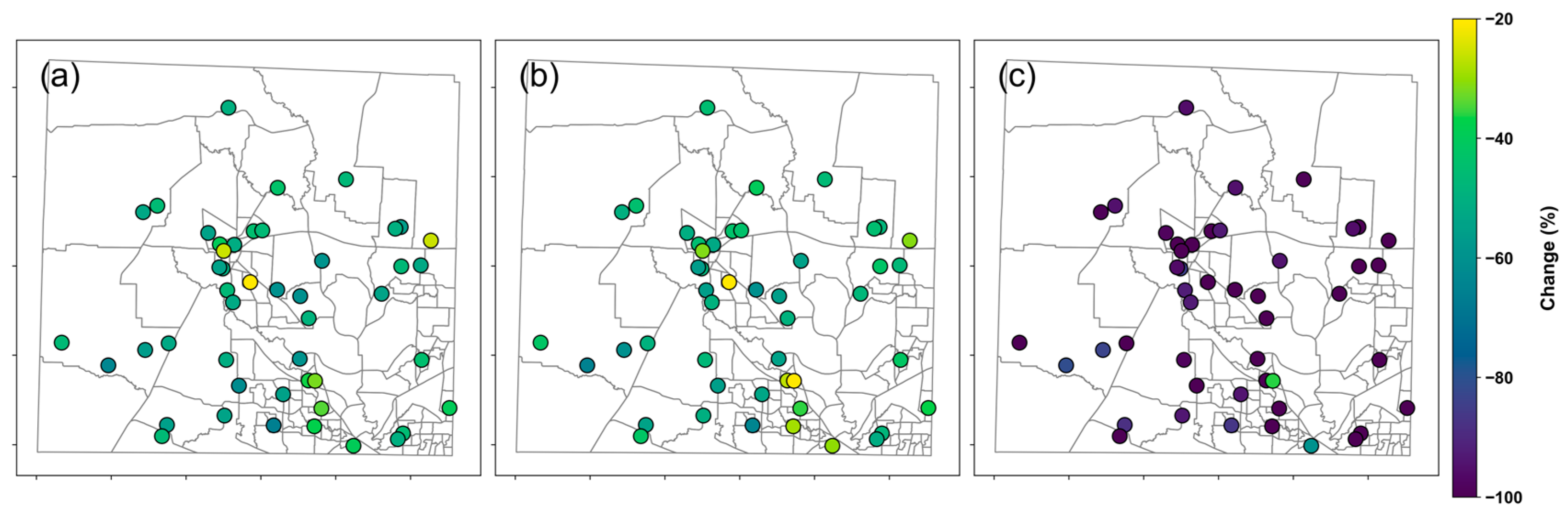
2.3. Spatial-Temporal Variations in Sensor Performance
2.4. Performance Metrics
2.5. Independent Variables
2.6. Developing Calibration Models
- Model 1: Simple linear regression
- Model 2: MLR with an additive RHPA term
- Model 3: MLR with an additive SW term
- Model 4: MLR with an additive LW term
- Model 5: MLR with additive SW and LW terms
- Model 6: MLR with additive RHPA, LW, and SW terms
- Model 7: MLR with additive RHPA, LW, SW, and WNDS terms
- Model 8: MLR with additive and multiplicative TPA and RHPA terms
2.7. Performance in Apparent Temperature Calculation
3. Results and Discussion
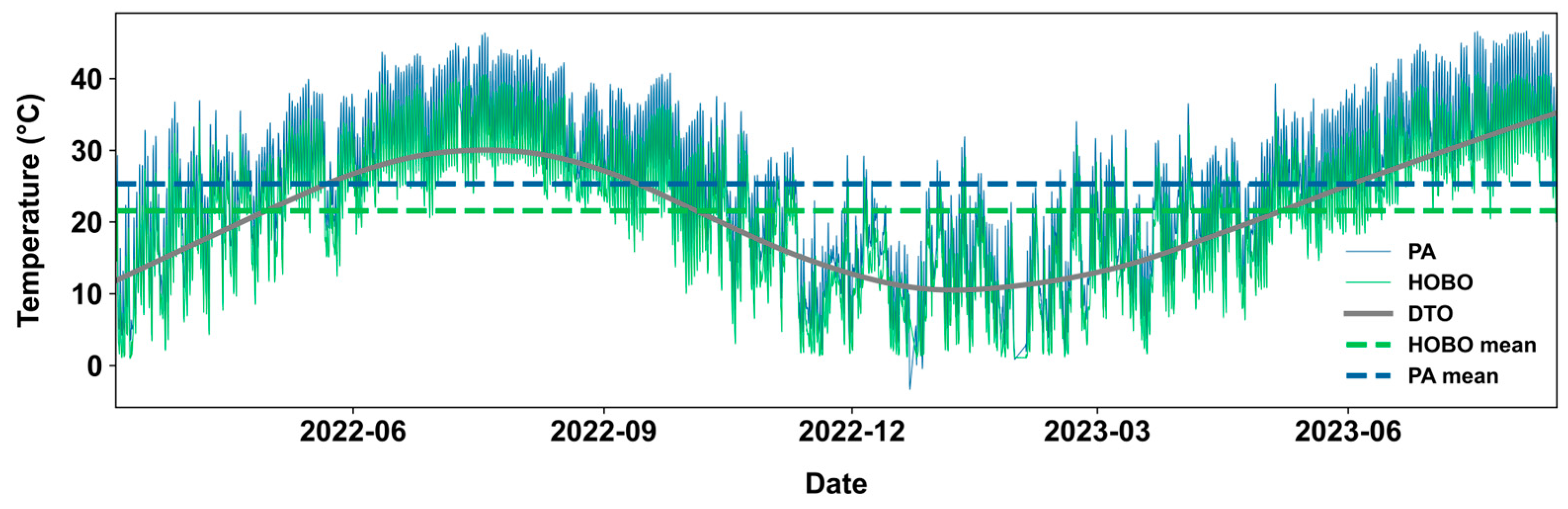
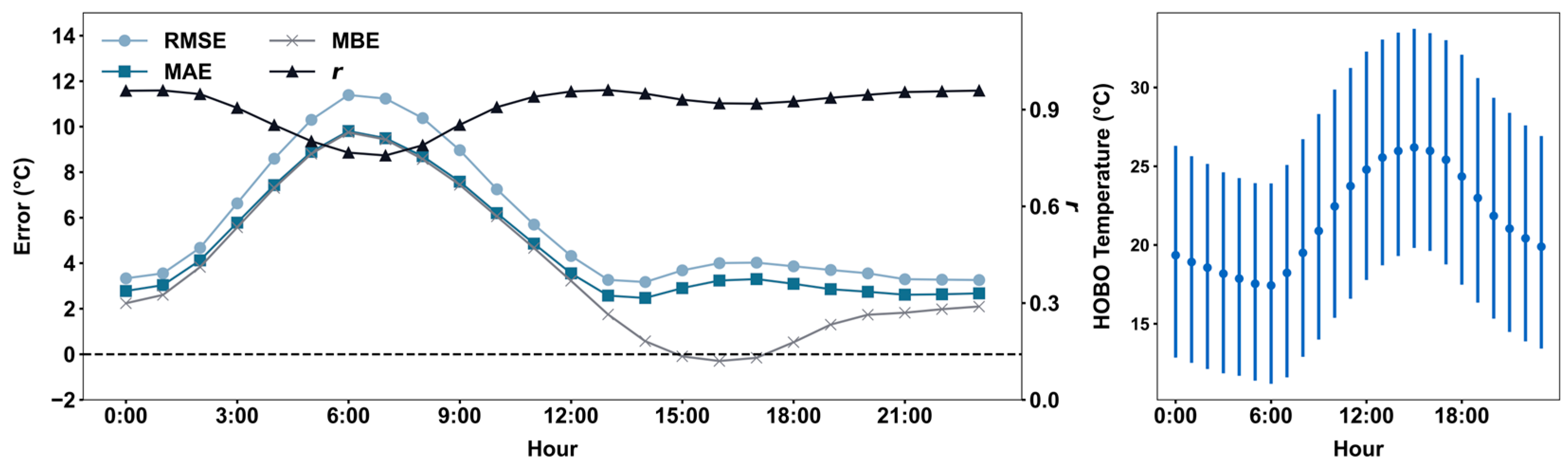
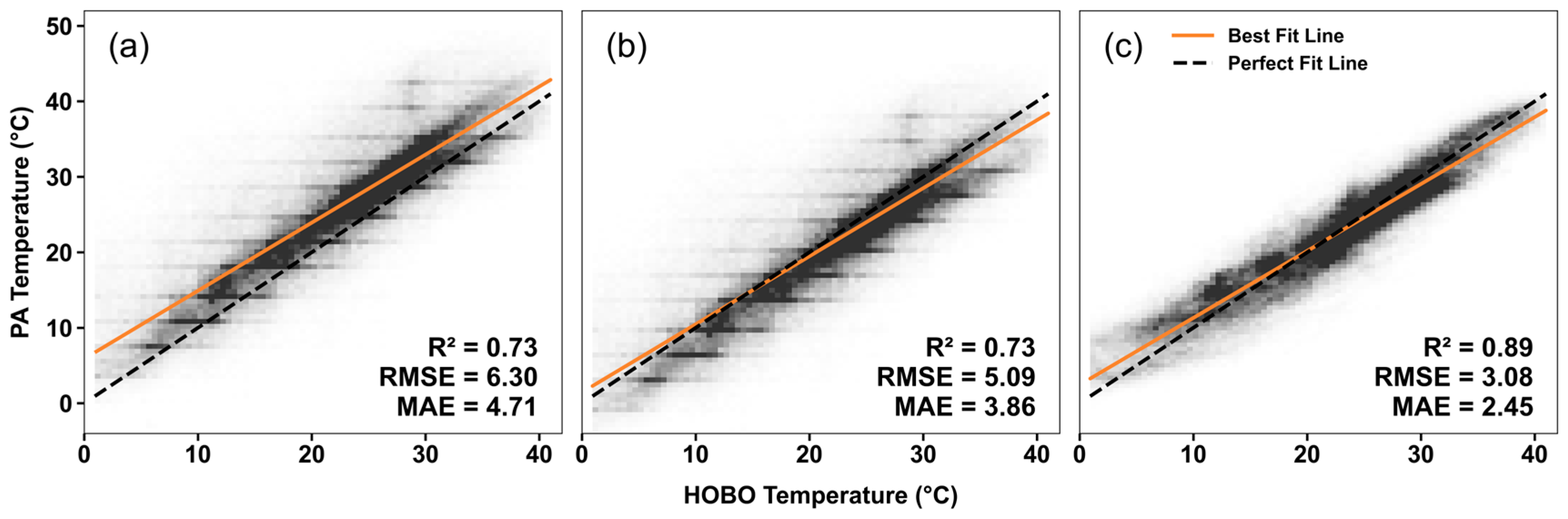
3.1. Evaluation of Uncalibrated PA Temperature Measurements
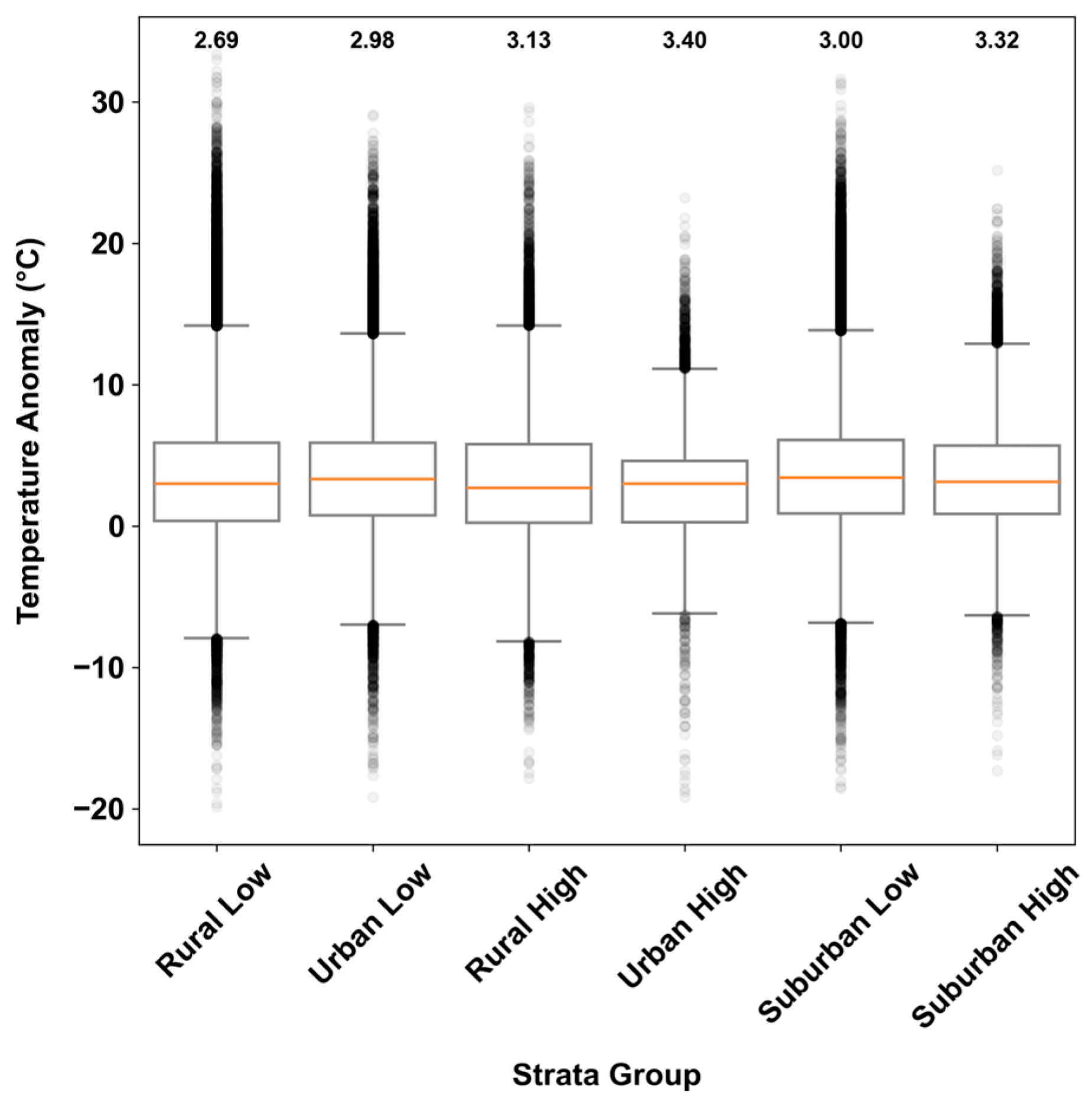
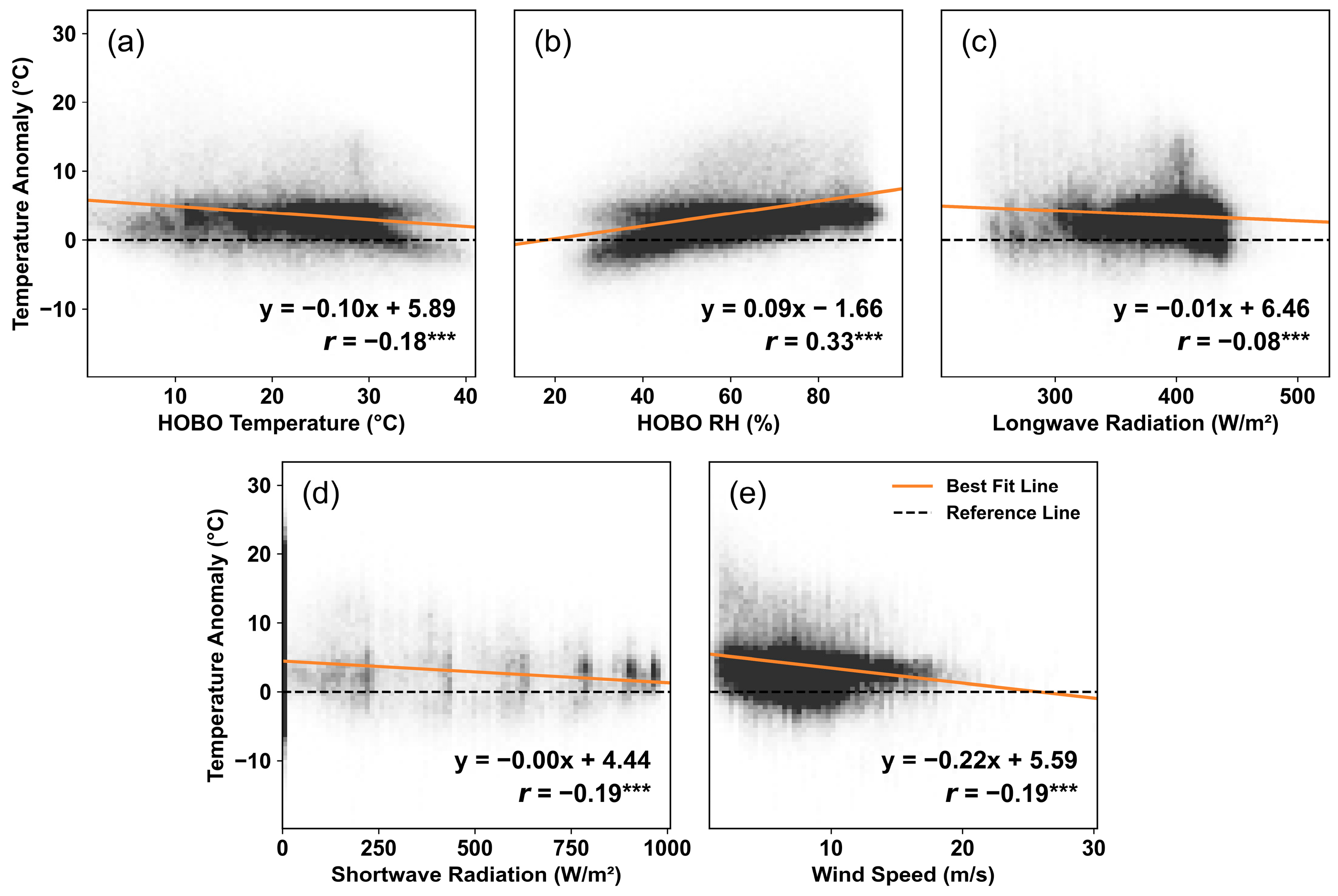
3.2. Factors Influencing Termpretuare Anomaly
3.3. Comparison of Calibration Models for PA Temperature Sensors
3.4. Evalutation in the Context of the Heat Index
4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LCS | Low-cost sensors |
| PA | PurpleAir |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| AIC | Akaike information criterion |
| RH | Relative humidity |
| WNDS | Wind speed |
| LW | Longwave downwelling surface irradiance |
| SW | Shortwave downwelling surface irradiance |
| UHI | Urban heat island |
| HI | Heat Index |
| MLR | Multiple linear regression |
| VIF | Variance inflation factor |
References
- Muller, C.L.; Chapman, L.; Johnston, S.; Kidd, C.; Illingworth, S.; Foody, G.; Overeem, A.; Leigh, R.R. Crowdsourcing for Climate and Atmospheric Sciences: Current Status and Future Potential. Int. J. Climatol. 2015, 35, 3185–3203. [Google Scholar] [CrossRef]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.W.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The Changing Paradigm of Air Pollution Monitoring. Environ. Sci. Technol. 2013, 47, 11369–11377. [Google Scholar] [CrossRef] [PubMed]
- Chapman, L.; Bell, S.; Randall, S. Can Crowdsourcing Increase the Durability of an Urban Meteorological Network? Urban Clim. 2023, 49, 101542. [Google Scholar] [CrossRef]
- Chapman, L.; Bell, C.; Bell, S. Can the Crowdsourcing Data Paradigm Take Atmospheric Science to a New Level? A Case Study of the Urban Heat Island of London Quantified Using Netatmo Weather Stations. Int. J. Climatol. 2017, 37, 3597–3605. [Google Scholar] [CrossRef]
- Liang, L.; Daniels, J.; Bailey, C.; Hu, L.; Phillips, R.; South, J. Integrating Low-Cost Sensor Monitoring, Satellite Mapping, and Geospatial Artificial Intelligence for Intra-Urban Air Pollution Predictions. Environ. Pollut. 2023, 331, 121832. [Google Scholar] [CrossRef]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The Rise of Low-Cost Sensing for Managing Air Pollution in Cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of Low-Cost Sensing Technologies for Air Quality Monitoring and Exposure Assessment: How Far Have They Gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef]
- Liang, L.; Gong, P.; Cong, N.; Li, Z.; Zhao, Y.; Chen, Y. Assessment of Personal Exposure to Particulate Air Pollution: The First Result of City Health Outlook (CHO) Project. BMC Public Health 2019, 19, 711. [Google Scholar] [CrossRef]
- Dodds, P.S.; Mitchell, L.; Reagan, A.J.; Danforth, C.M. Tracking Climate Change through the Spatiotemporal Dynamics of the Teletherms, the Statistically Hottest and Coldest Days of the Year. PLoS ONE 2016, 11, e0154184. [Google Scholar] [CrossRef]
- Lu, Y.; Giuliano, G.; Habre, R. Estimating Hourly PM2.5 Concentrations at the Neighborhood Scale Using a Low-Cost Air Sensor Network: A Los Angeles Case Study. Environ. Res. 2021, 195, 110653. [Google Scholar] [CrossRef]
- Yadav, N.; Sharma, C. Spatial Variations of Intra-City Urban Heat Island in Megacity Delhi. Sustain. Cities Soc. 2018, 37, 298–306. [Google Scholar] [CrossRef]
- Amegah, A.K.; Dakuu, G.; Mudu, P.; Jaakkola, J.J.K. Particulate Matter Pollution at Traffic Hotspots of Accra, Ghana: Levels, Exposure Experiences of Street Traders, and Associated Respiratory and Cardiovascular Symptoms. J. Expo. Sci. Environ. Epidemiol. 2022, 32, 333–342. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2018, 11, 48. [Google Scholar] [CrossRef]
- Paciorek, C.J.; Liu, Y. Limitations of Remotely Sensed Aerosol as a Spatial Proxy for Fine Particulate Matter. Environ. Health Perspect. 2009, 117, 904–909. [Google Scholar] [CrossRef]
- Liang, L. Calibrating Low-Cost Sensors for Ambient Air Monitoring: Techniques, Trends, and Challenges. Environ. Res. 2021, 197, 111163. [Google Scholar] [CrossRef] [PubMed]
- Zabow, M.; Jones, H.; Trtanj, J.; McMahon, K.; Schramm, P. The National Integrated Heat Health Information System: A Federal Approach to Addressing Extreme Heat and Health. In Proceedings of the 103rd AMS Annual Meeting, Denver, CO, USA, 8–12 January 2023. [Google Scholar]
- Li, H.; Sodoudi, S.; Liu, J.; Tao, W. Temporal Variation of Urban Aerosol Pollution Island and Its Relationship with Urban Heat Island. Atmos. Res. 2020, 241, 104957. [Google Scholar] [CrossRef]
- Li, H.; Meier, F.; Lee, X.; Chakraborty, T.; Liu, J.; Schaap, M.; Sodoudi, S. Interaction between Urban Heat Island and Urban Pollution Island during Summer in Berlin. Sci. Total Environ. 2018, 636, 818–828. [Google Scholar] [CrossRef]
- Ulpiani, G. On the Linkage between Urban Heat Island and Urban Pollution Island: Three-Decade Literature Review towards a Conceptual Framework. Sci. Total Environ. 2021, 751, 141727. [Google Scholar] [CrossRef]
- Johnson, K.; Holder, A.; Frederick, S.; Hagler, G.; Clements, A. PurpleAir PM2.5 Performance across the U.S.#2, 2020. In Proceedings of the Meeting between ORD, OAR/AirNow, and USFS, Research Triangle Park, NC, USA, 3 February 2020. [Google Scholar]
- Feenstra, B.; Papapostolou, V.; Hasheminassab, S.; Zhang, H.; Boghossian, B.D.; Cocker, D.; Polidori, A. Performance Evaluation of Twelve Low-Cost PM2.5 Sensors at an Ambient Air Monitoring Site. Atmos. Environ. 2019, 216, 116946. [Google Scholar] [CrossRef]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can Commercial Low-Cost Sensor Platforms Contribute to Air Quality Monitoring and Exposure Estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef]
- Ardon-Dryer, K.; Dryer, Y.; Williams, J.N.; Moghimi, N. Measurements of PM2.5 with PurpleAir under Atmospheric Conditions. Atmos. Meas. Tech. 2020, 13, 5441–5458. [Google Scholar] [CrossRef]
- Campmier, M.J.; Gingrich, J.; Singh, S.; Baig, N.; Gani, S.; Upadhya, A.; Agrawal, P.; Kushwaha, M.; Mishra, H.R.; Pillarisetti, A.; et al. Seasonally Optimized Calibrations Improve Low-Cost Sensor Performance: Long-Term Field Evaluation of PurpleAir Sensors in Urban and Rural India. Atmos. Meas. Tech. 2023, 16, 4357–4374. [Google Scholar] [CrossRef]
- Barkjohn, K.K.; Holder, A.L.; Frederick, S.G.; Clements, A.L. Correction and Accuracy of PurpleAir PM2.5 Measurements for Extreme Wildfire Smoke. Sensors 2022, 22, 9669. [Google Scholar] [CrossRef]
- Stavroulas, I.; Grivas, G.; Michalopoulos, P.; Liakakou, E.; Bougiatioti, A.; Kalkavouras, P.; Fameli, K.; Hatzianastassiou, N.; Mihalopoulos, N.; Gerasopoulos, E. Field Evaluation of Low-Cost PM Sensors (Purple Air PA-II) Under Variable Urban Air Quality Conditions, in Greece. Atmosphere 2020, 11, 926. [Google Scholar] [CrossRef]
- Couzo, E.; Valencia, A.; Gittis, P. Evaluation and Correction of PurpleAir Temperature and Relative Humidity Measurements. Atmosphere 2024, 15, 415. [Google Scholar] [CrossRef]
- PurpleAir. PurpleAir Sensors Functional Overview. Available online: https://community.purpleair.com/t/purpleair-sensors-functional-overview/150 (accessed on 15 December 2024).
- Liang, L.; Daniels, J. What Influences Low-Cost Sensor Data Calibration?—A Systematic Assessment of Algorithms, Duration, and Predictor Selection. Aerosol Air Qual. Res. 2022, 22, 220076. [Google Scholar] [CrossRef]
- McBroom, B.D.; Rahn, D.A.; Brunsell, N.A. Urban Fraction Influence on Local Nocturnal Cooling Rates from Low-Cost Sensors in Dallas-Fort Worth. Urban Clim. 2024, 53, 101823. [Google Scholar] [CrossRef]
- Onset Computer Corporation. HOBO MX1101 Data Logger. Available online: https://www.onsetcomp.com/products/data-loggers/mx1101 (accessed on 15 December 2024).
- Oke, T. Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites; World Meteorological Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Nayak, B.; Hazra, A. How to Choose the Right Statistical Test? Indian J. Ophthalmol. 2011, 59, 85. [Google Scholar] [CrossRef] [PubMed]
- Giordano, M.R.; Malings, C.; Pandis, S.N.; Presto, A.A.; McNeill, V.F.; Westervelt, D.M.; Beekmann, M.; Subramanian, R. From Low-Cost Sensors to High-Quality Data: A Summary of Challenges and Best Practices for Effectively Calibrating Low-Cost Particulate Matter Mass Sensors. J. Aerosol Sci. 2021, 158, 105833. [Google Scholar] [CrossRef]
- Barkjohn, K.K.; Gantt, B.; Clements, A.L. Development and Application of a United States-Wide Correction for PM2.5 Data Collected with the PurpleAir Sensor. Atmos. Meas. Tech. 2021, 14, 4617–4637. [Google Scholar] [CrossRef]
- Raheja, G.; Nimo, J.; Appoh, E.K.-E.; Essien, B.; Sunu, M.; Nyante, J.; Amegah, M.; Quansah, R.; Arku, R.E.; Penn, S.L.; et al. Low-Cost Sensor Performance Intercomparison, Correction Factor Development, and 2+ Years of Ambient PM2.5 Monitoring in Accra, Ghana. Environ. Sci. Technol. 2023, 57, 10708–10720. [Google Scholar] [CrossRef] [PubMed]
- Bi, J.; Wildani, A.; Chang, H.H.; Liu, Y. Incorporating Low-Cost Sensor Measurements into High-Resolution PM2.5 Modeling at a Large Spatial Scale. Environ. Sci. Technol. 2020, 54, 2152–2162. [Google Scholar] [CrossRef]
- Malings, C.; Tanzer, R.; Hauryliuk, A.; Saha, P.K.; Robinson, A.L.; Presto, A.A.; Subramanian, R. Fine Particle Mass Monitoring with Low-Cost Sensors: Corrections and Long-Term Performance Evaluation. Aerosol. Sci. Technol. 2020, 54, 160–174. [Google Scholar] [CrossRef]
- Patel, M.Y.; Vannucci, P.F.; Kim, J.; Berelson, W.M.; Cohen, R.C. Towards a Hygroscopic Growth Calibration for Low-Cost PM2.5 Sensors. Atmos. Meas. Tech. 2024, 17, 1051–1060. [Google Scholar] [CrossRef]
- Malm, W.C.; Schichtel, B.A.; Prenni, A.J.; Day, D.; Perkins, R.J.; Sullivan, A.; Tigges, M. The Dependence of PurpleAir Sensors on Particle Size Distribution and Meteorology and Their Relationship to Integrating Nephelometers. Atmos. Environ. 2024, 337, 120757. [Google Scholar] [CrossRef]
- Wild, M. The Global Energy Balance as Represented in CMIP6 Climate Models. Clim. Dyn. 2020, 55, 553–577. [Google Scholar] [CrossRef]
- GOES-E SSI. OSI SAF GOES-East Surface Solar Irradiance 2021-Onwards, OSI-306-b. EUMETSAT Ocean and Sea Ice Satellite Application Facility. Available online: https://osi-saf.eumetsat.int/products/osi-306-b (accessed on 5 May 2025).
- Ho, H.C.; Knudby, A.; Xu, Y.; Hodul, M.; Aminipouri, M. A Comparison of Urban Heat Islands Mapped Using Skin Temperature, Air Temperature, and Apparent Temperature (Humidex), for the Greater Vancouver Area. Sci. Total Environ. 2016, 544, 929–938. [Google Scholar] [CrossRef]
- Romps, D.M. Heat Index Extremes Increasing Several Times Faster than the Air Temperature. Environ. Res. Lett. 2024, 19, 041002. [Google Scholar] [CrossRef]
- Méndez-Lázaro, P.; Muller-Karger, F.E.; Otis, D.; McCarthy, M.J.; Rodríguez, E. A Heat Vulnerability Index to Improve Urban Public Health Management in San Juan, Puerto Rico. Int. J. Biometeorol. 2018, 62, 709–722. [Google Scholar] [CrossRef]
- Lu, Y.-C.; Romps, D.M. Extending the Heat Index. J. Appl. Meteorol. Climatol. 2022, 61, 1367–1383. [Google Scholar] [CrossRef]
- Concas, F.; Mineraud, J.; Lagerspetz, E.; Varjonen, S.; Liu, X.; Puolamäki, K.; Nurmi, P.; Tarkoma, S. Low-Cost Outdoor Air Quality Monitoring and Sensor Calibration: A Survey and Critical Analysis. ACM Trans. Sens. Netw. 2021, 17, 1–44. [Google Scholar] [CrossRef]
- Wallace, L.; Bi, J.; Ott, W.R.; Sarnat, J.; Liu, Y. Calibration of Low-Cost PurpleAir Outdoor Monitors Using an Improved Method of Calculating PM. Atmos. Environ. 2021, 256, 118432. [Google Scholar] [CrossRef]
- Zheng, T.; Bergin, M.H.; Johnson, K.K.; Tripathi, S.N.; Shirodkar, S.; Landis, M.S.; Sutaria, R.; Carlson, D.E. Field Evaluation of Low-Cost Particulate Matter Sensors in High- and Low-Concentration Environments. Atmos. Meas. Tech. 2018, 11, 4823–4846. [Google Scholar] [CrossRef]
- Oke, T.R. The Energetic Basis of the Urban Heat Island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]



| Variable (Acronym) | Source | Unit | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| Wind speed (WNDS) | Texas Commission on Environmental Quality | m/s | / | Hourly |
| Longwave downwelling surface irradiance (LW) | GOES-East Surface Solar Irradiance | W/m2 | 0.05° | |
| Shortwave downwelling surface irradiance (SW) | GOES-East Surface Solar Irradiance | W/m2 | 0.05° | |
| Relative Humidity (RHPA) | PurpleAir Sensor | % | / | |
| Air Temperature (TPA) | PurpleAir Sensor | °C | / |
| Model | Number of Training Sample | R2 | RMSE (°C) | MAE (°C) | MBE (°C) |
|---|---|---|---|---|---|
| 1 | 209,048 | 0.73 | 4.73 | 3.54 | 0.01 |
| 2 | 209,048 | 0.75 | 4.59 | 3.49 | 0.01 |
| 3 | 209,048 | 0.77 | 4.41 | 3.38 | 0.01 |
| 4 | 208,988 | 0.82 | 3.93 | 3.16 | −0.02 |
| 5 | 208,988 | 0.86 | 3.38 | 2.73 | 0 |
| 6 | 208,988 | 0.86 | 3.38 | 2.73 | 0 |
| 7 | 207,999 | 0.87 | 3.37 | 2.72 | 0.01 |
| 8 | 209,048 | 0.75 | 4.56 | 3.45 | 0.01 |
| 9 | 208,988 | 0.89 | 3.10 | 2.46 | −0.01 |
| Class | Range of HI (°F) | HOBO HI (% of Time) | PA HI (% of Time) |
|---|---|---|---|
| Caution | 80–90 | 17.6 | 18.8 |
| Extreme Caution | 90–103 | 14.0 | 20.3 |
| Danger | 103–124 | 3.9 | 9.6 |
| Extreme Danger | 125 | 0 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tse, J.; Liang, L. Evaluating PurpleAir Sensors: Do They Accurately Reflect Ambient Air Temperature? Sensors 2025, 25, 3044. https://doi.org/10.3390/s25103044
Tse J, Liang L. Evaluating PurpleAir Sensors: Do They Accurately Reflect Ambient Air Temperature? Sensors. 2025; 25(10):3044. https://doi.org/10.3390/s25103044
Chicago/Turabian StyleTse, Justin, and Lu Liang. 2025. "Evaluating PurpleAir Sensors: Do They Accurately Reflect Ambient Air Temperature?" Sensors 25, no. 10: 3044. https://doi.org/10.3390/s25103044
APA StyleTse, J., & Liang, L. (2025). Evaluating PurpleAir Sensors: Do They Accurately Reflect Ambient Air Temperature? Sensors, 25(10), 3044. https://doi.org/10.3390/s25103044









