Reducing Upper-Limb Muscle Effort with Model-Based Gravity Compensation During Robot-Assisted Movement
Abstract
1. Introduction
- (1)
- Compared with other upper limb weight compensation methods, such as the position-varying compensation strategy, the weight compensation strategy based on the arm dynamics model is adopted in this paper;
- (2)
- In the weight compensation method proposed in this paper, the weight estimation of the arm is calculated based on the real-time joint data of the arm, rather than using the equivalent weight estimation method;
- (3)
- In this paper, an arm weight compensation experiment based on a point-to-point task was carried out to observe the activation degree of the upper limb muscle group, and the performance of the proposed weight compensation method was compared with that of the method without compensation and the position-varying compensation method.
2. Arm Gravity Compensation Method
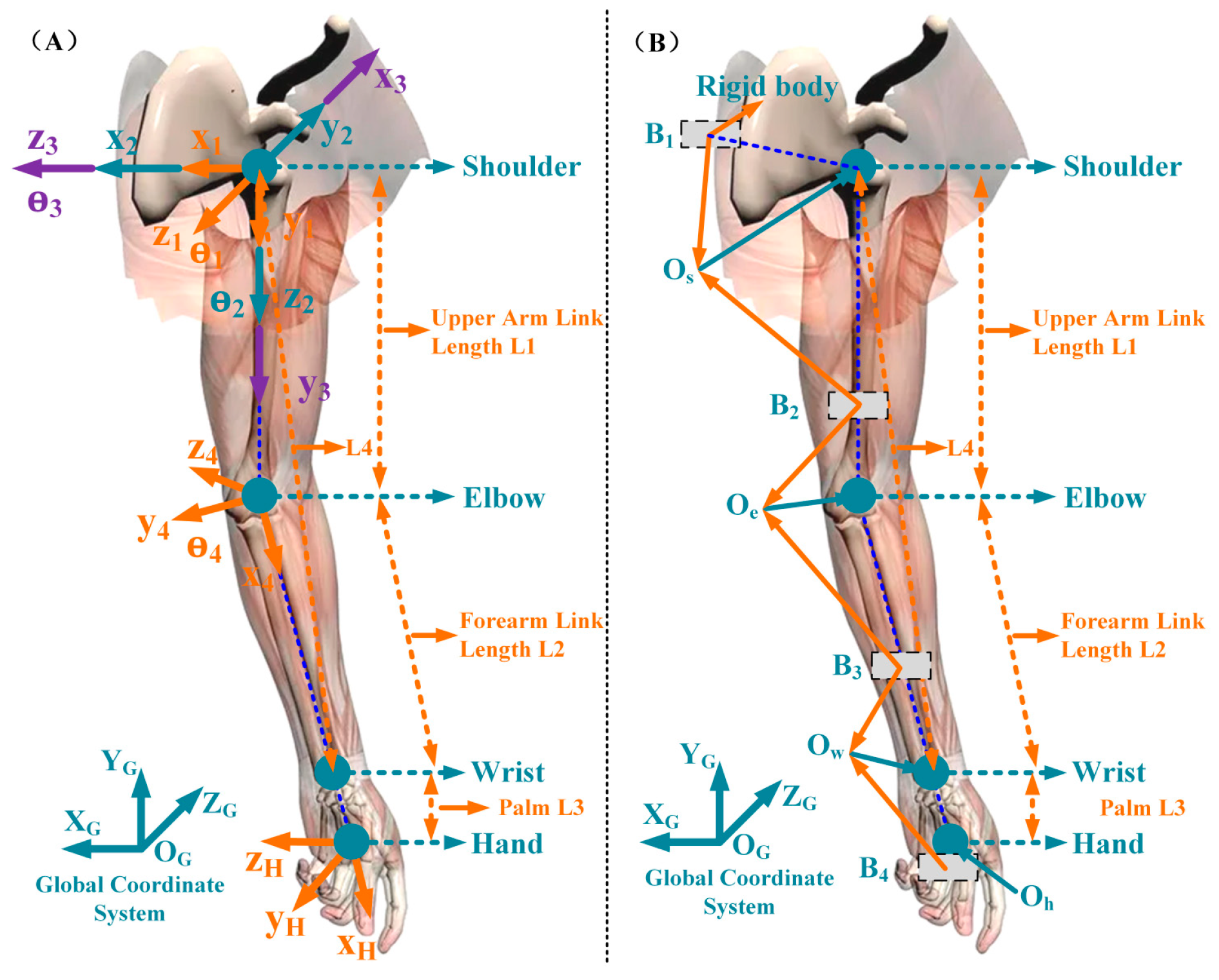
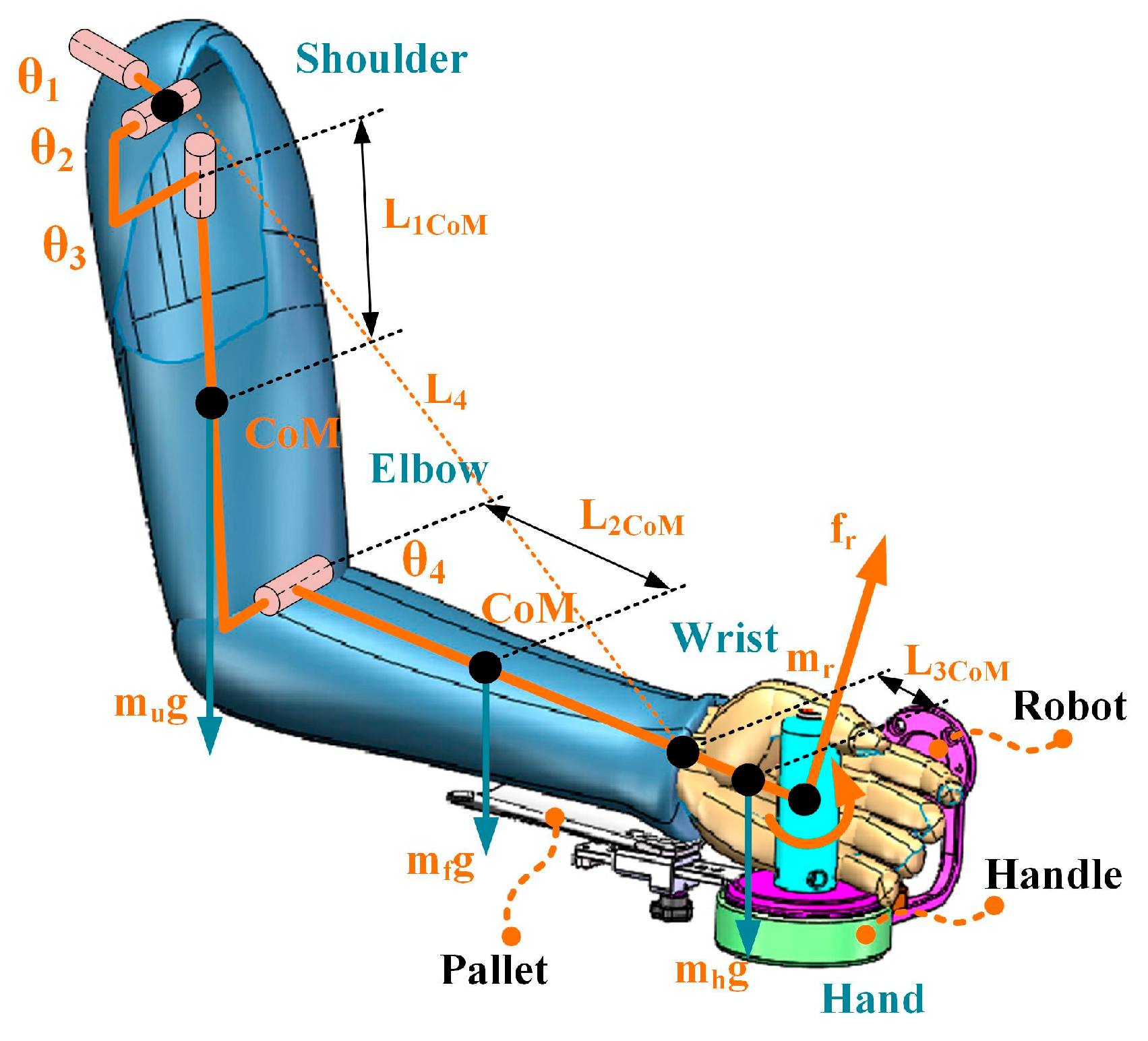
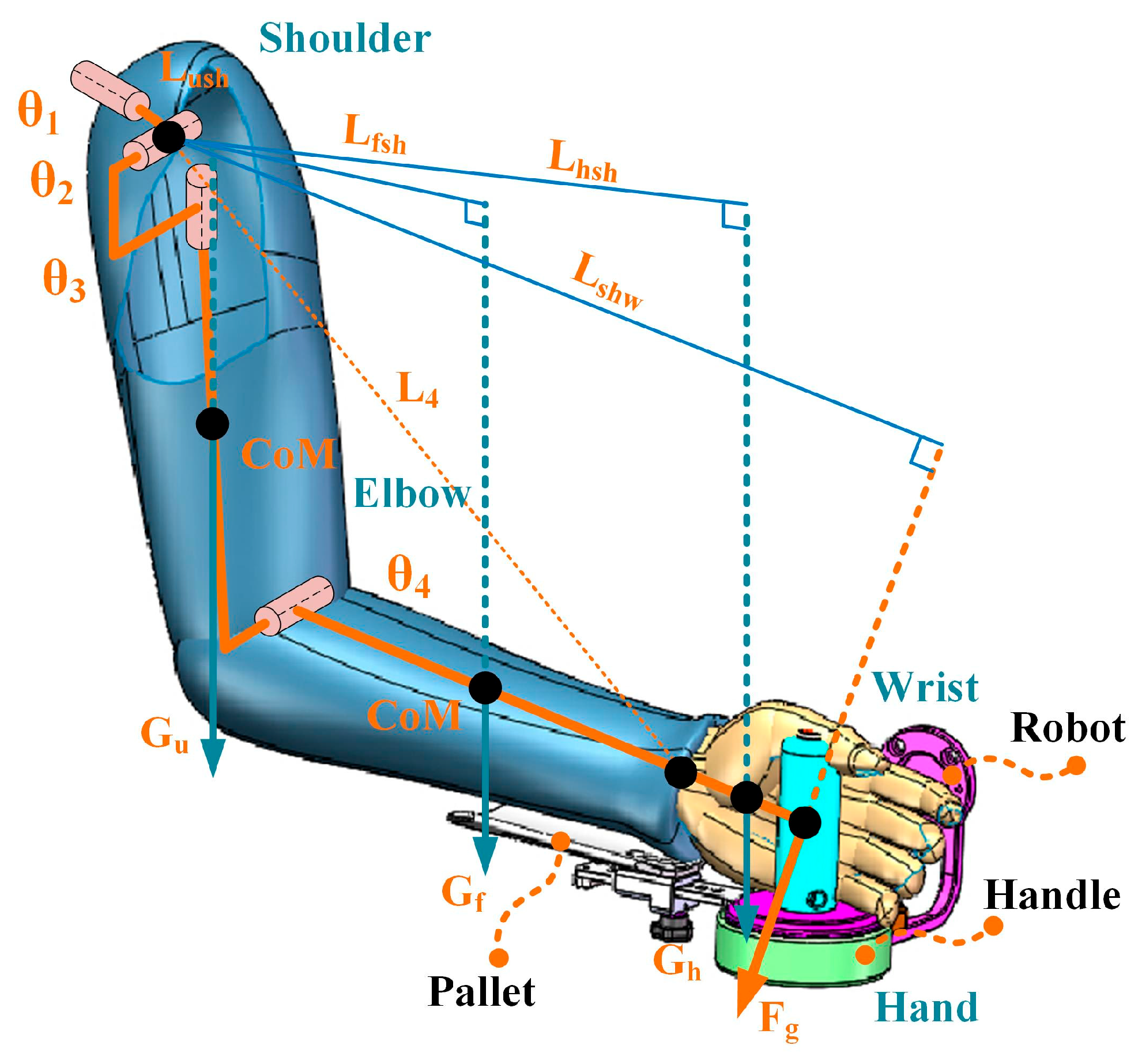
2.1. Arm Model Reconstruction
2.2. Gravity Compensation Strategies
3. Experiments
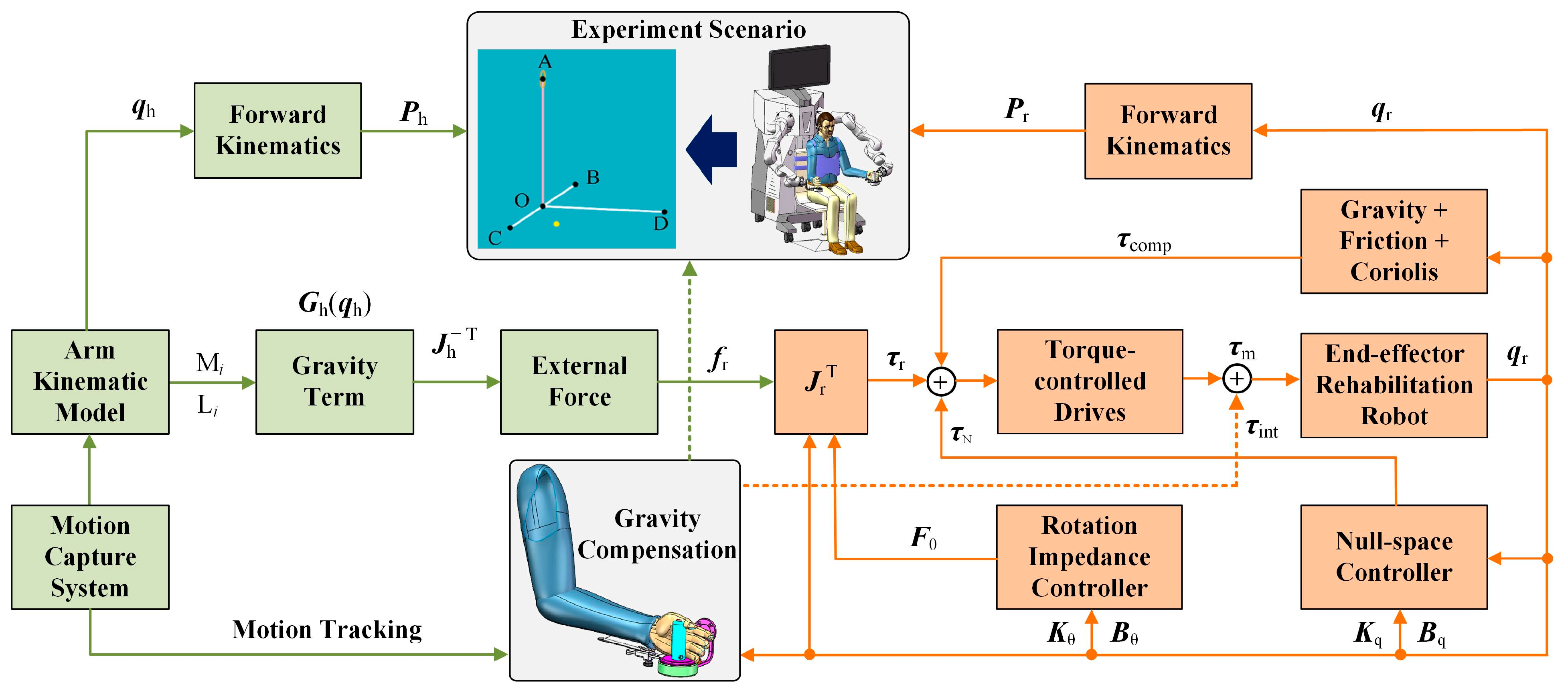
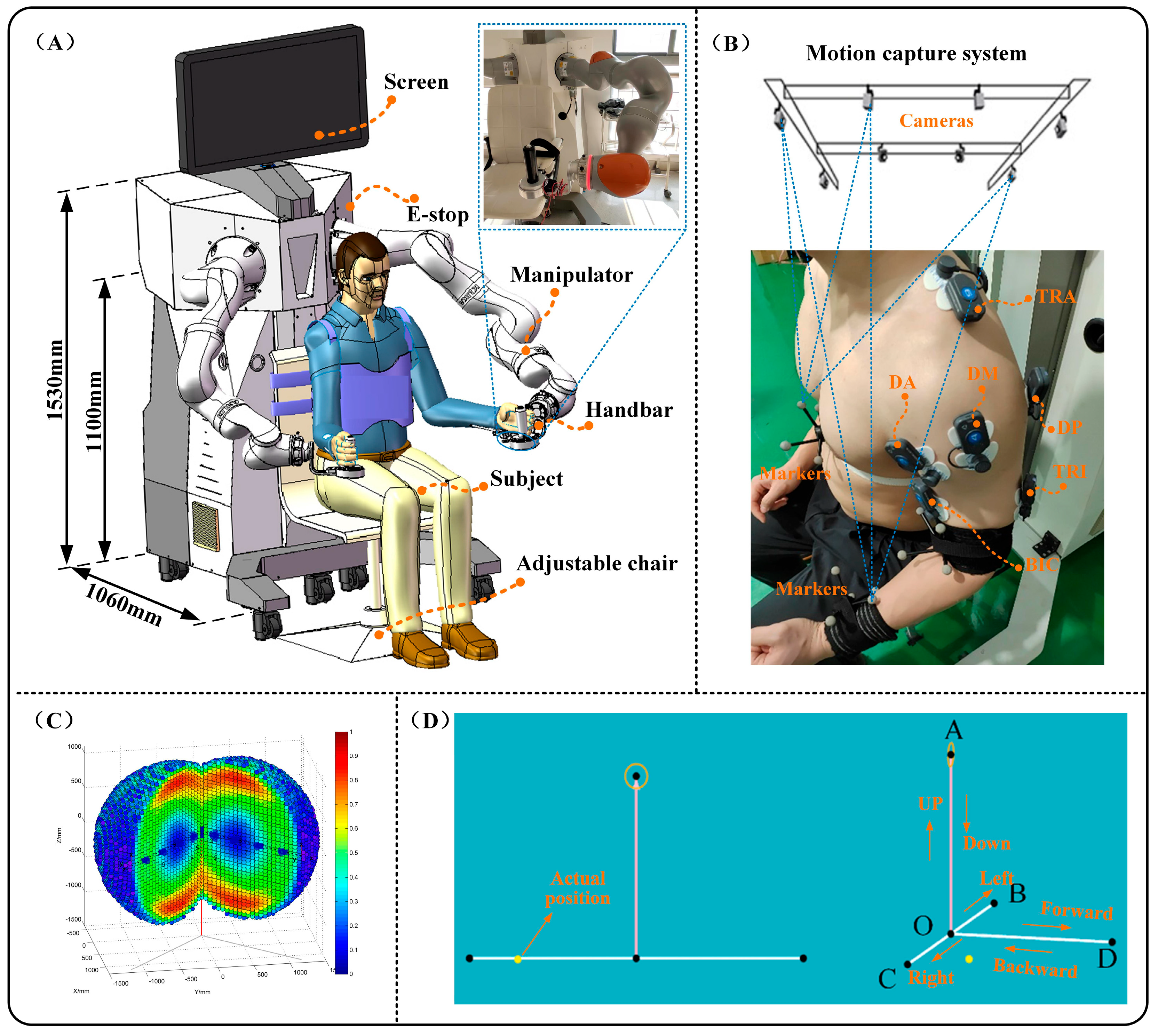
3.1. Experiment Setup
3.2. Experimental Protocols
3.3. Data Analysis
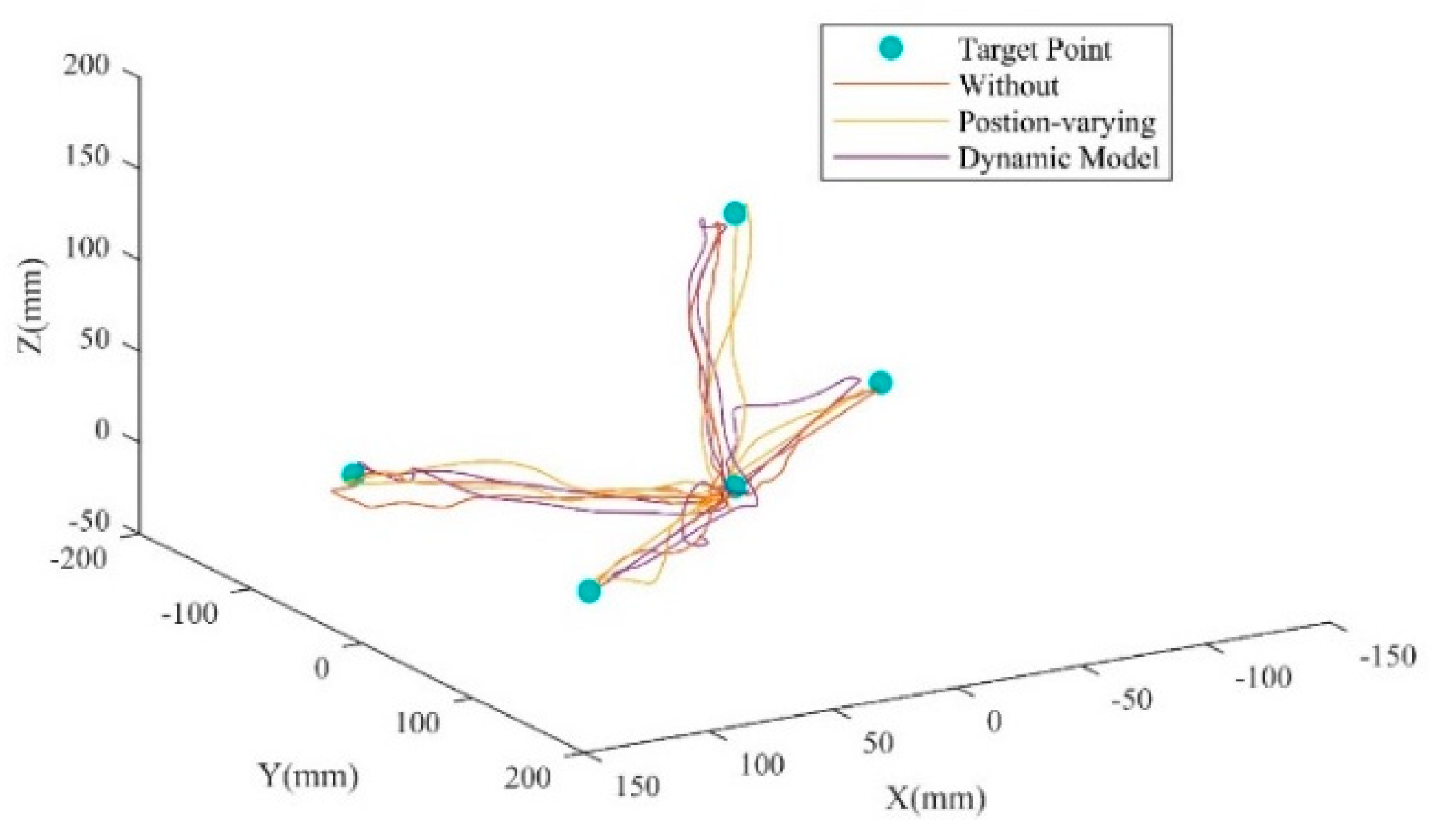
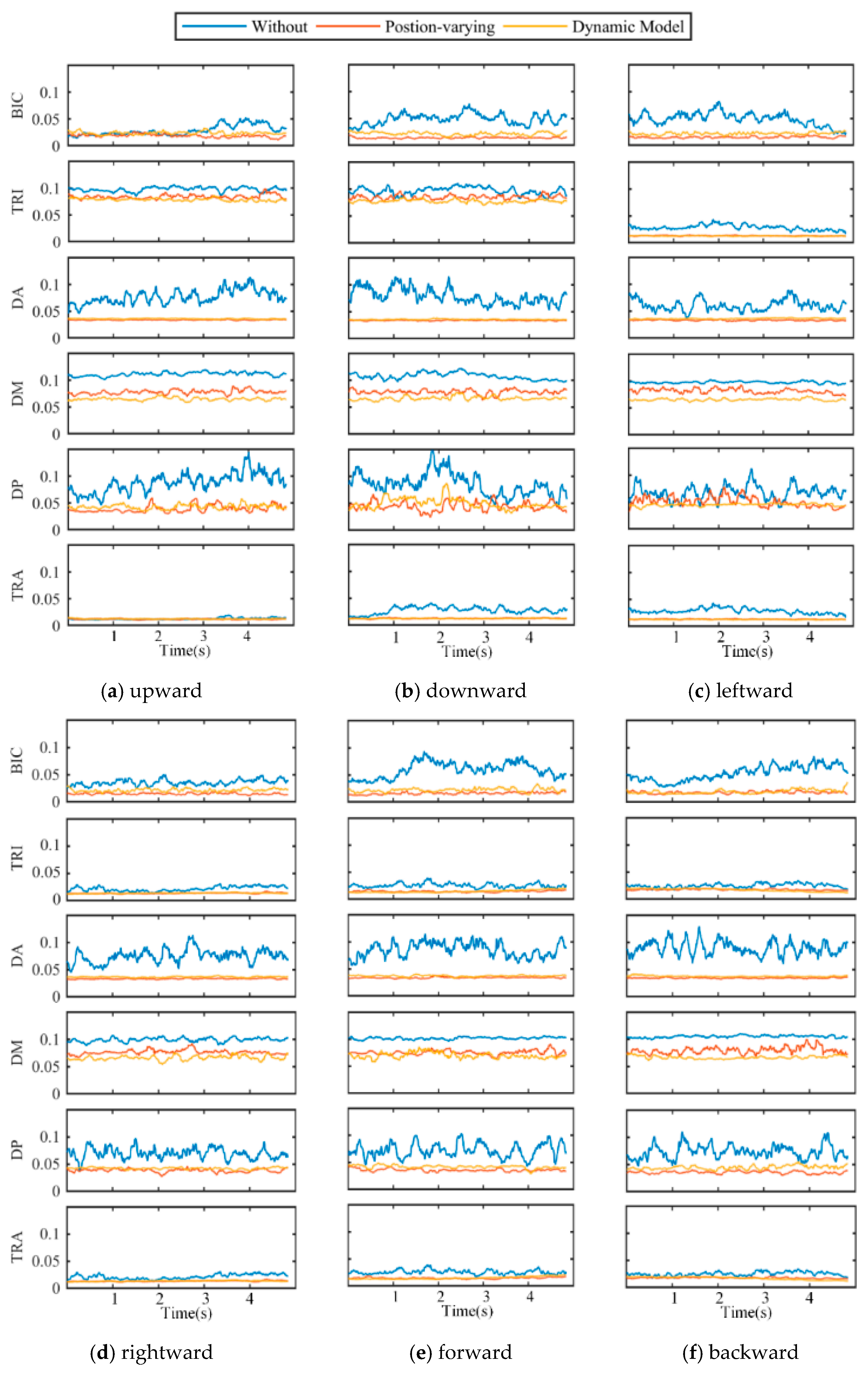
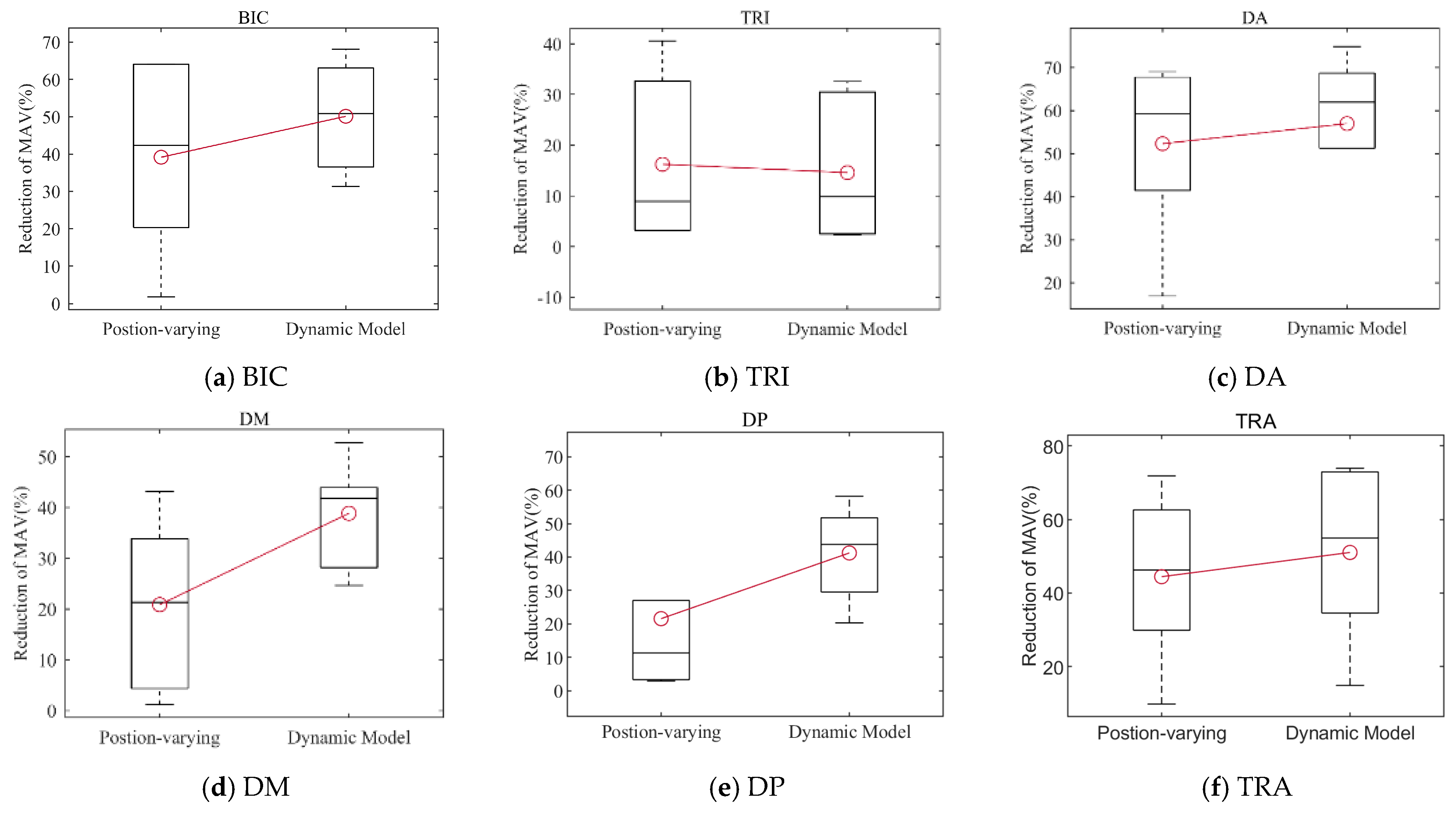
4. Results
5. Discussion
5.1. Existing Weight Compensation Strategies
5.2. Usability of the Weight Compensation Strategies
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Narayan, J.; Kalita, B.; Dwivedy, S.K. Development of Robot-based Upper Limb Devices for Rehabilitation Purposes: A Systematic Review. Augment. Hum. Res. 2021, 6, 4. [Google Scholar] [CrossRef]
- Morone, G.; Cocchi, I.; Paolucci, S.; Iosa, M. Robot-assisted therapy for arm recovery for stroke patients: State of the art and clinical implication. Expert Rev. Med. Devices 2020, 17, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Bucchieri, A.; Tessari, F.; Buccelli, S.; De Momi, E.; Laffranchi, M.; De Michieli, L. The impact of gravity on functional movements: Kinematic insights and features selection. bioRxiv 2023. bioRxiv:2023.12.05.570204. [Google Scholar] [CrossRef]
- Claude, L.; Moreno, J.C.; Luis, P.J. Human-robot interfaces in exoskeletons for gait training after stroke: State of the art and challenges. Appl. Bionics Biomech. 2014, 9, 193–203. [Google Scholar]
- Housman, S.J.; Scott, K.M.; Reinkensmeyer, D.J. A randomized controlled trial of gravity-supported, computer-enhanced arm exercise for individuals with severe hemiparesis. Neurorehabil. Neural Repair 2009, 23, 505–514. [Google Scholar] [CrossRef]
- Krabben, T.; Prange, G.B.; Molier, B.I.; Stienen, A.H.; Jannink, M.J.; Buurke, J.H.; Rietman, J.S. Influence of gravity compensation training on synergistic movement patterns of the upper extremity after stroke, a pilot study. J. Neuroeng. Rehabil. 2012, 9, 44. [Google Scholar] [CrossRef]
- Runnalls, K.D.; Anson, G.; Byblow, W.D. Partial weight support of the arm affects corticomotor selectivity of biceps brachii. J. Neuroeng. Rehabil. 2015, 12, 94. [Google Scholar] [CrossRef]
- Hussain, I.; Salvietti, G.; Spagnoletti, G.; Malvezzi, M.; Cioncoloni, D.; Rossi, S.; Prattichizzo, D. A soft supernumerary robotic finger and mobile arm support for grasping compensation and hemiparetic upper limb rehabilitation. Robot. Auton. Syst. 2017, 93, 1–12. [Google Scholar] [CrossRef]
- Perry, B.E.; Evans, E.K.; Stokic, D.S. Weight compensation characteristics of Armeo®Spring exoskeleton: Implications for clinical practice and research. J. Neuroeng. Rehabil. 2017, 14, 14. [Google Scholar] [CrossRef]
- Krebs, H.I.; Hogan, N.; Aisen, M.L.; Volpe, B.T. Robot-aided neurorehabilitation. IEEE Trans. Rehabil. Eng. 1998, 6, 75–87. [Google Scholar] [CrossRef]
- Loureiro, R.; Amirabdollahian, F.; Topping, M.; Driessen, B.; Harwin, W. Upper limb robot mediated stroke therapy-GENTLE/s approach. Auton. Robot. 2003, 15, 35–51. [Google Scholar] [CrossRef]
- Stienen, A.H.; Hekman, E.E.; Van der Helm, F.C.; Prange, G.B.; Jannink, M.J.; Aalsma, A.M.; Van der Kooij, H. Freebal: Dedicated gravity compensation for the upper extremities. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007. [Google Scholar]
- Kim, B.; Deshpande, A.D. An upper-body rehabilitation exoskeleton Harmony with an anatomical shoulder mechanism: Design, modeling, control, and performance evaluation. Int. J. Robot. Res. 2017, 36, 414–435. [Google Scholar] [CrossRef]
- Just, F.; Özen, Ö.; Tortora, S.; Riener, R.; Rauter, G. Feedforward model based arm weight compensation with the rehabilitation robot ARMin. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017. [Google Scholar]
- Just, F.; Özen, Ö.; Tortora, S.; Klamroth-Marganska, V.; Riener, R.; Rauter, G. Human arm weight compensation in rehabilitation robotics: Efficacy of three distinct methods. J. Neuroeng. Rehabil. 2020, 17, 13. [Google Scholar] [CrossRef] [PubMed]
- Crocher, V.; Fong, J.; Bosch, T.J.; Tan, Y.; Mareels, I.; Oetomo, D. Upper Limb Deweighting Using Underactuated End-Effector-Based Backdrivable Manipulanda. IEEE Robot. Autom. Lett. 2018, 3, 2116–2122. [Google Scholar] [CrossRef]
- Mukherjee, J.; Chatterjee, A.; Jena, S.; Kumar, N.; Muthukrishnan, S.P.; Roy, S.; Bhasin, S. Adaptive Gravity Compensation Control of a Cable-Driven Upper-Arm Soft Exosuit. arXiv 2023, arXiv:2304.14823. [Google Scholar]
- Huang, Y.; Yang, Q.; Chen, Y.; Song, R. Assessment of Motor Control during Three-Dimensional Movements Tracking with Position-Varying Gravity Compensation. Front. Neurosci. 2017, 11, 253. [Google Scholar] [CrossRef]
- Hull, J.; Turner, R.; Simon, A.A.; Asbeck, A.T. A novel method and exoskeletons for whole-arm gravity compensation. IEEE Access 2020, 8, 143144–143159. [Google Scholar] [CrossRef]
- Ketelhut, M.; Husmann, S.; Haas, J.; Abel, D. Iterative Learning Control of Gravity Compensation for Upper-Arm Robot-Assisted Rehabilitation. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020. [Google Scholar]
- Wu, G.; Van der Helm, F.C.; Veeger, H.D.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef]
- Jiang, J.; Guo, S.; Zhang, L.; Sun, Q. Motor Ability Evaluation of the Upper Extremity with Point-To-Point Training Movement Based on End-Effector Robot-Assisted Training System. J. Healthc. Eng. 2022, 2022, 1939884. [Google Scholar] [CrossRef]
- Guo, S.; Xiong, X.; Zhang, L.; Sun, Q. A Novel Algorithm of Kinematics Parameters Measurement for Upper Limb Based on Motion Capture. Int. J. Mechatron. Appl. Mech. 2020, 7, 144–151. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zhang, L.; Guo, S.; Huang, Y.; Xiong, X. Kinematic Singularity Analysis and Simulation for 7dof Anthropomorphic Manipulator. Int. J. Mechatron. Appl. Mech. 2019, 1, 157–164. [Google Scholar]
- Bertomeu-Motos, A.; Blanco, A.; Badesa, F.J.; Barios, J.A.; Zollo, L.; Garcia-Aracil, N. Human arm joints reconstruction algorithm in rehabilitation therapies assisted by end-effector robotic devices. J. Neuroeng. Rehabil. 2018, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Guo, S.; Xi, F. Performance-based assistance control for robot-mediated upper-limbs rehabilitation. Mechatronics 2022, in press. [Google Scholar] [CrossRef]
- Sun, Q.; Guo, S.; Zhang, L. Kinematic dexterity analysis of human-robot interaction of an upper limb rehabilitation robot. Technol. Health Care 2020, 29, 1029–1045. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, L.; Sun, Q. Development of a force-field-based control strategy for an upper-limb rehabilitation robot. Mech. Sci. 2022, 13, 949–959. [Google Scholar] [CrossRef]
- Caimmi, M.; Chiavenna, A.; Scano, A.; Gasperini, G.; Giovanzana, C.; Tosatti, L.M.; Molteni, F. Using robot fully assisted functional movements in upper-limb rehabilitation of chronic stroke patients: Preliminary results. Eur. J. Phys. Rehabil. Med. 2016, 53, 390–399. [Google Scholar] [CrossRef]
- Hughes, A.-M.; Freeman, C.T.; Burridge, J.H.; Chappell, P.H.; Lewin, P.L.; Rogers, E. Shoulder and elbow muscle activity during fully supported trajectory tracking in people who have had a stroke. J. Electromyogr. Kinesiol. 2010, 20, 465–476. [Google Scholar] [CrossRef]
- Prange, G.B.; Kallenberg, L.A.; Jannink, M.J.; Stienen, A.H.; van der Kooij, H.; IJzerman, M.J.; Hermens, H.J. Influence of gravity compensation on muscle activity during reach and retrieval in healthy elderly. J. Electromyogr. Kinesiol. 2009, 19, e40–e49. [Google Scholar] [CrossRef]
- Sabatini, A.M. Identification of neuromuscular synergies in natural upper-arm movements. Biol. Cybern. 2002, 86, 253–262. [Google Scholar] [CrossRef]
- Kloosterman, M.; Snoek, G.J.; Kouwenhoven, M.; Nene, A.V.; Jannink, M.J. Influence of gravity compensation on kinematics and muscle activation patterns during reach and retrieval in subjects with cervical spinal cord injury: An explorative study. J. Rehabil. Res. Dev. 2010, 47, 617–628. [Google Scholar] [CrossRef]
- Coscia, M.; Cheung, V.C.; Tropea, P.; Koenig, A.; Monaco, V.; Bennis, C.; Micera, S.; Bonato, P. The effect of arm weight support on upper limb muscle synergies during reaching movements. J. Neuroeng. Rehabil. 2014, 11, 22. [Google Scholar] [CrossRef] [PubMed]
- Fong, J.; Crocher, V.; Tan, Y.; Oetomo, D.; Mareels, I. EMU: A transparent 3D robotic manipulandum for upper-limb rehabilitation. IEEE Int. Conf. Rehabil. Robot 2017, 2017, 771–776. [Google Scholar] [PubMed]
- Leng, Y.; Huang, G.; Ma, L.; Qian, Y.; Chen, X.; Zhang, K.; Fu, C. A lightweight, integrated and portable force-controlled ankle exoskeleton for daily walking assistance. In Proceedings of the 2021 27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Shanghai, China, 26–28 November 2021; pp. 42–47. [Google Scholar]
- Chen, X.; Zhang, K.; Liu, H.; Leng, Y.; Fu, C. A probability distribution model-based approach for foot placement prediction in the early swing phase with a wearable imu sensor. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2595–2604. [Google Scholar] [CrossRef] [PubMed]


| Weight | Length | Center of Mass | |
|---|---|---|---|
| Upper arm | 0.028 | 0.436 | |
| Forearm | 0.016 | 0.430 | |
| Palms | 0.006 | 0.506 |
| Variable | Values | Units |
|---|---|---|
| F-Value | Main Effects | Interaction Effect | ||
|---|---|---|---|---|
| Outcome Measures | Compensation Method (DOF = 2) | Direction (DOF = 5) | Compensation Method × Direction (DOF = 10) | |
| Muscle Activation | BIC | 13.56 (p = 0.001) * | 1.55 (p > 0.050) | 0.59 (p > 0.050) |
| TRI | 1.34 (p > 0.050) | 0.86 (p > 0.050) | 0.55 (p > 0.050) | |
| DA | 22.71 (p = 0.000) * | 3.79 (p > 0.050) | 1.07 (p > 0.050) | |
| DM | 6.78 (p = 0.034) * | 3.44 (p > 0.050) | 0.77 (p > 0.050) | |
| DP | 2.82 (p = 0.007) * | 2.01 (p > 0.050) | 1.13 (p > 0.050) | |
| TRA | 9.58 (p = 0.008) * | 2.69 (p > 0.050) | 1.14 (p > 0.050) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Yu, H.; Li, D. Reducing Upper-Limb Muscle Effort with Model-Based Gravity Compensation During Robot-Assisted Movement. Sensors 2025, 25, 3032. https://doi.org/10.3390/s25103032
Zhang L, Yu H, Li D. Reducing Upper-Limb Muscle Effort with Model-Based Gravity Compensation During Robot-Assisted Movement. Sensors. 2025; 25(10):3032. https://doi.org/10.3390/s25103032
Chicago/Turabian StyleZhang, Leigang, Hongliu Yu, and Desheng Li. 2025. "Reducing Upper-Limb Muscle Effort with Model-Based Gravity Compensation During Robot-Assisted Movement" Sensors 25, no. 10: 3032. https://doi.org/10.3390/s25103032
APA StyleZhang, L., Yu, H., & Li, D. (2025). Reducing Upper-Limb Muscle Effort with Model-Based Gravity Compensation During Robot-Assisted Movement. Sensors, 25(10), 3032. https://doi.org/10.3390/s25103032








