Device-Driven Service Allocation in Mobile Edge Computing with Location Prediction
Abstract
1. Introduction
- This study constructs the ELPM model by combining Spatial-Temporal Graph Neural Networks (ST-GNN) with the attention mechanism [8]. Since user location changes in mobile edge computing scenarios exhibit both temporal and spatial characteristics, which traditional methods find difficult to capture, ST-GNN can compensate for these shortcomings. The attention mechanism adaptively weights historical trajectories, significantly improving prediction accuracy, providing reliable data for service allocation, and reducing service migration loss.
- On this basis, for the dynamic service allocation problem, in order to maximize the connection ratio between edge users and edge servers while minimizing service deployment costs while ensuring user experience, this paper designs the Mobile Edge Service Dynamic Allocation (MESDA) strategy based on an improved Grey Wolf Optimizer (GWO) [9]. By introducing a random factor and adaptive mechanism to strengthen the direction judgment in the later iteration, combined with prediction results, tasks are allocated in advance, reducing migration times, improving resource utilization, and lowering costs.
2. Related Work
2.1. Location Prediction
2.2. User Migration and Service Collaboration
2.3. Service Optimization and User Allocation
2.4. Service Migration and Offloading
2.5. Reservoir Dynamic Analysis Scenario
3. System Model
3.1. Problem Definition
3.2. Explanation of Key Parameters
3.3. Constraints and Optimization Objectives
4. Service Allocation Algorithm Based on Location Prediction: ELPM and MESDA
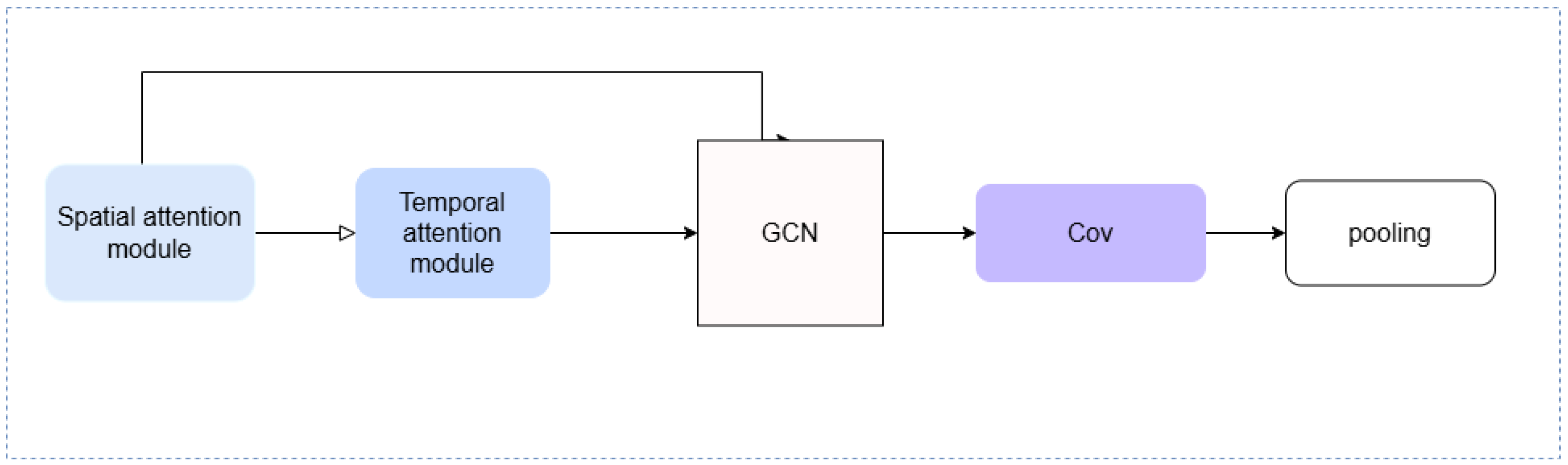
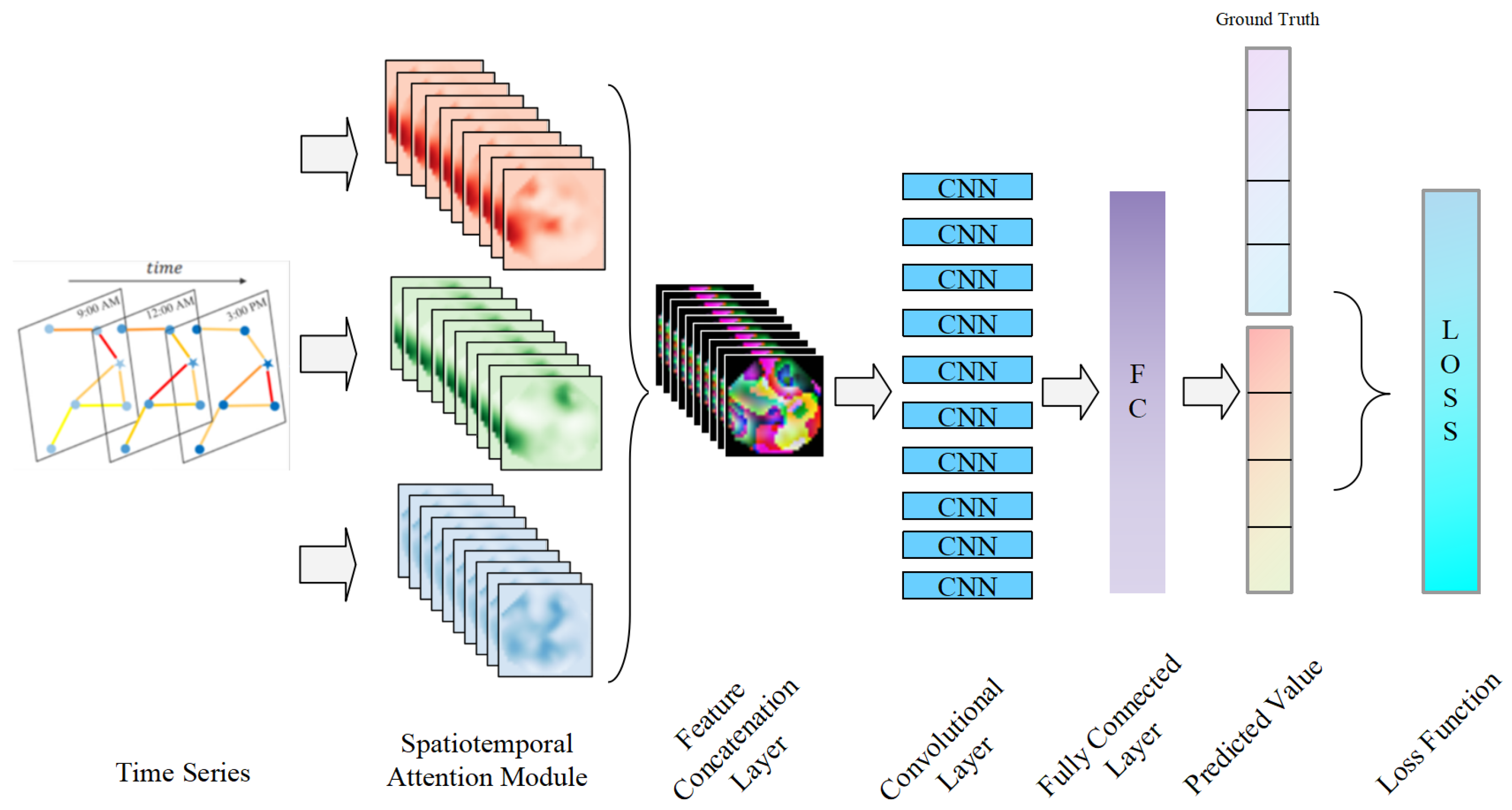
4.1. ELPM Location Prediction Model
4.2. The Calculation Method of Service Deployment Cost
- First, use the graph theory depth-first search algorithm to model the relationship network among edge servers;
- Then, use the Dijkstra algorithm to calculate the shortest path in the service allocation process (i.e., service deployment cost).First, abstract the relationship network composed of edge servers and define a k-cluster undirected relationship network , where V represents the global vertex set and E represents the initial edge set. The i-th cluster is represented as , where . Abstract the i-th cluster as a high-level node . Whenever the number of connecting edges between two clusters is greater than zero, an abstract edge with a weight of 1 is established between them. All high-level nodes and the abstracted edges form the high-level relationship network composed of edge servers.
| Algorithm 1 Finding all high-level nodes between start and end nodes in a graph. |
| Input: A graph G with high-level nodes, start node Start, and end node End Output: Set of all high-level nodes between Start and End, shown in Path[]
|
| Algorithm 2 Calculate service deployment cost using Dijkstra’s algorithm. |
| Input: Dijkstra(G, dist[], s) where G is the graph, dist[] stores distances from all nodes to s, and s is the starting node Output: The shortest path p
|
4.3. MESDA Service Dynamic Allocation Strategy
| Algorithm 3 Grey Wolf Optimization Algorithm with Adaptive Parameters. |
|
- (1)
- Before updating the position of each wolf, calculate the values of vectors A and C;
- (2)
- Perform unified normalization on the values of A and C, that is,where the normalized method uses the ‘min-max scaler‘ in the ‘sklearn‘ package, and its function is to normalize the values of A and C to the range ;
- (3)
- Embed the parameters A and C when simulating the surrounding behavior of the wolf pack, which is expressed by the following two formulas:where t represents the current iteration number, A and C are the exploration parameter and the exploitation parameter, respectively, is the position of the prey, and is the position of the grey wolf individual in the t-th generation. After the update, the improved GWO method with dynamic factors A and C is obtained, denoted as MESDA.
5. Experiment
5.1. Dataset
5.2. Control Experiment
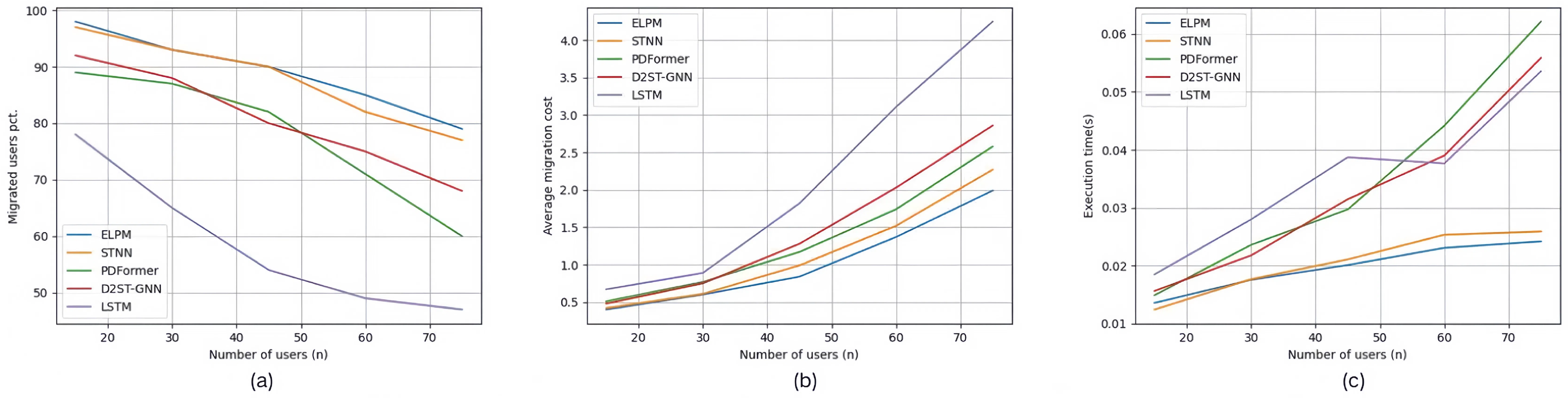
5.2.1. Control Group of Location Prediction Model
- ELPM: This refers to the location prediction model proposed in this paper for mobile edge computing environments. For the ELPM model, we used the following hyperparameters: a learning rate of 0.001, a batch size of 32, and 100 hidden layers.
- STNN: This is the Spatial-Temporal Neural Network model, which effectively combines the features of temporal data and spatial data. Using this model for location prediction is suitable for mobile edge computing scenarios and has certain typical advantages. By comparing with STNN, we are able to verify the accuracy and efficiency of our method in predicting user locations in dynamic environments.
- PDFormer [39]: This model utilizes a spatial self-attention module to capture dynamic spatial dependencies, introduces two graph masking matrices to highlight short- and long-range spatial dependencies, and uses a traffic delay-aware feature transformation module to accurately simulate the time delay in spatial information propagation, providing relatively accurate traffic prediction results. Choosing PDFormer as a baseline helps us compare the performance differences between self-attention-based models and our Spatial-Temporal Graph Neural Network approach, especially in modeling complex spatio-temporal dependencies.
- D2STGNN [8]: This model is a decoupled dynamic Spatial-Temporal Graph Neural Network that captures spatio-temporal correlations and learns dynamic features of traffic networks through a dynamic graph learning module. Choosing D2STGNN as a baseline can demonstrate the advantages of our method in dynamic spatio-temporal modeling and learning dynamic features.
- LSTM: This is the Long Short-Term Memory network model, which effectively captures long-term dependencies and temporal features in sequential data in mobile edge computing scenarios. It can also learn abstract features of data through a multi-layer neural network structure, thereby improving the accuracy of location prediction. Choosing LSTM as the benchmark model can help us compare the effects of traditional time-series prediction methods and our innovative method based on the Spatial-Temporal Graph Neural Network.
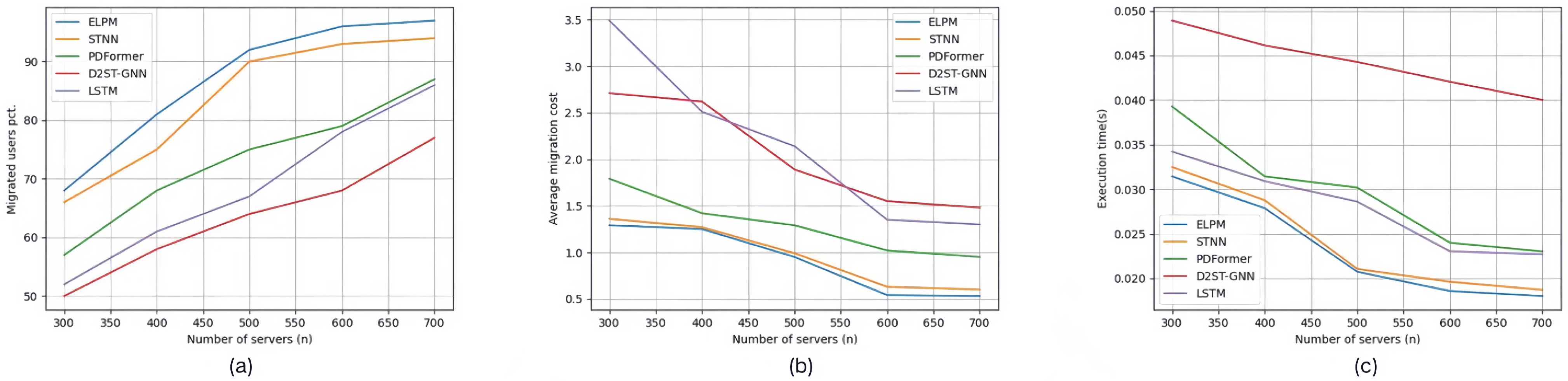
5.2.2. Control Group of Service Allocation Strategy
- MESDA: This refers to the service allocation strategy proposed in this paper for mobile edge computing environments. We set the following parameters for MESDA: a population size of 50, providing a balance between exploration and computational cost, and a maximum of 200 iterations, allowing sufficient time for the optimization process to converge.
- GWO: This is the Grey Wolf Optimizer, which is characterized by fast convergence and strong global search ability. It is suitable for optimizing and adjusting complex problems and can be effectively applied to the dynamic service allocation problem in mobile edge computing environments.
- MDQP [40]: This method considers the service request time and location of mobile clients, uses multi-dimensional indicators to predict service quality, and, thereby, achieves effective service recommendation for mobile clients. This method is referred to as MDQP in this paper.
- K Nearest: This is the k-Nearest Neighbors algorithm, which can select the K nearest neighbor nodes for service resource allocation based on demand in mobile edge computing scenarios.
- Logistic Regression: This is the Logistic Regression model, suitable for solving service allocation problems in mobile edge computing environments.
- Random Forest: This is the Random Forest algorithm, which can improve the accuracy and robustness of service allocation in this scenario by using the ensemble prediction ability of multiple decision trees.
5.2.3. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kong, X.; Wu, Y.; Wang, H.; Xia, F. Edge computing for internet of everything: A survey. IEEE Internet Things J. 2022, 9, 23472–23485. [Google Scholar] [CrossRef]
- Feng, C.; Han, P.; Zhang, X.; Yang, B.; Liu, Y.; Guo, L. Computation offloading in mobile edge computing networks: A survey. J. Netw. Comput. Appl. 2022, 202, 103366. [Google Scholar] [CrossRef]
- Du, H.; Liu, J.; Niyato, D.; Kang, J.; Xiong, Z.; Zhang, J.; Kim, D.I. Attention-aware resource allocation and QoE analysis for metaverse xURLLC services. IEEE J. Sel. Areas Commun. 2023, 41, 2158–2175. [Google Scholar] [CrossRef]
- Gebrekidan, T.Z.; Stein, S.; Norman, T.J. Combinatorial Client-Master Multiagent Deep Reinforcement Learning for Task Offloading in Mobile Edge Computing. arXiv 2024, arXiv:2402.11653. [Google Scholar]
- Mach, P.; Becvar, Z. Mobile edge computing: A survey on architecture and computation offloading. IEEE Commun. Surv. Tutorials 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Jiang, X.; Hou, P.; Zhu, H.; Li, B.; Wang, Z.; Ding, H. Dynamic and intelligent edge server placement based on deep reinforcement learning in mobile edge computing. Ad Hoc Netw. 2023, 145, 103172. [Google Scholar] [CrossRef]
- Zaman, S.K.U.; Jehangiri, A.I.; Maqsood, T.; Umar, A.I.; Khan, M.A.; Jhanjhi, N.Z.; Shorfuzzaman, M.; Masud, M. COME-UP: Computation offloading in mobile edge computing with LSTM based user direction prediction. Appl. Sci. 2022, 12, 3312. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, Z.; Wei, W.; Wang, F.; Xu, Y.; Cao, X.; Jensen, C.S. Decoupled dynamic spatial-temporal graph neural network for traffic forecasting. arXiv 2022, arXiv:2206.09112. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wang, J. Dynamic multiworkflow offloading and scheduling under soft deadlines in the cloud-edge environment. IEEE Syst. J. 2023, 17, 2077–2088. [Google Scholar] [CrossRef]
- Song, L.; Sun, G.; Yu, H.; Niyato, D. ESPD-LP: Edge Service Pre-Deployment Based on Location Prediction in MEC. IEEE Trans. Mob. Comput. 2025, 1–18. [Google Scholar] [CrossRef]
- Virdis, A.; Nardini, G.; Stea, G.; Sabella, D. End-to-end performance evaluation of MEC deployments in 5G scenarios. J. Sens. Actuator Netw. 2020, 9, 57. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Huang, X.; Li, J.; Min, G. GNN-based long and short term preference modeling for next-location prediction. Inf. Sci. 2023, 629, 1–14. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, Y.; Zhong, W.; Zhang, C.; Xin, B. A truncated SVD-based ARIMA model for multiple QoS prediction in mobile edge computing. Tsinghua Sci. Technol. 2021, 27, 315–324. [Google Scholar] [CrossRef]
- Liu, H.; Chen, K.; Ma, J. Incremental learning-based real-time trajectory prediction for autonomous driving via sparse gaussian process regression. In Proceedings of the 2024 IEEE Intelligent Vehicles Symposium (IV), Jeju Island, Republic of Korea, 2–5 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 737–743. [Google Scholar]
- Chen, C.; Liu, L.; Qiu, T.; Ren, Z.; Hu, J.; Ti, F. Driver’s intention identification and risk evaluation at intersections in the Internet of vehicles. IEEE Internet Things J. 2018, 5, 1575–1587. [Google Scholar] [CrossRef]
- Zeng, W.; Quan, Z.; Zhao, Z.; Xie, C.; Lu, X. A deep learning approach for aircraft trajectory prediction in terminal airspace. IEEE Access 2020, 8, 151250–151266. [Google Scholar] [CrossRef]
- Du, W.; He, Q.; Ji, Y.; Cai, C.; Zhao, X. Optimal user migration upon server failures in edge computing environment. In Proceedings of the 2021 IEEE International Conference on Web Services (ICWS), Chicago, IL, USA, 5–10 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 272–281. [Google Scholar]
- Wang, S.; Guo, Y.; Zhang, N.; Yang, P.; Zhou, A.; Shen, X. Delay-aware microservice coordination in mobile edge computing: A reinforcement learning approach. IEEE Trans. Mob. Comput. 2019, 20, 939–951. [Google Scholar] [CrossRef]
- Chen, S.; Hu, M.; Guo, S. Fast dynamic-programming algorithm for solving global optimization problems of hybrid electric vehicles. Energy 2023, 273, 127207. [Google Scholar] [CrossRef]
- Cang, Y.; Chen, M.; Pan, Y.; Yang, Z.; Hu, Y.; Sun, H.; Chen, M. Joint User Scheduling and Computing Resource Allocation Optimization in Asynchronous Mobile Edge Computing Networks. IEEE Trans. Commun. 2024, 72, 3378–3392. [Google Scholar] [CrossRef]
- Zou, G.; Liu, Y.; Qin, Z.; Chen, J.; Xu, Z.; Gan, Y.; Zhang, B.; He, Q. TD-EUA: Task-decomposable edge user allocation with QoE optimization. In Proceedings of the Service-Oriented Computing: 18th International Conference, ICSOC 2020, Dubai, United Arab Emirates, 14–17 December 2020; Proceedings 18. Springer: Berlin/Heidelberg, Germany, 2020; pp. 215–231. [Google Scholar]
- Panda, S.P.; Ray, K.; Banerjee, A. Dynamic edge user allocation with user specified QoS preferences. In Proceedings of the Service-Oriented Computing: 18th International Conference, ICSOC 2020, Dubai, United Arab Emirates, 14–17 December 2020; Proceedings 18. Springer: Berlin/Heidelberg, Germany, 2020; pp. 187–197. [Google Scholar]
- Peng, Q.; Xia, Y.; Feng, Z.; Lee, J.; Wu, C.; Luo, X.; Zheng, W.; Pang, S.; Liu, H.; Qin, Y.; et al. Mobility-aware and migration-enabled online edge user allocation in mobile edge computing. In Proceedings of the 2019 IEEE International Conference on Web Services (ICWS), Milan, Italy, 8–13 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 91–98. [Google Scholar]
- Liu, F.; Lv, B.; Huang, J.; Ali, S. Edge user allocation in overlap areas for mobile edge computing. Mob. Netw. Appl. 2021, 26, 2423–2433. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.; Wu, J.; Tang, Z. A multi-user service migration scheme based on deep reinforcement learning and SDN in mobile edge computing. Phys. Commun. 2021, 47, 101397. [Google Scholar] [CrossRef]
- Huang, L.; Feng, X.; Zhang, C.; Qian, L.; Wu, Y. Deep reinforcement learning-based joint task offloading and bandwidth allocation for multi-user mobile edge computing. Digit. Commun. Netw. 2019, 5, 10–17. [Google Scholar] [CrossRef]
- Knebel, F.P.; Trevisan, R.; do Nascimento, G.S.; Abel, M.; Wickboldt, J.A. A study on cloud and edge computing for the implementation of digital twins in the Oil & Gas industries. Comput. Ind. Eng. 2023, 182, 109363. [Google Scholar]
- Hussain, R.F.; Salehi, M.A.; Kovalenko, A.; Salehi, S.; Semiari, O. Robust resource allocation using edge computing for smart oil fields. In Proceedings of the 24th International Conference on Parallel and Distributed Processing Techniques & Applications, Singapore, 11–13 August 2018. [Google Scholar]
- Qiu, Y.; Niu, J.; Zhu, X.; Zhu, K.; Yao, Y.; Ren, B.; Ren, T. Mobile edge computing in space-air-ground integrated networks: Architectures, key technologies and challenges. J. Sens. Actuator Netw. 2022, 11, 57. [Google Scholar] [CrossRef]
- Hussain, R.F.; Salehi, M.A.; Kovalenko, A.; Feng, Y.; Semiari, O. Federated edge computing for disaster management in remote smart oil fields. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 929–936. [Google Scholar]
- Shmueli, G.; Tafti, A. How to “improve” prediction using behavior modification. Int. J. Forecast. 2023, 39, 541–555. [Google Scholar] [CrossRef]
- Lai, P.; He, Q.; Xia, X.; Chen, F.; Abdelrazek, M.; Grundy, J.; Hosking, J.; Yang, Y. Dynamic user allocation in stochastic mobile edge computing systems. IEEE Trans. Serv. Comput. 2021, 15, 2699–2712. [Google Scholar] [CrossRef]
- Haibeh, L.A.; Yagoub, M.C.; Jarray, A. A survey on mobile edge computing infrastructure: Design, resource management, and optimization approaches. IEEE Access 2022, 10, 27591–27610. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, H.; Qiu, C.; Zhou, Y.; Lu, J. Distributed task offloading in cooperative mobile edge computing networks. IEEE Trans. Veh. Technol. 2024, 73, 10487–10501. [Google Scholar] [CrossRef]
- Hao, H.; Xu, C.; Zhang, W.; Yang, S.; Muntean, G.M. Joint task offloading, resource allocation, and trajectory design for multi-uav cooperative edge computing with task priority. IEEE Trans. Mob. Comput. 2024, 23, 8649–8663. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Y.; Yuan, Q. Application of Dijkstra algorithm in robot path-planning. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1067–1069. [Google Scholar]
- Li, Y.; Zhou, A.; Ma, X.; Wang, S. Profit-aware edge server placement. IEEE Internet Things J. 2021, 9, 55–67. [Google Scholar] [CrossRef]
- Jiang, J.; Han, C.; Zhao, W.X.; Wang, J. Pdformer: Propagation delay-aware dynamic long-range transformer for traffic flow prediction. Proc. AAAI Conf. Artif. Intell. 2023, 37, 4365–4373. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Cheng, B.; Yang, F.; Chang, R.N. Multi-dimensional QoS prediction for service recommendations. IEEE Trans. Serv. Comput. 2016, 12, 47–57. [Google Scholar] [CrossRef]
- Dong, S.; Tang, J.; Abbas, K.; Hou, R.; Kamruzzaman, J.; Rutkowski, L.; Buyya, R. Task offloading strategies for mobile edge computing: A survey. Comput. Netw. 2024, 254, 110791. [Google Scholar] [CrossRef]
| Notation | Description |
|---|---|
| , the remaining available resources of edge server , where represents one of the resources ( etc.), | |
| D | , the available resource types of edge servers |
| The geographic area radius that edge server can cover, within which edge users may connect to this server to obtain services | |
| The service deployment cost generated by edge user u migrating service | |
| The number of hops on the shortest network path between edge servers and , used to measure the transmission distance between servers | |
| The delay experienced by edge user u when connected to a remote cloud | |
| The total cost integrating the migration cost and delay cost of edge user u | |
| R | , a set of predefined resource consumption amounts of service , where , and represents the consumption amount of one of the resources, |
| S | , a finite set composed of edge servers |
| U | , a finite set of edge users whose required services have the possibility of being allocated |
| , a finite set composed of services | |
| A finite set of edge servers whose service range covers edge user u | |
| A service required by edge user u, | |
| A finite set of edge servers that own the service required by edge user u | |
| A finite set of edge users whose required services are successfully allocated to edge server | |
| Whether the required service of edge user u is allocated to edge server () or not () | |
| Whether edge server owns service () or not () |
| Edge Users | Edge Servers | Initial Resources of Edge Servers | Location Prediction Model + Service Allocation Strategy | |
|---|---|---|---|---|
| ELPM + MESDA | ||||
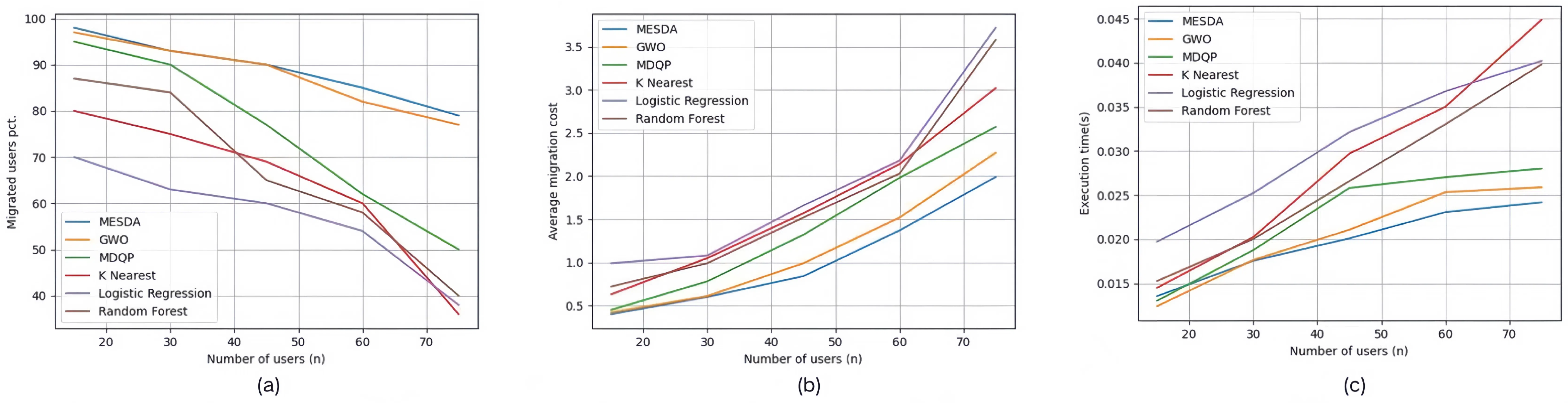
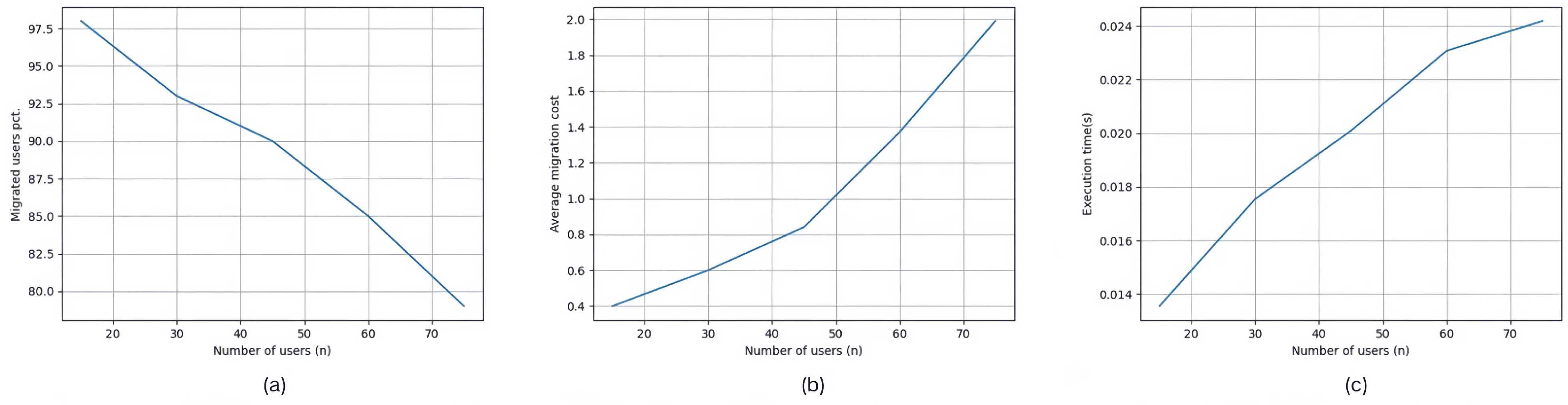
| Set #2.1 | 15, 30, 45, 60, 75 | 500 | 100% | STNN + GWO |
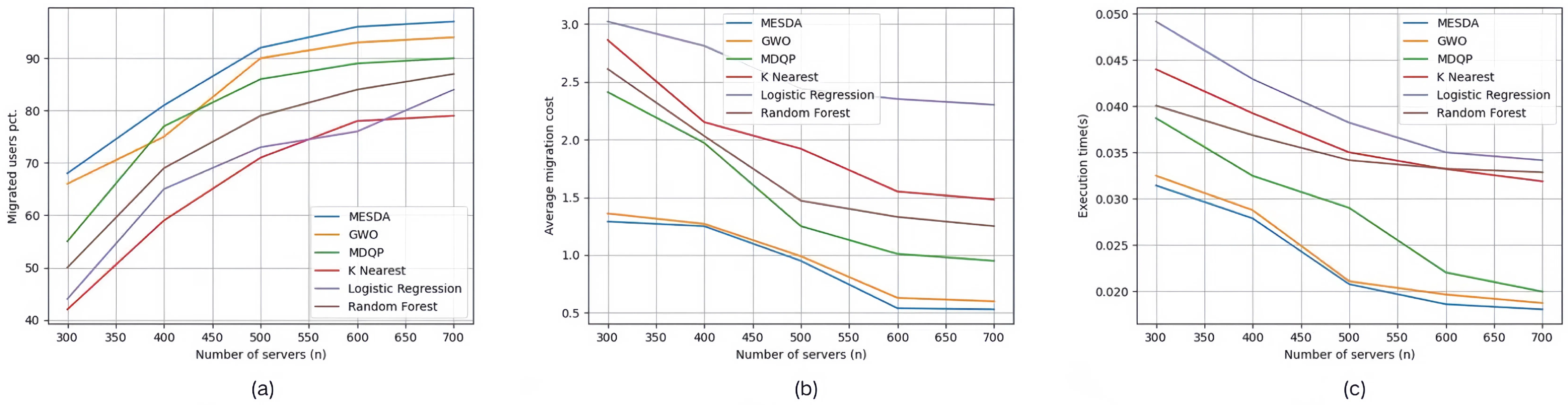
| Set #2.2 | 45 | 300, 400, 500, 600, 700 | 100% | PDFormer + MESDA |
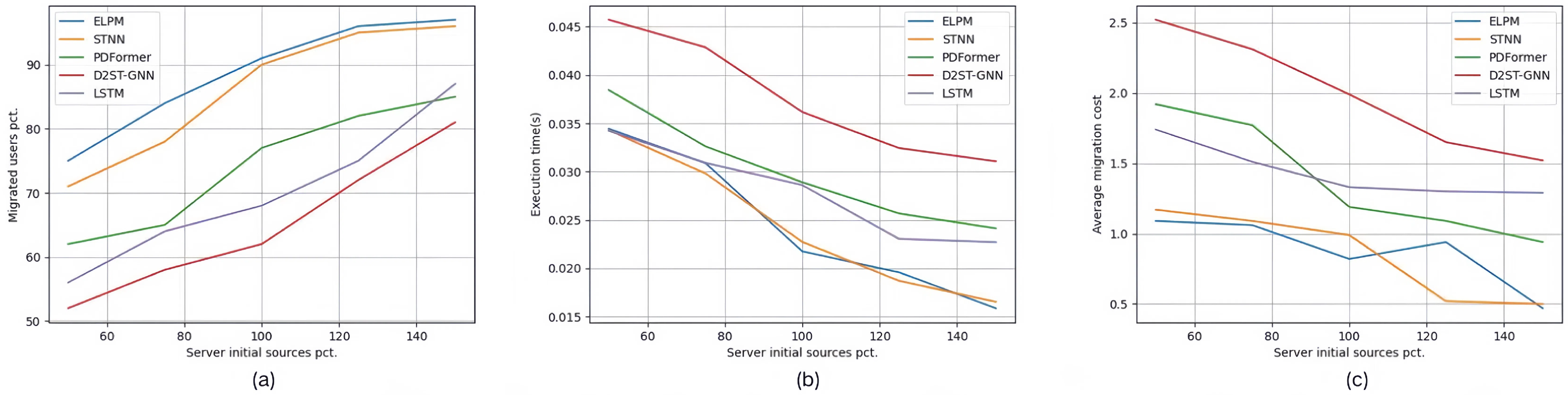
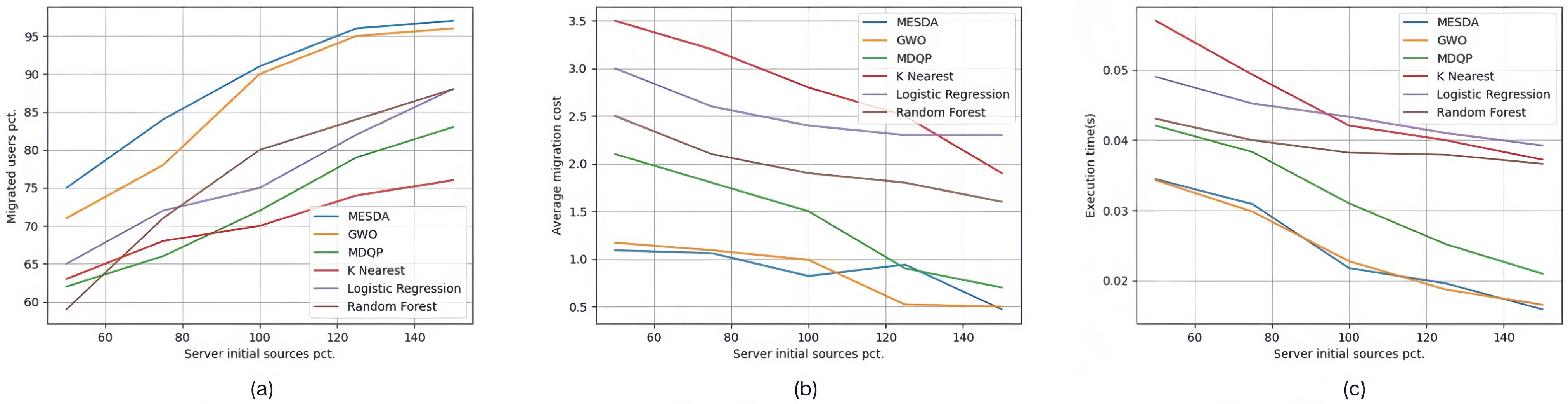
| Set #2.3 | 45 | 500 | 50%, 75%, 100%, 125%, 150% | D2STGNN + MESDA |
| LSTM + MESDA | ||||
| ELPM + MESDA | ||||
| Set #3.1 | 15, 30, 45, 60, 75 | 500 | 100% | STNN + GWO |
| Set #3.2 | 45 | 300, 400, 500, 600, 700 | 100% | ELPM + MDQP |
| Set #3.3 | 45 | 500 | 50%, 75%, 100%, 125%, 150% | ELPM + K Nearest |
| ELPM + Random Forest |
| Average Percentage of Users Connected to Edge Servers | Average Service Setup Cost | Average Service Allocation Execution Time | |
|---|---|---|---|
| ELPM + MESDA | 88% | 0.942667 | 0.022513 s |
| STNN + GWO | 85.80% | 0.995333 | 0.023009 s |
| PDFformer + MESDA | 75.07% | 1.343333 | 0.031479 s |
| D2STGNN + MESDA | 69.67% | 1.842667 | 0.038223 s |
| LSTM + MESDA | 65.80% | 1.913333 | 0.030363 s |
| Average Percentage of Users Connected to Edge Servers | Average Service Setup Cost | Average Service Allocation Execution Time | |
|---|---|---|---|
| ELPM + MESDA | 88% | 0.942667 | 0.022513 s |
| STNN + GWO | 85.80% | 0.995333 | 0.023009 s |
| ELPM + MDQP | 75.53% | 1.446 | 0.027487 s |
| ELPM + K Nearest | 67% | 2.151333 | 0.036887 s |
| ELPM + Logistic Regression | 67% | 2.343333 | 0.038095 s |
| ELPM + Random Forest | 72.33% | 1.828667 | 0.033855 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Li, X.; Chen, Y.; Yang, M.; Liu, X.; Liu, Y.; Xiu, S. Device-Driven Service Allocation in Mobile Edge Computing with Location Prediction. Sensors 2025, 25, 3025. https://doi.org/10.3390/s25103025
Zeng Q, Li X, Chen Y, Yang M, Liu X, Liu Y, Xiu S. Device-Driven Service Allocation in Mobile Edge Computing with Location Prediction. Sensors. 2025; 25(10):3025. https://doi.org/10.3390/s25103025
Chicago/Turabian StyleZeng, Qian, Xiaobo Li, Yixuan Chen, Minghao Yang, Xingbang Liu, Yuetian Liu, and Shiwei Xiu. 2025. "Device-Driven Service Allocation in Mobile Edge Computing with Location Prediction" Sensors 25, no. 10: 3025. https://doi.org/10.3390/s25103025
APA StyleZeng, Q., Li, X., Chen, Y., Yang, M., Liu, X., Liu, Y., & Xiu, S. (2025). Device-Driven Service Allocation in Mobile Edge Computing with Location Prediction. Sensors, 25(10), 3025. https://doi.org/10.3390/s25103025






