Detection and Recognition of Visual Geons Based on Specific Object-of-Interest Imaging Technology
Abstract
1. Introduction
1.1. Recognition-by-Components (RBCs) Framework Based on Marr
- Computational level: Geons as the minimal units of visual representation;
- Algorithmic level: Deep learning simulates hierarchical feature extraction;
- Implementation level: The optimization of weight in neural networks (, ) corresponds to synaptic plasticity.
- Constructing complex objects: By combining and arranging different basic geons, various complex visual objects can be created, offering high flexibility.
- Providing recognition cues: Basic geons not only form the shape and structure of objects, but also provide key cues for object recognition. When an observer sees an object, they first identify the basic geons of the object and then recognize the object based on the combination and arrangement of these elements.
- Supporting rapid recognition: Due to the limited number and types of basic geons and the relatively fixed ways they can be combined, the visual system can quickly recognize objects, making this process highly automated.
1.2. Deep Learning-Based CV Scholars
1.3. Psychology, Neuroscience, and Other Fields
1.4. Research Objectives and Contributions
- Constructing a dynamically adaptive geon representation system to overcome RBCs theory’s rigid classification constraints.
- Leveraging neural network plasticity to model hierarchical biological vision processing.
- Establishing a noise-robust evaluation framework to assess the model’s biological plausibility.
- Theoretical innovation: Introduction of an adaptive geon detection framework integrating RBCs theory with neural networks, bridging theory and practice for novel detection paradigms.
- Experimental validation: Empirical demonstration of geons as foundational units in multi-object scenes, confirming their essential role in complex visual tasks.
- Robustness analysis: Evaluation under Gaussian and salt-and-pepper noise demonstrates the method’s stability and reliability, supporting real-world applications.
2. Materials and Methods
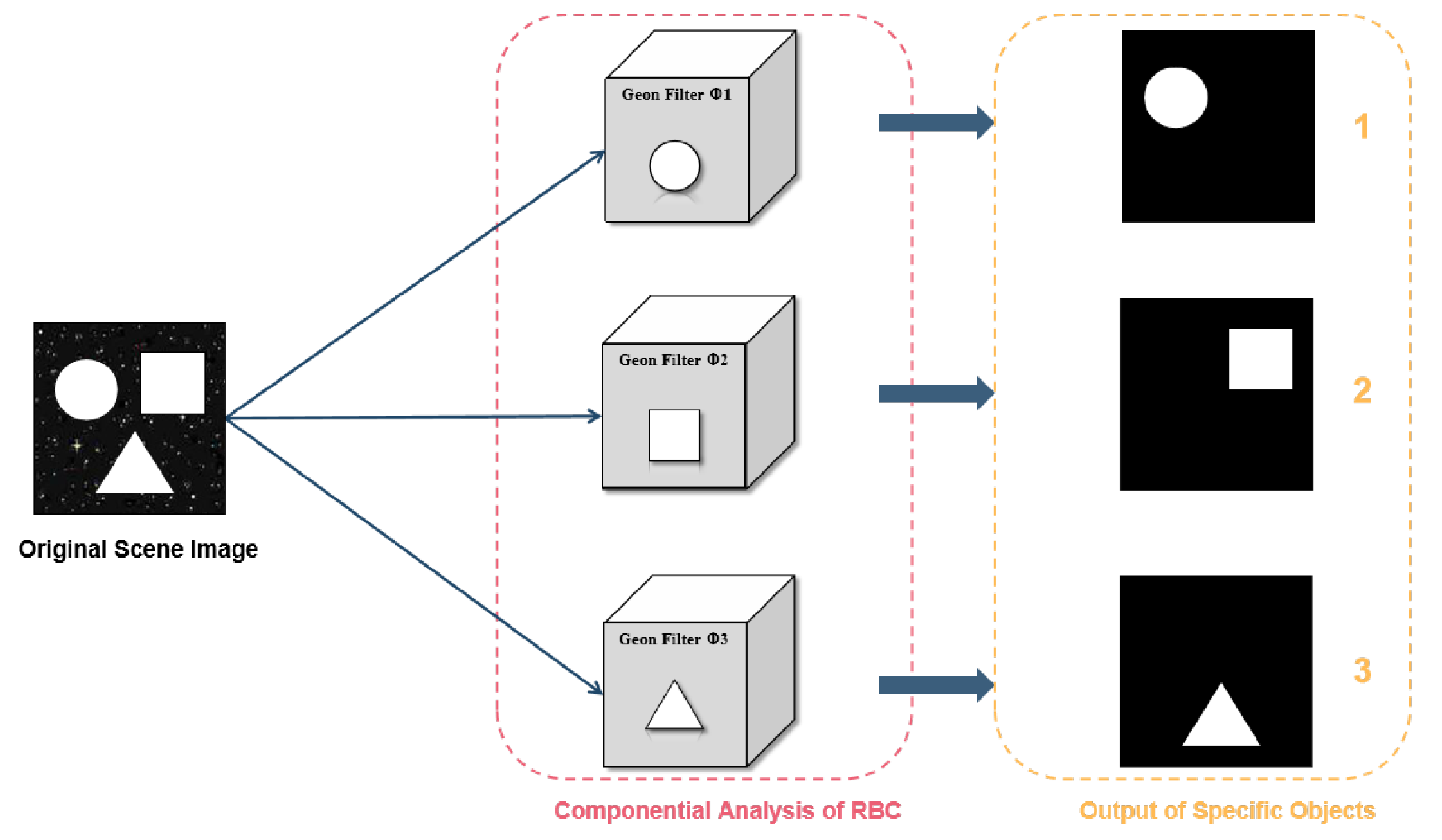
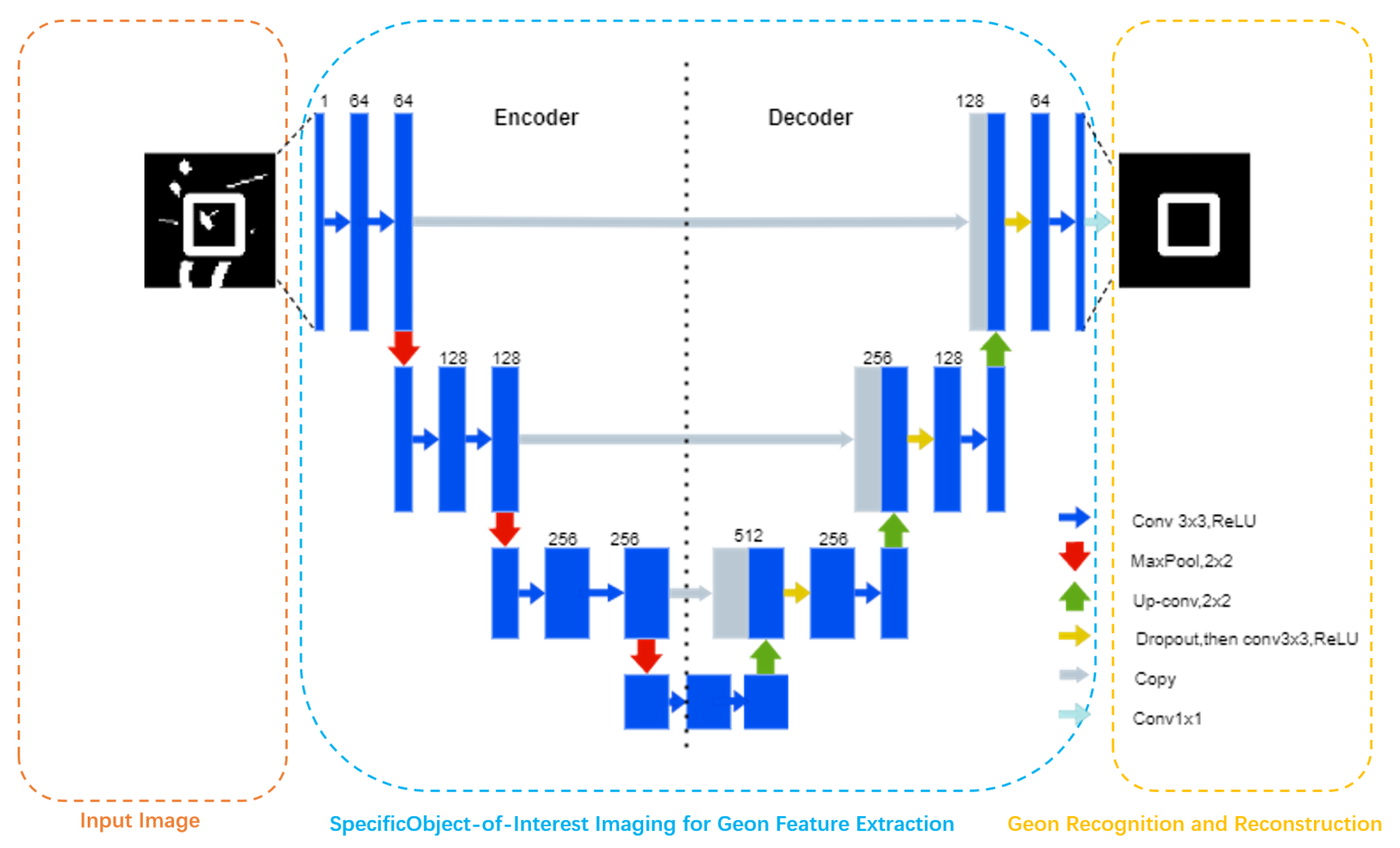
2.1. Principles of the Experiment
- Computational level: Consistent with RBCs theory, geons serve as minimal units of visual representation.
- Algorithmic level: Deep learning simulates hierarchical feature extraction, where U-Net’s encoder→decoder architecture corresponds to human V1→IT cortical pathways.
- Implementational level: Neural network weight optimization (, ) mirrors synaptic plasticity, partially validating Zhang et al.’s visual cortical activity modulation [58].
2.2. Datasheet
2.3. Evaluation Indicators
- Structural Similarity Index Measure (SSIM) [68]SSIM quantifies perceptual consistency by modeling the human visual system’s multi-channel characteristics. It is defined asBy comparing brightness, contrast, and structural similarity, visual perceptual consistency is quantified within the range of [0, 1].
- Peak Signal-to-Noise Ratio (PSNR) [69]PSNR measures fidelity in the frequency domain and is computed asHere, represents the maximum pixel value of the image (e.g., 255 for an 8-bit image). PSNR reflects the ratio of signal power to distortion.
- Mean Squared Error (MSE) [70]MSE quantifies the average squared difference between corresponding pixels:MSE indicates optimization convergence.
2.4. Experimental Setup Implementation Details
- Paired t-tests for within-condition comparisons.
- ANOVA with Tukey HSD for cross-condition analysis.
- Wilcoxon tests for non-normal distributions.
- Type I error control used Bonferroni correction ( = 0.05/9 = 0.0056 for 9 test sets).
3. Experiments and Results
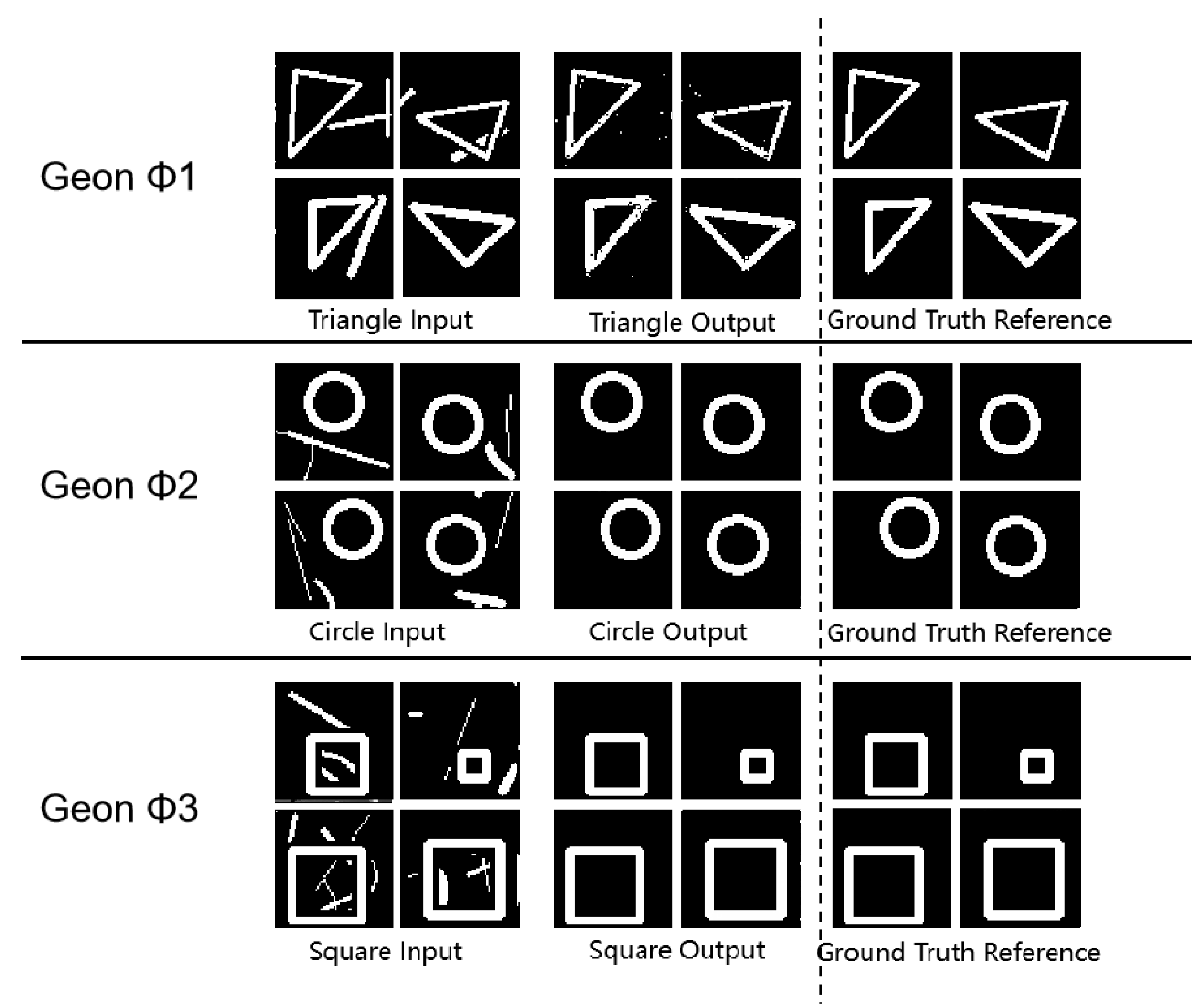
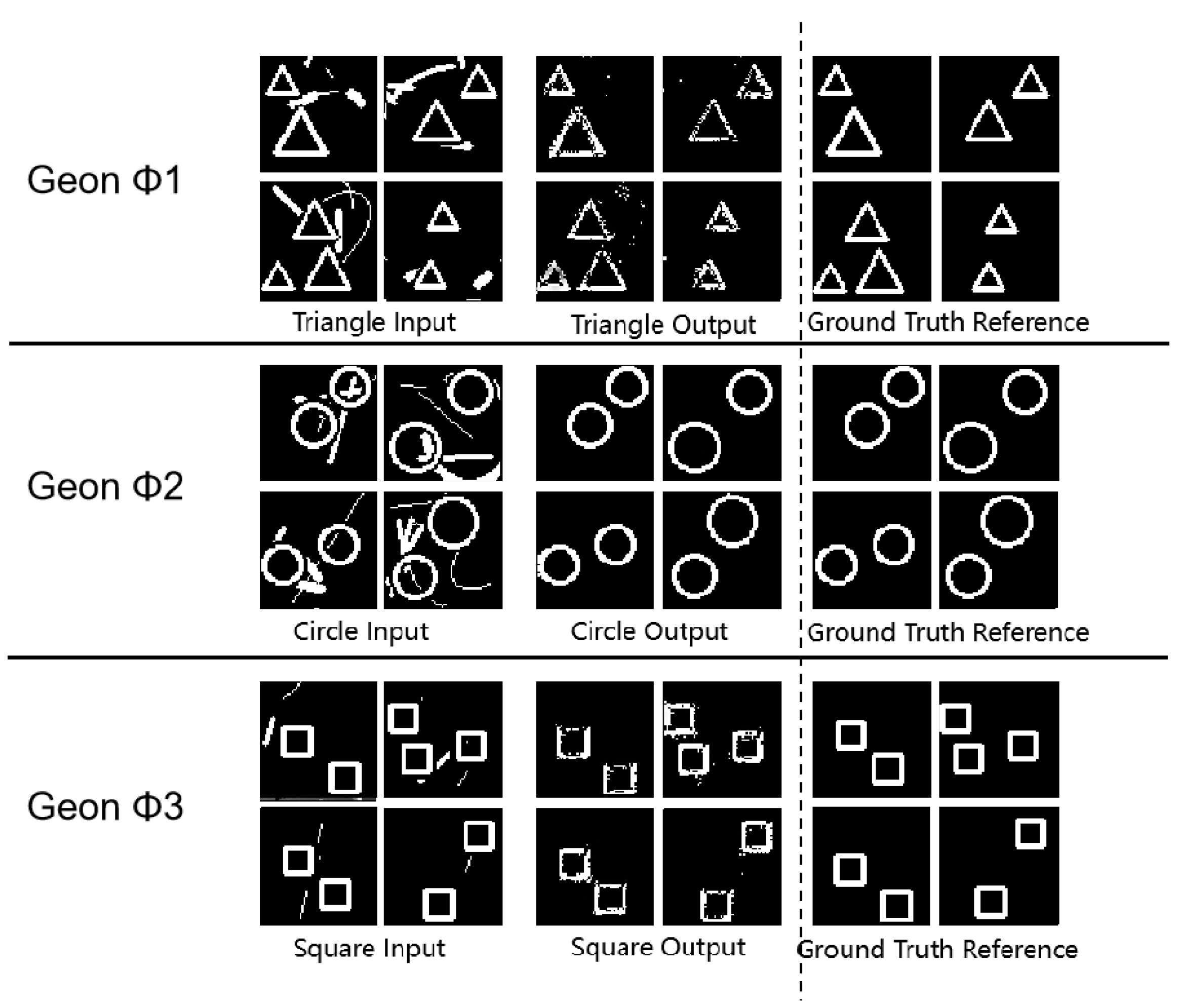
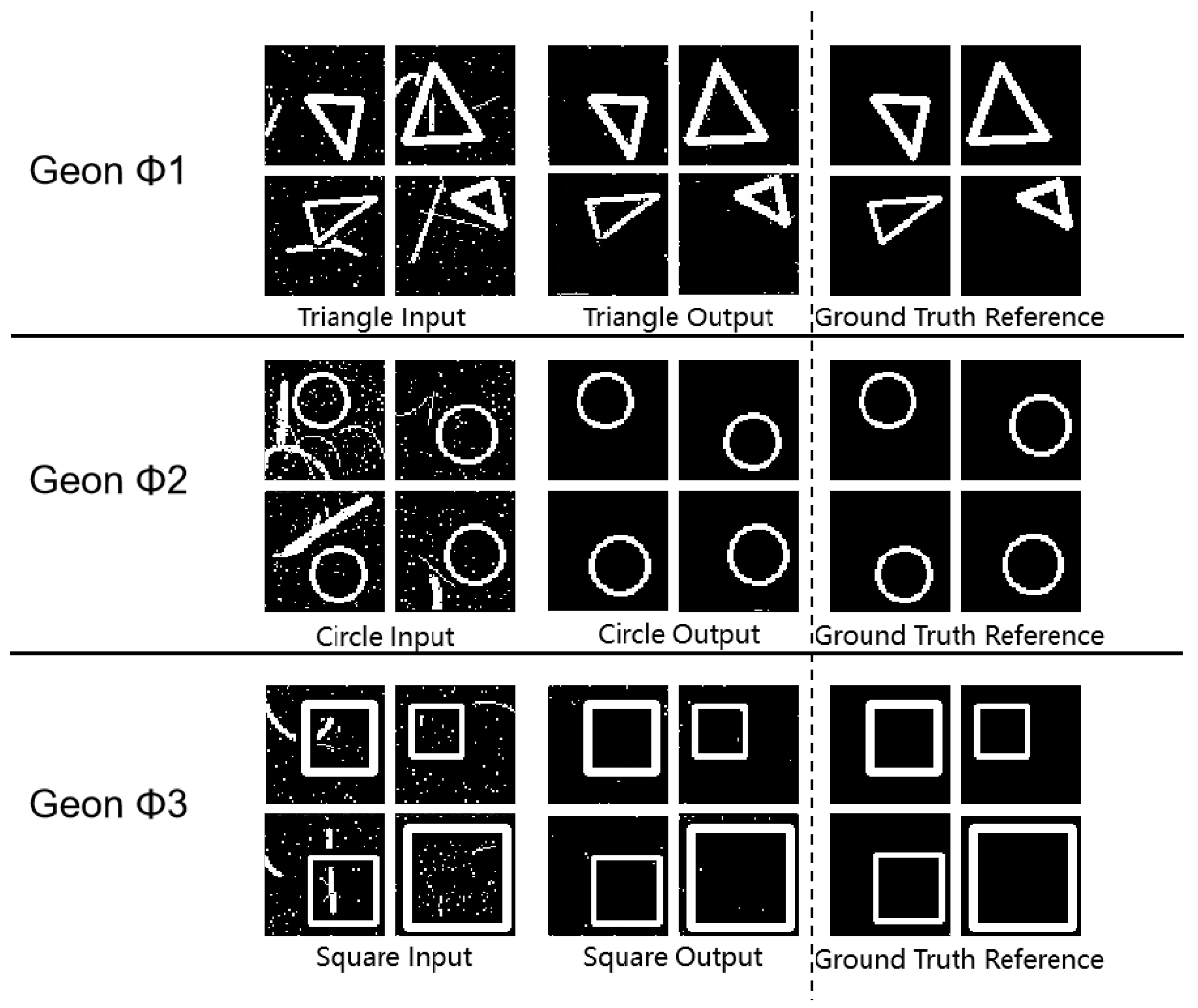
3.1. Fundamental Detection
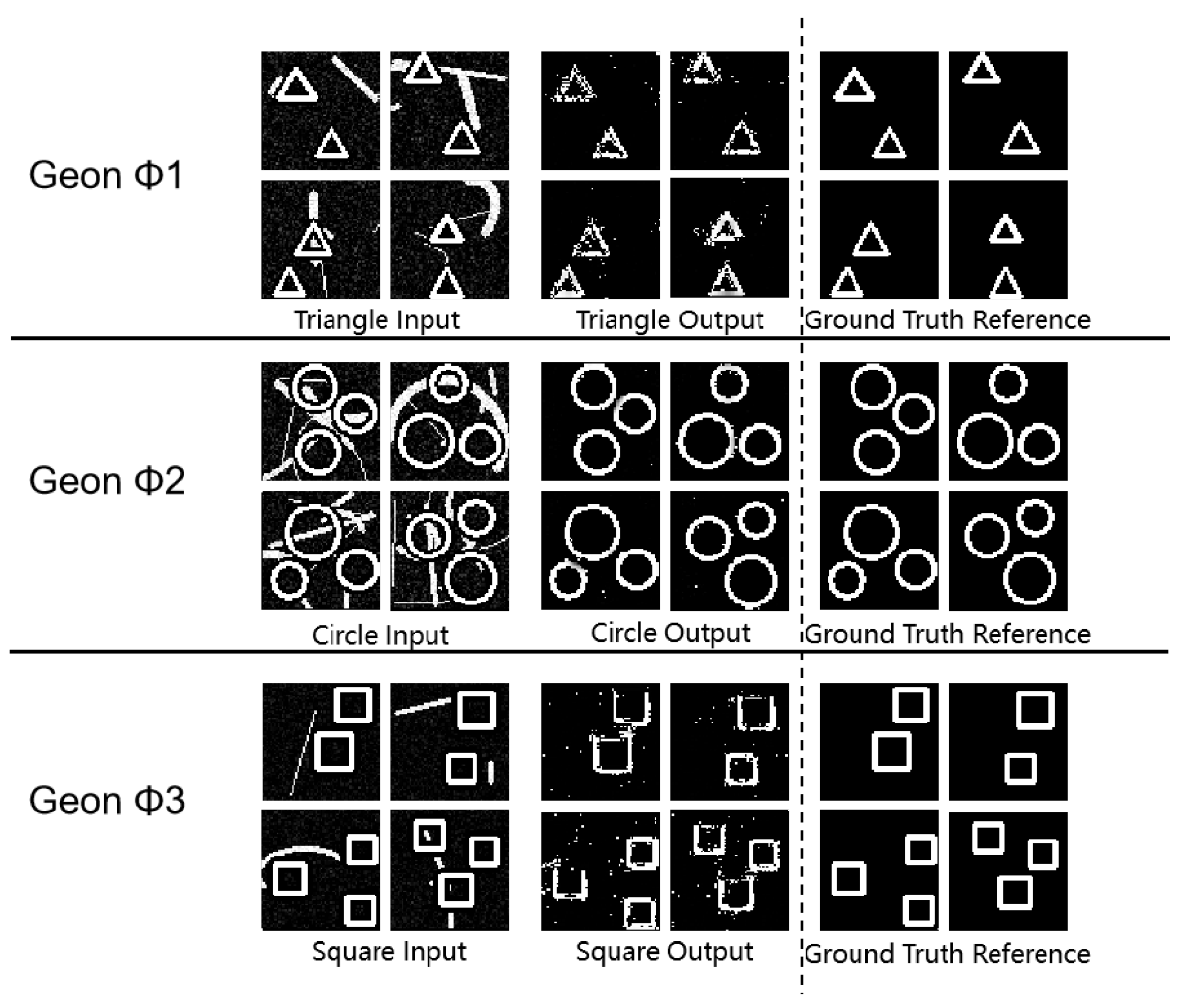
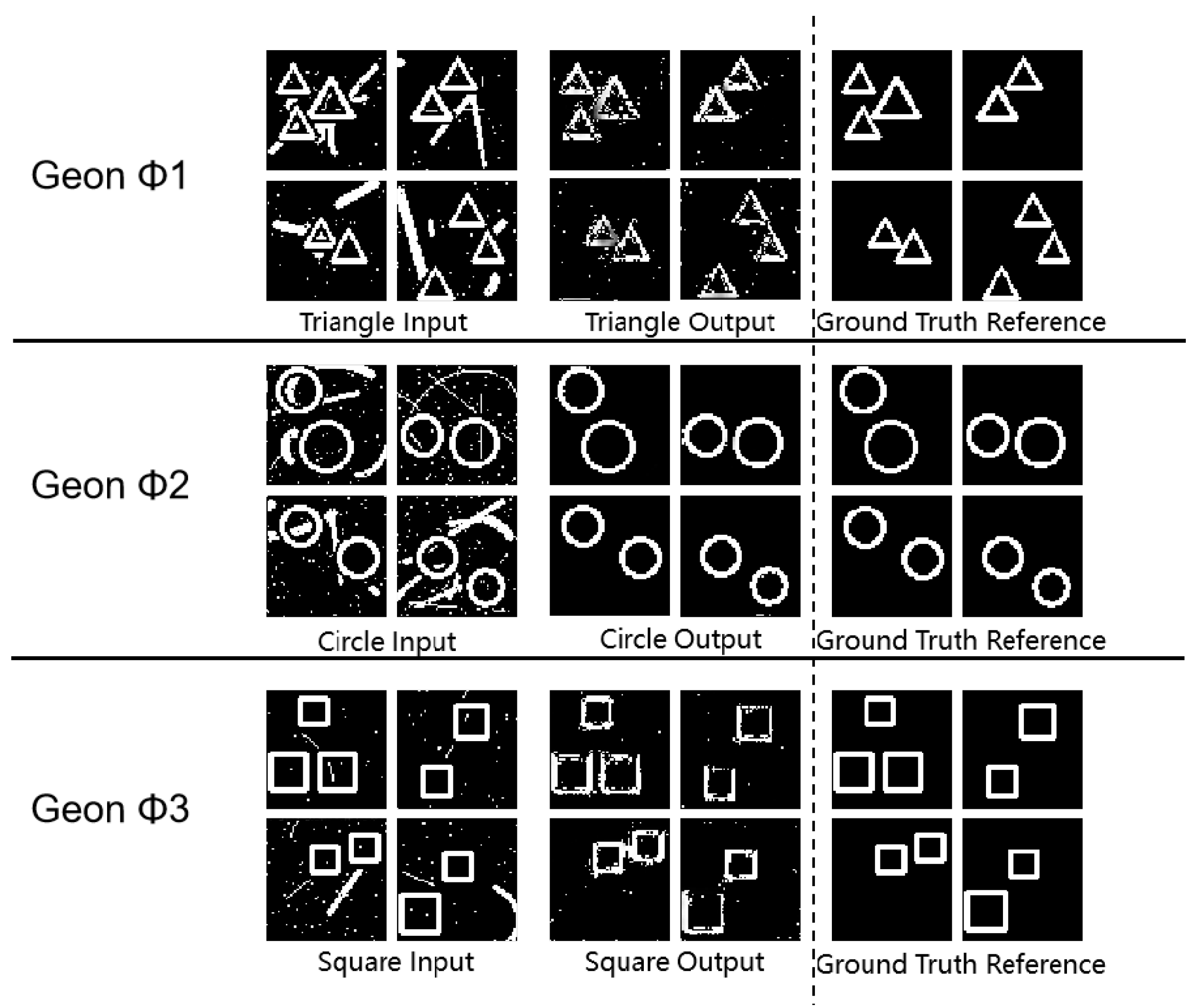
3.2. Geon Separation Detection
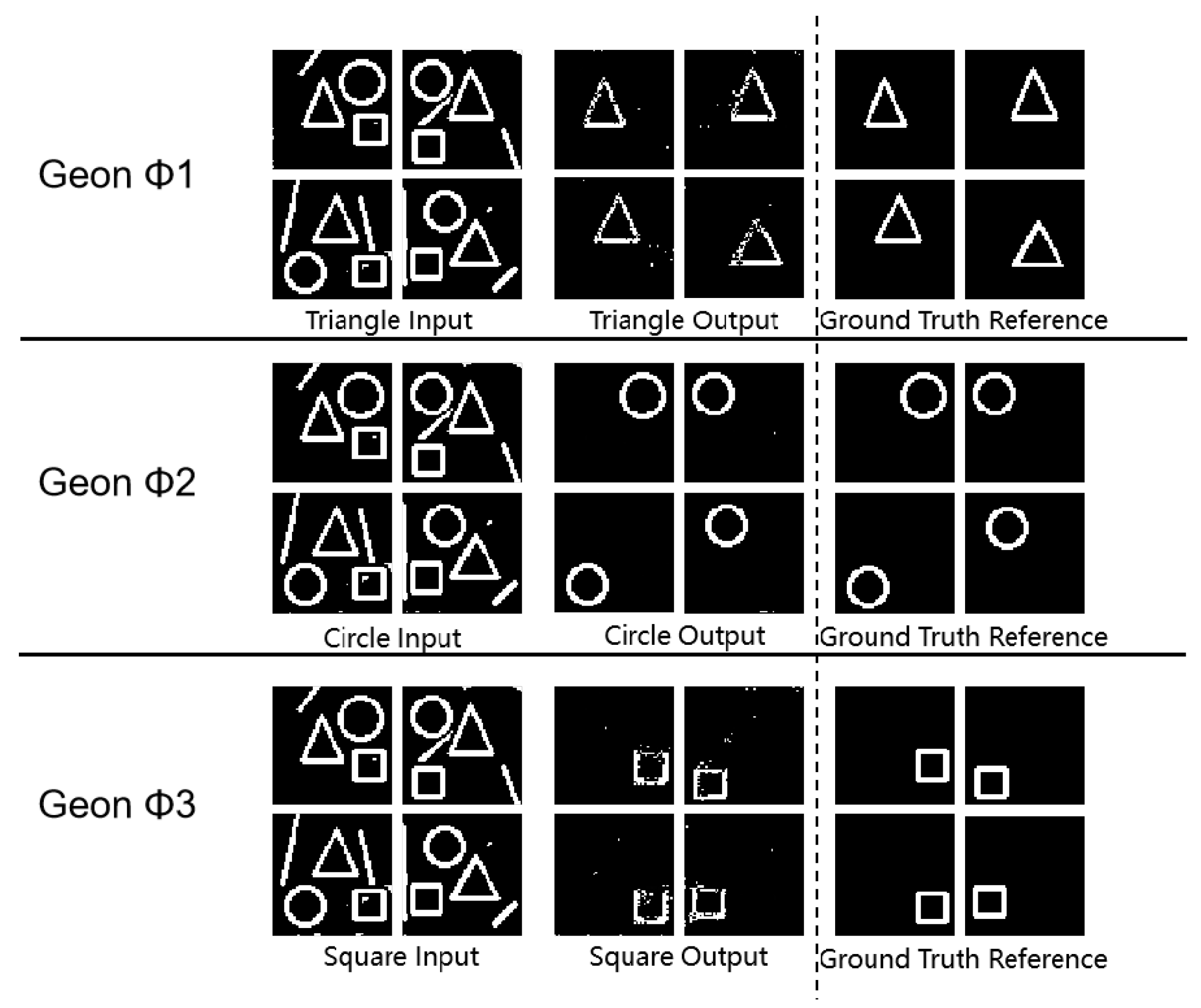
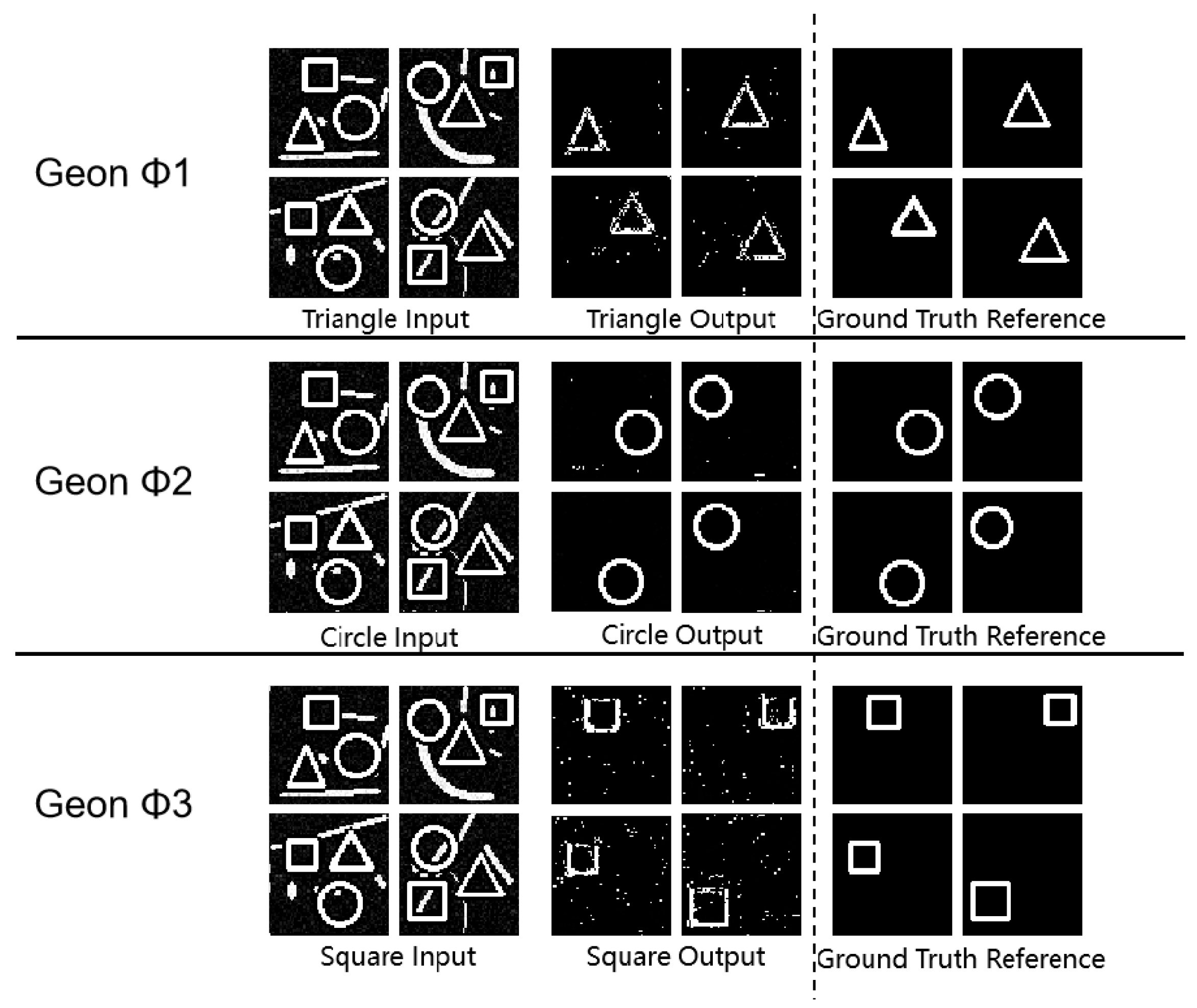
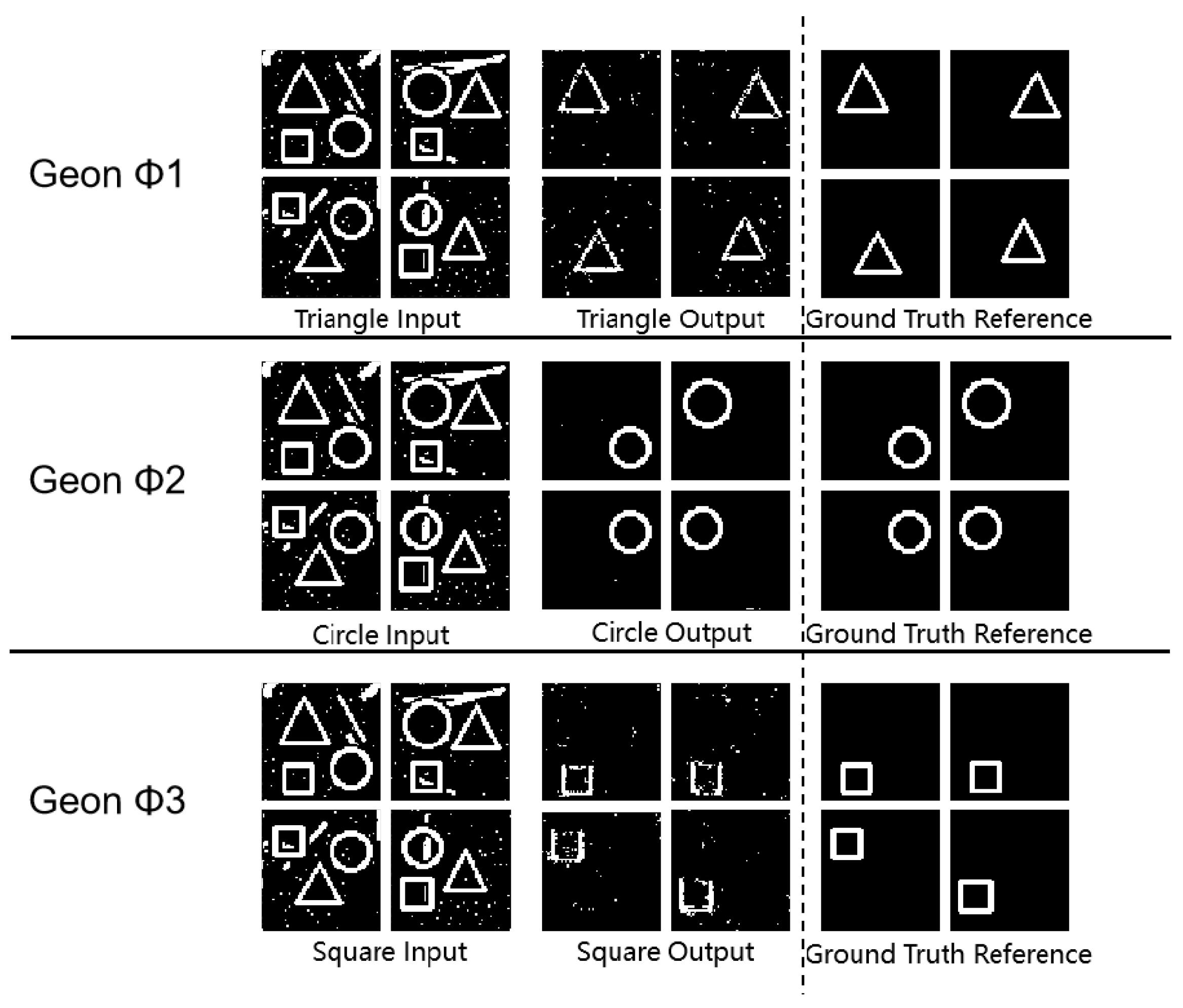
3.3. Multi-Geon Detection
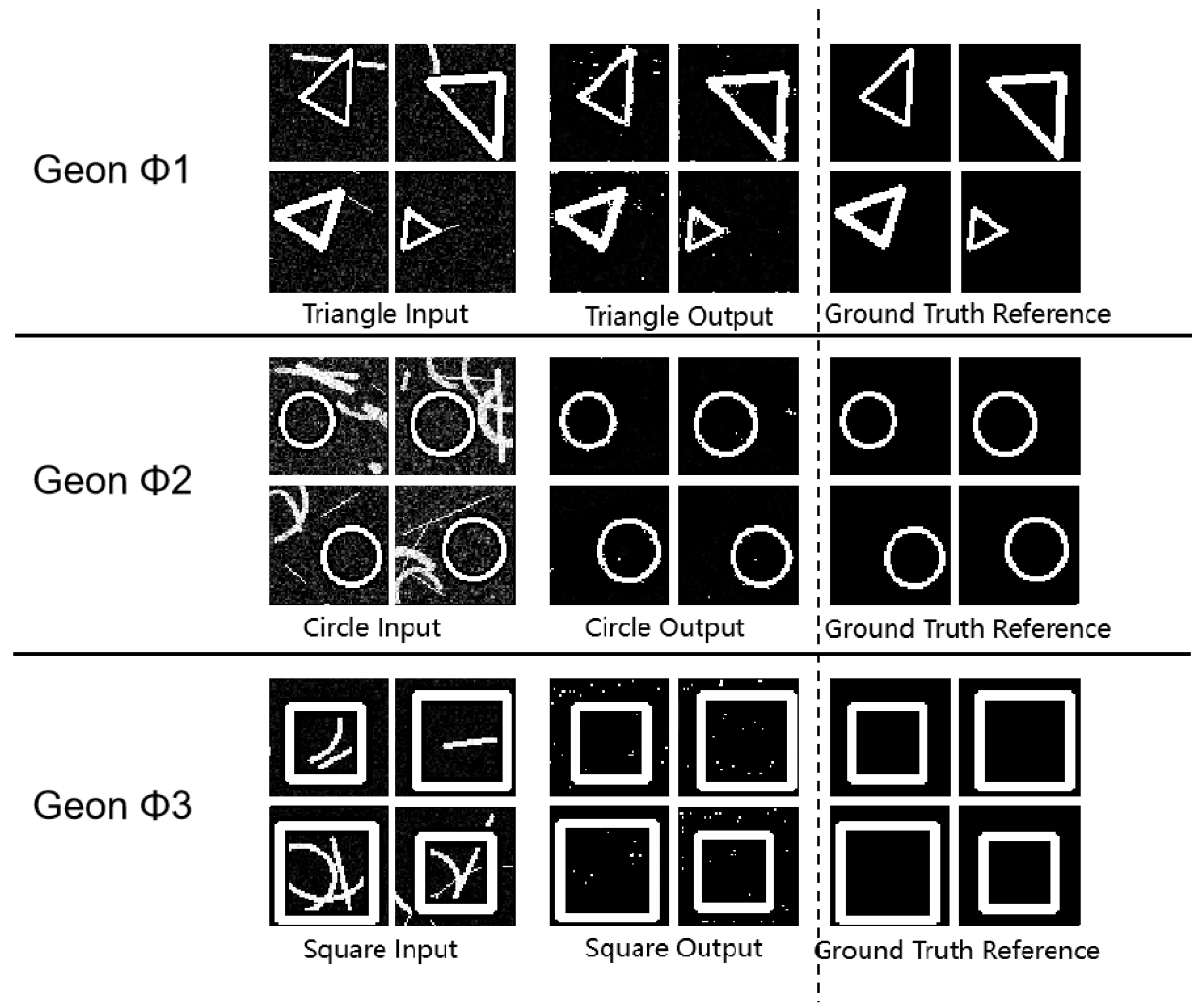
3.4. Robustness Evaluation
3.5. Discussion of Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biederman, I. Human image understanding: Recent research and a theory. Comput. Vision Graph. Image Process. 1985, 32, 29–73. [Google Scholar] [CrossRef]
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115–147. [Google Scholar] [CrossRef] [PubMed]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 207, 187–217. [Google Scholar] [CrossRef]
- Marr, D.; Poggio, T. From Understanding Computation to Understanding Neural Circuitry; Massachusetts Institute of Technology: Cambridge, MA, USA, 1976. [Google Scholar]
- Marr, D. Visual information processing: The structure and creation of visual representations. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1980, 290, 199–218. [Google Scholar] [CrossRef]
- Marr, D. Early processing of visual information. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1976, 275, 483–519. [Google Scholar] [CrossRef]
- Marr, D. A theory for cerebral neocortex. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1970, 176, 161–234. [Google Scholar]
- Marr, D. Representing visual information. Comput. Vis. Syst. 1978, 10, 101–180. [Google Scholar]
- Marr, D. A theory of cerebellar cortex. J. Physiol. 1969, 202, 437–470. [Google Scholar] [CrossRef]
- Marr, D. Analysis of occluding contour. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1977, 197, 441–475. [Google Scholar] [CrossRef]
- Marr, D.; Nishihara, H.K. Representation and recognition of the spatial organization of three-dimensional shapes. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1978, 200, 269–294. [Google Scholar] [CrossRef]
- Marr, D.; Poggio, T. A computational theory of human stereo vision. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 204, 301–328. [Google Scholar] [CrossRef]
- Marr, D.; Ullman, S. Directional selectivity and its use in early visual processing. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1981, 211, 151–180. [Google Scholar] [CrossRef]
- Marr, D. Artificial intelligence—A personal view. Artif. Intell. 1977, 9, 37–48. [Google Scholar] [CrossRef]
- Marr, D.; Vaina, L. Representation and recognition of the movements of shapes. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1982, 214, 501–524. [Google Scholar] [CrossRef]
- Torre, V.; Poggio, T.A. On edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 147–163. [Google Scholar] [CrossRef]
- Bertero, M.; Poggio, T.A.; Torre, V. Ill-posed problems in early vision. Proc. IEEE 1988, 76, 869–889. [Google Scholar] [CrossRef]
- Yuille, A.L.; Poggio, T.A. Scaling theorems for zero crossings. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 15–25. [Google Scholar] [CrossRef]
- Brunelli, R.; Poggio, T. Face recognition: Features versus templates. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1042–1052. [Google Scholar] [CrossRef]
- Sung, K.-K.; Poggio, T. Example-based learning for view-based human face detection. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 39–51. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Poggio, T. A trainable system for object detection. Int. J. Comput. Vis. 2000, 38, 15–33. [Google Scholar] [CrossRef]
- Riesenhuber, M.; Poggio, T. Hierarchical models of object recognition in cortex. Nat. Neurosci. 1999, 2, 1019–1025. [Google Scholar] [CrossRef] [PubMed]
- Patil-Takbhate, B.; Takbhate, R.; Khopkar-Kale, P.; Tripathy, S. Marvin Minsky: The Visionary Behind the Confocal Microscope and the Father of Artificial Intelligence. Cureus 2024, 16, e68434. [Google Scholar] [CrossRef]
- Minsky, M.L. Why people think computers can’t. AI Mag. 1982, 3, 3. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge; Massachusetts Institute of Technology: Cambridge, MA, USA, 1974. [Google Scholar] [CrossRef]
- Minsky, M.; Papert, S. Perceptrons: An Introduction to Computational Geometry; MIT Press: Cambridge, MA, USA, 1969; pp. 1–20. [Google Scholar] [CrossRef]
- Minsky, M. Commonsense-based interfaces. Commun. ACM 2000, 43, 66–73. [Google Scholar] [CrossRef]
- Minsky, M. Decentralized minds. Behav. Brain Sci. 1980, 3, 439–440. [Google Scholar] [CrossRef]
- Yan, S.; Yang, Z.; Ma, C.; Huang, H.; Vouga, E.; Huang, Q. Hpnet: Deep primitive segmentation using hybrid representations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; 17 October 2021; pp. 2753–2762. [Google Scholar] [CrossRef]
- Zou, C.; Yumer, E.; Yang, J.; Ceylan, D.; Hoiem, D. 3d-prnn: Generating shape primitives with recurrent neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 900–909. [Google Scholar] [CrossRef]
- Lin, Y.; Tang, C.; Chu, F.-J.; Vela, P.A. Using synthetic data and deep networks to recognize primitive shapes for object grasping. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 10494–10501. [Google Scholar] [CrossRef]
- Aliev, K.A.; Sevastopolsky, A.; Kolos, M.; Ulyanov, D.; Lempitsky, V. Neural Point-Based Graphics. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12367, pp. 42–61. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, B.; Yang, H.; Huang, Q. H3DNet: 3D Object Detection Using Hybrid Geometric Primitives. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12357, pp. 311–329. [Google Scholar] [CrossRef]
- Li, L.; Fu, H.; Tai, C.-L. Fast sketch segmentation and labeling with deep learning. IEEE Comput. Graph. Appl. 2019, 39, 38–51. [Google Scholar] [CrossRef]
- Huang, J.; Gao, J.; Ganapathi-Subramanian, V.; Su, H.; Liu, Y.; Tang, C.; Guibas, L.J. DeepPrimitive: Image decomposition by layered primitive detection. Comp. Visual Media 2018, 4, 385–397. [Google Scholar] [CrossRef]
- Sharma, G.; Goyal, R.; Liu, D.; Kalogerakis, E.; Maji, S. Neural Shape Parsers for Constructive Solid Geometry. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2628–2640. [Google Scholar] [CrossRef] [PubMed]
- Zunair, H.; Hamza, A.B. Sharp U-Net: Depthwise convolutional network for biomedical image segmentation. Comput. Biol. Med. 2021, 136, 104699. [Google Scholar] [CrossRef]
- Treisman, A. Preattentive processing in vision. Comput. Vision Graph. Image Process. 1985, 31, 156–177. [Google Scholar] [CrossRef]
- Treisman, A.; Gormican, S. Feature analysis in early vision: Evidence from search asymmetries. Psychol. Rev. 1988, 95, 15–48. [Google Scholar] [CrossRef] [PubMed]
- Treisman, A. Features and objects in visual processing. Sci. Am. 1986, 255, 114B–125. [Google Scholar] [CrossRef]
- Treisman, A. Perceptual grouping and attention in visual search for features and for objects. J. Exp. Psychol. Hum. Percept. Perform. 1982, 8, 194–214. [Google Scholar] [CrossRef]
- Treisman, A. How the deployment of attention determines what we see. Visual Cogn. 2006, 14, 411–443. [Google Scholar] [CrossRef]
- Treisman, A. Binocular rivalry and stereoscopic depth perception. In From Perception to Consciousness: Searching with Anne Treisman; Wolfe, J., Robertson, L., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 59–69. [Google Scholar] [CrossRef]
- Treisman, A. Feature binding, attention and object perception. Philos. Trans. R. Soc. B Biol. Sci. 1998, 353, 1295–1306. [Google Scholar] [CrossRef] [PubMed]
- Treisman, A. Features and objects: The Fourteenth Bartlett Memorial Lecture. Q. J. Exp. Psychol. A Hum. Exp. Psychol. 1988, 40A, 201–237. [Google Scholar] [CrossRef]
- Treisman, A.; DeSchepper, B. Object tokens, attention, and visual memory. In Attention and Performance 16: Information Integration in Perception and Communication; Inui, T., McClelland, J.L., Eds.; The MIT Press: Cambridge, MA, USA, 1996; pp. 15–46. [Google Scholar]
- Treisman, A.; Paterson, R. Emergent features, attention, and object perception. J. Exp. Psychol. Hum. Percept. Perform. 1984, 10, 12–31. [Google Scholar] [CrossRef]
- Treisman, A.M.; Gelade, G. A feature-integration theory of attention. Cogn. Psychol. 1980, 12, 97–136. [Google Scholar] [CrossRef] [PubMed]
- Treisman, A. Visual attention and the perception of features and objects. Can. Psychol./Psychol. Can. 1994, 35, 107–108. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194–203. [Google Scholar] [CrossRef]
- Borji, A.; Itti, L. State-of-the-Art in Visual Attention Modeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 185–207. [Google Scholar] [CrossRef] [PubMed]
- Itti, L.; Koch, C.; Braun, J. Revisiting spatial vision: Toward a unifying model. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2000, 17, 1899–1917. [Google Scholar] [CrossRef] [PubMed]
- Itti, L. Automatic foveation for video compression using a neurobiological model of visual attention. IEEE Trans. Image Process. Publ. IEEE Signal Process. Soc. 2004, 13, 1304–1318. [Google Scholar] [CrossRef]
- Itti, L. Quantitative modelling of perceptual salience at human eye position. Vis. Cogn. 2006, 14, 959–984. [Google Scholar] [CrossRef]
- Carmi, R.; Itti, L. The role of memory in guiding attention during natural vision. J. Vis. 2006, 6, 898–914. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Itti, L.; Gold, C.; Koch, C. Visual attention and target detection in cluttered natural scenes. Opt. Eng. 2001, 40, 1784–1793. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C. Comparison of feature combination strategies for saliency-based visual attention systems. In Proceedings of the SPIE 3644, Human Vision and Electronic Imaging IV, San Jose, CA, USA, 23–29 January 1999. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, X.; Zheng, C.; Zhao, Y.; Gao, J.; Deng, Z.; Zhang, X.; Chen, J. Effects of Vergence Eye Movement Planning on Size Perception and Early Visual Processing. J. Cogn. Neurosci. 2024, 36, 2793–2806. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, D.; Liang, B.; Wang, Z.; Li, J.; Gao, Z.; Gao, M.; Huang, R.; Liu, M. Visual Creativity Imagery Modulates Local Spontaneous Activity Amplitude of Resting-State Brain. In Proceedings of the 2016 Annual Meeting of the Organization for Human Brain Mapping, Geneva, Switzerland, 26–30 June 2016; Abstract 1525. [Google Scholar]
- Wen, X.; Zhang, D.; Liang, B.; Zhang, R.; Wang, Z.; Wang, J.; Liu, M.; Huang, R. Reconfiguration of the Brain Functional Network Associated with Visual Task Demands. PLoS ONE 2015, 10, e0132518. [Google Scholar] [CrossRef]
- Zhou, L.F.; Wang, K.; He, L.; Meng, M. Twofold advantages of face processing with or without visual awareness. J. Exp. Psychol. Hum. Percept. Perform. 2021, 47, 784–794. [Google Scholar] [CrossRef]
- Zhu, H.; Cai, T.; Xu, J.; Wu, S.; Li, X.; He, S. Neural correlates of stereoscopic depth perception: A fNIRS study. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 4442–4446. [Google Scholar]
- Li, J.; Chen, S.; Wang, S.; Lei, M.; Dai, X.; Liang, C.; Xu, K.Y.; Lin, S.; Li, Y.; Fan, Y.; et al. An optical biomimetic eyes with interested object imaging. arXiv 2021, arXiv:2108.04236. [Google Scholar] [CrossRef]
- Li, J.; Lei, M.; Dai, X.; Wang, S.; Zhong, T.; Liang, C.; Wang, C.; Xie, P.; Wang, R. Compressed Sensing Based Object Imaging System and Imaging Method Therefor. U.S. Patent 2021/0144278 A1, 13 May 2021. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9351. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Deep Plug-And-Play Super-Resolution for Arbitrary Blur Kernels. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1671–1681. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
| Theoretical Framework | Definition of Geons | Dynamic Adaptability | Noise Robustness | Improvements in This Paper |
|---|---|---|---|---|
| RBC (Biederman) | Fixed 36 geometric shapes | Low | Not involved | Adaptive learning of geons |
| I-Theory | Gradual abstraction of features | Medium | Partial | Incorporation of sparse coding |
| DeepPrimitive | Data-driven action segmentation | High | Data-dependent | Cross-modal bioinspired |
| Geon | SSIM (95% CI) | PSNR (95% CI) | MSE (95% CI) |
|---|---|---|---|
| Triangle | 0.93 ± 0.02 * | 59.14 ± 1.24 ** | 0.10 ± 0.03 * |
| Circle | 0.99 ± 0.01 ** | 54.64 ± 1.05 ** | 0.23 ± 0.05 ** |
| Square | 0.98 ± 0.01 ** | 58.40 ± 1.18 ** | 0.11 ± 0.02 ** |
| Geon | SSIM (SEM) | PSNR (SEM) | MSE (SEM) |
|---|---|---|---|
| Triangle | 0.88 ± 0.03 *** | 62.34 ± 0.89 *** | 0.05 ± 0.01 *** |
| Circle | 0.99 ± 0.005 *** | 60.05 ± 0.76 *** | 0.06 ± 0.01 *** |
| Square | 0.80 ± 0.04 ** | 58.88 ± 1.12 ** | 0.10 ± 0.02 ** |
| Geon | SSIM (SEM) | PSNR (SEM) | MSE (SEM) |
|---|---|---|---|
| Triangle | 0.79 ± 0.03 *** | 46.17 ± 0.89 *** | 2.64 ± 0.01 *** |
| Circle | 0.98 ± 0.005 *** | 48.58 ± 0.76 *** | 1.35 ± 0.01 *** |
| Square | 0.77 ± 0.04 ** | 51.55 ± 1.12 ** | 0.61 ± 0.02 ** |
| Geon | Scene | SSIM | PSNR | MSE |
|---|---|---|---|---|
| Basic Detection | 0.69 | 42.22 | 4.03 | |
| Triangle | Geon Separation | 0.83 | 61.45 | 0.06 |
| Multi-Target | 0.70 | 46.93 | 1.98 | |
| Basic Detection | 0.85 | 45.60 | 1.87 | |
| Circle | Geon Separation | 0.95 | 55.36 | 0.20 |
| Multi-Target | 0.89 | 46.19 | 1.85 | |
| Basic Detection | 0.56 | 56.06 | 0.18 | |
| Square | Geon Separation | 0.49 | 57.17 | 0.13 |
| Multi-Target | 0.46 | 51.10 | 0.67 |
| Geon | Scene | SSIM | PSNR | MSE |
|---|---|---|---|---|
| Basic Detection | 0.88 | 56.28 | 0.16 | |
| Triangle | Geon Separation | 0.65 | 59.35 | 0.08 |
| Multi-Target | 0.63 | 46.42 | 2.24 | |
| Basic Detection | 0.98 | 57.19 | 0.13 | |
| Circle | Geon Separation | 0.98 | 59.66 | 0.07 |
| Multi-Target | 0.98 | 48.55 | 1.34 | |
| Basic Detection | 0.88 | 57.83 | 0.11 | |
| Square | Geon Separation | 0.72 | 58.57 | 0.10 |
| Multi-Target | 0.68 | 51.15 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Liu, M.; Li, J. Detection and Recognition of Visual Geons Based on Specific Object-of-Interest Imaging Technology. Sensors 2025, 25, 3022. https://doi.org/10.3390/s25103022
Wu Y, Liu M, Li J. Detection and Recognition of Visual Geons Based on Specific Object-of-Interest Imaging Technology. Sensors. 2025; 25(10):3022. https://doi.org/10.3390/s25103022
Chicago/Turabian StyleWu, Yonghao, Minyi Liu, and Jun Li. 2025. "Detection and Recognition of Visual Geons Based on Specific Object-of-Interest Imaging Technology" Sensors 25, no. 10: 3022. https://doi.org/10.3390/s25103022
APA StyleWu, Y., Liu, M., & Li, J. (2025). Detection and Recognition of Visual Geons Based on Specific Object-of-Interest Imaging Technology. Sensors, 25(10), 3022. https://doi.org/10.3390/s25103022






