Long-Term Neonatal EEG Modeling with DSP and ML for Grading Hypoxic–Ischemic Encephalopathy Injury
Abstract
1. Introduction
- A novel method of long-term EEG representation by the usage of frequency and amplitude modulation data transformation, applied only for short-term EEG seizure detection prior to this research.
- A novel ML modeling pipeline that accurately models long-term EEG compressed spectrograms to leverage computer vision backbones, formulating the problem as a regression task (as opposed to classification) to leverage the monotonic relationship between grades.
- A novel postprocessing technique to convert regression values to grades based on optimized rounder thresholds.
2. Methods
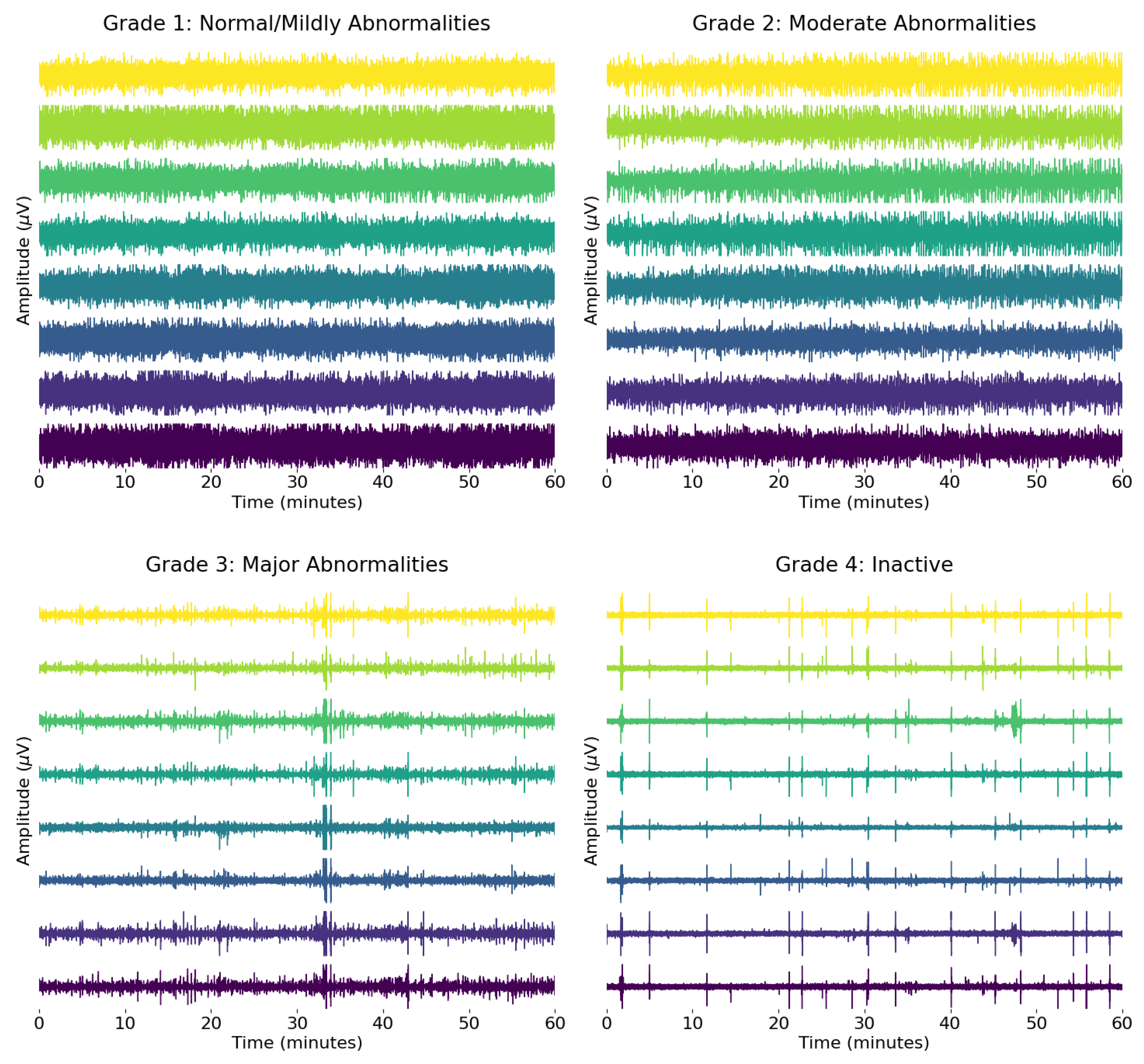
2.1. Dataset
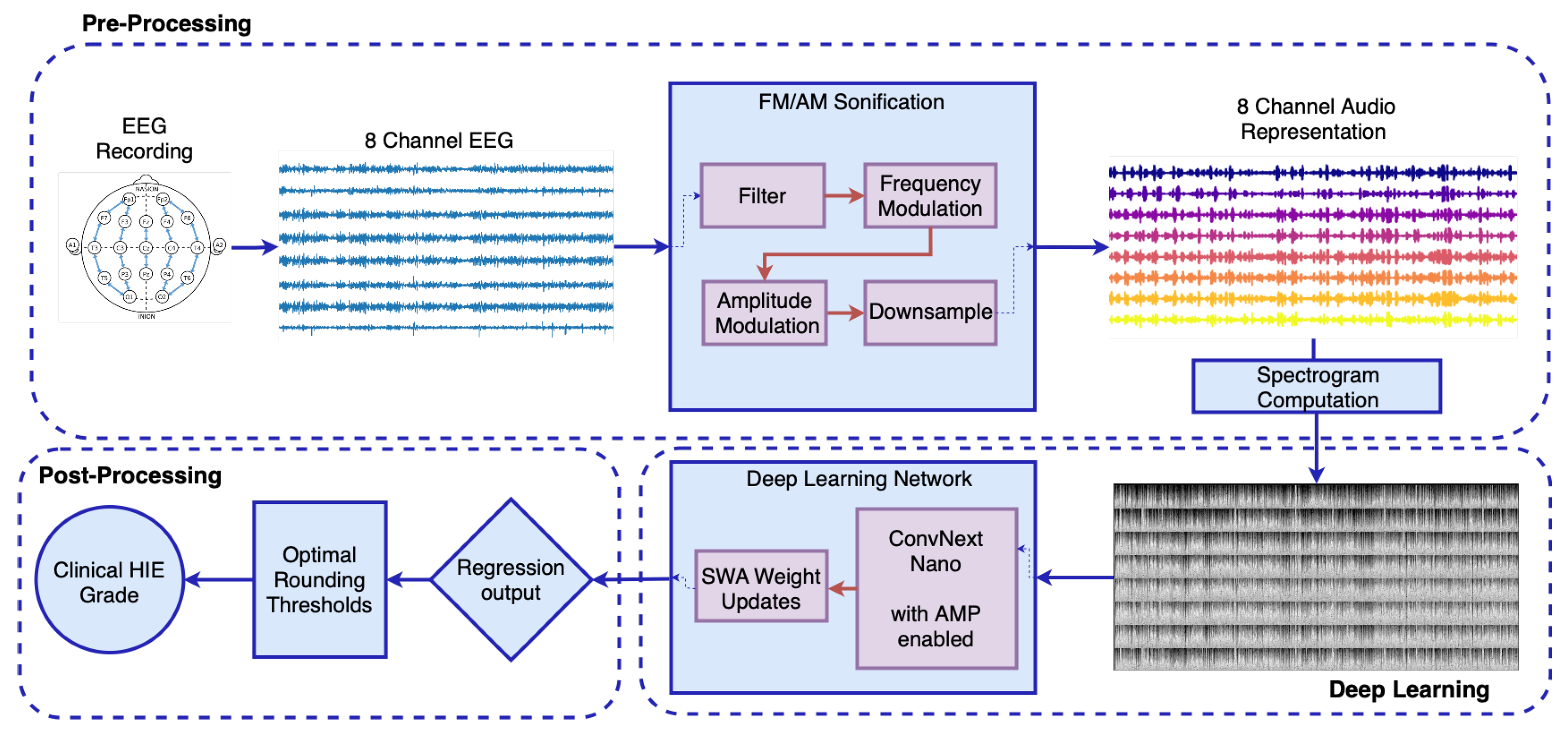
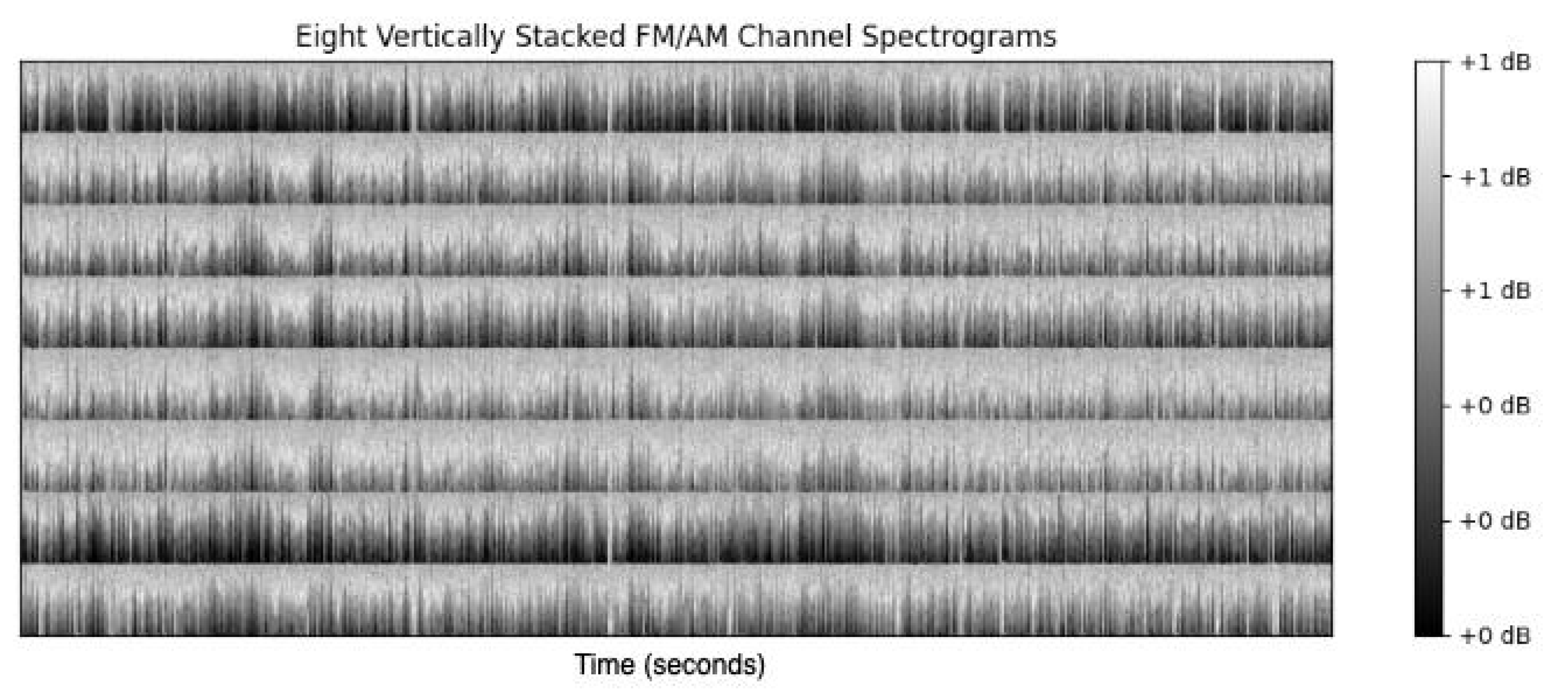
2.2. Proposed Workflow
2.2.1. Signal Preprocessing
- Preprocessing: The EEG signal is filtered between 0.5 to 7.5 Hz after the implementation of a notch filter and downsampled to reduce computational load [34]. This was carried out to preserve rhythmic activity predominantly found in the delta and theta bands of the neonatal EEG [42,43], while accommodating the constraints introduced by downsampling. The upper cutoff at 7.5 Hz was chosen to allow for an effective anti-aliasing filter with a reasonable transition band before the Nyquist limit, avoiding the need for an excessively sharp filter design. This trade-off ensures minimal loss of relevant signal content while maintaining computational efficiency and filter stability. Dynamic range compression is applied to the amplitude of the signal to prevent distortion during the frequency modulation (FM) stage. An envelope is applied to capture the signal energy, with the envelope compressed for any values exceeding a pre-defined threshold of −20 dB.
- Frequency Modulation: A carrier sinusoid centered at 500 Hz is modulated based on the processed EEG signal, with an exponential transform then applied to convert the EEG frequencies to semitones, following the musical definition of an octave.
- Amplitude Modulation: The FM signal is then modulated with the envelope of the EEG signal, emphasizing long-term rhythmic patterns in the EEG, a critical feature for defining the EEG grade.
- Downsampling: The audio signal is downsampled, based on Fourier Transform interpolation and satisfying the Shannon-Nyquist Sampling Theorem [44] to a frequency of 512 Hz.
2.2.2. Deep Learning Model
2.2.3. Postprocessing
2.3. Performance Metrics
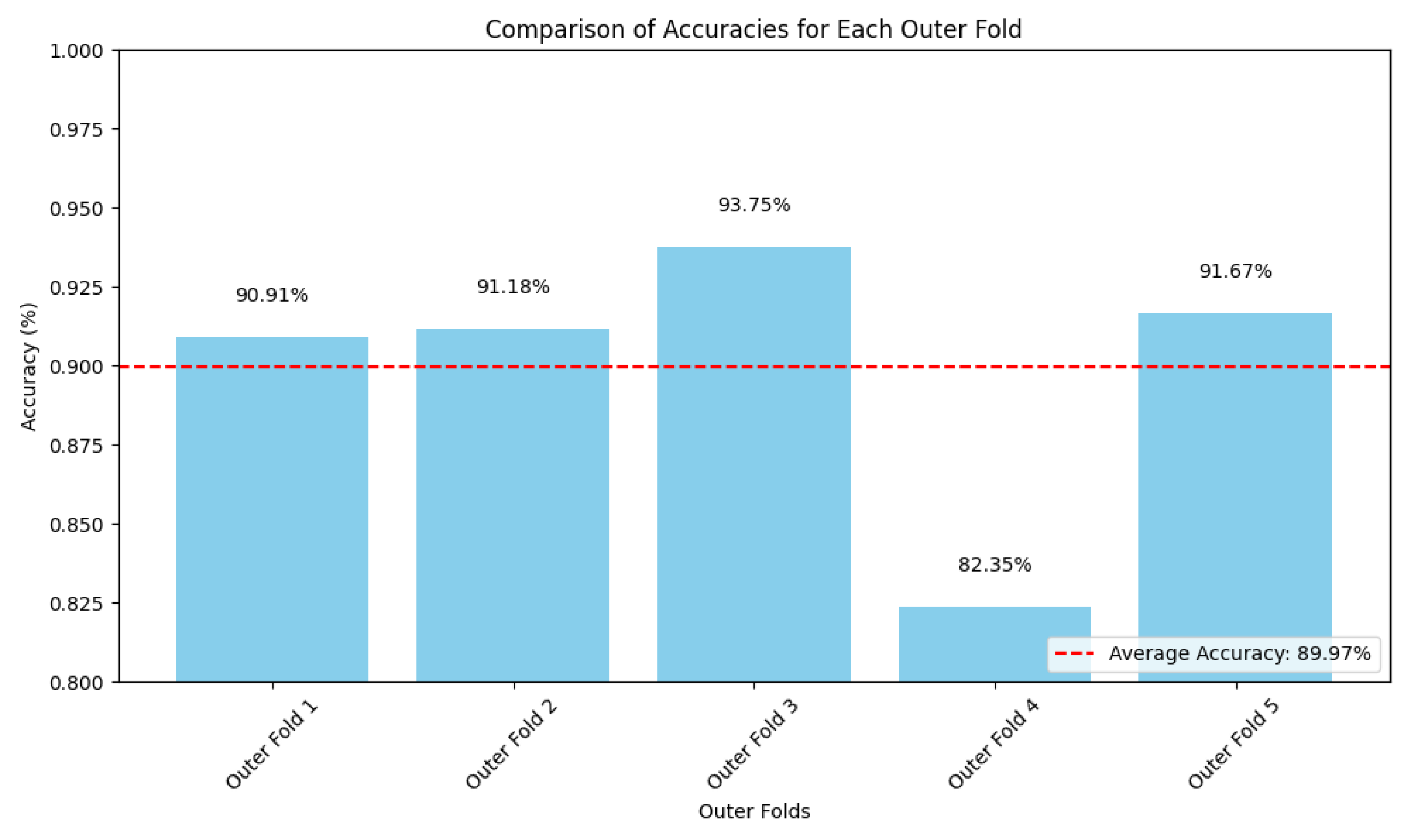
2.4. Nested Cross-Validation Evaluation Framework
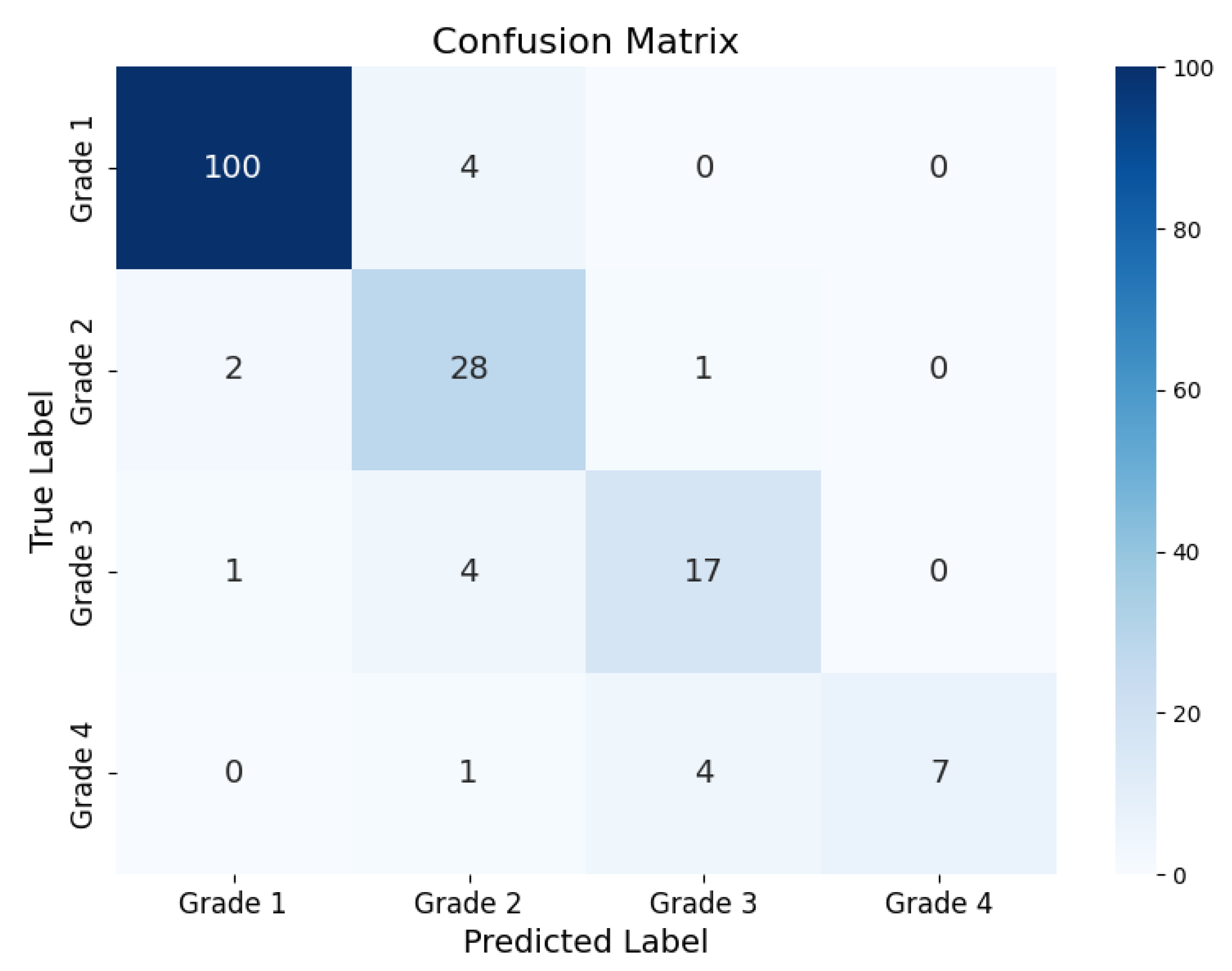
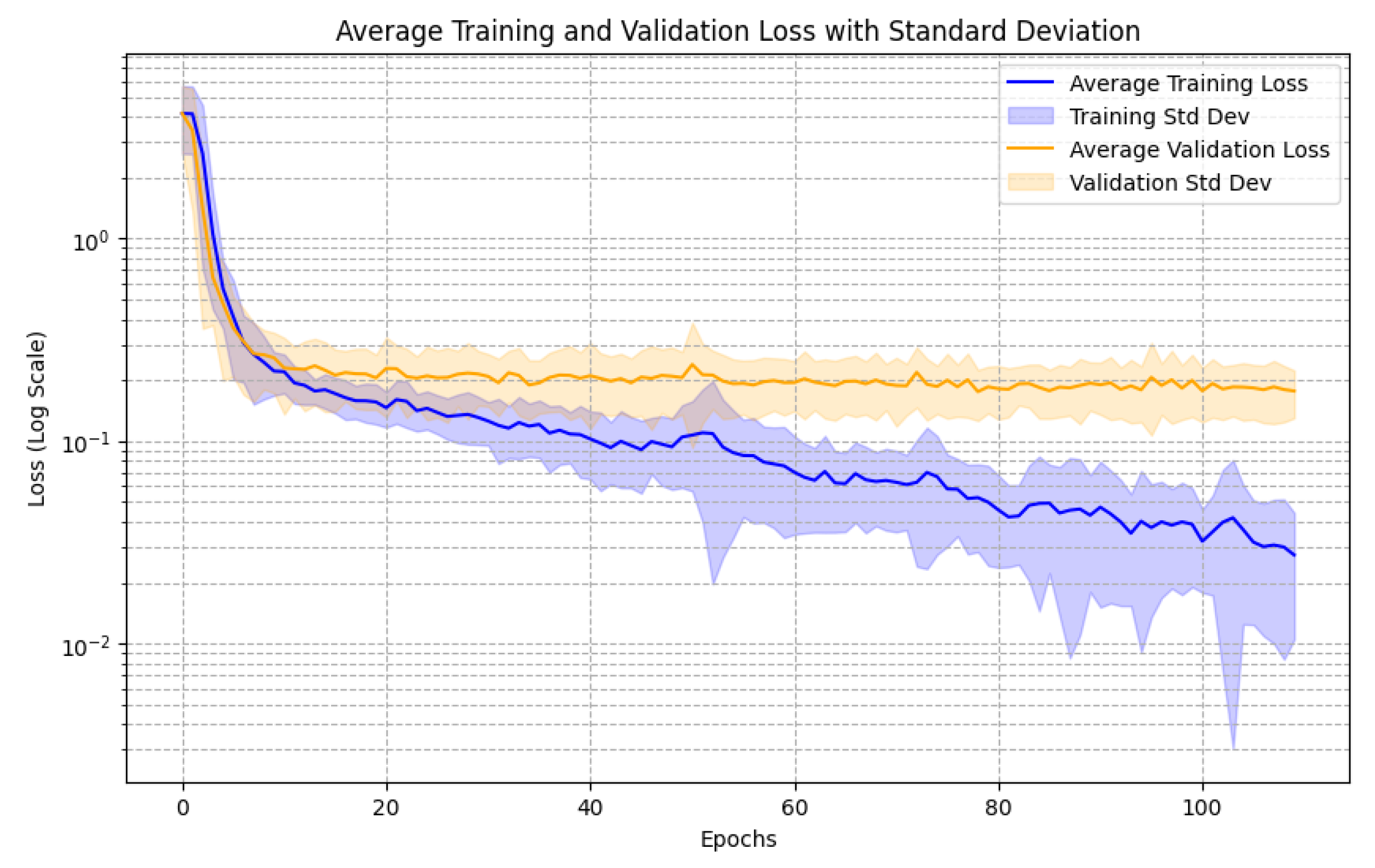
3. Results
4. Discussion
4.1. New State of the Art
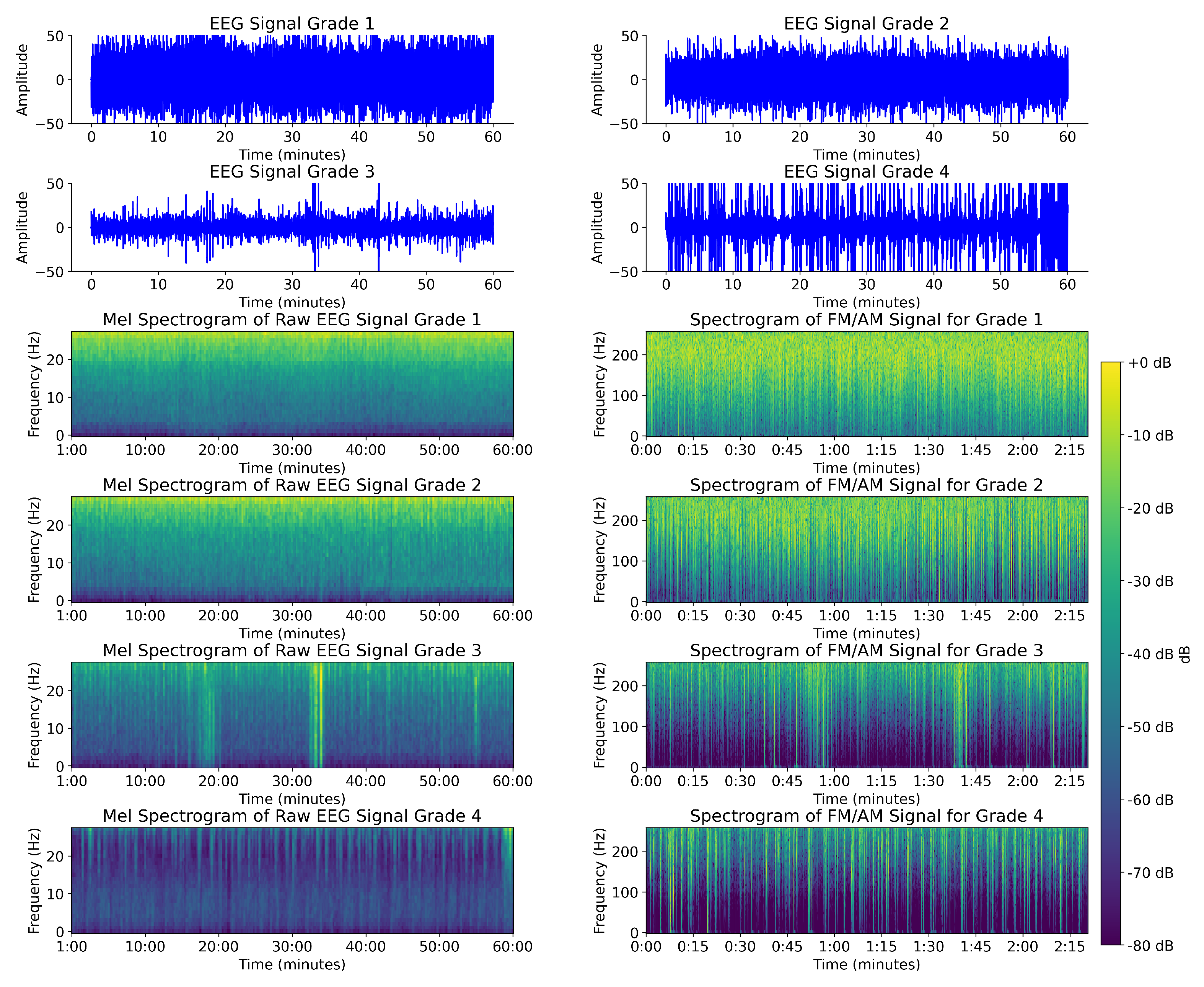
4.2. Comparison Between FM/AM Transformed EEG Spectrogram and Mel Spectrogram EEG
4.3. Regression vs. Classification Performance
4.4. Analysis of Errors
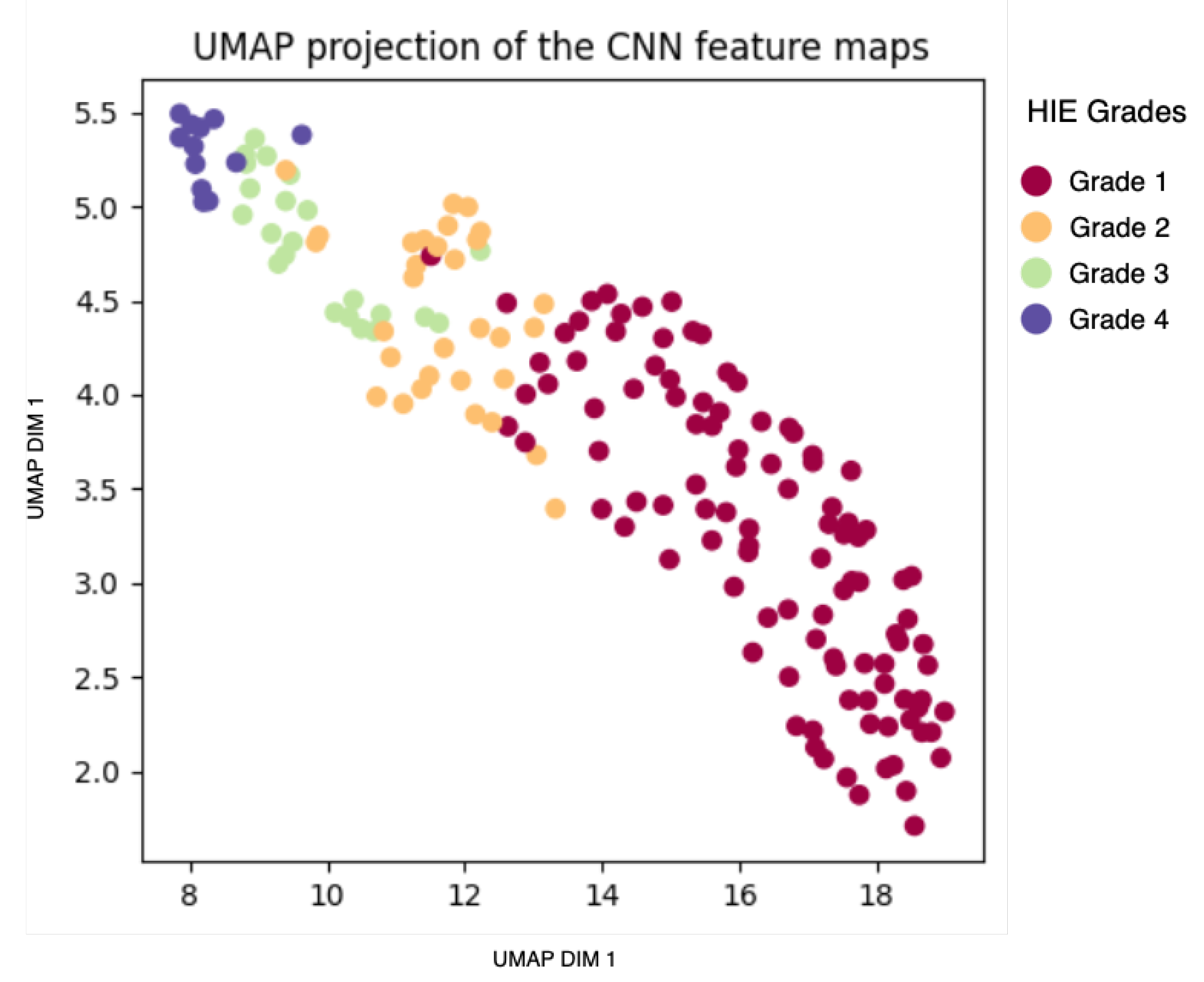
4.5. Analysis of Model-Based Representation
4.6. Methodology Refinement and Experimental Justification
4.7. Computational Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HIE | Hypoxic–Ischemic Encephalopathy |
| ML | Machine Learning |
| DSP | Digital Signal Processing |
| CNN | Convolutional Neural Network |
| EEG | Electroencephalogram |
| FM\AM | Frequency and Amplitude Modulation |
| CV | Cross-Validation |
| OOF | Out-Of-Fold |
| MSE | Mean-Squared Error |
References
- Greco, P.; Nencini, G.; Piva, I.; Scioscia, M.; Volta, C.A.; Spadaro, S.; Neri, M.; Bonaccorsi, G.; Greco, F.; Cocco, I.; et al. Pathophysiology of Hypoxic–Ischemic Encephalopathy: A Review of the Past and a View on the Future. Acta Neurol. Belg. 2020, 120, 277–288. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.C.; Kozuki, N.; Blencowe, H.; Vos, T.; Bahalim, A.; Darmstadt, G.L.; Niermeyer, S.; Ellis, M.; Robertson, N.J.; Cousens, S.; et al. Intrapartum-Related Neonatal Encephalopathy Incidence and Impairment at Regional and Global Levels for 2010 with Trends from 1990. Pediatr. Res. 2013, 74, 50–72. [Google Scholar] [CrossRef] [PubMed]
- Likitha, N.; Channabasavanna, N.; Mahendrappa, K.B. Immediate Complications of Hypoxic-Ischemic Encephalopathy in Term Neonates with Resistive Index as Prognostic Factor. Int. J. Contemp. Pediatr. 2021, 8, 711. [Google Scholar] [CrossRef]
- Chen, D.Y.; Lee, I.C.; Wang, X.A.; Wong, S.H. Early Biomarkers and Hearing Impairments in Patients with Neonatal Hypoxic–Ischemic Encephalopathy. Diagnostics 2021, 11, 2056. [Google Scholar] [CrossRef]
- Edmonds, C.J.; Helps, S.K.; Hart, D.; Zatorska, A.; Gupta, N.; Cianfaglione, R.; Vollmer, B. Minor Neurological Signs and Behavioural Function at Age 2 Years in Neonatal Hypoxic Ischaemic Encephalopathy (HIE). Eur. J. Paediatr. Neurol. 2020, 27, 78–85. [Google Scholar] [CrossRef]
- Okulu, E.; Hirfanoğlu, İ.; Satar, M.; Erdeve, O.; Koc, E.; Ozlu, F.; Gokce, M.; Armangil, D.; Tunç, G.; Demirel, N.; et al. An Observational, Multicenter, Registry-Based Cohort Study of Turkish Neonatal Society in Neonates with Hypoxic Ischemic Encephalopathy. PLoS ONE 2023, 18, e0295759. [Google Scholar] [CrossRef] [PubMed]
- Vega-Del-Val, C.; Arnaez, J.; Caserío, S.; Gutiérrez, E.P.; Benito, M.; Castañón, L.; Garcia-Alix, A.; on behalf of the IC-HIE Study Group. Temporal Trends in the Severity and Mortality of Neonatal Hypoxic-Ischemic Encephalopathy in the Era of Hypothermia. Neonatology 2021, 118, 685–692. [Google Scholar] [CrossRef]
- Wang, Q.; Lv, H.; Lu, L.; Ren, P.; Li, L. Neonatal Hypoxic–Ischemic Encephalopathy: Emerging Therapeutic Strategies Based on Pathophysiologic Phases of the Injury. J. Matern.-Fetal Neonatal Med. 2019, 32, 3685–3692. [Google Scholar] [CrossRef]
- Malai, T.; Khuwuthyakorn, V.; Kosarat, S.; Tantiprabha, W.; Manopunya, S.; Pomrop, M.; Katanyuwong, K.; Saguensermsri, C.; Wiwattanadittakul, N. Short-Term Outcome of Perinatal Hypoxic-Ischaemic Encephalopathy at Chiang Mai University Hospital, Thailand: A 15-Year Retrospective Study. Paediatr. Int. Child Health 2022, 42, 109–116. [Google Scholar] [CrossRef]
- Ristovska, S.; Stomnaroska, O.; Danilovski, D. Hypoxic Ischemic Encephalopathy (HIE) in Term and Preterm Infants. PRILOZI 2022, 43, 77–84. [Google Scholar] [CrossRef]
- Jia, W.; Lei, X.; Dong, W.; Li, Q. Benefits of Starting Hypothermia Treatment within 6 h vs. 6–12 h in Newborns with Moderate Neonatal Hypoxic-Ischemic Encephalopathy. BMC Pediatr. 2018, 18, 50. [Google Scholar] [CrossRef] [PubMed]
- Abend, N.S.; Licht, D.J. Predicting Outcome in Children with Hypoxic Ischemic Encephalopathy. Pediatr. Crit. Care Med. 2007, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- van Laerhoven, H.; de Haan, T.R.; Offringa, M.; Post, B.; van der Lee, J.H. Prognostic Tests in Term Neonates with Hypoxic-Ischemic Encephalopathy: A Systematic Review. Pediatrics 2013, 131, 88–98. [Google Scholar] [CrossRef]
- Douglas-Escobar, M.; Weiss, M.D. Hypoxic-Ischemic Encephalopathy: A Review for the Clinician. JAMA Pediatr. 2015, 169, 397–403. [Google Scholar] [CrossRef] [PubMed]
- Keene, J.C.; Benedetti, G.M.; Tomko, S.R.; Guerriero, R. Quantitative EEG in the Neonatal Intensive Care Unit: Current Application and Future Promise. Ann. Child Neurol. Soc. 2023, 1, 289–298. [Google Scholar] [CrossRef]
- McCoy, B.; Hahn, C.D. Continuous EEG Monitoring in the Neonatal Intensive Care Unit. J. Clin. Neurophysiol. 2013, 30, 106–114. [Google Scholar] [CrossRef]
- Boylan, G.; Burgoyne, L.; Moore, C.; O’Flaherty, B.; Rennie, J. An International Survey of EEG Use in the Neonatal Intensive Care Unit. Acta Paediatr. 2010, 99, 1150–1155. [Google Scholar] [CrossRef]
- Brogger, J.; Eichele, T.; Aanestad, E.; Olberg, H.; Hjelland, I.; Aurlien, H. Visual EEG Reviewing Times with SCORE EEG. Clin. Neurophysiol. Pract. 2018, 3, 59–64. [Google Scholar] [CrossRef]
- Ahmed, R.; Temko, A.; Marnane, W.; Lightbody, G.; Boylan, G. Grading Hypoxic–Ischemic Encephalopathy Severity in Neonatal EEG Using GMM Supervectors and the Support Vector Machine. Clin. Neurophysiol. 2016, 127, 297–309. [Google Scholar] [CrossRef]
- Raurale, S.A.; Boylan, G.B.; Mathieson, S.R.; Marnane, W.P.; Lightbody, G.; O’Toole, J.M. Grading Hypoxic-Ischemic Encephalopathy in Neonatal EEG with Convolutional Neural Networks and Quadratic Time–Frequency Distributions. J. Neural Eng. 2021, 18, 046007. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, X.; Wu, D. Grading Method for Hypoxic-Ischemic Encephalopathy Based on Neonatal EEG. Comput. Model. Eng. Sci. 2020, 122, 721–742. [Google Scholar] [CrossRef]
- Lacan, L.; Betrouni, N.; Lamblin, M.D.; Chaton, L.; Delval, A.; Bourriez, J.L.; Storme, L.; Derambure, P.; NguyenThe Tich, S. Quantitative Approach to Early Neonatal EEG Visual Analysis in Hypoxic-Ischemic Encephalopathy Severity: Bridging the Gap between Eyes and Machine. Neurophysiol. Clin. 2021, 51, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Marnane, W.P.; Boylan, G.B.; Lightbody, G. Neonatal Hypoxic-Ischemic Encephalopathy Grading from Multi-Channel EEG Time-Series Data Using a Fully Convolutional Neural Network. Technologies 2023, 11, 151. [Google Scholar] [CrossRef]
- Mandhouj, B.; Cherni, M.A.; Sayadi, M. An Automated Classification of EEG Signals Based on Spectrogram and CNN for Epilepsy Diagnosis. Analog. Integr. Circuits Signal Process. 2021, 108, 101–110. [Google Scholar] [CrossRef]
- Yan, P.Z.; Wang, F.; Kwok, N.; Allen, B.B.; Keros, S.; Grinspan, Z. Automated Spectrographic Seizure Detection Using Convolutional Neural Networks. Seizure Eur. J. Epilepsy 2019, 71, 124–131. [Google Scholar] [CrossRef]
- Tawhid, M.N.A.; Siuly, S.; Wang, K.; Wang, H. Automatic and Efficient Framework for Identifying Multiple Neurological Disorders From EEG Signals. IEEE Trans. Technol. Soc. 2023, 4, 76–86. [Google Scholar] [CrossRef]
- HMS—Harmful Brain Activity Classification. Available online: https://kaggle.com/competitions/hms-harmful-brain-activity-classification (accessed on 8 May 2025).
- Torres, J.; Buldain Pérez, J.D.; Beltrán Blázquez, J.R. Arrhythmia Detection Using Convolutional Neural Models; Springer: Cham, Switzerland, 2019; pp. 120–127. [Google Scholar] [CrossRef]
- Le, M.D.; Singh Rathour, V.; Truong, Q.S.; Mai, Q.; Brijesh, P.; Le, N. Multi-Module Recurrent Convolutional Neural Network with Transformer Encoder for ECG Arrhythmia Classification. In Proceedings of the 2021 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI), Athens, Greece, 27–30 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, J.; Chen, B.; Yao, B.; He, W. ECG Arrhythmia Classification Using STFT-Based Spectrogram and Convolutional Neural Network. IEEE Access 2019, 7, 92871–92880. [Google Scholar] [CrossRef]
- Korotchikova, I.; Stevenson, N.J.; Walsh, B.H.; Murray, D.M.; Boylan, G.B. Quantitative EEG Analysis in Neonatal Hypoxic Ischaemic Encephalopathy. Clin. Neurophysiol. 2011, 122, 1671–1678. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Ortigoza, E.B.; Kota, S.; Liu, Y.; Zhang, R.; Chalak, L.F. Feasibility of EEG Phase-Amplitude Coupling to Stratify Encephalopathy Severity in Neonatal HIE Using Short Time Window. Brain Sci. 2022, 12, 854. [Google Scholar] [CrossRef]
- Pavel, A.M.; Rennie, J.M.; de Vries, L.S.; Blennow, M.; Foran, A.; Shah, D.K.; Pressler, R.M.; Kapellou, O.; Dempsey, E.M.; Mathieson, S.R.; et al. Neonatal Seizure Management: Is the Timing of Treatment Critical? J. Pediatr. 2022, 243, 61–68.e2. [Google Scholar] [CrossRef]
- Gomez, S.; O’Sullivan, M.; Popovici, E.; Mathieson, S.; Boylan, G.; Temko, A. On Sound-Based Interpretation of Neonatal EEG. arXiv 2018, arXiv:1806.03047. [Google Scholar] [CrossRef]
- Loui, P.; Koplin-Green, M.; Frick, M.; Massone, M. Rapidly Learned Identification of Epileptic Seizures from Sonified EEG. Front. Hum. Neurosci. 2014, 8, 820. [Google Scholar] [CrossRef] [PubMed]
- Baier, G.; Hermann, T.; Stephani, U. Event-Based Sonification of EEG Rhythms in Real Time. Clin. Neurophysiol. 2007, 118, 1377–1386. [Google Scholar] [CrossRef]
- Chalak, L.F.; Ferriero, D.M.; Gunn, A.J.; Robertson, N.J.; Boylan, G.B.; Molloy, E.J.; Thoresen, M.; Inder, T.E. Mild HIE and Therapeutic Hypothermia: Gaps in Knowledge with under-Powered Trials. Pediatr. Res. 2024, 1–3. [Google Scholar] [CrossRef]
- Stevenson, N.J.; Korotchikova, I.; Temko, A.; Lightbody, G.; Marnane, W.P.; Boylan, G.B. An Automated System for Grading EEG Abnormality in Term Neonates with Hypoxic-Ischaemic Encephalopathy. Ann. Biomed. Eng. 2013, 41, 775–785. [Google Scholar] [CrossRef] [PubMed]
- O’Toole, J.M.; Mathieson, S.R.; Raurale, S.A.; Magarelli, F.; Marnane, W.P.; Lightbody, G.; Boylan, G.B. Neonatal EEG Graded for Severity of Background Abnormalities in Hypoxic-Ischaemic Encephalopathy. Sci. Data 2023, 10, 129. [Google Scholar] [CrossRef]
- O’Toole, J.M.; Mathieson, S.R.; Magarelli, F.; Marnane, W.P.; Lightbody, G.; Boylan, G.B. Neonatal EEG Graded for Severity of Background Abnormalities. Zenodo 2022. [Google Scholar] [CrossRef]
- Murray, D.; Boylan, G.; Ryan, A.C.; Connolly, S. Early EEG Findings in Hypoxic-Ischemic Encephalopathy Predict Outcomes at 2 Years. Pediatrics 2009, 124, e459–e467. [Google Scholar] [CrossRef]
- Kitayama, M.; Otsubo, H.; Parvez, S.; Lodha, A.; Ying, E.; Parvez, B.; Ishii, R.; Mizuno-Matsumoto, Y.; Zoroofi, R.A.; Snead, O.C. Wavelet Analysis for Neonatal Electroencephalographic Seizures. Pediatr. Neurol. 2003, 29, 326–333. [Google Scholar] [CrossRef]
- Tsuchida, T.N.; Wusthoff, C.J.; Shellhaas, R.A.; Abend, N.S.; Hahn, C.D.; Sullivan, J.E.; Nguyen, S.; Weinstein, S.; Scher, M.S.; Riviello, J.J.; et al. American Clinical Neurophysiology Society Standardized EEG Terminology and Categorization for the Description of Continuous EEG Monitoring in Neonates: Report of the American Clinical Neurophysiology Society Critical Care Monitoring Committee. J. Clin. Neurophysiol. 2013, 30, 161–173. [Google Scholar] [CrossRef]
- Hamill, J.; Caldwell, G.E.; Derrick, T.R. Reconstructing Digital Signals Using Shannon’s Sampling Theorem. J. Appl. Biomech. 1997, 13, 226–238. [Google Scholar] [CrossRef]
- Mesaros, A.; Heittola, T.; Benetos, E.; Foster, P.; Lagrange, M.; Virtanen, T.; Plumbley, M.D. Detection and Classification of Acoustic Scenes and Events: Outcome of the DCASE 2016 Challenge. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 379–393. [Google Scholar] [CrossRef]
- Arts, L.P.A.; van den Broek, E.L. The Fast Continuous Wavelet Transformation (fCWT) for Real-Time, High-Quality, Noise-Resistant Time–Frequency Analysis. Nat. Comput. Sci. 2022, 2, 47–58. [Google Scholar] [CrossRef]
- Donnelly, D.; Rogers, E. Time Series Analysis with the Hilbert–Huang Transform. Am. J. Phys. 2009, 77, 1154–1161. [Google Scholar] [CrossRef]
- Pinnegar, C.R.; Khosravani, H.; Federico, P. Time-Frequency Phase Analysis of Ictal EEG Recordings with the S-transform. IEEE Trans. Bio-Med. Eng. 2009, 56, 2583–2593. [Google Scholar] [CrossRef] [PubMed]
- Ghaderpour, E.; Pagiatakis, S.D. Least-Squares Wavelet Analysis of Unequally Spaced and Non-stationary Time Series and Its Applications. Math. Geosci. 2017, 49, 819–844. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. arXiv 2022, arXiv:2201.03545. [Google Scholar] [CrossRef]
- Wightman, R.; Raw, N.; Soare, A.; Arora, A.; Ha, C.; Reich, C.; Guan, F.; Kaczmarzyk, J.; MrT23; Mike; et al. Rwightman/Pytorch-Image-Models: V0.8.10dev0 Release. Zenodo 2023. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2017, arXiv:1608.03983. [Google Scholar]
- Izmailov, P.; Podoprikhin, D.; Garipov, T.; Vetrov, D.; Wilson, A.G. Averaging Weights Leads to Wider Optima and Better Generalization. arXiv 2019, arXiv:1803.05407. [Google Scholar] [CrossRef]
- Automatic Mixed Precision—PyTorch Tutorials 2.4.0+cu121 Documentation. Available online: https://pytorch.org/tutorials/recipes/recipes/amp_recipe.html (accessed on 8 May 2025).
- PetFinder.My Adoption Prediction. Available online: https://kaggle.com/competitions/petfinder-adoption-prediction (accessed on 8 May 2025).
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Mean Squared Error. In The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 337–339. [CrossRef]
- Draper, N.R.; Smith, H. On Worthwhile Regressions, Big F’s, and R2. In Applied Regression Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1998; Chapter 11; pp. 243–250. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-measure to ROC, Informedness, Markedness and Correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A Systematic Analysis of Performance Measures for Classification Tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Sasaki, Y. The Truth of the F-measure. Teach Tutor Mater 2007, 1, 1–5. [Google Scholar]
- A Coefficient of Agreement for Nominal Scales—Jacob Cohen. 1960. Available online: https://journals.sagepub.com/doi/10.1177/001316446002000104 (accessed on 8 May 2025).
- Singh, A.; Mittal, S.; Malhotra, P.; Srivastava, Y. Clustering Evaluation by Davies-Bouldin Index(DBI) in Cereal Data Using K-Means. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 11–13 March 2020; pp. 306–310. [Google Scholar] [CrossRef]
- Shahapure, K.R.; Nicholas, C. Cluster Quality Analysis Using Silhouette Score. In Proceedings of the 2020 IEEE 7th International Conference on Data Science and Advanced Analytics (DSAA), Sydney, NSW, Australia, 6–9 October 2020; pp. 747–748. [Google Scholar] [CrossRef]
- Pedregosa, F.; Pedregosa, F.; Varoquaux, G.; Varoquaux, G.; Org, N.; Gramfort, A.; Gramfort, A.; Michel, V.; Michel, V.; Fr, L.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ahmed, M.Z.I.; Sinha, N.; Ghaderpour, E.; Phadikar, S.; Ghosh, R. A Novel Baseline Removal Paradigm for Subject-Independent Features in Emotion Classification Using EEG. Bioengineering 2023, 10, 54. [Google Scholar] [CrossRef]
- Massar, H.; Stergiadis, C.; Nsiri, B.; Drissi, T.B.; Klados, M.A. EMD-BSS: A Hybrid Methodology Combining Empirical Mode Decomposition and Blind Source Separation to Eliminate the Ocular Artifacts from EEG Recordings. Biomed. Signal Process. Control 2024, 95, 106475. [Google Scholar] [CrossRef]



| True Value | Validation Predictions (Avg) | Test Predictions (Avg) |
|---|---|---|
| 4 | 3.5354, 3.2588, 3.7585, 2.9211 (3.3234) | 3.35 |
| 2 | 1.015, 0.982, 1.09, 1.078 (1.0418) | 1.079 |
| 1 | 2.0059, 1.0475, 1.7400, 2.22 (1.755) | 1.63 |
| 1 | 1.143, 2.4976, 2.387, 2.56 (2.14) | 2.504 |
| 3 | 1.0998, 1.625, 1.7237, 1.90576 (1.5887) | 1.733 |
| 3 | 2.589, 1.7465, 1.8679, 1.822 (2.0066) | 1.746 |
| Metric | FM/AM Transformed EEG Spectrogram | EEG Mel Spectrogram |
|---|---|---|
| Test Accuracy | 89.97% | 81.66% |
| Precision | 0.9079 | 0.7858 |
| Recall | 0.8994 | 0.7576 |
| F1-Score | 0.8985 | 0.7547 |
| R-Squared | 0.8507 | 0.7574 |
| Cohen’s Kappa Score | 0.8219 | 0.5622 |
| Metric | Regression Model | Classification Model |
|---|---|---|
| Train Accuracy (%) | 96.30 | 94.55 |
| Validation Accuracy (%) | 92.31 | 88.46 |
| Test Accuracy (%) | 93.94 | 90.91 |
| Metric | Raw EEG | Sonified EEG | Feature Map |
|---|---|---|---|
| Davies-Bouldin Index | 14.637 | 2.985 | 0.8 |
| Calinski–Harabasz Index | 0.8584 | 224.308 | 166.8 |
| Silhouette Score | −0.2602 | 0.06 | 0.3457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Twomey, L.; Gomez, S.; Popovici, E.; Temko, A. Long-Term Neonatal EEG Modeling with DSP and ML for Grading Hypoxic–Ischemic Encephalopathy Injury. Sensors 2025, 25, 3007. https://doi.org/10.3390/s25103007
Twomey L, Gomez S, Popovici E, Temko A. Long-Term Neonatal EEG Modeling with DSP and ML for Grading Hypoxic–Ischemic Encephalopathy Injury. Sensors. 2025; 25(10):3007. https://doi.org/10.3390/s25103007
Chicago/Turabian StyleTwomey, Leah, Sergi Gomez, Emanuel Popovici, and Andriy Temko. 2025. "Long-Term Neonatal EEG Modeling with DSP and ML for Grading Hypoxic–Ischemic Encephalopathy Injury" Sensors 25, no. 10: 3007. https://doi.org/10.3390/s25103007
APA StyleTwomey, L., Gomez, S., Popovici, E., & Temko, A. (2025). Long-Term Neonatal EEG Modeling with DSP and ML for Grading Hypoxic–Ischemic Encephalopathy Injury. Sensors, 25(10), 3007. https://doi.org/10.3390/s25103007






