Iterative Pulse–Echo Tomography for Ultrasonic Image Correction
Abstract
1. Introduction
2. Iterative CUTE Algorithm
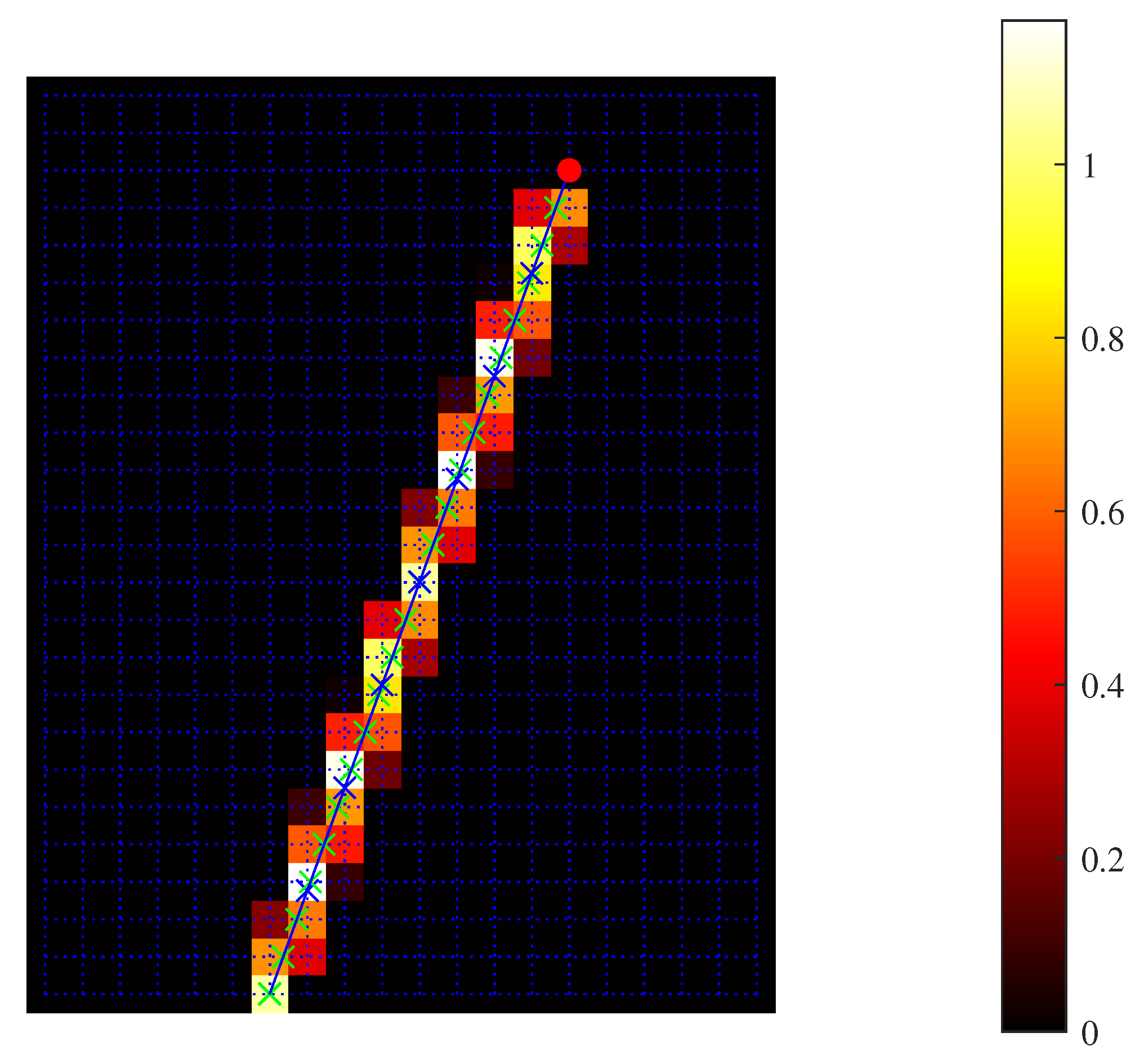
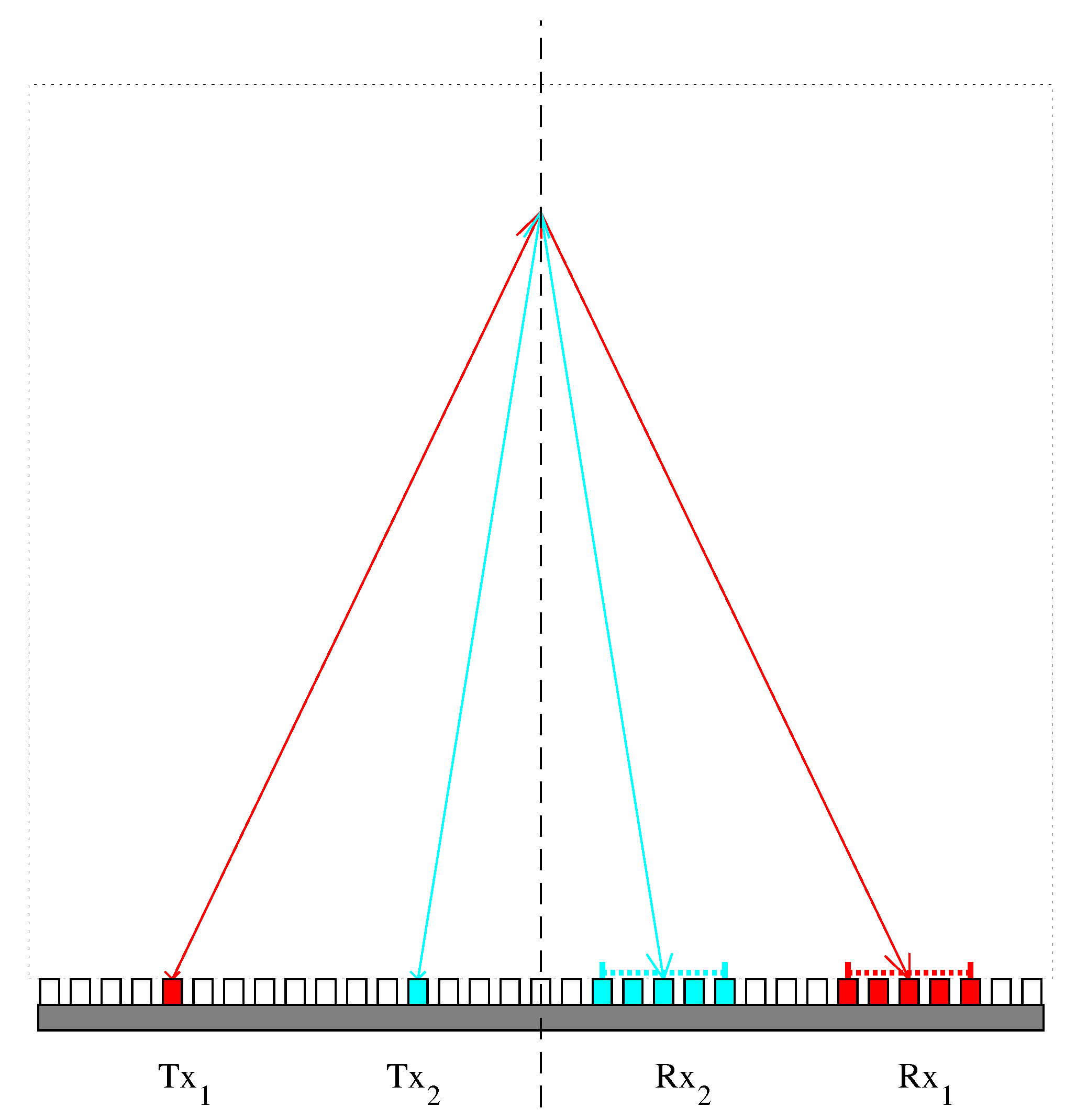
2.1. Numerical Realization and Inversion of Forward Model
2.2. Iterative Correction of SoS Estimate
| Algorithm 1: Iterative CUTE algorithm. |
 |
3. Simulation and Discussion
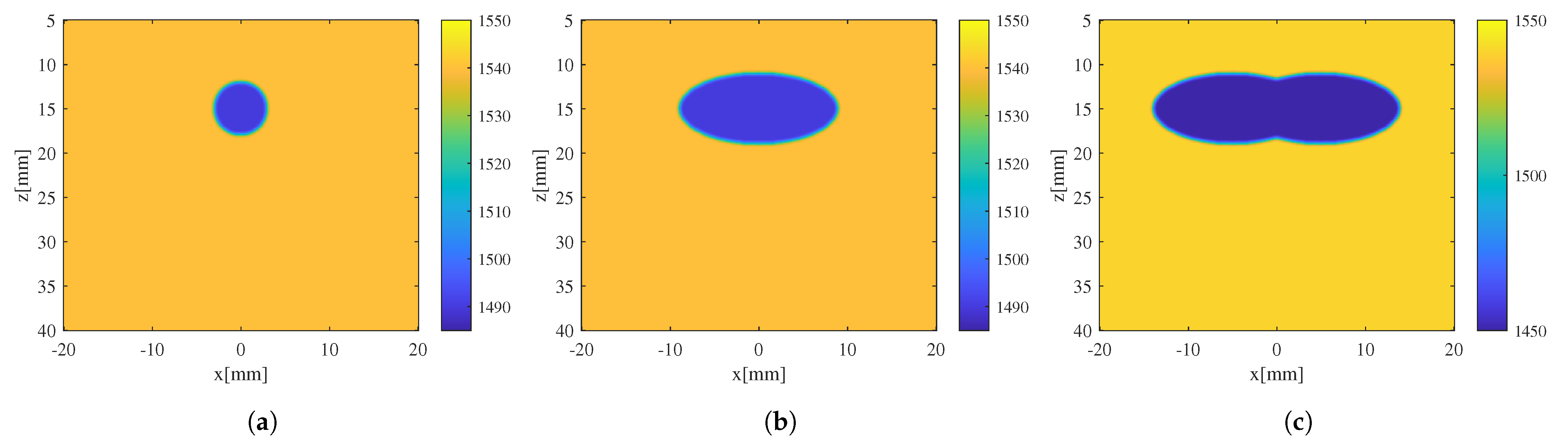
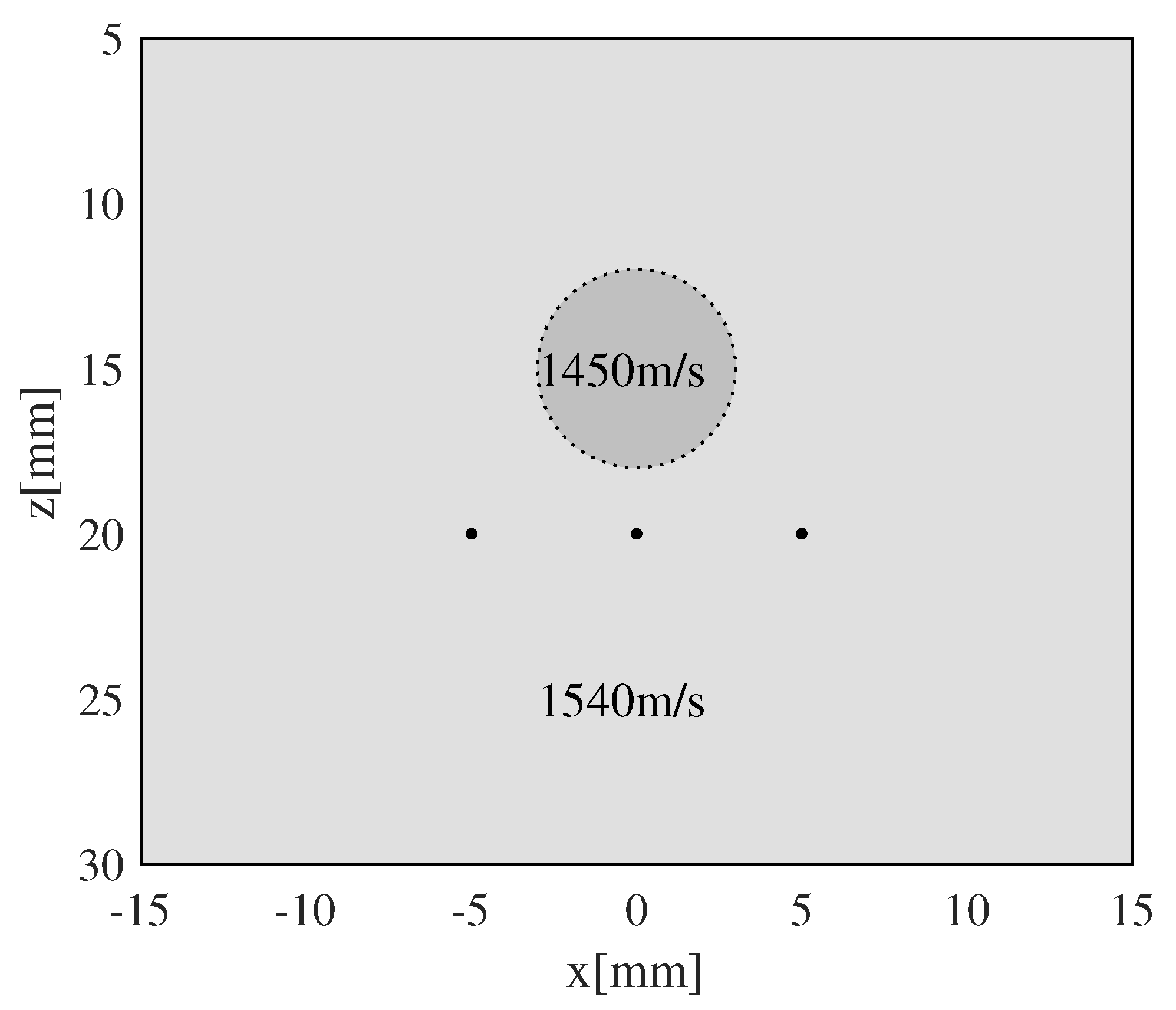
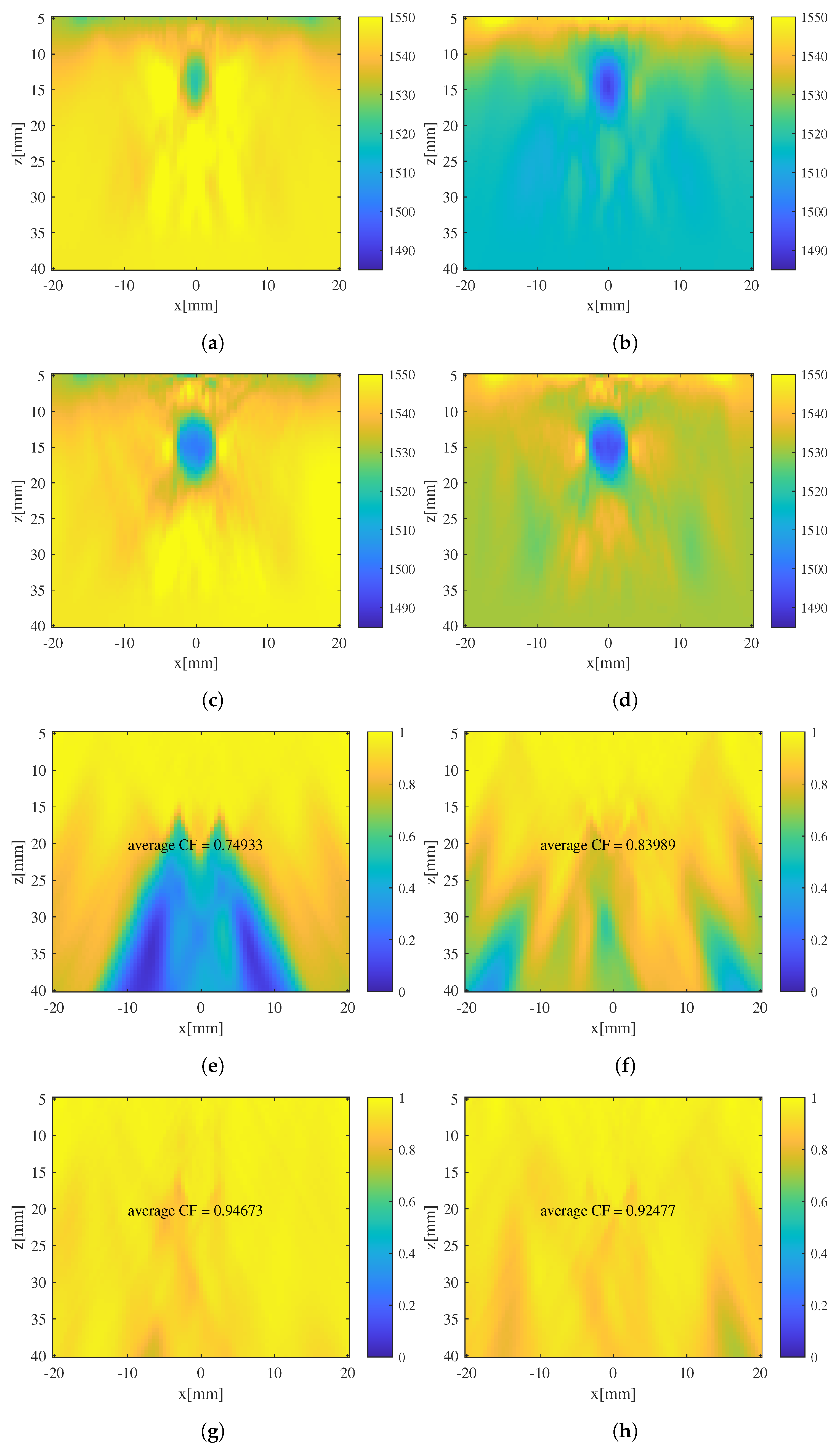
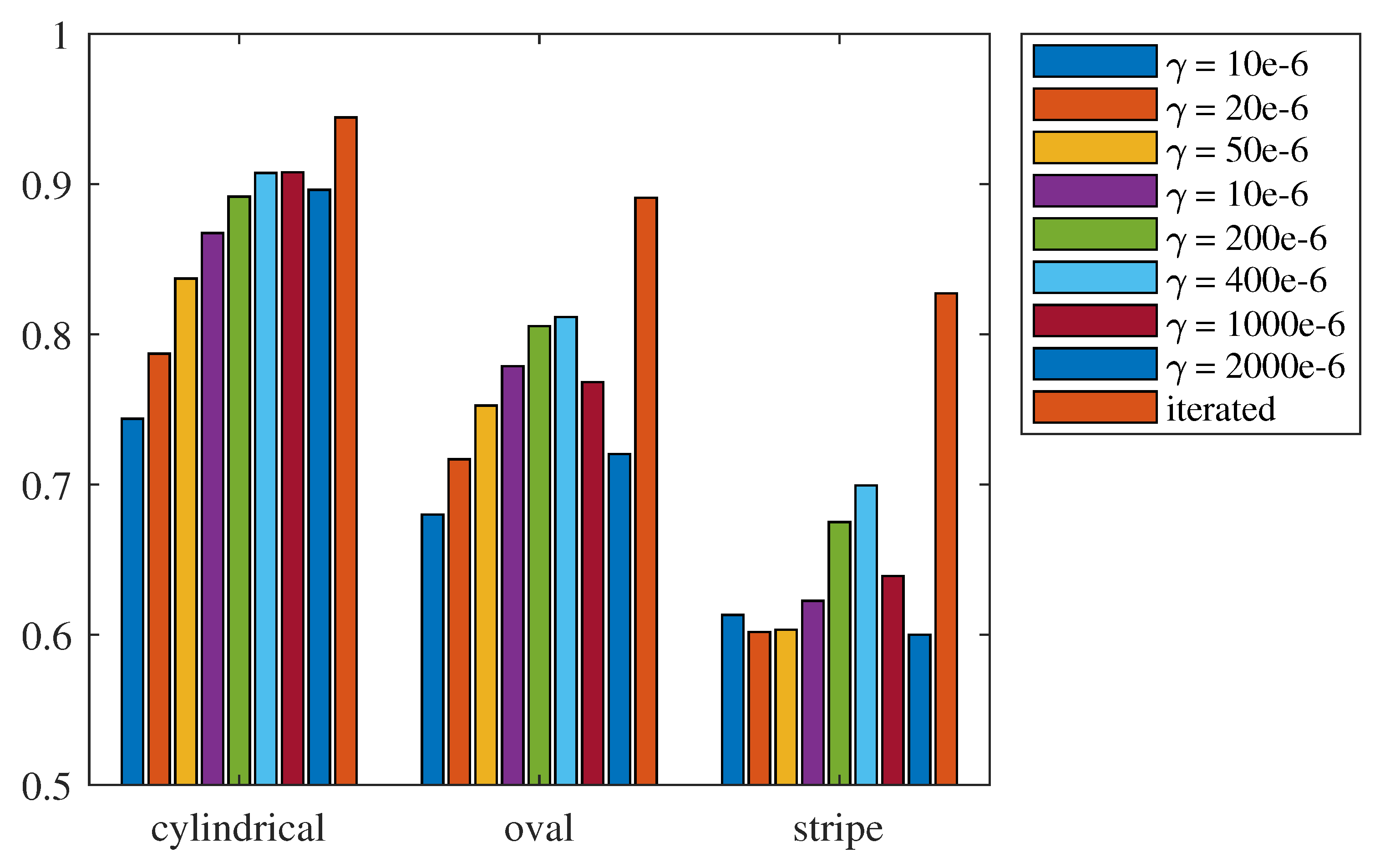
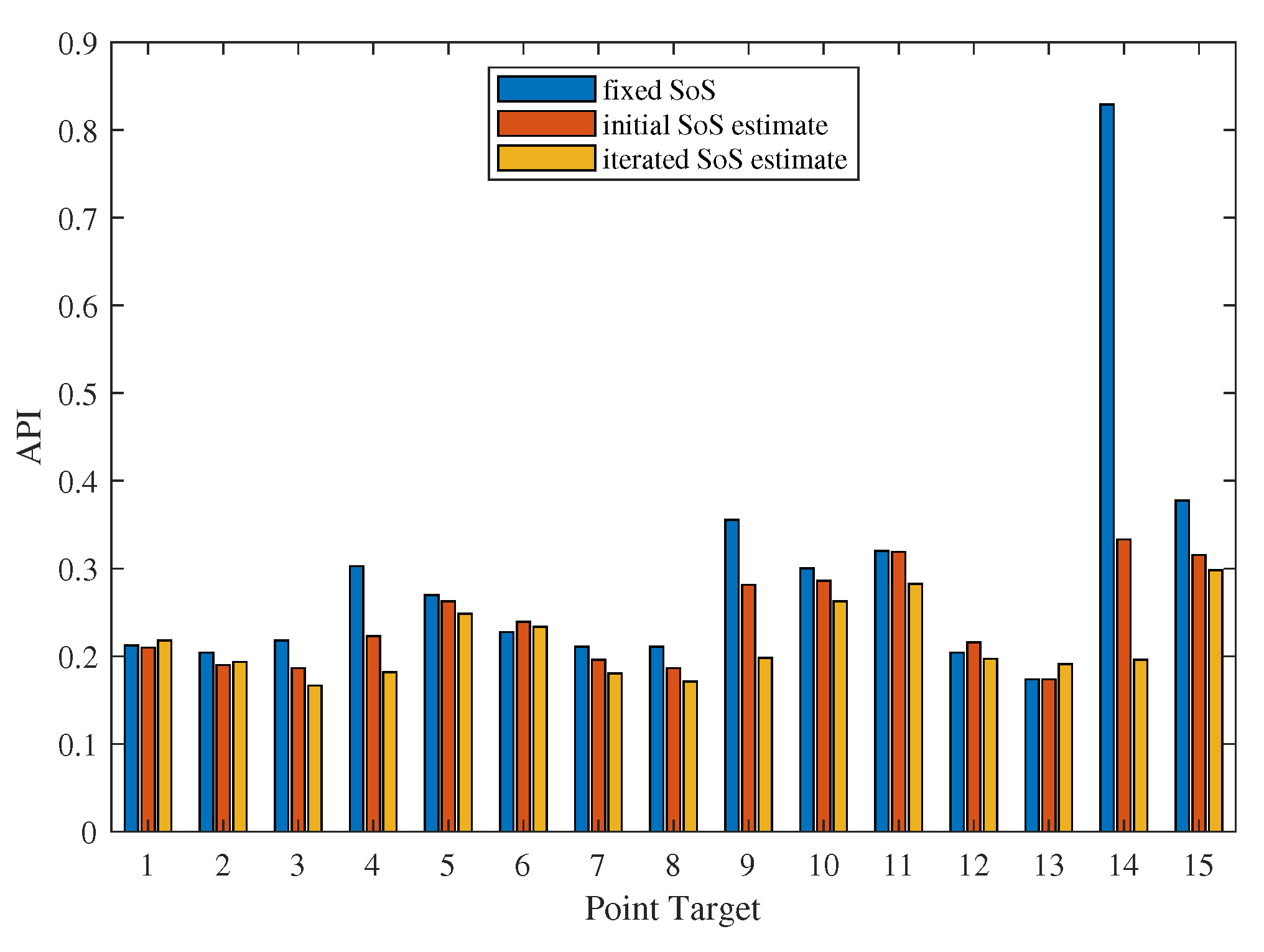
3.1. Evaluation of the Effectiveness of Local SoS Correction
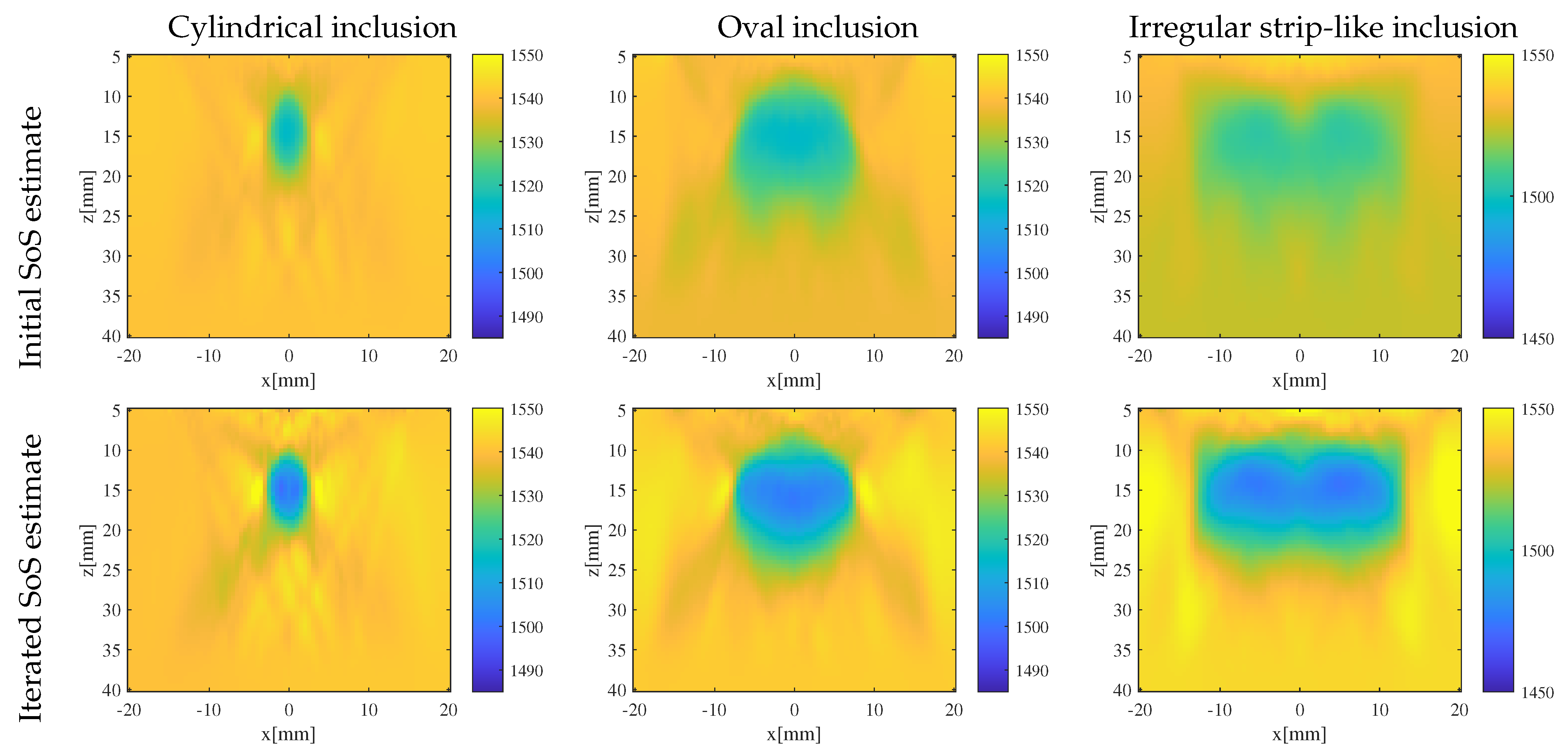
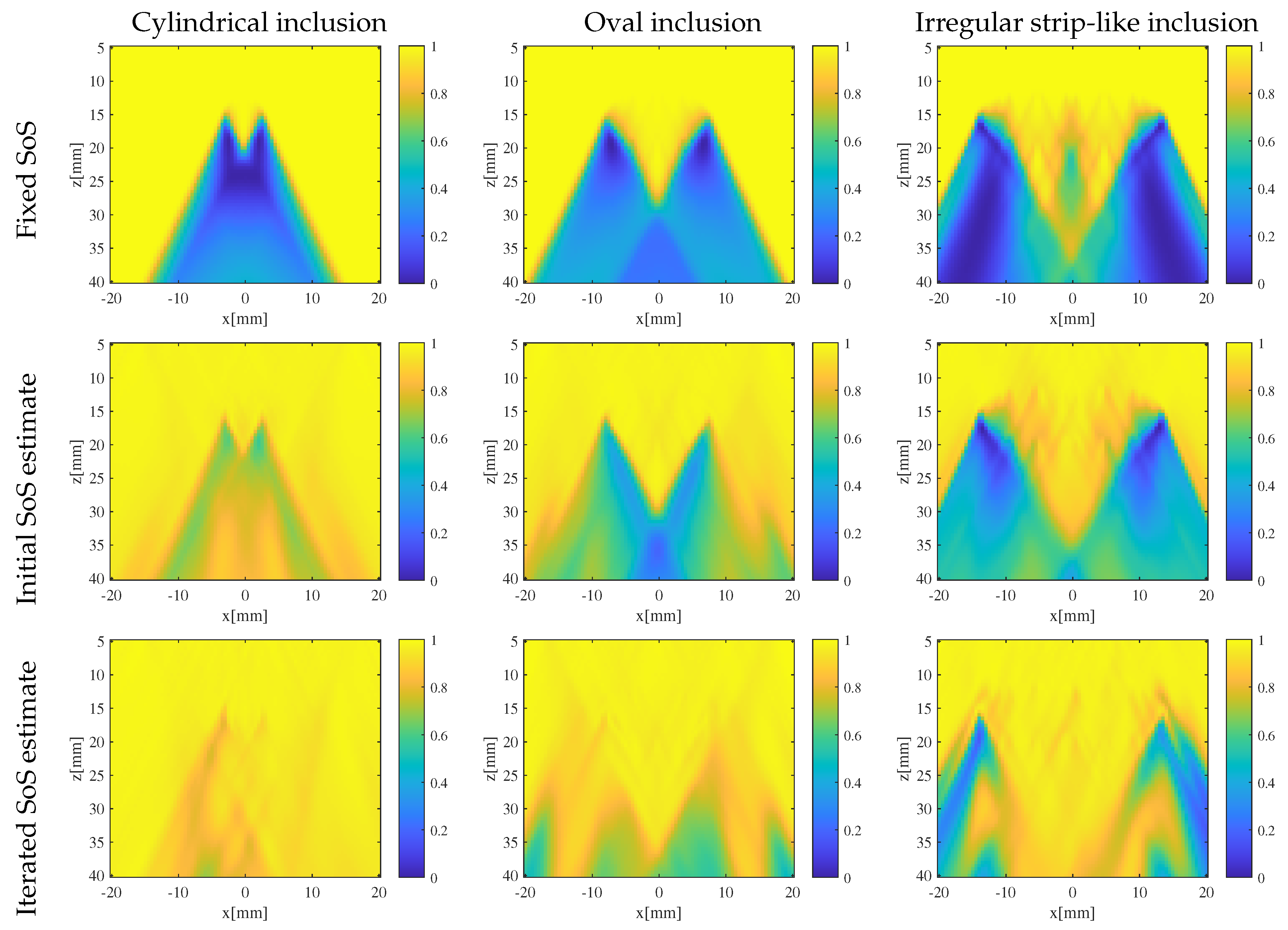
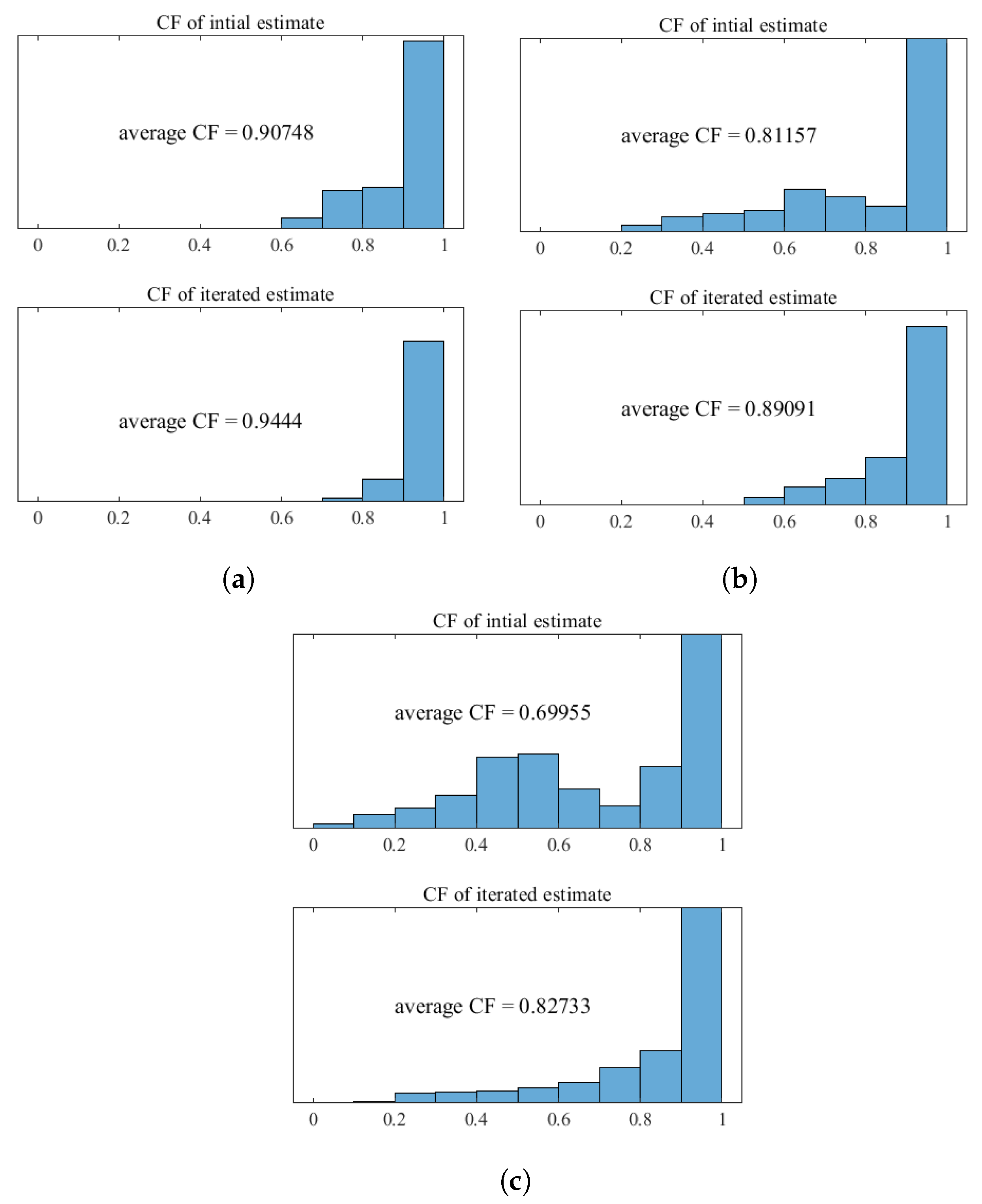
3.2. Results and Discussion
- Targeted error reduction in SoS estimation: the iterative approach of the CUTE algorithm methodically narrows the discrepancy between actual and estimated SoS, minimizing the specific errors caused by these discrepancies and thereby enhancing the precision of the SoS estimation in a targeted manner.
- Improved handling of regularization challenges: The iterative framework of the CUTE algorithm allows for iterative SoS correction with increased regularization strength. This approach mitigates interference related to insufficient regularization, as well as the under-correction of SoS results related to strong regularization.
- Enhanced reconstruction of irregularly shaped inclusions: through iterative error correction, the iterative CUTE algorithm demonstrates more precise reconstructions that are closer to the true characteristics of these inclusions.
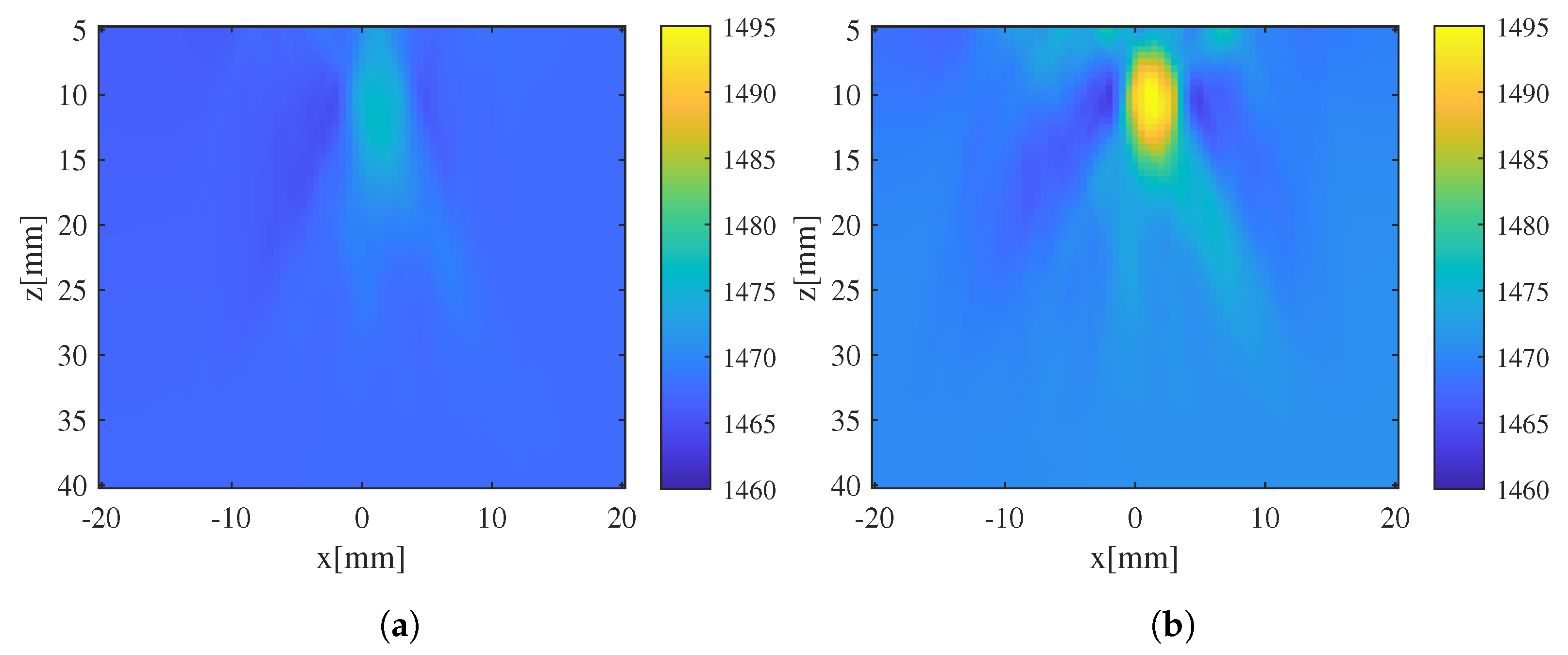
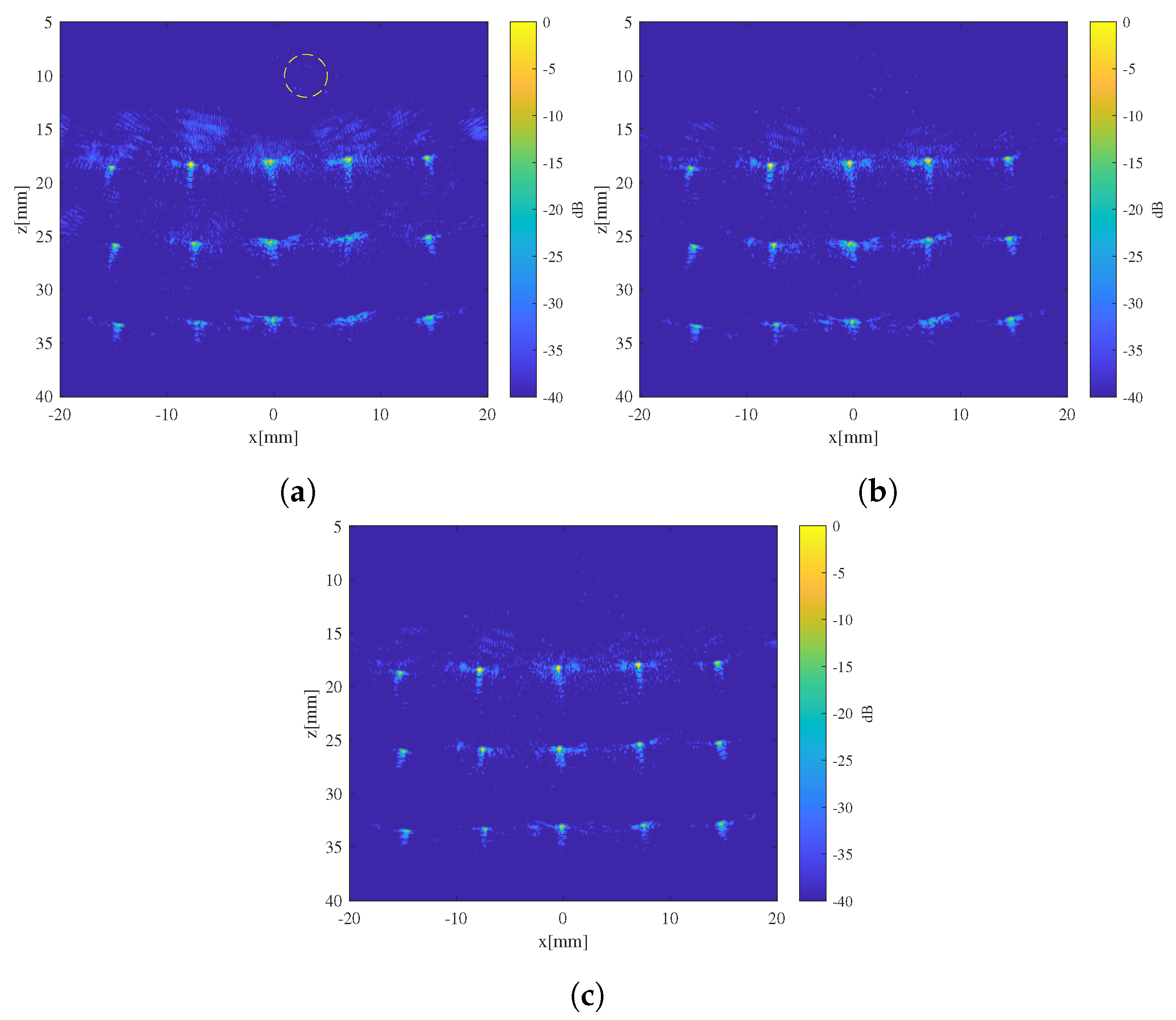
4. Validation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, M.E.; McKeag, M.S.; Trahey, G.E. The impact of sound speed errors on medical ultrasound imaging. J. Acoust. Soc. Am. 2000, 107, 3540–3548. [Google Scholar] [CrossRef]
- Trahey, G. Properties of acoustical speckle in the presence of phase aberration part I: First order statistics. Ultrason. Imaging 1988, 10, 12–28. [Google Scholar] [CrossRef]
- Smith, S.W.; Trahey, G.E.; Hubbard, S.M.; Wagner, R.F. Properties of acoustical speckle in the presence of phase aberration. Part II: Correlation lengths. Ultrason. Imaging 1988, 10, 29–51. [Google Scholar] [CrossRef]
- Ali, R.; Brevett, T.; Zhuang, L.; Bendjador, H.; Podkowa, A.S.; Hsieh, S.S.; Simson, W.; Sanabria, S.J.; Herickhoff, C.D.; Dahl, J.J. Aberration correction in diagnostic ultrasound: A review of the prior field and current directions. Z. Med. Phys. 2023, 33, 267–291. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, M.; Flax, S.W. Phase aberration measurements in medical ultrasound: Human studies. Ultrason. Imaging 1988, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Flax, S.W.; O’Donnell, M. Phase-aberration correction using signals from point reflectors and diffuse scatterers: Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 758–767. [Google Scholar] [CrossRef] [PubMed]
- Rachlin, D. Direct estimation of aberrating delays in pulse-echo imaging systems. J. Acoust. Soc. Am. 1990, 88, 191–198. [Google Scholar] [CrossRef]
- Jaeger, M.; Robinson, E.; Akarcay, H.G.; Frenz, M. Full correction for spatially distributed speed-of-sound in echo ultrasound based on measuring aberration delays via transmit beam steering. Phys. Med. Biol. 2015, 60, 4497–4515. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.; Kang, L.; Kim, J.; Lee, S. An efficient sound speed estimation method to enhance image resolution in ultrasound imaging. Ultrasonics 2009, 49, 774–778. [Google Scholar] [CrossRef]
- Malik, B.H.; Klock, J.C. Breast Cyst Fluid Analysis Correlations with Speed of Sound Using Transmission Ultrasound. Acad. Radiol. 2019, 26, 76–85. [Google Scholar] [CrossRef]
- Roy, O.; Jovanović, I.; Hormati, A.; Parhizkar, R.; Vetterli, M. Sound speed estimation using wave-based ultrasound tomography: Theory and GPU implementation. In Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy; D’hooge, J., McAleavey, S.A., Eds.; SPIE: Bellingham, WA, USA, 2010. [Google Scholar] [CrossRef]
- Duric, N.; Littrup, P.; Poulo, L.; Babkin, A.; Pevzner, R.; Holsapple, E.; Rama, O.; Glide, C. Detection of breast cancer with ultrasound tomography: First results with the Computed Ultrasound Risk Evaluation (CURE) prototype. Med. Phys. 2007, 34, 773–785. [Google Scholar] [CrossRef]
- Anderson, M.E.; Trahey, G.E. The direct estimation of sound speed using pulse-echo ultrasound. J. Acoust. Soc. Am. 1998, 104, 3099–3106. [Google Scholar] [CrossRef]
- Ali, R.; Telichko, A.V.; Wang, H.; Sukumar, U.K.; Vilches-Moure, J.G.; Paulmurugan, R.; Dahl, J.J. Local Sound Speed Estimation for Pulse-Echo Ultrasound in Layered Media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Azuma, T.; Liang, J.T.; Nakajima, Y. Average sound speed estimation using speckle analysis of medical ultrasound data. Int. J. Comput. Assist. Radiol. Surg. 2012, 7, 891–899. [Google Scholar] [CrossRef]
- Jaeger, M.; Held, G.; Peeters, S.; Preisser, S.; Grunig, M.; Frenz, M. Computed ultrasound tomography in echo mode for imaging speed of sound using pulse-echo sonography: Proof of principle. Ultrasound Med. Biol. 2015, 41, 235–250. [Google Scholar] [CrossRef] [PubMed]
- Sanabria, S.J.; Ozkan, E.; Rominger, M.; Goksel, O. Spatial domain reconstruction for imaging speed-of-sound with pulse-echo ultrasound: Simulation and in vivo study. Phys. Med. Biol. 2018, 63, 215015. [Google Scholar] [CrossRef]
- Stähli, P.; Kuriakose, M.; Frenz, M.; Jaeger, M. Improved forward model for quantitative pulse-echo speed-of-sound imaging. Ultrasonics 2020, 108, 106168. [Google Scholar] [CrossRef] [PubMed]
- Stähli, P.; Frenz, M.; Jaeger, M. Bayesian Approach for a Robust Speed-of-Sound Reconstruction Using Pulse-Echo Ultrasound. IEEE Trans. Med. Imaging 2021, 40, 457–467. [Google Scholar] [CrossRef]
- Rau, R.; Schweizer, D.; Vishnevskiy, V.; Goksel, O. Speed-of-sound imaging using diverging waves. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 1201–1211. [Google Scholar] [CrossRef]
- Jaeger, M.; Stähli, P.; Martiartu, N.K.; Yolgunlu, P.S.; Frappart, T.; Fraschini, C.; Frenz, M. Pulse-echo speed-of-sound imaging using convex probes. Phys. Med. Biol. 2022, 67, 215016. [Google Scholar] [CrossRef]
- Rau, R.; Schweizer, D.; Vishnevskiy, V.; Goksel, O. Ultrasound Aberration Correction based on Local Speed-of-Sound Map Estimation. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019. [Google Scholar] [CrossRef]
- Beuret, S.; Hériard-Dubreuil, B.; Martiartu, N.K.; Jaeger, M.; Thiran, J.P. Windowed Radon Transform for Robust Speed-of-Sound Imaging with Pulse-Echo Ultrasound. IEEE Trans. Med. Imaging 2023. [Google Scholar] [CrossRef]
- Mitchell, J.R.; Dickof, P.; Law, A.G. A comparison of line integral algorithms. Comput. Phys. 1990, 4, 166. [Google Scholar] [CrossRef]
- Podkowa, A.S.; Oelze, M.L. The convolutional interpretation of registration-based plane wave steered pulse-echo local sound speed estimators. Phys. Med. Biol. 2020, 65, 025003. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 375. [Google Scholar]
- Rau, R.; Ozkan, E.; Ozturkler, B.M.; Gastli, L.; Goksel, O. Displacement Estimation Methods for Speed-of-Sound Imaging in Pulse-Echo. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7–11 September 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Hassouna, M.S.; Farag, A.A. Multi-stencils fast marching methods: A highly accurate solution to the eikonal equation on cartesian domains. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1563–1574. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef] [PubMed]
- Hollman, K.W.; Rigby, K.W.; Donnell, M.O. Coherence factor of speckle from a multi-row probe. In Proceedings of the 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No.99CH37027), Tahoe, NV, USA, 17–20 October 1999; Volume 2, pp. 1257–1260. [Google Scholar] [CrossRef]
- Mallart, R.; Fink, M. Adaptive focusing in scattering media through sound-speed inhomogeneities: The van Cittert Zernike approach and focusing criterion. J. Acoust. Soc. Am. 1994, 96, 3721–3732. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
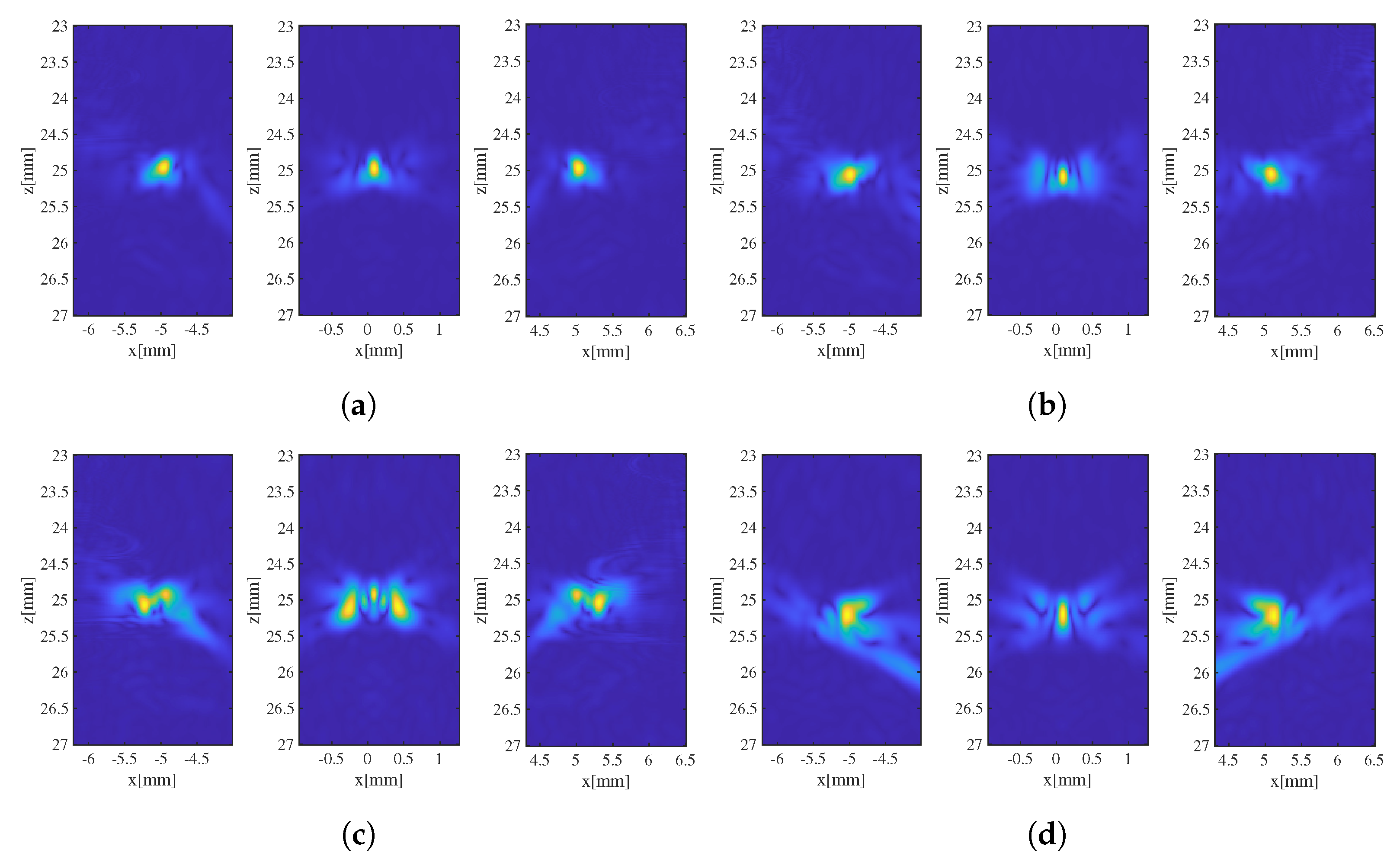

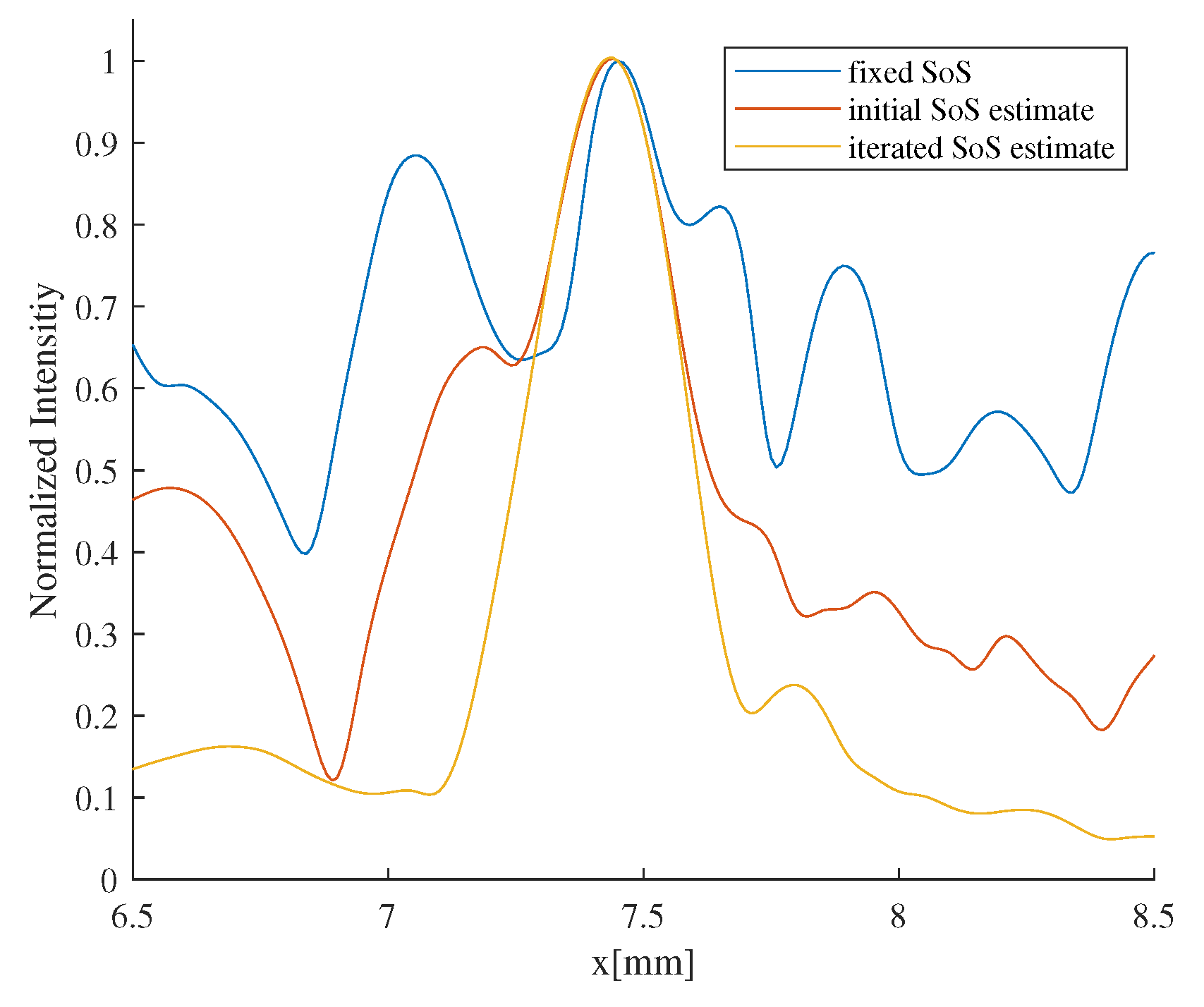
| Background SoS | Inclusion SoS | |
|---|---|---|
| SoS estimate 1 | 1500 m/s | 1540 m/s |
| SoS estimate 2 | 1407 m/s | 1545 m/s |
| SoS estimate 3 | 1549.7 m/s | 1549.7 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zengqiu, Y.; Wu, W.; Xiao, L.; Zhou, E.; Cao, Z.; Hua, J.; Wang, Y. Iterative Pulse–Echo Tomography for Ultrasonic Image Correction. Sensors 2024, 24, 1895. https://doi.org/10.3390/s24061895
Zengqiu Y, Wu W, Xiao L, Zhou E, Cao Z, Hua J, Wang Y. Iterative Pulse–Echo Tomography for Ultrasonic Image Correction. Sensors. 2024; 24(6):1895. https://doi.org/10.3390/s24061895
Chicago/Turabian StyleZengqiu, Yuchen, Wentao Wu, Ling Xiao, Erlei Zhou, Zheng Cao, Jiadong Hua, and Yue Wang. 2024. "Iterative Pulse–Echo Tomography for Ultrasonic Image Correction" Sensors 24, no. 6: 1895. https://doi.org/10.3390/s24061895
APA StyleZengqiu, Y., Wu, W., Xiao, L., Zhou, E., Cao, Z., Hua, J., & Wang, Y. (2024). Iterative Pulse–Echo Tomography for Ultrasonic Image Correction. Sensors, 24(6), 1895. https://doi.org/10.3390/s24061895





