Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method
Abstract
1. Introduction
2. Formulation for Parameter Identification
2.1. Modeling of Structural Frame Elements
2.2. Objective Function
2.3. Result Analysis
3. Parameter Identification of a Three-Span Single-Layer Rigid Frame
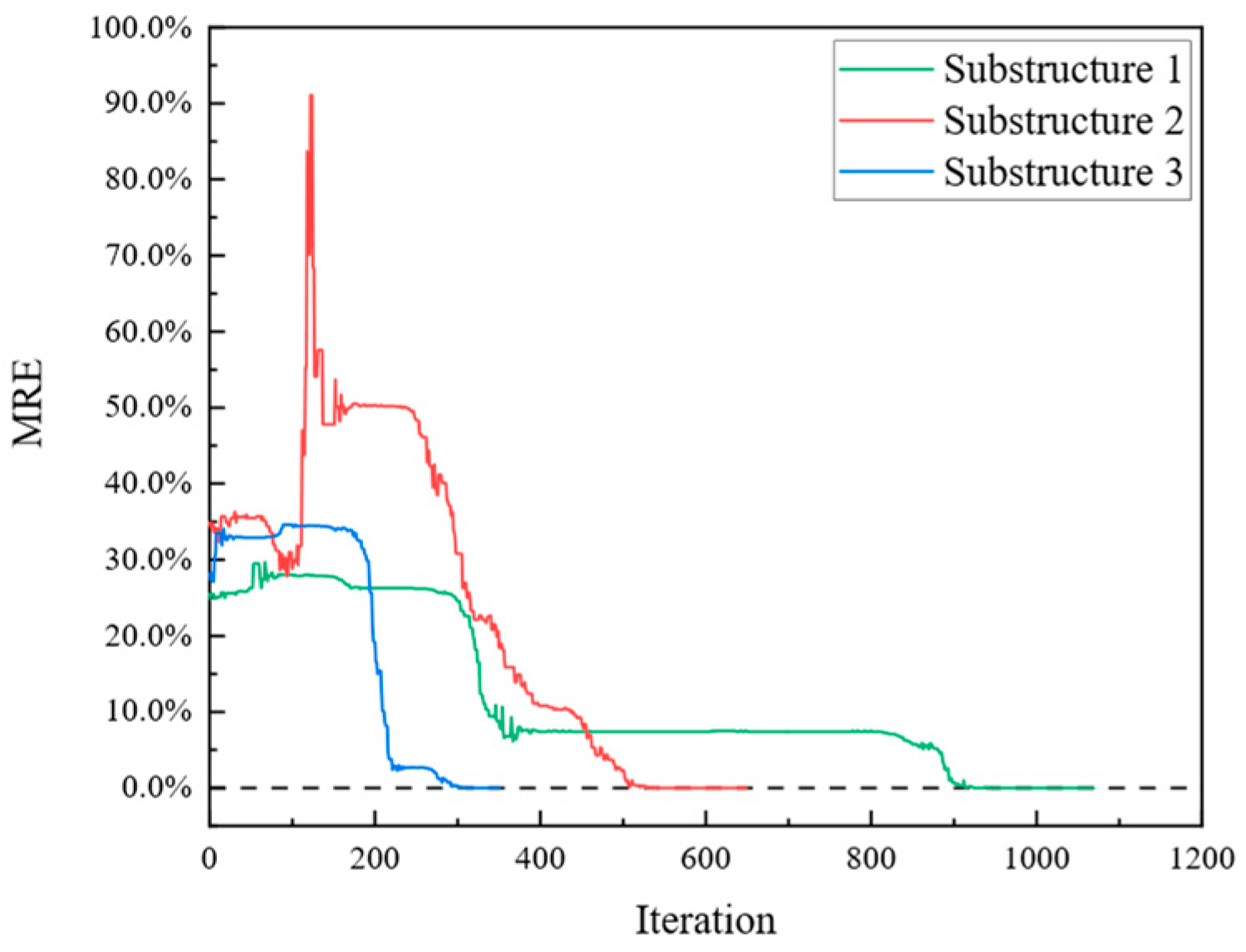
4. Parameter Identification Using the Stiffness Separation Method
4.1. Formulas of the Stiffness Separation Method
4.2. Parameter Identification Example
5. Example of a Large and Complex Rigid Frame
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Şakar, G.; Öztürk, H.; Sabuncu, M. Dynamic stability of multi-span frames subjected to periodic loading. J. Constr. Steel Res. 2012, 70, 65–70. [Google Scholar] [CrossRef]
- Zeng, Y.; Zeng, Y.; Jiang, D.; Liu, S.; Tan, H.; Zhou, J. Curing Parameters’ Influences of Early-age Temperature Field in Concrete Continuous Rigid Frame Bridge. J. Clean. Prod. 2021, 313, 127571. [Google Scholar] [CrossRef]
- Liang, Y.; Yan, J.L.; Qian, W.X.; Cheng, Z.Q.; Chen, H. Analysis of collapse resistance of offshore rigid frame—Continuous girder bridge based on time-varying fragility. Mar. Struct. 2021, 75, 102844. [Google Scholar] [CrossRef]
- Li, Y.; Lai, Y.; Lu, G.; Yan, F.; Wei, P.; Xie, Y.M. Innovative design of long-span steel–concrete composite bridge using multi-material topology optimization. Eng. Struct. 2022, 269, 114838. [Google Scholar] [CrossRef]
- Yoshikawa, M.; Hayashi, H.; Kawakita, S.; Hayashida, M. Construction of Benten Viaduct, rigid-frame bridge with seismic isolators at the foot of piers. Cem. Concr. Compos. 2000, 22, 39–46. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, Y.; Liu, J.; Jing, Y. Unified calculation model for the longitudinal fundamental frequency of continuous rigid frame bridge. Struct. Eng. Mech. 2021, 3, 343–354. [Google Scholar]
- Liu, W.; Lai, H.; Dai, G.; Rao, S.; Wang, D.; Wu, B. Numerical study on track–bridge interaction of integral railway rigid-frame bridge. Appl. Sci. 2021, 11, 922. [Google Scholar] [CrossRef]
- Kravanja, S.; Žula, T. Cost optimization of industrial steel building structures. Adv. Eng. Softw. 2010, 41, 442–450. [Google Scholar] [CrossRef]
- Scozzese, F.; Terracciano, G.; Zona, A.; Della Corte, G.; Dall’Asta, A.; Landolfo, R. Analysis of seismic non-structural damage in single-storey industrial steel buildings. Soil Dyn. Earthq. Eng. 2018, 114, 505–519. [Google Scholar] [CrossRef]
- Kravanja, S.; Turkalj, G.; Šilih, S.; Žula, T. Optimal design of single-story steel building structures based on parametric MINLP optimization. J. Constr. Steel Res. 2013, 81, 86–103. [Google Scholar] [CrossRef]
- Nick, H.; Ashrafpoor, A.; Aziminejad, A. Damage identification in steel frames using dual-criteria vibration-based damage detection method and artificial neural network. Structures 2023, 51, 1833–1851. [Google Scholar] [CrossRef]
- Azam, S.E.; Rageh, A.; Linzell, D. Damage detection in structural systems utilizing artificial neural networks and proper orthogonal decomposition. Struct. Control Health Monit. 2019, 26, e2288. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J. Sound Vib. 2021, 491, 115741. [Google Scholar] [CrossRef]
- Mosallam, A.; Zirakian, T.; Abdelaal, A.; Bayraktar, A. Health monitoring of a steel moment-resisting frame subjected to seismic loads. J. Constr. Steel Res. 2018, 140, 34–46. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, C.; Gu, X.; Li, J. A novel deep learning-based method for damage identification of smart building structures. Struct. Health Monit. 2018, 18, 143–163. [Google Scholar] [CrossRef]
- Xiao, F.; Fan, J.; Chen, G.S.; Hulsey, J.L. Bridge health monitoring and damage identification of truss bridge using strain measurements. Adv. Mech. Eng. 2019, 11, 1–7. [Google Scholar] [CrossRef]
- Xiao, F.; Zhu, W.; Meng, X.; Chen, G.S. Parameter identification of frame structures by considering shear deformation. Int. J. Distrib. Sens. Netw. 2023, 2023, 6631716. [Google Scholar] [CrossRef]
- Fan, C.; Zheng, Y.; Wang, B.; Zhou, Y.; Sun, M. Damage identification method for tied arch bridge suspender based on quasi-static displacement influence line. Mech. Syst. Signal Process. 2023, 200, 110518. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, J.; Lu, Z. A fast friction-model-inspired sparse regularization approach for damage identification with modal data. Comput. Struct. 2020, 227, 106142. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Livaoğlu, R. Modal strain energy based enhanced approaches for damage detection and severity estimation. Eng. Fail. Anal. 2023, 146, 107142. [Google Scholar] [CrossRef]
- Capponi, L.; Slavič, J.; Rossi, G.; Boltežar, M. Thermoelasticity-based modal damage identification. Int. J. Fatigue 2020, 137, 105661. [Google Scholar] [CrossRef]
- Sanayei, M.M.; Saletnik, M.J.; Member, A.A. Parameter estimation of structures from static strain measurements. I: Formulation Struct. Eng. 1996, 122, 555–562. [Google Scholar]
- Sanayei, M.; Phelps, J.E.; Sipple, J.D.; Bell, E.S.; Brenner, B.R. Instrumentation, nondestructive testing, and finite-element model updating for bridge evaluation using strain measurements. J. Bridge Eng. 2012, 17, 130–138. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717707929. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, C.; Li, X. Structural damage detection of the bridge under moving loads with the quasi-static displacement influence line from one sensor. Measurement 2023, 211, 112599. [Google Scholar] [CrossRef]
- Terlaje, A.S.; Truman, K.Z. Parameter identification and damage detection using structural optimization and static response data. Adv. Struct. Eng. 2007, 10, 607–621. [Google Scholar] [CrossRef]
- Kourehli, S.S. Structural damage diagnosis using incomplete static responses and LS-SVM. Inverse Probl. Sci. Eng. 2016, 25, 418–433. [Google Scholar] [CrossRef]
- Zhang, J.; Maes, K.; De Roeck, G.; Lombaert, G. Model updating for a large multi-span quasi-periodic viaduct based on free wave characteristics. J. Sound Vib. 2021, 506, 116161. [Google Scholar] [CrossRef]
- Cheng, X.; Liao, Y. Structural safety assessment oriented modal experiments on Renyihe Bridge using vehicle excitations. Structures 2023, 56, 105016. [Google Scholar] [CrossRef]
- Deng, F.; Wei, S.; Jin, X.; Chen, Z.; Li, H. Damage identification of long-span bridges based on the correlation of probability distribution of monitored quasi-static responses. Mech. Syst. Signal Process. 2023, 186, 109908. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Tang, L.; Liu, Y.; Jiang, Z.; Fang, D. Localized reliability analysis on a large-span rigid frame bridge based on monitored strains from the long-term SHM system. Smart Struct. Syst. 2014, 14, 209–224. [Google Scholar] [CrossRef]
- Weng, S.; Xia, Y.; Xu, Y.-L.; Zhou, X.-Q.; Zhu, H.-P. Improved substructuring method for eigensolutions of large-scale structures. J. Sound Vib. 2009, 323, 718–736. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
- Jaishi, B.; Ren, W.-X. Damage detection by finite element model updating using modal flexibility residual. J. Sound Vib. 2006, 290, 369–387. [Google Scholar] [CrossRef]
- Sanayei, M.; Onipede, O. Damage assessment of structures using static test data. AIAA J. 2001, 29, 1174–1179. [Google Scholar] [CrossRef]
- Xiao, F.; Zhu, W.; Meng, X.; Chen, G.S. Parameter identification of structures with different connections using static responses. Appl. Sci. 2022, 12, 5896. [Google Scholar] [CrossRef]
- Yun, C.-B.; Yi, J.-H.; Bahng, E.Y. Joint damage assessment of framed structures using a neural networks technique. Eng. Struct. 2001, 23, 425–435. [Google Scholar] [CrossRef]
- Lei, Y.; Li, Q.; Chen, F.; Chen, Z. Damage Identification of frame structures with joint damage under earthquake excitation. Adv. Struct. Eng. 2014, 17, 1075–1087. [Google Scholar] [CrossRef]
- Weng, J.H.; Loh, C.H.; Yang, J.N. Experimental study of damage detection by data-driven subspace identification and finite-element model updating. J. Struct. Eng. 2009, 135, 1533–1544. [Google Scholar] [CrossRef]
- Nanda, B.; Maity, D.; Maiti, D.K. Modal parameter based inverse approach for structural joint damage assessment using unified particle swarm optimization. Appl. Math. Comput. 2014, 242, 407–422. [Google Scholar] [CrossRef]
- Aval, S.B.B.; Mohebian, P. Combined joint and member damage identification of skeletal structures by an improved biology migration algorithm. J. Civ. Struct. Health Monit. 2020, 10, 357–375. [Google Scholar] [CrossRef]
- Tofallis, C. A better measure of relative prediction accuracy for model selection and model estimation. J. Oper. Res. Soc. 2015, 66, 1352–1362. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]




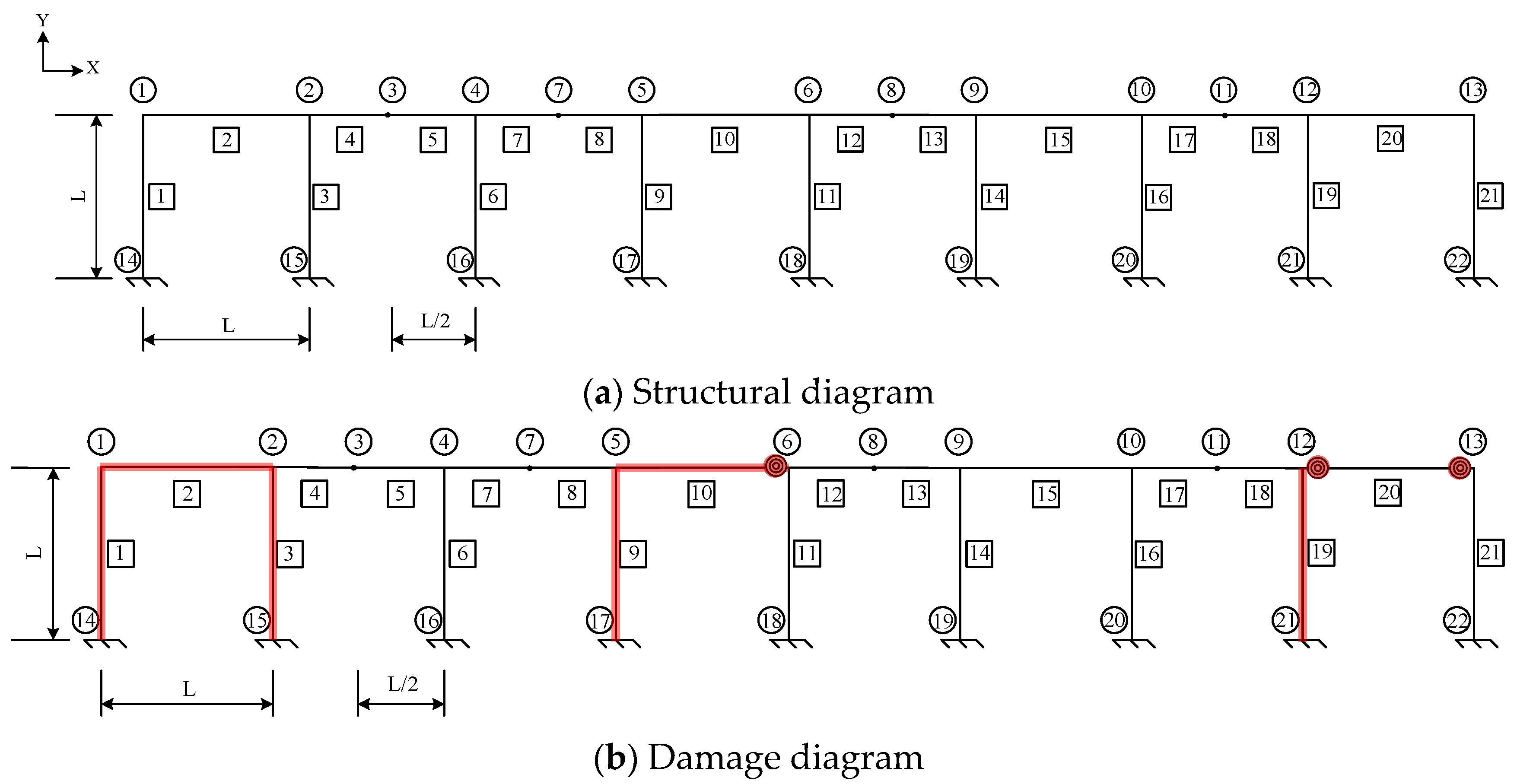


| Damage Scenario | Damage Parameter | Value | Damage Parameter | Value |
|---|---|---|---|---|
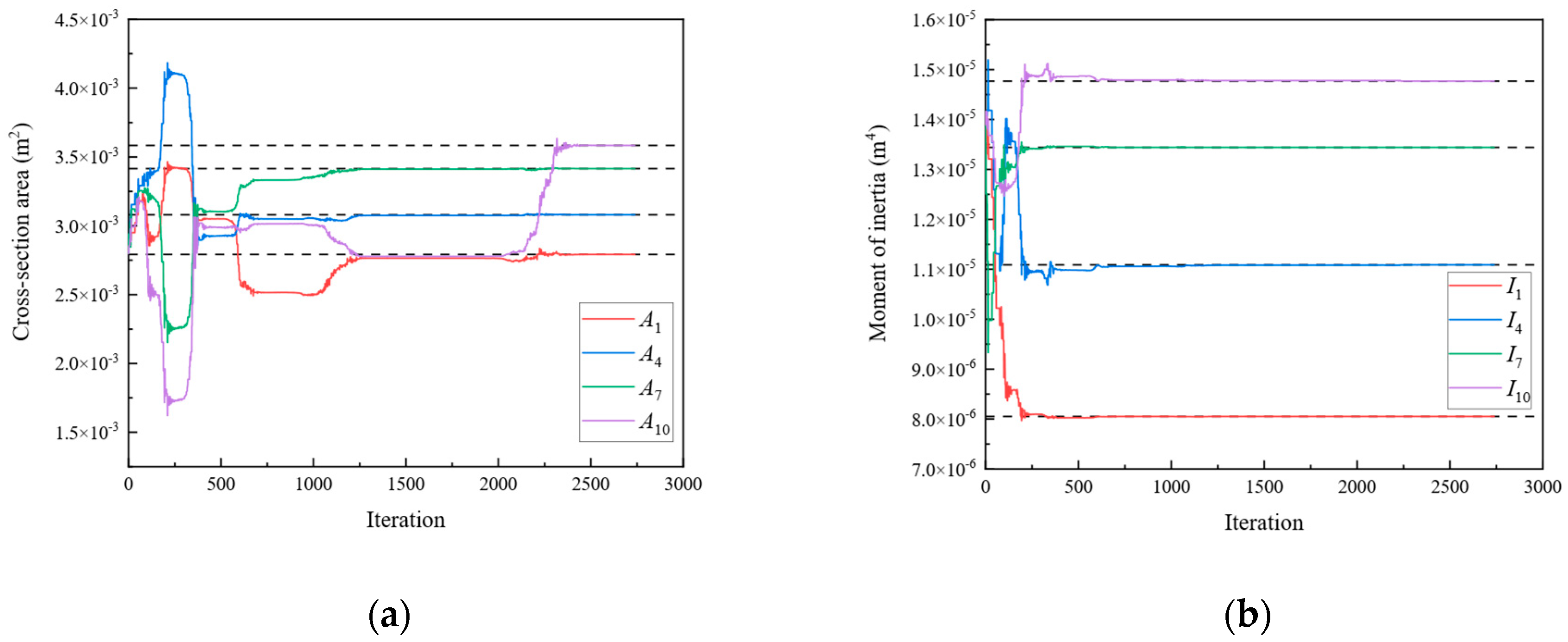
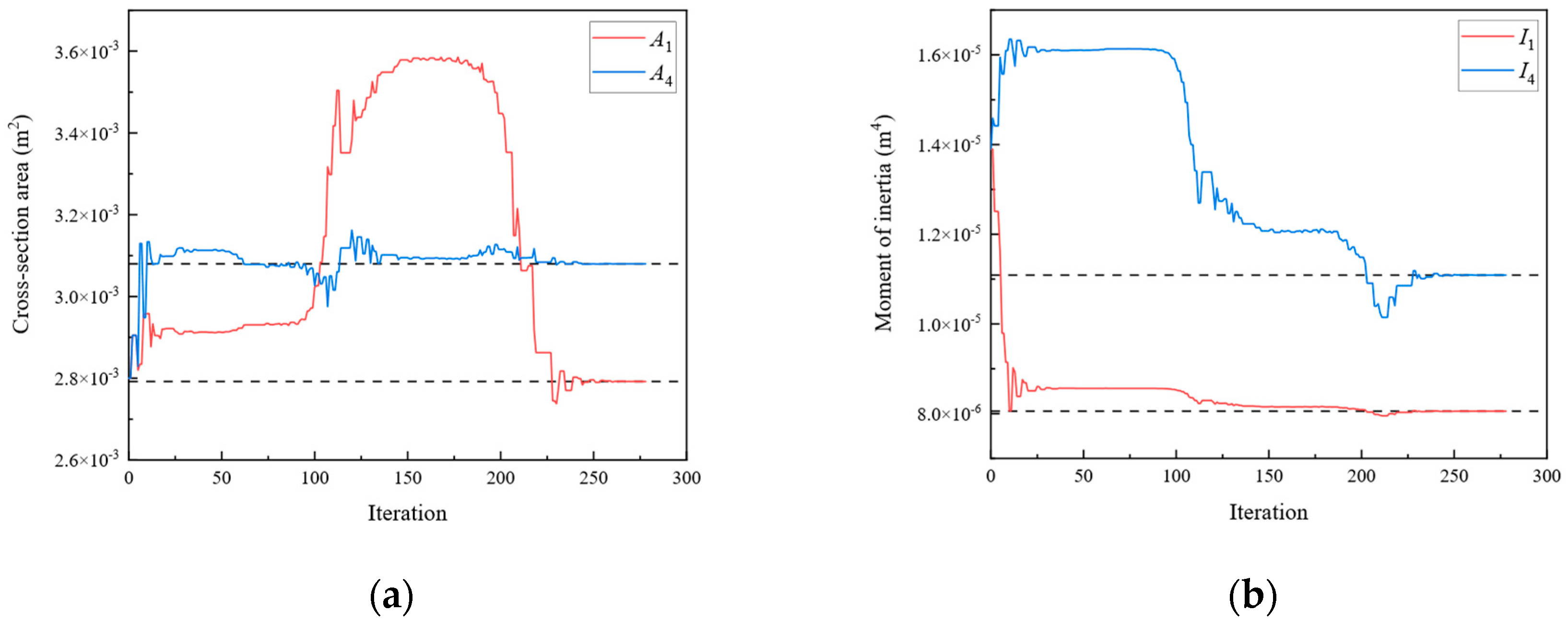
| 1 | A1 | 2.792 × 10−3 | I1 | 8.053 × 10−6 |
| A4 | 3.080 × 10−3 | I4 | 1.109 × 10−5 | |
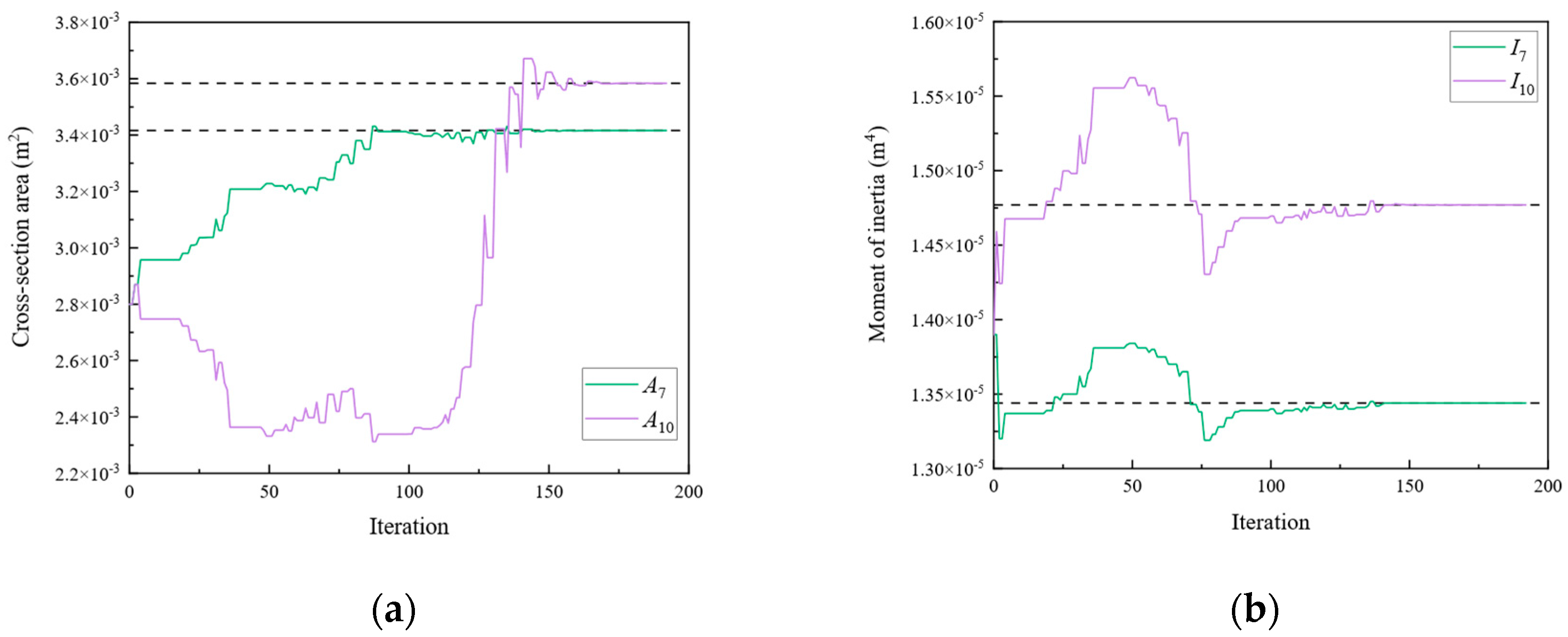
| A7 | 3.416 × 10−3 | I7 | 1.344 × 10−5 | |
| A10 | 3.584 × 10−3 | I10 | 1.477 × 10−5 | |
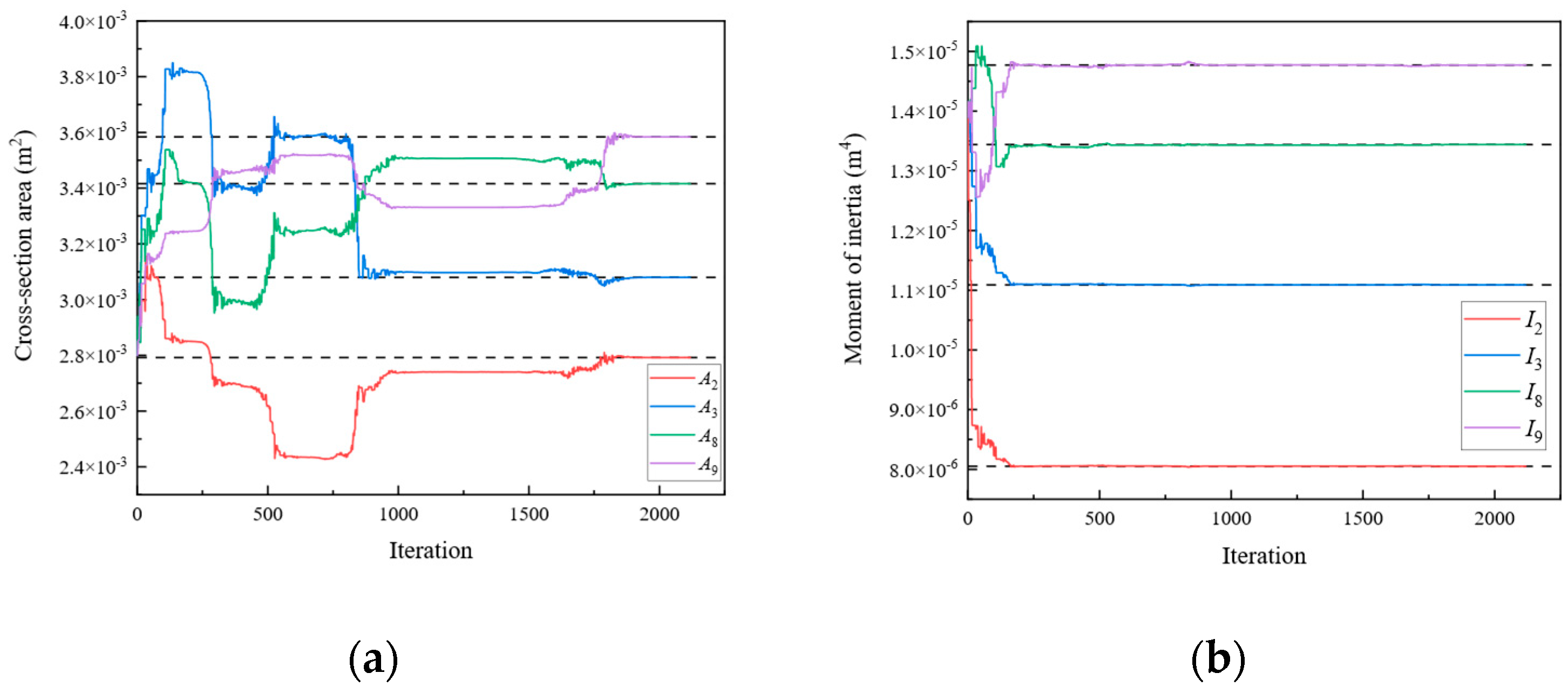
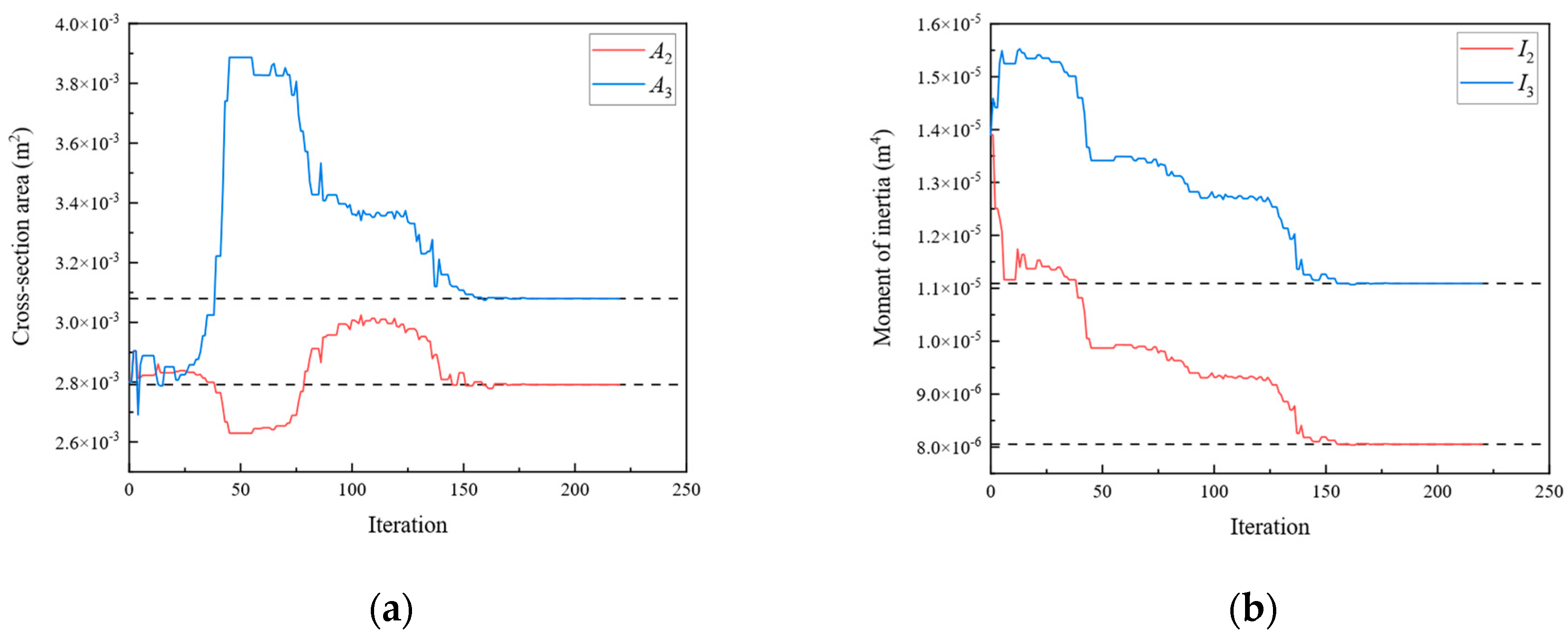
| 2 | A2 | 2.792 × 10−3 | I2 | 8.053 × 10−6 |
| A3 | 3.080 × 10−3 | I3 | 1.109 × 10−5 | |
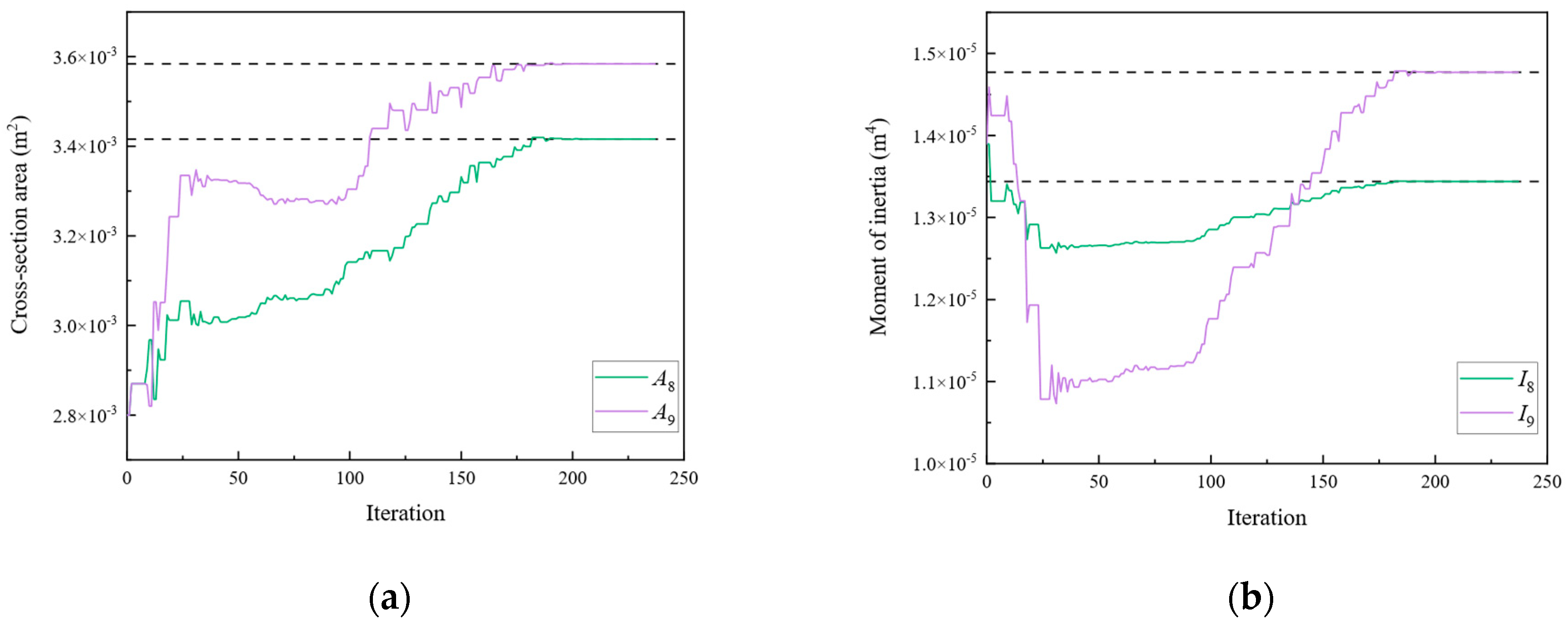
| A8 | 3.416 × 10−3 | I8 | 1.344 × 10−5 | |
| A9 | 3.584 × 10−3 | I9 | 1.477 × 10−5 | |
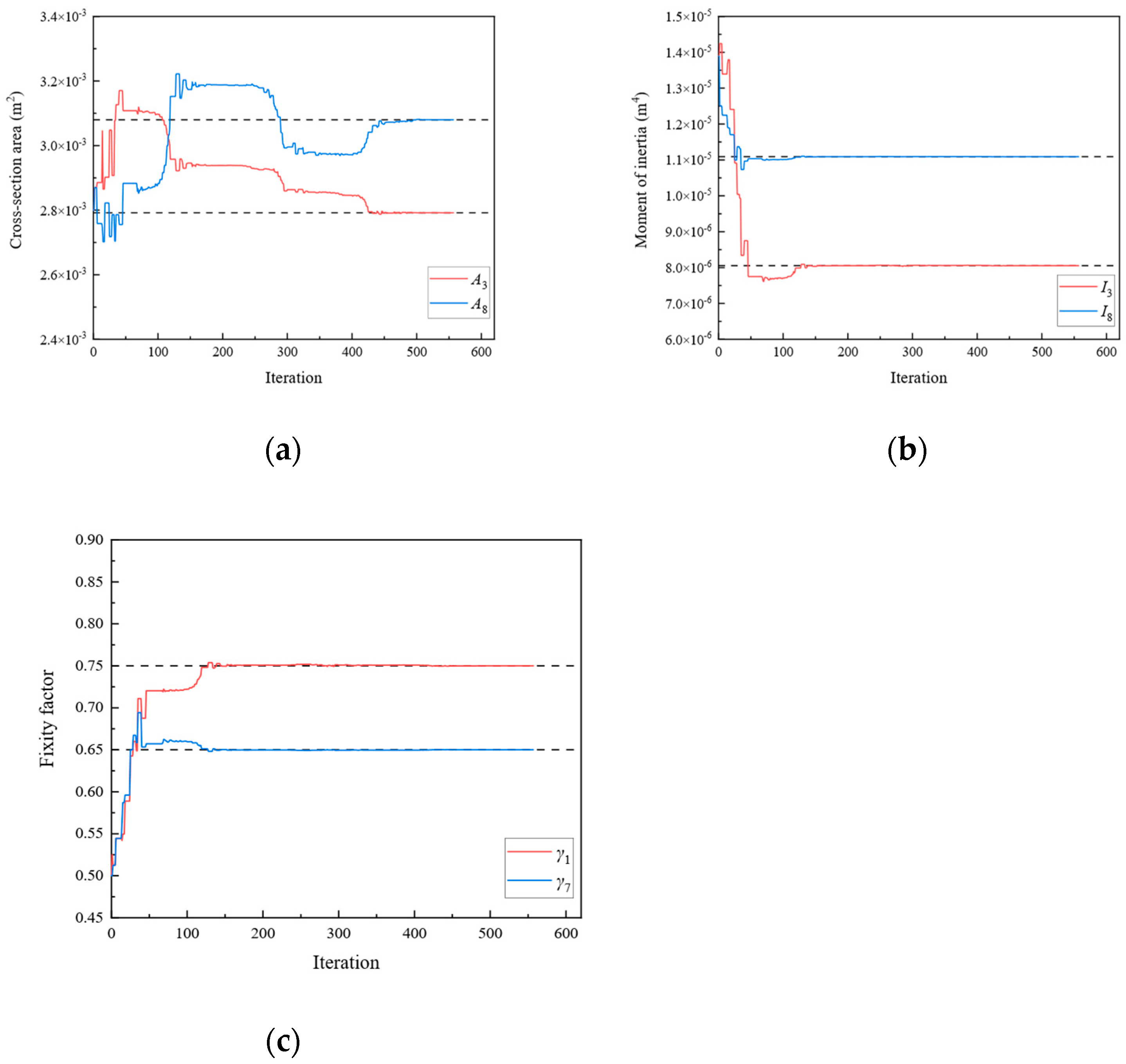
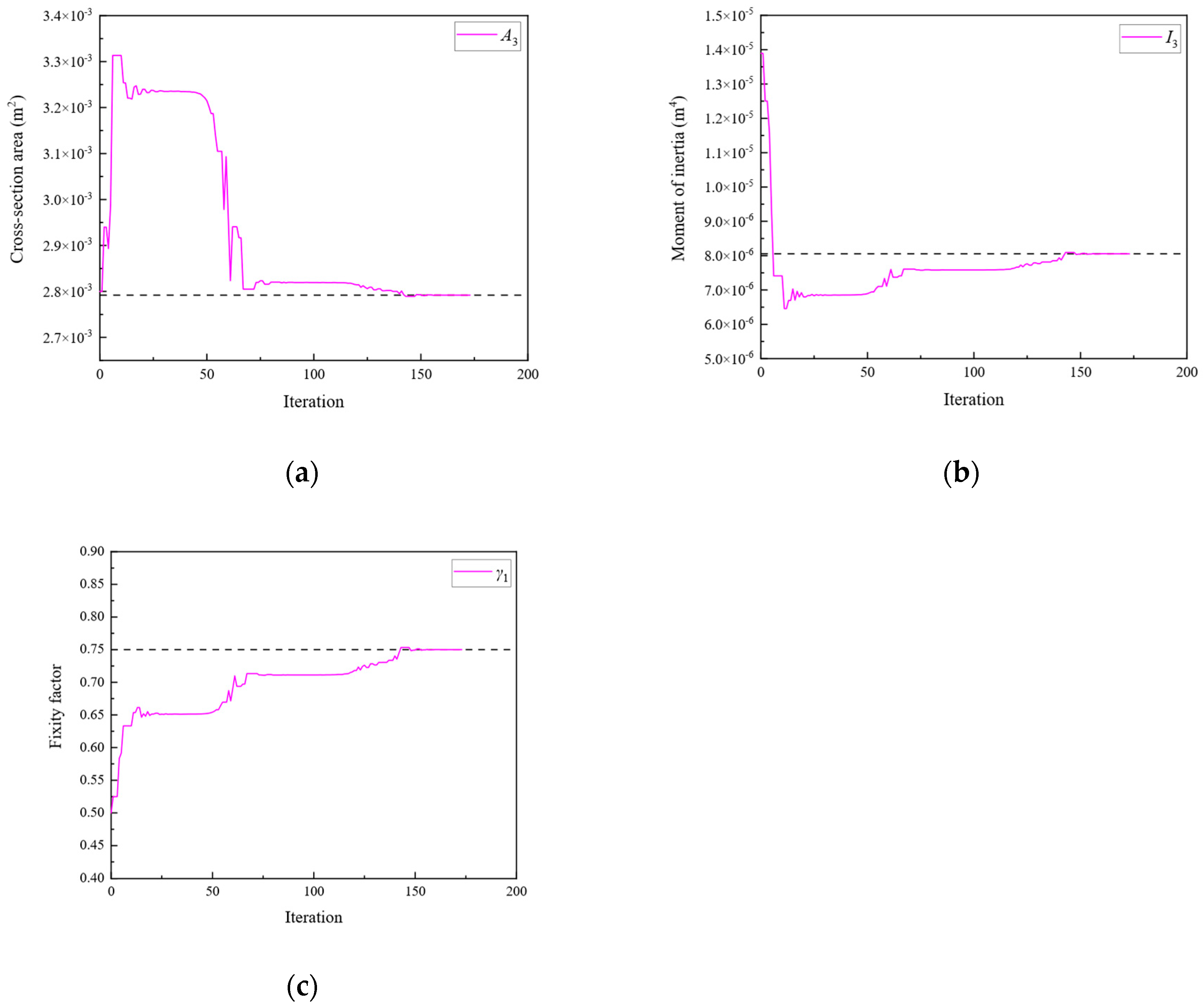
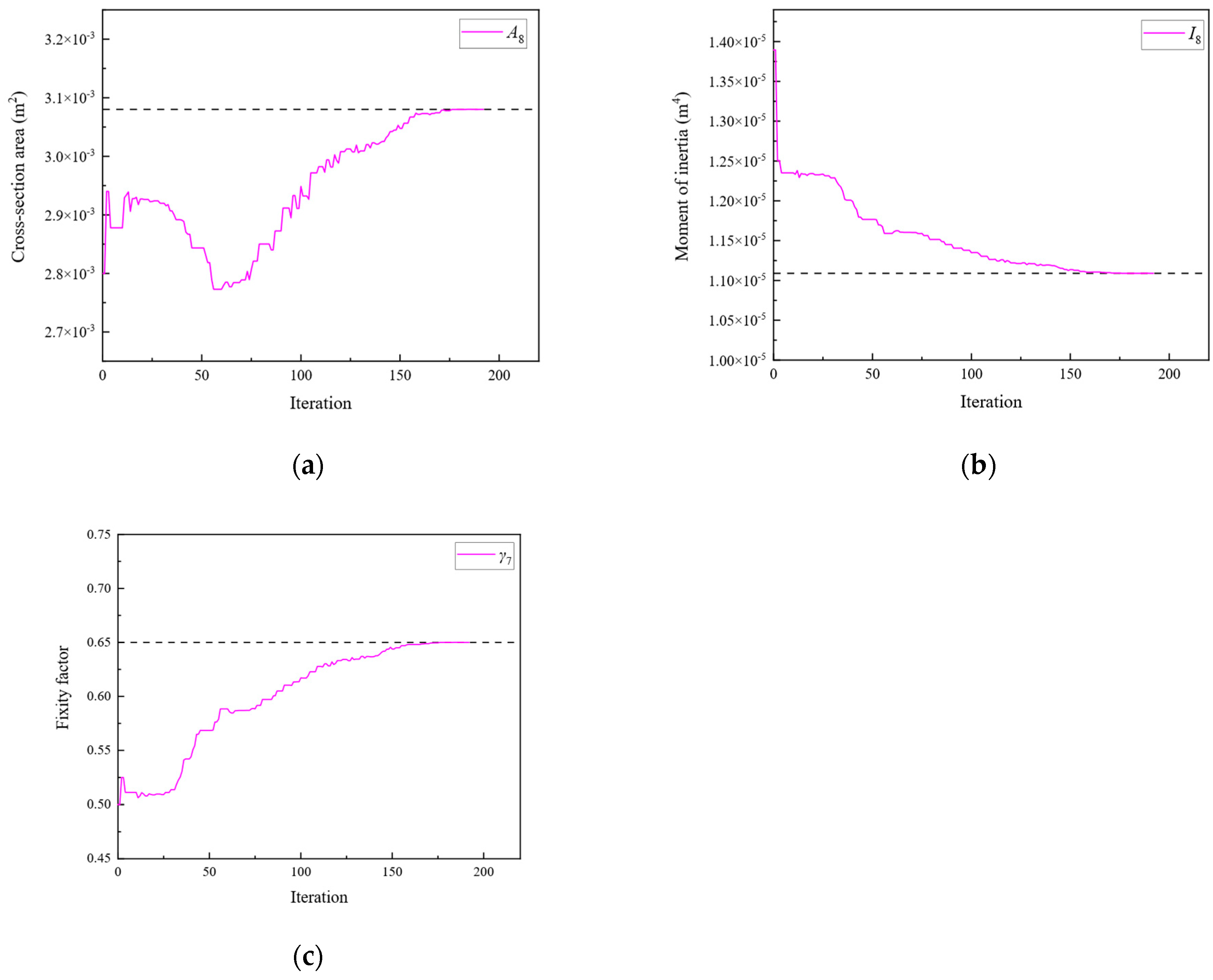
| 3 | A3 | 2.792 × 10−3 | I3 | 8.053 × 10−6 |
| A8 | 3.080 × 10−3 | I8 | 1.109 × 10−5 | |
| γ1 | 0.75 | γ7 | 0.65 | |
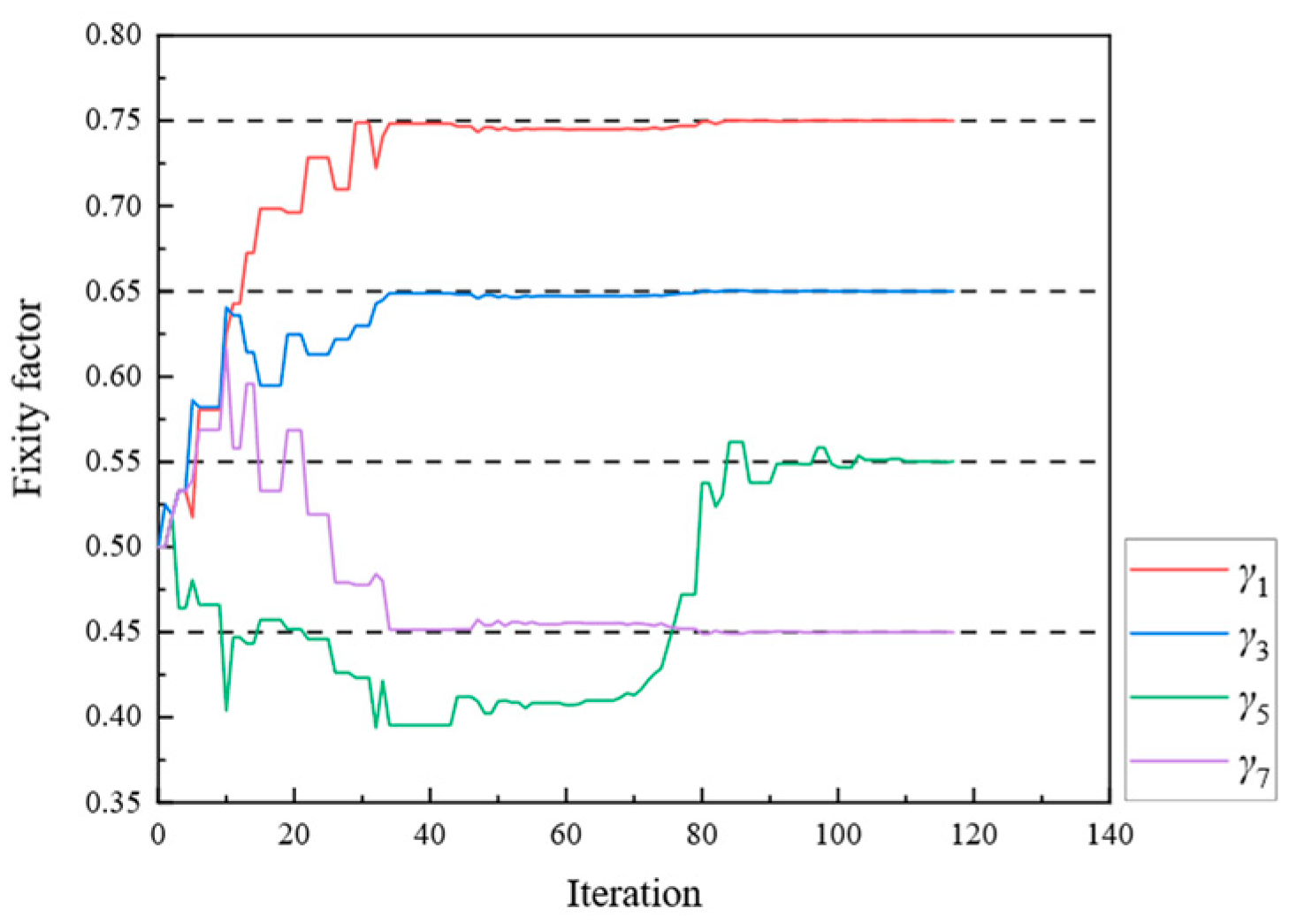
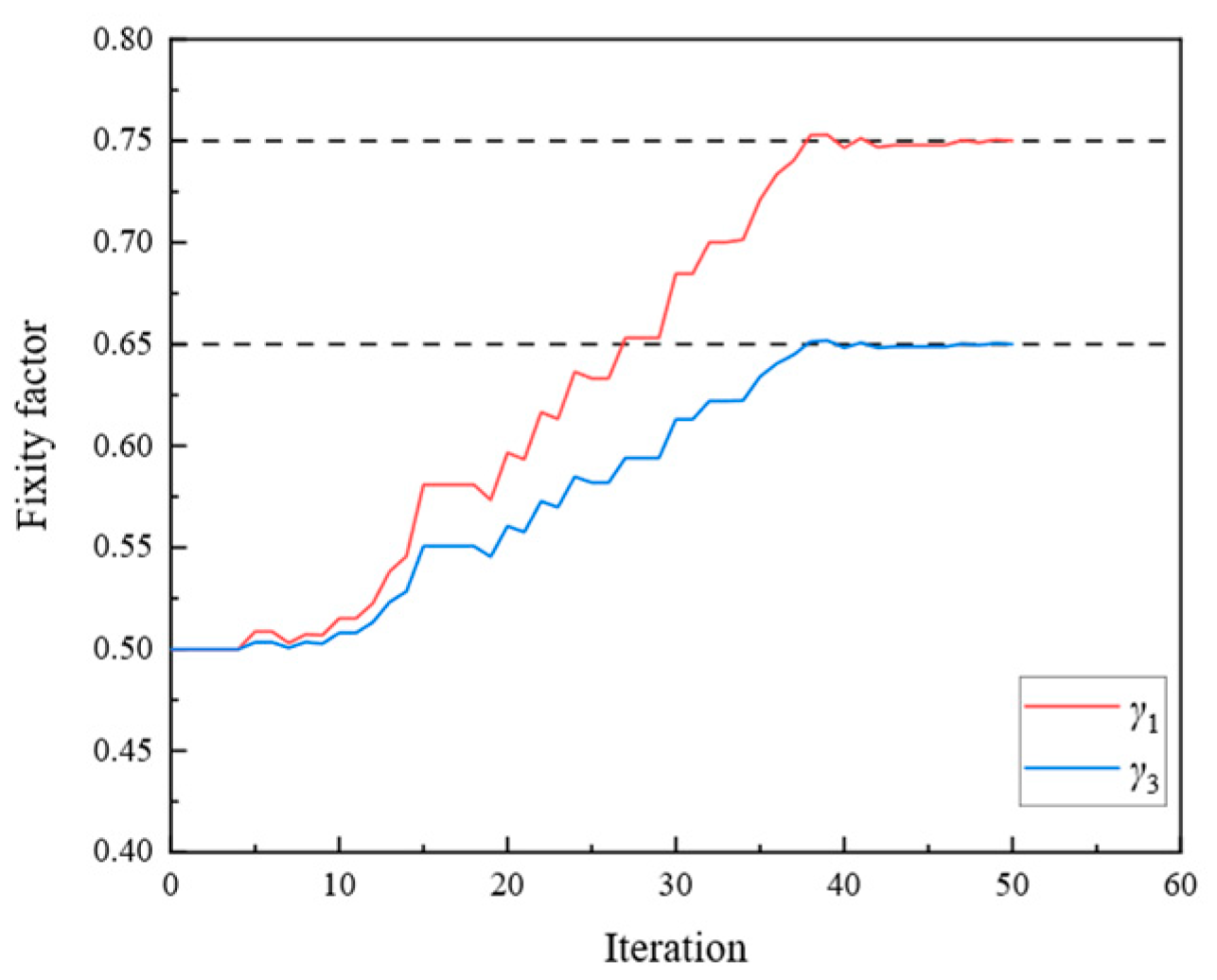
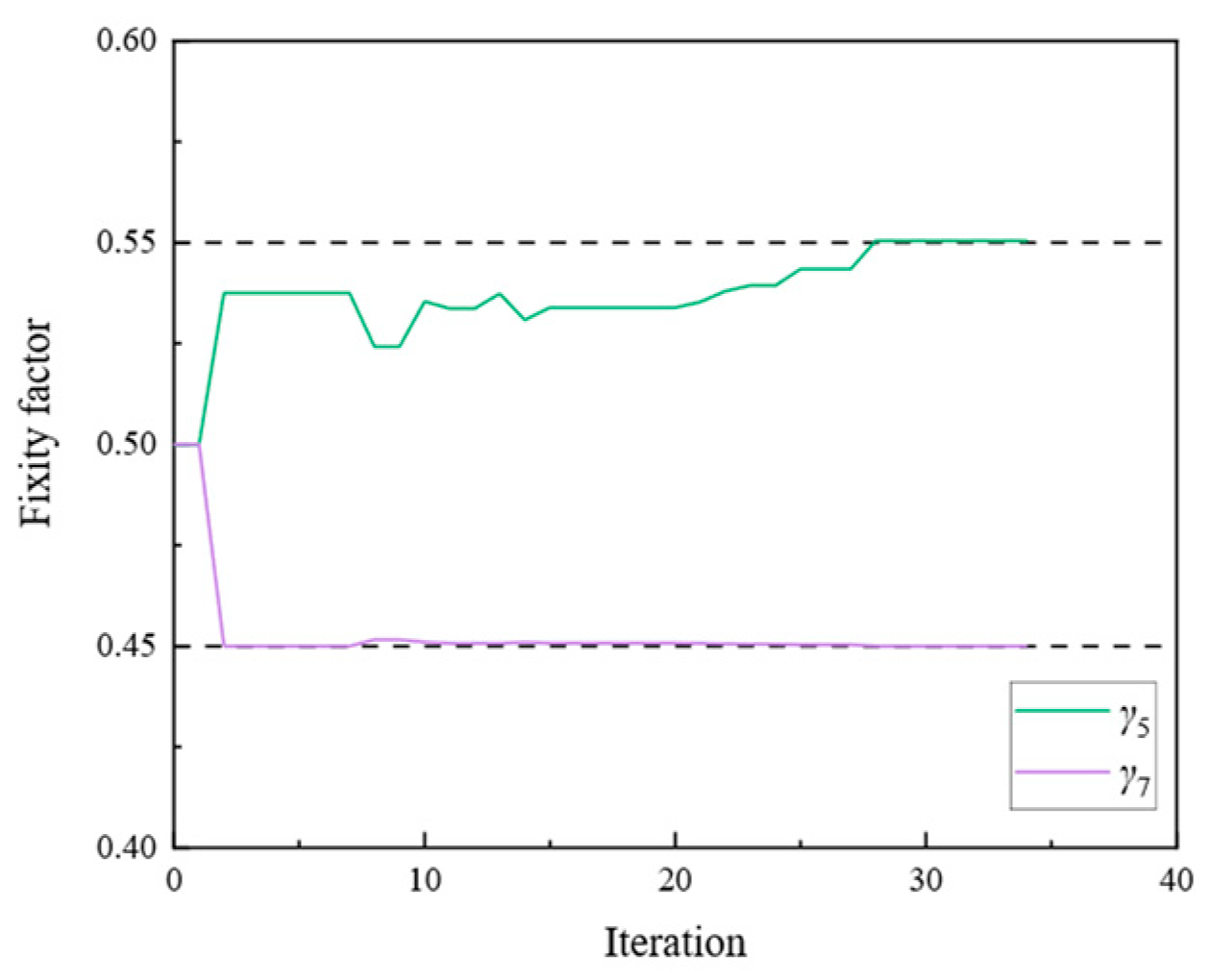
| 4 | γ1 | 0.75 | γ5 | 0.55 |
| γ3 | 0.65 | γ7 | 0.45 |
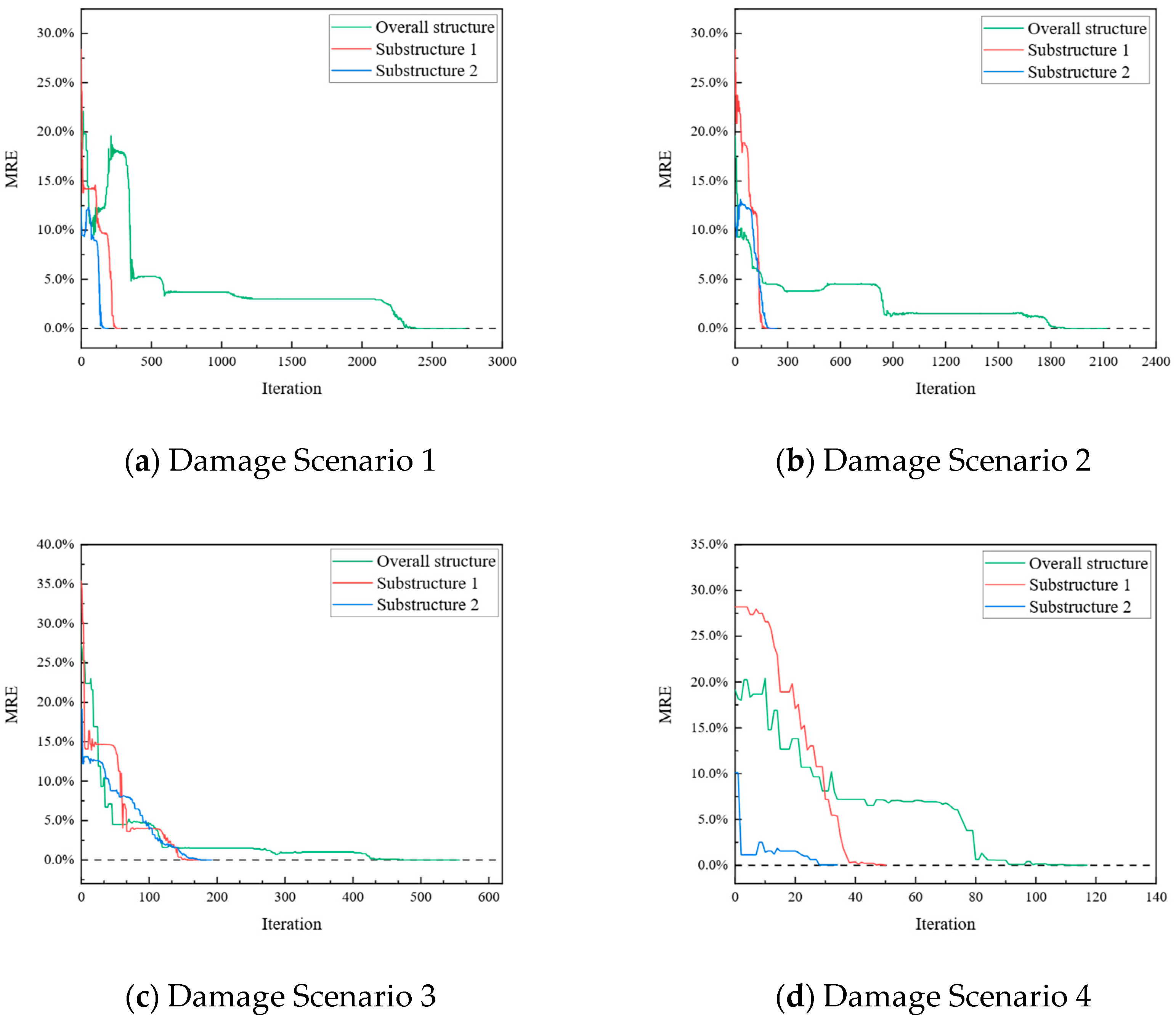
| Damage Scenario | Damage Elements | Member Damage | Joint Damage | Unknown Parameters | Iterations |
|---|---|---|---|---|---|
| Scenario 1 | 4 | 4 | 0 | 8 | 2738 |
| Scenario 2 | 4 | 4 | 0 | 8 | 2118 |
| Scenario 3 | 4 | 2 | 2 | 6 | 557 |
| Scenario 4 | 4 | 0 | 4 | 4 | 117 |
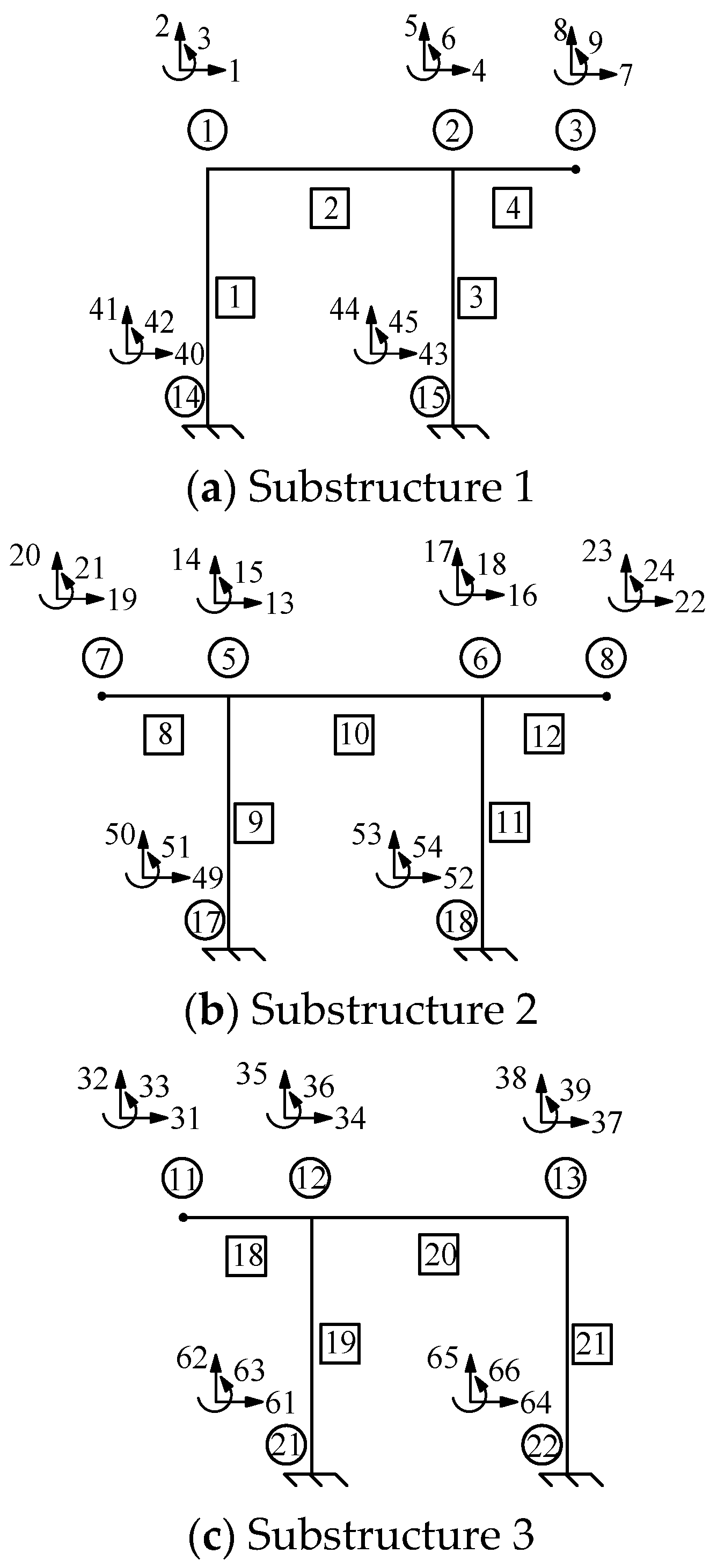
| Substructure | Damage Parameter | Value | Damage Parameter | Value |
|---|---|---|---|---|
| 1 | A1 | 3.904 × 10−3 | I1 | 1.535 × 10−5 |
| A2 | 4.068 × 10−3 | I2 | 1.813 × 10−5 | |
| A3 | 4.224 × 10−3 | I3 | 1.896 × 10−5 | |
| 2 | A9 | 4.480 × 10−3 | I9 | 2.223 × 10−5 |
| A10 | 4.800 × 10−3 | I10 | 1.840 × 10−5 | |
| γ6 | 0.75 | |||
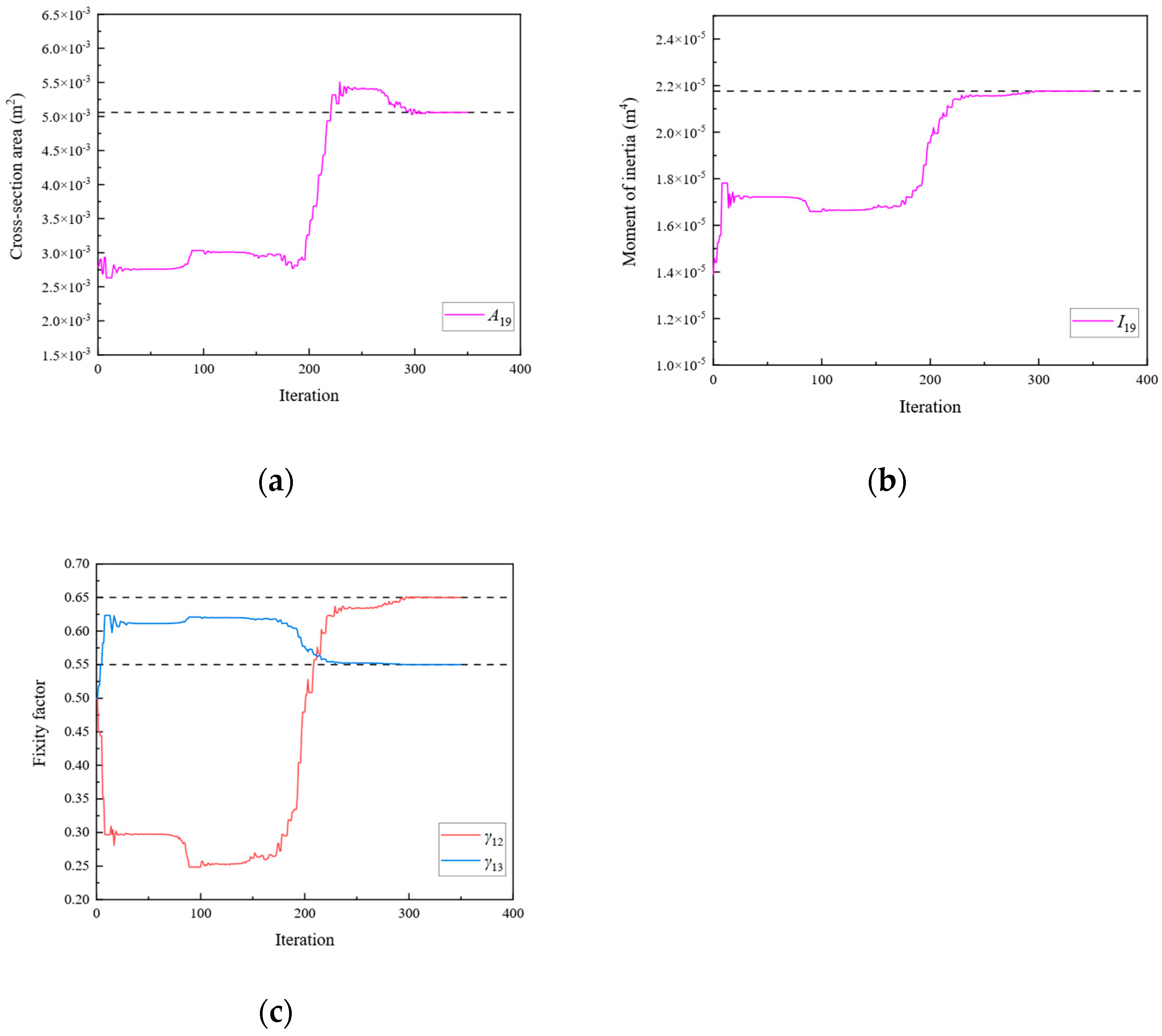
| 3 | A19 | 5.060 × 10−3 | I19 | 2.176 × 10−5 |
| γ12 | 0.65 | γ13 | 0.55 |
| Damage Scenario | Damage Elements | Member Damage | Joint Damage | Unknown Parameters | Iterations |
|---|---|---|---|---|---|
| Substructure 1 | 3 | 3 | 0 | 6 | 1069 |
| Substructure 2 | 3 | 2 | 1 | 5 | 649 |
| Substructure 3 | 3 | 1 | 2 | 4 | 350 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, F.; Yan, Y.; Meng, X.; Mao, Y.; Chen, G.S. Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method. Sensors 2024, 24, 1884. https://doi.org/10.3390/s24061884
Xiao F, Yan Y, Meng X, Mao Y, Chen GS. Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method. Sensors. 2024; 24(6):1884. https://doi.org/10.3390/s24061884
Chicago/Turabian StyleXiao, Feng, Yu Yan, Xiangwei Meng, Yuxue Mao, and Gang S. Chen. 2024. "Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method" Sensors 24, no. 6: 1884. https://doi.org/10.3390/s24061884
APA StyleXiao, F., Yan, Y., Meng, X., Mao, Y., & Chen, G. S. (2024). Parameter Identification of Multispan Rigid Frames Using a Stiffness Separation Method. Sensors, 24(6), 1884. https://doi.org/10.3390/s24061884












