Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function
Abstract
1. Introduction
- The first FPGA implementation of an adaptive-activation-function (AAF)-based neural network for regression.
- An adaptive activation function applied to digital predistortion and implemented in FPGA hardware.
- An optimized segmented spline curve layer that has been designed with the target hardware in mind to provide an implementation true to the mathematical basis of the segmented spline curve layer.
- The results show that the implementation of the AAF for DPD using the SSCNN is capable of effective linearization while consuming minimal resources.
- A thorough comparison of different neural network structures and their FPGA implementations that compares the performance and resources used. The comparison shows that the SSCNN has similar performance to a deep neural network (DNN) while using far fewer hardware resources.
2. Background
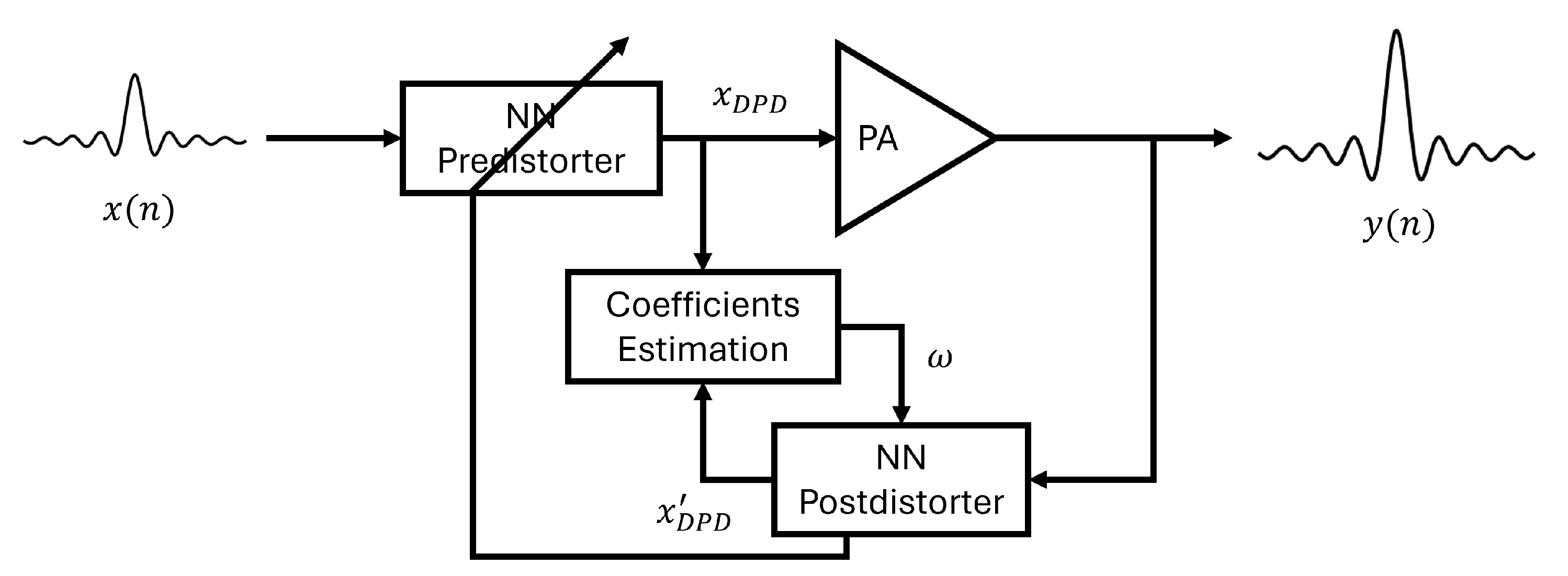
2.1. DPD
2.2. Direct Learning and Indirect Learning Architectures
2.3. Real-Valued Time-Delay Neural Network
2.4. Deep Neural Networks
2.5. Segmented Spline Curve Neural Network
3. Activation Functions
3.1. Related Work on Activation Functions
3.2. Adaptive Activation Functions
4. Hardware Design and Implementation
4.1. SSCNN Model Analysis
- Step 1:
- Choose the coefficient array length L;
- Step 2:
- Calculate the inverse of the x-axis width of a single segment ;
- Step 3:
- Find the coefficient index ;
- Step 4:
- Access coefficients and ;
- Step 5:
- Achieve the activation function .
4.2. SSC Layer Structure
4.3. Saturation
4.4. Systolic Processing
4.5. Implementation
Parameters
5. Results and Discussion
5.1. Experimental Setup
5.2. DPD Performance
5.3. Resource Utilization
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Boumaiza, S.; Mkadem, F. Wideband RF power amplifier predistortion using real-valued time-delay neural networks. In Proceedings of the 2009 European Microwave Conference (EuMC), Rome, Italy, 29 September–1 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1449–1452. [Google Scholar]
- Zhang, Y.; Li, Y.; Liu, F.; Zhu, A. Vector decomposition based time-delay neural network behavioral model for digital predistortion of RF power amplifiers. IEEE Access 2019, 7, 91559–91568. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Li, G.; Liu, F. Vector decomposed long short-term memory model for behavioral modeling and digital predistortion for wideband RF power amplifiers. IEEE Access 2020, 8, 63780–63789. [Google Scholar] [CrossRef]
- Hongyo, R.; Egashira, Y.; Hone, T.M.; Yamaguchi, K. Deep neural network-based digital predistorter for Doherty power amplifiers. IEEE Microw. Wirel. Components Lett. 2019, 29, 146–148. [Google Scholar] [CrossRef]
- Jung, S.; Kim, Y.; Woo, Y.; Lee, C. A two-step approach for DLA-based digital predistortion using an integrated neural network. Signal Process. 2020, 177, 107736. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, X.; Xu, L.; Wang, W.; Ghannouchi, F.M. Low computational complexity digital predistortion based on convolutional neural network for wideband power amplifiers. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1702–1706. [Google Scholar] [CrossRef]
- Liu, Z.; Dou, Y.; Jiang, J.; Wang, Q.; Chow, P. An FPGA-based processor for training convolutional neural networks. In Proceedings of the 2017 International Conference on Field Programmable Technology (ICFPT), Melbourne, VIC, Australia, 11–13 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 207–210. [Google Scholar]
- Kim, K.; Jang, S.J.; Park, J.; Lee, E.; Lee, S.S. Lightweight and Energy-Efficient Deep Learning Accelerator for Real-Time Object Detection on Edge Devices. Sensors 2023, 23, 1185. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Wu, C.; Cui, Z.; Niu, C. A new lightweight deep neural network for surface scratch detection. Int. J. Adv. Manuf. Technol. 2022, 123, 1999–2015. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sharma, A.; Bharti, V.; Singh, A.K.; Singh, S.K.; Saxena, S. MobiHisNet: A lightweight CNN in mobile edge computing for histopathological image classification. IEEE Internet Things J. 2021, 8, 17778–17789. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 2020, 404, 109136. [Google Scholar] [CrossRef]
- Lau, M.M.; Lim, K.H. Review of adaptive activation function in deep neural network. In Proceedings of the 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), Sarawak, Malaysia, 3–6 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 686–690. [Google Scholar]
- Jagtap, A.D.; Shin, Y.; Kawaguchi, K.; Karniadakis, G.E. Deep Kronecker neural networks: A general framework for neural networks with adaptive activation functions. Neurocomputing 2022, 468, 165–180. [Google Scholar] [CrossRef]
- Qian, S.; Liu, H.; Liu, C.; Wu, S.; San Wong, H. Adaptive activation functions in convolutional neural networks. Neurocomputing 2018, 272, 204–212. [Google Scholar] [CrossRef]
- Özbay, Y.; Tezel, G. A new method for classification of ECG arrhythmias using neural network with adaptive activation function. Digit. Signal Process. 2010, 20, 1040–1049. [Google Scholar] [CrossRef]
- AMD. Xilinx RFSoC DFE. Available online: https://www.xilinx.com/products/silicon-devices/soc/rfsoc/zynq-ultrascale-plus-rfsoc-dfe.html (accessed on 7 March 2024).
- Morgan, D.; Ma, Z.; Kim, J.; Zierdt, M.; Pastalan, J. A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers. IEEE Trans. Signal Process 2006, 54, 3852–3860. [Google Scholar] [CrossRef]
- Vaicaitis, A.; Hu, A.; Dooley, J. Direct Input-to-Output Neural Network for Efficient Digital Predistortion of MIMO Transmitters. In Proceedings of the 2021 51st European Microwave Conference, EuMC 2021, London, UK, 4–6 April 2022. [Google Scholar]
- Jiang, Y.; Vaicaitis, A.; Leeser, M.; Dooley, J. Neural Network on the Edge: Efficient and Low Cost FPGA Implementation of Digital Predistortion in MIMO Systems. In Proceedings of the 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 17–19 April 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–2. [Google Scholar]
- Braithwaite, R.N. A comparison of indirect learning and closed loop estimators used in digital predistortion of power amplifiers. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA, 17–22 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Hesami, S.; Dooley, J.; Farrell, R. Digital predistorter in crosstalk compensation of MIMO transmitters. In Proceedings of the 2016 27th Irish Signals and Systems Conference (ISSC), Londonderry, UK, 21–22 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Abi Hussein, M.; Bohara, V.A.; Venard, O. On the system level convergence of ILA and DLA for digital predistortion. In Proceedings of the 2012 International Symposium on Wireless Communication Systems (ISWCS), Paris, France, 28–31 August 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 870–874. [Google Scholar]
- Liu, T.; Boumaiza, S.; Ghannouchi, F.M. Dynamic behavioral modeling of 3G power amplifiers using real-valued time-delay neural networks. IEEE Trans. Microw. Theory Tech. 2004, 52, 1025–1033. [Google Scholar] [CrossRef]
- Wang, D.; Aziz, M.; Helaoui, M.; Ghannouchi, F.M. Augmented real-valued time-delay neural network for compensation of distortions and impairments in wireless transmitters. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 242–254. [Google Scholar] [CrossRef]
- Fawzy, A.; Sun, S.; Lim, T.J.; Guo, Y.X. An Efficient Deep Neural Network Structure for RF Power Amplifier Linearization. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Vaicaitis, A.; Dooley, J. Segmented Spline Curve Neural Network for Low Latency Digital Predistortion of RF Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2022, 70, 4910–4915. [Google Scholar] [CrossRef]
- Blott, M.; Preußer, T.B.; Fraser, N.J.; Gambardella, G.; O’brien, K.; Umuroglu, Y.; Leeser, M.; Vissers, K. FINN-R: An end-to-end deep-learning framework for fast exploration of quantized neural networks. ACM Trans. Reconfigurable Technol. Syst. (TRETS) 2018, 11, 1–23. [Google Scholar] [CrossRef]
- Sun, M.; Zhao, P.; Gungor, M.; Pedram, M.; Leeser, M.; Lin, X. 3D CNN acceleration on FPGA using hardware-aware pruning. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Zhang, M.; Vassiliadis, S.; Delgado-Frias, J.G. Sigmoid generators for neural computing using piecewise approximations. IEEE Trans. Comput. 1996, 45, 1045–1049. [Google Scholar] [CrossRef]
- Tatas, K.; Gemenaris, M. High-Performance and Low-Cost Approximation of ANN Sigmoid Activation Functions on FPGAs. In Proceedings of the 2023 12th International Conference on Modern Circuits and Systems Technologies (MOCAST), Athens, Greece, 28–30 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–4. [Google Scholar]
- Abdelsalam, A.M.; Langlois, J.P.; Cheriet, F. A configurable FPGA implementation of the tanh function using DCT interpolation. In Proceedings of the 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, 30 April–2 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 168–171. [Google Scholar]
- Si, J.; Harris, S.L.; Yfantis, E. Neural networks on an FPGA and hardware-friendly activation functions. J. Comput. Commun. 2020, 8, 251. [Google Scholar] [CrossRef]
- Ngah, S.; Bakar, R.A.; Embong, A.; Razali, S. Two-steps implementation of sigmoid function for artificial neural network in field programmable gate array. ARPN J. Eng. Appl. Sci 2016, 7, 4882–4888. [Google Scholar]
- Gao, Y.; Luan, F.; Pan, J.; Li, X.; He, Y. Fpga-based implementation of stochastic configuration networks for regression prediction. Sensors 2020, 20, 4191. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Raj, A.N.J.; Hu, Z.; Huang, S.; Fan, Z.; Joler, M. A twofold lookup table architecture for efficient approximation of activation functions. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 2540–2550. [Google Scholar] [CrossRef]
- Al-Rikabi, H.M.; Al-Ja’afari, M.A.; Ali, A.H.; Abdulwahed, S.H. Generic model implementation of deep neural network activation functions using GWO-optimized SCPWL model on FPGA. Microprocess. Microsyst. 2020, 77, 103141. [Google Scholar] [CrossRef]
- Pasca, B.; Langhammer, M. Activation function architectures for FPGAs. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 43–437. [Google Scholar]
- Decherchi, S.; Gastaldo, P.; Leoncini, A.; Zunino, R. Efficient digital implementation of extreme learning machines for classification. IEEE Trans. Circuits Syst. II Express Briefs 2012, 59, 496–500. [Google Scholar] [CrossRef]
- Liu, S.; Fan, H.; Luk, W. Accelerating fully spectral CNNs with adaptive activation functions on FPGA. In Proceedings of the 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 1–5 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1530–1535. [Google Scholar]
- Bohra, P.; Campos, J.; Gupta, H.; Aziznejad, S.; Unser, M. Learning Activation Functions in Deep (Spline) Neural Networks. IEEE Open J. Signal Process. 2020, 1, 295–309. [Google Scholar] [CrossRef]
- Xilinx. ZCU111 Evaluation Board User Guide; UG1271 (v1.4); Xilinx: San Jose, CA, USA, 2023. [Google Scholar]

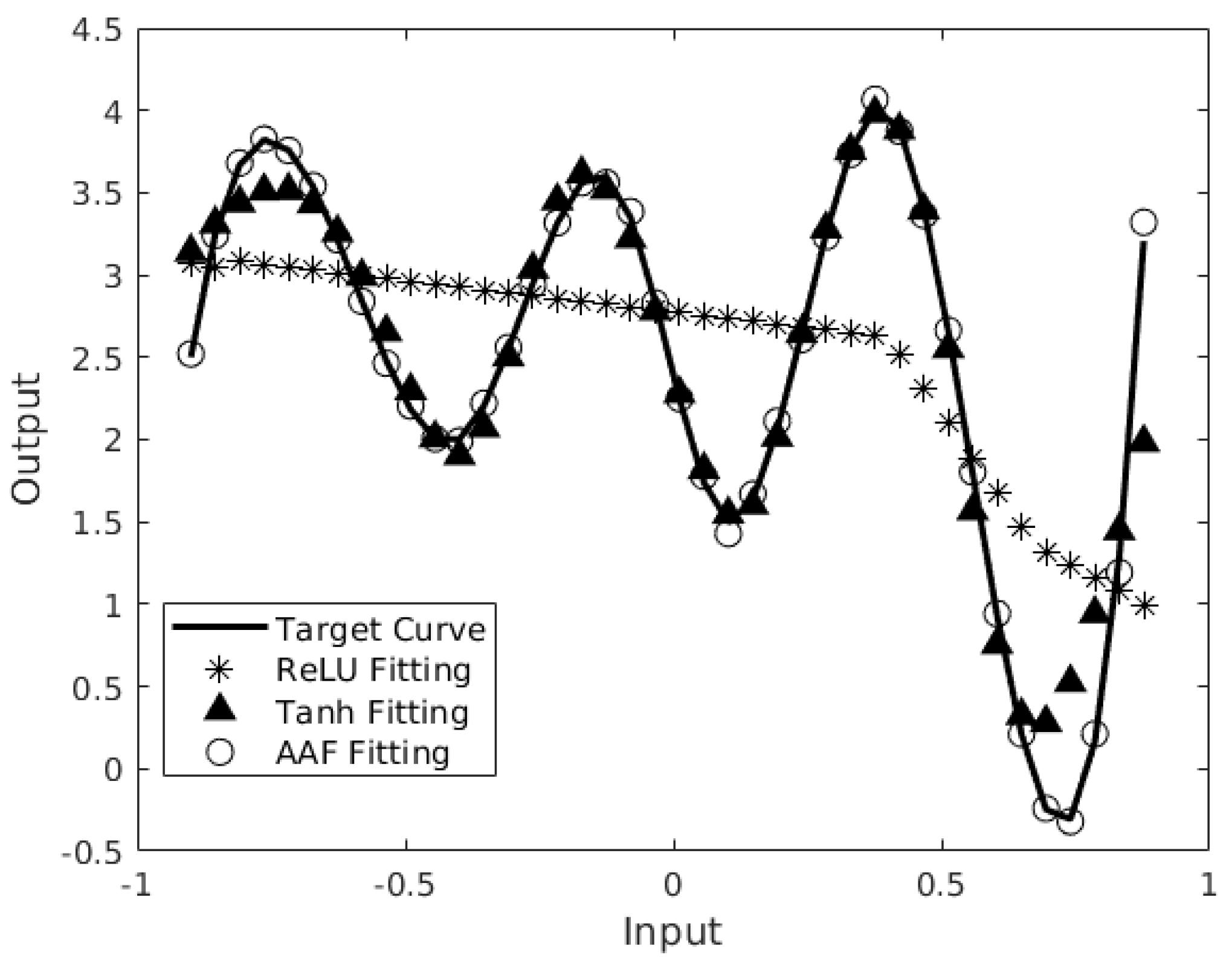






| Activation Function | Definition |
|---|---|
| ReLU | |
| Sigmoid | |
| Hyperbolic Tangent | |
| Segmented Spline |
| Model | # of Coefficients | EVM (%) | ACPR (dBm) | NMSE (dB) |
|---|---|---|---|---|
| No DPD | - | 4.0725 | −35.487 | −27.803 |
| RVTDNN (9) | 83 | 2.7758 | −37.752 | −31.132 |
| ARVTDNN (9) | 110 | 2.4284 | −40.748 | −32.295 |
| DNN (9, 4) | 140 | 2.4310 | −40.138 | −32.284 |
| DNN (9, 4, 4) | 160 | 2.2545 | −41.650 | −32.939 |
| SSCNN (9) | 85 | 2.3340 | −41.886 | −32.653 |
| Model | Slice LUTs | FFs | BRAMs | DSPs | Clock Speed (MHz) |
|---|---|---|---|---|---|
| RVTDNN (9) | 6123 (1.44%) | 7880 (0.93%) | 4.5 (0.42%) | 90 (2.11%) | 118.73 |
| ARVTDNN (9) | 7289 (1.71%) | 10,935 (1.29%) | 4.5 (0.42%) | 117 (2.74%) | 116.71 |
| DNN (9, 4) | 9355 (2.2%) | 12,425 (1.46%) | 6 (0.56%) | 152 (3.56%) | 102.25 |
| DNN (9, 4, 4) | 12,080 (2.84%) | 14,072 (1.65%) | 8 (0.74%) | 184 (4.31%) | 100.68 |
| SSCNN(9) | 8258 (1.94%) | 8084 (0.95%) | 0 (0%) | 108 (2.53%) | 221.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Vaicaitis, A.; Dooley, J.; Leeser, M. Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function. Sensors 2024, 24, 1829. https://doi.org/10.3390/s24061829
Jiang Y, Vaicaitis A, Dooley J, Leeser M. Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function. Sensors. 2024; 24(6):1829. https://doi.org/10.3390/s24061829
Chicago/Turabian StyleJiang, Yiyue, Andrius Vaicaitis, John Dooley, and Miriam Leeser. 2024. "Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function" Sensors 24, no. 6: 1829. https://doi.org/10.3390/s24061829
APA StyleJiang, Y., Vaicaitis, A., Dooley, J., & Leeser, M. (2024). Efficient Neural Networks on the Edge with FPGAs by Optimizing an Adaptive Activation Function. Sensors, 24(6), 1829. https://doi.org/10.3390/s24061829






