An Underwater Source Localization Method Using Bearing Measurements
Abstract
1. Introduction
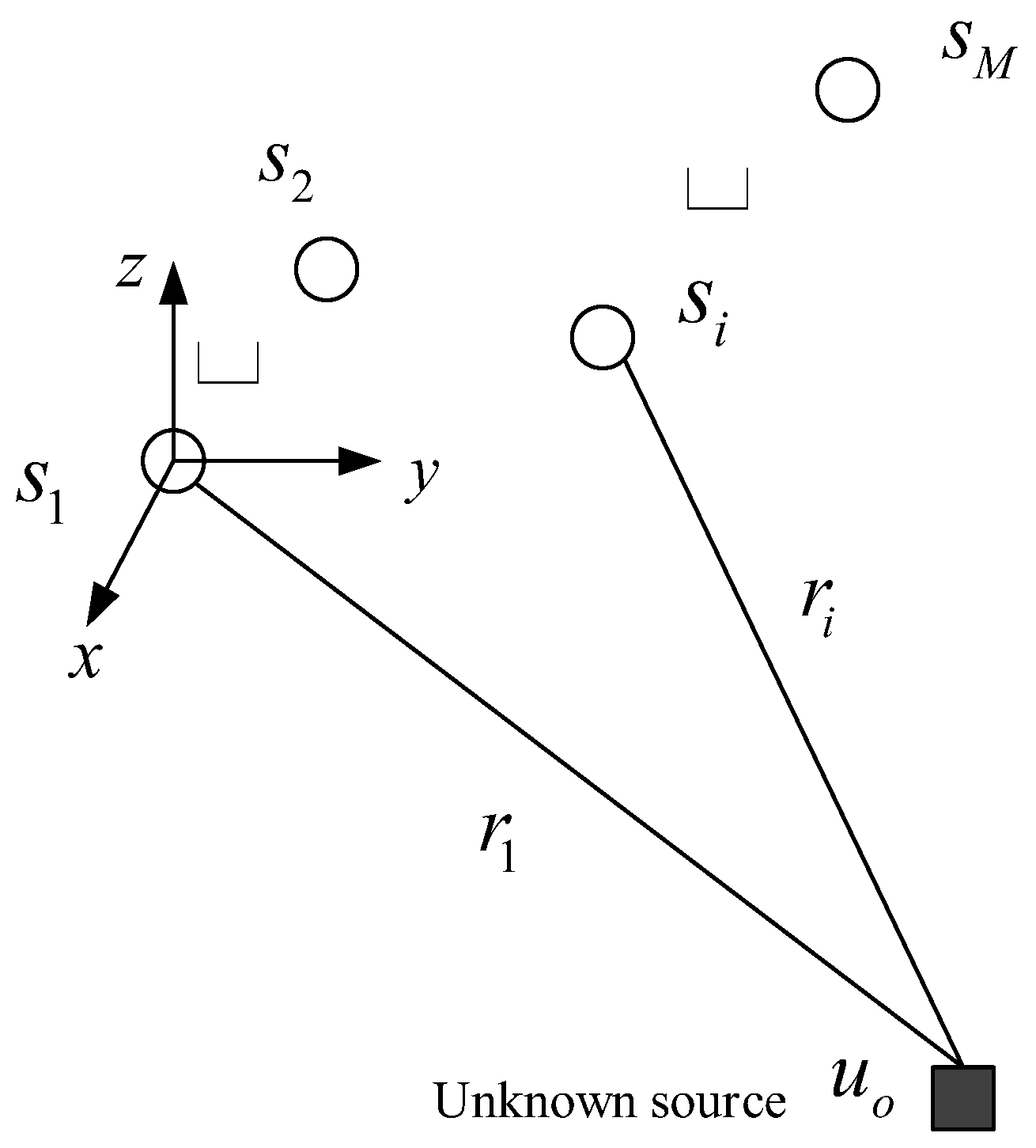
2. System Model
3. Localization Method
3.1. Initial Solution
3.2. Bias Compensation Method Based on Taylor Expansion
| Algorithm 1: The AOA-based localization method based on bias compensation |
| Step 1: Set as an identity matrix and solve the optimization problem using (10). A rough value can be obtained. |
| Step 2: Reformulate the weighting matrix W with the rough value |
| Step 3: Construct constraints based on the (13)–(15). |
| Step 4: Get the closed-form of the localization problem using (16) based on the SDP method. |
| Step 5: Based on the closed-form solution, construct a constrained optimization equation based on the Taylor expansion as (25) shows. |
| Step 6: Use Lagrange multiplier technology to get the bias as (27) shows. |
| Step 7: Revise the result using (29) and an improved result can be obtained. |
3.3. CRLB Analysis
4. Simulation and Field Test
4.1. Simulation Test
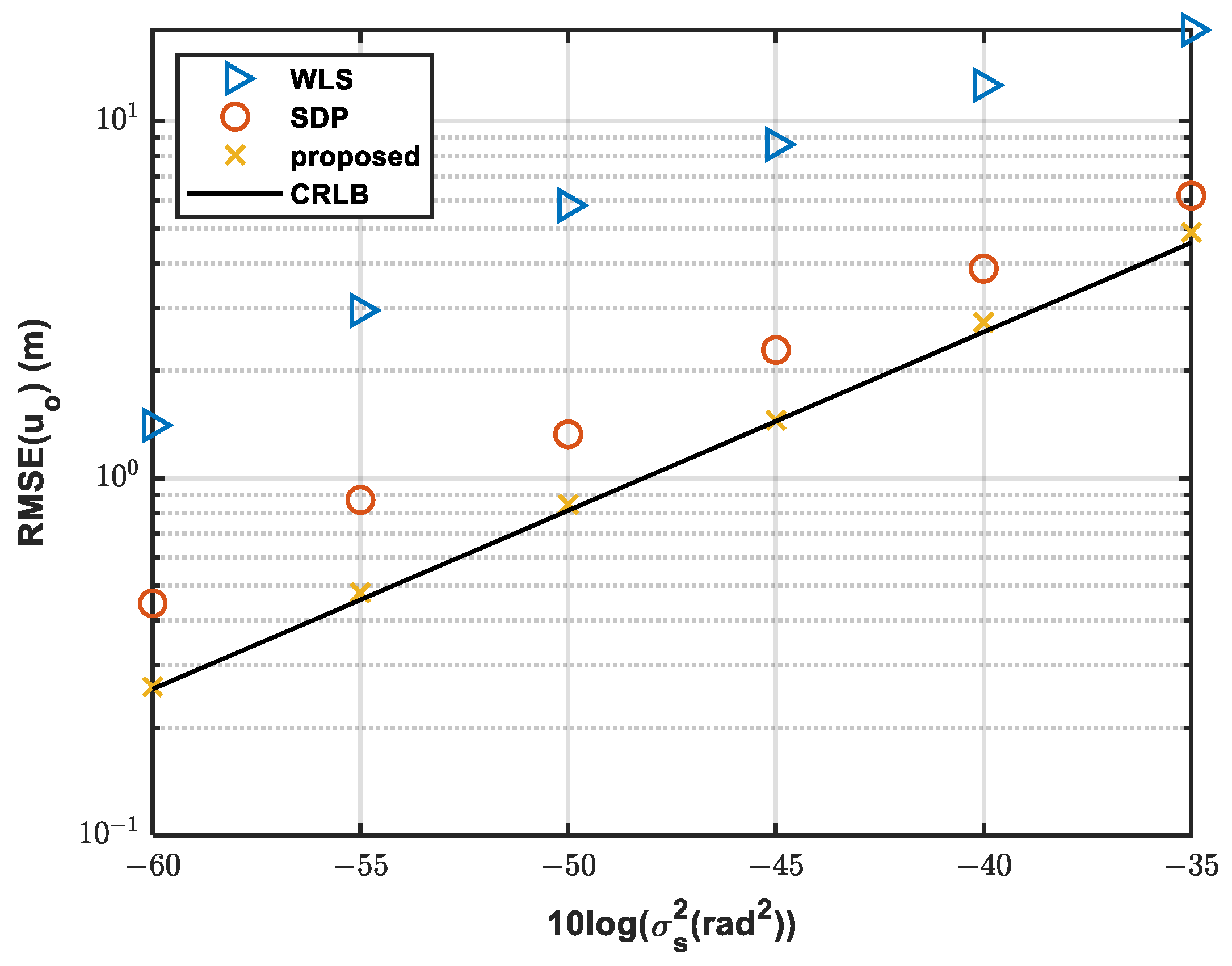
4.1.1. Simulation 1—Analysis under Different AOA Noises
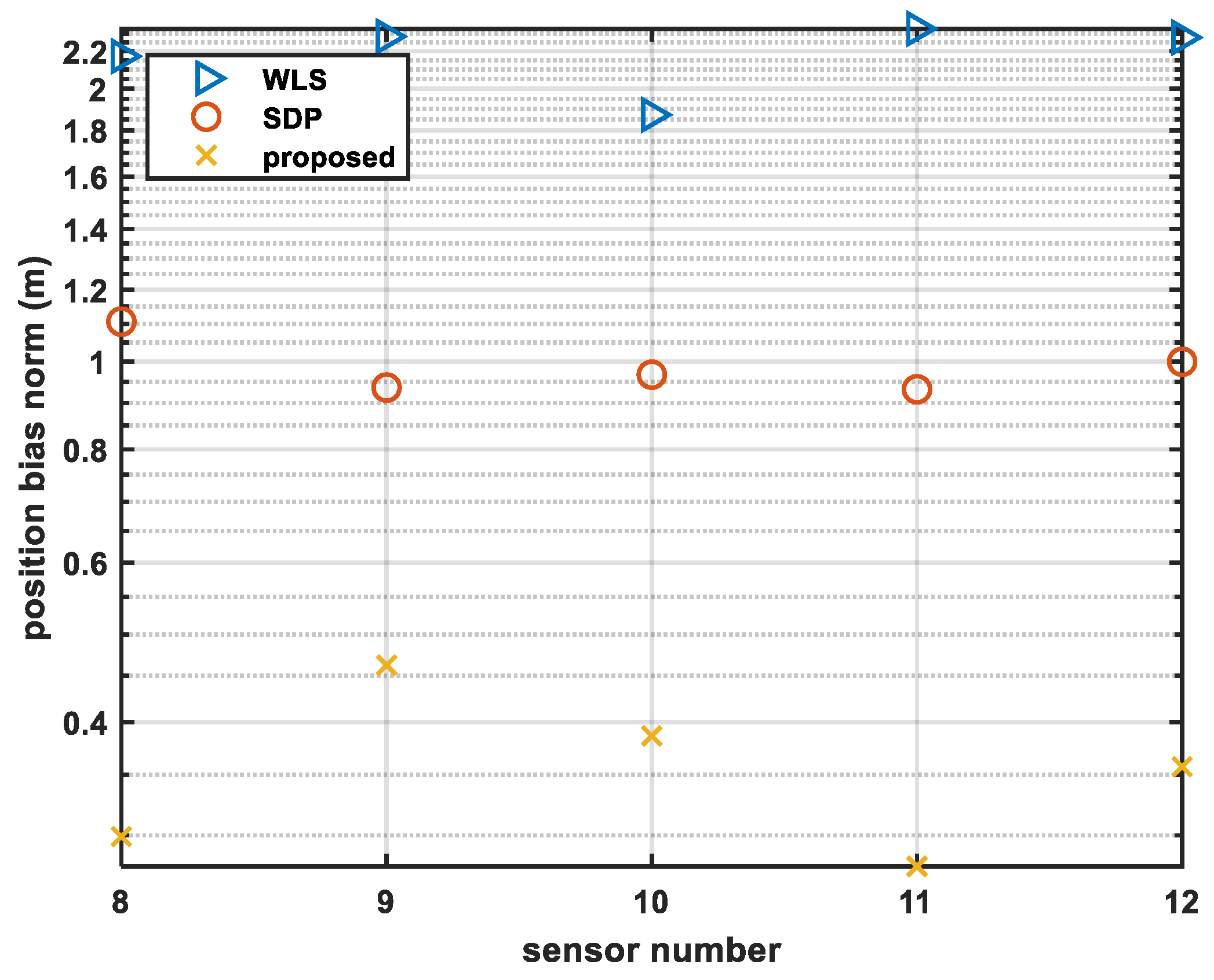
4.1.2. Simulation 2—Analysis under Different Sensor Numbers
4.1.3. Simulation 3—Analysis of the Algorithms’ Computational Efficiency
4.2. Field Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Amiri, R.; Behnia, F.; Noroozi, A. Efficient Joint Moving Target and Antenna Localization in Distributed MIMO Radars. IEEE Trans. Wirel. Commun. 2019, 18, 4425–4435. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Cheng, N.; Hao, B.; Shi, J.; Zhang, R.; Shen, X. Multiobjective Optimization Based Sensor Selection for TDOA Tracking in Wireless Sensor Network. IEEE Trans. Veh. Technol. 2019, 68, 12360–12374. [Google Scholar] [CrossRef]
- Jin, B.; Xu, X.; Zhu, Y.; Zhang, T.; Fei, Q. Single-Source Aided Semi-Autonomous Passive Location for Correcting the Position of an Underwater Vehicle. IEEE Sens. J. 2019, 19, 3267–3275. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, X.; Zheng, C.; Fu, J.; Zhao, C. Underwater Acoustical Localization of the Black Box Utilizing Single Autonomous Underwater Vehicle Based on the Second-Order Time Difference of Arrival. IEEE J. Ocean Eng. 2020, 45, 1268–1279. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Liu, Z.X.; Wang, R.; Zhao, Y.J.; Liu, Z.; Wang, R.; Zhao, Y. A Bias Compensation Method for Distributed Moving Source Localization Using TDOA and FDOA with Sensor Location Errors. Sensors 2018, 18, 3747. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, T.; Shin, H.-S. An Efficient Constrained Weighted Least Squares Method with Bias Reduction for TDOA-Based Localization. IEEE Sens. J. 2021, 21, 10122–10131. [Google Scholar] [CrossRef]
- Cong, L.; Zhuang, W. Hybrid TDOA/AOA mobile user location for wideband CDMA cellular systems. IEEE Trans. Wirel. Commun. 2002, 1, 439–447. [Google Scholar] [CrossRef]
- Yu, H.; Huang, G.; Gao, J.; Liu, B. An Efficient Constrained Weighted Least Squares Algorithm for Moving Source Location Using TDOA and FDOA Measurements. IEEE Trans. Wirel. Commun. 2012, 11, 44–47. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, X.; Wang, Z. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Wen, F.; Liu, P.; Wei, H.; Zhang, Y.; Qiu, R.C. Joint Azimuth, Elevation, and Delay Estimation for 3-D Indoor Localization. IEEE Trans. Veh. Technol. 2018, 67, 4248–4261. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wirel. Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Doğançay, K. Bearings-only target localization using total least squares. Signal Process 2005, 85, 1695–1710. [Google Scholar] [CrossRef]
- Zou, J.; Sun, Y.; Wan, Q. A Novel 3-D Localization Scheme Using 1-D Angle Measurements. IEEE Sens. Lett. 2020, 4, 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. An Asymptotically Efficient Estimator in Closed-Form for 3-D AOA Localization Using a Sensor Network. IEEE Trans. Wirel. Commun. 2015, 14, 6524–6535. [Google Scholar] [CrossRef]
- Amiri, R.; Behnia, F.; Zamani, H. Efficient 3-D Positioning Using Time-Delay and AOA Measurements in MIMO Radar Systems. IEEE Commun. Lett. 2017, 21, 2614–2617. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Ho, C. Semidefinite relaxation method for unified near-Field and far-Field localization by AOA. Signal Process. 2021, 181, 107916. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, T.; Tong, J.; Weng, C.; Li, Y. A calibration method of ultra-short baseline installation error with large misalignment based on variational Bayesian unscented Kalman filter. Rev. Sci. Instrum. 2019, 90, 055003. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Jin, B.; Zhu, Y.; Tong, J. Student’s t-Based Robust Kalman Filter for a SINS/USBL Integration Navigation Strategy. IEEE Sens. J. 2020, 20, 5540–5553. [Google Scholar] [CrossRef]
- Wang, G.; Li, Y.; Ansari, N. A Semidefinite Relaxation Method for Source Localization Using TDOA and FDOA Measurements. IEEE Trans. Veh. Technol. 2013, 62, 853–862. [Google Scholar] [CrossRef]
- Zheng, C. Application of USBL Positioning Technology on Underwater Submersible Interfacing. Ph.D. Dissertation, Harbin Engineering University, Harbin, China, 2007. [Google Scholar]
- Zhang, L.; Zhang, T.; Wei, H. A Novel Robust Inertial and Ultra-Short Baseline Integrated Navigation Strategy Under the Influence of Motion Effect. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19323–19334. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, L.; Shin, H.-S. A Novel and Robust Calibration Method for the Underwater Transponder Position. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]







| Algorithm | WLS (s) | SDP (s) | Proposed (s) |
|---|---|---|---|
| Running Time | 0.02 | 3.97 | 3.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Liu, Y.; Yan, T.; Yang, S.; Li, R. An Underwater Source Localization Method Using Bearing Measurements. Sensors 2024, 24, 1627. https://doi.org/10.3390/s24051627
Li P, Liu Y, Yan T, Yang S, Li R. An Underwater Source Localization Method Using Bearing Measurements. Sensors. 2024; 24(5):1627. https://doi.org/10.3390/s24051627
Chicago/Turabian StyleLi, Peijuan, Yiting Liu, Tingwu Yan, Shutao Yang, and Rui Li. 2024. "An Underwater Source Localization Method Using Bearing Measurements" Sensors 24, no. 5: 1627. https://doi.org/10.3390/s24051627
APA StyleLi, P., Liu, Y., Yan, T., Yang, S., & Li, R. (2024). An Underwater Source Localization Method Using Bearing Measurements. Sensors, 24(5), 1627. https://doi.org/10.3390/s24051627





