Ultra-High Sensitivity Methane Gas Sensor Based on Cryptophane-A Thin Film Depositing in Double D-Shaped Photonic Crystal Fiber Using the Vernier Effect
Abstract
1. Introduction
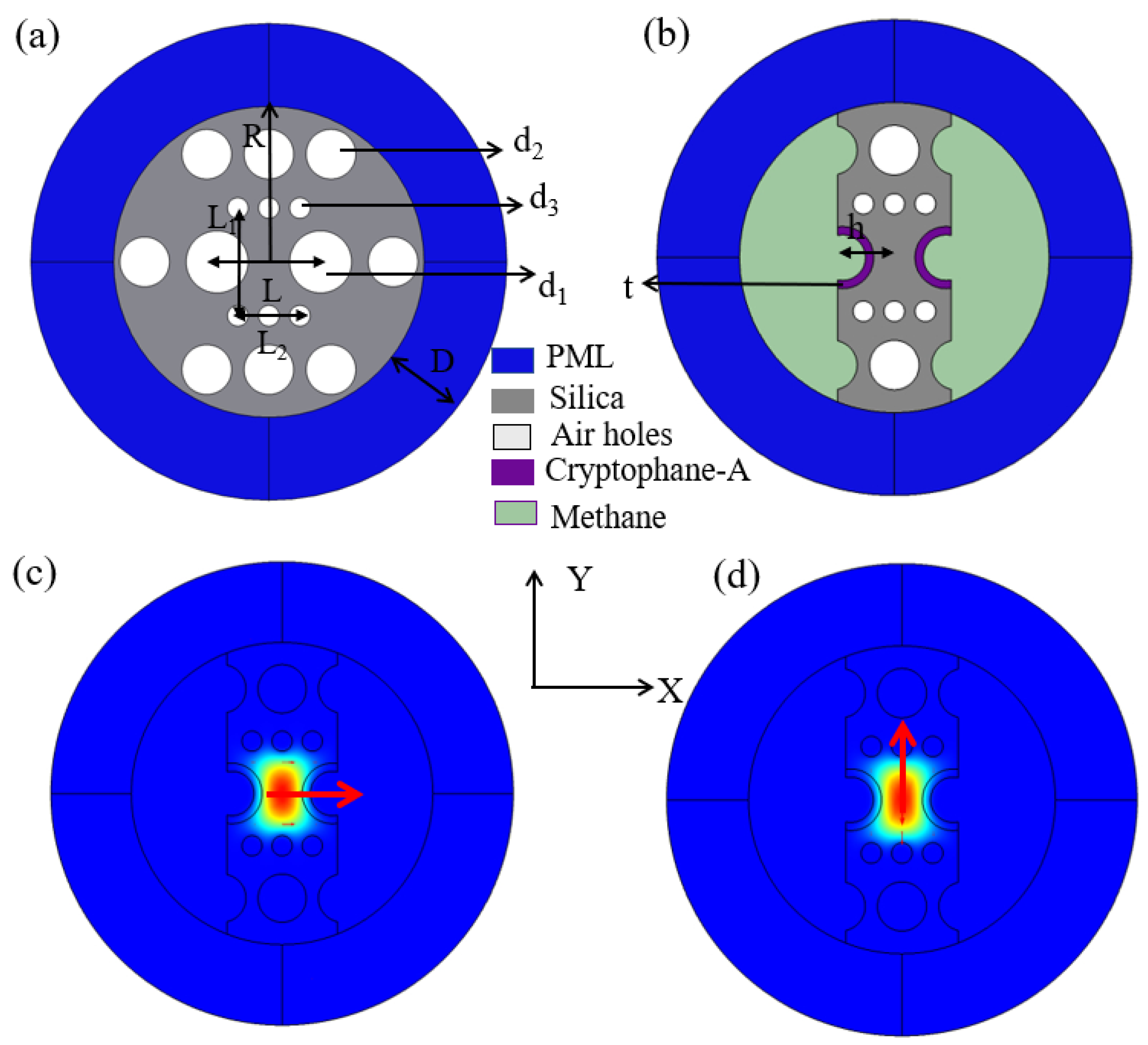
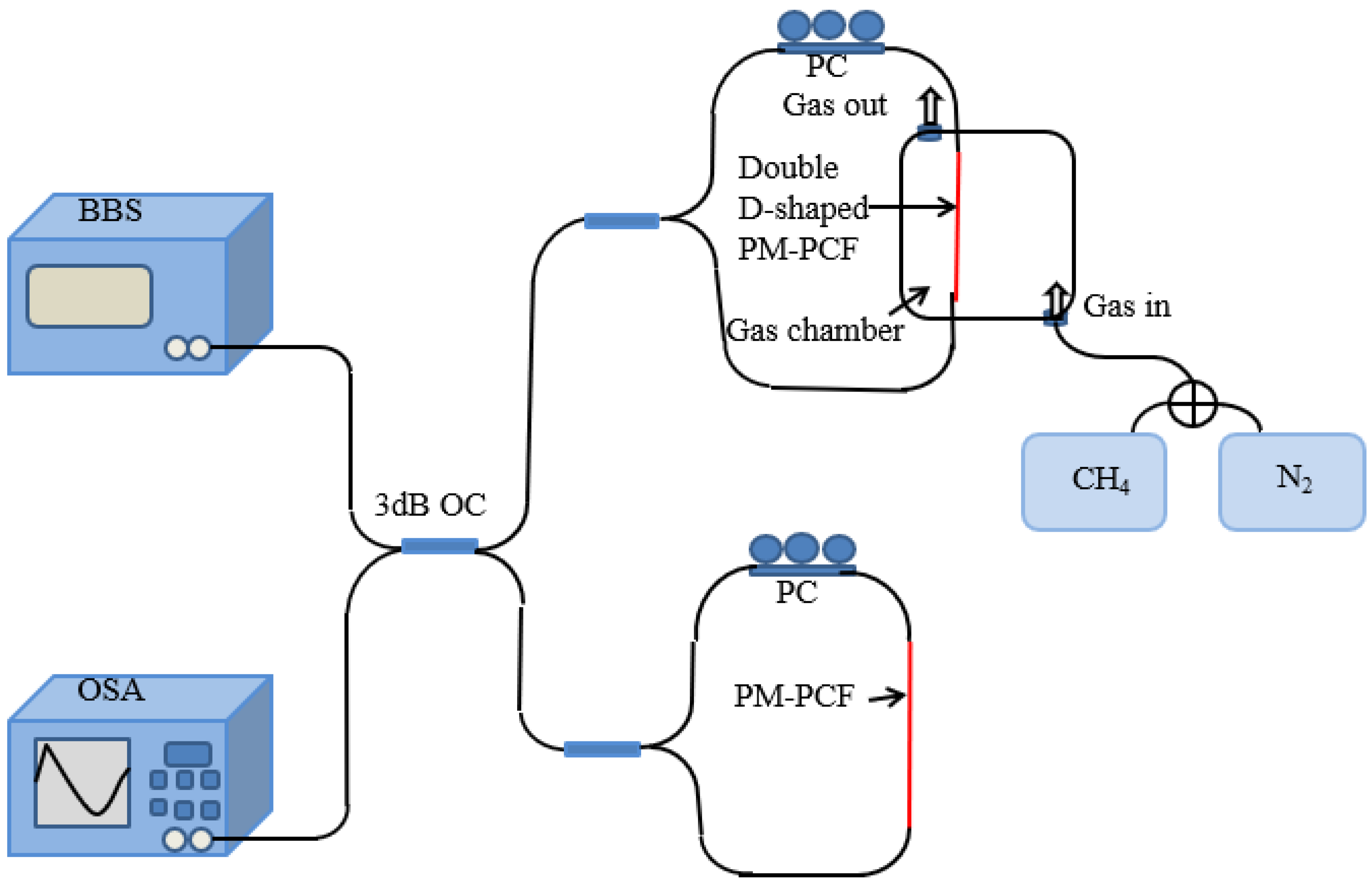
2. PCF Design and Numerical Analysis Methods
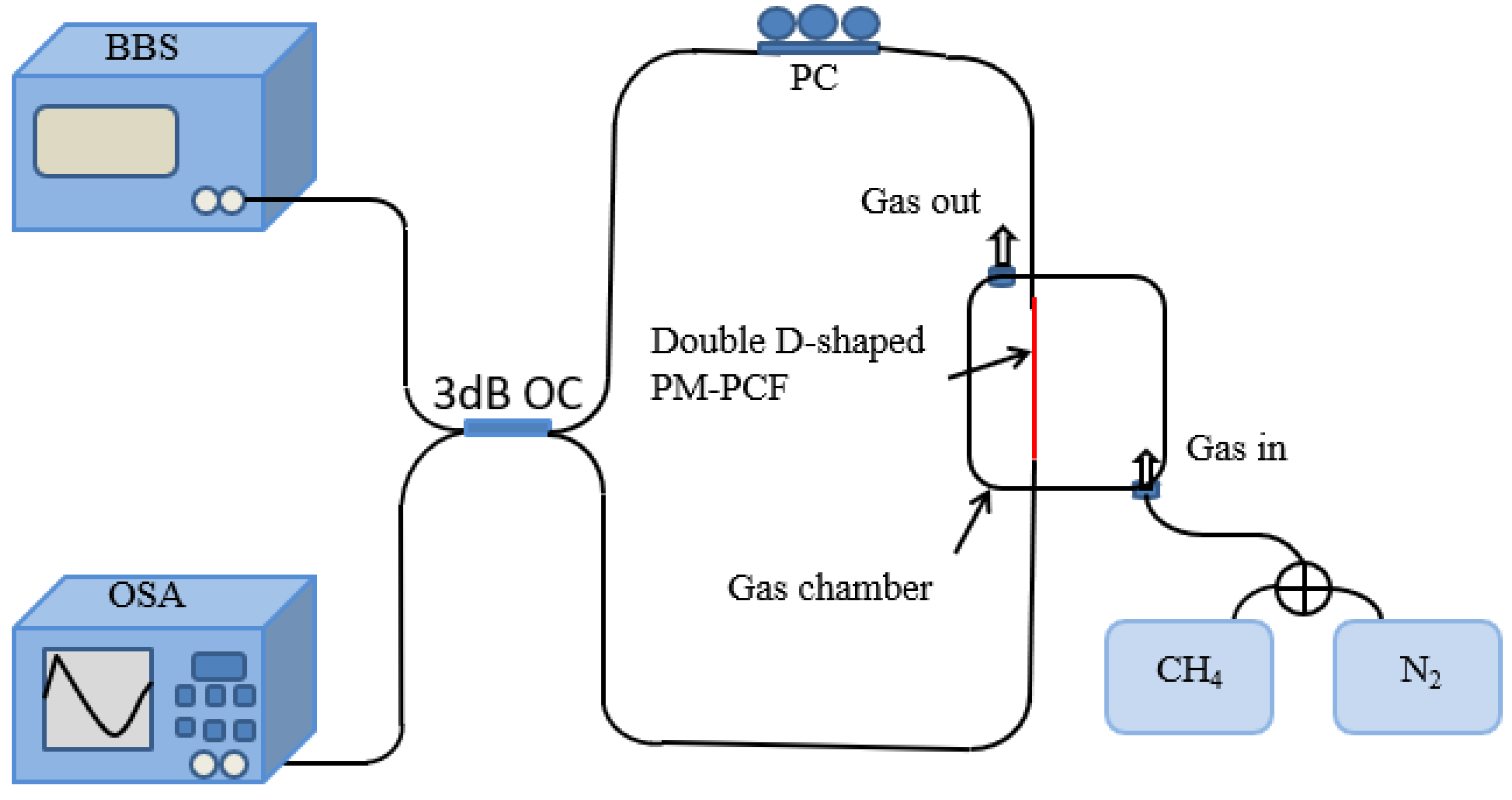
3. Discussion on Sensing Principles and Results
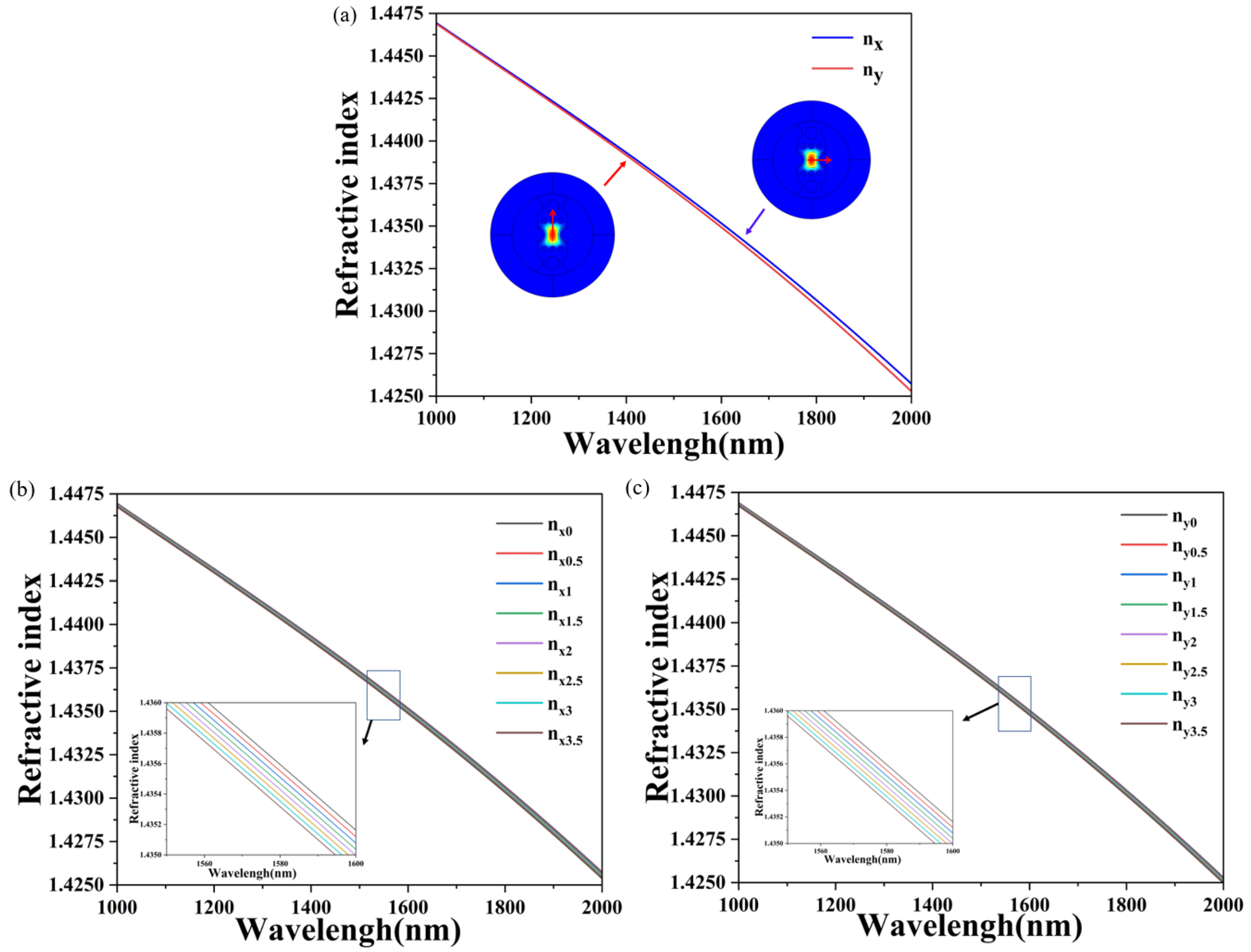
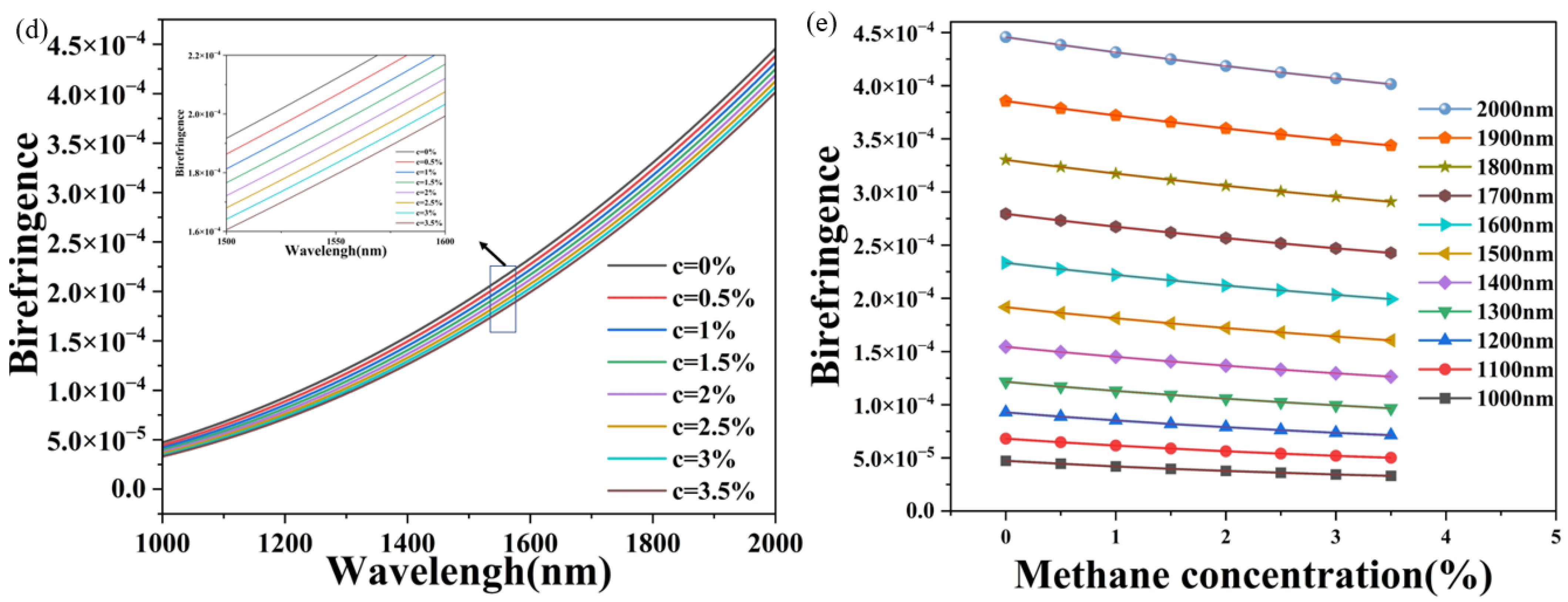
3.1. Single Sagnac Interferometer
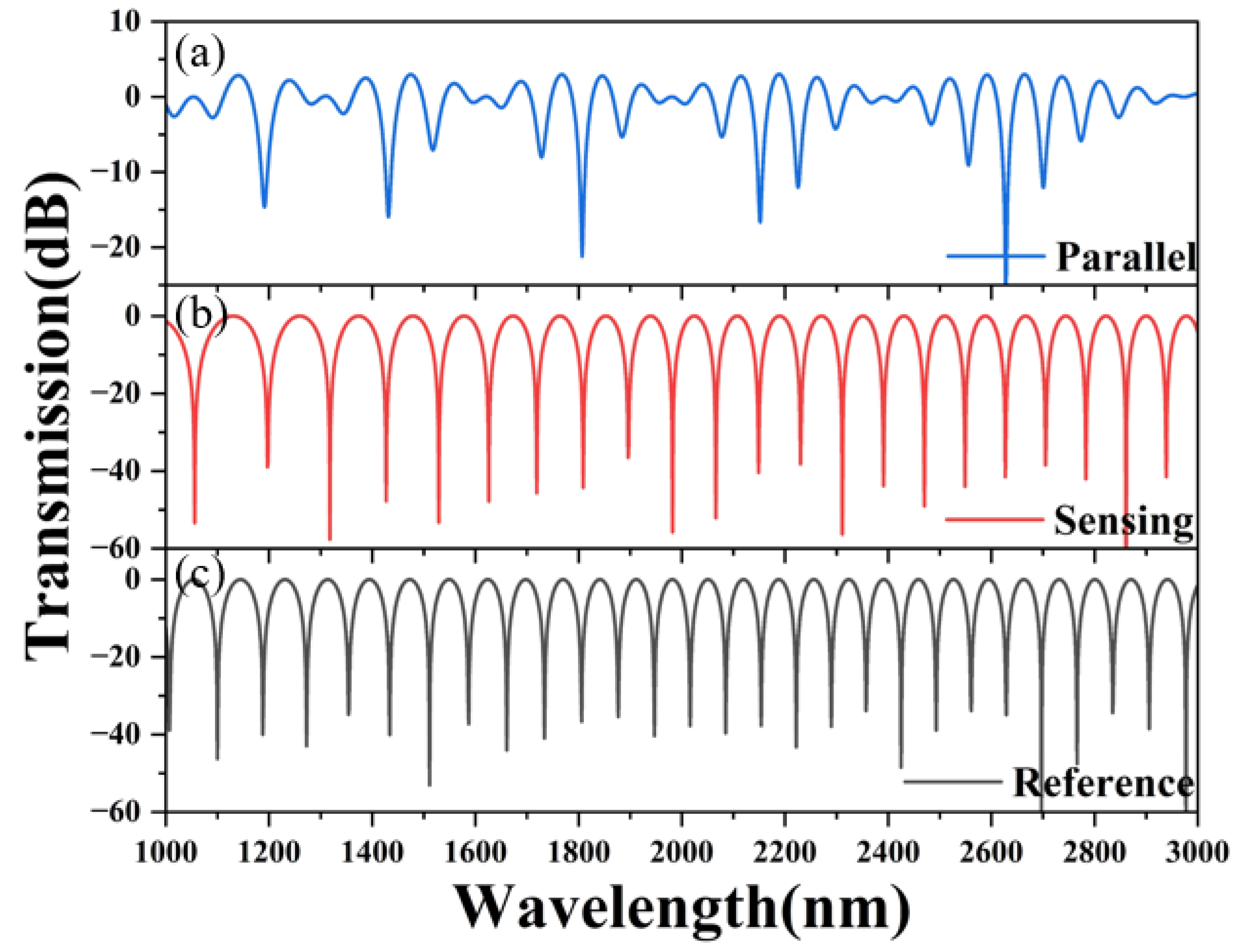
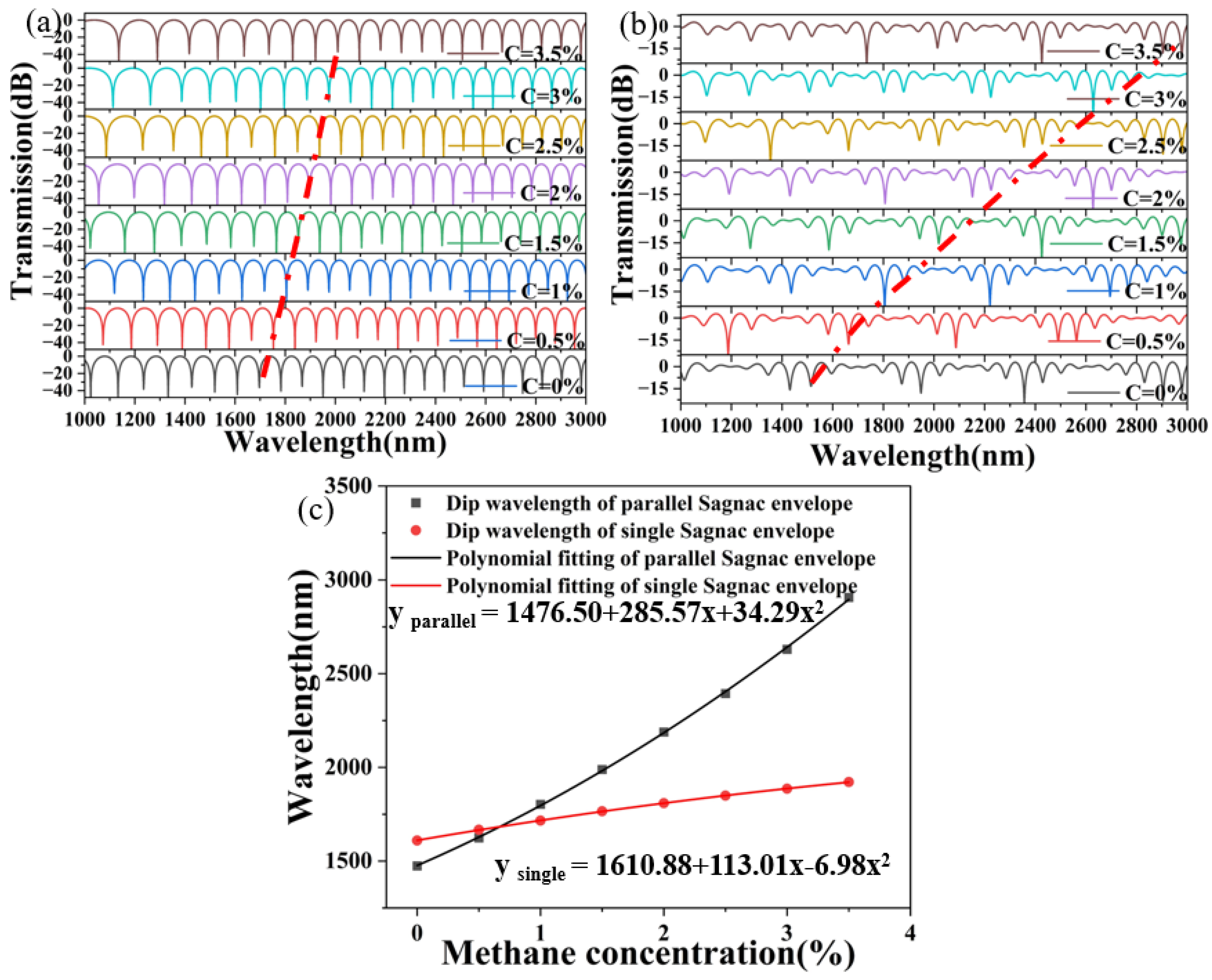
3.2. Two Parallel Sagnac Interferometers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, D.; Qiao, X.; Rong, Q.; Shao, Z. Wavelength switchable fiber-optic Sagnac filter. Opt. Fiber Technol. 2018, 41, 222–226. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Tong, Z.; Wang, X.; Tao, Y.; Yu, H.; Mu, J. Balloon-Shaped SMF Blood Glucose Concentration and Temperature Sensor Based on Core-Offset Structure. Sensors 2024, 24, 6344. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Li, S.; Chen, Q.; Yin, Z. An ultrasensitive twist sensor based on parallel dual HMSF-SIs with Vernier effect. Optik 2023, 286, 171012. [Google Scholar] [CrossRef]
- Wang, X.-Z.; Wang, Q. A high-birefringence microfiber Sagnac-interferometer biosensor based on the Vernier effect. Sensors 2018, 18, 4114. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Lechtenböhmer, S.; Assonov, S.S.; Brenninkmeijer, C.A.; Dienst, C.; Fischedick, M.; Hanke, T. Low methane leakage from gas pipelines. Nature 2005, 434, 841–842. [Google Scholar] [CrossRef] [PubMed]
- Comert, B.; Akin, N.; Donmez, M.; Saglam, S.; Ozcelik, S. Titanium dioxide thin films as methane gas sensors. IEEE Sens. J. 2016, 16, 8890–8896. [Google Scholar] [CrossRef]
- Ghanbari, R.; Safaiee, R.; Sheikhi, M.H.; Golshan, M.M.; Horastani, Z.K. Graphene decorated with silver nanoparticles as a low-temperature methane gas sensor. ACS Appl. Mater. Interfaces 2019, 11, 21795–21806. [Google Scholar] [CrossRef]
- Liu, H.; Wang, M.; Wang, Q.; Li, H.; Ding, Y.; Zhu, C. Simultaneous measurement of hydrogen and methane based on PCF-SPR structure with compound film-coated side-holes. Opt. Fiber Technol. 2018, 45, 1–7. [Google Scholar] [CrossRef]
- Chen, X.; Huang, Z.; Li, J.; Wu, C.; Wang, Z.; Cui, Y. Methane gas sensing behavior of lithium ion doped carbon nanotubes sensor. Vacuum 2018, 154, 120–128. [Google Scholar] [CrossRef]
- Liu, D.; Fu, S.; Tang, M.; Shum, P.; Liu, D. Comb Filter-Based Fiber-Optic Methane Sensor System With Mitigation of Cross Gas Sensitivity. J. Light. Technol. 2012, 30, 3103–3109. [Google Scholar] [CrossRef]
- Hoo, Y.L.; Liu, S.; Ho, H.L.; Jin, W. Fast Response Microstructured Optical Fiber Methane Sensor With Multiple Side-Openings. IEEE Photonics Technol. Lett. 2010, 22, 296–298. [Google Scholar] [CrossRef]
- Iseki, T.; Tai, H.; Kimura, K. A portable remote methane sensor using a tunable diode laser. Meas. Sci. Technol. 2000, 11, 594–602. [Google Scholar] [CrossRef]
- Massie, C.; Stewart, G.; McGregor, G.; Gilchrist, J.R. Design of a portable optical sensor for methane gas detection. Sens. Actuators B Chem. 2006, 113, 830–836. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, L.; Che, X.; Huang, J.; Li, X.; Chen, W. Photonic crystal fiber methane sensor based on modal interference with an ultraviolet curable fluoro-siloxane nano-film incorporating cryptophane A. Sens. Actuators B Chem. 2016, 235, 717–722. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Chen, C.; Bai, B.; Shao, Q.; Wang, H.; Zhang, W.; Chen, C.; Tang, S. Transverse-Stress Compensated Methane Sensor Based on Long-Period Grating in Photonic Crystal Fiber. IEEE Access 2019, 7, 175522–175530. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, L.; Huang, J.; Tao, C.; Li, X.; Chen, W. Sensitivity enhancing of transition mode long-period fiber grating as methane sensor using high refractive index polycarbonate/cryptophane A overlay deposition. Sens. Actuators B Chem. 2015, 207, 477–480. [Google Scholar] [CrossRef]
- Liu, H.; Wu, B.; Zhang, X.; Zhao, B.; Zhang, H.; Tang, S. A highly sensitive sensor of methane and hydrogen in tellurite photonic crystal fiber based on four-wave mixing. Opt. Quantum Electron. 2022, 54, 215. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, C.; Chen, H.; Wang, Y.; Sun, S.; Zhang, H.; Wang, P.; Huang, A.H. Highly sensitive gas pressure sensor based on the enhanced Vernier effect through a cascaded Fabry-Perot and Mach-Zehnder interferometer. Opt. Express 2022, 30, 34956–34972. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Zhang, Y.-n.; Zhao, Y. Fiber-optic sensors based on Vernier effect. Measurement 2021, 167, 108451. [Google Scholar] [CrossRef]
- Li, J.; Li, S.; Chen, H.; Yin, Z.; Shao, P.; Li, K.; Gao, T. High sensitivity twist sensor based on Sagnac interference with a helical elliptical core fiber. IEEE Sens. J. 2024, 24, 14335–14342. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Fan, X.; Li, H.; Li, L.; Shi, R.; Gu, M.; Li, S. Ultra-sensitive fiber optic sensor for glucose concentration measurement based on Vernier effect in cascaded Mach–Zehnder interferometers. J. Phys. D Appl. Phys. 2024, 57, 245109. [Google Scholar] [CrossRef]
- Lopez-Vargas, J.D.; Dante, A.; Allil, R.C.; Del Villar, I.; Matias, I.R.; Werneck, M.M. Ag@Fe3O4-coated U-shaped plastic optical fiber sensor for H2S detection. Sens. Actuators B Chem. 2024, 401, 135054. [Google Scholar] [CrossRef]
- Zhang, Y.-n.; Zhao, Y.; Wang, Q. Measurement of methane concentration with cryptophane E infiltrated photonic crystal microcavity. Sens. Actuators B Chem. 2015, 209, 431–437. [Google Scholar] [CrossRef]
- Wei, W.; Nong, J.; Zhang, G.; Tang, L.; Jiang, X.; Chen, N.; Luo, S.; Lan, G.; Zhu, Y. Graphene-based long-period fiber grating surface plasmon resonance sensor for high-sensitivity gas sensing. Sensors 2016, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Che, X.; Shen, R.; Wang, C.; Li, X.; Chen, W. High-sensitivity photonic crystal fiber long-period grating methane sensor with cryptophane-A-6Me absorbed on a PAA-CNTs/PAH nanofilm. Opt. Express 2017, 25, 20258–20267. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, W.; Chen, C.; Tang, S.; Liu, H. A new methane sensor based on compound film-coated photonic crystal fiber and Sagnac interferometer with higher sensitivity. Results Phys. 2019, 15, 102817. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, J.; Sun, Y.; Liu, W.; Liu, C.; Lv, J.; Lv, T.; Jiang, Y.; Li, B.; Wang, F. High-sensitivity methane sensor composed of photonic quasi-crystal fiber based on surface plasmon resonance. JOSA A 2021, 38, 1438–1442. [Google Scholar] [CrossRef]
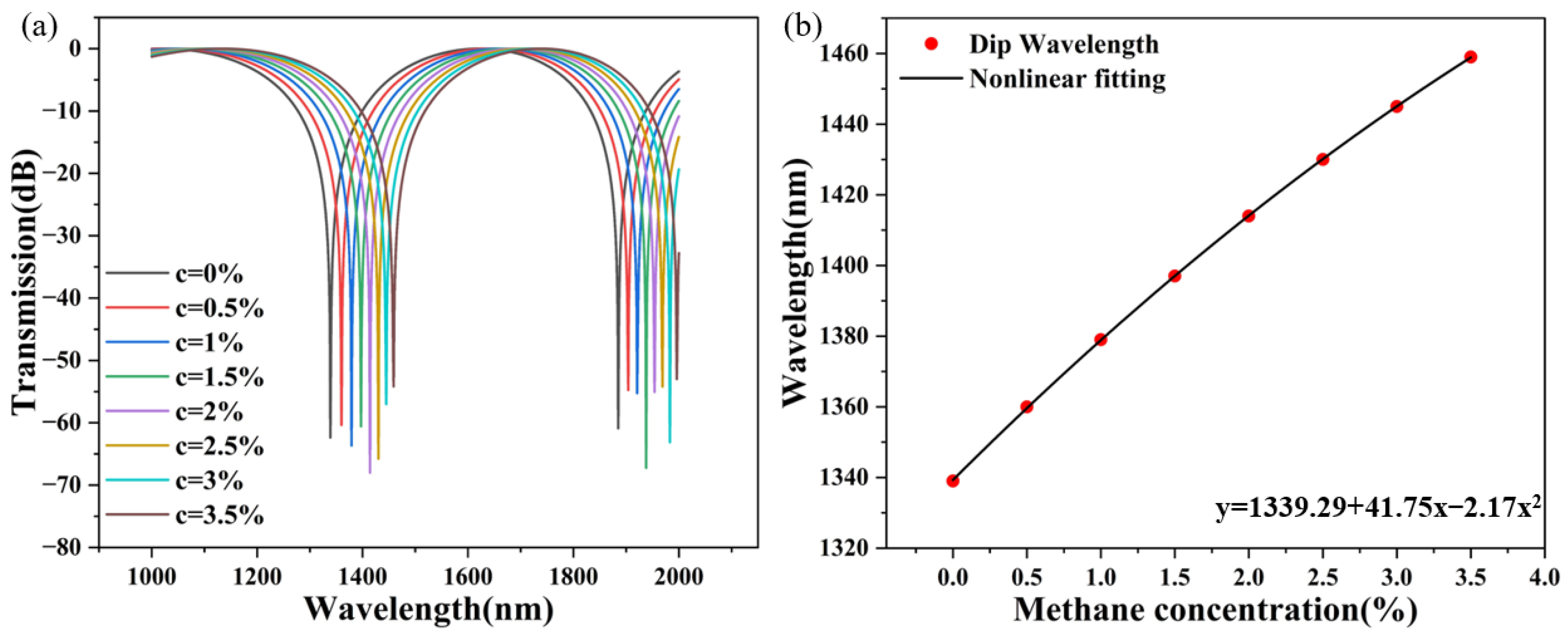


| y = a + b1 × x − b2 × x2 | |||||
|---|---|---|---|---|---|
| t | Parameters | ||||
| a | b1 | b2 | R2 | Average Sensitivities (nm/%) | |
| t = 500 nm | 1339.29 | 41.75 | 2.17 | 0.99998 | 34.28 |
| t = 600 nm | 1320.13 | 57.11 | 3.36 | 0.99999 | 45.42 |
| t = 700 nm | 1401.29 | 73.80 | 4.64 | 0.99996 | 57.71 |
| t = 800 nm | 1485.71 | 92.06 | 5.93 | 0.99995 | 71.71 |
| t = 900 nm | 1574.71 | 111.04 | 7.12 | 0.99995 | 86.57 |
| y = a + b1 × x − b2 × x2 | |||||
|---|---|---|---|---|---|
| h | Parameters | ||||
| a | b1 | b2 | R2 | Average Sensitivities (nm/%) | |
| h = 5 × 103 nm | 1574.71 | 111.04 | 7.12 | 0.99996 | 86.57 |
| h = 5.5 × 103 nm | 1613.79 | 113.25 | 7.17 | 0.99995 | 88.57 |
| h = 6 × 103 nm | 1638.92 | 114.29 | 7.24 | 0.99995 | 89.43 |
| y = a + b1 × x+ b2 × x2 | |||||
|---|---|---|---|---|---|
| Effective Lengths of PCF in the Reference SI Loop | Parameters | ||||
| a | b1 | b2 | R2 | Average Sensitivities (nm/%) | |
| 4 × 107 nm | 1476.50 | 285.57 | 34.29 | 0.99971 | 409.43 |
| 4.1 × 107 nm | 1384.54 | 283.04 | 16.98 | 0.99983 | 343.71 |
| 4.2 × 107 nm | 1295.08 | 282.71 | 5.52 | 0.99956 | 302.29 |
| Type of Sensor | Sensitivity | Method | Gas | Reference |
|---|---|---|---|---|
| PCF | 0.514 nm/% | Experiment with methane and nitrogen mixed gas | methane | [14] |
| PCF-LPFG | 2.5 nm/% | Experiment with methane and nitrogen mixed gas | methane | [16] |
| PC micro-cavity | 1.67 nm/% | Simulation | methane | [23] |
| LPFG-SPR | 0.344 nm/% | Experiment with methane and nitrogen mixed gas | methane | [24] |
| PCF-LPG | 1.078 nm/% | Experiment with methane and nitrogen mixed gas | methane | [25] |
| PCF | 36.64 nm/% | Simulation with methane and nitrogen mixed gas | methane | [26] |
| PCF-SPR | 1.99 nm/% | Simulation with methane and hydrogen mixed gas | methane | [8] |
| PQF-SPR | 8 nm/% | Simulation | methane | [27] |
| Tellurite-PCF | 2.052 nm/% | Simulation with methane and hydrogen mixed gas | methane | [17] |
| PCF-LPG incorporating cryptophane-A | 6:39 nm/% | Simulation with methane gas | methane | [15] |
| PCF | 409.43 nm/% | Simulation with methane and nitrogen mixed gas | methane | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Ullah, S.; Zhang, S.; Li, S. Ultra-High Sensitivity Methane Gas Sensor Based on Cryptophane-A Thin Film Depositing in Double D-Shaped Photonic Crystal Fiber Using the Vernier Effect. Sensors 2024, 24, 8132. https://doi.org/10.3390/s24248132
Zhou D, Ullah S, Zhang S, Li S. Ultra-High Sensitivity Methane Gas Sensor Based on Cryptophane-A Thin Film Depositing in Double D-Shaped Photonic Crystal Fiber Using the Vernier Effect. Sensors. 2024; 24(24):8132. https://doi.org/10.3390/s24248132
Chicago/Turabian StyleZhou, Di, Sajid Ullah, Sa Zhang, and Shuguang Li. 2024. "Ultra-High Sensitivity Methane Gas Sensor Based on Cryptophane-A Thin Film Depositing in Double D-Shaped Photonic Crystal Fiber Using the Vernier Effect" Sensors 24, no. 24: 8132. https://doi.org/10.3390/s24248132
APA StyleZhou, D., Ullah, S., Zhang, S., & Li, S. (2024). Ultra-High Sensitivity Methane Gas Sensor Based on Cryptophane-A Thin Film Depositing in Double D-Shaped Photonic Crystal Fiber Using the Vernier Effect. Sensors, 24(24), 8132. https://doi.org/10.3390/s24248132






