GeometryFormer: Semi-Convolutional Transformer Integrated with Geometric Perception for Depth Completion in Autonomous Driving Scenes
Abstract
1. Introduction
- To prevent the loss of local information on the grid line during tokenization and maintain local continuity, we propose semi-convolutional style vision transformer, which utilizes a convolution layer to calculate the self-attention matrices and add depth-wise convolution to the feed-forward module.
- For the accurate recovery of edges and details, we propose a geometric perception module that learns the distribution of geometric structures such as edges and planes by encoding the three-dimensional geometric features of sparse points and integrates them with transformer to improve network performance.
- We designed a better double-stage fusion of convolution and transformer than the previous single-stage method; our GTLC block is employed as the basic unit that constitutes the whole U-Net backbone. Our model achieves SoTA performance on public datasets and still has excellent performance even when the depth data are extremely sparse.
2. Related Research
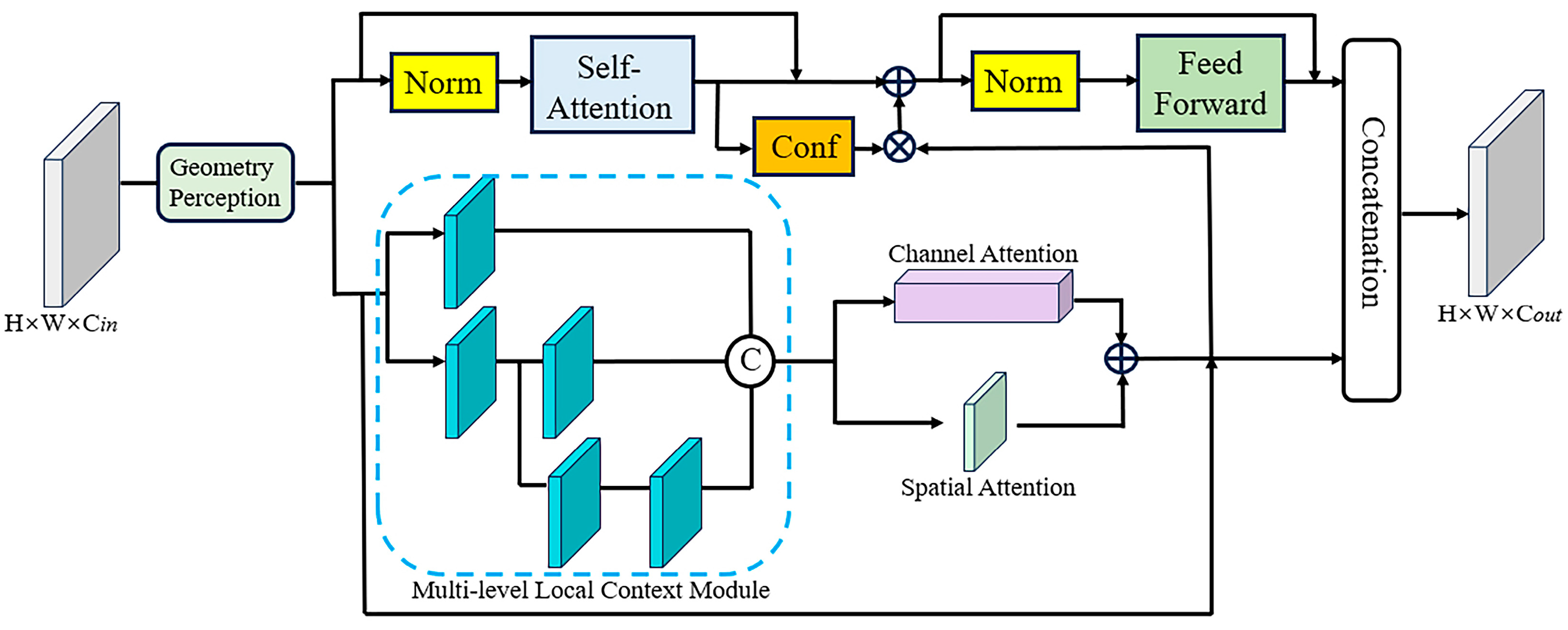
3. Method
3.1. Semi-Convolutional Transformer
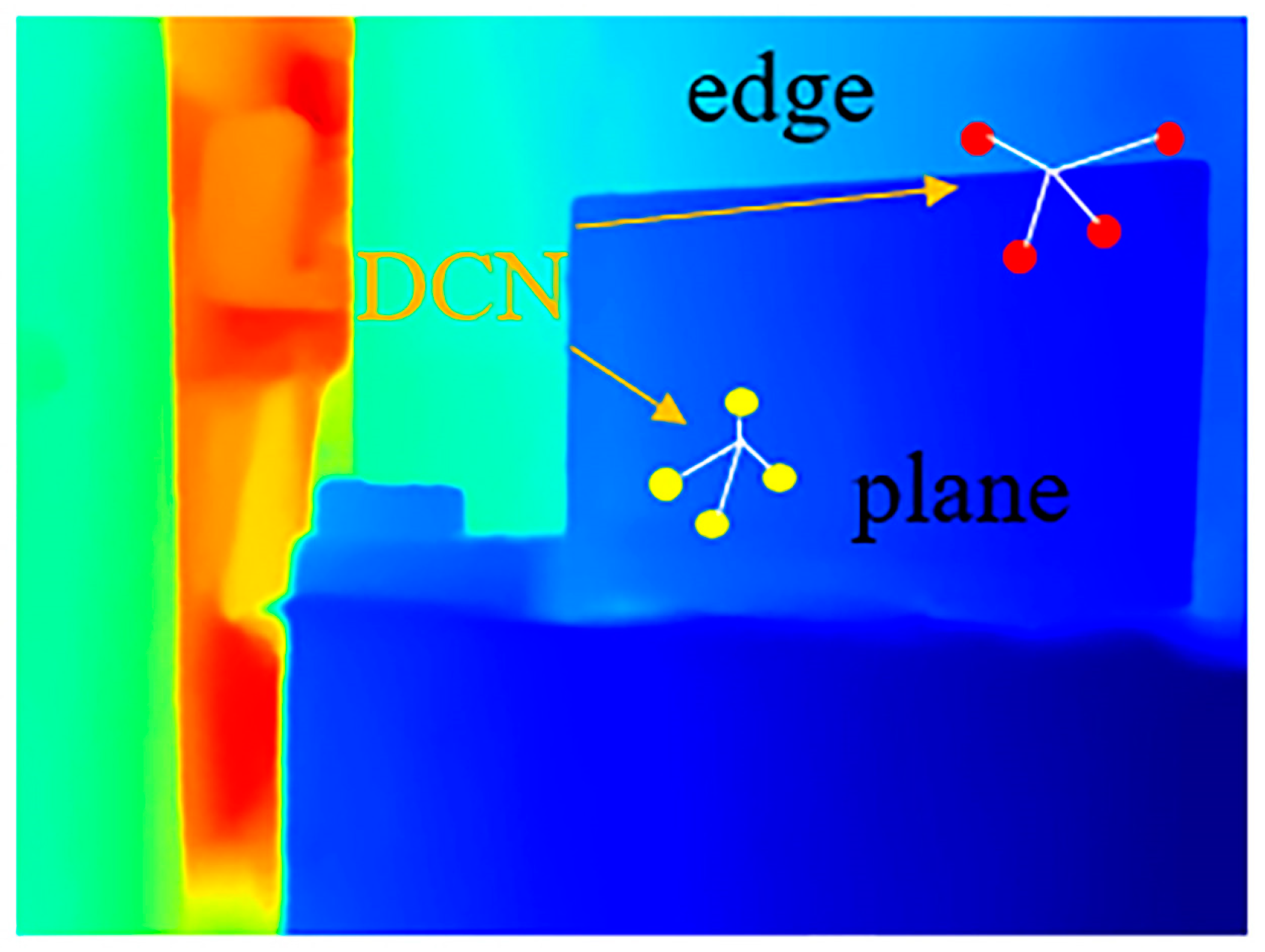
3.2. Geometric Perception Module
3.3. Multi-Level Local Context Module
3.4. Fusion Strategy of Transformer and Convolution
3.5. Encoder
3.6. Decoder
3.7. Depth Refinement and Loss Function
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Comparison with SoTA Methods
4.4. Ablation Studies and Analysis
4.5. Sparsity Level Analysis
5. Real Vehicle Test and Generalization Ability Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferstl, D.; Reinbacher, C.; Ranftl, R.; Rüther, M.; Bischof, H. Image guided depth upsampling using anisotropic total generalized variation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 993–1000. [Google Scholar]
- Herrera, C.D.; Kannala, J.; Ladický, L.; Heikkilä, J. Depth map inpainting under a second-order smoothness prior. In Image Analysis: 18th Scandinavian Conference, SCIA 2013, Espoo, Finland, 17–20 June 2013, Proceedings 18; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schneider, N.; Schneider, L.; Pinggera, P.; Franke, U.; Pollefeys, M.; Stiller, C. Semantically guided depth upsampling. In Pattern Recognition: 38th German Conference, GCPR 2016, Hannover, Germany, 12–15 September 2016, Proceedings 38; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ma, F.; Cavalheiro, G.V.; Karaman, S. Self-supervised sparse-to-dense: Self-supervised depth completion from lidar and monocular camera. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), IEEE, Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Yan, Z.; Wang, K.; Li, X.; Zhang, Z.; Li, J.; Yang, J. RigNet: Repetitive image guided network for depth completion. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Hu, M.; Wang, S.; Li, B.; Ning, S.; Fan, L.; Gong, X. Penet: Towards precise and efficient image guided depth completion. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), IEEE, Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Liu, L.; Song, X.; Lyu, X.; Diao, J.; Wang, M.; Liu, Y.; Zhang, L. Fcfr-net: Feature fusion based coarse-to-fine residual learning for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35. [Google Scholar]
- Qiu, J.; Cui, Z.; Zhang, X.; Liu, S.; Zeng, B.; Pollefeys, M. Deeplidar: Deep surface normal guided depth prediction for outdoor scene from sparse lidar data and single color image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Xu, Y.; Zhu, X.; Shi, J.; Zhang, G.; Bao, H.; Li, H. Depth completion from sparse lidar data with depth-normal constraints. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Van Gansbeke, W.; Neven, D.; De Brabandere, B.; Van Gool, L. Sparse and noisy lidar completion with rgb guidance and uncertainty. In Proceedings of the 2019 16th International Conference on Machine Vision Applications (MVA), IEEE, Tokyo, Japan, 27–31 May 2019. [Google Scholar]
- Eldesokey, A.; Felsberg, M.; Khan, F.S. Confidence propagation through cnns for guided sparse depth regression. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2423–2436. [Google Scholar] [CrossRef]
- Zhao, S.; Gong, M.; Fu, H.; Tao, D. Adaptive context-aware multi-modal network for depth completion. IEEE Trans. Image Process. 2021, 30, 5264–5276. [Google Scholar] [CrossRef]
- Tang, J.; Tian, F.P.; Feng, W.; Li, J.; Tan, P. Learning guided convolutional network for depth completion. IEEE Trans. Image Process. 2020, 30, 1116–1129. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Huang, W.; Gu, S.; Xie, L.; Wang, Y.; Jiao, J.; Ye, Q. Conformer: Local features coupling global representations for visual recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Rho, K.; Ha, J.; Kim, Y. Guideformer: Transformers for image guided depth completion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Zhao, C.; Zhang, Y.; Poggi, M.; Tosi, F.; Guo, x.; Zhu, Z.; Huang, G.; Tang, Y.; Mattoccia, S. Monovit: Self-supervised monocular depth estimation with a vision transformer. In Proceedings of the 2022 International Conference on 3D Vision (3DV), Prague, Czech Republic, 12–16 September 2022. [Google Scholar]
- Dosovitskiy, A. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhang, Y.; Guo, X.; Poggi, M.; Zhu, Z. Completionformer: Depth completion with convolutions and vision transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Lin, X.; Yan, Z.; Deng, X.; Zheng, C.; Yu, L. ConvFormer: Plug-and-Play CNN-Style Transformers for Improving Medical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Woo, S.; Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Uhrig, J.; Schneider, N.; Schneider, L.; Franke, U.; Brox, T.; Geiger, A. Sparsity invariant cnns. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Liu, L.-K.; Stanley, H.C.; Truong, Q.N. Depth reconstruction from sparse samples: Representation, algorithm, and sampling. IEEE Trans. Image Process. 2015, 24, 1983–1996. [Google Scholar] [CrossRef] [PubMed]
- Ku, J.; Harakeh, A.; Waslander, S.L. In defense of classical image processing: Fast depth completion on the cpu. In Proceedings of the 2018 15th Conference on Computer and Robot Vision (CRV), Toronto, ON, Canada, 9–11 May 2018. [Google Scholar]
- Eldesokey, A.; Felsberg, M.; Khan, F.S. Propagating confidences through cnns for sparse data regression. arXiv 2018, arXiv:1805.11913. [Google Scholar]
- Chodosh, N.; Wang, C.; Lucey, S. Deep convolutional compressed sensing for lidar depth completion. In Proceedings of the Computer Vision–ACCV 2018: 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Revised Selected Papers; Part I 14. Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Dong, X.; Bao, J.; Chen, D.; Zhang, W.; Yu, N.; Yuan, L.; Chen, D.; Guo, B. Cswin transformer: A general vision transformer backbone with cross-shaped windows. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Ramachandran, P.; Parmar, N.; Vaswani, A.; Bello, I. Stand-alone self-attention in vision models. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pvt v2: Improved baselines with pyramid vision transformer. Comput. Vis. Media 2022, 8, 415–424. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Ranftl, R.; Bochkovskiy, A.; Koltun, V. Vision transformers for dense prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Guo, J.; Han, K.; Wu, H.; Tang, Y.; Chen, X.; Wang, Y.; Xu, C. Cmt: Convolutional neural networks meet vision transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Lee, Y.; Kim, J.; Willette, J.; Hwang, S.J. Mpvit: Multi-path vision transformer for dense prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Su, S.; Wu, J.; Yan, H.; Liu, H. AF 2 R Net: Adaptive Feature Fusion and Robust Network for Efficient and Precise Depth Completion. IEEE Access 2023, 11, 111347–111357. [Google Scholar] [CrossRef]
- Liu, R.; Lehman, J.; Molino, P.; Petroski Such, F.; Frank, E.; Sergeev, A.; Yosinski, J. An intriguing failing of convolutional neural networks and the coordconv solution. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Najibi, M.; Samangouei, P.; Chellappa, R.; Davis, L.S. Ssh: Single stage headless face detector. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016, Proceedings, Part IV 14; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Xu, Z.; Yin, H.; Yao, J. Deformable spatial propagation networks for depth completion. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 913–917. [Google Scholar]
- Lin, Y.; Cheng, T.; Zhong, Q.; Zhou, W.; Yang, H. Dynamic spatial propagation network for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36. [Google Scholar]
- Park, J.; Joo, K.; Hu, Z.; Liu, C.K.; So Kweon, I. Non-local spatial propagation network for depth completion. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020, Proceedings, Part XIII 16; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Cheng, X.; Wang, P.; Yang, R. Depth estimation via affinity learned with convolutional spatial propagation network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Cheng, X.; Wang, P.; Guan, C.; Yang, R. Cspn++: Learning context and resource aware convolutional spatial propagation networks for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34. [Google Scholar]
- Liu, X.; Shao, X.; Wang, B.; Li, Y.; Wang, S. Graphcspn: Geometry-aware depth completion via dynamic gcns. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012, Proceedings, Part V 12; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rahman, M. Beginning Microsoft Kinect for Windows SDK 2.0: Motion and Depth Sensing for Natural User Interfaces; Springer Nature: Cham, Switzerland, 2017. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, L.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Imran, S.; Liu, X.; Morris, D. Depth completion with twin surface extrapolation at occlusion boundaries. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Lee, B.U.; Lee, K.; Kweon, I.S. Depth completion using plane-residual representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Wang, Y.; Mao, Y.; Liu, Q.; Dai, Y. Decomposed Guided Dynamic Filters for Efficient RGB-Guided Depth Completion. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 1186–1198. [Google Scholar] [CrossRef]
- Li, X.; He, R.; Wu, J.; Yan, H.; Chen, X. LEES-Net: Fast, lightweight unsupervised curve estimation network for low-light image enhancement and exposure suppression. Displays 2023, 80, 102550. [Google Scholar] [CrossRef]











| Scales | Layers | Params (M) | FLOPs (G) |
|---|---|---|---|
| Tiny | [2, 2, 2, 2] | 56.8 | 334.0 |
| Small | [2, 3, 3, 4] | 94.1 | 354.3 |
| Base | [3, 3, 4, 6] | 130.5 | 374.7 |
| Method | KITTI DC | NYUv2 | Reference | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | MAE (mm) | iRMSE (1/km) | iMAE (1/km) | RMSE (m) | REL | ||
| ACMNet [12] | 732.99 | 206.80 | 2.08 | 0.90 | 0.105 | 0.015 | TIP2021 |
| GuideNet [13] | 736.24 | 218.83 | 2.25 | 0.99 | 0.101 | 0.015 | TIP2021 |
| PENet [6] | 730.08 | 210.55 | 2.17 | 0.94 | - | - | ICRA2021 |
| TWISE [51] | 840.20 | 195.58 | 2.08 | 0.82 | 0.097 | 0.013 | CVPR2021 |
| PRNet [52] | 867.12 | 204.68 | 2.17 | 0.85 | 0.104 | 0.014 | CVPR2021 |
| RigNet [5] | 712.66 | 203.25 | 2.08 | 0.90 | 0.090 | 0.013 | ECCV2022 |
| GuideFormer [15] | 721.48 | 207.76 | 2.14 | 0.97 | - | - | CVPR2022 |
| DySPN [42] | 709.12 | 192.71 | 1.88 | 0.82 | 0.090 | 0.012 | AAAI2022 |
| Decomposition [53] | 707.93 | 205.11 | 2.01 | 0.91 | 0.098 | 0.014 | TCSVT2023 |
| CFormer [18] | 708.87 | 203.45 | 2.01 | 0.88 | 0.090 | 0.012 | CVPR2023 |
| Ours | 702.64 | 190.86 | 1.92 | 0.82 | 0.0879 | 0.0114 | - |
| GeometryFormer | RMSE (mm) | MAE (mm) | Params. (M) | FLOPs (G) | ||
|---|---|---|---|---|---|---|
| (1) | origin ViT | 88.9 | 34.6 | 125.8 | 370.4 | |
| (2) | w/semi-convolution | 88.1 | 34.3 | 130.5 | 374.7 | |
| Dilation Rates | Refinement Method | RMSE (mm) | MAE (mm) | Params. (M) | FLOPs (G) | |
| (3) | - | DySPN | 89.3 | 35.2 | 121.4 | 394.5 |
| (4) | - | GraphCSPN | 90.2 | 35.8 | 147.5 | 459.7 |
| (5) | {1} | NLSPN | 88.1 | 34.3 | 130.5 | 374.7 |
| (6) | {1, 2} | NLSPN | 88.0 | 34.3 | 130.5 | 379.4 |
| (7) | {1, 2, 3} | NLSPN | 87.9 | 34.1 | 130.5 | 384.2 |
| Backbone Type | Refinement Iterations | RMSE (mm) | MAE (mm) | Params. (M) | FLOPs (G) | |
| (8) | ConvFormer | 18 | 92.8 | 36.6 | 101.5 | 375.5 |
| (9) | PVTv2-Base | 18 | 91.2 | 35.4 | 126.7 | 446.8 |
| (10) | CFormer-Small | 18 | 90.1 | 35.2 | 82.6 | 439.1 |
| (11) | Ours-Small | 18 | 89.5 | 35.0 | 94.1 | 363.8 |
| (12) | CFormer-Tiny | 6 | 90.9 | 35.3 | 45.8 | 389.4 |
| (13) | CFormer-Small | 6 | 90.0 | 35.0 | 82.6 | 429.6 |
| (14) | CFormer-Base | 6 | 90.1 | 35.1 | 146.7 | 499.6 |
| (15) | Ours-Tiny | 6 | 90.2 | 35.0 | 56.8 | 334.0 |
| (16) | Ours-Small | 6 | 89.3 | 34.8 | 94.1 | 354.3 |
| (17) | Ours-Base | 6 | 88.1 | 34.3 | 130.5 | 374.7 |
| Geometric Perception | Fusion Strategy | Attention | Decoder | RMSE (mm) | MAE (mm) | |
|---|---|---|---|---|---|---|
| (18) | × | 1 | Cascade | Deconvolution | 89.4 | 34.8 |
| (19) | × | 1 | Cascade | Pixel-shuffle | 89.1 | 34.7 |
| (20) | × | 1 | Parallel | Pixel-shuffle | 88.8 | 34.6 |
| (21) | √ | 1 | Parallel | Pixel-shuffle | 88.4 | 34.4 |
| (22) | √ | 2 | Parallel | Pixel-shuffle | 88.1 | 34.3 |
| Method | RMSE (m) | |||||
|---|---|---|---|---|---|---|
| NLSPN | DySPN | CFormer | Ours-ViT | Ours | ||
| Sample Number | 0 | 0.562 | 0.521 | 0.490 | 0.482 | 0.480 |
| 50 | 0.223 | 0.203 | 0.208 | 0.201 | 0.198 | |
| 200 | 0.129 | 0.126 | 0.127 | 0.123 | 0.121 | |
| 500 | 0.092 | 0.090 | 0.090 | 0.0889 | 0.0879 | |
| Scanning Lines | Method | RMSE (mm) | MAE (mm) | iRMSE (1/km) | iMAE (1/km) |
|---|---|---|---|---|---|
| 1 | NLSPN | 3507.7 | 1849.1 | 13.8 | 8.9 |
| DySPN | 3625.5 | 1924.7 | 13.8 | 8.9 | |
| CFormer | 3250.2 | 1582.6 | 10.4 | 6.6 | |
| Ours-ViT | 3211.9 | 1574.6 | 10.4 | 6.5 | |
| Ours | 3189.4 | 1561.3 | 10.4 | 6.5 | |
| 4 | NLSPN | 2293.1 | 831.3 | 7.0 | 3.4 |
| DySPN | 2285.8 | 834.3 | 6.3 | 3.2 | |
| CFormer | 2150.0 | 740.1 | 5.4 | 2.6 | |
| Ours-ViT | 2117.6 | 736.1 | 5.4 | 2.5 | |
| Ours | 2098.8 | 733.6 | 5.3 | 2.5 | |
| 16 | NLSPN | 1288.9 | 377.2 | 3.4 | 1.4 |
| DySPN | 1274.8 | 366.4 | 3.2 | 1.3 | |
| CFormer | 1218.6 | 337.4 | 3.0 | 1.2 | |
| Ours-ViT | 1191.7 | 332.5 | 3.0 | 1.2 | |
| Ours | 1178.5 | 327.0 | 2.9 | 1.2 | |
| 64 | NLSPN | 889.4 | 238.8 | 2.6 | 1.0 |
| DySPN | 878.5 | 228.6 | 2.5 | 1.0 | |
| CFormer | 848.7 | 215.9 | 2.5 | 0.9 | |
| Ours-ViT | 827.3 | 210.4 | 2.4 | 0.9 | |
| Ours | 819.4 | 206.9 | 2.3 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, S.; Wu, J. GeometryFormer: Semi-Convolutional Transformer Integrated with Geometric Perception for Depth Completion in Autonomous Driving Scenes. Sensors 2024, 24, 8066. https://doi.org/10.3390/s24248066
Su S, Wu J. GeometryFormer: Semi-Convolutional Transformer Integrated with Geometric Perception for Depth Completion in Autonomous Driving Scenes. Sensors. 2024; 24(24):8066. https://doi.org/10.3390/s24248066
Chicago/Turabian StyleSu, Siyuan, and Jian Wu. 2024. "GeometryFormer: Semi-Convolutional Transformer Integrated with Geometric Perception for Depth Completion in Autonomous Driving Scenes" Sensors 24, no. 24: 8066. https://doi.org/10.3390/s24248066
APA StyleSu, S., & Wu, J. (2024). GeometryFormer: Semi-Convolutional Transformer Integrated with Geometric Perception for Depth Completion in Autonomous Driving Scenes. Sensors, 24(24), 8066. https://doi.org/10.3390/s24248066






