Network Dismantling on Signed Network by Evolutionary Deep Reinforcement Learning
Abstract
1. Introduction
2. Related Works
2.1. Network Dismantling Methods
2.2. Evolutionary Deep Reinforcement Learning Algorithms
3. Problem Formulation
3.1. Network Connectivity
3.2. Signed Networks
3.3. The Objective Function
4. Deep Reinforcement Learning
4.1. Network Embedding
4.2. Deep Q-Network
4.3. Markov Seed Selection
| Algorithm 1 MSS (Markov seed selection) Algorithm |
|
5. The DSEDR Algorithm
5.1. Evolution of DQN Populations
5.1.1. Solution Representation and Evaluation
5.1.2. Initialization Operations
| Algorithm 2 Initialization Algorithm |
|
5.1.3. Evolutionary Operations
| Algorithm 3 Evolution Algorithm |
|
5.2. Reinforcement Learning Operation
| Algorithm 4 DRL (deep reinforcement learning) Algorithm |
5.3. DSEDR Algorithm
5.4. Complexity Analysis
- MSS: The time complexity of MSS can be computed as , where is the number of nodes to be removed, is the average connectivity of nodes in the target network, d and l denote the number of neurons in the first and the second layers of the DQN, respectively.
- Initialization: The time complexity of Initialization can be computed as , where is the initial population size.
- EA: The time complexity of EA can be computed as .
- DRL: The time complexity of DRL can be computed as , where is the batch size in the DRL Algorithm.
| Algorithm 5 DSEDR Algorithm |
|
6. Experiments
6.1. Experimental Settings
6.1.1. Baseline Algorithm
- Degree: The degree of a node, i.e., the number of neighboring nodes directly connected to the node [35].
- Betweenness: Betweenness Centrality (BC) reflects how often a node appears on the shortest paths between pairs of other nodes. The BC of a node is defined as follows:where is the number of all shortest paths from node to , and is the number of shortest paths passing through among the shortest paths from node to [36].
- K-shell: K-shell centrality categorizes nodes based on their degrees to assess their importance in a network. Assuming there are no isolated nodes in the network, we eliminate nodes with one connection until no such nodes remain and assign them to the 1-shell. Similarly, we recursively eliminate nodes with degree 2 to form the 2-shell. This process ends when all nodes have been assigned to one of the shells [37].
- Closeness: Closeness Centrality reflects the distance between a node and all other nodes in the network and measures the average shortest path length from the node to all other nodes. A higher closeness value indicates a more central position within the network. It can be computed as follows:where is the length of the shortest path between node and node [38].
- Positive degree (P-DEG): The number of positive edges connected to the i-th node, denoted as .
- Negative degree (N-DEG): The number of negative edges connected to the i-th node, denoted as .
- Net degree (Net-DEG): This metric represents the difference between P-DEG and N-DEG:
- Ratio degree (Ratio-DEG): It indicates the proportion of positive edges connected to node relative to its total edges in the network, as follows:
- Prestige: Prestige is determined by both the positive and negative incoming links to a node [39]. The prestige of node i () is calculated as follows:
- PageRank: PageRank, which was inspired by Larry Page of Google, is among the most prevalent ranking algorithms in use today [40]. We can represent the PageRank score of node i as . This rank value is computed (in an iterative manner) as follows:where is a forgetting factor. N is the number of nodes in the network. represents the set of nodes that have edges pointing to node i, and represents the number of outgoing links from node j.
6.1.2. Parameter Setting
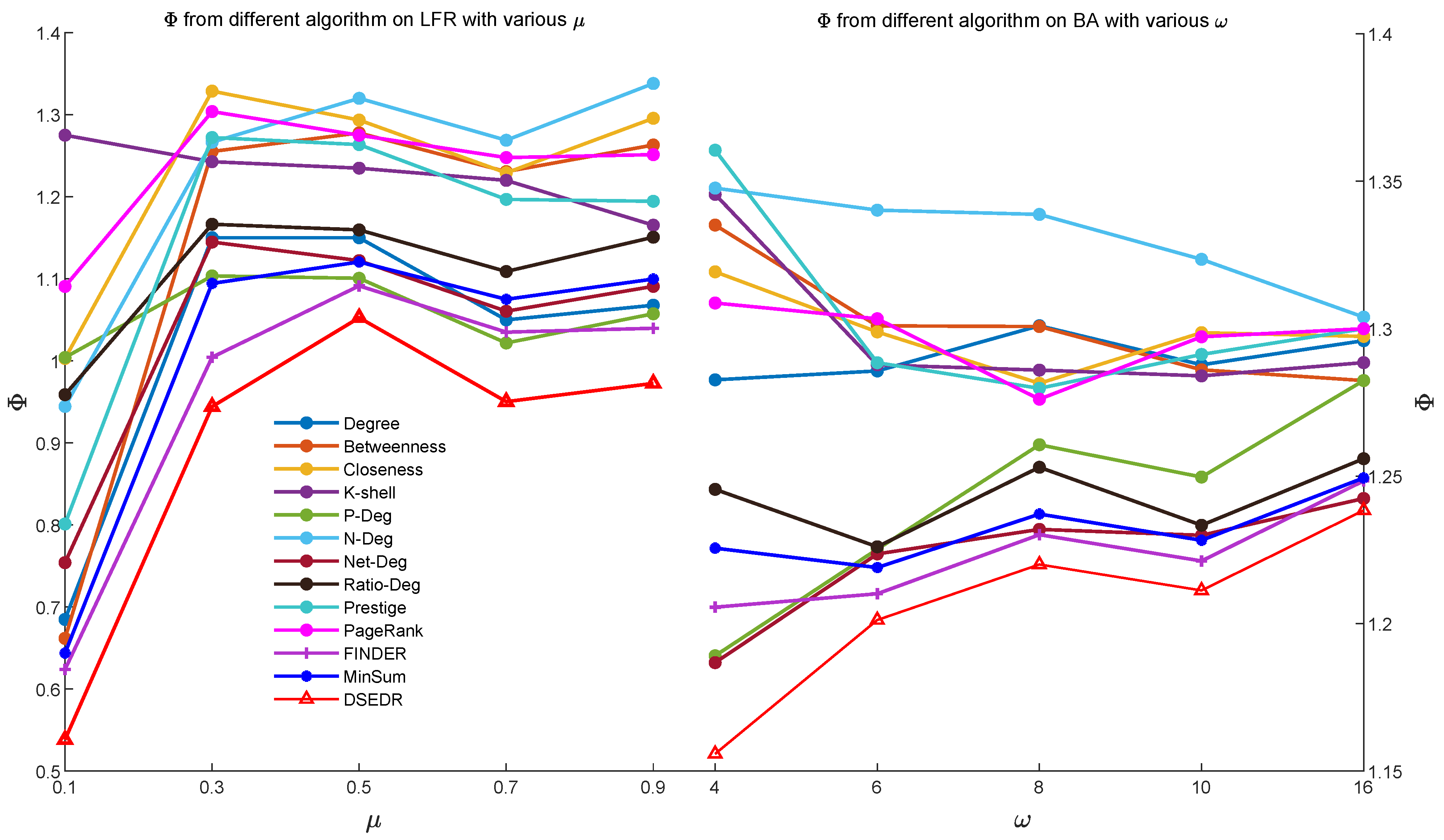
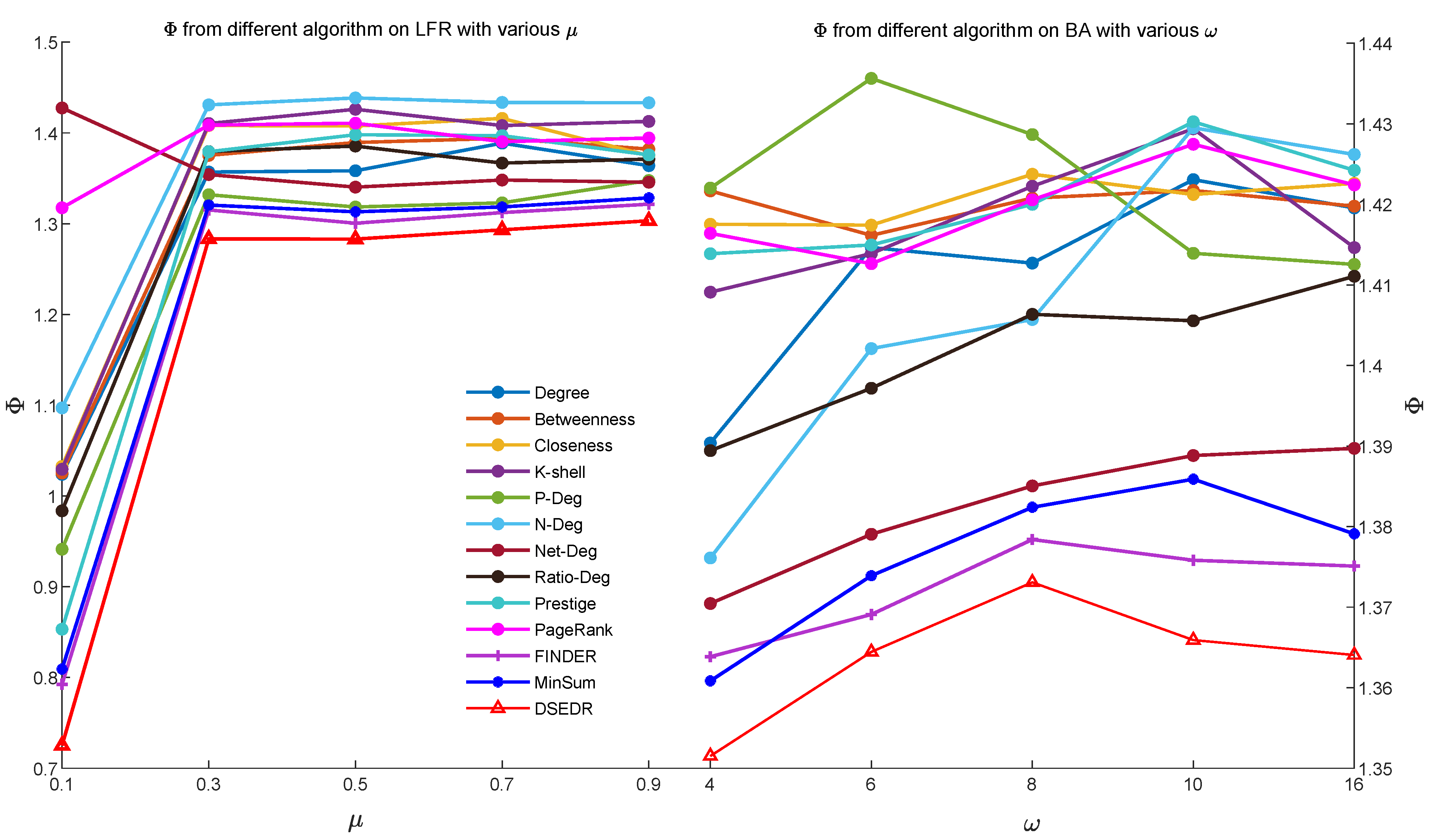
6.2. Artificial Network
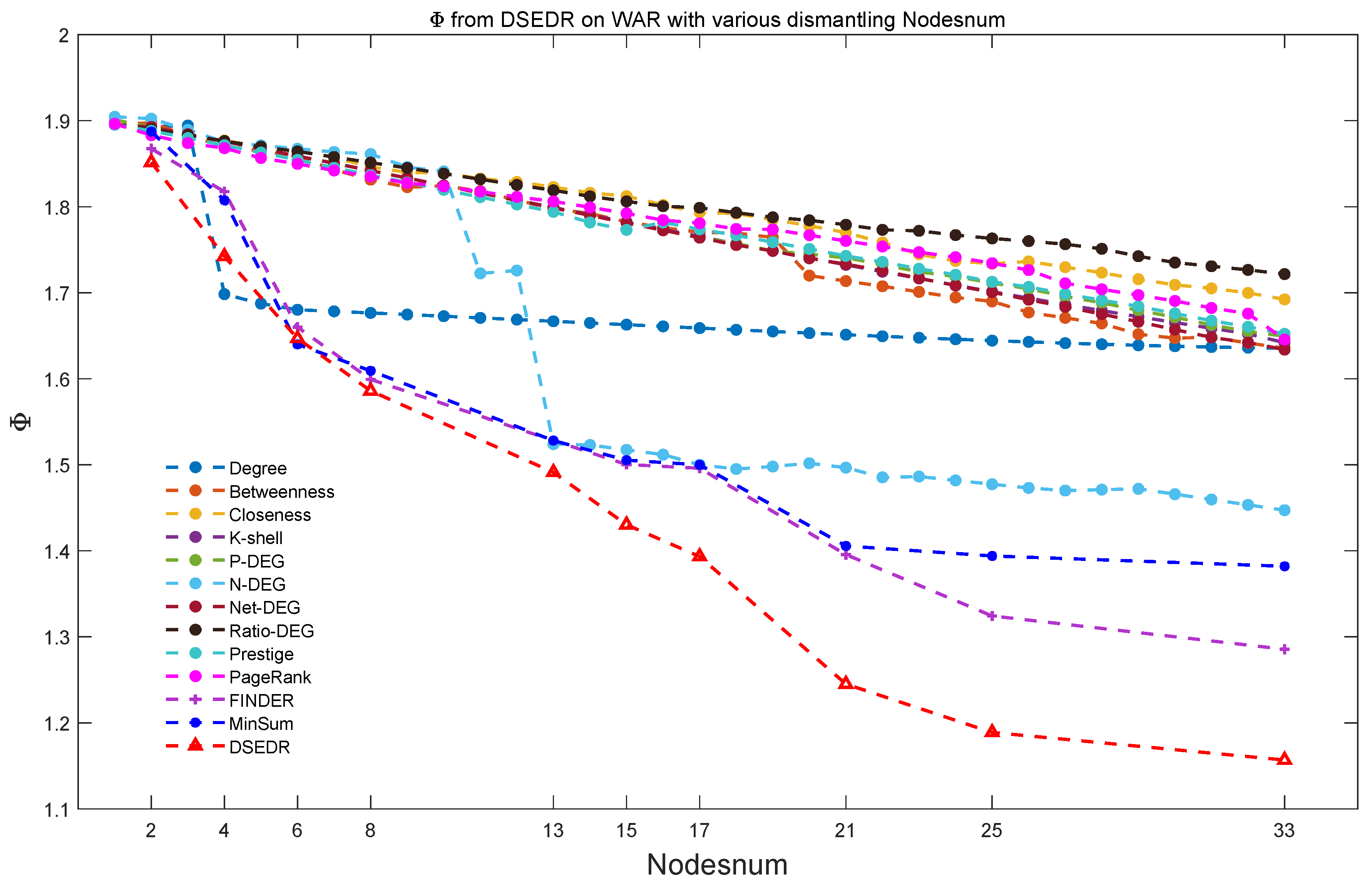
6.3. Real-World Network
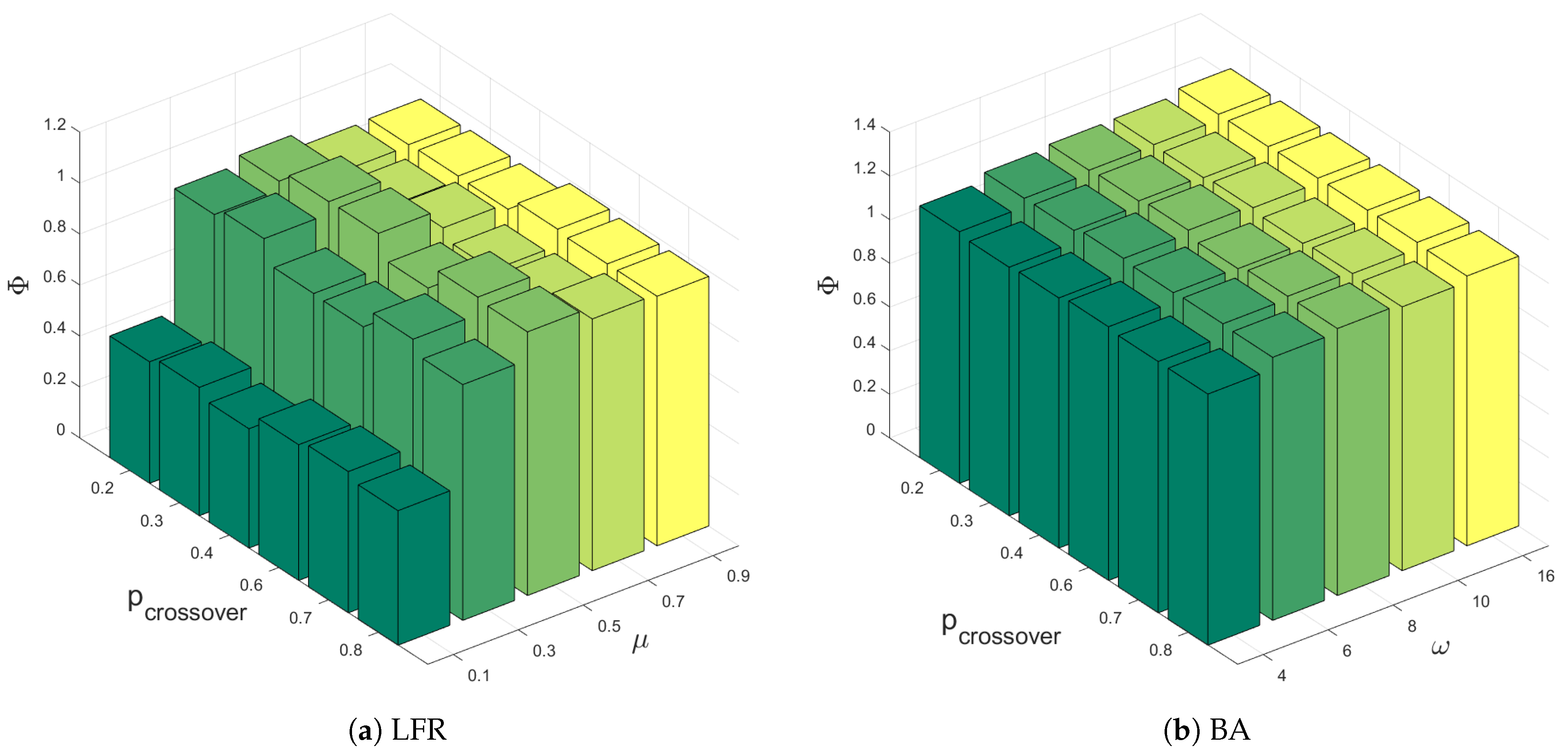
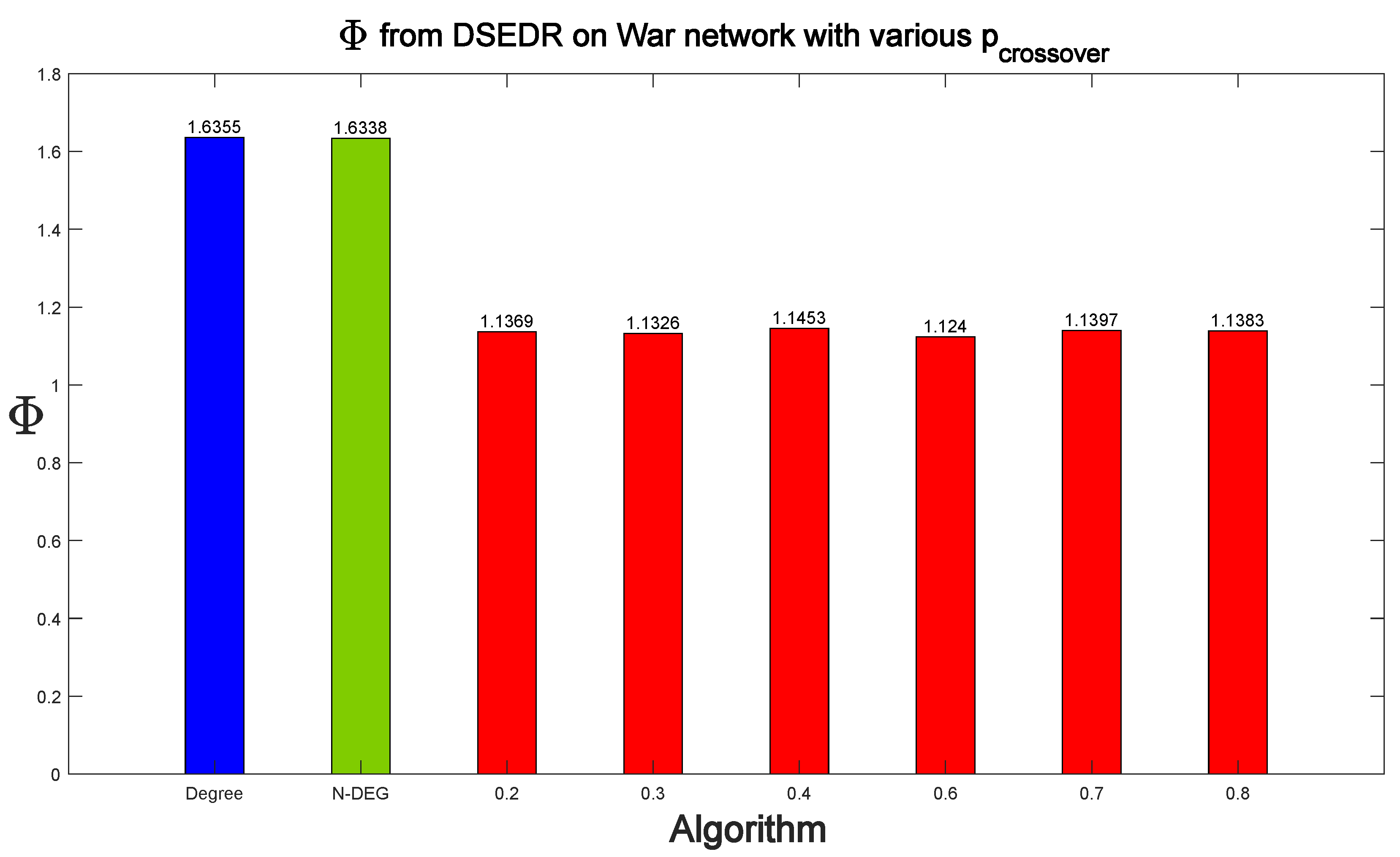
6.3.1. Efficiency and Parameter Analysis
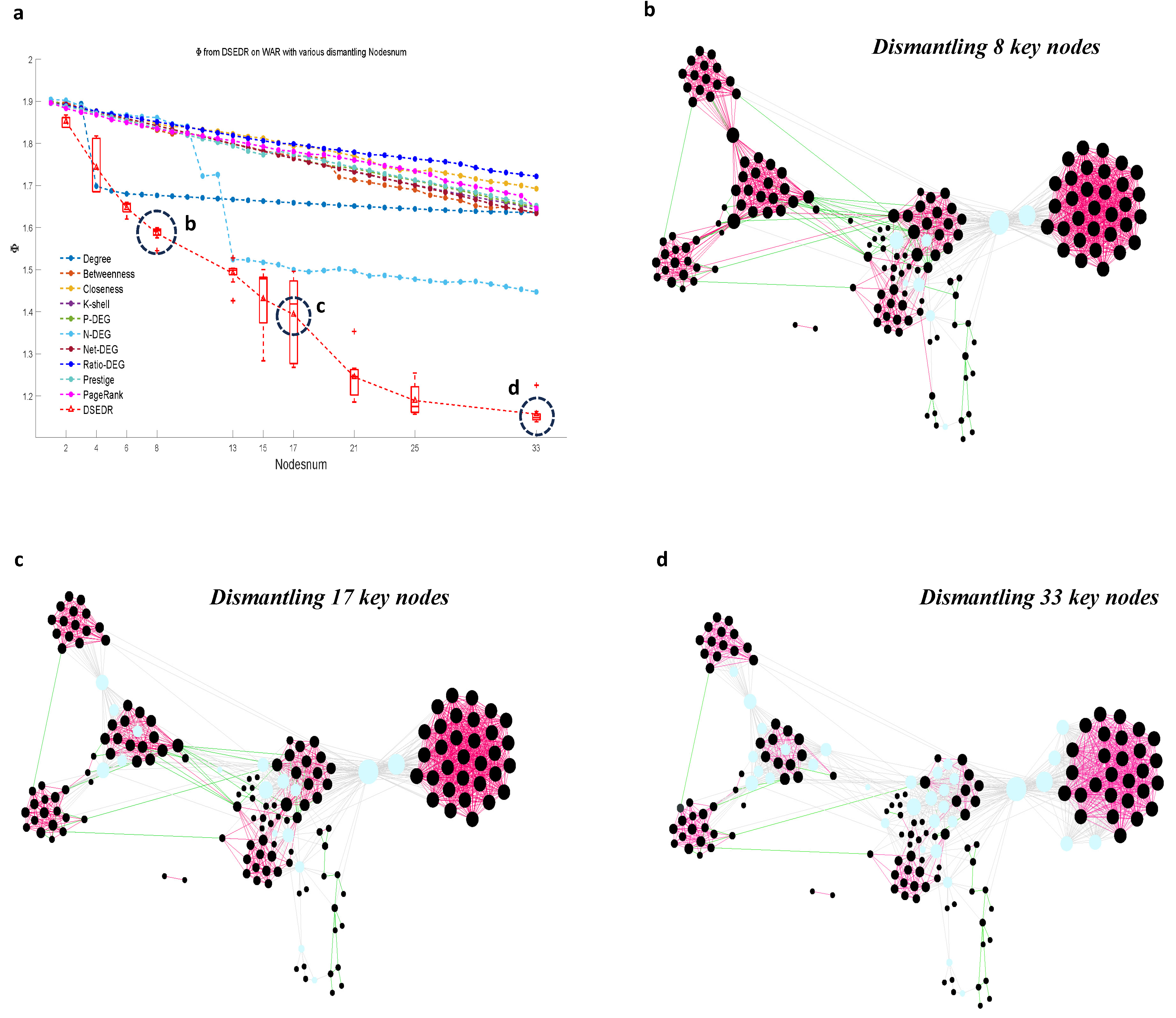
6.3.2. Visualization and Real Meaning Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akhtar, M.U.; Liu, J.; Liu, X.; Ahmed, S.; Cui, X. NRAND: An efficient and robust dismantling approach for infectious disease network. Inf. Process. Manag. 2023, 60, 103221. [Google Scholar] [CrossRef]
- Qi, M.; Chen, P.; Wu, J.; Liang, Y.; Duan, X. Robustness measurement of multiplex networks based on graph spectrum. Chaos 2023, 33, 021102. [Google Scholar] [CrossRef] [PubMed]
- Collins, B.; Hoang, D.T.; Nguyen, N.T.; Hwang, D. A new model for predicting and dismantling a complex terrorist network. IEEE Access 2022, 10, 126466–126478. [Google Scholar] [CrossRef]
- Duijn, P.A.; Kashirin, V.; Sloot, P.M. The relative ineffectiveness of criminal network disruption. Sci. Rep. 2014, 4, 4238. [Google Scholar] [CrossRef]
- Tripathy, R.M.; Bagchi, A.; Mehta, S. A study of rumor control strategies on social networks. In Proceedings of the ACM International Conference on Information & Knowledge Management, Toronto, ON, Canada, 26–30 October 2010. [Google Scholar]
- Zhan, X.-X.; Zhang, K.; Ge, L.; Huang, J.; Zhang, Z.; Wei, L.; Sun, G.-Q.; Liu, C.; Zhang, Z.-K. Exploring the effect of social media and spatial characteristics during the COVID-19 pandemic in china. IEEE Trans. Netw. Sci. Eng. 2022, 10, 553–564. [Google Scholar] [CrossRef]
- Rahman, K.C. A survey on sensor network. J. Comput. Inf. Technol. 2010, 1, 76–87. [Google Scholar]
- Bui, T.N.; Jones, C. Finding good approximate vertex and edge partitions is np-hard. Inf. Process. Lett. 1992, 42, 153–159. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Osat, S.; Faqeeh, A.; Radicchi, F. Optimal percolation on multiplex networks. Nat. Commun. 2017, 8, 1540. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; Huttenlocher, D.; Kleinberg, J. Signed networks in social media. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Atlanta, GA, USA, 10–15 April 2010; pp. 1361–1370. [Google Scholar]
- Li, H.-J.; Feng, Y.; Xia, C.; Cao, J. Overlapping graph clustering in attributed networks via generalized cluster potential games. ACM Trans. Knowl. Discov. Data 2024, 18, 1–26. [Google Scholar] [CrossRef]
- Tang, J.; Chang, Y.; Aggarwal, C.; Liu, H. A survey of signed network mining in social media. ACM Comput. Surv. 2016, 49, 1–37. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Ma, L.; Shao, Z.; Li, X.; Lin, Q.; Li, J.; Leung, V.C.; Nandi, A.K. Influence Maximization in Complex Networks by Using Evolutionary Deep Reinforcement Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 995–1009. [Google Scholar] [CrossRef]
- Osat, S.; Papadopoulos, F.; Teixeira, A.S.; Radicchi, F. Embedding-aided network dismantling. Phys. Rev. Res. 2023, 5, 013076. [Google Scholar] [CrossRef]
- Wandelt, S.; Lin, W.; Sun, X.; Zanin, M. From random failures to targeted attacks in network dismantling. Reliab. Eng. Syst. Saf. 2022, 218, 108146. [Google Scholar] [CrossRef]
- Braunstein, A.; Dall’Asta, L.; Semerjian, G.; Zdeborová, L. Network dismantling. Proc. Natl. Acad. Sci. USA 2016, 113, 12368–12373. [Google Scholar] [CrossRef]
- Yan, D.; Xie, W.; Zhang, Y.; He, Q.; Yang, Y. Hypernetwork dismantling via deep reinforcement learning. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3302–3315. [Google Scholar] [CrossRef]
- Fan, C.; Zeng, L.; Sun, Y.; Liu, Y.Y. Finding key players in complex networks through deep reinforcement learning. Nat. Mach. Intell. 2020, 2, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Deepali, J.J.; Ishaan, K.; Sadanand, G.; Omkar, K.; Divya, P.; Shivkumar, P. Reinforcement Learning: A Survey. In Machine Learning and Information Processing; Springer: Berlin, Germany, 2021; pp. 297–308. [Google Scholar]
- Liu, F.Y.; Li, Z.N.; Qian, C. Self-Guided Evolution Strategies with Historical Estimated Gradients. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI-20) IJCAI, Yokohama, Japan, 11–17 July 2020; pp. 1474–1480. [Google Scholar]
- Khadka, S.; Tumer, K. Evolution-guided policy gradient in reinforcement learning. In Advances in Neural Information Processing Systems 31; Neural Information Processing Systems Foundation, Inc. (NeurIPS): Montreal, QC, Canada, 2018. [Google Scholar]
- Zhan, Z.; Li, J.; Zhang, J. Evolutionary deep learning: A survey. Neurocomputing 2022, 483, 42–58. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, W.; Tüske, Z.; Picheny, M. Evolutionary stochastic gradient descent for optimization of deep neural networks. In Advances in Neural Information Processing Systems 31; Neural Information Processing Systems Foundation, Inc. (NeurIPS): Montreal, QC, Canada, 2018. [Google Scholar]
- Such, F.P.; Madhavan, V.; Conti, E.; Lehman, J.; Stanley, K.O.; Clune, J. Deep neuroevolution: Genetic algorithms are a competitive alternative for training deep neural networks for reinforcement learning. arXiv 2017, arXiv:1712.06567. [Google Scholar] [CrossRef]
- Khadka, S.; Majumdar, S.; Nassar, T.; Dwiel, Z.; Tumer, E.; Miret, S.; Liu, Y.; Tumer, K. Collaborative evolutionary reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Li, H.-J.; Xu, W.; Qiu, C.; Pei, J. Fast Markov Clustering Algorithm Based on Belief Dynamics. IEEE Trans. Cybern. 2023, 53, 3716–3725. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-J.; Cao, H.; Feng, Y.; Li, X.; Pei, J. Optimization of Graph Clustering Inspired by Dynamic Belief Systems. IEEE Trans. Knowl. Data Eng. 2024, 36, 6773–6785. [Google Scholar] [CrossRef]
- Borgatti, S.P. Identifying sets of key players in a social network. Comput. Math. Organ. Theory 2006, 12, 21–34. [Google Scholar] [CrossRef]
- Cheng, S.Q.; Shen, H.W.; Zhang, G.Q.; Cheng, X.Q. Survey of signed network research. Ruan Jian Xue Bao/J. Softw. 2013, 25, 1–15. [Google Scholar]
- Shen, X.; Chung, F.L. Deep network embedding for graph representation learning in signed networks. IEEE Trans. Cybern. 2020, 50, 1556–1568. [Google Scholar] [CrossRef] [PubMed]
- Han, X.N.; Liu, H.P.; Sun, F.C.; Zhang, X.Y. Active object detection with multistep action prediction using deep Q-network. IEEE Trans. Ind. Inform. 2019, 15, 3723–3731. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Zhao, D.B. Online minimax Q network learning for two-player zero-sum Markov games. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1228–1241. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Carmi, S.; Havlin, S.; Kirkpatrick, S.; Shavitt, Y.; Shir, E. A model of Internet topology using k-shell decomposition. Proc. Natl. Acad. Sci. USA 2007, 104, 11150–11154. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Zolfaghar, K.; Aghaie, A. Mining trust and distrust relationships in social Web applications. In Proceedings of the 2010 IEEE 6th International Conference on Intelligent Computer Communication and Processing, Cluj-Napoca, Romania, 26–28 August 2010; pp. 73–80. [Google Scholar]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web. In Proceedings of the Web Conference, Toronto, ON, Canada, 11–14 May 1999. [Google Scholar]
- Lancichinetti, A.; Fortunato, S.; Radicchi, F. Benchmark graphs for testing community detection algorithms. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 78, 046110. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Ghosn, F.; Palmer, G.; Bremer, S.A. The MID3 data set, 1993–2001: Procedures, coding rules, and description. Confl. Manag. Peace Sci. 2004, 21, 133–154. [Google Scholar] [CrossRef]


| Notation | Instruction |
|---|---|
| Target network | |
| Set of nodes | |
| Set of edges | |
| Number of nodes | |
| Number of edges | |
| Size of giant connected component | |
| The i-th connected component of | |
| Size of | |
| Objective function | |
| Set of nodes to be dismantled | |
| Weights of DQN neural network | |
| Action of DQN at t | |
| Seed node selection state of DRL at time t | |
| Selected nodes set to be removed at t | |
| Degree vector of each node | |
| Positive out-degree vector | |
| Decision reward | |
| Initial population size | |
| Batch size in DRL algorithm | |
| Maximum number of iterations | |
| Population size in the EA algorithm | |
| Population in evolution | |
| The number of nodes to be removed | |
| The average connectivity of nodes | |
| d | The 1st layer neurons’ number of the DQN |
| l | The 2nd layer neurons’ number of the DQN |
| Parameter | Value |
|---|---|
| Iteration number | 100 |
| Evolutionary population size | 100 |
| Crossover probability | 0.8 |
| Mutation probability | 0.2 |
| Network embedding dimension d | 64 |
| Training batch size | 512 |
| Training discount rate | 0.8 |
| Training learning rate | 0.001 |
| Importance of positive edge share in | 1 |
| Network Parameter | Value |
|---|---|
| number of nodes n | 166 |
| number of sides k | 1433 |
| number of positive sides | 1295 |
| number of negative side | 138 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Xiong, F.; Zhang, H.; Li, H. Network Dismantling on Signed Network by Evolutionary Deep Reinforcement Learning. Sensors 2024, 24, 8026. https://doi.org/10.3390/s24248026
Ou Y, Xiong F, Zhang H, Li H. Network Dismantling on Signed Network by Evolutionary Deep Reinforcement Learning. Sensors. 2024; 24(24):8026. https://doi.org/10.3390/s24248026
Chicago/Turabian StyleOu, Yuxuan, Fujing Xiong, Hairong Zhang, and Huijia Li. 2024. "Network Dismantling on Signed Network by Evolutionary Deep Reinforcement Learning" Sensors 24, no. 24: 8026. https://doi.org/10.3390/s24248026
APA StyleOu, Y., Xiong, F., Zhang, H., & Li, H. (2024). Network Dismantling on Signed Network by Evolutionary Deep Reinforcement Learning. Sensors, 24(24), 8026. https://doi.org/10.3390/s24248026








