Anomaly Detection and Remaining Useful Life Prediction for Turbofan Engines with a Key Point-Based Approach to Secure Health Management
Abstract
1. Introduction
2. Related Work
2.1. Convolution and Its Properties
2.1.1. One-Dimensional “Full” Convolution
2.1.2. One-Dimensional “Same” Convolution
2.2. C-MAPSS Dataset
2.3. Custom Description
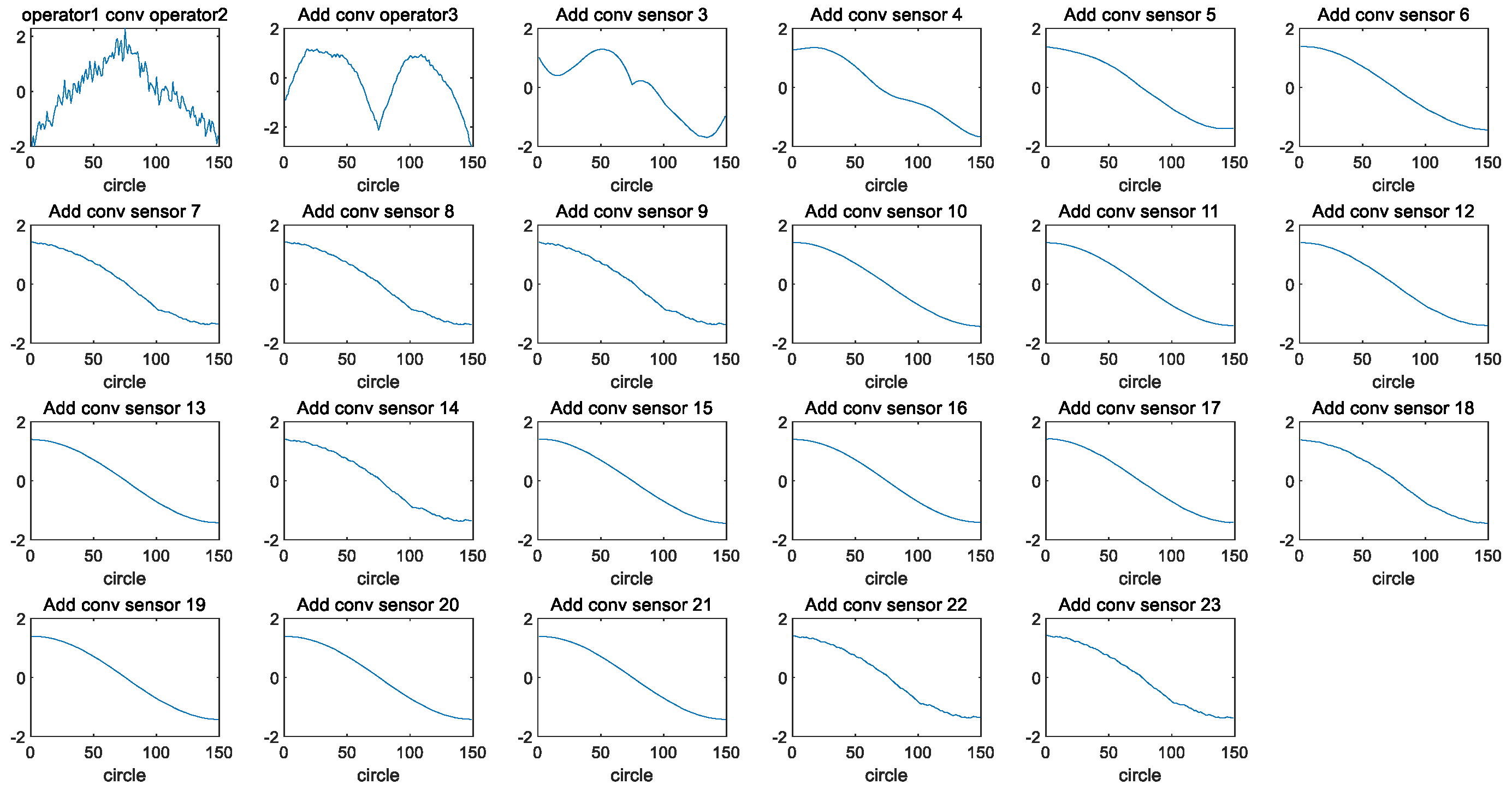
3. Acquisition and Inference of Key Points
3.1. Acquisition of Key Points
3.2. Inference
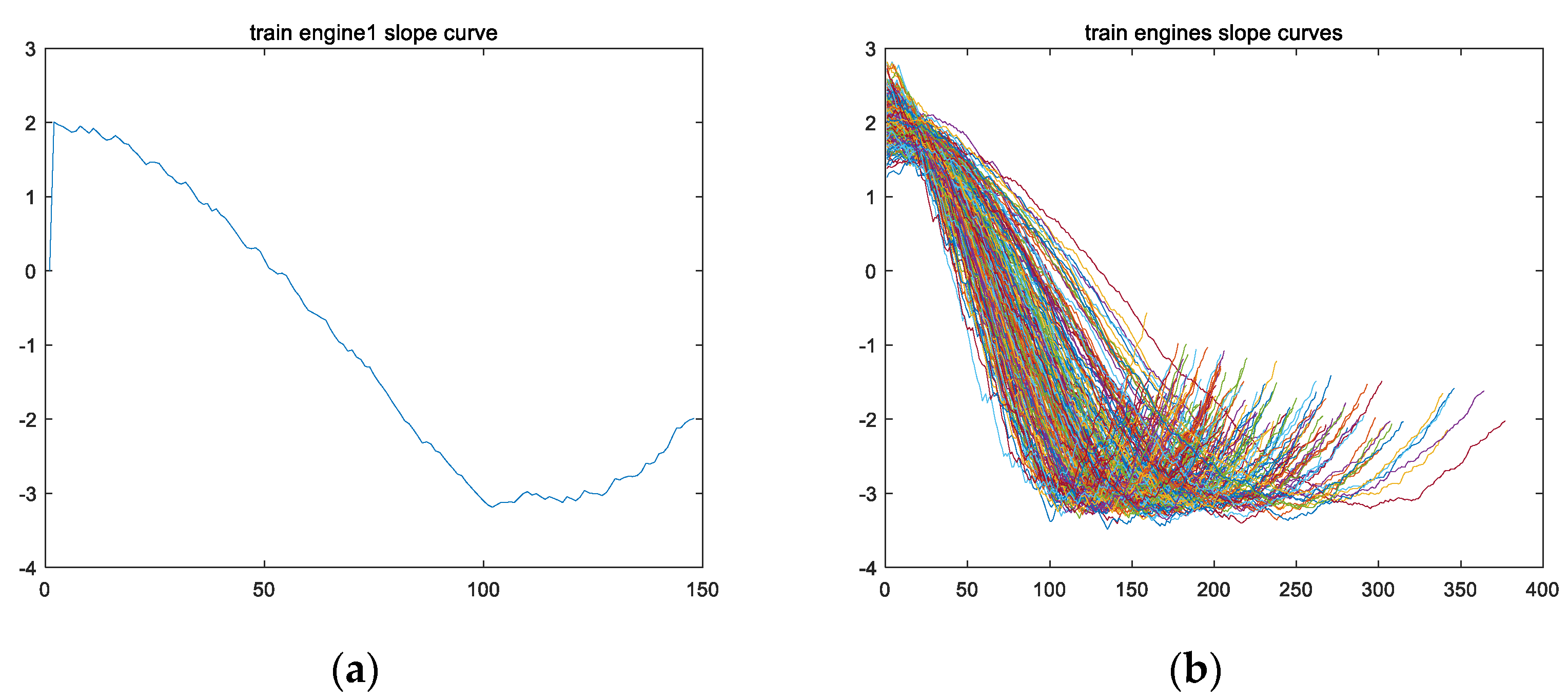
4. An Analysis of the Key Points
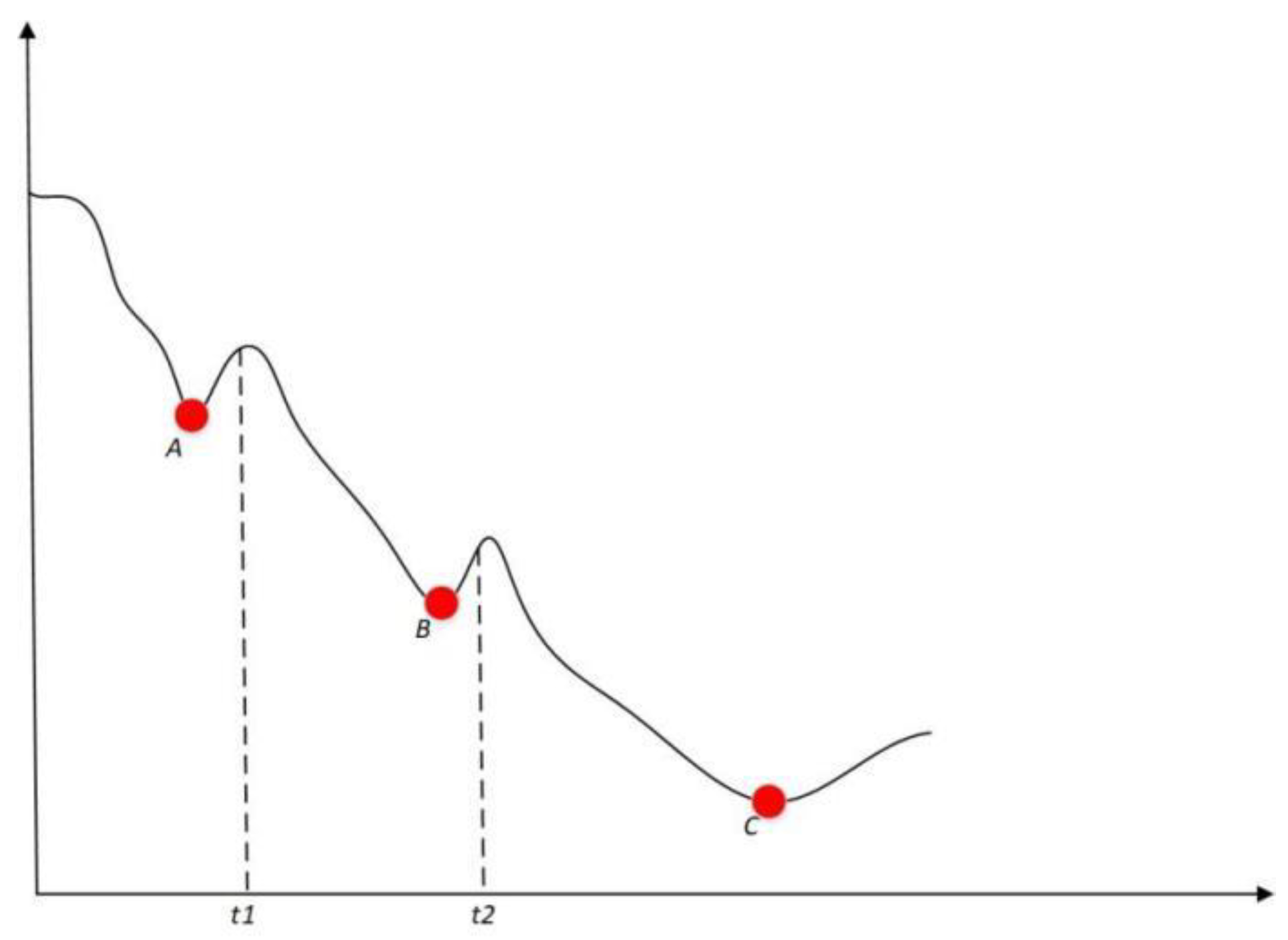
4.1. The First Key Point Analysis
4.2. The Second Key Point Analysis
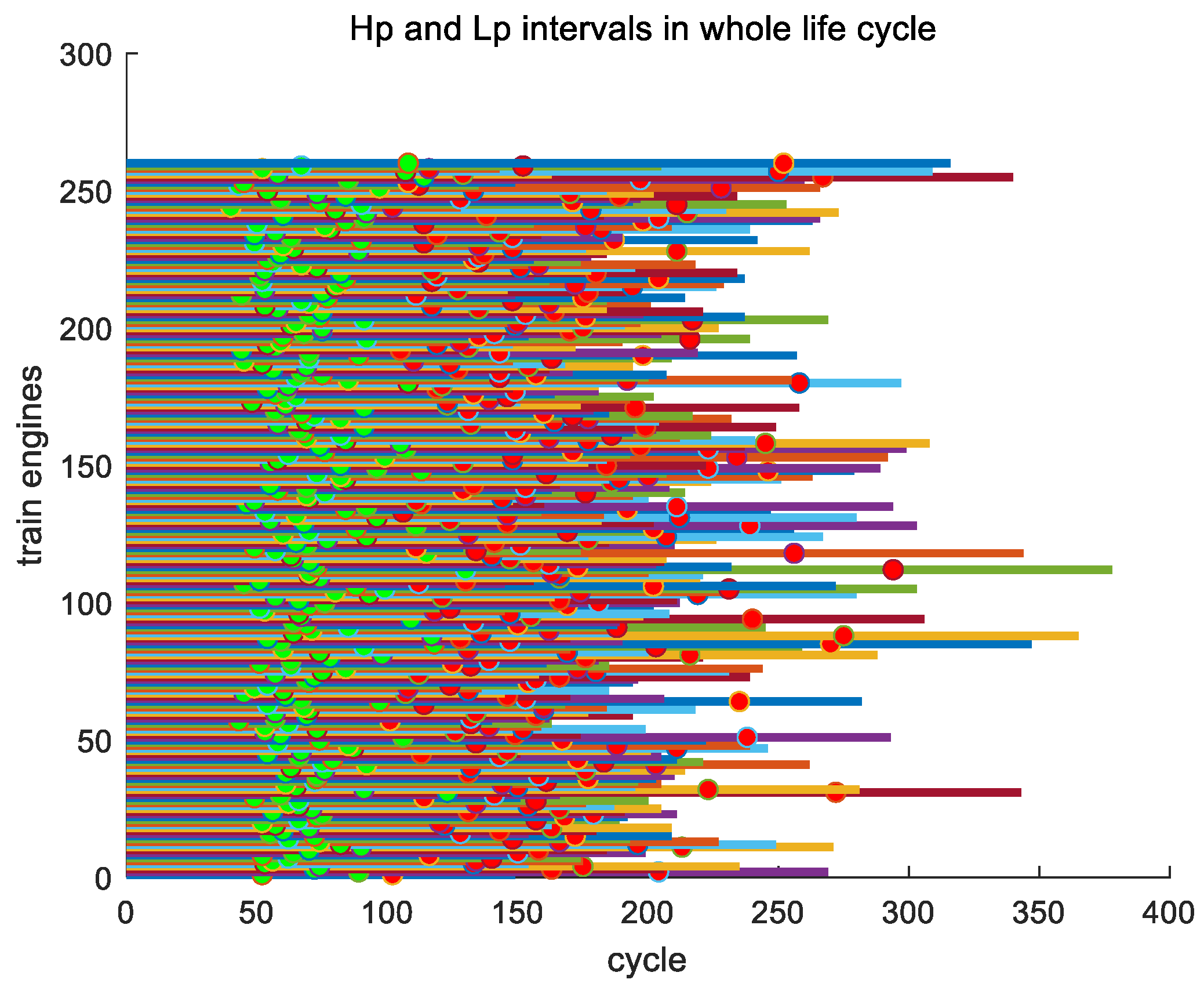
4.3. Time Interval Analysis of Key Points to
4.4. Time Interval Analysis of to
4.5. Three Stages
5. Application Based on Key Points
5.1. PHM Application
5.2. RUL Prediction
5.2.1. Evaluating Indicator
5.2.2. Obtaining Key Points of the Test Set
5.2.3. Using the Method in Conjunction with Other Prediction Algorithms
5.2.4. Using the Key Point Method Alone to Predict the RUL
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| RUL | Remaining Useful Life |
| AI | Artificial Intelligence |
| PHM | Prognostics and Health Management |
| MSDFM | Multi-Sensor Data Fusion Model |
| EKF | Extended Kalman Filter |
| SKF | Switching Kalman Filter |
| IVBI | Iterative Variational Bayesian Inference |
| MLP | Multilayer Perceptron |
| CNN | Convolutional Neural Networks |
| DCNN | Deep Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| FMLP | Functional Multilayer Perceptron |
| GRU | Gate Recurrent Unit |
| CBM | Condition-Based Maintenance |
| RMSE | Root Mean Square Error |
References
- Peng, C.; Chen, Y.; Chen, Q.; Tang, Z.; Li, L.; Gui, W. A Remaining Useful Life Prognosis of Turbofan Engine Using Temporal and Spatial Feature Fusion. Sensors 2021, 21, 418. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Shen, J.; Qiu, H. Fault Detection Filter Design of Dual-Rotor Turbofan Aero-Engine: A Positive System Approach. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4216–4220. [Google Scholar] [CrossRef]
- de Pater, I.; Reijns, A.; Mitici, M. Alarm-based predictive maintenance scheduling for aircraft engines with imperfect Remaining Useful Life prognostics. Reliab. Eng. Syst. Saf. 2022, 221, 108341. [Google Scholar] [CrossRef]
- Yan, R.; Li, W.; Lu, S.; Xia, M.; Chen, Z.; Zhou, Z.; Li, Y.; Lu, J. Transfer Learning for Prognostics and Health Management: Advances, Challenges, and Opportunities. J. Dyn. Monit. Diagnostics 2024, 3, 2. [Google Scholar] [CrossRef]
- Hoeppner, D.W.; Krupp, W.E. Prediction of component life by application of fatigue crack growth knowledge. Eng. Fract. Mech. 1974, 6, 47–70. [Google Scholar] [CrossRef]
- Le Son, K.; Fouladirad, M.; Barros, A.; Levrat, E.; Iung, B. Remaining useful life estimation based on stochastic deterioration models: A comparative study. Reliab. Eng. Syst. Saf. 2013, 112, 165–175. [Google Scholar] [CrossRef]
- Sánchez, L.; Costa, N.; Otero, J.; Couso, I. Physics-Informed Learning Under Epistemic Uncertainty with an Application to System Health Modeling. Int. J. Approx. Reasoning 2023, 161, 108988. [Google Scholar] [CrossRef]
- Daigle, M.J.; Goebel, K. A model-based prognostics approach applied to pneumatic valves. Int. J. Progn. Health Manag. 2011, 2, 84. Available online: https://www.researchgate.net/publication/262971961_A_Model-based_Prognostics_Approach_Applied_to_Pneumatic_Valves (accessed on 5 December 2024).
- Gao, T.; Li, Y.; Huang, X.; Wang, C. Data-Driven Method for Predicting Remaining Useful Life of Bearing Based on Bayesian Theory. Sensors 2021, 21, 182. [Google Scholar] [CrossRef]
- Wei, J.; Bai, P.; Qin, D.; Lim, T.C.; Yang, P.; Zhang, H. Study on vibration characteristics of fan shaft of geared turbofan engine with sudden imbalance caused by blade off. J. Vib. Acoust. 2018, 140, 041010. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H. Engine remaining useful life prediction model based on R-Vine copula with multi-sensor data. Heliyon 2023, 9, e17118. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Gebraeel, N.; Lei, Y.; Fang, X.; Cai, X.; Yan, T. Remaining Useful Life Prediction based on a Multi-Sensor Data Fusion Model. Reliab. Eng. Syst. Saf. 2020, 208, 107249. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, J.; Luo, C.; Xiong, L.; Pan, Q. Aero-engine health degradation estimation based on an underdetermined extended Kalman filter and convergence proof. ISA Transactions 2021, 125, 528–538. [Google Scholar] [CrossRef] [PubMed]
- Tran, G.Q.B.; Bernard, P. Kalman-like Observer for Hybrid Systems with Linear Maps and Known Jump Times. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, Singapore, 13–15 December 2023; pp. 1865–1872. [Google Scholar] [CrossRef]
- Solís-Martín, D.; Galán-Páez, J.; Borrego-Díaz, J. A Stacked Deep Convolutional Neural Network to Predict the Remaining Useful Life of a Turbofan Engine. Annu. Conf. PHM Soc. 2021, 2111.12689. [Google Scholar] [CrossRef]
- Lim, P.; Goh, C.K.; Tan, K.C.; Dutta, P. Estimation of Remaining Useful Life Based on Switching Kalman Filter Neural Network Ensemble. In Proceedings of the PHM 2014–Proceedings of the Annual Conference of the Prognostics and Health Management Society, Fort Worth, TX, USA, 29 September–2 October 2014; pp. 2–9. [Google Scholar] [CrossRef]
- Hu, Y.; Bai, Y.; Fu, E.; Liu, P. A Novel Remaining Useful Life Probability Prediction Approach for Aero-Engine with Improved Bayesian Uncertainty Estimation Based on Degradation Data. Appl. Sciences 2023, 13, 9194. [Google Scholar] [CrossRef]
- Mosallam, A.; Medjaher, K.; Zerhouni, N. Data-driven prognostic method based on Bayesian approaches for direct remaining useful life prediction. J. Intell. Manuf. 2016, 27, 1037–1048. [Google Scholar] [CrossRef]
- Ahmadzadeh, F.; Lundberg, J. Remaining useful life estimation. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 461–474. [Google Scholar] [CrossRef]
- Heimes, F. Recurrent neural networks for remaining useful life estimation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X.L. Deep convolutional neural network-based regression approach for estimation of remaining useful life. In Proceedings of the International Conference on Database Systems for Advanced Applications, Dallas, TX, USA, 16–19 April 2016; Springer: Cham, Switzerland, 2016; pp. 214–228. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng.Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Chaoub, A.; Voisin, A.; Cerisara, C.; Iung, B. Learning representations with end-to-end models for improved remaining useful life prognostics. arXiv 2021. [Google Scholar] [CrossRef]
- Llasag Rosero, R.; Silva, C.; Ribeiro, B. Forecasting Functional Time Series Using Federated Learning. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Corfu, Greece, 7 June 2023. [Google Scholar] [CrossRef]
- Sánchez Ruiz, Á. Estimation of the Remaining Useful Life (RUL) of a turbofan using CNN-GRU Neural Networks. Ph.D. Thesis, College of Aerospace Engineering and Technology, Universidad Politécnica de Madrid, Madrid, Spain, 2020. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Chen, W.; Gu, Y. A CNN-LSTM-based Domain Adaptation Model for Remaining Useful Life Prediction. Meas. Sci. Technol. 2022, 33, 115118. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, X.; Li, Y.; Iqbal, M.Y. A Double-Channel Hybrid Deep Neural Network Based on CNN and BiLSTM for Remaining Useful Life Prediction. Sensors 2020, 20, 7109. [Google Scholar] [CrossRef]
- Lee, J.; Mitici, M. Deep reinforcement learning for predictive aircraft maintenance using Probabilistic Remaining-Useful-Life prognostics. Reliab. Eng. Syst. Safety. 2022, 230, 108908. [Google Scholar] [CrossRef]
- Libretexts Technology Website 7.2: Sums of Continuous Random Variables. Available online: https://stats.libretexts.org/Bookshelves/Probability_Theory/Book%3A_Introductory_Probability_(Grinstead_and_Snell)/07%3A_Sums_of_Random_Variables/7.02%3A_Sums_of_Continuous_Random_Variables (accessed on 12 July 2024).
- Yan, X.; Liu, X.; Li, J.; Hu, H.; Lin, M.; Wang, X. Recoding double-phase holograms with the full convolutional neural network. Opt. Laser Technol. 2024, 174, 110667. [Google Scholar] [CrossRef]
- Jiang, H.; Li, S.; Li, H. Parallel ‘same’ and ‘valid’ convolutional block and input-collaboration strategy for histopathological image classification. Appl. Soft Comput. 2022, 117, 108417. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Kefalas, M.; Yang, K.; Apostolidis, A.; Olhofer, M.; Limmer, S.; B¨ack, T. A Review: Prognostics and Health Management in Automotive and Aerospace. Int. J. Progn. Health Manag. 2019, 10, 35. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, J.; Li, Z.; Zhao, X.; Guo, D.; Fu, H. Study on Prognostics and Health Management of Fluid Loop System for Space Application. J. Phys. Conf. Ser. 2022, 2184, 012059. [Google Scholar] [CrossRef]
- Frederick, D.; de Castro, J.; Litt, J. User’s Guide for the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS); NASA/ARL: Hanover, MD, USA, 2007. Available online: https://ntrs.nasa.gov/api/citations/20120003211/downloads/20120003211.pdf (accessed on 5 December 2024).
- Zhang, C.; Lim, P.; Qin, A.K.; Tan, K.C. Multiobjective deep belief networks ensemble for remaining useful life estimation in prognostics. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2306–2318. [Google Scholar] [CrossRef]
- Wang, T.; Guo, D.; Sun, X.-M. Remaining useful life predictions for turbofan engine degradation based on concurrent semi-supervised model. Neural Comput. Appl. 2022, 34, 5151–5160. [Google Scholar] [CrossRef]



















| Dataset | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Training engines | 100 | 260 | 100 | 249 |
| Testing engines | 100 | 259 | 100 | 248 |
| Operating conditions | 1 | 6 | 1 | 6 |
| Fault modes | 1 | 1 | 2 | 2 |
| Number of training samples | 20,632 | 53,760 | 24,721 | 61,250 |
| Number of testing samples | 13,097 | 33,992 | 16,597 | 41,215 |
| Sensor No | Sensor Description | Units |
|---|---|---|
| 1 | Total temperature at fan inlet | °R |
| 2 | Total temperature at LPC outlet | °R |
| 3 | Total temperature at HPT outlet | °R |
| 4 | Total temperature at LPT outlet | °R |
| 5 | Pressure at fan inlet | psia |
| 6 | Total pressure in bypass duct | psia |
| 7 | Total pressure at HPC outlet | psia |
| 8 | Physical fan speed | rpm |
| 9 | Physical core speed | rpm |
| 10 | Engine pressure ratio | - |
| 11 | Static pressure at HPC outlet | rpm |
| 12 | Ratio of fuel flow to Ps30 | pps/psi |
| 13 | Corrected fan speed | rpm |
| 14 | Corrected core speed | rpm |
| 15 | Bypass ratio | - |
| 16 | Burner fuel/air ratio | - |
| 17 | Bleed enthalpy | - |
| 18 | Demanded fan speed | rpm |
| 19 | Demanded corrected fan speed | rpm |
| 20 | HPT coolant bleed | lbm/s |
| 21 | LPT coolant bleed | lbm/s |
| Columns | 1 | 2 | 3–5 | 6–26 |
|---|---|---|---|---|
| Parameter Name | Engine id | Current lifecycle of engine | Operating conditions | Sensor data |
| Convolutional Fusion Process | |
|---|---|
| Input: train_cell{}, include all train engine data, every engine data size is features × length Output: conv result, in which every engine data size is 1 × length | |
| 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: | for i = 1: numer of engines in the train sets Get the i-th engine data of the train_cell; the i-th engine data size is features × length; Get the i-th engine data’s first feature, the size is 1 × length, named h1; for j = 2: features Get the ith engine data’s j-th feature, and convolution with h1, then reassign the result to h1, Central part of the convolution of the same size as h1,that is the h1’s size is 1 × length. end the h1 is the i-th engine convolution result and is saved in variable train_conv_cell. end |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Y.; Zhang, T.; Shi, D. Anomaly Detection and Remaining Useful Life Prediction for Turbofan Engines with a Key Point-Based Approach to Secure Health Management. Sensors 2024, 24, 8022. https://doi.org/10.3390/s24248022
Duan Y, Zhang T, Shi D. Anomaly Detection and Remaining Useful Life Prediction for Turbofan Engines with a Key Point-Based Approach to Secure Health Management. Sensors. 2024; 24(24):8022. https://doi.org/10.3390/s24248022
Chicago/Turabian StyleDuan, Yuntao, Tao Zhang, and Dunhuang Shi. 2024. "Anomaly Detection and Remaining Useful Life Prediction for Turbofan Engines with a Key Point-Based Approach to Secure Health Management" Sensors 24, no. 24: 8022. https://doi.org/10.3390/s24248022
APA StyleDuan, Y., Zhang, T., & Shi, D. (2024). Anomaly Detection and Remaining Useful Life Prediction for Turbofan Engines with a Key Point-Based Approach to Secure Health Management. Sensors, 24(24), 8022. https://doi.org/10.3390/s24248022






