A Combined CNN-LSTM Network for Ship Classification on SAR Images
Abstract
1. Introduction
- Specific focus on single-view SAR imagery: Unlike other studies, our research targets the challenges of synthetic aperture radar (SAR) imagery, such as limited labeled datasets, imbalanced class distributions, and non-sequential images.
- Proposed optimizations: We propose a shallow CNN combined with LSTM to reduce network complexity, minimize training time, and improve classification accuracy for SAR datasets. This contrasts with standard CNN-LSTM implementations, which often prioritize depth and complexity. Through a systematic evaluation of CNN components, such as the number and size of filters, we aim to optimize the model’s performance while minimizing computational cost and training time.
- Comprehensive validation: We validated our architecture on three distinct SAR datasets (FUSAR-Ship, OpenSARShip, and MSTAR), showcasing its adaptability and competitive performance in handling datasets of varying size, balance, and difficulty.
2. Convolutional Neural Networks (CNNs)
2.1. Description of CNN
2.1.1. Description of CNN Architecture Adopted
- Zero-padding step: Ensures no information is lost at the borders during convolution. If (,) denotes the number of zeros added to the last two tensor dimensions, the zero-padding step constructs the tensor .
- Convolutional step: Extracts features by applying filters to the input tensor. Each filter moves across the tensor with defined strides, producing an output that highlights key spatial patterns. The process is parameterized by the number, size, and strides of the filters, optimizing feature extraction for the classification task.If K denotes the number of filters, represents the filter where (,) is the size of all filters, and (,) denotes the strides of filters along the last two dimensions, then the output of the convolutional step is mathematically given bywhereThen, the resulting tensor is given byAn activation function is then applied to this tensor. The Rectified Linear Unit (ReLU) activation function is used.
- Max-pooling step: Downsamples the feature maps by retaining the highest value within a defined window, reducing dimensionality while preserving the most significant features. This process enhances computational efficiency and focuses on dominant spatial patterns.If (,) is the size of the max-pooling window and (,) are its strides along the last two dimensions, respectively, the output of max-pooling applied on the activated CONV tensorcan be expressed bywhere
- Dropout step: Mitigates overfitting by randomly setting a fraction of the tensor’s elements to zero during training. This regularization technique reduces the network’s reliance on specific neurons, improving its generalization to unseen data.
2.1.2. Model Selection for the CNN (Methodology)
3. Recurrent Neural Networks (RNNs)
3.1. Description of RNN
3.2. Long Short-Term Memory Network (LSTM)
3.3. Combined CNN-LSTM Hybrid Network Adopted
3.3.1. Description of CNN-LSTM Architecture Adopted
3.3.2. Model Selection for the CNN-LSTM (Methodology)
4. Brief Presentation of the SAR Datasets
4.1. MSTAR Data and Pre-Processing
4.2. OpenSARShip Data and Pre-Processing
- Type OD product: GRD.
- Polarization: VV.
- Image size: , and we resized the images to pixels.
- Class: {Cargo, Bulk Carrier, Container Ship}.
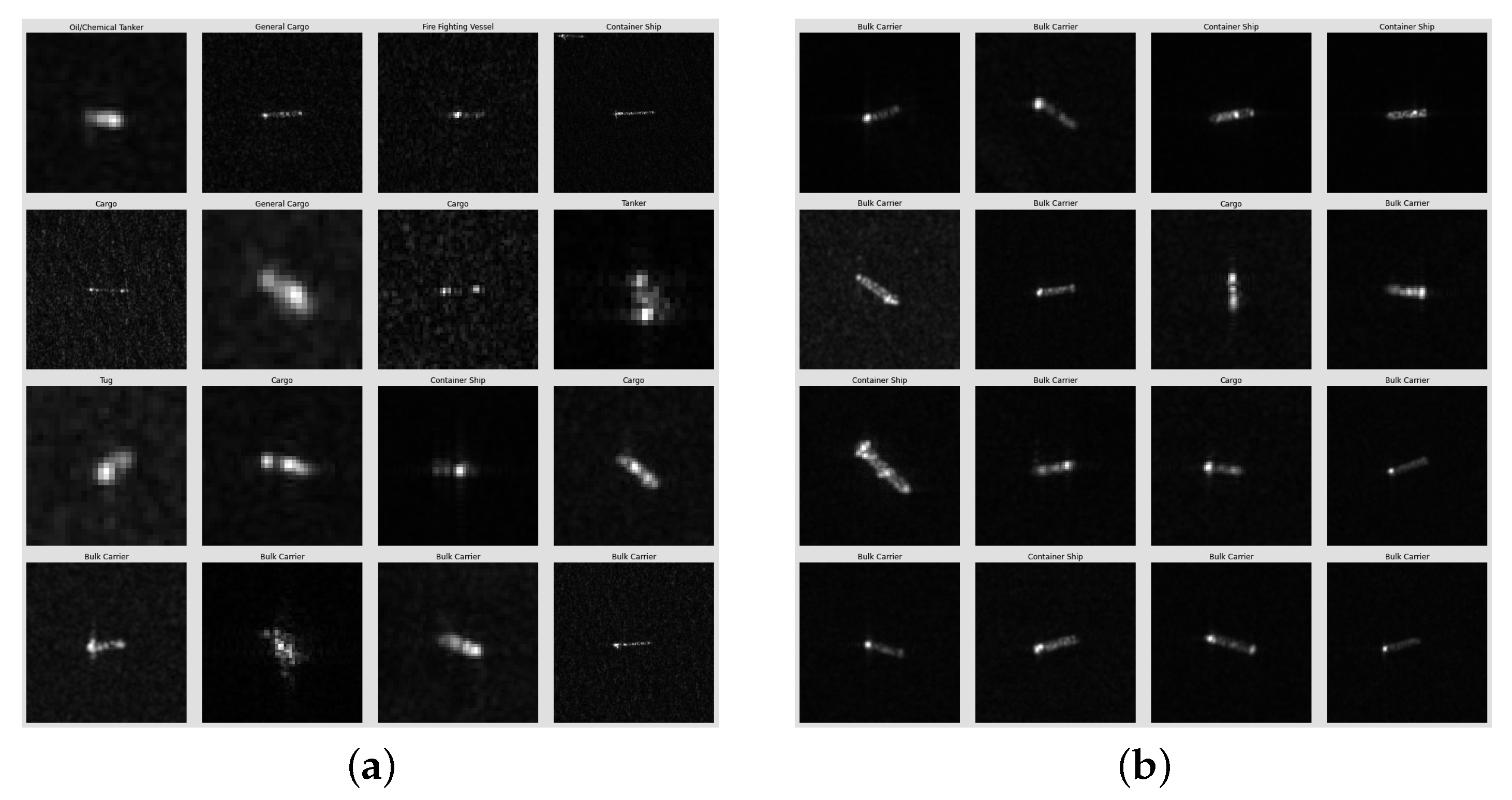
4.3. FUSAR-Ship Data and Pre-Processing
5. Experiments and Results on SAR Images
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| MS-CNN | Multi-Stream CNN |
| Conv-BiLSTM | Convolutional bidirectional long short-term memory |
| CBLPN | Conv-BiLSTM Prototypical Network |
| SAR | Synthetic aperture radar |
| MSTAR | Moving and Stationary Target Acquisition and Recognition |
| AIS | Automatic identification system |
| DNN | Deep neural network |
| FC | Fully connected |
| CE | Cross Entropy |
| GPU | Graphics processing unit |
| FPGA | Field-Programmable Gate Array |
| ASIC | Application-Specific Integrated Circuit |
| RNN | Recurrent neural network |
| GRD | Ground Range Detected |
| SLC | Single Look Complex |
| VV | Vertical–Vertical polarization |
| VH | Vertical–Horizontal polarization |
| HDC | Hybrid Dilated CNN |
| GAN | Generative Adversarial Network |
| ReLU | Rectified Linear Unit |
| MIMO | Multiple input multiple output |
| IT | Inferotemporal Cortex |
| RGC | Retinal Ganglion Cells |
| LGN | Lateral Geniculate Nucleus |
| IoT | Internet of Things |
| CSI | Channel State Information |
| RF | Radio Frequency |
| SSID | Service Set Identifier |
| BPTT | Backpropagation Through Time |
| HOG | Histogram of Oriented Gradients |
| GRSS | Geoscience and Remote Sensing Society |
| ATR | Automatic target recognition |
| CUDA | Compute Unified Device Architecture |
| SMI | System Management Interface |
| VGG | Visual Geometry Group |
| ResNet | Residual Network |
| Xception | Extreme Inception |
| DenseNet | Densely Connected Convolutional Networks |
| EfficientNet | Efficient Network |
| MobileNet | Mobile Network |
| FUSAR-Ship | Fudan University SAR-Ship |
| HH | Horizontal–Horizontal polarization |
References
- Zhang, X.; Ramachandran, A.; Zhuge, C.; He, D.; Zuo, W.; Cheng, Z.; Rupnow, K.; Chen, D. Machine learning on FPGAs to face the IoT revolution. In Proceedings of the 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, CA, USA, 13–16 November 2017; pp. 819–826. [Google Scholar] [CrossRef]
- Andri, R.; Cavigelli, L.; Rossi, D.; Benini, L. YodaNN: An Ultra-Low Power Convolutional Neural Network Accelerator Based on Binary Weights. In Proceedings of the 2016 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Pittsburgh, PA, USA, 11–13 July 2016; pp. 236–241. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Neural Networks; Kremer, S.C., Kolen, J.F., Eds.; IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.Z.; Islam, M.M.F.; Asraf, A. A Combined Deep CNN-LSTM Network for the Detection of Novel Coronavirus (COVID-19) Using X-ray Images. medRxiv 2020, 20, 100412. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Li, W. Ship Classification in High-Resolution SAR Images via Transfer Learning with Small Training Dataset. Sensors 2019, 19, 63. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Qu, C.; Peng, S. Ship classification for unbalanced SAR dataset based on convolutional neural network. J. Appl. Remote Sens. 2018, 12, 035010. [Google Scholar] [CrossRef]
- Xiao, Q.; Liu, B.; Li, Z.; Ni, W.; Yang, Z.; Li, L. Progressive Data Augmentation Method for Remote Sensing Ship Image Classification Based on Imaging Simulation System and Neural Style Transfer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9176–9186. [Google Scholar] [CrossRef]
- Geng, Z.; Xu, Y.; Wang, B.N.; Yu, X.; Zhu, D.Y.; Zhang, G. Target Recognition in SAR Images by Deep Learning with Training Data Augmentation. Sensors 2023, 23, 941. [Google Scholar] [CrossRef] [PubMed]
- Lang, H.; Yang, G.; Li, C.; Xu, J. Multisource Heterogeneous Transfer Learning via Feature Augmentation for Ship Classification in SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, Y.; Fu, Q. Semi-Supervised Deep Transfer Learning-Based on Adversarial Feature Learning for Label Limited SAR Target Recognition. IEEE Access 2019, 7, 152412–152420. [Google Scholar] [CrossRef]
- Zaied, S.; Toumi, A.; Khenchaf, A. Target classification using convolutional deep learning and auto-encoder models. In Proceedings of the 2018 4th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 21–24 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Q.; Teng, Z.; Xing, J.; Gao, J.; Hu, W.; Maybank, S. Learning Attentions: Residual Attentional Siamese Network for High Performance Online Visual Tracking. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4854–4863. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Squeeze-and-Excitation Laplacian Pyramid Network With Dual-Polarization Feature Fusion for Ship Classification in SAR Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D.; et al. HOG-ShipCLSNet: A Novel Deep Learning Network With HOG Feature Fusion for SAR Ship Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Khenchaf, Y.; Toumi, A. Siamese Neural Network for Automatic Target Recognition Using Synthetic Aperture Radar. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Pasadena, CA, USA, 16–21 July 2023. [Google Scholar]
- Zhang, T.; Zhang, X. Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How. Remote Sens. 2021, 13, 2091. [Google Scholar] [CrossRef]
- Toumi, A.; Cexus, J.C.; Khenchaf, A. A proposal learning strategy on CNN architectures for targets classification. In Proceedings of the 2022 6th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sfax, Tunisia, 24–27 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Raj, J.A.; Idicula, S.M.; Paul, B. One-Shot Learning-Based SAR Ship Classification Using New Hybrid Siamese Network. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Lang, H.; Wang, R.; Zheng, S.; Wu, S.; Li, J. Ship Classification in SAR Imagery by Shallow CNN Pre-Trained on Task-Specific Dataset with Feature Refinement. Remote Sens. 2022, 14, 5986. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Su, H.; Gao, L.; Wang, T. Deep Learning for SAR Ship Detection: Past, Present and Future. Remote Sens. 2022, 14, 2712. [Google Scholar] [CrossRef]
- Er, M.; Zhang, Y.; Chen, J.; Gao, W. Ship detection with deep learning: A survey. Artif. Intell. Rev. 2023, 56, 1–41. [Google Scholar] [CrossRef]
- Zhao, P.; Liu, K.; Zou, H.; Zhen, X. Multi-Stream Convolutional Neural Network for SAR Automatic Target Recognition. Remote Sens. 2018, 10, 1473. [Google Scholar] [CrossRef]
- Wang, L.; Bai, X.; Zhou, F. Few-Shot SAR ATR Based on Conv-BiLSTM Prototypical Networks. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Baird, Z.; Mcdonald, M.K.; Rajan, S.; Lee, S.J. A CNN-LSTM Network for Augmenting Target Detection in Real Maritime Wide Area Surveillance Radar Data. IEEE Access 2020, 8, 179281–179294. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, K.; Chen, B.; Liu, C.; Li, W.; Zou, Z.; Shi, Z. RSMamba: Remote Sensing Image Classification with State Space Model. arXiv 2024, arXiv:2403.19654. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv 2024, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Yang, G.; Lang, H. Semisupervised Heterogeneous Domain Adaptation via Dynamic Joint Correlation Alignment Network for Ship Classification in SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3175056. [Google Scholar] [CrossRef]
- Ma, L.; Tian, S. A Hybrid CNN-LSTM Model for Aircraft 4D Trajectory Prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Alsanwy, S.; Asadi, H.; Qazani, M.R.C.; Mohamed, S.; Nahavandi, S. A CNN-LSTM Based Model to Predict Trajectory of Human-Driven Vehicle. In Proceedings of the 2023 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Honolulu, HI, USA, 1–4 October 2023; pp. 3097–3103. [Google Scholar] [CrossRef]
- Wang, M.; Guo, X.; She, Y.; Zhou, Y.; Liang, M.; Chen, Z.S. Advancements in Deep Learning Techniques for Time Series Forecasting in Maritime Applications: A Comprehensive Review. Information 2024, 15, 507. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, J.; Heng, W.; Ren, K.; Song, J. Transfer Learning with Convolutional Neural Networks for SAR Ship Recognition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 322, 072001. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings; Bengio, Y., LeCun, Y., Eds.; DBLP: Trier, Germany, 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Sandler, M.; Howard, A.G.; Zhu, M.; Zhmoginov, A.; Chen, L. Inverted Residuals and Linear Bottlenecks: Mobile Networks for Classification, Detection and Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Basha, S.S.; Dubey, S.R.; Pulabaigari, V.; Mukherjee, S. Impact of fully connected layers on performance of convolutional neural networks for image classification. Neurocomputing 2020, 378, 112–119. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; Proceedings of Machine Learning Research; Gordon, G., Dunson, D., Dudík, M., Eds.; AISTATS: Amherst, MA, USA, 2011; Volume 15, pp. 315–323. [Google Scholar]
- Olah, C. Understanding LSTM Networks. 2015. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 12 March 2022).
- Keydel, E.R.; Lee, S.W.; Moore, J.T. MSTAR extended operating conditions: A tutorial. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery III, Orlando, FL, USA, 8–12 April 1996; Zelnio, E.G., Douglass, R.J., Eds.; International Society for Optics and Photonics—SPIE: Bellingham, WA, USA, 1996; Volume 2757, pp. 228–242. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. AutoAugment: Learning Augmentation Policies from Data. arXiv 2019, arXiv:1805.09501. [Google Scholar] [CrossRef]
- Huang, L.; Liu, B.; Li, B.; Guo, W.; Yu, W.; Zhang, Z.; Yu, W. OpenSARShip: A Dataset Dedicated to Sentinel-1 Ship Interpretation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 195–208. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. What, Where, and How to Transfer in SAR Target Recognition Based on Deep CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2324–2336. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition. Sci. China Inf. Sci. 2020, 63, 1–19. [Google Scholar] [CrossRef]
- Lei, X.; Pan, H.; Huang, X. A Dilated CNN Model for Image Classification. IEEE Access 2019, 7, 124087–124095. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Chen, D. CSRNet: Dilated Convolutional Neural Networks for Understanding the Highly Congested Scenes. arXiv 2018, arXiv:1802.10062. [Google Scholar] [CrossRef]











| CNN Layer | Layer Steps | Parameters |
|---|---|---|
| Input | ||
| CONV #1 | Zero padding 2D Conv 2D Max-pooling 2D Dropout | = (1,1) = 64, = (2,2) = (1,1) act = ’ReLU’ = (4,4), = (4,4) 25% |
| CONV #2 | Zero padding 2D Conv 2D Max-pooling 2D Dropout | = (1,1) = 64, = (2,2) = (1,1) act = ’ReLU’ = (4,4), = (4,4) 25% |
| CONV #3 | Zero padding 2D Conv 2D Max-pooling 2D Dropout | = (1,1) = 128, = (2,2) = (1,1) act = ’ReLU’ = (4,4), = (4,4) 25% |
| FC #1 | Dense Dropout | = N, act = ’ReLU’ 50% |
| FC #2 | Dense Dropout | = , act = ’ReLU’ 50% |
| Output | Dense | = = C, act = ’identity’ |
| (, , ) | Validation Accuracy (%) | ||
|---|---|---|---|
| FUSAR-Ship | OpenSARShip | MSTAR | |
| (32,32,64) | 64.95 | 73.04 | 97.55 |
| (32,64,64) | 65.03 | 73.19 | 97.92 |
| (64,64,128) | 65.94 | 74.81 | 97.96 |
| (64,128,128) | 65.51 | 75.56 | 98.65 |
| (128,128,256) | 65.03 | 74.07 | 98.72 |
| (128,256,256) | 63.57 | 73.93 | 98.69 |
| (256,256,512) | 64.34 | 74.07 | 98.65 |
| (256,512,512) | 63.61 | 74.22 | 99.12 |
| N | Validation Accuracy (%) | ||
|---|---|---|---|
| FUSAR-Ship | OpenSARShip | MSTAR | |
| 128 | 64.60 | 73.48 | 98.91 |
| 256 | 65.94 | 75.56 | 99.12 |
| 384 | 64.82 | 75.41 | 98.83 |
| 512 | 64.34 | 74.22 | 98.69 |
| Dataset | Optimal Parameters | Validation Accuracy (%) | ||
|---|---|---|---|---|
| (,) | (,,) | N | ||
| FUSAR-Ship | (4,4) | (64,64,128) | 256 | 65.94 |
| OpenSARShip | (20,20) | (64,128,128) | 256 | 75.56 |
| MSTAR | (25,25) | (128,128,256) | 256 | 99.12 |
| Layer | Type | Kernel | Kernel Size | Stride | Input Size |
|---|---|---|---|---|---|
| 1 | Convolution2D | 1 | |||
| 2 | Pool | - | 4 | ||
| 3 | Convolution2D | 1 | |||
| 4 | Pool | - | 4 | ||
| 5 | Convolution2D | 1 | |||
| 6 | Pool | - | 4 | ||
| 7 | LSTM | - | - | - | |
| 8 | FC | N | - | - | . |
| 9 | Softmax | - | - | N |
| (, , ) | Validation Accuracy (%) | ||
|---|---|---|---|
| FUSAR-Ship | OpenSARShip | MSTAR | |
| (32,32,64) | 63.78 | 74.53 | 97.72 |
| (32,64,64) | 64.04 | 74.06 | 98.35 |
| (64,64,128) | 65.29 | 75.78 | 99.04 |
| (64,128,128) | 63.48 | 74.84 | 98.64 |
| (128,128,256) | 65.20 | 74.84 | 98.90 |
| (128,256,256) | 64.82 | 74.53 | 99.15 |
| (256,256,512) | 63.74 | 74.84 | 99.01 |
| (256,512,512) | 64.17 | 75.00 | 99.04 |
| Validation Accuracy (%) | |||
|---|---|---|---|
| FUSAR-Ship | OpenSARShip | MSTAR | |
| 32 | 65.16 | 75.31 | 99.23 |
| 64 | 64.52 | 75.47 | 99.08 |
| 96 | 63.78 | 73.91 | 99.19 |
| 128 | 65.29 | 75.78 | 99.15 |
| 160 | 64.34 | 74.69 | 99.15 |
| 192 | 64.69 | 74.84 | 98.71 |
| N | Validation Accuracy (%) | ||
|---|---|---|---|
| FUSAR-Ship | OpenSARShip | MSTAR | |
| 64 | 64.82 | 75.32 | 99.16 |
| 128 | 65.29 | 75.78 | 99.15 |
| 184 | 64.85 | 75.11 | 99.34 |
| 256 | 64.94 | 74.98 | 99.43 |
| 320 | 64.88 | 75.21 | 99.52 |
| 384 | 64.91 | 74.84 | 99.49 |
| Dataset | Optimal Parameters | Validation Accuracy (%) | |||
|---|---|---|---|---|---|
| (,) | (,,) | N | |||
| FUSAR-Ship | (11,11) | (64,64,128) | 128 | 128 | 65.29 |
| OpenSARShip | (18,18) | (64,64,128) | 128 | 128 | 75.78 |
| MSTAR | (24,24) | (128,256,256) | 32 | 320 | 99.52 |
| Targets | 2S1 | BMP2 | BRDM2 | BTR60 | BTR70 | D7 | T62 | T72 | ZIL131 | ZSU234 |
|---|---|---|---|---|---|---|---|---|---|---|
| Entire training | 299 | 233 | 298 | 256 | 233 | 299 | 299 | 232 | 299 | 299 |
| Test | 274 | 195 | 274 | 195 | 196 | 274 | 273 | 196 | 274 | 274 |
| Training | Validation | Entire Training | Test | |
|---|---|---|---|---|
| Entire Training | Entire Training | Dataset | Dataset | |
| Cargo | 99 | 25 | 124 | 31 |
| Bulk Carrier | 335 | 84 | 419 | 105 |
| Container Ship | 104 | 26 | 130 | 33 |
| Training | Validation | Entire Training | Test | |
|---|---|---|---|---|
| Entire Training | Entire Training | Dataset | Dataset | |
| Cargo | 1083 | 271 | 1354 | 339 |
| Bulk Carrier | 174 | 44 | 218 | 55 |
| Fishing | 502 | 126 | 628 | 157 |
| Tanker | 94 | 24 | 118 | 30 |
| Architecture | Number of | Training | Number | Test Loss | Test |
|---|---|---|---|---|---|
| Parameters | Time (s) | of Epochs | Accuracy (%) | ||
| VGG16 | 134.28M | 711.18 | 99 | 4.3436 | 65.23 |
| ResNet50 | 23.52M | 4602.78 | 763 | 3.8623 | 67.99 |
| Xception | 20.82M | 2822.80 | 505 | 2.8643 | 67.13 |
| DenseNet121 | 6.96M | 5250.83 | 388 | 3.4620 | 71.08 |
| EfficientNetB0 | 4.01M | 1178.61 | 131 | 2.3526 | 61.45 |
| MobileNetV2 | 2.23M | 1090.02 | 250 | 2.9414 | 57.31 |
| Proposed CNN | 363k | 3447.87 | 4109 | 4.8501 | 67.47 |
| Proposed CNN-LSTM | 3.66M | 377.54 | 163 | 4.1756 | 65.58 |
| Architecture | Number of | Training | Number | Test Loss | Test |
|---|---|---|---|---|---|
| Parameters | Time (s) | of Epochs | Accuracy (%) | ||
| VGG16 | 134.27M | 718.57 | 270 | 2.0185 | 72.19 |
| ResNet50 | 23.51M | 3502.18 | 1854 | 5.8233 | 57.99 |
| Xception | 20.81M | 1958.26 | 978 | 4.1148 | 65.09 |
| DenseNet121 | 6.96M | 5578.21 | 1447 | 8.4319 | 56.80 |
| EfficientNetB0 | 4.01M | 254.74 | 111 | 2.9316 | 52.07 |
| MobileNetV2 | 2.23M | 621.78 | 398 | 2.5883 | 56.21 |
| Proposed CNN | 10.02M | 1375.10 | 1642 | 6.9658 | 69.82 |
| Proposed CNN-LSTM | 6.17M | 132.61 | 166 | 2.5124 | 70.41 |
| Architecture | Number of | Training | Number | Test Loss | Test |
|---|---|---|---|---|---|
| Parameters | Time (s) | of Epochs | Accuracy (%) | ||
| VGG16 | 138.30M | 1073.35 | 132 | 0.1532 | 98.14 |
| ResNet50 | 23.53M | 2902.83 | 425 | 0.2698 | 95.67 |
| Xception | 20.83M | 3397.96 | 504 | 0.1836 | 95.34 |
| DenseNet121 | 6.96M | 11188.50 | 731 | 0.1543 | 97.77 |
| EfficientNetB0 | 4.02M | 1541.87 | 155 | 0.5745 | 86.85 |
| MobileNetV2 | 2.24M | 1671.27 | 275 | 4.2541 | 40.74 |
| Proposed CNN | 31.10M | 1880.30 | 289 | 0.1239 | 98.52 |
| Proposed CNN-LSTM | 59.33M | 686.19 | 74 | 0.0910 | 98.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toumi, A.; Cexus, J.-C.; Khenchaf, A.; Abid, M. A Combined CNN-LSTM Network for Ship Classification on SAR Images. Sensors 2024, 24, 7954. https://doi.org/10.3390/s24247954
Toumi A, Cexus J-C, Khenchaf A, Abid M. A Combined CNN-LSTM Network for Ship Classification on SAR Images. Sensors. 2024; 24(24):7954. https://doi.org/10.3390/s24247954
Chicago/Turabian StyleToumi, Abdelmalek, Jean-Christophe Cexus, Ali Khenchaf, and Mahdi Abid. 2024. "A Combined CNN-LSTM Network for Ship Classification on SAR Images" Sensors 24, no. 24: 7954. https://doi.org/10.3390/s24247954
APA StyleToumi, A., Cexus, J.-C., Khenchaf, A., & Abid, M. (2024). A Combined CNN-LSTM Network for Ship Classification on SAR Images. Sensors, 24(24), 7954. https://doi.org/10.3390/s24247954









