Few-Mode Fiber with Low Spontaneous Raman Scattering for Quantum Key Distribution and Classical Optical Communication Coexistence Systems
Abstract
1. Introduction
2. The SpRS When QKD Coexists with Classical Signals in FMF
2.1. Derivation of the SpRS in FMF
2.2. Impact of the SpRS on QKD
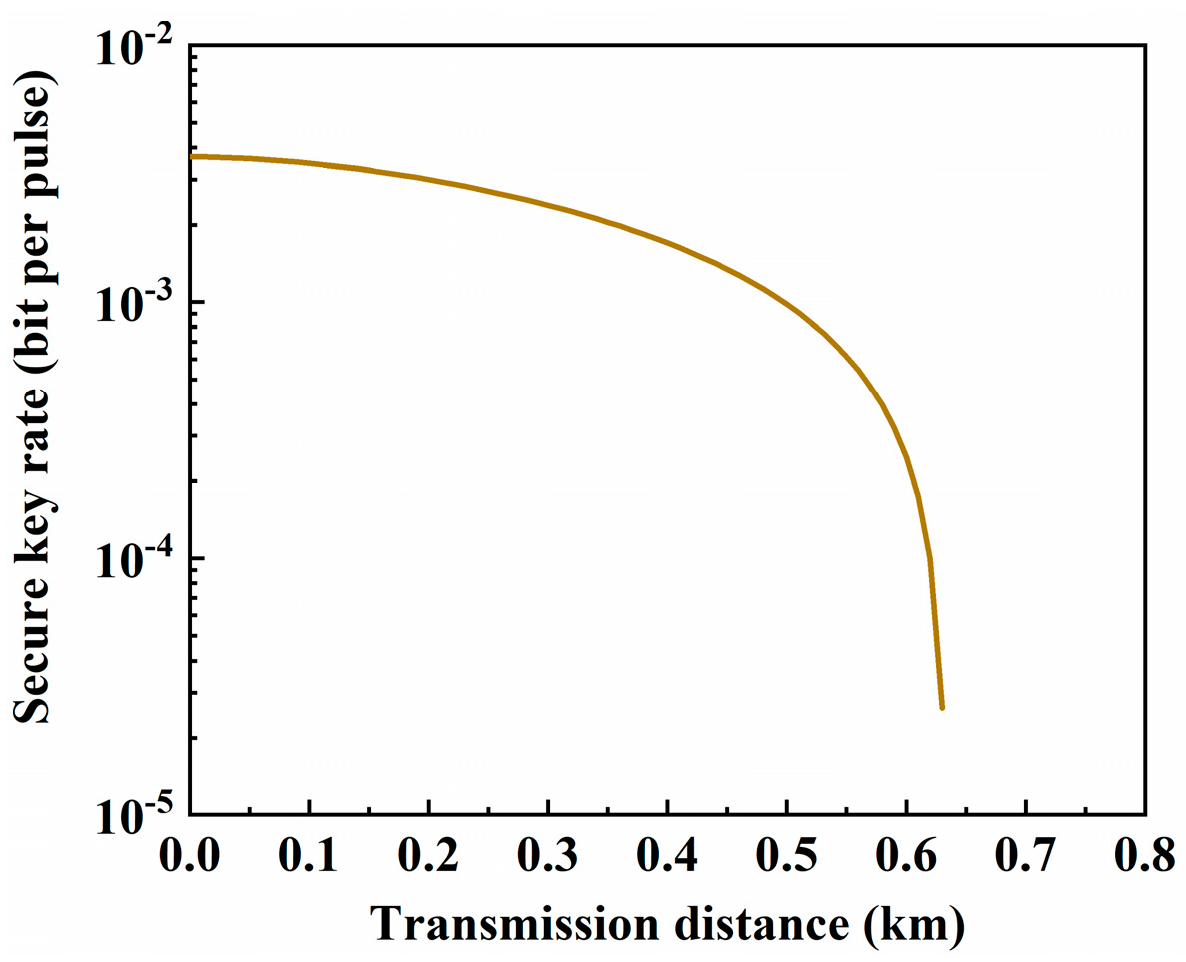
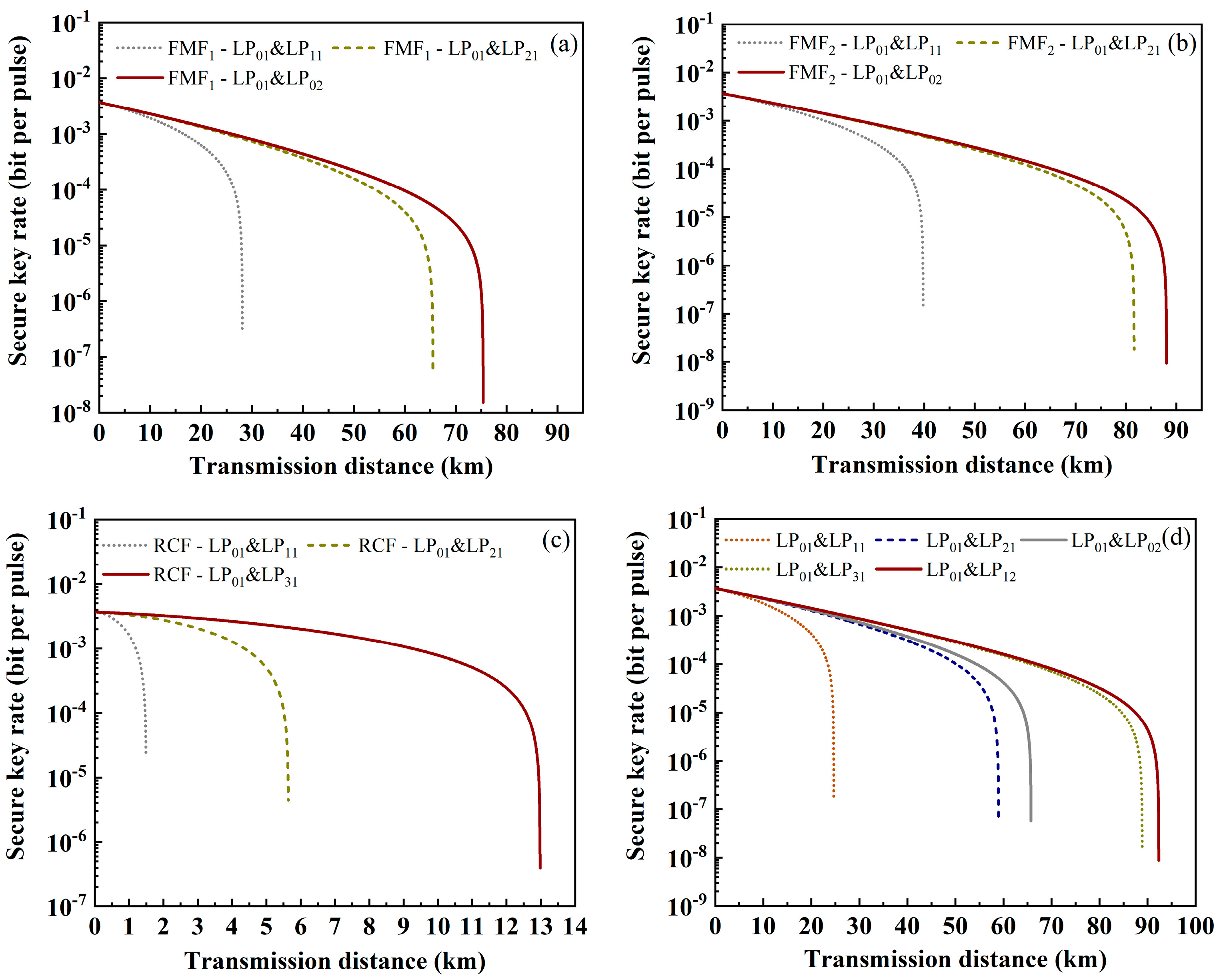
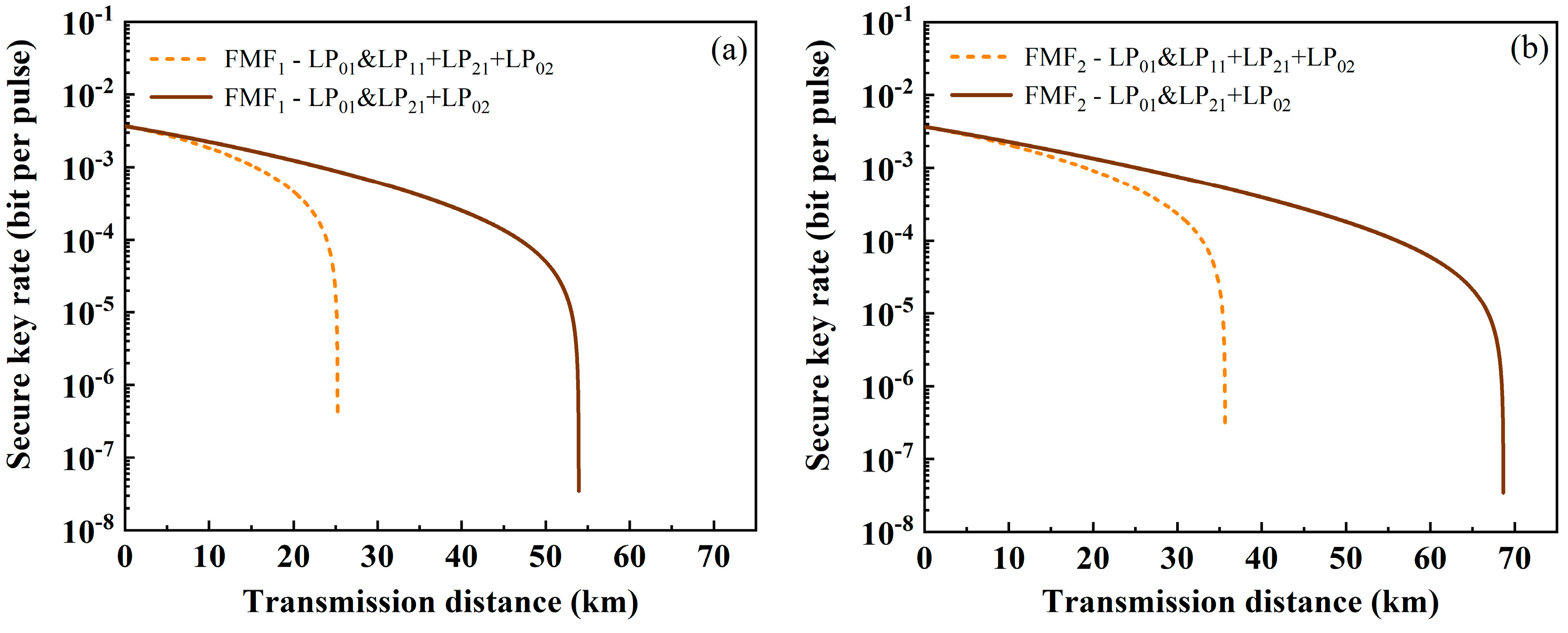
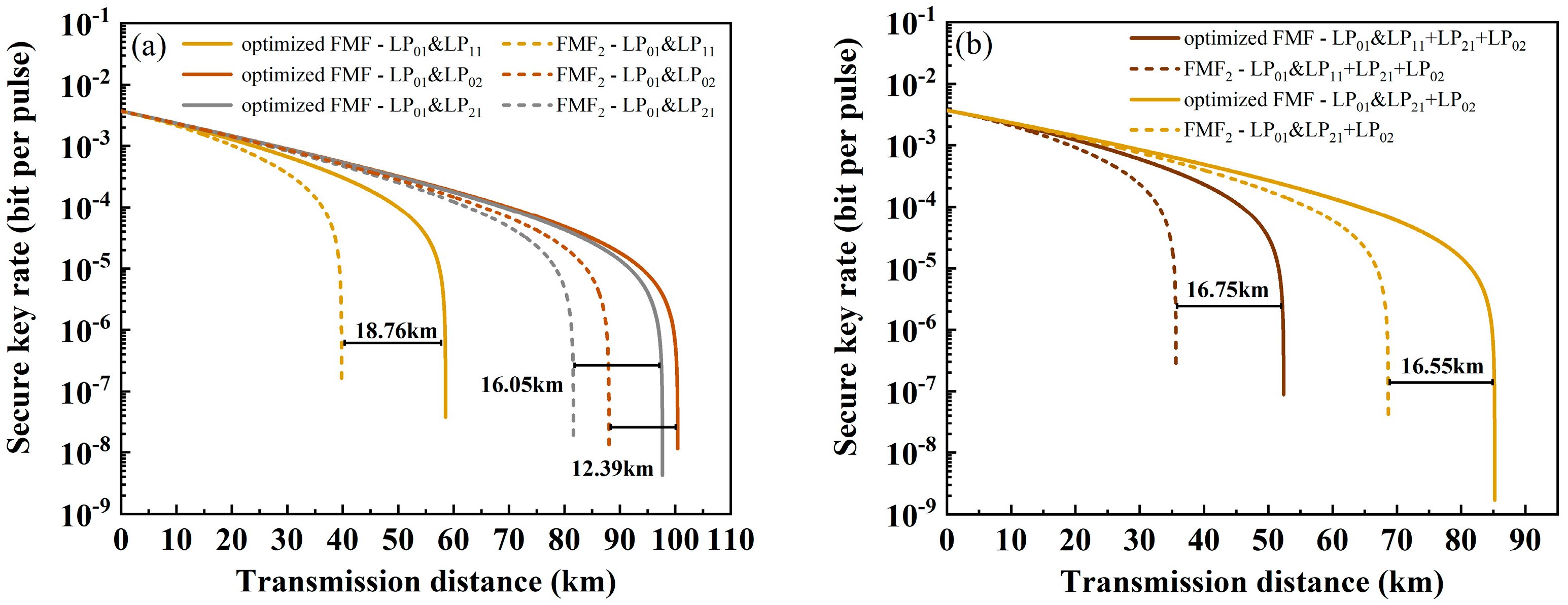
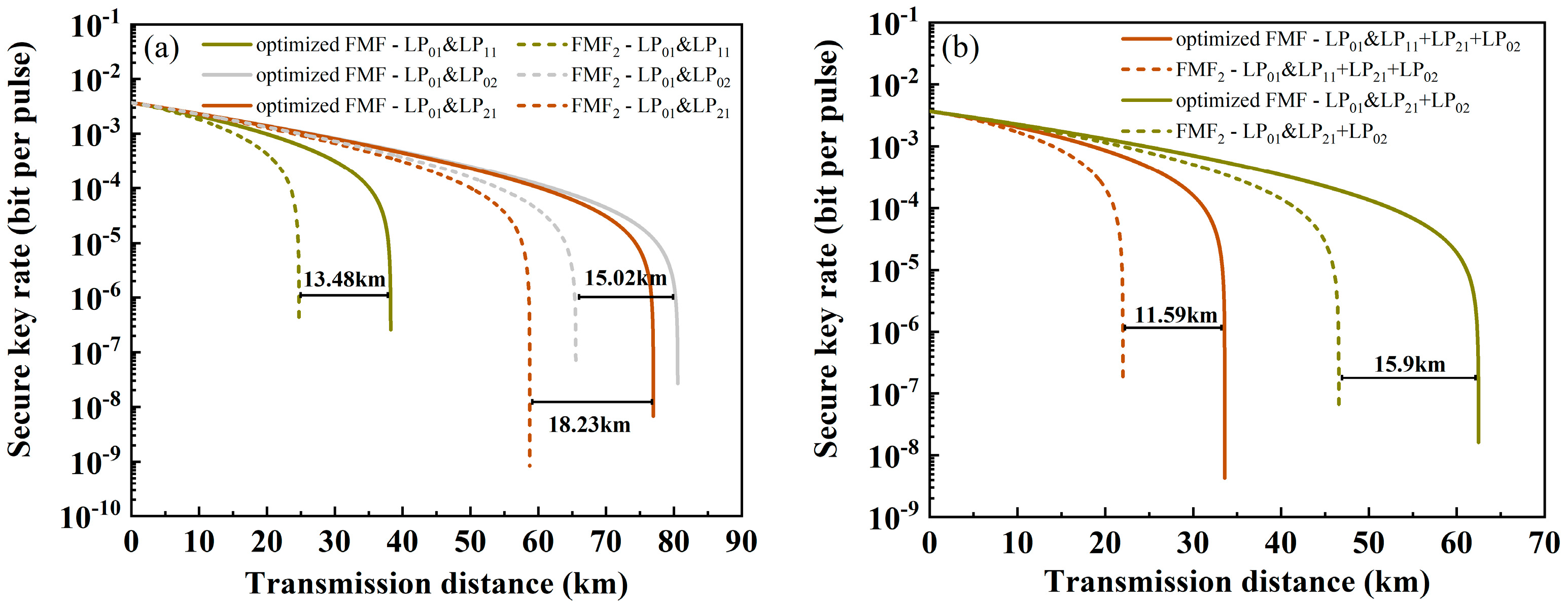
3. Performance of QKD in FMFs
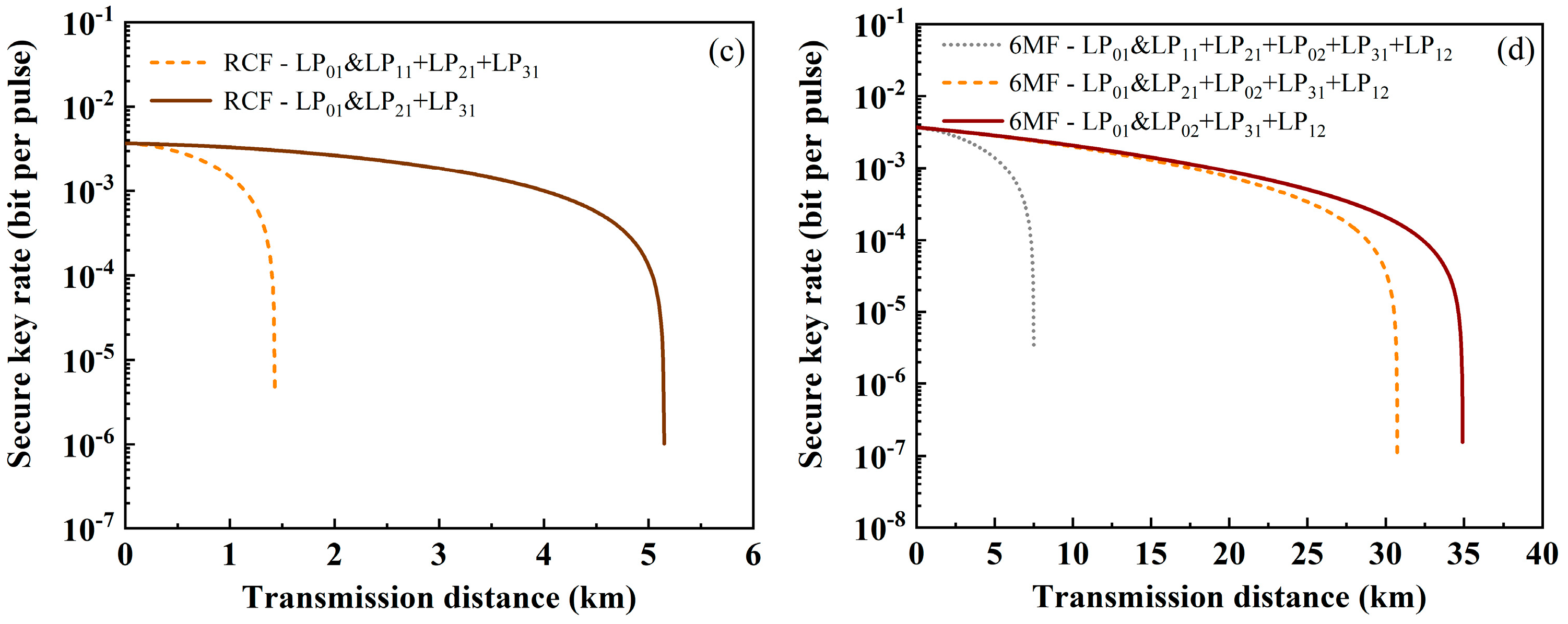
4. Performance of QKD in the Ring-Assisted FMF
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Dynes, J.F.; Wonfor, A.; Tam, W.W.-S.; Sharpe, A.W.; Takahashi, R.; Lucamarini, M.; Plews, A.; Yuan, Z.L.; Dixon, A.R.; Cho, J.; et al. Cambridge quantum network. Npj Quantum Inf. 2019, 5, 101. [Google Scholar] [CrossRef]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
- Fan-Yuan, G.-J.; Lu, F.-Y.; Wang, S.; Yin, Z.-Q.; He, D.-Y.; Chen, W.; Zhou, Z.; Wang, Z.-H.; Teng, J.; Guo, G.-C.; et al. Robust and adaptable quantum key distribution network without trusted nodes. Optica 2022, 9, 812–823. [Google Scholar] [CrossRef]
- Xu, F.; Xu, H.; Lo, H.-K. Protocol choice and parameter optimization in decoy-state measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052333. [Google Scholar] [CrossRef]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef]
- Kong, W.; Sun, Y.; Gao, Y.; Ji, Y. Core and Wavelength Allocation Schemes for Noise Suppression in Quantum Key Distribution Over Multicore Fiber. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–12. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Li, J.; Lin, R.; Zhang, J.; Chen, J. Hybrid Trusted/Untrusted Relay-Based Quantum Key Distribution Over Optical Backbone Networks. IEEE J. Sel. Areas Commun. 2021, 39, 2701–2718. [Google Scholar] [CrossRef]
- Tang, J.-S.; Tang, L.; Xia, K. Three methods for the single-photon transport in a chiral cavity quantum electrodynamics system. Chin. Opt. Lett. 2022, 20, 062701. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.-J.; Jiang, C.; Chen, J.-P.; Zhang, C.; Pan, W.-X.; Ma, D.; Dong, H.; Xiong, J.-M.; Zhang, C.-J.; et al. Experimental Twin-Field Quantum Key Distribution over 1000 km Fiber Distance. Phys. Rev. Lett. 2023, 130, 210801. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Tan, H.; Lu, Y.; Liao, S.-K.; Huang, J.; Li, H.; Wang, Z.; Mao, H.-K.; Yan, B.; et al. High-rate quantum key distribution exceeding 110 Mb s–1. Nat. Photonics 2023, 17, 416–421. [Google Scholar] [CrossRef]
- Geng, J.-Q.; Fan-Yuan, G.-J.; Li, K.-J.; Tang, M.; Wang, S.; He, D.-Y.; Chen, W.; Yin, Z.-Q.; Guo, G.-C.; Han, Z.-F. Integration in the C-band between quantum key distribution and the classical channel of 25 dBm launch power over multicore fiber media. Opt. Lett. 2022, 47, 3111–3114. [Google Scholar] [CrossRef]
- Li, N.; Hu, C.; Lu, X.-M. Information-theoretic perspective on performance assessment and fundamental limit of quantum imaging. Chin. Opt. Lett. 2024, 22, 060009. [Google Scholar] [CrossRef]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.-K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103042. [Google Scholar] [CrossRef]
- Eraerds, P.; Walenta, N.; Legré, M.; Gisin, N.; Zbinden, H. Quantum key distribution and 1 Gbps data encryption over a single fibre. New J. Phys. 2010, 12, 063027. [Google Scholar] [CrossRef]
- Peters, N.A.; Toliver, P.; Chapuran, T.E.; Runser, R.J.; McNown, S.R.; Peterson, C.G.; Rosenberg, D.; Dallmann, N.; Hughes, R.J.; McCabe, K.P.; et al. Dense wavelength multiplexing of 1550 nm QKD with strong classical channels in reconfigurable networking environments. New J. Phys. 2009, 11, 045012. [Google Scholar] [CrossRef]
- Karinou, F.; Comandar, L.; Brunner, H.H.; Hillerkuss, D.; Fung, F.; Bettelli, S.; Mikroulis, S.; Wang, D.; Yi, Q.; Kuschnerov, M.; et al. Experimental Evaluation of the Impairments on a QKD System in a 20-Channel WDM Co-Existence Scheme. In Proceedings of the 2017 IEEE Photonics Society Summer Topical Meeting Series (SUM), San Juan, PR, USA, 10–12 July 2017; pp. 145–146. [Google Scholar]
- Dynes, J.F.; Kindness, S.J.; Tam, S.W.-B.; Plews, A.; Sharpe, A.W.; Lucamarini, M.; Fröhlich, B.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Quantum key distribution over multicore fiber. Opt. Express 2016, 24, 8081–8087. [Google Scholar] [CrossRef]
- Winzer, P.J. Making spatial multiplexing a reality. Nat. Photonics 2014, 8, 345–348. [Google Scholar] [CrossRef]
- Wang, B.-X.; Mao, Y.; Shen, L.; Zhang, L.; Lan, X.-B.; Ge, D.; Gao, Y.; Li, J.; Tang, Y.-L.; Tang, S.-B.; et al. Long-distance transmission of quantum key distribution coexisting with classical optical communication over a weakly-coupled few-mode fiber. Opt. Express 2020, 28, 12558–12565. [Google Scholar] [CrossRef]
- Stolen, R.H. Relation between the effective area of a single-mode fiber and the capture fraction of spontaneous Raman scattering. J. Opt. Soc. Am. B 2002, 19, 498–501. [Google Scholar] [CrossRef]
- Bacco, D.; Ding, Y.; Dalgaard, K.; Rottwitt, K.; Oxenløwe, L.K. Space division multiplexing chip-to-chip quantum key distribution. Sci. Rep. 2017, 7, 12459. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Su, J.; Li, X.; Ou, Z.Y. Distribution of entangled photon pairs over few-mode fibers. Sci. Rep. 2017, 7, 14954. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, M.; Tokuda, M.; Negishi, Y. Measurement of polarization mode coupling along a polarization-maintaining optical fiber using a backscattering technique. Opt. Lett. 1983, 8, 546–548. [Google Scholar] [CrossRef] [PubMed]
- Sano, A.; Takara, H.; Kobayashi, T.; Miyamoto, Y. Crosstalk-Managed High Capacity Long Haul Multicore Fiber Transmission With Propagation-Direction Interleaving. J. Light. Technol. 2014, 32, 2771–2779. [Google Scholar] [CrossRef]
- Koshiba, M.; Saitoh, K.; Takenaga, K.; Matsuo, S. Analytical Expression of Average Power-Coupling Coefficients for Estimating Intercore Crosstalk in Multicore Fibers. IEEE Photonics J. 2012, 4, 1987–1995. [Google Scholar] [CrossRef]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Marcuse, D. Derivation of Coupled Power Equations. Bell Syst. Tech. J. 1972, 51, 229–237. [Google Scholar] [CrossRef]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 413–487. [Google Scholar] [CrossRef]
- Bures, J. Guided Optics: Optical Fibers and All-Fiber Components; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-Mode Fibers for Mode-Division-Multiplexed Systems. J. Light. Technol. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Jiang, S.; Ma, L.; Zhang, Z.; Xu, Z.; Shuai, W.; Du, J.; Yang, C.; Tong, W.; He, Z. Design and characterization of ring-assisted few-mode fibers for weakly coupled mode-division multiplexing transmission. J. Light. Technol. 2018, 36, 5547–5555. [Google Scholar] [CrossRef]
- Lu, G.; Liu, S.; Lv, D.; Chen, M.; Zhang, Z. Design of ring-assisted few-mode fiber with low loss for improved mode-division multiplexing. Laser Phys. 2021, 31, 105101. [Google Scholar] [CrossRef]
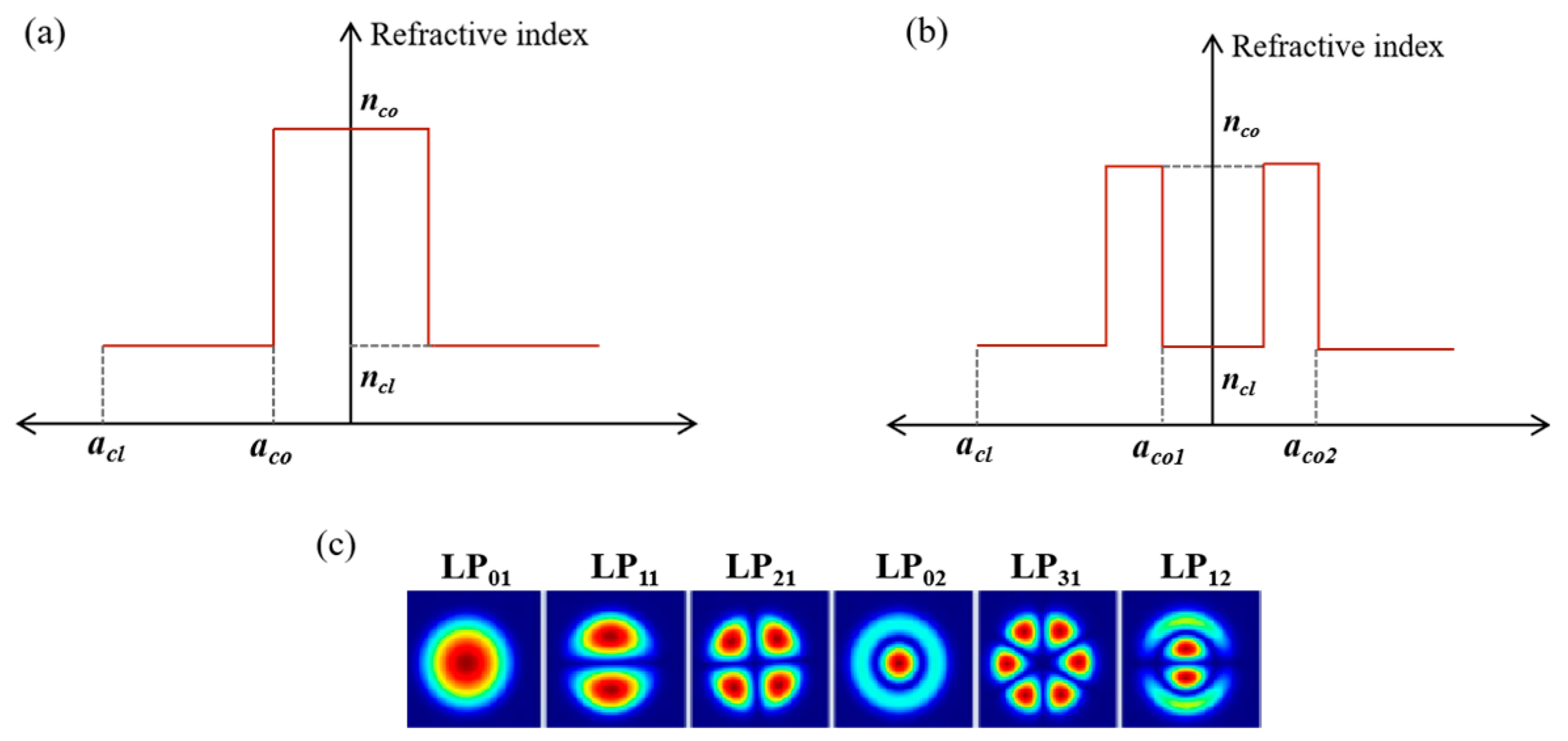
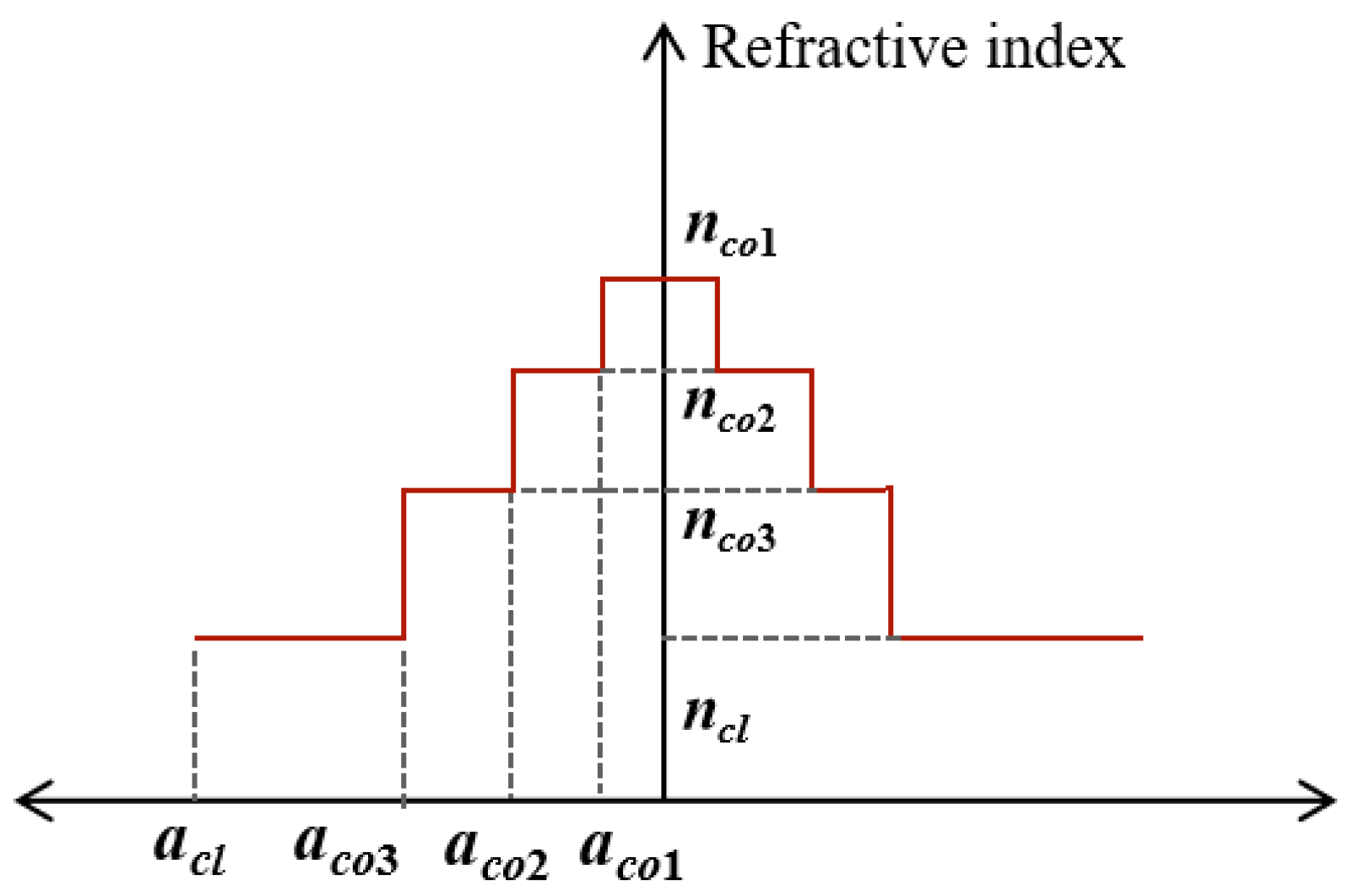


| nco | ncl | acl (μm) | aco (μm) | |
|---|---|---|---|---|
| SMF | 1.452 | 1.444 | 62.5 | 3 |
| FMF1 | 1.452 | 1.444 | 62.5 | 7 |
| FMF2 | 1.459 | 1.444 | 62.5 | 6 |
| RCF | 1.459 | 1.444 | 62.5 | aco1 = 4, aco2 = 7.5 |
| 6MF | 1.456 | 1.444 | 62.5 | 8 |
| Δneff (×10−3) | ||||||
|---|---|---|---|---|---|---|
| LP01 and LP11 | LP11 and LP21 | LP21 and LP02 | LP31 and LP21 | LP02 and LP31 | LP31 and LP12 | |
| FMF1 | 2.4 | 2.9 | 0.6 | - | - | - |
| FMF2 | 3.5 | 4.5 | 1.2 | - | - | - |
| RCF | 0.7 | 2.1 | - | 3.1 | - | - |
| 6MF | 2.1 | 2.8 | 0.9 | - | 2.4 | 1.6 |
| hij (km−1) | |||||
|---|---|---|---|---|---|
| LP01 and LP11 | LP01 and LP21 | LP01 and LP02 | LP01 and LP31 | LP01 and LP12 | |
| FMF1 | 3.72 × 10−4 | 5.40 × 10−5 | 3.55 × 10−5 | - | - |
| FMF2 | 1.7962 × 10−4 | 2.7054 × 10−5 | 2.0182 × 10−5 | - | - |
| RCF | 1.41 × 10−1 | 9.14 × 10−3 | - | 1.74 × 10−3 | - |
| 6-MF | 4.8449 × 10−4 | 7.1666 × 10−5 | 5.3517 × 10−5 | 1.9382 × 10−5 | 1.6384 × 10−5 |
| Δneff (×10−3) | hij (km−1) | |||||
|---|---|---|---|---|---|---|
| LP01 and LP11 | LP11 and LP02 | LP21 and LP02 | LP01 and LP11 | LP01 and LP02 | LP01 and LP21 | |
| ring-assisted FMF | 5.4 | 4.2 | 0.5 | 6.83 × 10−5 | 9.27 × 10−6 | 1.01 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Tang, J.; Kong, W.; Zhao, Z.; Zheng, J.; Liu, Y. Few-Mode Fiber with Low Spontaneous Raman Scattering for Quantum Key Distribution and Classical Optical Communication Coexistence Systems. Sensors 2024, 24, 7645. https://doi.org/10.3390/s24237645
Zhao Q, Tang J, Kong W, Zhao Z, Zheng J, Liu Y. Few-Mode Fiber with Low Spontaneous Raman Scattering for Quantum Key Distribution and Classical Optical Communication Coexistence Systems. Sensors. 2024; 24(23):7645. https://doi.org/10.3390/s24237645
Chicago/Turabian StyleZhao, Qi, Jianjun Tang, Weiwen Kong, Zhenyu Zhao, Jingjing Zheng, and Yang Liu. 2024. "Few-Mode Fiber with Low Spontaneous Raman Scattering for Quantum Key Distribution and Classical Optical Communication Coexistence Systems" Sensors 24, no. 23: 7645. https://doi.org/10.3390/s24237645
APA StyleZhao, Q., Tang, J., Kong, W., Zhao, Z., Zheng, J., & Liu, Y. (2024). Few-Mode Fiber with Low Spontaneous Raman Scattering for Quantum Key Distribution and Classical Optical Communication Coexistence Systems. Sensors, 24(23), 7645. https://doi.org/10.3390/s24237645







