An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques
Abstract
1. Introduction
2. An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques
2.1. Conjugate Gradient Method
2.2. Fast Conjugate Gradient-Based RDRCB
2.3. The Upper and Lower Boundaries of the Lagrange Multiplier
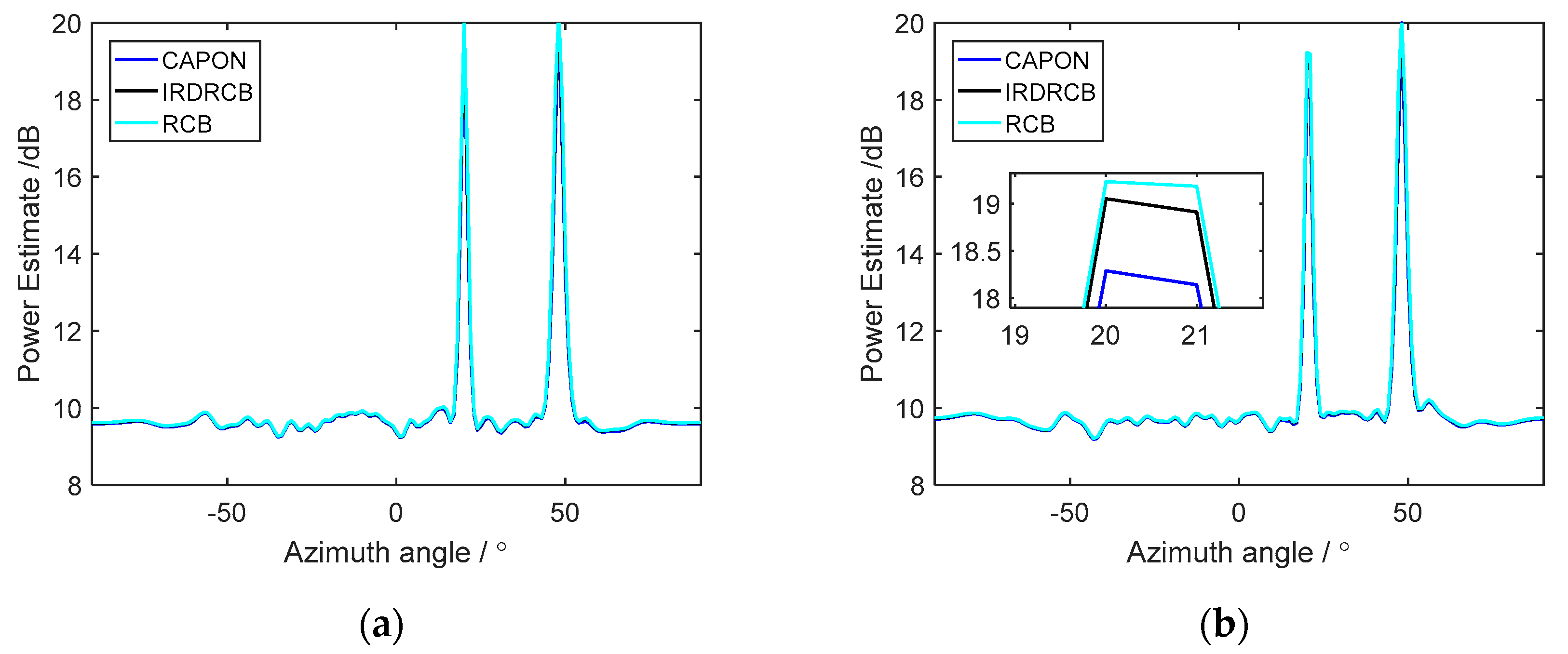
3. Numerical Examples
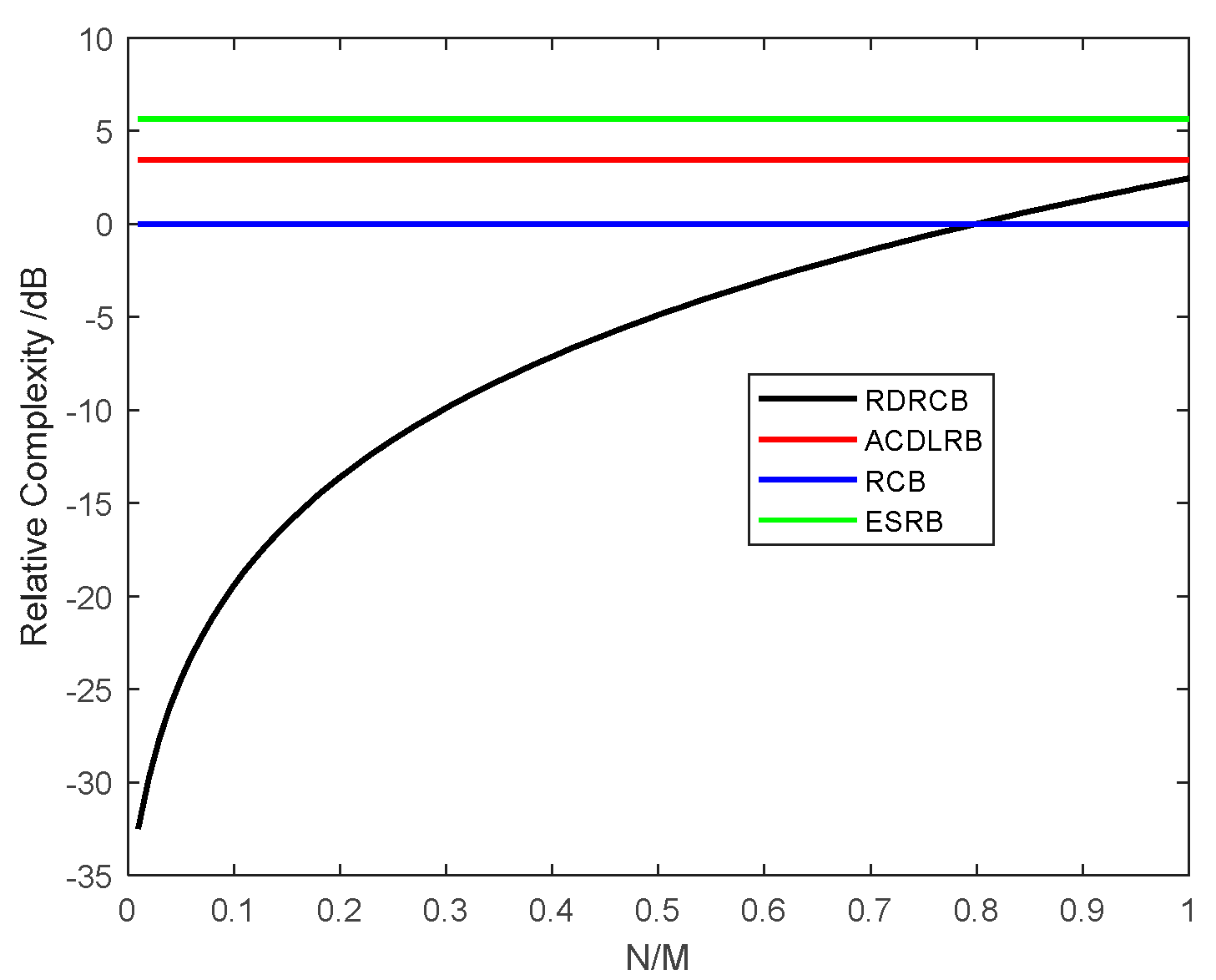
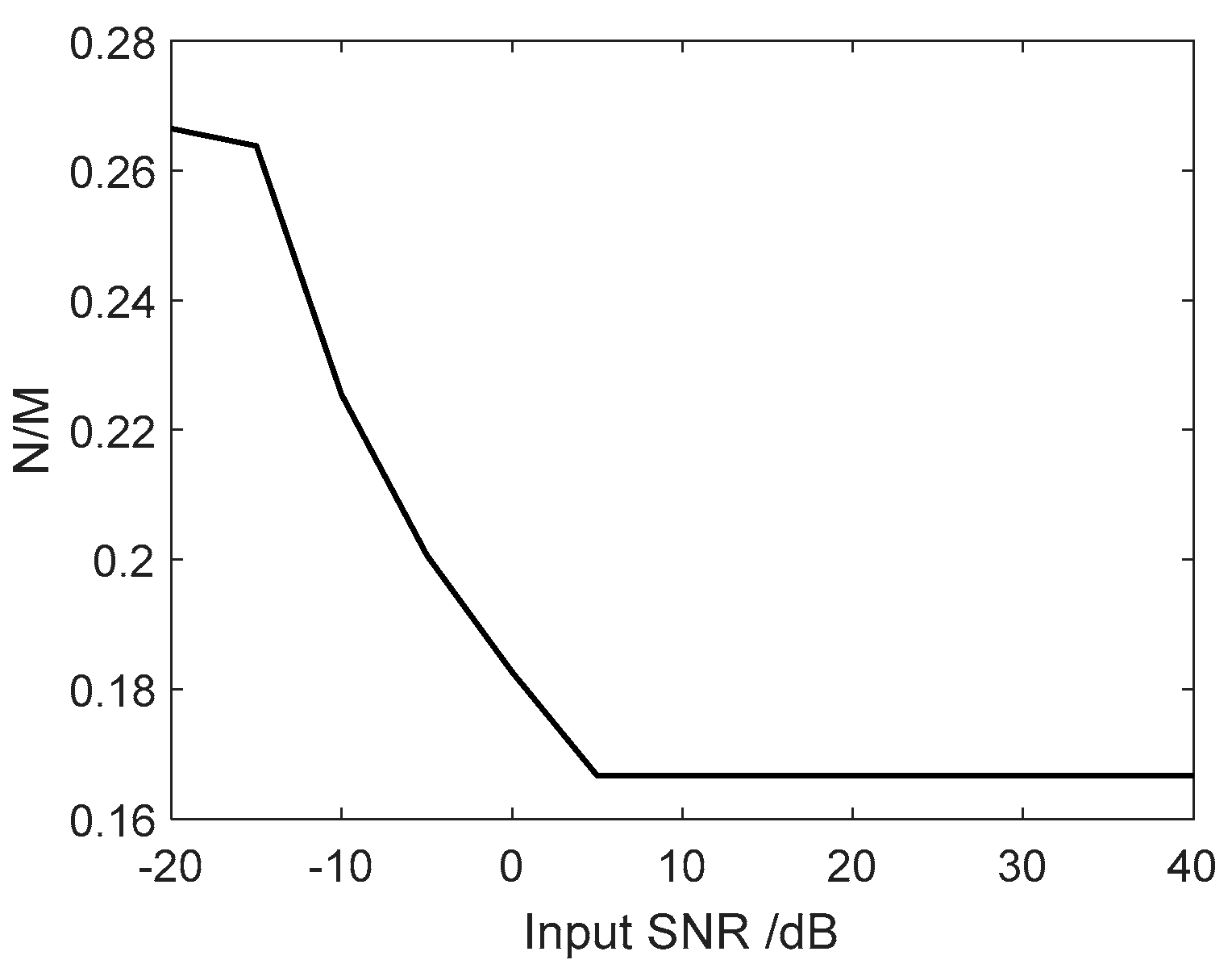
3.1. Complexity Analysis
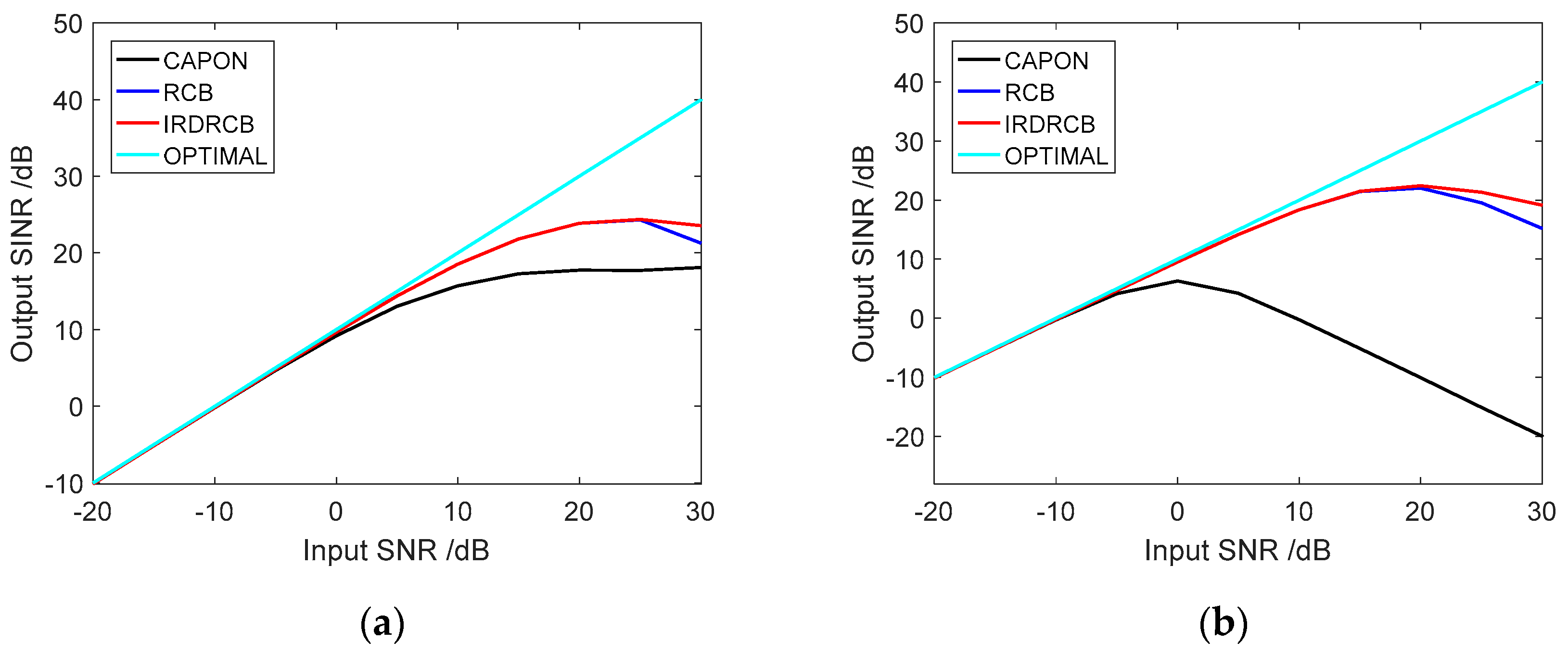
3.2. Output SINR Versus Input SNR
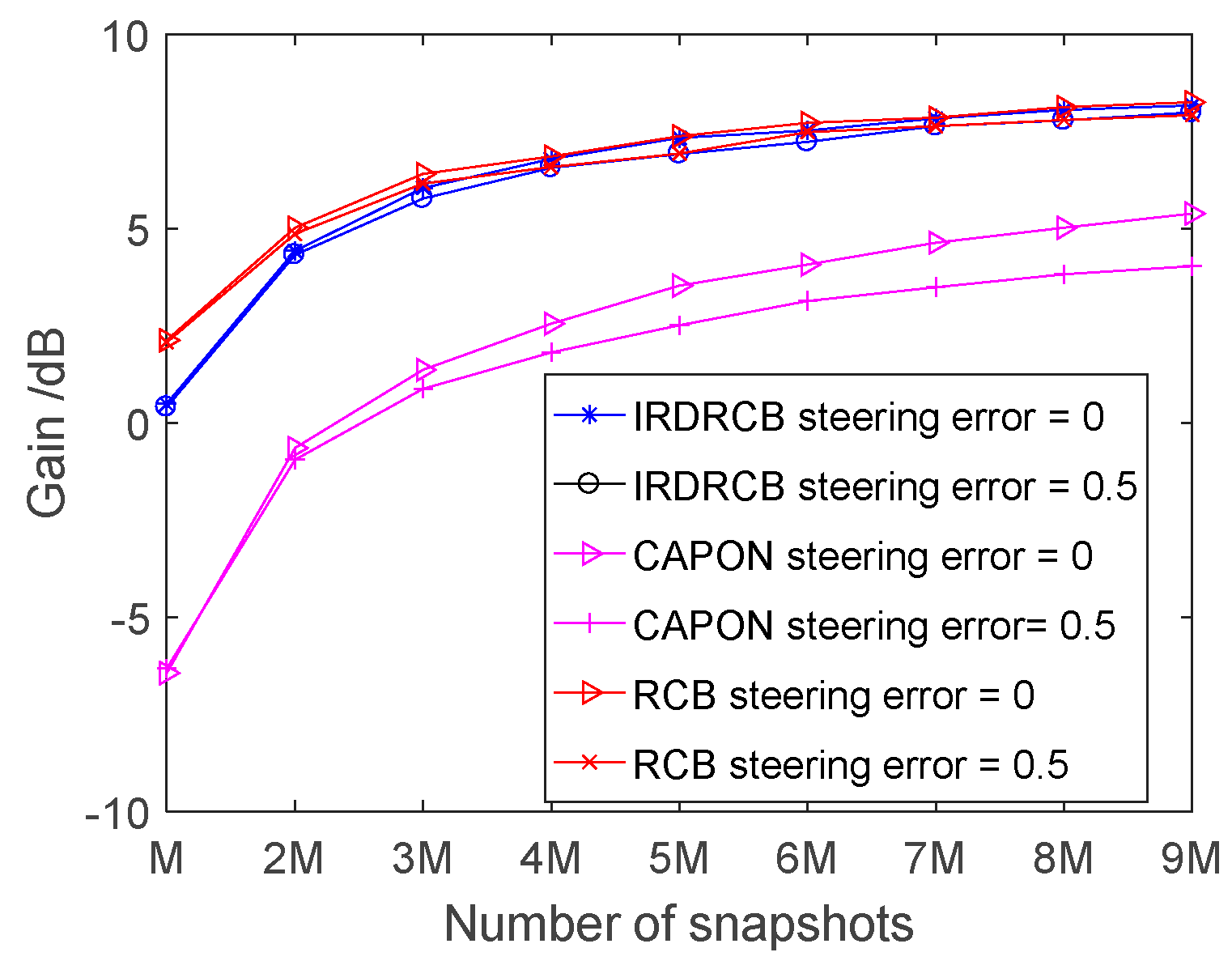
3.3. Output SINR Versus the Number of Snapshots
3.4. Azimuth Spectra
3.5. Experimental Data Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Long, T.; Chen, J.; Huang, G.; Benesty, J.; Cohen, I. Acoustic source localization based on geometric projection in reverberant and noisy environments. IEEE J. Sel. Top. Signal Process. 2019, 13, 143–155. [Google Scholar] [CrossRef]
- Karo, I.Y.; Dvorkind, T.G.; Cohen, I. Source Localization with Feedback Beamforming. IEEE Trans. Signal Process. 2021, 69, 631–640. [Google Scholar] [CrossRef]
- Montalbano, G.M.; Serebryakov, G.V. Optimum Beamforming Performance Degradation in the Presence of Imperfect Spatial Coherence of Wavefronts. IEEE Trans. Antennas Propag. 2003, 51, 1030–1039. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, T.; Wang, W.-Q.; So, H.C. Robust Adaptive Beamforming via Simplified Interference Power Estimation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3139–3152. [Google Scholar] [CrossRef]
- Lee, C.-C.; Lee, J.-H. Eigenspace-based adaptive array beamforming with robust capabilities. IEEE Trans. Antennas Propag. 1997, 45, 1711–1716. [Google Scholar] [CrossRef]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Dong, J.; Hu, P.; Feng, J. Double constraint Time-domain MVDR adaptive beamforming algorithm. Ship Sci. Technol. 2021, 43, 127–130. [Google Scholar]
- Bo, L.; Zhang, X.; Xiong, J. Robust Capon Beamforming for Towed Array Sonar During Maneuvering. J. Electron. Inf. Technol. 2018, 40, 2423–2429. [Google Scholar]
- Tang, B.; Tang, J.; Peng, Y. Convergence Rate of LSMI in Amplitude Heterogeneous Clutter Environment. IEEE Signal Process. Lett. 2010, 17, 481–484. [Google Scholar] [CrossRef]
- Swathi Sharma, S.S. SMI Algorithm Adaptive Beamforming for Radar Systems. In Proceedings of the 2017 International Conference on Wireless Communications, Signal Processing and Networking, Chennai, India, 22–24 March 2017; pp. 2065–2069. [Google Scholar]
- Feng, Y.; Liao, G.; Xu, J. Robust adaptive beamforming against large steering vector mismatch based on minimum dispersion. Digit. Signal Process. 2020, 99, 102676. [Google Scholar] [CrossRef]
- Ruan, H.; de Lamare, R.C. Robust Adaptive Beamforming Based on Low-Rank and Cross-Correlation Techniques. IEEE Trans. Signal Process. 2016, 64, 3919–3932. [Google Scholar] [CrossRef]
- Liu, C.; Liao, G. Robust Capon beamformer under norm constraint. Signal Process. 2010, 90, 1573–1581. [Google Scholar] [CrossRef]
- Vorobyov, S.; Gershman, A.; Luo, Z.-Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. Doubly constrained robust Capon beamformer. IEEE Trans. Signal Process. 2004, 52, 2407–2423. [Google Scholar] [CrossRef]
- Nai, S.E.; Ser, W.; Yu, Z.L.; Chen, H. Iterative Robust Minimum Variance Beamforming. IEEE Trans. Signal Process. 2011, 59, 1601–1611. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, A.; Yang, Q. Robust Adaptive Beamforming Based on Conjugate Gradient Algorithms. IEEE Trans. Signal Process. 2016, 64, 6046–6057. [Google Scholar] [CrossRef]
- Zhang, J.; Shu, Q. Constrained adaptive beamforming algorithm based on set-membership and conjugate gradient. Syst. Eng. Electron. 2019, 41, 27–34. [Google Scholar]
- Wang, H.; Liao, G.; Xu, J.; Zhu, S. Subarray-based coherent pulsed-LFM frequency diverse array for range resolution enhancement. IET Signal Process. 2020, 14, 251–258. [Google Scholar] [CrossRef]
- Wang, W.Q. Subarray-Based Frequency Diverse Array Radar for Target Range-Angle Estimation. IEEE Trans Aerosp. Electron. Syst. 2014, 50, 3057–3067. [Google Scholar] [CrossRef]
- Somasundaram, S.D.; Butt, N.R.; Jakobsson, A.; Hart, L. Low-Complexity Uncertainty-Set-Based Robust Adaptive Beamforming for Passive Sonar. IEEE J. Ocean. Eng. 2015, 1–17. [Google Scholar] [CrossRef]
- Somasundaram, S.D. A framework for reduced dimension robust Capon beamforming. In Proceedings of the Statistical Signal Processing Workshop, Nice, France, 28–30 June 2011. [Google Scholar]
- Somasundaram, S.D.; Parsons, N.H.; Li, P.; de Lamare, R.C. Reduced-dimension robust capon beamforming using Krylov-subspace techniques. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 270–289. [Google Scholar] [CrossRef]
- Somasundaram, S.D.; Parsons, N.H.; Li, P.; de Lamare, R.C. Data-Adaptive Reduced-Dimension Robust Beamforming Algorithms. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Ding, T.; Qu, M.; Bai, J.; Li, F. Negative Reactance Impacts Power Flow Convergence Using Conjugate Gradient Method. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2527–2531. [Google Scholar] [CrossRef]
- Xiong, K.; Herbert, H.C.; Wang, S. Kernel Correntropy Conjugate Gradient Algorithms Based on Half-Quadratic Optimization. IEEE Trans. Cybern. 2021, 51, 5497–5510. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, J.; Reed, I.; Scharf, L. A multistage representation of the Wiener filter based on orthogonal projections. IEEE Trans. Inf. Theory 1998, 44, 2943–2959. [Google Scholar] [CrossRef]
- Qiang, X.; Liu, Y.; Feng, Q.; Zhang, Y.; Qiu, T.; Jin, M. Adaptive DOA Estimation with Low Complexity for Wideband Signals of Massive MIMO Systems. Signal Process. 2020, 176, 107702. [Google Scholar] [CrossRef]
- Besson, O.; Montesinos, J.; de Tournemine, C.L. On Convergence of the Auxiliary-Vector Beamformer With Rank-Deficient Covariance Matrices. IEEE Signal Process. Lett. 2009, 16, 249–252. [Google Scholar] [CrossRef]
- Pados, D.; Batalama, S. Joint space-time auxiliary-vector filtering for DS/CDMA systems with antenna arrays. IEEE Trans. Commun. 1999, 47, 1406–1415. [Google Scholar] [CrossRef]
- Honig, M.; Goldstein, J. Adaptive reduced-rank interference suppression based on the multistage Wiener filter. IEEE Trans. Commun. 2002, 50, 986–994. [Google Scholar] [CrossRef]


| Solve for | |
| Evaluate DRT | |
| EVD(M) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jiang, X.; Chen, Y. An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques. Sensors 2024, 24, 7152. https://doi.org/10.3390/s24227152
Wang X, Jiang X, Chen Y. An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques. Sensors. 2024; 24(22):7152. https://doi.org/10.3390/s24227152
Chicago/Turabian StyleWang, Xiaolin, Xihai Jiang, and Yaowu Chen. 2024. "An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques" Sensors 24, no. 22: 7152. https://doi.org/10.3390/s24227152
APA StyleWang, X., Jiang, X., & Chen, Y. (2024). An Improved Reduced-Dimension Robust Capon Beamforming Method Using Krylov Subspace Techniques. Sensors, 24(22), 7152. https://doi.org/10.3390/s24227152





