CrackNet: A Hybrid Model for Crack Segmentation with Dynamic Loss Function
Abstract
1. Introduction
- CrackNet proposes a novel architecture in which: (1) The encoder structure is based on an improved hybrid model of CNN and transformer, enabling the establishment of remote dependencies at a high level while retaining local feature extraction capabilities; (2) A novel spatial attention module is added to each skip connection. This module emphasizes the overlapping regions of two feature maps and supplements fine-grained features, effectively reducing background interference; (3) We propose using strip pooling instead of traditional square pooling. This adaptation is specifically tailored to the elongated nature of cracks, enhancing the model’s ability to detect fine, narrow features while minimizing interference from irrelevant background noise.
- We introduce a dynamic loss function to address the issue of imbalanced data distribution, in which the loss weights are dynamically updated based on the model’s different learning stages. This adaptive approach not only enhances the model’s performance by improving recall rates for underrepresented classes, but also reduces the likelihood of overfitting to the dominant classes. Furthermore, the proposed weight updating mechanism can be easily extended to other application scenarios, making it a versatile solution for various tasks involving imbalanced datasets.
- The proposed method has been validated on multiple public crack datasets, demonstrating overall performance superior to that of other models.
2. Related Work
2.1. CNN-Based Segmentation Network
2.2. Transformer-Based Segmentation Network
2.3. CNN and Transformer Hybrid Segmentation Network
2.4. Loss Function
3. Methods
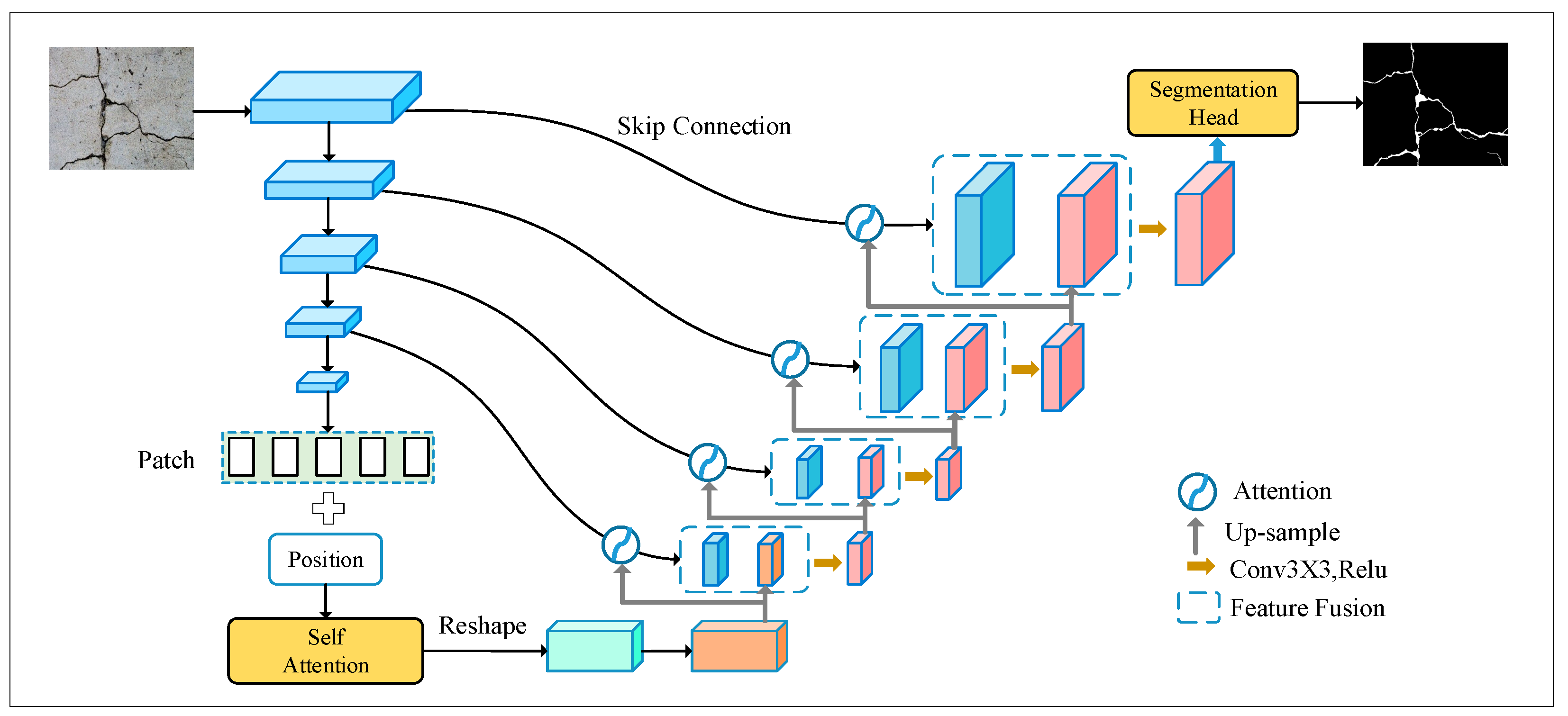
3.1. Overview of the Proposed Method
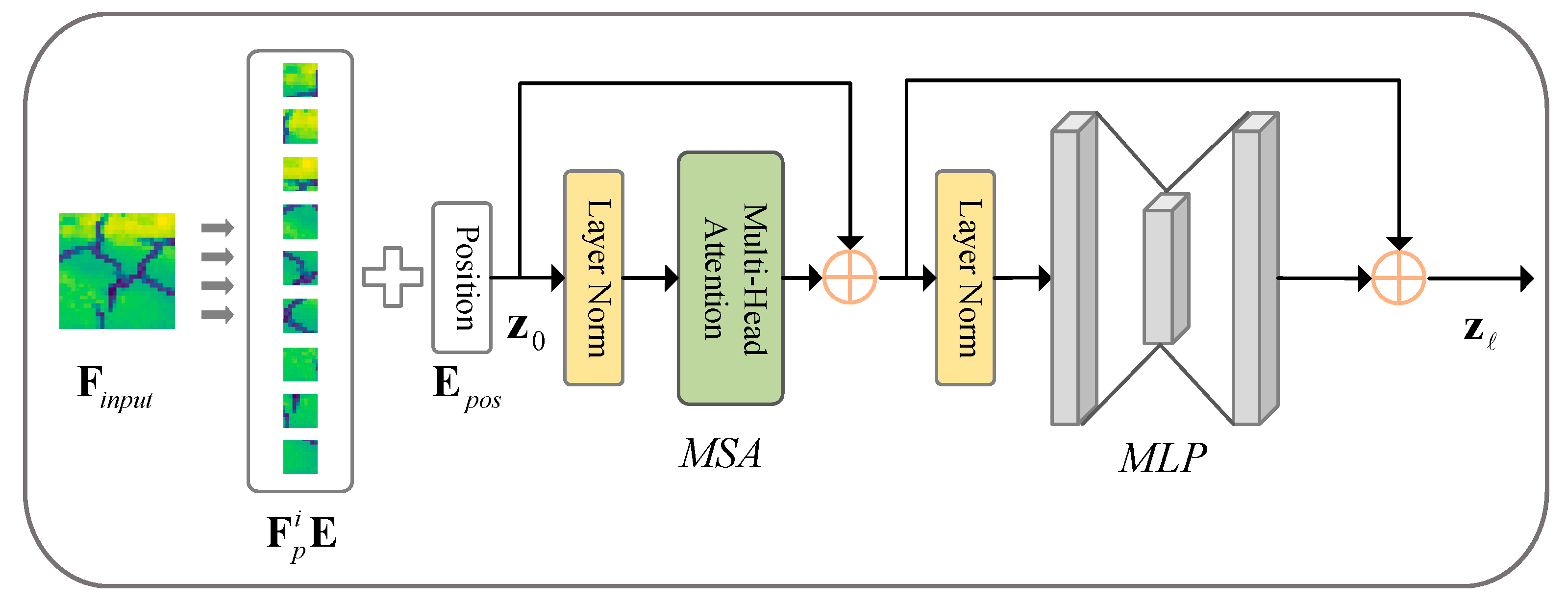
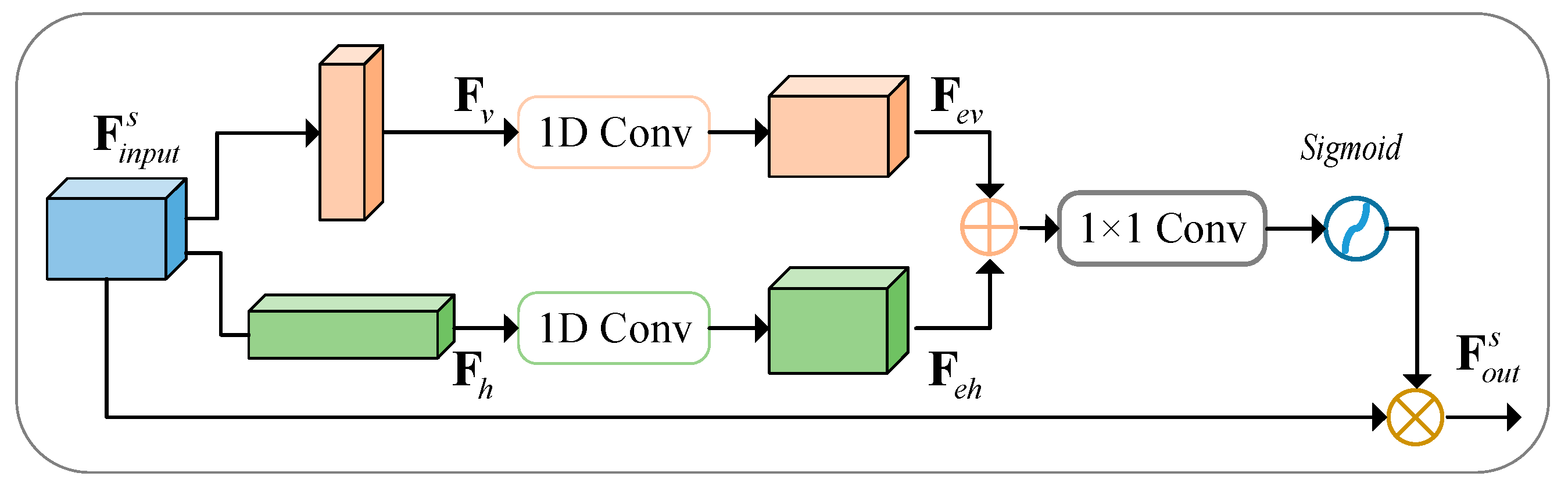
3.2. Hybrid Encoder
- (1)
- CNN-Module
- (2)
- Trans-Module
3.3. Bottleneck Layer
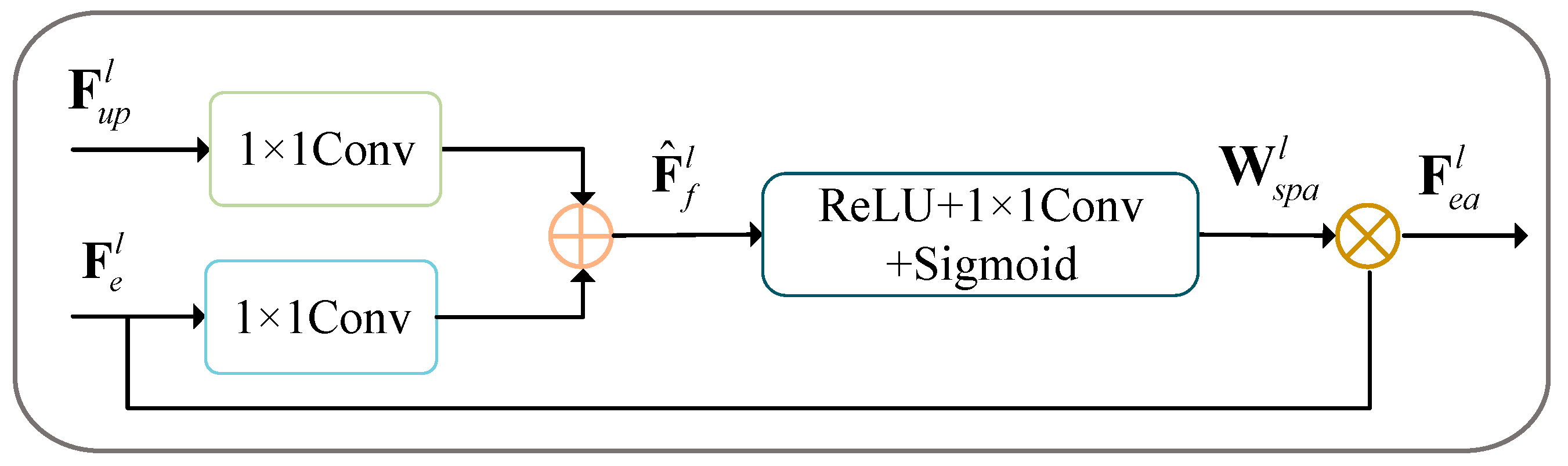
3.4. Attention Decoder Module
3.5. Dynamic Loss Function
| Algorithm 1. Dynamic cross-entropy weight updating. |
| 1. Input: The maximum numbers of iterations and epochs ; update interval ; mean loss in one interval , initialized by the last iterations; the number of loss decreases ; the number of loss increases ; initial values are 0. Output: The updated weight parameters 2. For do 3. Compute according to Equation (9) 4. if // 5. ; // the number of loss decreases 6. else if 7. ; // the number of loss increases 8. End if 9. if // the number of iterations meets the interval. 10. if // 11. // increase weight 12. else // decrease weight 13. end if 14. ; update ; 15. end if 16. 17. End for |
4. Experimental Results and Discussion
4.1. Datasets and Preprocessing
- (1)
- DeepCrack: The dataset is composed of 537 RGB color images with manually annotated segmentations, which are of a fixed size of 544 × 384 pixels. The dataset was divided into a training set with 300 images and a testing set with 237 images.
- (2)
- Crack500: This dataset contains 500 images and corresponding pixel-level annotations of size around 2000 × 1500 pixels, all taken by mobile phone. The dataset is divided into 250 images of training data, 50 images of validation data, and 200 images for testing.
- (3)
- CFD: This dataset consists of 118 images of size 480 × 320, which was taken by an iPhone 5 on an urban road surface in Beijing, China. All images were annotated at pixel level. This dataset is very challenging due to the complex background, including shadows, oil spots, water stains, and lane lines. We divide 60% and 40% of this dataset into training and testing, respectively.
4.2. Data Augmentation
4.3. Parameters
4.4. Performance Metrics
4.5. Results Comparisons
- (1)
- Performance on the DeepCrack Dataset
- (2)
- Performance on the Crack500 Dataset:
- (3)
- Performance on the CFD Dataset:
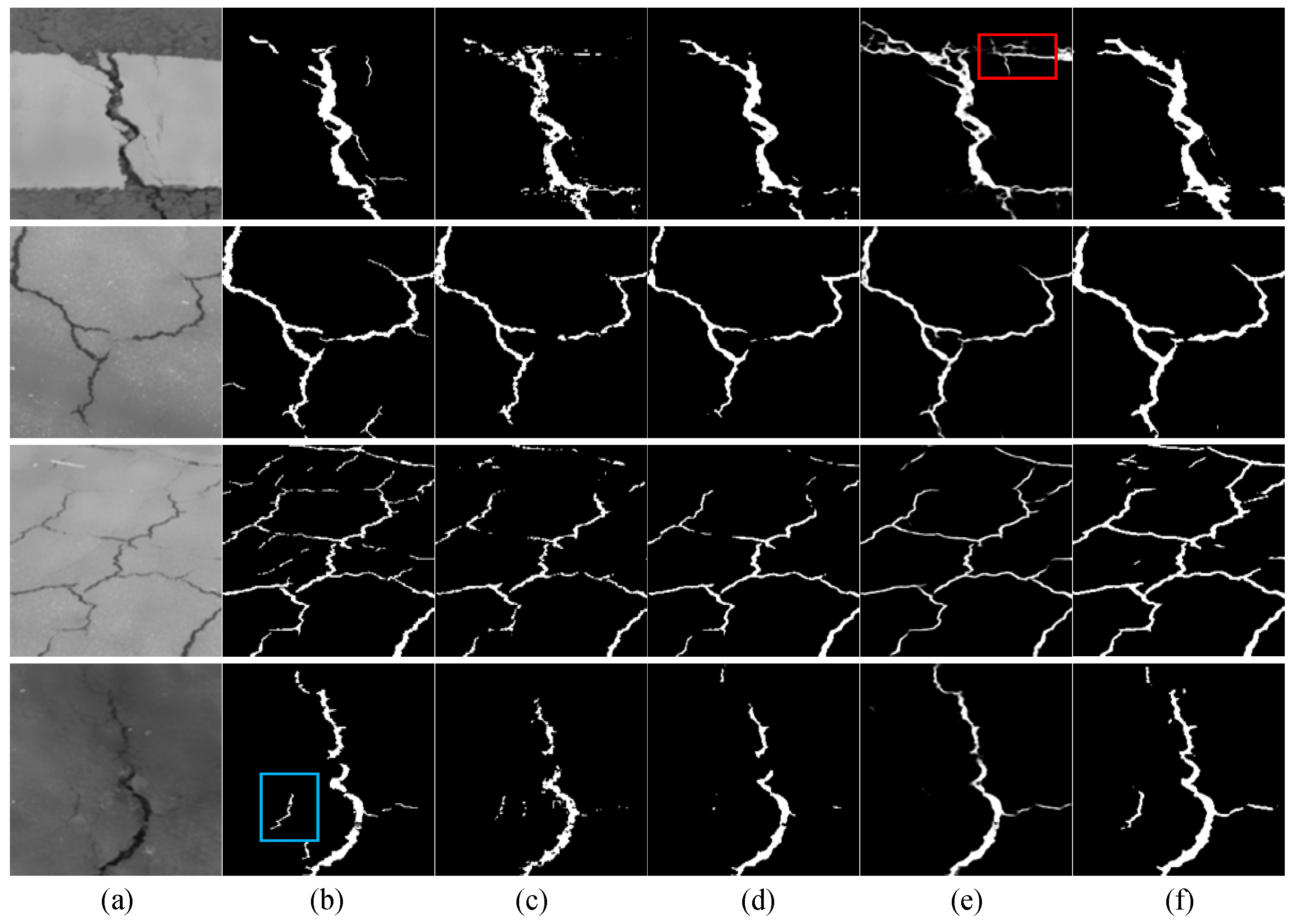
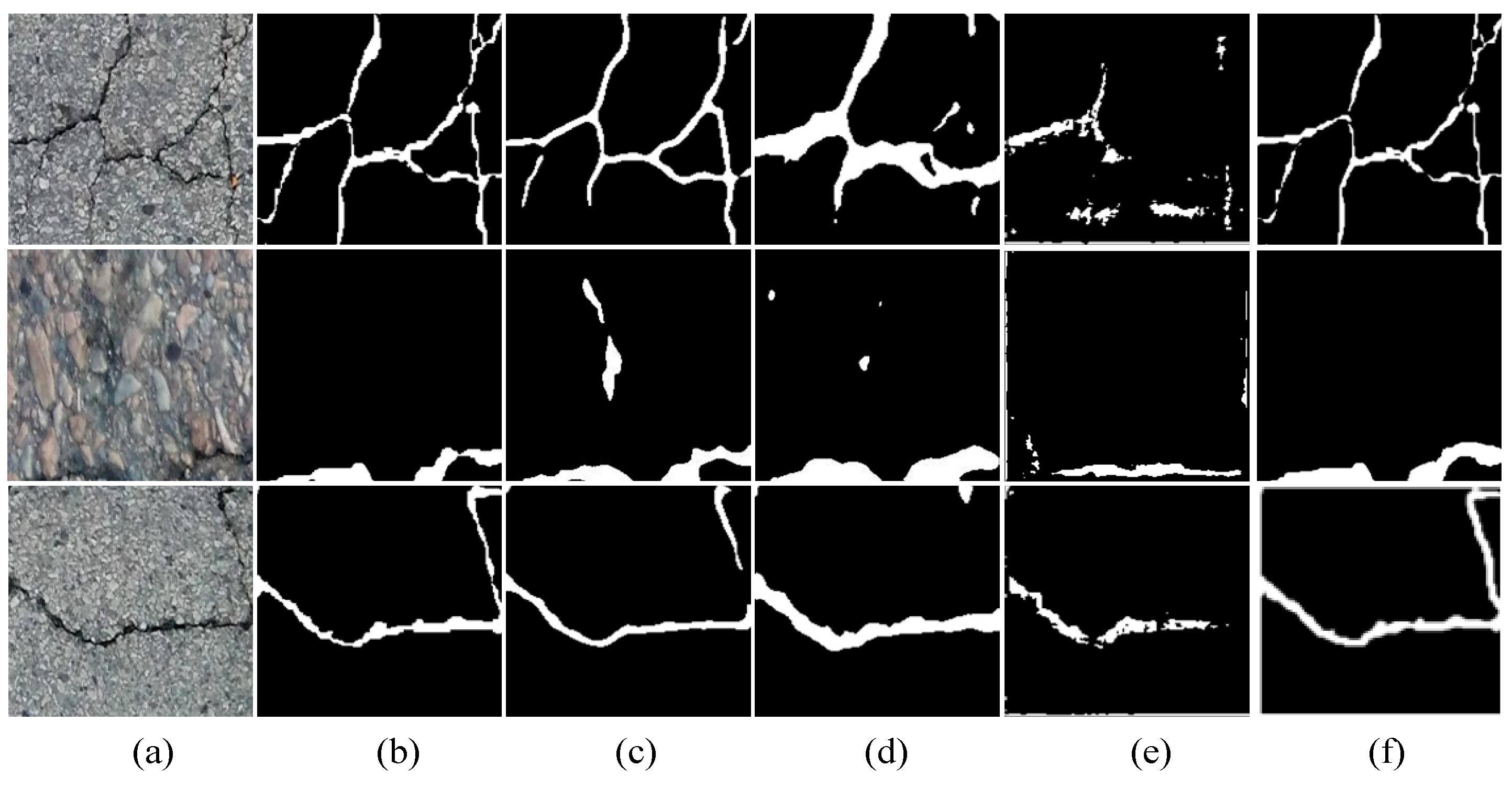
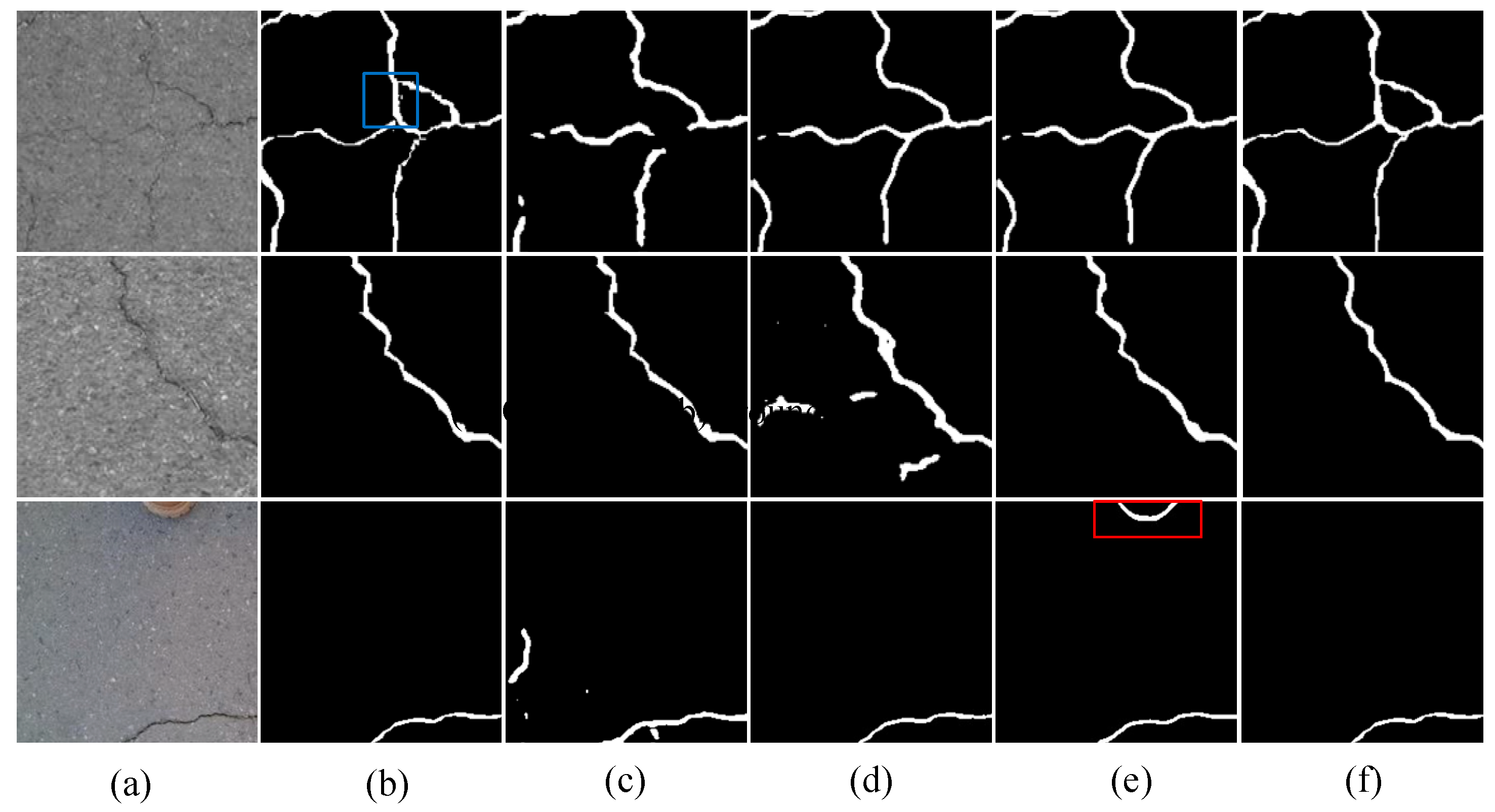
4.6. Qualitative Results Comparisons
- (1)
- Qualitative results on the DeepCrack
- (2)
- Qualitative results on the Crack500
- (3)
- Qualitative results on the CFD
4.7. Comparisons with Other Methods
4.8. Ablation Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mohan, A.; Poobal, S. Crack detection using image processing: A critical review and analysis. Alex. Eng. J. 2018, 57, 787–798. [Google Scholar] [CrossRef]
- König, J.; Jenkins, M.; Mannion, M.; Barrie, P.; Morison, G. What’s Cracking? A Review and Analysis of Deep Learning Methods for Structural Crack Segmentation, Detection and Quantification. arXiv 2022, arXiv:2202.03714. [Google Scholar]
- Pan, Y.; Zhang, X.; Cervone, G.; Yang, L. Detection of asphalt pavement potholes and cracks based on the unmanned aerial vehicle multispectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3701–3712. [Google Scholar] [CrossRef]
- Dung, C.V.; Anh, L.D. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Xinghao, C.; Wang, G.; Guo, H.; Zhang, C.; Wang, H.; Zhang, L. Mfa-net: Motion feature augmented network for dynamic hand gesture recognition from skeletal data. Sensors 2019, 19, 239. [Google Scholar] [CrossRef] [PubMed]
- Wooram, C.; Cha, Y.-J. SDDNet: Real-time crack segmentation. IEEE Trans. Ind. Electron. 2019, 67, 8016–8025. [Google Scholar]
- Cui, X.; Wang, Q.; Dai, J.; Xue, Y.; Duan, Y. Intelligent crack detection based on attention mechanism in convolution neural network. Adv. Struct. Eng. 2021, 24, 1859–1868. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. arXiv 2015, arXiv:1504.08083. [Google Scholar]
- Redmon, J. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Huyan, J.; Li, W.; Tighe, S.; Xu, Z.; Zhai, J. CrackU-net: A novel deep convolutional neural network for pixelwise pavement crack detection. Struct. Control Health Monit. 2020, 27, e2551. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, J.; Lu, X.; Xie, R.; Li, L. DeepCrack: A deep hierarchical feature learning architecture for crack segmentation. Neurocomputing 2019, 338, 139–153. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Schütt, K.T.; Sauceda, H.E.; Kindermans, P.J.; Tkatchenko, A.; Müller, K.R. Schnet–a deep learning architecture for molecules and materials. J. Chem. Phys. 2018, 148, 241722. [Google Scholar] [CrossRef] [PubMed]
- Vijay, B.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar]
- Olaf, R.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention, Proceedings of the MICCAI 2015: 18th International Conference, Part III 18, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Wang, L.; Ye, Y. Computer vision-based road crack detection using an improved I-UNet convolutional networks. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Fangyu, L.; Wang, L. UNet-based model for crack detection integrating visual explanations. Constr. Build. Mater. 2022, 322, 126265. [Google Scholar]
- Fan, L.; Zhao, H.; Li, Y.; Li, S.; Zhou, R.; Chu, W. RAO-UNet: A residual attention and octave UNet for road crack detection via balance loss. IET Intell. Transp. Syst. 2022, 16, 332–343. [Google Scholar] [CrossRef]
- Lau, S.L.; Chong, E.K.; Yang, X.; Wang, X. Automated pavement crack segmentation using u-net-based convolutional neural network. IEEE Access 2020, 8, 114892–114899. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Z.; Zhao, X.; Chen, C.; Liang, X.; Zou, T.; Wang, P. Pavement crack detection and recognition using the architecture of segNet. J. Ind. Inf. Integr. 2020, 18, 100144. [Google Scholar] [CrossRef]
- Shengyuan, L.; Zhao, X.; Zhou, G. Automatic pixel-level multiple damage detection of concrete structure using fully convolutional network. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 616–634. [Google Scholar]
- Kang, D.; Benipal, S.S.; Gopal, D.L.; Cha, Y.J. Hybrid pixel-level concrete crack segmentation and quantification across complex backgrounds using deep learning. Autom. Constr. 2020, 118, 103291. [Google Scholar] [CrossRef]
- Honghu, C.; Wang, W.; Deng, L. Tiny-Crack-Net: A multiscale feature fusion network with attention mechanisms for segmentation of tiny cracks. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1914–1931. [Google Scholar]
- Ashish, V.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Guyon, I., Von Luxburg, U., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2017. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021. [Google Scholar]
- Nikita, K.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Wenjun, W.; Su, C. Automatic concrete crack segmentation model based on transformer. Autom. Constr. 2022, 139, 104275. [Google Scholar]
- Shamsabadi, E.A.; Xu, C.; Rao, A.S.; Nguyen, T.; Ngo, T.; Dias-da-Costa, D. Vision transformer-based autonomous crack detection on asphalt and concrete surfaces. Autom. Constr. 2022, 140, 104316. [Google Scholar] [CrossRef]
- Dang, L.M.; Wang, H.; Li, Y.; Nguyen, T.N.; Moon, H. DefectTR: End-to-end defect detection for sewage networks using a transformer. Constr. Build. Mater. 2022, 325, 126584. [Google Scholar] [CrossRef]
- Qi, H.; Kong, X.; Jin, Z.; Zhang, J.; Wang, Z. A Vision-Transformer-Based Convex Variational Network for Bridge Pavement Defect Segmentation. In Proceedings of the IEEE Transactions on Intelligent Transportation Systems, Edmonton, AB, Canada, 15–17 October 2024; Volume 25, pp. 13820–13832. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Computer Vision, Proceedings of the ECCV 2022 Workshops, Part III, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Guo, X.; Lin, X.; Yang, X.; Yu, L.; Cheng, K.-T.; Yan, Z. UCTNet: Uncertainty-guided CNN-Transformer hybrid networks for medical image segmentation. Pattern Recognit. 2024, 152, 110491. [Google Scholar] [CrossRef]
- Wu, M.; Jia, M.; Wang, J. TMCrack-Net: A U-shaped network with a feature pyramid and transformer for mural crack segmentation. Appl. Sci. 2022, 12, 10940. [Google Scholar] [CrossRef]
- Xiang, C.; Guo, J.; Cao, R.; Deng, L. A crack-segmentation algorithm fusing transformers and convolutional neural networks for complex detection scenarios. Autom. Constr. 2023, 152, 104894. [Google Scholar] [CrossRef]
- Liu, H.; Miao, X.; Mertz, C.; Xu, C.; Kong, H. Crackformer: Transformer network for fine-grained crack detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021. [Google Scholar]
- Wang, J.; Zeng, Z.; Sharma, P.K.; Alfarraj, O.; Tolba, A.; Zhang, J.; Wang, L. Dual-path network combining CNN and transformer for pavement crack segmentation. Autom. Constr. 2024, 158, 105217. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Jie, F.; Qu, B.; Yuan, Y. Distribution equalization learning mechanism for road crack detection. Neurocomputing 2021, 424, 193–204. [Google Scholar]
- Li, K.; Wang, B.; Tian, Y.; Qi, Z. Fast and Accurate Road Crack Detection Based on Adaptive Cost-Sensitive Loss Function. IEEE Trans. Cybern. 2021, 53, 1051–1062. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Zhang, L.; Cheng, M.M.; Feng, J. Strip pooling: Rethinking spatial pooling for scene parsing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Shi, Y.; Cui, L.; Qi, Z.; Meng, F.; Chen, Z. Automatic road crack detection using random structured forests. IEEE Tran. Intel. Trans. Syst. 2016, 17, 3434–3445. [Google Scholar] [CrossRef]
- Mengyang, P.; Huang, Y.; Guan, Q.; Ling, H. Rindnet: Edge detection for discontinuity in reflectance, illumination, normal and depth. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 6879–6888. [Google Scholar]
- Koonce, B. EfficientNet. In Convolutional Neural Networks with Swift for Tensorflow: Image Recognition and Dataset Categorization; Apress: New York, NY, USA, 2021; pp. 109–123. [Google Scholar]

| Model | F1 | IoU | Pr | Re | Acc |
|---|---|---|---|---|---|
| DeepCrack [11] | 0.7473 | 0.6132 | 0.6342 | 0.9604 | 0.9737 |
| U-Net [15] | 0.7887 | 0.6832 | 0.8852 | 0.7504 | 0.9837 |
| TransUNet [32] | 0.8338 | 0.7243 | 0.9034 | 0.7902 | 0.9865 |
| Swin-Unet [33] | 0.7789 | 0.6513 | 0.8691 | 0.7328 | 0.9819 |
| CrackNet | 0.8425 | 0.7406 | 0.8690 | 0.8424 | 0.9872 |
| Model | F1 | IoU | Pr | Re | Acc |
|---|---|---|---|---|---|
| DeepCrack [11] | 0.4911 | 0.3425 | 0.3607 | 0.8982 | 0.9254 |
| U-Net [15] | 0.6693 | 0.5279 | 0.6998 | 0.6876 | 0.9672 |
| TransUNet [32] | 0.6520 | 0.5053 | 0.7014 | 0.6587 | 0.9577 |
| Swin-Unet [33] | 0.6426 | 0.4971 | 0.6915 | 0.6519 | 0.9529 |
| CrackNet | 0.6744 | 0.5293 | 0.6474 | 0.7595 | 0.9611 |
| Model | F1 | IoU | Pr | Re | Acc |
|---|---|---|---|---|---|
| DeepCrack [11] | 0.6125 | 0.4536 | 0.5151 | 0.8174 | 0.9782 |
| U-Net [15] | 0.6723 | 0.5182 | 0.6257 | 0.7519 | 0.9392 |
| TransUNet [32] | 0.6791 | 0.5243 | 0.6639 | 0.7122 | 0.9484 |
| Swin-Unet [33] | 0.6297 | 0.4690 | 0.6344 | 0.6574 | 0.9416 |
| CrackNet | 0.7035 | 0.5509 | 0.6381 | 0.7957 | 0.9502 |
| Methods | Pr | Re | F1 |
|---|---|---|---|
| RIND [44] | 0.6456 | 0.7534 | 0.6954 |
| UCTNet [34] | 0.6701 | 0.7205 | 0.6944 |
| Crackmer [38] | 0.6370 | 0.7237 | 0.6776 |
| CrackNet | 0.6381 | 0.7957 | 0.7035 |
| Methods | Pr | Re | F1 |
|---|---|---|---|
| RIND [44] | 0.7896 | 0.8920 | 0.8377 |
| EfficientNet [45] | 0.6925 | 0.8614 | 0.7678 |
| UCTNet [34] | 0.8217 | 0.8857 | 0.8525 |
| Crackmer [38] | 0.8931 | 0.8233 | 0.8568 |
| CrackNet | 0.8690 | 0.8424 | 0.8425 |
| Method | F1 | IoU | Pr | Re | ||
|---|---|---|---|---|---|---|
| Baseline | SP | DWL | ||||
| √ | 0.6704 | 0.5177 | 0.7130 | 0.6765 | ||
| √ | √ | 0.6782 | 0.5245 | 0.7080 | 0.6893 | |
| √ | √ | √ | 0.7035 | 0.5509 | 0.6381 | 0.7957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Hu, Z.; Li, Q.; Sun, Y.; Chen, J.; Zhou, Q. CrackNet: A Hybrid Model for Crack Segmentation with Dynamic Loss Function. Sensors 2024, 24, 7134. https://doi.org/10.3390/s24227134
Fan Y, Hu Z, Li Q, Sun Y, Chen J, Zhou Q. CrackNet: A Hybrid Model for Crack Segmentation with Dynamic Loss Function. Sensors. 2024; 24(22):7134. https://doi.org/10.3390/s24227134
Chicago/Turabian StyleFan, Yawen, Zhengkai Hu, Qinxin Li, Yang Sun, Jianxin Chen, and Quan Zhou. 2024. "CrackNet: A Hybrid Model for Crack Segmentation with Dynamic Loss Function" Sensors 24, no. 22: 7134. https://doi.org/10.3390/s24227134
APA StyleFan, Y., Hu, Z., Li, Q., Sun, Y., Chen, J., & Zhou, Q. (2024). CrackNet: A Hybrid Model for Crack Segmentation with Dynamic Loss Function. Sensors, 24(22), 7134. https://doi.org/10.3390/s24227134





