Charge Diffusion and Repulsion in Semiconductor Detectors
Abstract
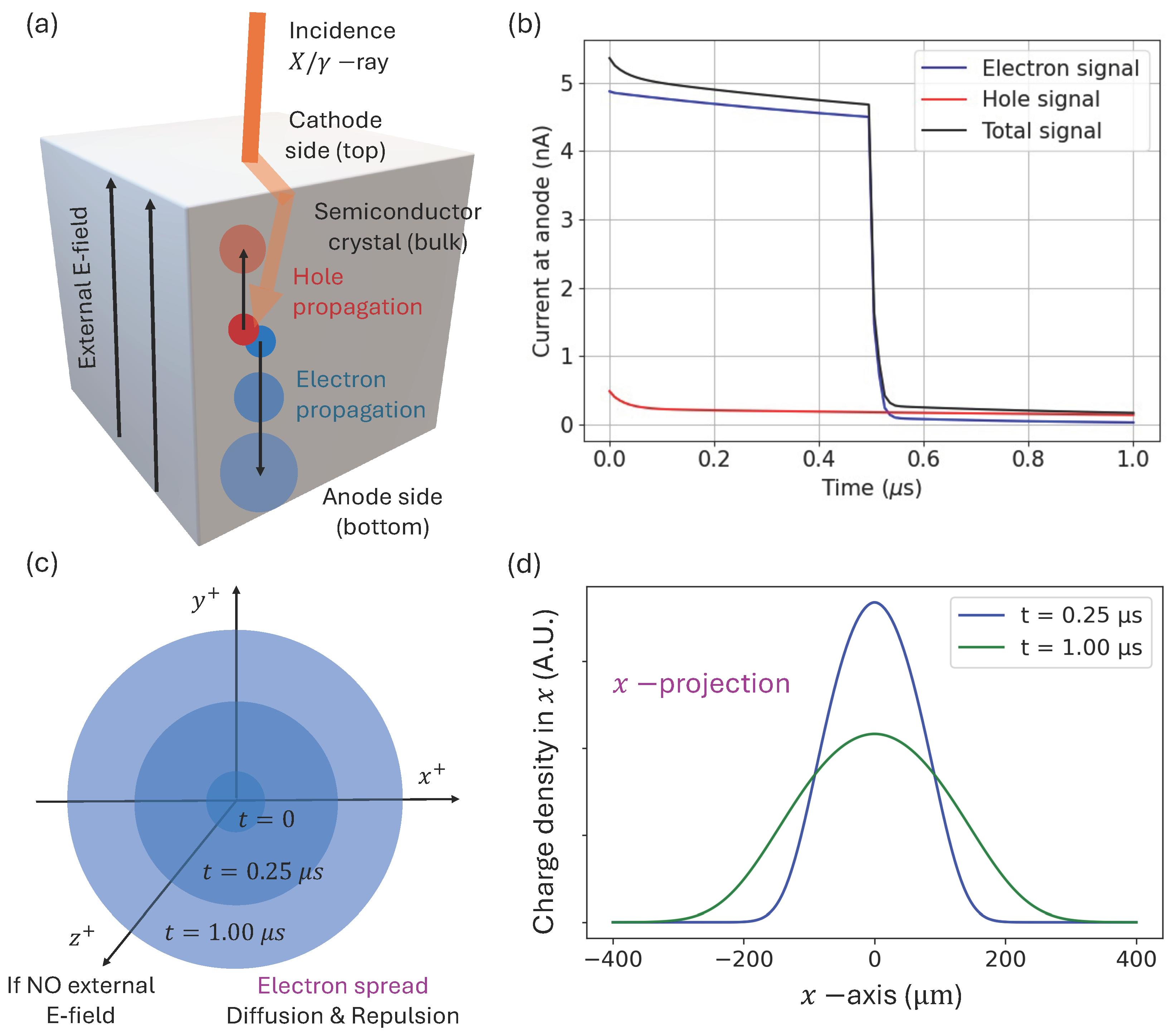
1. Introduction
2. Theoretical Background
3. Gatti Model: Decoupling Processes
3.1. Diffusion
3.2. Repulsion
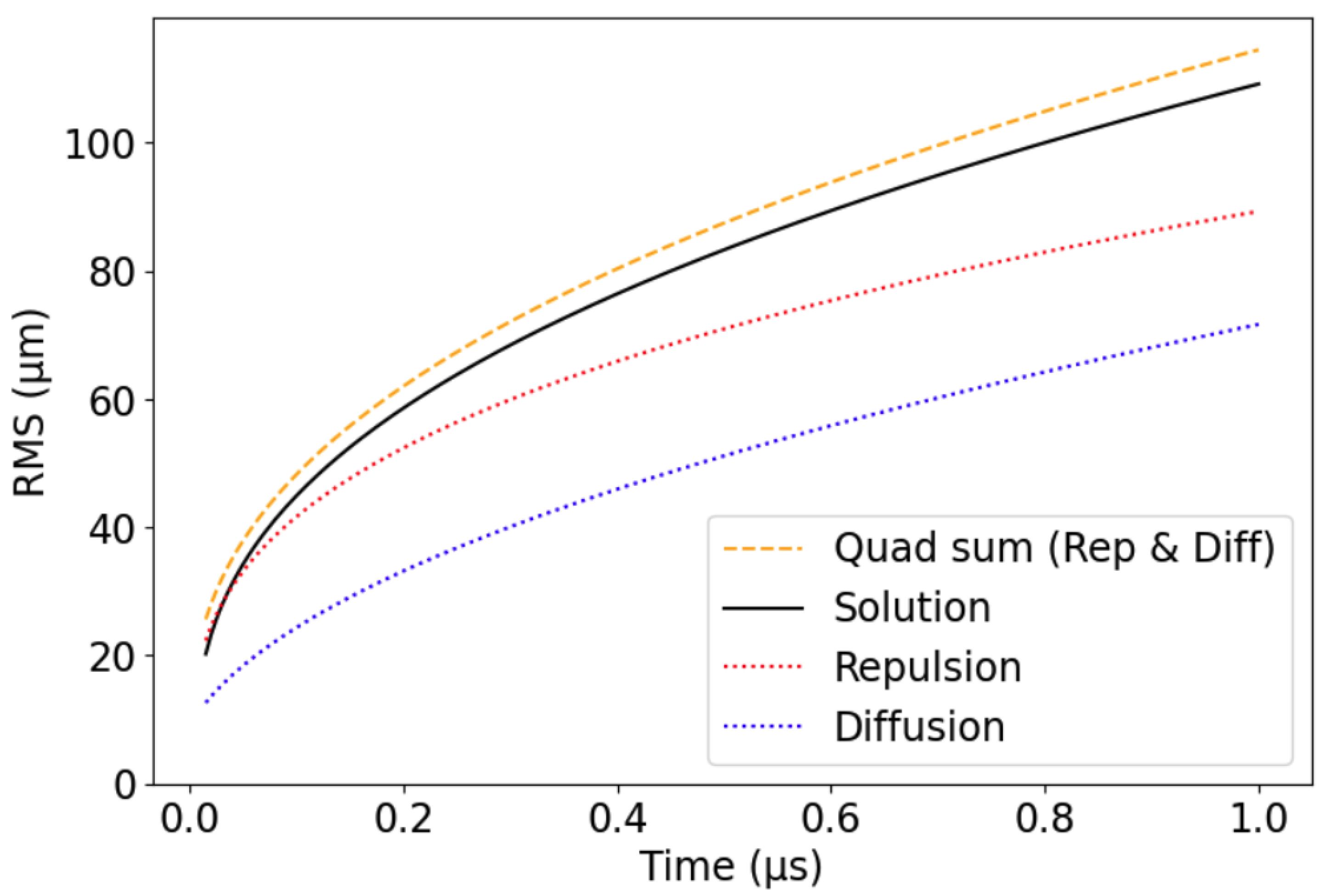
3.3. Root Mean Square Metric
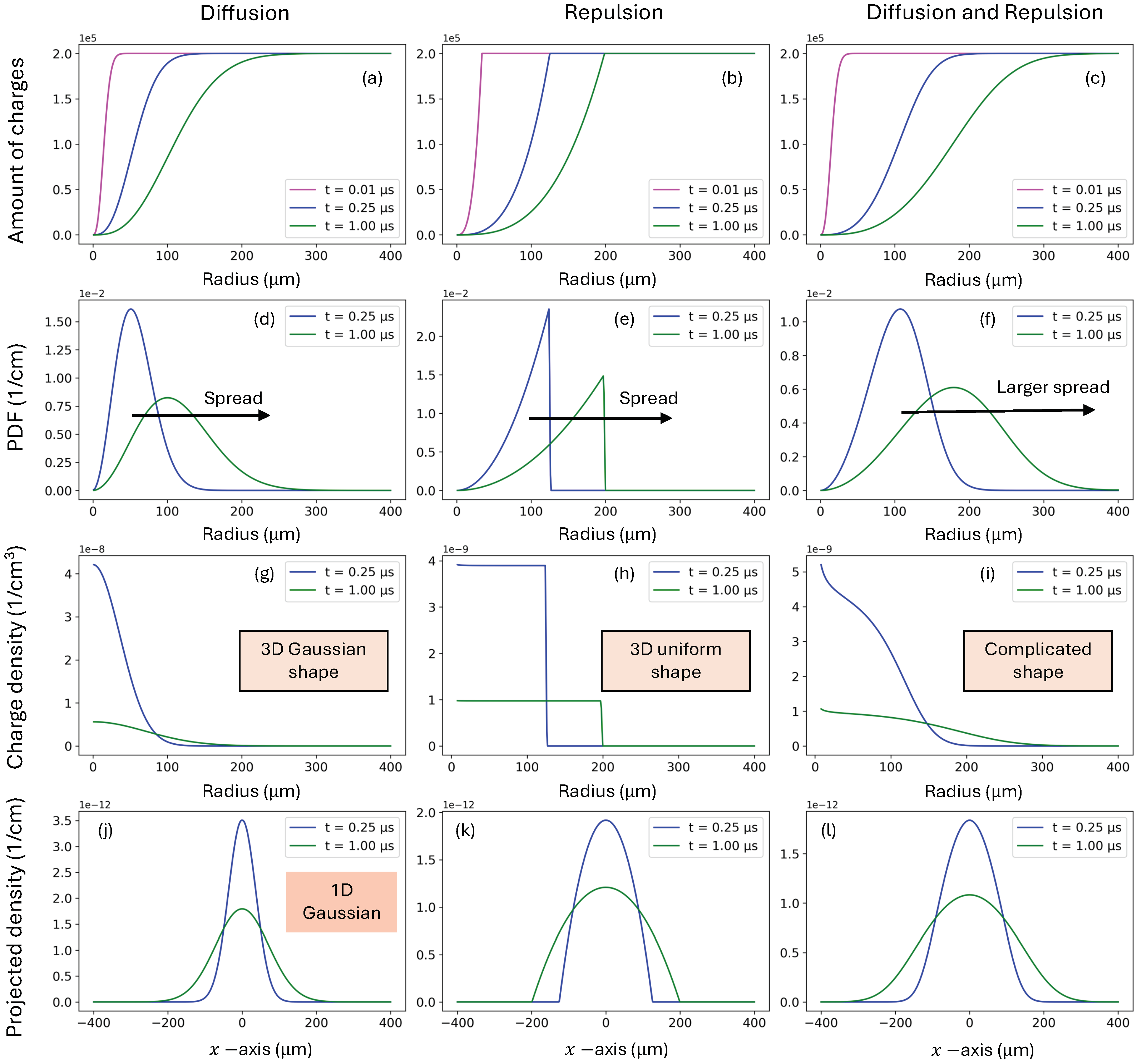
- The number of elementary charges, , within a given radial distance R from the center of the charge cloud, is displayed in Figure 2a–c. For R values larger than the charge cloud, will approximate the total number of generated electron–hole pairs (in this representative case, charges). Alternatively, this variable can be expressed as the total Coulomb charge, , or as the normalized charge distribution, .
- The probability density function (PDF) of the charge distribution, , is shown in Figure 2d–f.
- The charge densities , expressed in C/c, are displayed in Figure 2g–i.
- The charge densities projected over the x-coordinate (due to symmetry, this projection is identical for all coordinates) becomewhere one needs to consider the spherical symmetry of the density and .
4. BH Model: Gaussian Distribution
4.1. Analytical Derivations
- As mentioned above, charges diffusing in three dimensions adopt a Gaussian distribution with a variance of . The marginal density along the x-axis remains Gaussian and has the same identical variance, so . For reasons that will become apparent in Section 4.3, expressing this formula as a time-dependent differential equation is more advantageous. Thus, we could represent it as
- On the other hand, the charges spread as a result of repulsion in a uniform three-dimensional shape. The charge density due to repulsion-only is described in Equation (15), but note that the marginal density along the x-axis has a more intricate mathematical description: As seen in Figure 2k, it is no longer uniform. Despite its complicated shape, the variance of this marginal density can still be calculated by definition. For instance, after a few calculations in the intermediate steps, one can derive the following:As mentioned in the point above, we are now looking for an expression of the temporal derivative of the variance. Therefore, we easily derive the following expression:
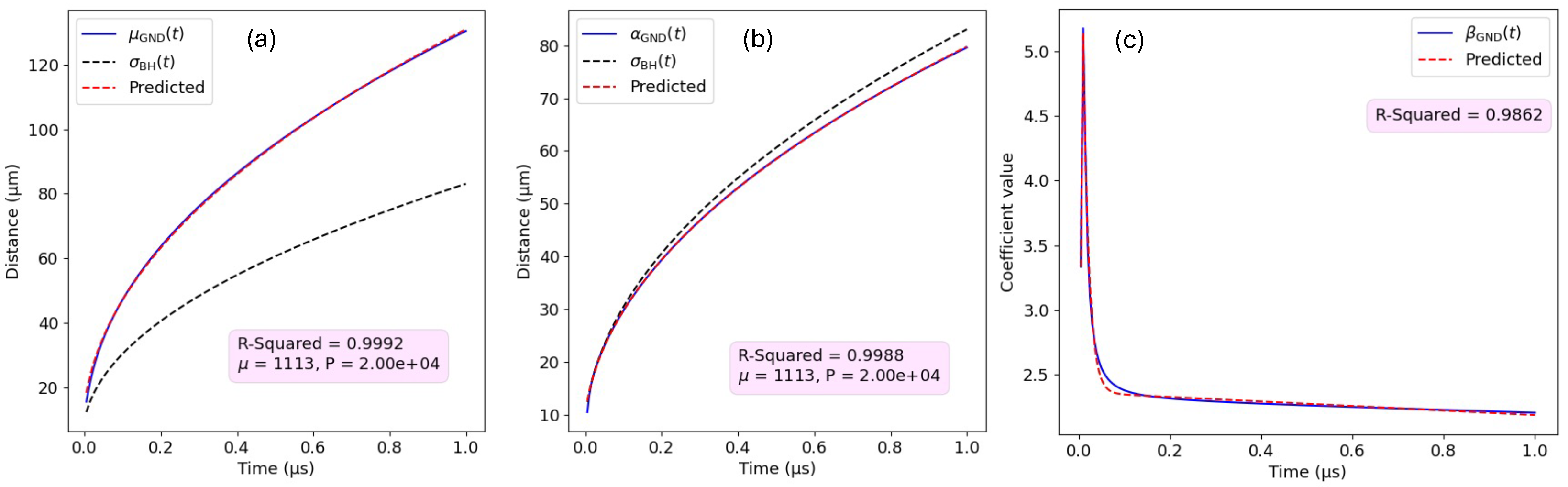
4.2. Numerical Evaluation
4.3. Monte Carlo Algorithm
| Algorithm 1 BH approach: Diffusion and repulsion |
|
5. Our Proposed GND Model
5.1. Generalized Normal Distributions
5.2. Gaussian Mixture Model
- We can find a reasonable value for (and therefore also) by matching the first three moments (mean, variance, and skewness) of the GMM with the GND. In particular, if we defineNote that both results are valid for any value (we will decide on a particular value below). Because both the GMM and the GND are symmetric, there is also a match of the third moment (the skewness is zero).
- We can now find a convenient value by matching the peak of the GMM density with the peak of the GND density at the central point, , meaningSubstituting the value of from Equation (29) and considering the known peak value of the GND distribution, one findsThis non-linear algebraic equation can be efficiently solved as a least squares minimization problem, where the objective function represents the residuals of the equation. Specifically, we employed the Python package SciPy and utilized again the efficient trust-region optimizer, incorporating box constraints to ensure that remains within the physically meaningful range of positive values less than the known parameter .
5.3. Monte Carlo Algorithm
| Algorithm 2 Novel approach: Diffusion and repulsion |
|
5.4. Extending the Algorithm for Different Scenarios
6. Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- , , ;
- , , ;
- , , ;
- , , ;
- , , , , .
References
- Haller, E. Germanium: From its discovery to SiGe devices. Mater. Sci. Semicond. Process. 2006, 9, 408–422. [Google Scholar] [CrossRef]
- Hayashi, K.; Park, I.; Dotsu, K.; Ueno, I.; Nishino, S.; Matsuoka, M.; Yasuda, H.; Fukazawa, Y.; Ohsugi, T.; Mizuno, T.; et al. Radiation effects on the silicon semiconductor detectors for the ASTRO–H mission. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 699, 225–229. [Google Scholar] [CrossRef]
- Luke, P.N.; Amman, M.; Tindall, C.; Lee, J.S. Recent developments in semiconductor gamma-ray detectors. J. Radioanal. Nucl. Chem. 2005, 264, 145–153. [Google Scholar] [CrossRef]
- Ponpon, J.; Sieskind, M. Recent advances in γ-and X-ray spectrometry by means of mercuric iodide detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 380, 173–178. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y. Growth of lead iodide single crystals used for nuclear radiation detection of Gamma-rays. Cryst. Res. Technol. 2017, 52, 1600370. [Google Scholar] [CrossRef]
- Kim, H.; Cirignano, L.; Churilov, A.; Ciampi, G.; Higgins, W.; Olschner, F.; Shah, K. Developing larger TlBr detectors—detector performance. IEEE Trans. Nucl. Sci. 2009, 56, 819–823. [Google Scholar] [CrossRef]
- Ikegami, K.; Nishizawa, H.; Takashima, K.; Usami, T.; Hayakawa, T.; Yamamoto, T.; Nakamura, K.; Matsuoka, Y. CZT semiconductor radiation sensor for high energy gamma rays. Radiat. Eff. Defects Solids 1998, 146, 161–173. [Google Scholar] [CrossRef]
- Kalemci, E.; Matteson, J.L.; Skelton, R.T.; Hink, P.L.; Slavis, K.R. Model calculations of the response of CZT strip detectors. In Proceedings of the Hard X-Ray, Gamma-Ray, and Neutron Detector Physics, Denver, CO, USA, 18–23 July 1999; Volume 3768, pp. 360–373. [Google Scholar]
- Du, Y.; LeBlanc, J.; Possin, G.E.; Yanoff, B.D.; Bogdanovich, S. Temporal response of CZT detectors under intense irradiation. In Proceedings of the 2002 IEEE Nuclear Science Symposium Conference Record, Norfolk, VA, USA, 10–16 November 2002; Volume 1, pp. 480–484. [Google Scholar]
- Picone, M.; Glière, A.; Massé, P. A three-dimensional model of CdZnTe gamma-ray spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 504, 313–316. [Google Scholar] [CrossRef]
- Mathy, F.; Glière, A.; d’Aillon, E.G.; Massé, P.; Picone, M.; Tabary, J.; Verger, L. A three-dimensional model of CdZnTe gamma-ray detector and its experimental validation. IEEE Trans. Nucl. Sci. 2004, 51, 2419–2426. [Google Scholar] [CrossRef]
- Fink, J.; Krueger, H.; Lodomez, P.; Wermes, N. Characterization of charge collection in CdTe and CZT using the transient current technique. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2006, 560, 435–443. [Google Scholar] [CrossRef]
- Guerra, P.; Santos, A.; Darambara, D. Development of a simplified simulation model for performance characterization of a pixellated CdZnTe multimodality imaging system. Phys. Med. Biol. 2008, 53, 1099. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wei, Y.X. Monte Carlo simulations of the SNM spectra for CZT and NaI spectrometers. Appl. Radiat. Isot. 2008, 66, 1146–1150. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Anderson, S.E.; He, Z. Sub-pixel position sensing for pixelated, 3-D position sensitive, wide band-gap, semiconductor, gamma-ray detectors. IEEE Trans. Nucl. Sci. 2011, 58, 1400–1409. [Google Scholar] [CrossRef]
- Myronakis, M.E.; Darambara, D.G. Monte Carlo investigation of charge-transport effects on energy resolution and detection efficiency of pixelated CZT detectors for SPECT/PET applications. Med. Phys. 2011, 38, 455–467. [Google Scholar] [CrossRef]
- Montémont, G.; Lux, S.; Monnet, O.; Stanchina, S.; Verger, L. Studying spatial resolution of CZT detectors using sub-pixel positioning for SPECT. IEEE Trans. Nucl. Sci. 2014, 61, 2559–2566. [Google Scholar] [CrossRef]
- Bettelli, M.; Amadè, N.S. A first principles method to simulate the spectral response of CdZnTe-based X-and Gamma-ray detectors. In Radiation Detection Systems; CRC Press: Boca Raton, FL, USA, 2021; pp. 33–60. [Google Scholar]
- Abt, I.; Fischer, F.; Hagemann, F.; Hauertmann, L.; Schulz, O.; Schuster, M.; Zsigmond, A.J. Simulation of semiconductor detectors in 3D with SolidStateDetectors. jl. J. Instrum. 2021, 16, P08007. [Google Scholar] [CrossRef]
- Ballester, M.; Kaspar, J.; Massanes, F.; Banerjee, S.; Vija, A.H.; Katsaggelos, A.K. Modeling and Simulation of Charge-Induced Signals in Photon-Counting CZT Detectors for Medical Imaging Applications. arXiv 2024, arXiv:2405.13168. [Google Scholar]
- Ballester, M.; Banerjee, S.; Rodrigues, M.; Kaspar, J.; Vija, A.H.; Katsaggelos, A.K. Materials and defects characterization of CdZnTe sensors using the inverse synthesis method. In Proceedings of the 2022 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Milano, Italy, 5–12 November 2022; pp. 1–2. [Google Scholar]
- Banerjee, S.; Rodrigues, M.; Ballester, M.; Vija, A.H.; Katsaggelos, A.K. Machine Learning Approaches in Room Temperature Semiconductor Detectors. In X-Ray Photon Processing Detectors: Space, Industrial, and Medical Applications; Springer: Berlin/Heidelberg, Germany, 2023; pp. 67–94. [Google Scholar]
- Banerjee, S.; Rodrigues, M.; Ballester, M.; Vija, A.H.; Katsaggelos, A. Identifying Defects without a priori Knowledge in a Room-Temperature Semiconductor Detector Using Physics Inspired Machine Learning Model. Sensors 2023, 24, 92. [Google Scholar] [CrossRef]
- Banerjee, S.; Rodrigues, M.; Ballester, M.; Vija, A.H.; Katsaggelos, A.K. Learning-based physical models of room-temperature semiconductor detectors with reduced data. Sci. Rep. 2023, 13, 168. [Google Scholar] [CrossRef]
- Banerjee, S.; Rodrigues, M.; Ballester, M.; Vija, A.H.; Katsaggelos, A.K. A physics based machine learning model to characterize room temperature semiconductor detectors in 3D. Sci. Rep. 2024, 14, 7803. [Google Scholar] [CrossRef]
- Ballester, M.; Kaspar, J.; Massanes, F.; Banerjee, S.; Vija, A.H.; Katsaggelos, A.K. Characterization of Crystal Properties and Defects in CdZnTe Radiation Detectors. Crystals 2024, 14, 935. [Google Scholar] [CrossRef]
- Barrett, H.; Eskin, J.; Barber, H. Charge transport in arrays of semiconductor gamma-ray detectors. Phys. Rev. Lett. 1995, 75, 156. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Bolotnikov, A.; Camarda, G.; Hossain, A.; Yang, G.; James, R. CZT virtual Frisch-grid detector: Principles and applications. In Proceedings of the 2009 IEEE Long Island Systems, Applications and Technology Conference, Farmingdale, NY, USA, 1 May 2009; pp. 1–5. [Google Scholar]
- Shockley, W. Currents to conductors induced by a moving point charge. J. Appl. Phys. 1938, 9, 635–636. [Google Scholar] [CrossRef]
- Ramo, S. Currents induced by electron motion. Proc. IRE 1939, 27, 584–585. [Google Scholar] [CrossRef]
- He, Z. Review of the Shockley–Ramo theorem and its application in semiconductor gamma-ray detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2001, 463, 250–267. [Google Scholar] [CrossRef]
- Brigida, M.; Favuzzi, C.; Fusco, P.; Gargano, F.; Giglietto, N.; Giordano, F.; Loparco, F.; Marangelli, B.; Mazziotta, M.; Mirizzi, N.; et al. A new Monte Carlo code for full simulation of silicon strip detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2004, 533, 322–343. [Google Scholar] [CrossRef]
- Gaubas, E.; Ceponis, T.; Kalesinskas, V.; Pavlov, J.; Vysniauskas, J. Simulations of operation dynamics of different type GaN particle sensors. Sensors 2015, 15, 5429–5473. [Google Scholar] [CrossRef]
- Eisen, Y.; Shor, A. CdTe and CdZnTe materials for room-temperature X-ray and gamma ray detectors. J. Cryst. Growth 1998, 184, 1302–1312. [Google Scholar] [CrossRef]
- Zanichelli, M.; Santi, A.; Pavesi, M.; Zappettini, A. Charge collection in semi-insulator radiation detectors in the presence of a linear decreasing electric field. J. Phys. D Appl. Phys. 2013, 46, 365103. [Google Scholar] [CrossRef]
- Fritz, S.G.; Shikhaliev, P.M. CZT detectors used in different irradiation geometries: Simulations and experimental results. Med. Phys. 2009, 36, 1098–1108. [Google Scholar] [CrossRef]
- Washington, A.L.; Teague, L.C.; Duff, M.C.; Burger, A.; Groza, M.; Buliga, V. The effect of various detector geometries on the performance of CZT using one crystal. J. Electron. Mater. 2011, 40, 1744–1748. [Google Scholar] [CrossRef]
- Yao, H.W.; Anderson, R.J.; James, R.B. Optical characterization of the internal electric field distribution under bias of CdZnTe radiation detectors. In Proceedings of the Hard X-Ray and Gamma-Ray Detector Physics, Optics, and Applications, San Diego, CA, USA, 27 July–1 August 1997; Volume 3115, pp. 62–68. [Google Scholar]
- Pavesi, M.; Santi, A.; Bettelli, M.; Zappettini, A.; Zanichelli, M. Electric field reconstruction and transport parameter evaluation in CZT X-ray detectors. IEEE Trans. Nucl. Sci. 2017, 64, 2706–2712. [Google Scholar] [CrossRef]
- Uxa, Š.; Belas, E.; Grill, R.; Praus, P.; James, R.B. Determination of electric-field profile in CdTe and CdZnTe detectors using transient-current technique. IEEE Trans. Nucl. Sci. 2012, 59, 2402–2408. [Google Scholar] [CrossRef]
- Jung, M.; Morel, J.; Fougeres, P.; Hage-Ali, M.; Siffert, P. A new method for evaluation of transport properties in CdTe and CZT detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 428, 45–57. [Google Scholar] [CrossRef]
- Buurma, C.; Krishnamurthy, S.; Sivananthan, S. Shockley-read-hall lifetimes in CdTe. J. Appl. Phys. 2014, 116, 013102. [Google Scholar] [CrossRef]
- Höhr, T.; Schenk, A.; Fichtner, W. Revised Shockley–Read–Hall lifetimes for quantum transport modeling. J. Appl. Phys. 2004, 95, 4875–4882. [Google Scholar] [CrossRef]
- Kasap, S.; Ramaswami, K.O.; Kabir, M.; Johanson, R. Corrections to the Hecht collection efficiency in photoconductive detectors under large signals: Non-uniform electric field due to drifting and trapped unipolar carriers. J. Phys. D Appl. Phys. 2019, 52, 135104. [Google Scholar] [CrossRef]
- Ramaswami, K.O. Monte Carlo Simulation of Drifting Charge Carriers in Photoconductive Integrating Detectors. Ph.D. Thesis, University of Saskatchewan Saskatoon, Saskatoon, SK, Canada, 2019. [Google Scholar]
- Gatti, E.; Longoni, A.; Rehak, P.; Sampietro, M. Dynamics of electrons in drift detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1987, 253, 393–399. [Google Scholar] [CrossRef]
- Benoit, M.; Hamel, L. Simulation of charge collection processes in semiconductor CdZnTe γ-ray detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 606, 508–516. [Google Scholar] [CrossRef]
- Bolotnikov, A.; Camarda, G.; Carini, G.; Cui, Y.; Li, L.; James, R. Cumulative effects of Te precipitates in CdZnTe radiation detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2007, 571, 687–698. [Google Scholar] [CrossRef]
- Bolotnikov, A.; Camarda, G.; Cui, Y.; Yang, G.; Hossain, A.; Kim, K.; James, R. Characterization and evaluation of extended defects in CZT crystals for gamma-ray detectors. J. Cryst. Growth 2013, 379, 46–56. [Google Scholar] [CrossRef]
- Spartiotis, K.; Leppänen, A.; Pantsar, T.; Pyyhtiä, J.; Laukka, P.; Muukkonen, K.; Männistö, O.; Kinnari, J.; Schulman, T. A photon counting CdTe gamma-and X-ray camera. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 550, 267–277. [Google Scholar] [CrossRef]
- Gatti, E.; Rehak, P. Review of semiconductor drift detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 541, 47–60. [Google Scholar] [CrossRef]
- Sundberg, C.; Persson, M.; Wikner, J.J.; Danielsson, M. 1-μm spatial resolution in silicon photon-counting CT detectors. J. Med. Imaging 2021, 8, 063501. [Google Scholar] [CrossRef]
- Van Zeghbroeck, B.J. Principles of Semiconductor Devices; University of Colorado Boulder: Boulder, CO, USA, 2011. [Google Scholar]
- Marsden, J.E.; Tromba, A. Vector Calculus; Macmillan: New York, NY, USA, 2003. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Strikwerda, J.C. Finite Difference Schemes and Partial Differential Equations. SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Blitzstein, J.K.; Hwang, J. Introduction to Probability; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Ross, S.M.; Ross, S.M.; Ross, S.M.; Ross, S.M. A First Course in Probability; Macmillan: New York, NY, USA, 1976; Volume 2. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
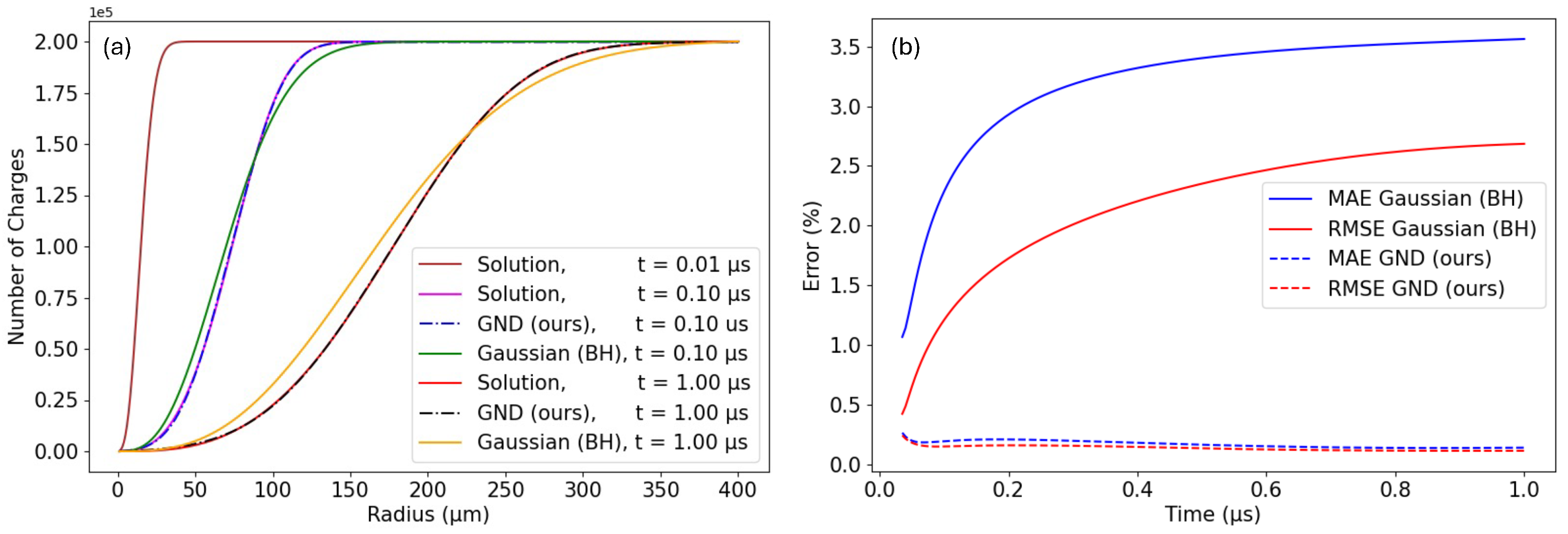

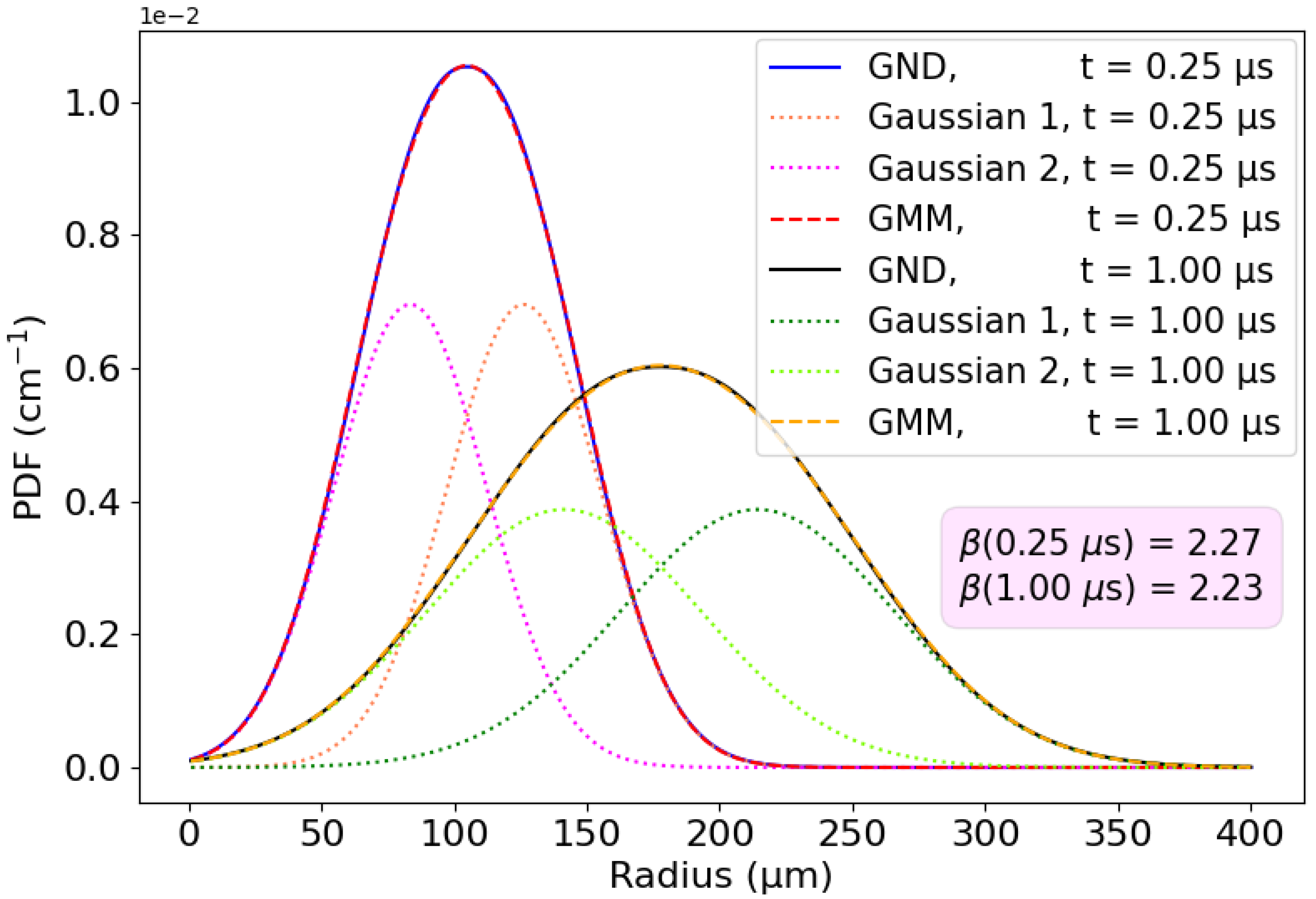
| Metrics | Gaussian (BH) | GND (Ours) |
|---|---|---|
| RMS absolute error (m) | 0.40 | 0.18 |
| MAE (%) | 3.21 | 0.17 |
| RMSE (%) | 2.19 | 0.14 |
| Cosine similarity | 1– | 1– |
| Correlation coefficient | 1– | 1– |
| KL divergence |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballester, M.; Kaspar, J.; Massanés, F.; Vija, A.H.; Katsaggelos, A.K. Charge Diffusion and Repulsion in Semiconductor Detectors. Sensors 2024, 24, 7123. https://doi.org/10.3390/s24227123
Ballester M, Kaspar J, Massanés F, Vija AH, Katsaggelos AK. Charge Diffusion and Repulsion in Semiconductor Detectors. Sensors. 2024; 24(22):7123. https://doi.org/10.3390/s24227123
Chicago/Turabian StyleBallester, Manuel, Jaromir Kaspar, Francesc Massanés, Alexander Hans Vija, and Aggelos K. Katsaggelos. 2024. "Charge Diffusion and Repulsion in Semiconductor Detectors" Sensors 24, no. 22: 7123. https://doi.org/10.3390/s24227123
APA StyleBallester, M., Kaspar, J., Massanés, F., Vija, A. H., & Katsaggelos, A. K. (2024). Charge Diffusion and Repulsion in Semiconductor Detectors. Sensors, 24(22), 7123. https://doi.org/10.3390/s24227123






