Continuous Gait Phase Estimation for Multi-Locomotion Tasks Using Ground Reaction Force Data
Abstract
1. Introduction
- Real-time classification of WCs is performed by analyzing FSR data using machine learning methods.
- Accurate real-time cGPE is performed to correspond to continuously varying WCs using a combination of WC classification results and FSR data.
- Walking experiments involving healthy adults are performed to verify the source-specific application of the proposed cGPE, irrespective of WCs.
2. Methods
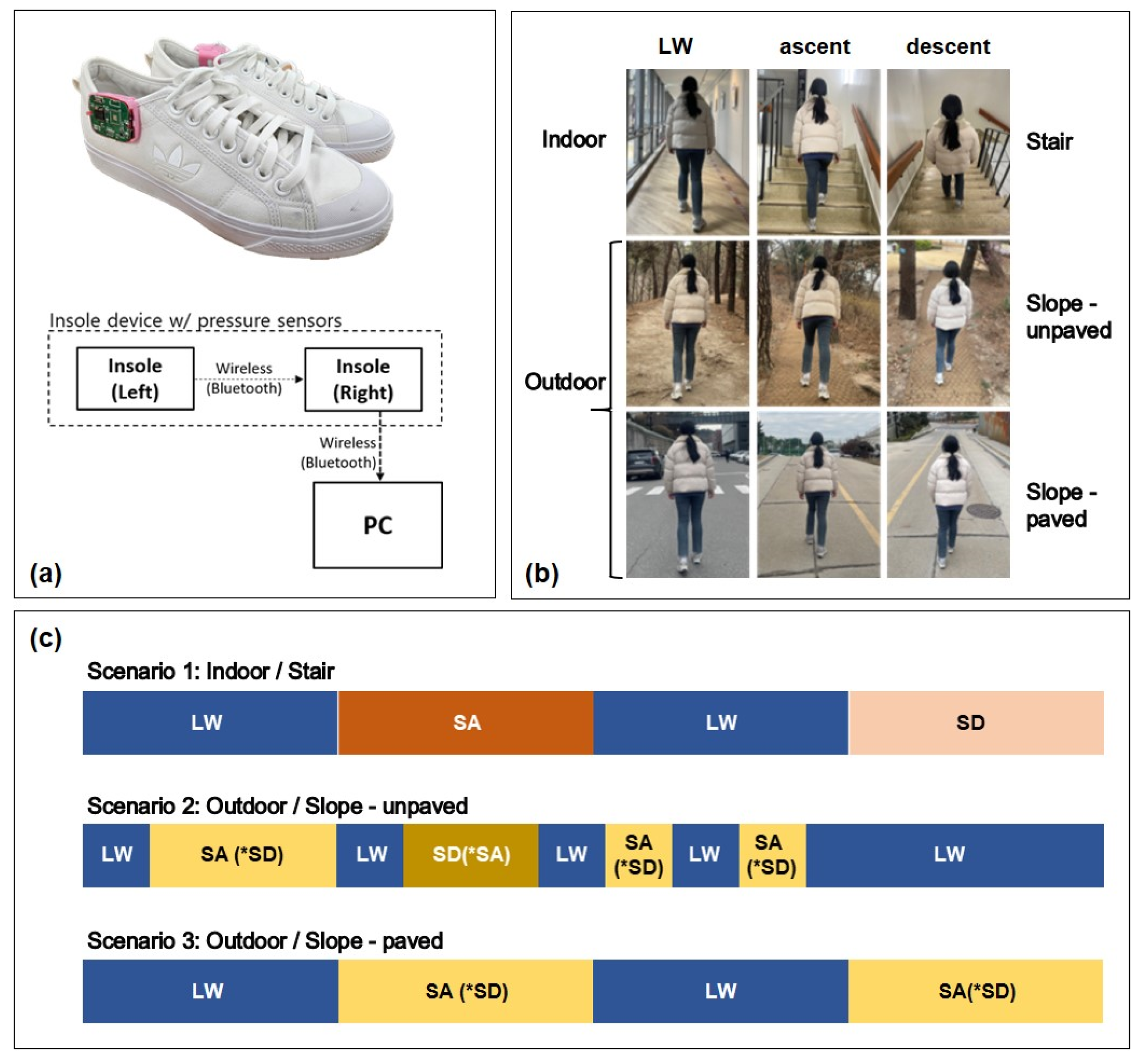
2.1. DAS
2.2. Experimental Conditions and Protocol
2.3. Walking Condition Classification and cGPE
3. Results
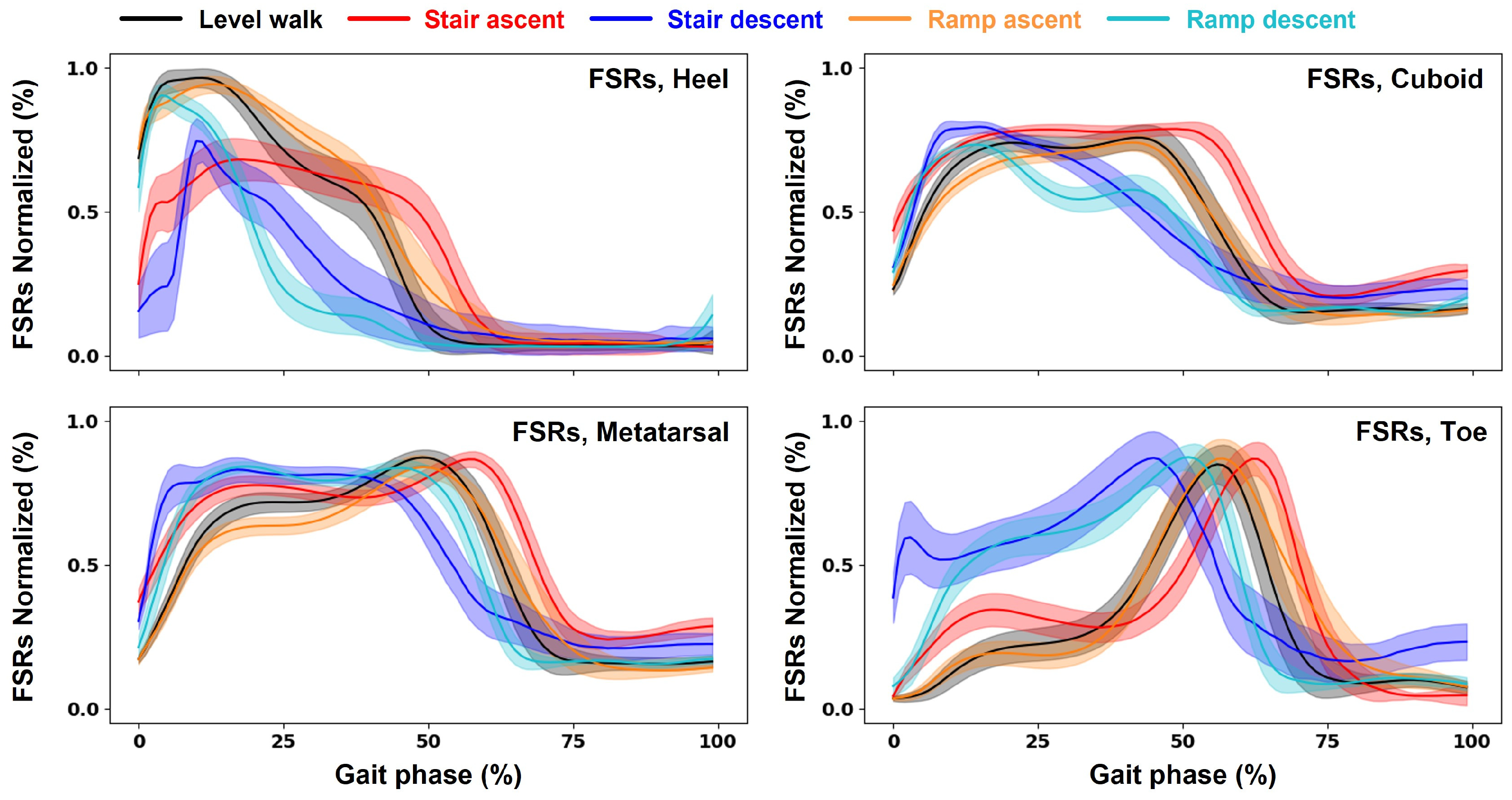
3.1. Experimental Measurement of FSRs
3.2. Walking Condition Classification Results
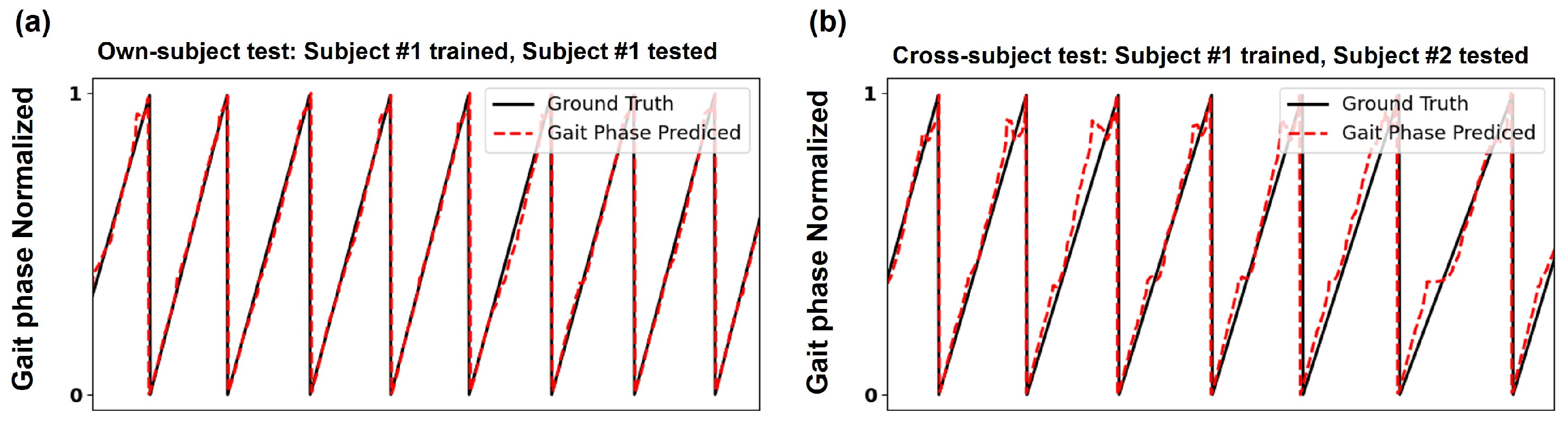
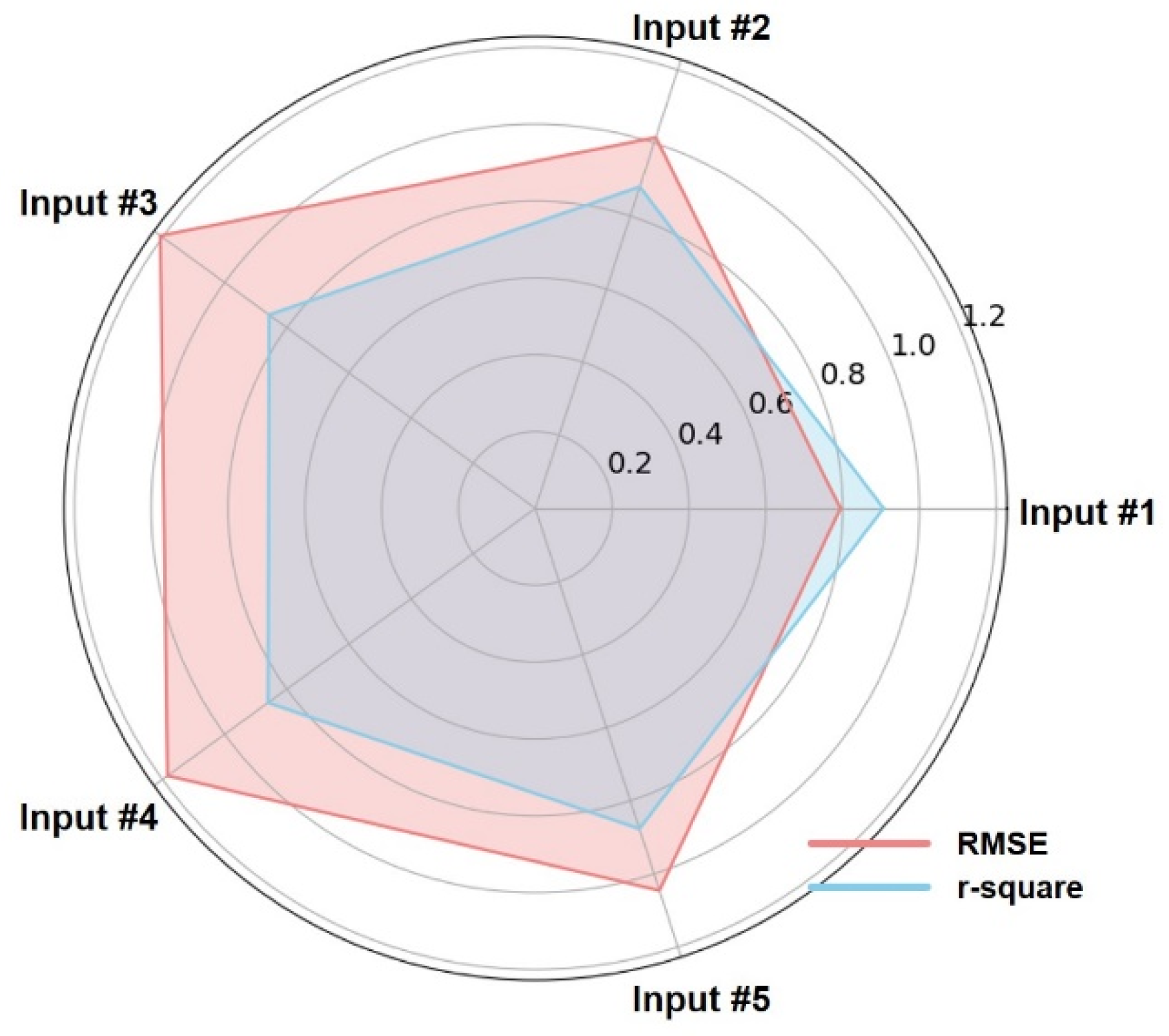
3.3. cGPE Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Whittle, M.W. Gait Analysis: An Introduction; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Wang, C.; Kim, Y.; Shin, H.; Min, S.D. Preliminary clinical application of textile insole sensor for hemiparetic gait pattern analysis. Sensors 2019, 19, 3950. [Google Scholar] [CrossRef] [PubMed]
- Seo, M.; Shin, M.J.; Park, T.S.; Park, J.H. Clinometric gait analysis using smart insoles in patients with hemiplegia after stroke: Pilot study. JMIR mHealth uHealth 2020, 8, e22208. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Wang, R.; Qi, D.; Xie, J.; Cao, J.; Liao, W.H. Wearable gait monitoring for diagnosis of neurodegenerative diseases. Measurement 2022, 202, 111839. [Google Scholar] [CrossRef]
- Han, Y.C.; Wong, K.I.; Murray, I. Gait phase detection for normal and abnormal gaits using IMU. IEEE Sens. J. 2019, 19, 3439–3448. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.W.; Ko, J. Gait disorder detection and classification method using inertia measurement unit for augmented feedback training in wearable devices. Sensors 2021, 21, 7676. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.; Kumar, N.A.; Hur, P. A phase-shifting based human gait phase estimation for powered transfemoral prostheses. IEEE Robot. Autom. Lett. 2021, 6, 5113–5120. [Google Scholar] [CrossRef]
- Chen, X.; Chen, C.; Wang, Y.; Yang, B.; Ma, T.; Leng, Y.; Fu, C. A piecewise monotonic gait phase estimation model for controlling a powered transfemoral prosthesis in various locomotion modes. IEEE Robot. Autom. Lett. 2022, 7, 9549–9556. [Google Scholar] [CrossRef]
- Kang, I.; Molinaro, D.D.; Duggal, S.; Chen, Y.; Kunapuli, P.; Young, A.J. Real-time gait phase estimation for robotic hip exoskeleton control during multimodal locomotion. IEEE Robot. Autom. Lett. 2021, 6, 3491–3497. [Google Scholar] [CrossRef]
- Medrano, R.L.; Thomas, G.C.; Keais, C.G.; Rouse, E.J.; Gregg, R.D. Real-time gait phase and task estimation for controlling a powered ankle exoskeleton on extremely uneven terrain. IEEE Trans. Robot. 2023, 39, 2170–2182. [Google Scholar] [CrossRef]
- Seo, K.; Park, Y.J.; Lee, J.; Hyung, S.; Lee, M.; Kim, J.; Shim, Y. RNN-based on-line continuous gait phase estimation from shank-mounted IMUs to control ankle exoskeletons. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019. [Google Scholar]
- Zhang, B.; Zhou, M.; Xu, W. An adaptive framework of real-time continuous gait phase variable estimation for lower-limb wearable robots. Robot. Auton. Syst. 2021, 143, 103842. [Google Scholar] [CrossRef]
- Choi, S.; Ko, C.; Kong, K. Walking-speed-adaptive gait phase estimation for wearable robots. Sensors 2023, 23, 8276. [Google Scholar] [CrossRef]
- Quintero, D.; Lambert, D.J.; Villarreal, D.J.; Gregg, R.D. Real-time continuous gait phase and speed estimation from a single sensor. In Proceedings of the 2017 IEEE Conference on Control Technology and Applications (CCTA), Maui, HI, USA, 27–30 August 2017. [Google Scholar]
- Villarreal, D.J.; Poonawala, H.A.; Gregg, R.D. A robust parameterization of human gait patterns across phase-shifting perturbations. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Livolsi, C.; Conti, R.; Giovacchini, F.; Vitiello, N.; Crea, S. A novel wavelet-based gait segmentation method for a portable hip exoskeleton. IEEE Trans. Robot. 2021, 38, 1503–1517. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Hu, J.; Zheng, J.; Wang, X.; Deng, J.; Wang, Y. Gait pattern identification and phase estimation in continuous multilocomotion mode based on inertial measurement units. IEEE Sens. J. 2022, 22, 16952–16962. [Google Scholar] [CrossRef]
- Wu, X.; Ma, Y.; Yong, X.; Wang, C.; He, Y.; Li, N. Locomotion mode identification and gait phase estimation for exoskeletons during continuous multilocomotion tasks. IEEE Trans. Cogn. Dev. Syst. 2019, 13, 45–56. [Google Scholar] [CrossRef]
- Seo, K.; Hyung, S.; Choi, B.K.; Lee, Y.; Shim, Y. A new adaptive frequency oscillator for gait assistance. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Seo, K.; Lee, J.; Lee, Y.; Ha, T.; Shim, Y. Fully autonomous hip exoskeleton saves metabolic cost of walking. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Xu, D.; Zhang, Z.; Crea, S.; Vitiello, N.; Wang, Q. Adaptive estimation of continuous gait phase based on capacitive sensors. Wearable Technol. 2022, 3, e11. [Google Scholar] [CrossRef]
- Lee, J.; Hong, W.; Hur, P. Continuous gait phase estimation using LSTM for robotic transfemoral prosthesis across walking speeds. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1470–1477. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Hu, J.; Wang, Y. Continuous human gait phase estimation considering individual diversity. In Proceedings of the 2023 15th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 26–27 August 2023. [Google Scholar]
- Thatte, N.; Shah, T.; Geyer, H. Robust and adaptive lower limb prosthesis stance control via extended kalman filter based gait phase estimation. IEEE Robot. Autom. Lett. 2019, 4, 3129–3136. [Google Scholar] [CrossRef]
- Mazon, D.M.; Groefsema, M.; Schomaker, L.R.; Carloni, R. IMU-based classification of locomotion modes, transitions, and gait phase with convolutional recurrent neural networks. Sensors 2022, 22, 8871. [Google Scholar] [CrossRef]
- Choi, W.; Yang, W.; Na, J.; Park, J.; Lee, G.; Nam, W. Unsupervised gait phase estimation with domain-adversarial neural network and adaptive window. IEEE J. Biomed. Health Inform. 2021, 26, 3373–3384. [Google Scholar] [CrossRef]
- Yu, S.; Yang, J.; Huang, T.H.; Zhu, J.; Visco, C.J.; Hameed, F.; Su, H. Artificial neural network-based activities classification, gait phase estimation, and prediction. Ann. Biomed. Eng. 2023, 51, 1471–1484. [Google Scholar] [CrossRef]
- Hong, W.; Lee, J.; Hur, P. Piecewise linear labeling method for speed-adaptability enhancement in human gait phase estimation. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 31, 628–635. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Liu, S.; Zhou, Z.; Sun, J.; Melendez-Calderon, A.; Guo, Z. Continuous gait phase recognition and prediction using lstm network across walking speeds and inclinations. In Proceedings of the 2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China, 9–11 July 2022. [Google Scholar]
- Park, J.S.; Kim, C.H. Ground-reaction-force-based gait analysis and its application to gait disorder assessment: New indices for quantifying walking behavior. Sensors 2022, 22, 7558. [Google Scholar] [CrossRef] [PubMed]
- Park, J.S.; Lee, C.M.; Koo, S.M.; Kim, C.H. Gait phase detection using force sensing resistors. IEEE Sens. J. 2020, 20, 6516–6523. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, W.; Wang, Q. A strain gauge based locomotion mode recognition method using convolutional neural network. Adv. Robot. 2019, 33, 254–263. [Google Scholar] [CrossRef]


| Model | Layer | Shape |
|---|---|---|
| Walking Condition Classification | Bi-LSTM | (128, 100 (1), 10 (3)) |
| Drop out | 0.25 | |
| Bi-LSTM | 64 | |
| Drop out | 0.25 | |
| Fully Connected | 64 | |
| Output layer | 5 | |
| Continuous Gait Phase Estimation | Bi-LSTM | (128, 100 (2), 10 (4)) |
| Drop out | 0.25 | |
| Bi-LSTM | 32 | |
| Drop out | 0.25 | |
| Fully Connected | 2 | |
| Output layer | 2 |
| Actual Class | Predict Class | ||||
|---|---|---|---|---|---|
| Level Walk | Stair Ascent | Stair Descent | Ramp Ascent | Ramp Descent | |
| Level walk | 90 ± 1% | 0 ± 0% | 0 ± 0% | 5 ± 2% | 4 ± 2% |
| Stair ascent | 6 ± 2% | 91 ± 4% | 1 ± 1% | 2 ± 2% | 1 ± 2% |
| Stair descent | 5 ± 4% | 1 ± 1% | 90 ± 5% | 0 ± 0% | 4 ± 4% |
| Ramp ascent | 9 ± 3% | 0 ± 0% | 0 ± 0% | 90 ± 3% | 1 ± 1% |
| Ramp descent | 8 ± 3% | 0 ± 0% | 0 ± 0% | 0 ± 0% | 91 ± 3% |
| Subject Used for Learning | Subject Used for Testing | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | ||
| #1 | LW | 0.607 (0.928) | 1.750 (0.793) | 1.487 (0.824) | 2.988 (0.648) | 1.083 (0.872) | 1.149 (0.864) | 0.633 (0.926) | 0.824 (0.903) | 0.795 (0.907) | 0.717 (0.916) |
| SA | 0.895 (0.894) | 1.833 (0.783) | 1.277 (0.851) | 3.070 (0.638) | 2.177 (0.746) | 2.438 (0.714) | 2.581 (0.695) | 2.404 (0.717) | 3.936 (0.534) | 3.349 (0.604) | |
| SD | 1.359 (0.841) | 1.668 (0.804) | 1.142 (0.864) | 2.968 (0.646) | 1.225 (0.855) | 1.523 (0.819) | 0.956 (0.887) | 1.438 (0.830) | 1.486 (0.827) | 1.523 (0.820) | |
| RA | 0.985 (0.884) | 0.669 (0.921) | 0.696 (0.918) | 2.678 (0.685) | 1.134 (0.866) | 0.802 (0.906) | 0.546 (0.935) | 0.379 (0.955) | 0.672 (0.921) | 0.707 (0.916) | |
| RD | 0.598 (0.929) | 1.286 (0.848) | 1.464 (0.827) | 2.978 (0.648) | 1.143 (0.865) | 1.503 (0.822) | 0.798 (0.906) | 1.271 (0.850) | 0.988 (0.883) | 0.520 (0.938) | |
| #2 | LW | 0.886 (0.895) | 0.692 (0.918) | 0.785 (0.907) | 1.717 (0.798) | 0.819 (0.903) | 2.038 (0.759) | 1.028 (0.879) | 0.850 (0.900) | 1.159 (0.864) | 2.086 (0.755) |
| SA | 3.244 (0.617) | 0.979 (0.884) | 2.549 (0.702) | 3.018 (0.644) | 2.216 (0.742) | 5.199 (0.390) | 3.994 (0.529) | 3.520 (0.586) | 7.061 (0.164) | 4.757 (0.437) | |
| SD | 6.430 (0.246) | 1.172 (0.862) | 1.599 (0.810) | 1.977 (0.764) | 1.483 (0.825) | 1.544 (0.816) | 1.667 (0.803) | 1.007 (0.881) | 3.324 (0.612) | 2.117 (0.749) | |
| RA | 1.647 (0.806) | 0.821 (0.903) | 0.668 (0.921) | 1.617 (0.810) | 1.311 (0.846) | 2.917 (0.658) | 1.296 (0.847) | 1.272 (0.851) | 1.706 (0.800) | 1.770 (0.790) | |
| RD | 1.154 (0.864) | 0.736 (0.913) | 0.757 (0.911) | 1.388 (0.836) | 0.747 (0.911) | 1.745 (0.794) | 0.939 (0.889) | 1.064 (0.875) | 1.231 (0.855) | 1.490 (0.824) | |
| #3 | LW | 1.334 (0.843) | 1.129 (0.866) | 0.618 (0.927) | 5.778 (0.319) | 0.793 (0.906) | 3.317 (0.608) | 1.166 (0.863) | 1.150 (0.864) | 0.964 (0.887) | 1.614 (0.811) |
| SA | 2.999 (0.646) | 2.350 (0.721) | 1.424 (0.833) | 4.576 (0.461) | 1.983 (0.769) | 4.529 (0.469) | 2.853 (0.663) | 2.617 (0.692) | 5.447 (0.355) | 3.765 (0.555) | |
| SD | 4.245 (0.502) | 1.190 (0.860) | 0.952 (0.887) | 3.593 (0.572) | 0.907 (0.893) | 2.778 (0.670) | 1.518 (0.820) | 1.186 (0.860) | 2.901 (0.662) | 2.703 (0.680) | |
| RA | 2.001 (0.765) | 1.546 (0.818) | 0.847 (0.900) | 3.943 (0.537) | 0.931 (0.890) | 2.260 (0.735) | 1.261 (0.851) | 1.422 (0.833) | 1.417 (0.834) | 1.344 (0.840) | |
| RD | 1.287 (0.848) | 1.545 (0.818) | 0.558 (0.934) | 5.330 (0.369) | 0.760 (0.910) | 3.262 (0.614) | 1.031 (0.878) | 1.108 (0.869) | 0.981 (0.884) | 1.202 (0.858) | |
| #4 | LW | 1.967 (0.768) | 1.507 (0.822) | 4.254 (0.498) | 0.433 (0.949) | 1.991 (0.765) | 3.545 (0.581) | 1.012 (0.881) | 0.659 (0.922) | 0.933 (0.890) | 0.991 (0.884) |
| SA | 1.892 (0.777) | 2.989 (0.646) | 1.800 (0.790) | 0.977 (0.885) | 1.950 (0.773) | 2.757 (0.677) | 2.557 (0.698) | 1.122 (0.868) | 4.581 (0.457) | 4.231 (0.500) | |
| SD | 11.929 (−0.399) | 1.679 (0.803) | 2.754 (0.673) | 0.906 (0.892) | 3.081 (0.636) | 1.623 (0.807) | 1.143 (0.865) | 1.185 (0.860) | 1.760 (0.795) | 1.591 (0.812) | |
| RA | 2.782 (0.673) | 0.936 (0.890) | 1.177 (0.861) | 0.628 (0.926) | 2.050 (0.759) | 2.748 (0.677) | 0.894 (0.894) | 0.537 (0.937) | 1.201 (0.859) | 0.814 (0.903) | |
| RD | 2.319 (0.726) | 1.189 (0.860) | 5.750 (0.322) | 0.564 (0.933) | 4.150 (0.508) | 2.594 (0.693) | 0.912 (0.892) | 1.231 (0.855) | 1.037 (0.877) | 0.731 (0.914) | |
| #5 | LW | 1.155 (0.864) | 1.013 (0.880) | 0.970 (0.886) | 1.654 (0.805) | 0.727 (0.914) | 3.501 (0.587) | 1.309 (0.846) | 1.531 (0.819) | 1.215 (0.857) | 2.081 (0.756) |
| SA | 2.745 (0.676) | 1.316 (0.844) | 1.389 (0.838) | 2.289 (0.730) | 1.040 (0.879) | 4.116 (0.517) | 1.964 (0.768) | 1.586 (0.813) | 5.551 (0.343) | 4.166 (0.507) | |
| SD | 9.937 (−0.165) | 1.268 (0.851) | 1.712 (0.797) | 1.921 (0.771) | 0.919 (0.891) | 2.451 (0.709) | 1.441 (0.829) | 1.449 (0.829) | 2.686 (0.687) | 2.620 (0.690) | |
| RA | 1.598 (0.812) | 0.891 (0.895) | 0.643 (0.924) | 1.260 (0.852) | 0.798 (0.906) | 2.206 (0.741) | 1.223 (0.855) | 1.506 (0.823) | 1.889 (0.778) | 1.388 (0.835) | |
| RD | 1.532 (0.819) | 0.815 (0.904) | 1.031 (0.878) | 1.191 (0.859) | 0.736 (0.913) | 3.445 (0.593) | 1.166 (0.862) | 1.811 (0.787) | 1.290 (0.848) | 1.234 (0.854) | |
| Subject Used for Learning | Subject Used for Testing | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | ||
| #6 | LW | 2.010 (0.763) | 2.631 (0.689) | 1.888 (0.777) | 2.233 (0.737) | 2.504 (0.705) | 0.955 (0.887) | 1.946 (0.771) | 0.795 (0.906) | 1.242 (0.854) | 0.587 (0.931) |
| SA | 10.036 (−0.185) | 3.164 (0.625) | 4.864 (0.431) | 4.742 (0.441) | 3.057 (0.644) | 1.104 (0.870) | 3.050 (0.640) | 4.529 (0.467) | 2.269 (0.731) | 4.609 (0.455) | |
| SD | 12.719 (−0.491) | 3.866 (0.546) | 2.267 (0.731) | 1.925 (0.770) | 7.350 (0.132) | 0.792 (0.906) | 1.325 (0.843) | 1.496 (0.823) | 1.344 (0.843) | 1.350 (0.840) | |
| RA | 10.081 (−0.186) | 5.471 (0.355) | 2.817 (0.668) | 2.471 (0.710) | 4.541 (0.465) | 0.438 (0.949) | 2.642 (0.688) | 0.505 (0.941) | 0.737 (0.913) | 0.642 (0.924) | |
| RD | 1.648 (0.806) | 2.321 (0.726) | 1.083 (0.872) | 1.822 (0.784) | 4.646 (0.449) | 1.320 (0.844) | 2.885 (0.659) | 1.087 (0.872) | 1.395 (0.835) | 0.647 (0.923) | |
| #7 | LW | 1.985 (0.766) | 1.435 (0.828) | 2.042 (0.759) | 5.838 (0.312) | 1.442 (0.930) | 4.309 (0.491) | 0.545 (0.936) | 0.654 (0.923) | 0.745 (0.913) | 1.148 (0.865) |
| SA | 7.603 (0.103) | 3.618 (0.571) | 1.728 (0.798) | 6.780 (0.201) | 4.002 (0.534) | 4.291 (0.497) | 0.592 (0.930) | 2.222 (0.739) | 3.723 (0.559) | 2.398 (0.716) | |
| SD | 9.771 (−0.146) | 2.610 (0.693) | 1.188 (0.859) | 5.720 (0.318) | 2.394 (0.717) | 4.435 (0.473) | 0.756 (0.910) | 1.260 (0.851) | 2.103 (0.755) | 1.791 (0.788) | |
| RA | 2.753 (0.676) | 1.436 (0.831) | 1.636 (0.807) | 4.516 (0.469) | 2.105 (0.752) | 2.654 (0.688) | 0.722 (0.915) | 0.903 (0.894) | 1.211 (0.858) | 1.120 (0.867) | |
| RD | 2.248 (0.735) | 1.592 (0.812) | 2.455 (0.710) | 5.248 (0.379) | 2.032 (0.759) | 4.332 (0.488) | 0.564 (0.933) | 1.492 (0.824) | 0.949 (0.888) | 0.811 (0.904) | |
| #8 | LW | 2.270 (0.732) | 1.476 (0.825) | 2.771 (0.673) | 5.000 (0.411) | 1.303 (0.846) | 2.434 (0.713) | 1.269 (0.851) | 0.721 (0.915) | 1.662 (0.805) | 1.252 (0.853) |
| SA | 5.530 (0.347) | 4.611 (0.453) | 2.857 (0.666) | 4.400 (0.482) | 2.248 (0.738) | 4.138 (0.515) | 1.113 (0.869) | 0.584 (0.931) | 3.685 (0.564) | 2.289 (0.729) | |
| SD | 4.261 (0.500) | 1.829 (0.785) | 2.621 (0.689) | 4.751 (0.433) | 3.654 (0.568) | 3.951 (0.530) | 1.059 (0.875) | 0.962 (0.886) | 3.144 (0.633) | 2.277 (0.730) | |
| RA | 2.255 (0.735) | 1.541 (0.818) | 1.947 (0.771) | 4.832 (0.432) | 2.418 (0.715) | 7.870 (0.076) | 1.485 (0.824) | 0.667 (0.922) | 2.498 (0.707) | 0.997 (0.882) | |
| RD | 2.280 (0.731) | 2.070 (0.756) | 3.704 (0.563) | 4.161 (0.508) | 1.209 (0.857) | 2.581 (0.695) | 1.121 (0.868) | 0.957 (0.887) | 1.452 (0.828) | 1.044 (0.876) | |
| #9 | LW | 2.488 (0.707) | 2.873 (0.660) | 3.336 (0.606) | 1.984 (0.766) | 4.820 (0.432) | 1.703 (0.799) | 0.909 (0.893) | 0.705 (0.917) | 0.794 (0.907) | 0.420 (0.951) |
| SA | 4.358 (0.486) | 2.717 (0.678) | 2.606 (0.695) | 1.849 (0.782) | 6.069 (0.293) | 2.174 (0.745) | 1.508 (0.822) | 1.796 (0.789) | 0.797 (0.906) | 3.075 (0.636) | |
| SD | 12.343 (−0.447) | 3.041 (0.643) | 1.454 (0.827) | 1.593 (0.810) | 2.297 (0.729) | 1.136 (0.865) | 1.457 (0.827) | 1.144 (0.865) | 0.660 (0.923) | 1.765 (0.791) | |
| RA | 3.169 (0.627) | 4.738 (0.442) | 2.714 (0.680) | 4.092 (0.519) | 2.845 (0.665) | 6.273 (0.264) | 2.096 (0.752) | 0.406 (0.952) | 0.535 (0.937) | 0.422 (0.950) | |
| RD | 2.399 (0.717) | 3.354 (0.605) | 1.859 (0.781) | 2.477 (0.707) | 7.358 (0.128) | 1.654 (0.804) | 0.851 (0.900) | 1.176 (0.861) | 1.341 (0.842) | 0.456 (0.946) | |
| #10 | LW | 2.032 (0.760) | 1.821 (0.785) | 3.630 (0.572) | 4.447 (0.476) | 3.589 (0.577) | 3.137 (0.630) | 0.518 (0.939) | 0.635 (0.925) | 0.837 (0.902) | 0.486 (0.943) |
| SA | 3.742 (0.558) | 3.304 (0.608) | 2.832 (0.669) | 4.341 (0.489) | 2.243 (0.739) | 5.493 (0.355) | 1.166 (0.862) | 1.722 (0.797) | 5.566 (0.341) | 0.995 (0.882) | |
| SD | 8.383 (0.017) | 1.896 (0.608) | 1.969 (0.766) | 3.500 (0.583) | 3.579 (0.577) | 5.342 (0.365) | 0.736 (0.913) | 1.077 (0.873) | 2.249 (0.738) | 0.689 (0.918) | |
| RA | 8.031 (0.055) | 1.508 (0.822) | 3.537 (0.583) | 2.617 (0.693) | 8.233 (0.030) | 1.933 (0.773) | 0.394 (0.953) | 0.667 (0.922) | 0.829 (0.903) | 0.382 (0.955) | |
| RD | 2.339 (0.724) | 2.289 (0.730) | 2.935 (0.654) | 3.872 (0.542) | 6.821 (0.192) | 4.114 (0.514) | 0.785 (0.907) | 1.089 (0.872) | 1.085 (0.872) | 0.377 (0.955) | |
| Input Data Used for Learning | Subject Used for Own-Subject Prediction | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | ||
| each FSR FSRFore FSRBack WC (input#1) | LW | 0.607 (0.928) | 0.692 (0.918) | 0.618 (0.927) | 0.433 (0.949) | 0.727 (0.914) | 0.955 (0.887) | 0.545 (0.936) | 0.721 (0.915) | 0.794 (0.907) | 0.486 (0.943) |
| SA | 0.895 (0.894) | 0.979 (0.884) | 1.424 (0.833) | 0.977 (0.885) | 1.040 (0.879) | 1.104 (0.870) | 0.592 (0.930) | 0.584 (0.931) | 0.797 (0.906) | 0.995 (0.882) | |
| SD | 1.359 (0.841) | 1.172 (0.862) | 0.952 (0.887) | 0.906 (0.892) | 0.919 (0.891) | 0.792 (0.906) | 0.756 (0.910) | 0.962 (0.886) | 0.660 (0.923) | 0.689 (0.918) | |
| RA | 0.985 (0.884) | 0.821 (0.903) | 0.847 (0.900) | 0.628 (0.926) | 0.798 (0.906) | 0.438 (0.949) | 0.722 (0.915) | 0.667 (0.922) | 0.535 (0.937) | 0.382 (0.955) | |
| RD | 0.598 (0.929) | 0.736 (0.913) | 0.558 (0.934) | 0.564 (0.933) | 0.736 (0.913) | 1.320 (0.844) | 0.564 (0.933) | 0.957 (0.887) | 1.341 (0.842) | 0.377 (0.955) | |
| each FSR FSRFore FSRBack (input#2) | LW | 0.799 (0.906) | 0.827 (0.927) | 0.632 (0.905) | 0.808 (0.905) | 1.158 (0.863) | 0.886 (0.895) | 0.645 (0.924) | 0.835 (0.902) | 0.762 (0.911) | 0.372 (0.956) |
| SA | 1.366 (0.839) | 2.786 (0.670) | 1.403 (0.797) | 1.822 (0.785) | 1.887 (0.780) | 1.997 (0.766) | 0.658 (0.922) | 0.951 (0.888) | 0.945 (0.888) | 1.478 (0.825) | |
| SD | 1.661 (0.805) | 0.936 (0.890) | 1.060 (0.879) | 1.311 (0.844) | 1.541 (0.818) | 0.821 (0.902) | 0.662 (0.922) | 0.824 (0.903) | 0.673 (0.922) | 0.933 (0.889) | |
| RA | 1.269 (0.851) | 1.367 (0.839) | 0.958 (0.940) | 0.842 (0.901) | 1.226 (0.856) | 0.474 (0.944) | 0.723 (0.914) | 0.764 (0.910) | 0.670 (0.921) | 0.445 (0.947) | |
| RD | 0.754 (0.911) | 1.059 (0.875) | 0.548 (0.888) | 0.664 (0.921) | 1.082 (0.872) | 1.424 (0.832) | 0.590 (0.930) | 0.815 (0.904) | 1.206 (0.857) | 0.424 (0.950) | |
| each FSR WC (input#3) | LW | 1.001 (0.882) | 1.254 (0.852) | 1.277 (0.849) | 0.849 (0.900) | 1.003 (0.882) | 0.940 (0.889) | 1.077 (0.873) | 1.580 (0.814) | 0.596 (0.930) | 1.023 (0.880) |
| SA | 1.814 (0.709) | 1.316 (0.844) | 1.630 (0.809) | 1.733 (0.796) | 1.686 (0.804) | 1.249 (0.853) | 1.390 (0.836) | 1.186 (0.861) | 1.004 (0.881) | 1.279 (0.849) | |
| SD | 2.480 (0.709) | 1.240 (0.854) | 1.484 (0.824) | 0.985 (0.883) | 1.357 (0.840) | 0.966 (0.885) | 1.392 (0.835) | 1.142 (0.865) | 1.042 (0.878) | 1.126 (0.867) | |
| RA | 1.525 (0.820) | 1.589 (0.813) | 1.333 (0.843) | 0.991 (0.884) | 0.944 (0.889) | 0.783 (0.908) | 0.995 (0.882) | 1.385 (0.837) | 0.852 (0.932) | 0.995 (0.882) | |
| RD | 1.123 (0.867) | 1.237 (0.854) | 1.137 (0.866) | 0.842 (0.900) | 1.123 (0.867) | 1.430 (0.831) | 0.886 (0.895) | 1.471 (0.827) | 0.781 (0.908) | 0.827 (0.902) | |
| FSRFore FSRBack WC (input#4) | LW | 0.786 (0.907) | 1.053 (0.875) | 1.133 (0.866) | 1.265 (0.851) | 1.468 (0.827) | 0.966 (0.886) | 0.844 (0.901) | 1.570 (0.815) | 0.593 (0.930) | 0.930 (0.891) |
| SA | 1.346 (0.841) | 1.515 (0.820) | 1.647 (0.807) | 2.183 (0.743) | 2.041 (0.762) | 1.410 (0.835) | 0.806 (0.905) | 1.762 (0.793) | 0.905 (0.893) | 1.260 (0.851) | |
| SD | 1.366 (0.840) | 1.113 (0.869) | 0.988 (0.883) | 0.957 (0.886) | 1.635 (0.807) | 0.887 (0.895) | 0.913 (0.892) | 1.526 (0.820) | 1.052 (0.877) | 0.916 (0.891) | |
| RA | 1.210 (0.858) | 1.779 (0.790) | 1.570 (0.815) | 1.388 (0.837) | 1.441 (0.830) | 0.719 (0.916) | 0.817 (0.903) | 1.514 (0.822) | 0.586 (0.931) | 0.813 (0.903) | |
| RD | 0.715 (0.916) | 1.253 (0.852) | 0.909 (0.893) | 1.003 (0.881) | 1.584 (0.812) | 1.403 (0.834) | 0.768 (0.909) | 1.490 (0.824) | 0.783 (0.908) | 0.608 (0.928) | |
| FSRFore FSRBack COP WC (input#5) | LW | 0.870 (0.897) | 1.048 (0.876) | 0.632 (0.925) | 0.420 (0.951) | 1.581 (0.814) | 1.093 (0.871) | 0.806 (0.905) | 1.034 (0.878) | 1.139 (0.866) | 0.395 (0.954) |
| SA | 2.190 (0.741) | 1.336 (0.842) | 1.403 (0.836) | 1.289 (0.848) | 2.006 (0.766) | 1.176 (0.862) | 0.763 (0.910) | 1.308 (0.846) | 0.929 (0.890) | 0.883 (0.896) | |
| SD | 1.554 (0.818) | 1.198 (0.859) | 1.060 (0.874) | 0.778 (0.907) | 1.518 (0.821) | 0.640 (0.924) | 0.791 (0.906) | 0.844 (0.900) | 1.085 (0.874) | 0.806 (0.905) | |
| RA | 0.715 (0.916) | 1.215 (0.857) | 0.958 (0.887) | 0.554 (0.935) | 1.850 (0.782) | 0.373 (0.956) | 0.963 (0.886) | 1.071 (0.874) | 0.792 (0.907) | 0.444 (0.947) | |
| RD | 0.836 (0.901) | 1.056 (0.876) | 0.548 (0.935) | 0.702 (0.917) | 1.661 (0.803) | 1.540 (0.818) | 0.811 (0.904) | 0.923 (0.891) | 2.271 (0.732) | 0.408 (0.952) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.S.; Kim, C.H. Continuous Gait Phase Estimation for Multi-Locomotion Tasks Using Ground Reaction Force Data. Sensors 2024, 24, 6318. https://doi.org/10.3390/s24196318
Park JS, Kim CH. Continuous Gait Phase Estimation for Multi-Locomotion Tasks Using Ground Reaction Force Data. Sensors. 2024; 24(19):6318. https://doi.org/10.3390/s24196318
Chicago/Turabian StylePark, Ji Su, and Choong Hyun Kim. 2024. "Continuous Gait Phase Estimation for Multi-Locomotion Tasks Using Ground Reaction Force Data" Sensors 24, no. 19: 6318. https://doi.org/10.3390/s24196318
APA StylePark, J. S., & Kim, C. H. (2024). Continuous Gait Phase Estimation for Multi-Locomotion Tasks Using Ground Reaction Force Data. Sensors, 24(19), 6318. https://doi.org/10.3390/s24196318






