A Novel Waveform Optimization Method for Orthogonal-Frequency Multiple-Input Multiple-Output Radar Based on Dual-Channel Neural Networks
Abstract
1. Introduction
- The causes of the periodic high sidelobes in the OFDM-LFM waveform applied in MIMO radar systems were analyzed in detail, which revealed that the periodicity is related to pulse width.
- In order to design OFDM-LFM waveforms with good correlation properties, a ResNeXt-based dual-channel CNNs method is presented, to optimize the phase and bandwidth of the OFDM-LFM waveforms. Meanwhile, a new adjustable objective function is proposed, which can optimize both the PSL and the ISL simultaneously by utilizing the optimization factor.
- Extensive numerical simulations were employed to validate the performance of the proposed CNNs method for OFDM-LFM waveform design. The experimental results show that the designed waveforms have better target detection performance compared to the traditional OFDM-LFM waveforms.
2. MIMO Radar Signal Model
2.1. OFDM-LFM Signal
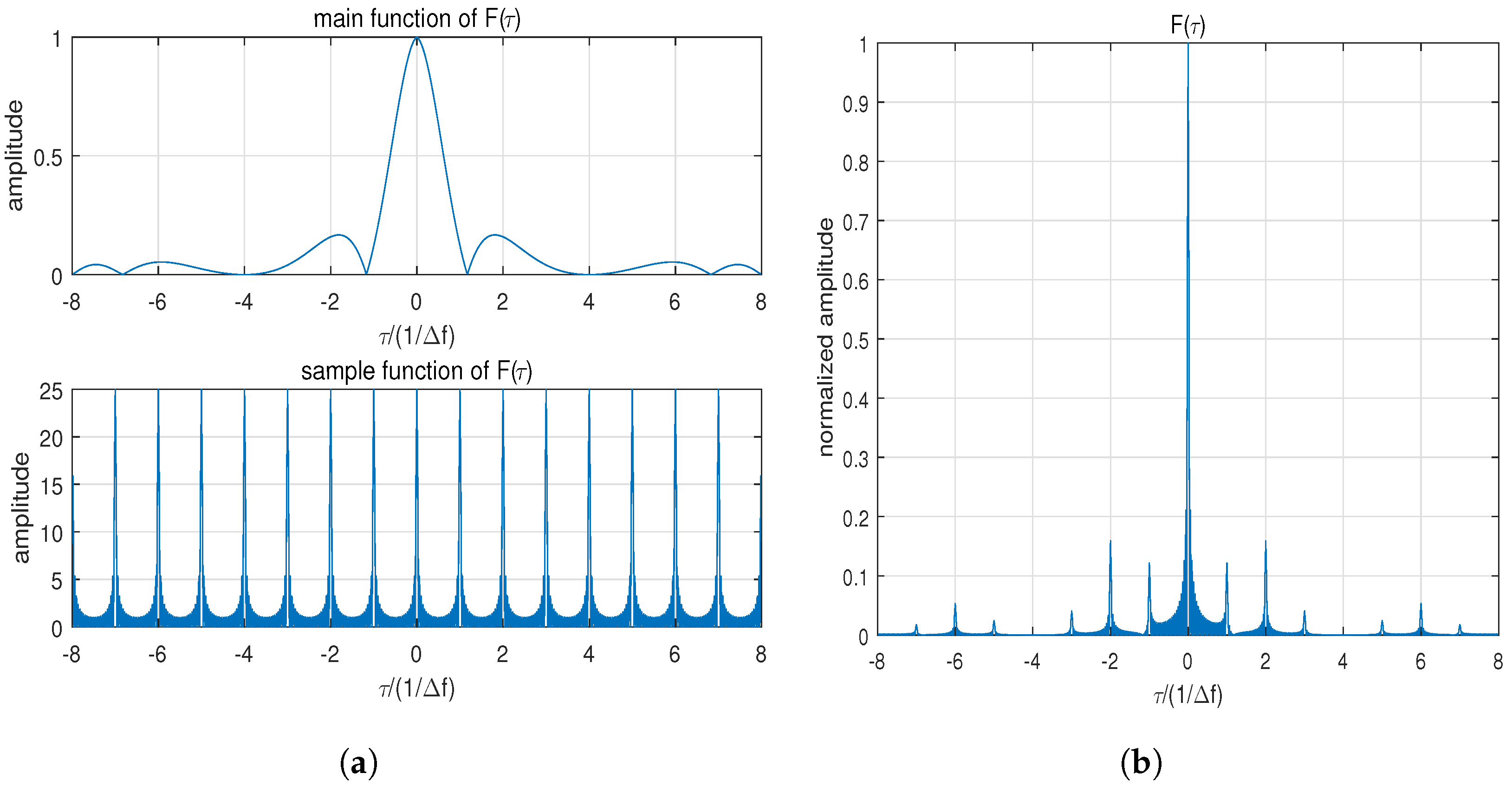
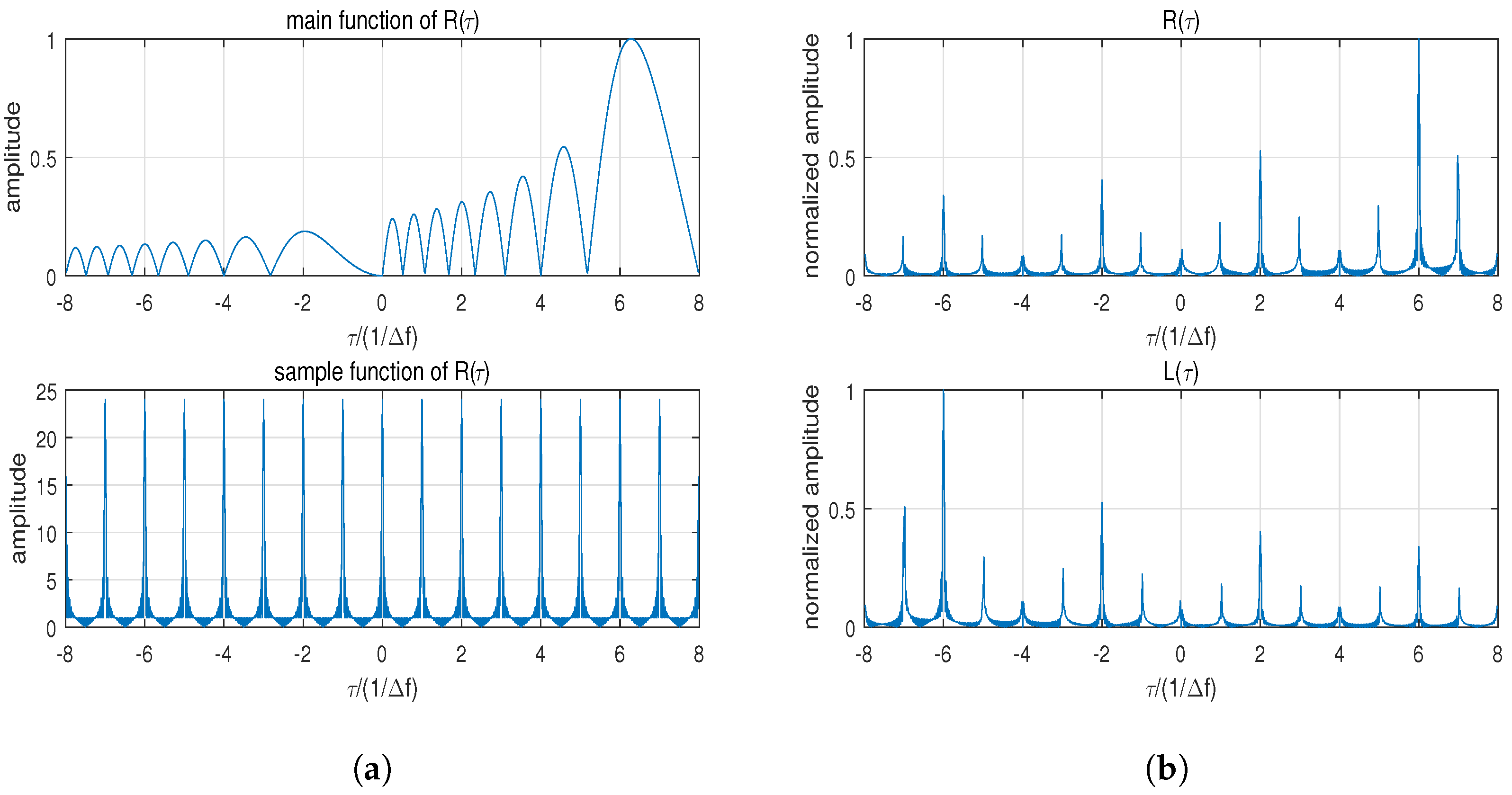
2.2. Analysis of Sidelobe Performance
3. Structure of Neural Networks
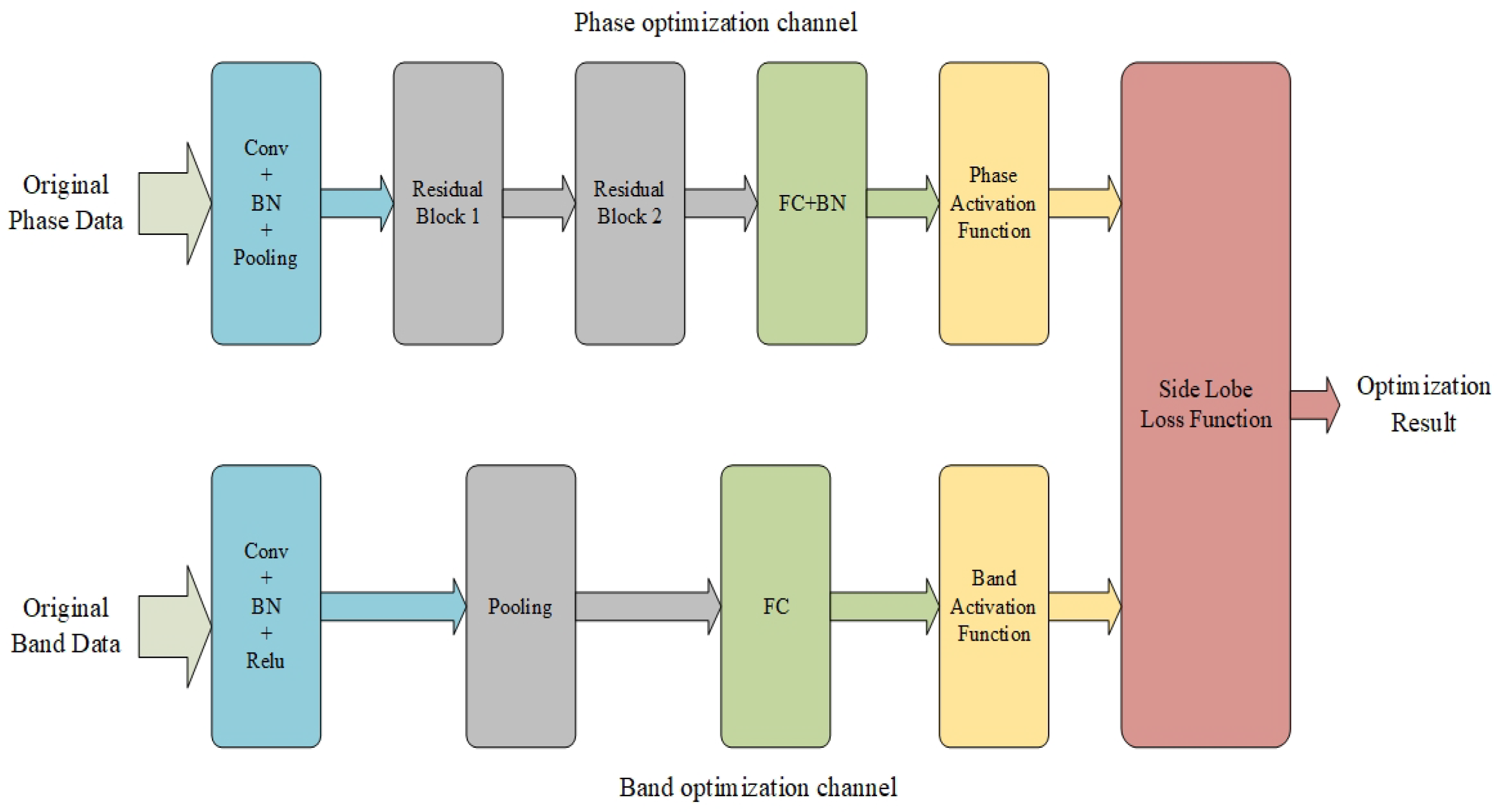
3.1. Dual-Channel CNNs Model
3.2. Loss Function
| Algorithm 1 In the dual-channel neural networks-based waveform optimization method, N represents the number of transmitting antennas, is a specific optimization factor, and D denotes the total number of iterations. Convolution kernel parameters are initialized by truncated random normal distribution data. |
|
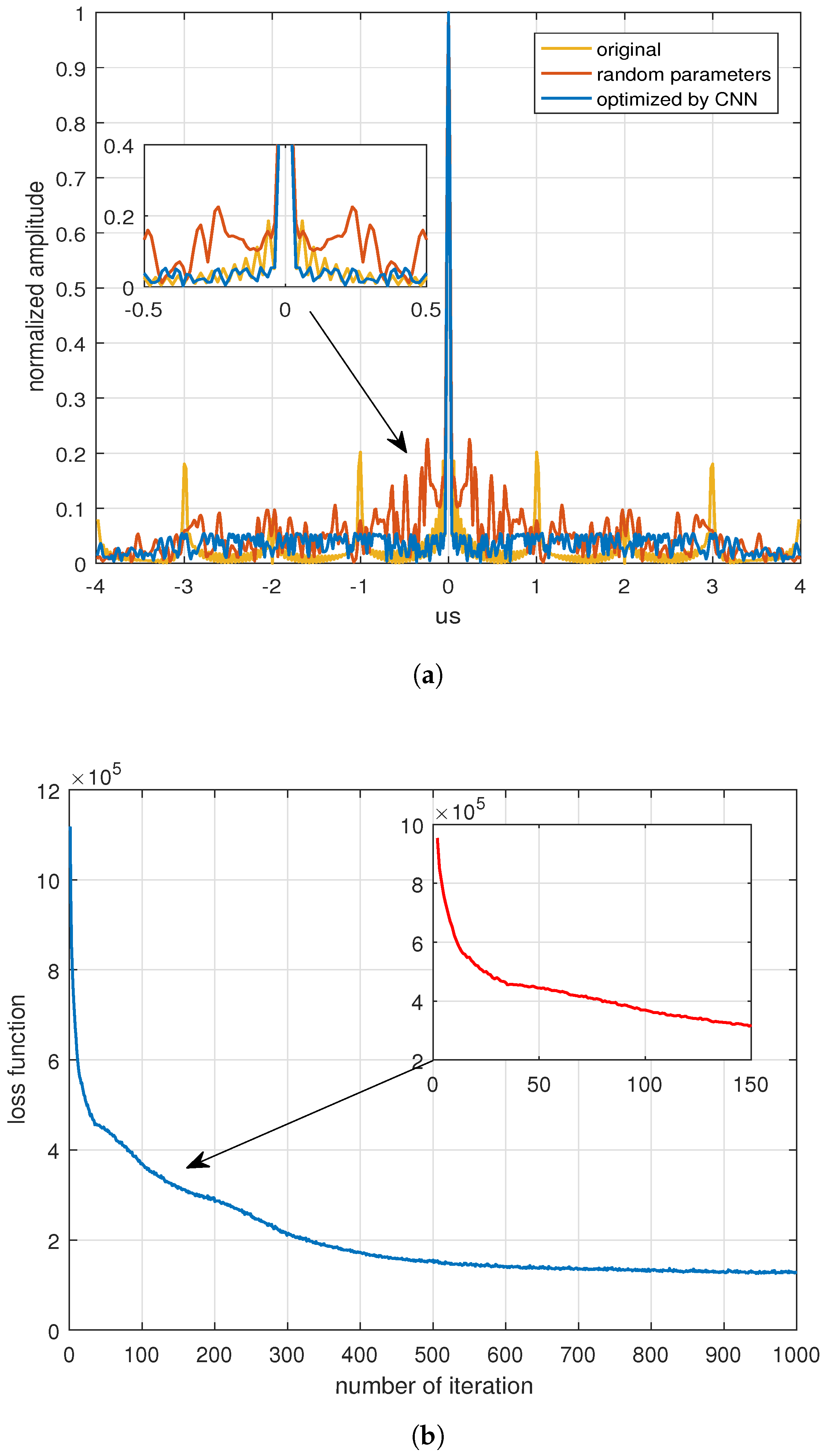
4. Numerical Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Derivation of R(τ)
References
- De Maio, A.; Lops, M. Design Principles of MIMO Radar Detectors. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 886–898. [Google Scholar]
- Pan, J.; Zheng, Z.; Zhao, D.; Yan, K.; Nie, J.; Zhou, B.; Fang, G. A Multi-Target Detection Method Based on Improved U-Net for UWB MIMO Through-Wall Radar. Remote Sens. 2023, 15, 3434. [Google Scholar] [CrossRef]
- Rojhani, N.; Shaker, G. Comprehensive Review: Effectiveness of MIMO and Beamforming Technologies in Detecting Low RCS UAVs. Remote Sens. 2024, 16, 1016. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; Huang, L.; So, H. Joint Range and Angle Estimation Using MIMO Radar With Frequency Diverse Array. IEEE Trans. Signal Process. 2015, 63, 3396–3410. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Fuhrmann, D.R.; San Antonio, G. Transmit beamforming for MIMO radar systems using signal cross-correlation. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 171–186. [Google Scholar] [CrossRef]
- Cui, G.; Li, H.; Rangaswamy, M. MIMO Radar Waveform Design with Constant Modulus and Similarity Constraints. IEEE Trans. Signal Process. 2014, 62, 343–353. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.; Ahmad, F. Dual-Function Radar-Communications: Information Embedding Using Sidelobe Control and Waveform Diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Yang, Y.; Blum, R.S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 330–343. [Google Scholar] [CrossRef]
- Stoica, P.; He, H.; Li, J. New Algorithms for Designing Unimodular Sequences with Good Correlation Properties. IEEE Trans. Signal Process. 2009, 57, 1415–1425. [Google Scholar] [CrossRef]
- Song, J.; Babu, P.; Palomar, D.P. Optimization Methods for Designing Sequences with Low Autocorrelation Sidelobes. IEEE Trans. Signal Process. 2015, 63, 3998–4009. [Google Scholar] [CrossRef]
- Aubry, A.; De, M.A.; Huang, Y. MIMO Radar Beampattern Design via PSL/ISL Optimization. IEEE Trans. Signal Process. 2016, 64, 3955–3967. [Google Scholar] [CrossRef]
- Fan, W.; Liang, J.; Li, J. Constant Modulus MIMO Radar Waveform Design with Minimum Peak Sidelobe Transmit Beampattern. IEEE Trans. Signal Process. 2018, 66, 4207–4222. [Google Scholar] [CrossRef]
- Hague, D.A. Adaptive Transmit Waveform Design Using Multitone Sinusoidal Frequency Modulation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1274–1287. [Google Scholar] [CrossRef]
- Wang, X.; Tang, B.; Zhang, M. Optimisation of practically constrained waveforms for rician target detection with multiple-input-multiple-output radar. IET Radar Sonar Navig. 2022, 16, 1116–1130. [Google Scholar] [CrossRef]
- Jiang, W.; Haimovich, A.M.; Simeone, O. Joint Design of Radar Waveform and Detector via End-to-End Learning with Waveform Constraints. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 552–567. [Google Scholar] [CrossRef]
- Raei, E.; Sedighi, S.; Alaee-Kerahroodi, M.; Bhavani Shankar, M.R. MIMO Radar Transmit Beampattern Shaping for Spectrally Dense Environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1007–1020. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Cheng, Z.; Feng, D. Orthogonal frequency division multiplexing linear frequency modulation signal design with optimised pulse compression property of spatial synthesised signals. IET Radar Sonar Navig. 2016, 10, 1319–1326. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Cheng, Z.; Feng, D. Correlated LFM Waveform Set Design for MIMO Radar Transmit Beampattern. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 329–333. [Google Scholar] [CrossRef]
- Dash, D.; Jayaraman, V. Ambiguity Function Analysis for Orthogonal-LFM Waveform Based Multistatic Radar. IEEE Sens. Lett. 2021, 5, 7501204. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Luo, F.; Wu, W. Waveform Design and DoA-DoD Estimation of OFDM-LFM Signal Based on SDFnT for MIMO Radar. IEEE Access 2023, 11, 1348–1358. [Google Scholar] [CrossRef]
- Wang, S.; He, F.; Dong, Z. A Novel Intrapulse Beamsteering SAR Imaging Mode Based on OFDM-Chirp Signals. Remote Sens. 2024, 16, 126. [Google Scholar] [CrossRef]
- Ding, M.; Li, Y.; Wei, J.; Zhu, E. Joint Design of OFDM-LFM Waveforms and Receive Filter for MIMO Radar in Spatial Heterogeneous Clutter. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3500105. [Google Scholar] [CrossRef]
- Pei, J.; Huang, Y.; Huo, W.; Zhang, Y.; Yang, J.; Yeo, T.-S. SAR Automatic Target Recognition Based on Multiview Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2196–2210. [Google Scholar] [CrossRef]
- Cui, Z.; Li, Q.; Cao, Z.; Liu, N. Dense Attention Pyramid Networks for Multi-Scale Ship Detection in SAR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8983–8997. [Google Scholar] [CrossRef]
- Li, Y.; Peng, C.; Chen, Y.; Jiao, L.; Zhou, L. A Deep Learning Method for Change Detection in Synthetic Aperture Radar Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5751–5763. [Google Scholar] [CrossRef]
- Wu, Z.; Hou, B.; Ren, B.; Ren, Z.; Wang, S.; Jiao, L. A Deep Detection Network Based on Interaction of Instance Segmentation and Object Detection for SAR Images. Remote Sens. 2021, 13, 2582. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. MIMO Radar Imaging Method with Non-Orthogonal Waveforms Based on Deep Learning. Algorithms 2022, 15, 306. [Google Scholar] [CrossRef]
- Bao, R.; Yang, Z. CNN-Based Regional People Counting Algorithm Exploiting Multi-Scale Range-Time Maps with an IR-UWB Radar. IEEE Sens. J. 2021, 21, 13704–13713. [Google Scholar] [CrossRef]
- Loran, T.; da Silva, A.B.C.; Joshi, S.K.; Baumgartner, S.V.; Krieger, G. Ship Detection Based on Faster R-CNN Using Range-Compressed Airborne Radar Data. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3500205. [Google Scholar] [CrossRef]
- Liang, R.; Cen, Y. Radar Signal Classification with Multi-Frequency Multi-Scale Deformable Convolutional Networks and Attention Mechanisms. Remote Sens. 2024, 44, 1431. [Google Scholar] [CrossRef]
- Hu, J.; Wei, Z.; Li, Y.; Li, H.; Wu, J. Designing Unimodular Waveform(s) for MIMO Radar by Deep Learning Method. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1184–1196. [Google Scholar] [CrossRef]
- Cong, J.; Wang, X.; Huang, M.; Wan, L. Robust DOA Estimation Method for MIMO Radar via Deep Neural Networks. IEEE Sens. J. 2021, 21, 7498–7507. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, J.; Zhong, K.; Zuo, Y.; Li, H. MIMO Radar Waveform Design for Range-ISL Optimization via Iterative Deep Unfolding Network. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3503405. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 June 2017; pp. 5987–5995. [Google Scholar]


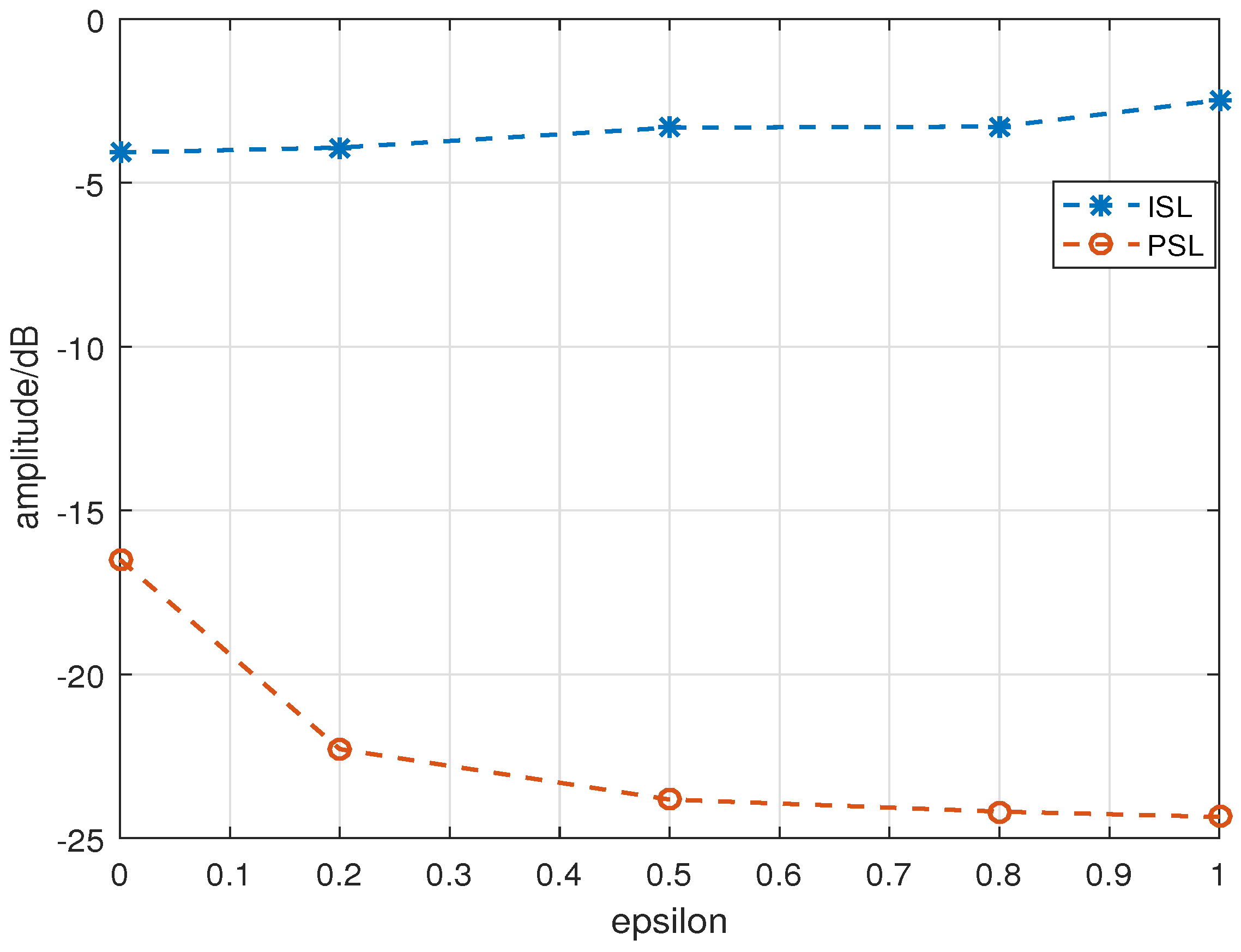
| 0 | 0.2 | 0.5 | 0.8 | 1.0 | |
|---|---|---|---|---|---|
| ISL | −4.075 dB | −3.926 dB | −3.317 dB | −3.284 dB | −2.476 dB |
| PSL | −16.499 dB | −22.281 dB | −23.818 dB | −24.186 dB | −24.348 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, M.; Gong, W.; Yang, L. A Novel Waveform Optimization Method for Orthogonal-Frequency Multiple-Input Multiple-Output Radar Based on Dual-Channel Neural Networks. Sensors 2024, 24, 5471. https://doi.org/10.3390/s24175471
Xia M, Gong W, Yang L. A Novel Waveform Optimization Method for Orthogonal-Frequency Multiple-Input Multiple-Output Radar Based on Dual-Channel Neural Networks. Sensors. 2024; 24(17):5471. https://doi.org/10.3390/s24175471
Chicago/Turabian StyleXia, Meng, Wenrong Gong, and Lichao Yang. 2024. "A Novel Waveform Optimization Method for Orthogonal-Frequency Multiple-Input Multiple-Output Radar Based on Dual-Channel Neural Networks" Sensors 24, no. 17: 5471. https://doi.org/10.3390/s24175471
APA StyleXia, M., Gong, W., & Yang, L. (2024). A Novel Waveform Optimization Method for Orthogonal-Frequency Multiple-Input Multiple-Output Radar Based on Dual-Channel Neural Networks. Sensors, 24(17), 5471. https://doi.org/10.3390/s24175471






