Simulation of Modal Control of Metal Mode-Filtered Vertical-Cavity Surface-Emitting Laser
Abstract
1. Introduction
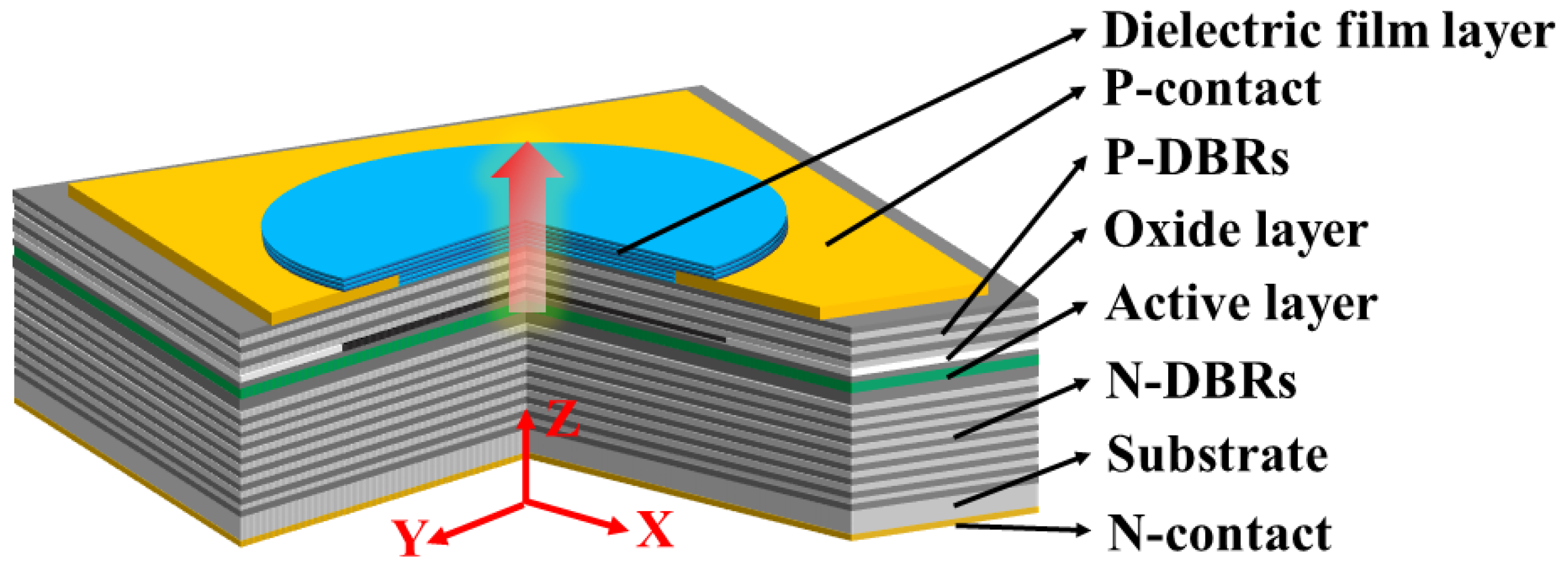
2. Structure of MMF-VCSEL
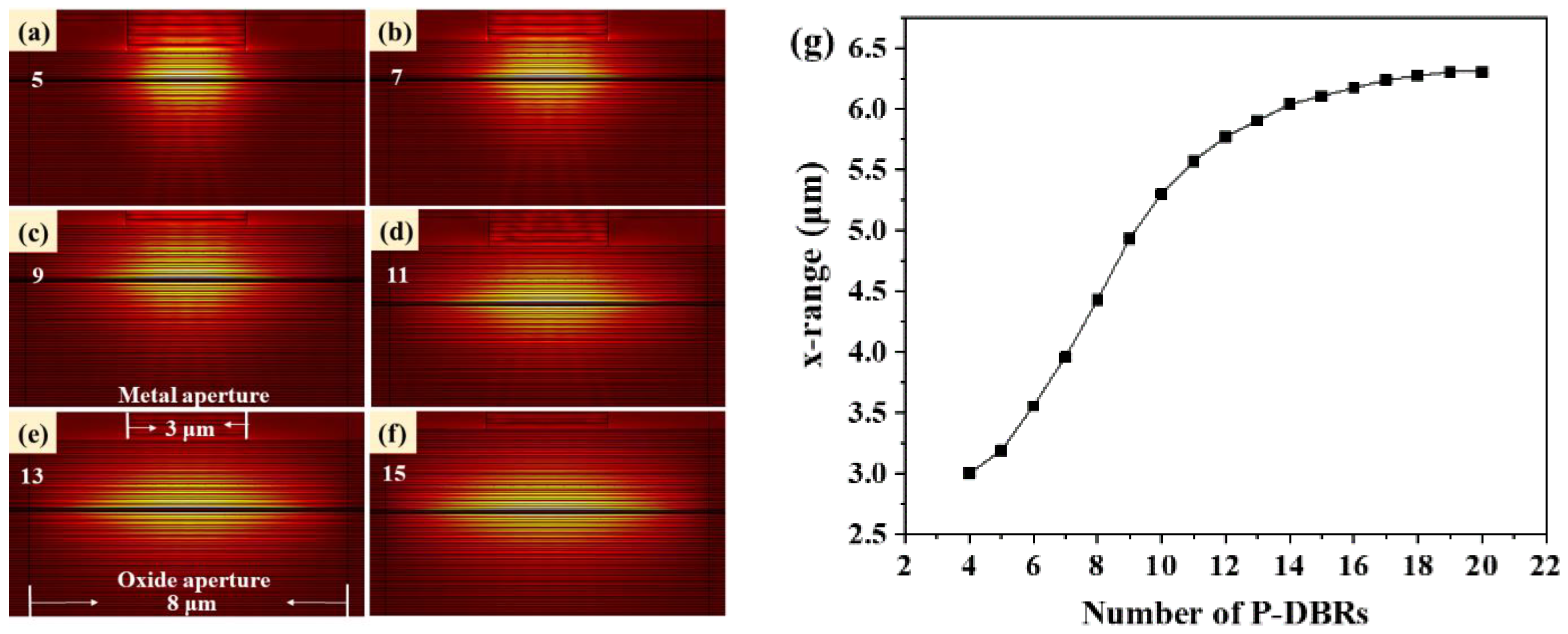
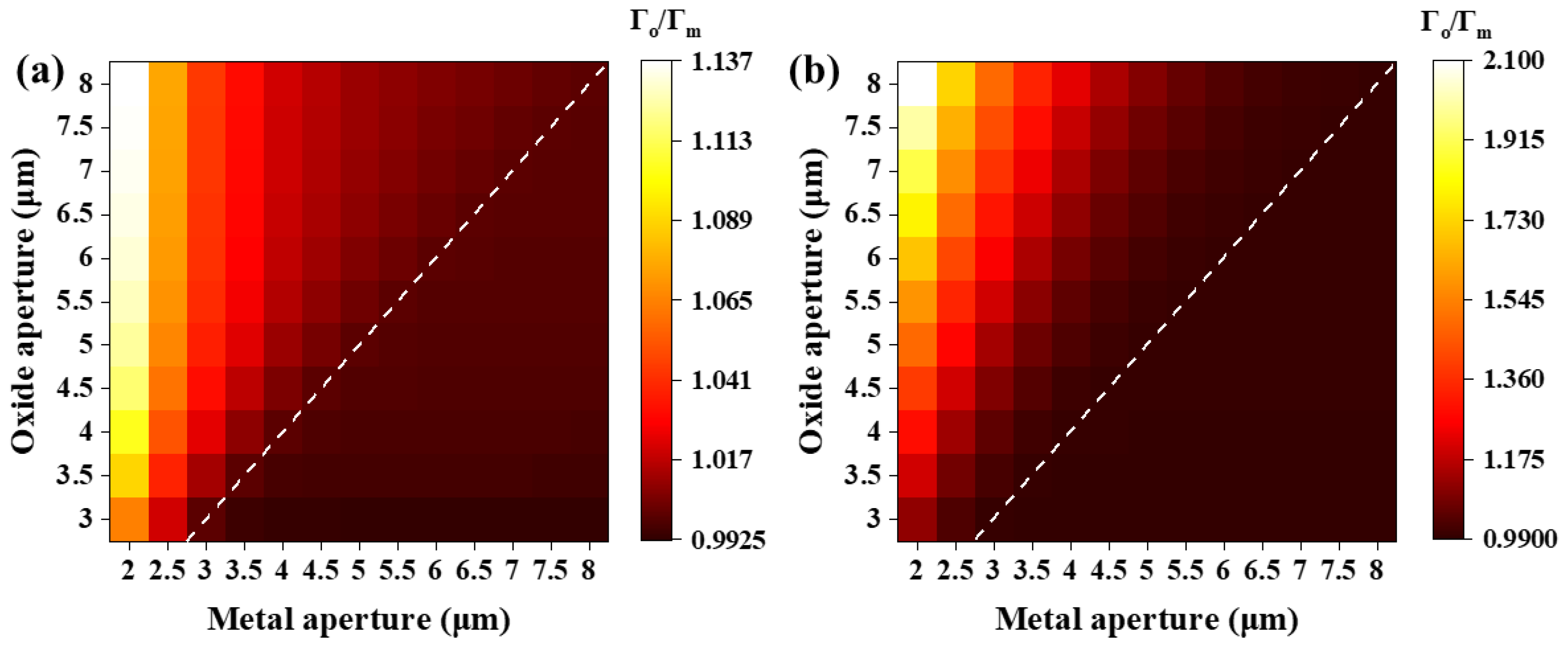
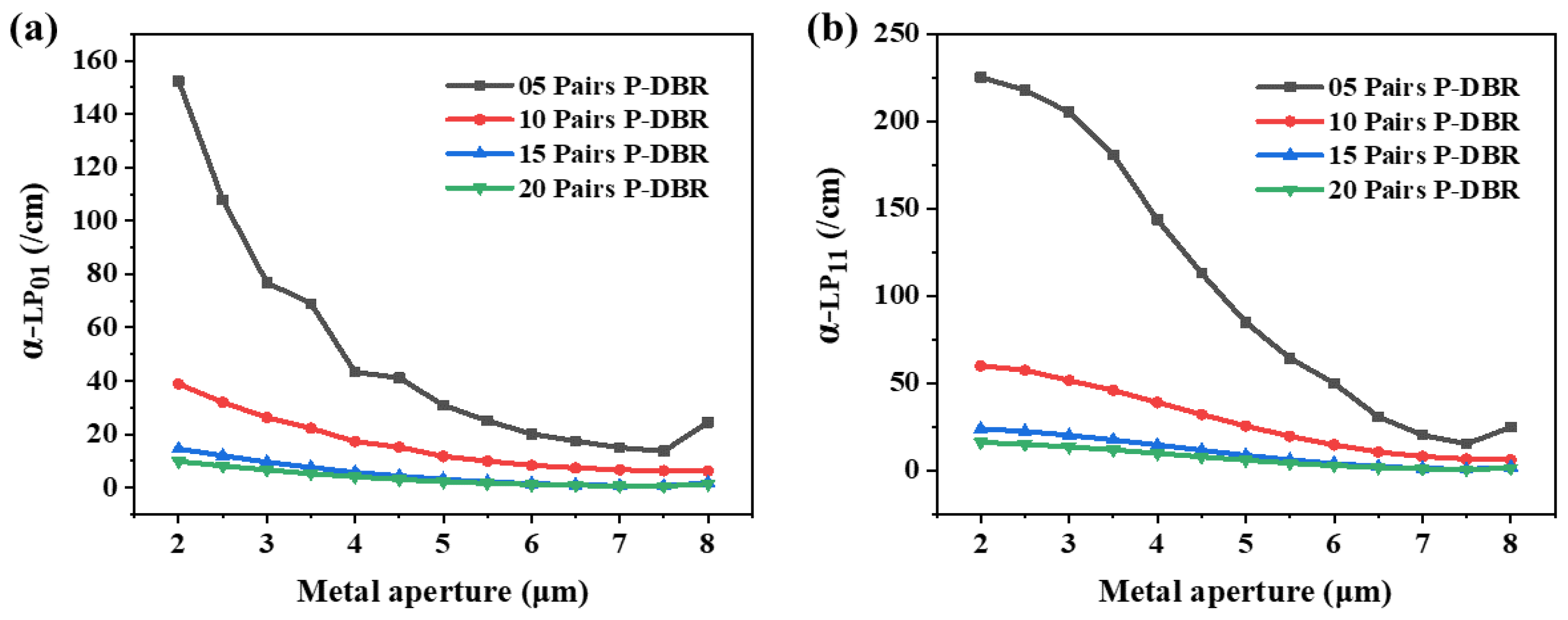
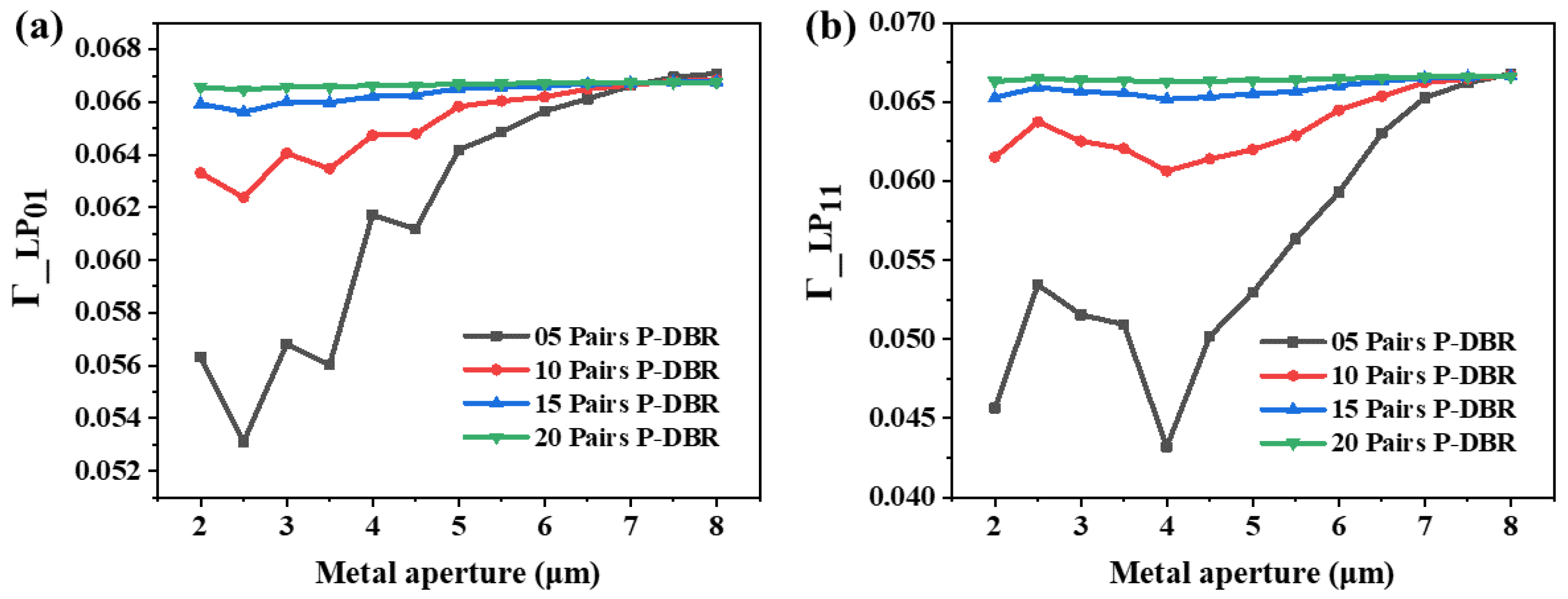
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Larsson, A. Advances in VCSELs for Communication and Sensing. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1552–1567. [Google Scholar] [CrossRef]
- Ueki, N.; Mukoyama, N. VCSEL-Based Laser Printing System. In VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Michalzik, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 539–548. [Google Scholar]
- Juodėnas, M.; Strandberg, E.; Grabowski, A.; Gustavsson, J.; Šípová-Jungová, H.; Larsson, A.; Käll, M. High-angle deflection of metagrating-integrated laser emission for high-contrast microscopy. Light Sci. Appl. 2023, 12, 251. [Google Scholar] [CrossRef] [PubMed]
- Koyama, F. Advances and new functions of VCSEL photonics. Opt. Rev. 2014, 21, 893–904. [Google Scholar] [CrossRef]
- Yang, Y.; Seong, J.; Choi, M.; Park, J.; Kim, G.; Kim, H.; Jeong, J.; Jung, C.; Kim, J.; Jeon, G.; et al. Integrated metasurfaces for re-envisioning a near-future disruptive optical platform. Light Sci. Appl. 2023, 12, 152. [Google Scholar] [CrossRef] [PubMed]
- Larsson, A.; Gustavsson, J.S. Single-Mode VCSELs. In VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Michalzik, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 119–144. [Google Scholar]
- Liao, W.-Y.; Li, J.; Li, C.-C.; Guo, X.-F.; Guo, W.-T.; Liu, W.-H.; Zhang, Y.-J.; Wei, X.; Tan, M.-Q. Oxide-aperture-dependent output characteristics of circularly symmetric VCSEL structure. Chin. Phys. B 2020, 29, 024201. [Google Scholar] [CrossRef]
- Ii, X.; Zhou, Y.; Zhang, X.; Zhang, J.; Zeng, Y.; Ning, Y.; Wang, L. High-power single-mode 894 nm VCSELs operating at high temperature (>2 mW @ 365 K). Appl. Phys. B 2022, 128, 16. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, X.; Zhang, J.-W.; Ning, Y.-Q.; Hofmann, W.; Wang, L.-J. Stable single-mode operation of 894.6 nm VCSEL at high temperatures for Cs atomic sensing. Chin. Phys. B 2017, 26, 074209. [Google Scholar] [CrossRef]
- Griffin, B.G.; Arbabi, A.; Tan, M.P.; Kasten, A.M.; Choquette, K.D.; Goddard, L.L. Demonstration of enhanced side-mode suppression in metal-filled photonic crystal vertical cavity lasers. Opt. Lett. 2013, 38, 1936–1938. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.; Shih, J.-C.; Cheng, C.-L.; Shi, J.-W. High-Power and Highly Single-Mode Zn-Diffusion VCSELs at 940 nm Wavelength. In Proceedings of the 2019 IEEE Photonics Conference (IPC), San Antonio, TX, USA, 29 September–3 October 2019. [Google Scholar]
- Patrick, S.; Kevin, P.P.; Fu-Chen, H.; Thomas, O.B., Jr.; John, M.D. Strain-Controlled Impurity-Induced Disordered Apertures for High-Power Single-Mode VCSELs; Proc.SPIE: San Francisco, CA, USA, 2020; p. 113000B. [Google Scholar]
- Ledentsov, N.N.; Shchukin, V.A.; Kalosha, V.P.; Ledentsov, N.N., Jr.; Kropp, J.R.; Agustin, M.; Chorchos, L.; Stepniak, G.; Turkiewicz, J.P.; Shi, J.W. Anti-waveguiding vertical-cavity surface-emitting laser at 850 nm: From concept to advances in high-speed data transmission. Opt. Express 2018, 26, 445–453. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhong, Y.F.; Dong, X.W.; Huang, Y.Q.; Duan, X.F.; Ren, X.M.; Cai, S.W.; Wang, Q. Single-Mode Vertical Cavity Surface Emitting Laser via High-Order Transverse Mode Expansion. J. Light. Technol. 2023, 41, 6735–6740. [Google Scholar] [CrossRef]
- Chase, C.; Rao, Y.; Hofmann, W.; Chang-Hasnain, C.J. 1550 nm high contrast grating VCSEL. Opt. Express 2010, 18, 15461–15466. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.T.; Min, S.Y.; Yang, Y.C.; Lin, H.Y.; Pan, J.S.; Wu, C.H. Single-Mode-VCSEL with a Ring-Shaped Self-Aligned Recessed Metal Mode Filter. IEEE Electron. Device Lett. 2023, 44, 1316–1319. [Google Scholar] [CrossRef]
- Nakamura, T.; Nakayama, H.; Omori, S.; Sakamoto, A.; Kondo, T.; Mukoyama, N.; Ueki, N.; Kuwata, Y.; Murakami, A.; Otoma, H. Single-mode oxide-confined VCSEL for printers and sensors. In Proceedings of the 2006 1st Electronic Systemintegration Technology Conference, Dresden, Germany, 5–7 September 2006; pp. 80–85. [Google Scholar]
- Ibrahim, H.R.; Hassan, A.M.; Ahmed, M.; Koyama, F. Single-mode and high-speed intracavity metal aperture VCSEL with transverse coupled cavity effect. In Proceedings of the 2020 European Conference on Optical Communications (ECOC), Brussels, Belgium, 6–10 December 2020; pp. 1–4. [Google Scholar]
- Mu, J.; Zhou, Y.; Zhang, X.; Zhang, J.; Chen, C.; Zhang, Z.; Liu, T.; Xia, Y.; Xu, Y.; Sun, J.; et al. A novel metal-mode-filtered vertical-cavity surface-emitting laser with 8 μm oxide aperture and single mode output. Results Phys. 2023, 54, 107107. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Xing, Z.; Yi, Z.; Jian-Wei, Z.; Jian, Z.; Chu-Yu, Z.; You-Wen, H.; Yong-Qiang, N.; Si-Hong, G.; Li-Jun, W. 894 nm high temperature operating vertical-cavity surface-emitting laser and its application in Cs chip-scale atomic-clock system. Acta Phys. Sin. 2016, 65, 134204. [Google Scholar] [CrossRef]
- Zhou, Y.; Jia, Y.; Zhang, X.; Zhang, J.; Liu, Z.; Ning, Y.; Wang, L. Large-aperture single-mode 795 nm VCSEL for chip-scale nuclear magnetic resonance gyroscope with an output power of 4.1 mW at 80 °C. Opt. Express 2022, 30, 8991–8999. [Google Scholar] [CrossRef] [PubMed]
- Michalzik, R. VCSEL Fundamentals. In VCSELs: Fundamentals, Technology and Applications of Vertical-Cavity Surface-Emitting Lasers; Michalzik, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 19–75. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, J.; Zhou, Y.; Chen, C.; Zhang, X.; Zhang, J.; Liu, T.; Zhang, Z.; Xu, Y.; Yuan, G.; Zhang, J.; et al. Simulation of Modal Control of Metal Mode-Filtered Vertical-Cavity Surface-Emitting Laser. Sensors 2024, 24, 4700. https://doi.org/10.3390/s24144700
Mu J, Zhou Y, Chen C, Zhang X, Zhang J, Liu T, Zhang Z, Xu Y, Yuan G, Zhang J, et al. Simulation of Modal Control of Metal Mode-Filtered Vertical-Cavity Surface-Emitting Laser. Sensors. 2024; 24(14):4700. https://doi.org/10.3390/s24144700
Chicago/Turabian StyleMu, Jingfei, Yinli Zhou, Chao Chen, Xing Zhang, Jianwei Zhang, Tianjiao Liu, Zhuo Zhang, Yuehui Xu, Gaohui Yuan, Jiye Zhang, and et al. 2024. "Simulation of Modal Control of Metal Mode-Filtered Vertical-Cavity Surface-Emitting Laser" Sensors 24, no. 14: 4700. https://doi.org/10.3390/s24144700
APA StyleMu, J., Zhou, Y., Chen, C., Zhang, X., Zhang, J., Liu, T., Zhang, Z., Xu, Y., Yuan, G., Zhang, J., Ning, Y., & Wang, L. (2024). Simulation of Modal Control of Metal Mode-Filtered Vertical-Cavity Surface-Emitting Laser. Sensors, 24(14), 4700. https://doi.org/10.3390/s24144700







