Neural Colour Correction for Indoor 3D Reconstruction Using RGB-D Data
Abstract
1. Introduction
2. Related Work
2.1. Pairwise Colour Correction
2.2. Colour Consistency Correction
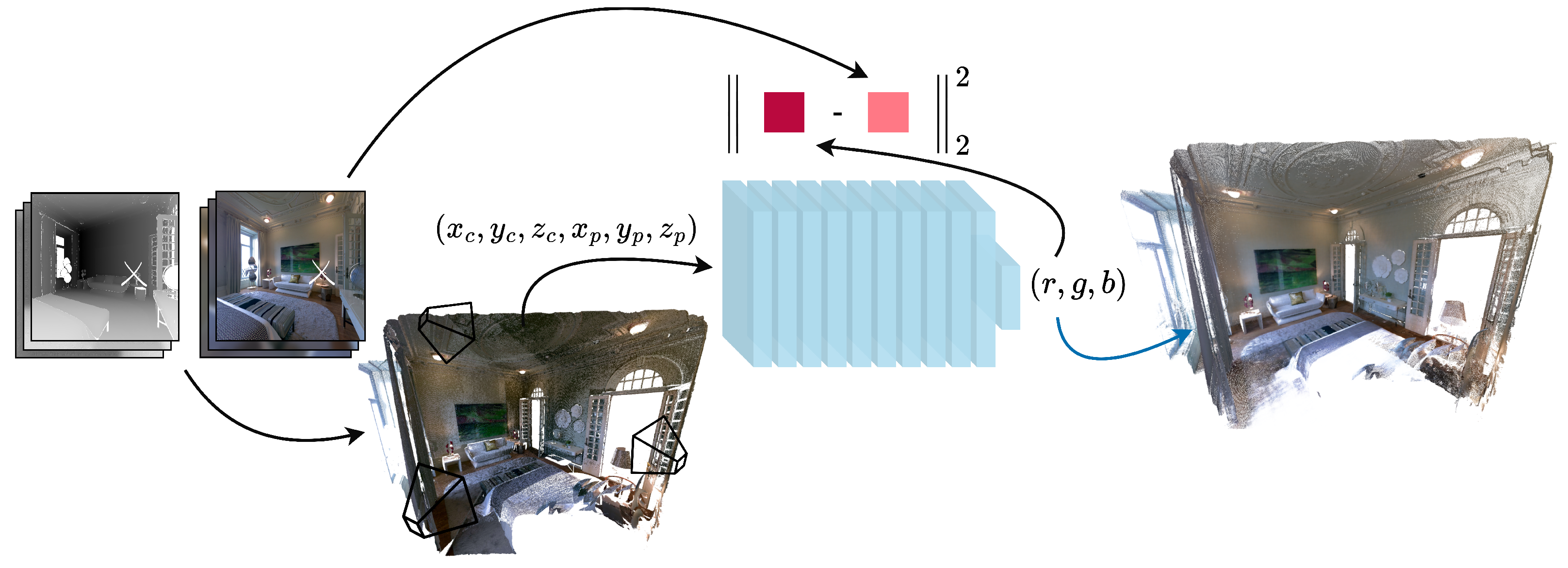
3. Proposed Approach
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Brown, M.; Lowe, D. Automatic Panoramic Image Stitching using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Xia, M.; Yao, J.; Xie, R.; Zhang, M.; Xiao, J. Color Consistency Correction Based on Remapping Optimization for Image Stitching. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2017; pp. 2977–2984. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Xia, M.; Li, Y.; Yao, J.; Wang, B. Grid Model-Based Global Color Correction for Multiple Image Mosaicking. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2006–2010. [Google Scholar] [CrossRef]
- HaCohen, Y.; Shechtman, E.; Goldman, D.B.; Lischinski, D. Optimizing color consistency in photo collections. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Pitie, F.; Kokaram, A.; Dahyot, R. N-dimensional probability density function transfer and its application to color transfer. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Washington, DC, USA, 17–20 October 2005; Volume 2, pp. 1434–1439. [Google Scholar] [CrossRef]
- Su, Z.; Deng, D.; Yang, X.; Luo, X. Color transfer based on multiscale gradient-aware decomposition and color distribution mapping. In Proceedings of the 20th ACM International Conference on Multimedia, Nara, Japan, 29 October–2 November 2012; pp. 753–756. [Google Scholar] [CrossRef]
- De Marchi, S. Polynomials arising in factoring generalized Vandermonde determinants: An algorithm for computing their coefficients. Math. Comput. Model. 2001, 34, 271–281. [Google Scholar] [CrossRef]
- Hwang, Y.; Lee, J.Y.; Kweon, I.S.; Kim, S.J. Color Transfer Using Probabilistic Moving Least Squares. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3342–3349. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, L.; Xu, S.; Du, S. Palette-Based Recoloring of Natural Images Under Different Illumination. In Proceedings of the 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), Chengdu, China, 23–26 April 2021; pp. 347–351. [Google Scholar] [CrossRef]
- Wu, F.; Dong, W.; Kong, Y.; Mei, X.; Paul, J.C.; Zhang, X. Content-based colour transfer. Comput. Graph. Forum 2013, 32, 190–203. [Google Scholar] [CrossRef]
- Finlayson, G.D.; Mackiewicz, M.; Hurlbert, A. Color Correction Using Root-Polynomial Regression. IEEE Trans. Image Process. 2015, 24, 1460–1470. [Google Scholar] [CrossRef]
- Hwang, Y.; Lee, J.Y.; Kweon, I.S.; Kim, S.J. Probabilistic moving least squares with spatial constraints for nonlinear color transfer between images. Comput. Vis. Image Underst. 2019, 180, 1–12. [Google Scholar] [CrossRef]
- Niu, Y.; Zheng, X.; Zhao, T.; Chen, J. Visually Consistent Color Correction for Stereoscopic Images and Videos. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 697–710. [Google Scholar] [CrossRef]
- Reinhard, E.; Adhikhmin, M.; Gooch, B.; Shirley, P. Color transfer between images. IEEE Comput. Graph. Appl. 2001, 21, 34–41. [Google Scholar] [CrossRef]
- Xiao, X.; Ma, L. Gradient-Preserving Color Transfer. Comput. Graph. Forum 2009, 28, 1879–1886. [Google Scholar] [CrossRef]
- Nguyen, R.M.; Kim, S.J.; Brown, M.S. Illuminant aware gamut-based color transfer. Comput. Graph. Forum 2014, 33, 319–328. [Google Scholar] [CrossRef]
- He, M.; Liao, J.; Chen, D.; Yuan, L.; Sander, P.V. Progressive Color Transfer With Dense Semantic Correspondences. ACM Trans. Graph. 2019, 38, 1–18. [Google Scholar] [CrossRef]
- Wu, Z.; Xue, R. Color Transfer With Salient Features Mapping via Attention Maps Between Images. IEEE Access 2020, 8, 104884–104892. [Google Scholar] [CrossRef]
- Lee, J.; Son, H.; Lee, G.; Lee, J.; Cho, S.; Lee, S. Deep color transfer using histogram analogy. Vis. Comput. 2020, 36, 2129–2143. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Yao, J.; Gong, Y.; Li, L. Global Color Consistency Correction for Large-Scale Images in 3-D Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3074–3088. [Google Scholar] [CrossRef]
- Li, Y.; Fang, C.; Yang, J.; Wang, Z.; Lu, X.; Yang, M.H. Universal style transfer via feature transforms. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 385–395. [Google Scholar]
- Chen, C.; Chen, Z.; Li, M.; Liu, Y.; Cheng, L.; Ren, Y. Parallel relative radiometric normalisation for remote sensing image mosaics. Comput. Geosci. 2014, 73, 28–36. [Google Scholar] [CrossRef]
- Dal’Col, L.; Coelho, D.; Madeira, T.; Dias, P.; Oliveira, M. A Sequential Color Correction Approach for Texture Mapping of 3D Meshes. Sensors 2023, 23, 607. [Google Scholar] [CrossRef]
- Xiong, Y.; Pulli, K. Color matching of image sequences with combined gamma and linear corrections. In Proceedings of the International Conference on Multimedia, Firenze Italy, 25–29 October 2010; pp. 261–270. [Google Scholar]
- Yu, L.; Zhang, Y.; Sun, M.; Zhou, X.; Liu, C. An auto-adapting global-to-local color balancing method for optical imagery mosaic. ISPRS J. Photogramm. Remote Sens. 2017, 132, 1–19. [Google Scholar] [CrossRef]
- Xie, R.; Xia, M.; Yao, J.; Li, L. Guided color consistency optimization for image mosaicking. ISPRS J. Photogramm. Remote Sens. 2018, 135, 43–59. [Google Scholar] [CrossRef]
- Moulon, P.; Duisit, B.; Monasse, P. Global multiple-view color consistency. In Proceedings of the Conference on Visual Media Production, London, UK, 30 November–1 December 2013. [Google Scholar]
- Shen, T.; Wang, J.; Fang, T.; Zhu, S.; Quan, L. Color Correction for Image-Based Modeling in the Large. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016. [Google Scholar]
- Park, J.; Tai, Y.W.; Sinha, S.N.; Kweon, I.S. Efficient and Robust Color Consistency for Community Photo Collections. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 430–438. [Google Scholar] [CrossRef]
- Yang, J.; Liu, L.; Xu, J.; Wang, Y.; Deng, F. Efficient global color correction for large-scale multiple-view images in three-dimensional reconstruction. ISPRS J. Photogramm. Remote Sens. 2021, 173, 209–220. [Google Scholar] [CrossRef]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. Deepsdf: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 165–174. [Google Scholar]
- Tancik, M.; Srinivasan, P.P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.T.; Ng, R. Fourier features let networks learn high frequency functions in low dimensional domains. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Online, 6–12 December 2020. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Sharma, G.; Wu, W.; Dalal, E.N. The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations. Color Res. Appl. 2005, 30, 21–30. [Google Scholar] [CrossRef]
- Xu, W.; Mulligan, J. Performance evaluation of color correction approaches for automatic multi-view image and video stitching. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 263–270. [Google Scholar] [CrossRef]
- Chang, A.; Dai, A.; Funkhouser, T.; Halber, M.; Niessner, M.; Savva, M.; Song, S.; Zeng, A.; Zhang, Y. Matterport3D: Learning from RGB-D Data in Indoor Environments. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]






| CIEDE2000 | PSNR | |||||
|---|---|---|---|---|---|---|
| Method | ||||||
| Original images | 10.87 | 10.71 | 2.66 | 18.44 | 18.36 | 2.51 |
| Reinhard et al. [14] | 10.52 | 10.33 | 2.39 | 18.30 | 18.29 | 2.34 |
| De Marchi et al. [7] | 8.96 | 9.14 | 4.05 | 20.20 | 19.92 | 4.27 |
| Brown and Lowe [1] | 10.38 | 10.15 | 2.24 | 19.10 | 19.07 | 2.15 |
| Moulon et al. [27] | 6.49 | 6.41 | 1.37 | 23.73 | 23.71 | 2.19 |
| Finlayson et al. [11] | 8.77 | 8.84 | 2.93 | 20.12 | 19.96 | 3.00 |
| Lee et al. [19] | 11.39 | 11.17 | 2.66 | 17.94 | 17.99 | 2.30 |
| Ours | 3.36 | 3.45 | 0.78 | 26.77 | 26.54 | 2.66 |
| CIEDE2000 | PSNR | |||||
|---|---|---|---|---|---|---|
| Method | ||||||
| Original images | 15.20 | 15.19 | 4.85 | 15.55 | 15.56 | 2.29 |
| Reinhard et al. [14] | 10.99 | 11.00 | 2.37 | 17.87 | 17.85 | 1.81 |
| De Marchi et al. [7] | 12.41 | 12.44 | 4.79 | 17.53 | 17.51 | 3.33 |
| Brown and Lowe [1] | 13.51 | 13.53 | 3.97 | 16.71 | 16.73 | 1.89 |
| Moulon et al. [27] | 7.24 | 7.22 | 1.52 | 21.50 | 21.55 | 1.80 |
| Finlayson et al. [11] | 11.19 | 11.22 | 3.46 | 17.81 | 17.77 | 2.36 |
| Lee et al. [19] | 12.11 | 12.10 | 2.09 | 17.38 | 17.38 | 1.34 |
| Ours | 3.59 | 3.57 | 1.23 | 26.83 | 26.86 | 2.79 |
| CIEDE2000 | PSNR | |||||
|---|---|---|---|---|---|---|
| Method | ||||||
| Original images | 9.74 | 9.56 | 4.36 | 20.74 | 20.62 | 4.85 |
| Reinhard et al. [14] | 11.07 | 10.87 | 3.30 | 18.00 | 17.99 | 3.16 |
| De Marchi et al. [7] | 8.43 | 8.51 | 5.58 | 22.06 | 21.58 | 5.51 |
| Brown and Lowe [1] | 8.21 | 8.36 | 3.30 | 22.70 | 22.21 | 5.16 |
| Moulon et al. [27] | 7.32 | 7.74 | 3.64 | 24.57 | 23.82 | 6.34 |
| Finlayson et al. [11] | 7.68 | 7.79 | 5.48 | 22.86 | 22.31 | 5.96 |
| Lee et al. [19] | 13.00 | 12.67 | 3.38 | 16.44 | 16.56 | 2.33 |
| Ours | 2.49 | 2.55 | 1.26 | 30.60 | 30.04 | 6.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madeira, T.; Oliveira, M.; Dias, P. Neural Colour Correction for Indoor 3D Reconstruction Using RGB-D Data. Sensors 2024, 24, 4141. https://doi.org/10.3390/s24134141
Madeira T, Oliveira M, Dias P. Neural Colour Correction for Indoor 3D Reconstruction Using RGB-D Data. Sensors. 2024; 24(13):4141. https://doi.org/10.3390/s24134141
Chicago/Turabian StyleMadeira, Tiago, Miguel Oliveira, and Paulo Dias. 2024. "Neural Colour Correction for Indoor 3D Reconstruction Using RGB-D Data" Sensors 24, no. 13: 4141. https://doi.org/10.3390/s24134141
APA StyleMadeira, T., Oliveira, M., & Dias, P. (2024). Neural Colour Correction for Indoor 3D Reconstruction Using RGB-D Data. Sensors, 24(13), 4141. https://doi.org/10.3390/s24134141










