A Simulation Method for Underwater SPAD Depth Imaging Datasets
Abstract
1. Introduction
2. Theory of Underwater SPAD Imaging Simulation
2.1. Underwater Imaging Model
2.2. Theory for SPAD Simulation
2.3. Simulation of SPAD Depth Map
2.4. Simulation of Backward Scattering
3. Method for Simulation of Underwater SPAD Dataset
3.1. Underwater Virtual Environment Setup
3.2. System Parameter Settings
3.3. Procedure of Underwater SPAD Simulation
- (a)
- Using the virtual environment software Unreal Engine, construct a three-dimensional target object with a plastic material. Place a camera in the virtual environment at a distance of 15 m and 50 m, respectively, from the target and export the target’s RGB image, depth map, surface normal map, etc., from the software. The exported RGB image represents the intensity information ground truth of the target, the depth map represents the depth information ground truth of the target, and the surface normal map represents the material, reflectance, and other ground truths of the target.
- (b)
- Multiply the values in the depth image by 2 and divide them by the underwater speed of light to obtain the theoretical ground truth of the time at which photons arrive at each pixel in the underwater environment. Since each pixel contains a TCSPC histogram channel, the ground truth of the photon arrival time is considered to be the position of the histogram peak.
- (c)
- Substitute all known parameters into Equation (7) to obtain the number of photons detected per pulse. Calculate the proportion of back-scattered photons detected after each pulse using Equation (11).
- (d)
- Use Equations (8) and (9) to calculate the Fisher information and the average number of photons measured per pixel within [0, T]. Calculate the lower bound of the standard deviation of the estimated peak position of the histogram arrival time using Equation (10), i.e., the Cramer–Rao bound.
- (e)
- Add a random number following a normal distribution with a mean of 0 and a standard deviation of to each pixel’s ground truth of the photon arrival time. This yields the result of the underwater SPAD simulation.
4. Practice Underwater SPAD Simulation Dataset
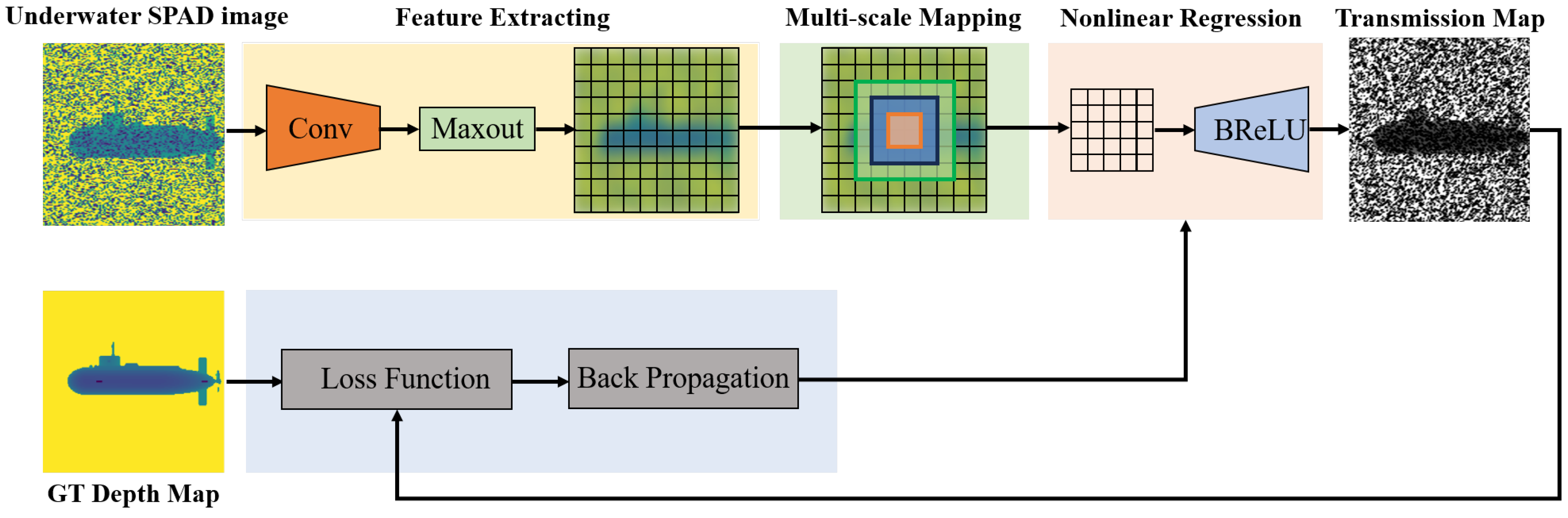
4.1. Denoising Network
4.2. Metrics
4.3. Results and Analysis
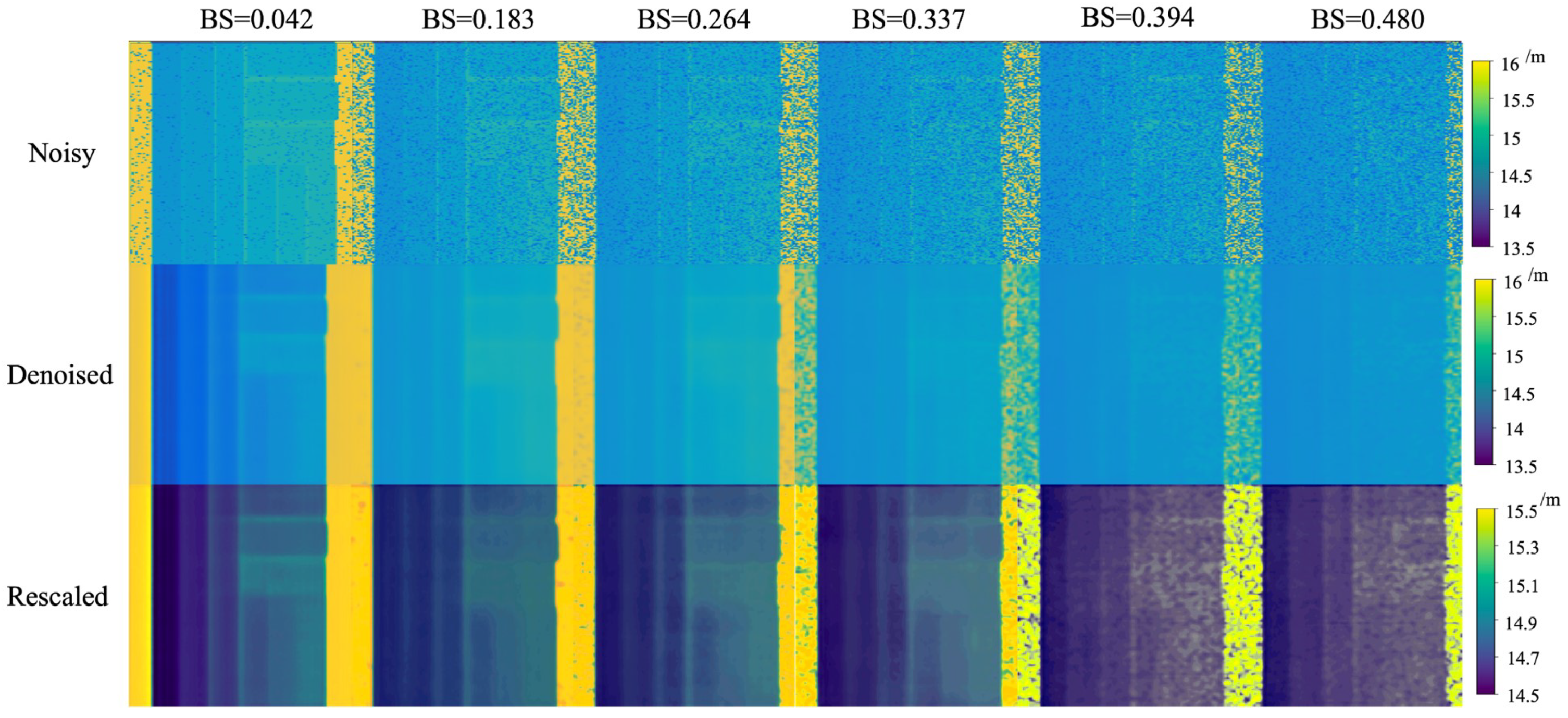
4.3.1. Visual Analysis
4.3.2. Inference on Real Underwater SPAD Data
5. Discussion
- We propose a simple and efficient simulation method for underwater SPAD depth images and TCSPC histograms. Addressing the difficulties in underwater SPAD imaging experiments and the high cost of SPAD devices, this study utilizes the Monte Carlo simulation to obtain underwater SPAD data. By combining the underwater light transmission model based on Fisher information estimation with the Monte Carlo simulation of underwater backward scattering, virtual environment software is used to obtain information about target objects, thereby generating a large amount of generalized underwater SPAD data. In the experiments, a dataset containing 20 target objects and 20,000 frames of depth images under different water scattering concentrations, as well as several frames of histogram data, is successfully obtained.
- We propose the USDN, a deep learning-based denoising network for underwater SPAD. In underwater environments, due to the influence of backward-scattered light from impurity particles in water, SPAD devices are susceptible to receiving backward-scattered photons, triggering responses. In this scenario, the SPAD depth images and histograms obtained through scattering media carry a large number of noise signals, leading to decreased image contrast, making it difficult for traditional image denoising algorithms to effectively remove these interferences. Deep learning is an effective method to address this issue. This study simplifies the problem of removing backward-scattering interference in underwater SPAD images to a supervised deep learning model. By continuously allowing the neural network to learn the characteristics of backward-scattering noise based on prior knowledge of the underwater background light, the model can effectively remove the backward-scattering interference to obtain clear and restored images. The experimental results show that the USDN improves the peak signal-to-noise ratio (PSNR), Structural Similarity Index (SSIM), and entropy by 5.59 dB, 9.03%, and 0.84, respectively. The minimum depth resolution of the denoised underwater SPAD images can reach 10 cm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, S.; Liu, T. Underwater rescue target detection based on acoustic images. Sensors 2024, 24, 1780. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Qiu, S.; Wang, H. Algorithm for de-scattering 3D images from infrared time-of-flight (ToF) cameras. Adv. Fiber Laser Conf. 2024, 13104, 1269–1279. [Google Scholar]
- Wang, H.; Qiu, S.; Lu, T. Reconstruction of high-resolution depth profiling from single-photon data based on PCA. Real-Time Photonic Meas. Data Manag. Process. VII 2023, 12772, 72–79. [Google Scholar]
- Tobin, R.; Halimi, A.; McCarthy, A.; Laurenzis, M.; Christnacher, F.; Buller, G.S. Three-dimensional single-photon imaging through obscurants. Opt. Express 2019, 27, 4590–4611. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; Della Rocca, F.M.; McCarthy, A.; Henderson, R.; Buller, G.S. Three-dimensional imaging of stationary and moving targets in turbid underwater environments using a single-photon detector array. Opt. Express 2019, 27, 28437–28456. [Google Scholar] [CrossRef] [PubMed]
- Maccarone, A.; Drummond, K.; McCarthy, A.; Steinlehner, U.K.; Tachella, J.; Garcia, D.A.; Pawlikowska, A.; Lamb, R.A.; Henderson, R.K.; McLaughlin, S.; et al. Submerged single-photon LiDAR imaging sensor used for real-time 3D scene reconstruction in scattering underwater environments. Opt. Express 2023, 31, 16690–16708. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Li, C.; Dai, J.; Shu, R.; Zhang, L.; Wang, J. Real-time and high-speed underwater photon-counting communication based on SPAD and PPM symbol synchronization. IEEE Photonics J. 2021, 13, 7300209. [Google Scholar] [CrossRef]
- Panglosse, A.; Martin-Gonthier, P.; Marcelot, O.; Virmontois, C.; Saint-Pé, O.; Magnan, P. Modeling, simulation methods and characterization of photon detection probability in cmos-spad. Sensors 2021, 21, 5860. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Kong, X.; Cong, J.; Mao, X.; Fu, Y. Design and simulation of a near-infrared enhanced Si-based SPAD for an automotive LiDAR. Appl. Opt. 2023, 62, 7380–7386. [Google Scholar] [CrossRef]
- Sun, F.; Xu, Y.; Wu, Z.; Zhang, J. A simple analytic modeling method for SPAD timing jitter prediction. IEEE J. Electron. Devices Soc. 2019, 7, 261–267. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, M.; Zhang, K. Underwater Turbid Media Stokes-Based Polarimetric Recovery. Sensors 2024, 24, 1367. [Google Scholar] [CrossRef]
- Jaffe, J.S. Computer modeling and the design of optimal underwater imaging systems. IEEE J. Ocean. Eng. 1990, 15, 101–111. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhang, T.; Yang, K.; Zhang, J.; Wang, X. A Study on Refraction Error Compensation Method for Underwater Spinning Laser Scanning Three-Dimensional Imaging. Sensors 2024, 24, 343. [Google Scholar] [CrossRef] [PubMed]
- Scholes, S.; Mora-Martín, G.; Zhu, F.; Gyongy, I.; Soan, P.; Leach, J. Simulating single-photon detector array sensors for depth imaging. arXiv 2022, arXiv:2210.05644. [Google Scholar]
- Chen, X.; Wang, X.; Gao, C. Analysis of diffuse light field based on Monte Carlo simulation. Laser J. 2016, 37, 50–53. [Google Scholar]
- Xin, Y.L.; Ge, G.P.; Du, W.; Wu, H.; Zhao, Y. Design of an Optical Physics Virtual Simulation System Based on Unreal Engine 5. Appl. Sci. 2024, 14, 955. [Google Scholar] [CrossRef]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. Dehazenet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Wei, Y.; Guo, K.; Han, H. Removal of Mixed Noise in Hyperspectral Images Based on Subspace Representation and Nonlocal Low-Rank Tensor Decomposition. Sensors 2024, 24, 327. [Google Scholar] [CrossRef] [PubMed]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—a comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Tsai, D.Y.; Lee, Y.; Matsuyama, E. Information entropy measure for evaluation of image quality. J. Digit. Imaging 2008, 21, 338–347. [Google Scholar] [CrossRef]
- Gupta, G. Algorithm for image processing using improved median filter and comparison of mean, median and improved median filter. Int. J. Soft Comput. Eng. (IJSCE) 2011, 1, 304–311. [Google Scholar]
- Danielyan, A.; Katkovnik, V.; Egiazarian, K. BM3D frames and variational image deblurring. IEEE Trans. Image Process. 2011, 21, 1715–1728. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]



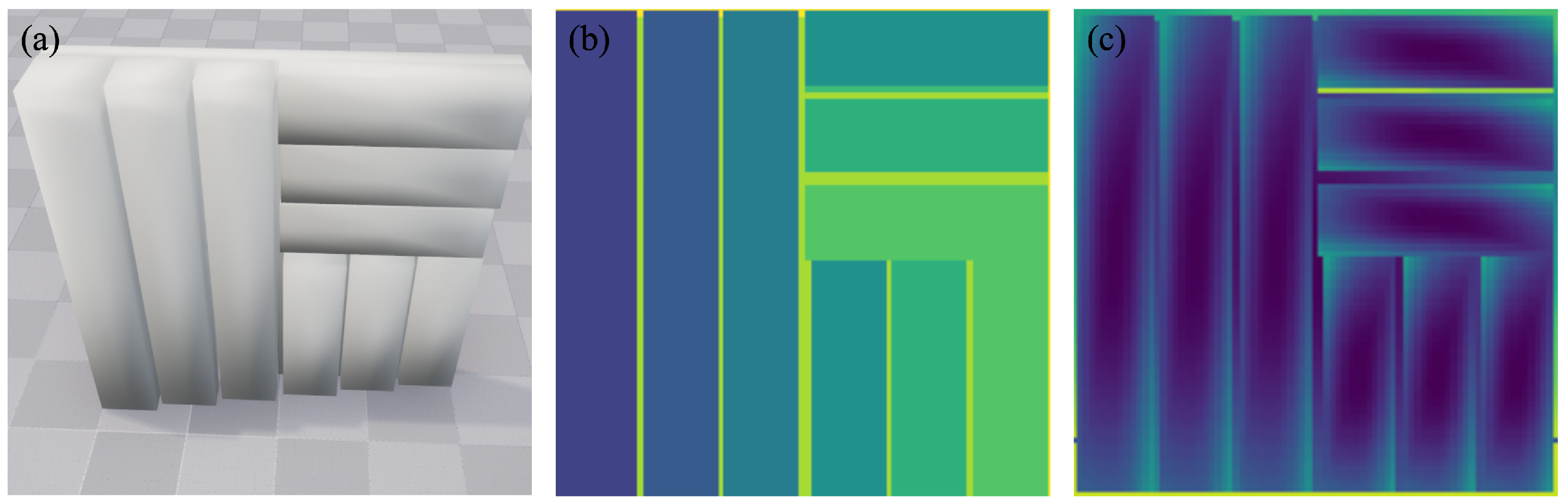








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wavelength | 532 nm | Average power | 300 mW |
| Repetition rate | 20 MHz | Pulse energy | 5 nJ |
| Pulse width | <85 ps | Beam diameter | mm |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Sensor size | 32 × 32 | Fill factor | 20% |
| Photon efficiency | 28%@500 nm | Bin width | 55 ps |
| Max FPS | 500 kHz | Jitter | <200 ps FWHM |
| Dark count rate | <100 Hz |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Focal length | 150 mm | F number | 1.8 |
| Target range | 15 m | Target reflectance | 78% |
| Backward scattering coefficient | Attenuation coefficient | 0.035 |
| Ours | Median Filter | BM3D | DnCNN | |
|---|---|---|---|---|
| PSNR | 5.59 ↑ | 4.2 ↑ | 5.18 ↑ | 4.73 ↑ |
| SSIM | 9.03% ↑ | 3.41% ↑ | 6.84% ↑ | 8.72% ↑ |
| Entropy | 0.84 ↓ | 0.51 ↓ | 0.59 ↓ | 0.73 ↓ |
| 1.2AL | 4.4AL | 5.7AL | |
|---|---|---|---|
| Entropy | 0.31 ↓ | 0.57 ↓ | 1.22 ↓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, T.; Qiu, S.; Wang, H.; Zhu, S.; Jin, W. A Simulation Method for Underwater SPAD Depth Imaging Datasets. Sensors 2024, 24, 3886. https://doi.org/10.3390/s24123886
Lu T, Qiu S, Wang H, Zhu S, Jin W. A Simulation Method for Underwater SPAD Depth Imaging Datasets. Sensors. 2024; 24(12):3886. https://doi.org/10.3390/s24123886
Chicago/Turabian StyleLu, Taoran, Su Qiu, Hui Wang, Shihao Zhu, and Weiqi Jin. 2024. "A Simulation Method for Underwater SPAD Depth Imaging Datasets" Sensors 24, no. 12: 3886. https://doi.org/10.3390/s24123886
APA StyleLu, T., Qiu, S., Wang, H., Zhu, S., & Jin, W. (2024). A Simulation Method for Underwater SPAD Depth Imaging Datasets. Sensors, 24(12), 3886. https://doi.org/10.3390/s24123886






