A Process Algebraic Approach to Predict and Control Uncertainty in Smart IoT Systems for Smart Cities Based on Permissible Probabilistic Equivalence
Abstract
1. Introduction
1.1. Smart System
- Unreliable interactions—smart systems are interacting with other systems or processes throughout the Internet, which are not always predictable, due to internet failure or congestion, causing deadlock.
- Environmental factors—the environmental changes may influence the operations of smart systems. For example, autonomous driving systems may be influenced by weather or traffic conditions.
1.2. Process Algebra in Digital Twins for Smart Cities
1.3. Previous Research on Probabilities
- (1)
- (1-1) The probabilistic OReqs (operational requirements) of smart IoT systems are defined by dTP-Calculus with the ITL (In-The-Large) system model and ITS (In-The-Small) process models. The nondeterminism of the systems is determined by the probabilistic choice operations in the process models.
- (2)
- (1-2) A probabilistic EX (execution) model is determined from the ITL model and its ITS models, and all the execution paths are generated. The nondeterministic behavior of the system is constructed by the compositions of the probabilistic choice operations among the ITS models.
- (3)
- (1-3) The simulation outcome of each execution path is generated in the form of a GTS (geo-temporal space) model. Each behavior of the system is represented by the composite value of probabilities from the corresponding probabilistic choice operations between the interacting ITS process models.
- (4)
- (1-4) The SSReqs (safety and security requirements) are defined by GTS visual logic. Furthermore, the requirements are defined with probabilities too.
- (5)
- (1-5) The SSReqs are analyzed and verified on GTSs, especially with respect to the probabilities of the SSReq over the probabilities in the probabilistic EX models.
- (6)
- (1-6) In the case where the SSReqs are not satisfied probabilistically, the probabilities of the choice operations in the ITS process models are enhanced to a certain high level, repeating the previous steps until all the SSReqs are satisfied probabilistically.

- Continuousness—the value of probability was defined to some value in the continuous range of values between zero and one that is conceptually away from the real situation;
- Arbitrariness—the target value for the new probability to satisfy the requirements was arbitrarily determined without any logical correlation to the physical world.
1.4. Approach
- (1)
- Probabilistic equivalence is the basic concept used to verify probabilistic requirements as a justification for the enhancement of probability, which overcomes the limitation of the arbitrariness from the previous approach. The equivalences can be classified into two classes.
- Process equivalence is for the equivalence between two processes representing two IoT devices in smart systems. It implies that two processes are statically identical and are dynamically bisimulative within the range of a probability difference or increment;
- System equivalence is for the equivalence between two systems representing two smart IoT systems. It implies that two systems are statically identical and are dynamically bisimulative within the range of a set of probability differences or increments for their corresponding processes.
- (2)
- (2-1) Incremental enhancement/improvement is the approach to improve the performance or capability of smart IoT systems to the level where all the SSReqs are satisfied probabilistically. Basically, the system improvement is based on process enhancement.
- Incremental process enhancement is the enhancement of a process representing each IoT device by increasing the values of probabilities on nondeterministic choice operations, representing replacing the units of the IoT device with a higher version, in terms of the probabilistic process equivalence;
- Incremental system improvement is the improvement for a system representing each smart IoT system by replacing its processes with the incrementally enhanced processes in terms of the probabilistic system equivalence.
- (1)
- Satisfied—the probability for SSReqs is in the range of validation probability and the validation is completed;
- (2)
- Unsatisfied—the probability for SSReqs is out of the range of validation probability; it goes through incremental enhancement and improvement, then another round of validation performs on SSReq until the final decision is made.
- Satisfiable—the new probability for SSReqs is in the range of validation probability and the validation is completed;
- Unsatisfiable—the new probability for SSReqs is out of the range of validation probability.
1.5. Proof of Concepts
- Modeler—It allows the visual specification of the operational requirements of the target smart IoT system with dTP-Calculus, consisting of the ITL (In-The-Large) system and ITS (In-The-Small) process models. The ITL model defines a set of processes in the system, interconnected with a set of communication channels, and the ITS model defines a set of interactions, that is, communication and movements, with other processes in the system. The nondeterministic behavior of the processes is defined by the probability of the choice operation.
- Generator—It generates an EX (execution) model for the system from a ITL system model with its ITS process models. The EX model contains all the execution paths possible for the system. The probabilistic behavior of the system is defined by generating execution paths with probabilities, composing nondeterministic interactions between processes with probabilities.
- Simulator—It simulates any selected execution path from the EX model and generates a GTS (geo-temporal space) model. The simulation is performed probabilistically as generated by the Generator for the EX model.
- Verifier—All the SSReqs (safety and security Requirements) are specified with GTS logic and verified by the Verifier. All the requirements are verified with respect to their corresponding probabilities.
- Validator—All the SSReqs with probabilities are validated to the system probabilities. If the probabilities are not satisfied, the system improvement starts with process enhancement.
1.6. Contribution
1.7. Organization
2. Theoretical Background
2.1. dTP-Calculus
- d (delta)—movement;
- T—time;
- P—probability.
2.1.1. Properties of dTP-Calculus
Mobility Property
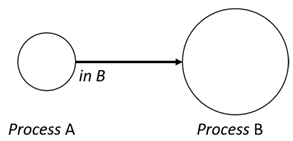
- Subjectivity—There are two types of movements in dTP-Calculus, (1) active movement, where a process moves autonomously by itself, and (2) passive movement, where a process is moved heteronomously by another process;
- Directivity—There are two types of movements in dTP-Calculus, (1) inward movement, where a process moves into another sibling process, and (2) outward movement, where a process moves out of its parent process.
- In—A subjective process moves autonomously into another sibling process and the subjective process needs to obtain permission from the sibling process;
- Out—A subjective process moves autonomously out of its parent sibling process and the subjective process needs to obtain permission from the parent process;
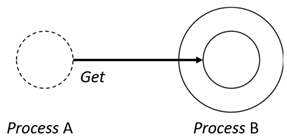
- Get—An objective process is moved into another sibling process heteronomously by the sibling process and the sibling process needs to obtain permission from the subjective process;
- Put—An objective process is moved out of its parent process heteronomously by the parent and the parent process needs to obtain permission from the objective process.
| Movement Types | Subjectivity | Directivity | Visual Presentation |
|---|---|---|---|
| In | Autonomous (Active) | Inward |  |
| Out | Outward |  | |
| Get | Heteronomous (Passive) | Inward | 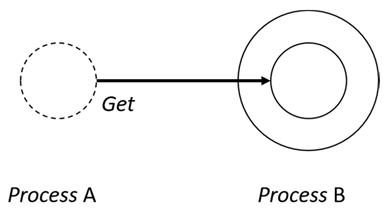 |
| Put | Outward |  |
Temporality Property
- Ready Time—The minimum time that a process must wait before performing a specific action, that is, interaction or movement;
- Timeout—The maximum time that a process must wait before performing a specific action, that is, interaction or movement;
- Execution Time—The time that a process consumes to execute a specific action;
- Deadline—The time within which a process must finish a specific action;
- Period—The time that a process repeats a specific action iteratively, like recursion.
Probability Property
- Discrete distribution—It allows to specify the choice to be made for its alternatives in the range of discrete values, where the summation of all the alternatives of the choice is 100%;
- Normal distribution—It allows the choice to be distributed normally for its alternatives with a mean () and a deviation (), whose dense function is defined as ;
- Exponential distribution—It allows the choice to be distributed exponentially for its alternatives with a frequency (), whose dense function is ;
- Uniform distribution—It allows the choice to be distributed uniformly for its alternatives in the range of , whose dense function is .
Priority Property
Synchronicity Property
2.1.2. dTP-Calculus Syntax
- It is one of the actions for A shown in (1) and (16) of the table: null (empty (16)), communication (send (17), receive (18)), movement ((19): (23)~(26)), control ((20): (27)~(29)).
- (a)
- Empty (16)—It represents a null action, where no action occurs.
- (b)
- Communication (send (17), receive (18))—It represents a synchronous communication between sender and receiver. In order to perform a communication between two processes, a set of synchronous actions, that is, send and receive, must occur in an overlapping time between them through a communication channel with the same type of message.
- (c)
- Movement (19)—It represents a movement interaction between a requesting process (21) and a permitting process (22). In order to perform a movement, the request action for the movement from the requesting process must be granted by the corresponding permitting action for the movement from the permitting process. There are a total of four types of such actions in dTP-Calculus—In (23), Out (24), Get (25), and Put (26).
- (d)
- Control (20)—It represents a set of control actions as follows:
- (i)
- New (27)—It represents an action for a process to create its child process. The child process cannot have a priority that is higher than that of the parent.
- (ii)
- Kill (28)—It represents an action for a process to terminate another process. The former must have a priority that is higher than that of the latter.
- (iii)
- Exit (29)—It represents an action for a process to terminate itself. The child processes with less priorities will be terminated in depth-first order. If there is any child process with a higher priority, this action must be propagated until the child process terminates.
- Timed Action (2)—It represents a time action, where the action is specified with the temporal properties [r, to, e, d], representing ready time, timeout, execution time, and deadline, respectively, and the recursion properties p and n, representing the period and number of repetitions, respectively.
- Timed Process (3)—This is the same notion for a process, instead of an action.
- Priority (4)—It represents the priority that has been stated in the previous subsection. It is expressed with a set of positive integers, where the high number represents a higher priority. Exceptionally, zero represents the highest priority. Note that, as described in the previous subsection, it is used to control asynchronous interactions and multiple synchronous situations.
- Nesting (5)—It represents inclusion relations among processes, where P includes Q. The included processes are controlled by an including process. If an inner process has a higher priority than that of its parent, that is, the including process, the inner process can move autonomously out of the including process, that is, its parent. All the processes, that is, parent and child, are running concurrently. When a parent process moves, its child processes move accordingly as included.
- Channel (6)—It represents a list of channels among processes. A communication occurs as a channel between processes.
- Choice (7)—It represents a choice operation, a branch of which is nondeterministically taken by a process for an action or interaction. For example, one of P and Q performs its action nondeterministically.
- Probabilistic Choice (8)—It represents a probabilistic choice operation, a branch of which is nondeterministically, but probabilistically, taken by a process for an action or interaction. The probabilistic distributions are defined in (12), (13), (14) and (15), respectively, as described in the previous subsection.
- Parallel (9)—It represents a number of independent processes to be run concurrently at the same time period.
- Exception (10)—It represent the exceptional handling actions or processes to be performed at the time of an exception being occurred, for example, the violation of temporal requirements for an action or a process.
- Sequence (11)—It represents the sequential execution of actions in temporal order.
2.1.3. dTP-Calculus Semantics
- Sequence (1)—Process P can perform its action without any premise or condition.
- ChoiceL, ChoiceR (2)—Only the chosen process can perform its own action as a premise without any condition.
- Probability Choice (3)—Only the chosen process can perform its own action probabilistically as a premise without any condition under a specified probability distribution.
- ParlL, ParlR (4)—Each process is independent and runs concurrently without interference as a premise without any condition.
- Parcom (5)—Synchronous communication occurs between two processes, P and Q. As a result of the communication interaction, each process makes its respective transition, as shown in the premises, without any side condition.
- NestingO, NestingI (6)—Both nesting and nested processes can perform their own transitions independently, as defined in the premises without any side condition.
- NestingCom (7)—A synchronous communication interaction is possible between the nesting and nested processes.
- In (8), Out (9), Get (10), Put (11)—Each movement is defined as a synchronous interaction between a requesting process and a permitting process for the action. As stated, In and Out are for autonomous movements and Get and Put are for heteronomous movements. Note that the inclusion relations are modified as a result of the movements.
- InP (12), OutP (13), GetP (14), PutP (15)—Each movement is defined as an asynchronous interaction between a requesting process and a permitting process for the action. The difference is that if the request process has a higher priority, it does not have to wait for permission from the permitting process, but it can move asynchronously without permission.
- TickTimeR (16)—As time ticks with , the ready time r and deadline d are elapsed by the ticks .
- TickTimeTO (17)—As time ticks idly with , timeout to and deadline d are elapsed by the ticks .
- TickTimeEnd (18)—An action is completed after the execution time e.
- TickTimeSyncE (19)—As time ticks for the synchronous interaction with , the execution time e and deadline d are elapsed by the ticks .
- TickTimeAsyncE (20)—As time ticks for the asynchronous interaction with , the execution time e and deadline d are elapsed by the ticks after ready time r.
- Timeout (21)—When timeout to becomes zero, a fault occurs. Exception handler P should be activated.
- Deadline (22)—When deadline d becomes zero, a fault occurs. Exception handler P should be activated.
- Period (23)—After recursion, repetition n is decremented by one.
- PeriodEnd (24)—If repetition n becomes zero, the recursion ends.
2.1.4. dTP-Calculus Rules
- Choice1 (1), Choice2 (2), Choice3 (3)—commutative and distributive rules for the choice operation;
- Parallel1 (4), Parallel2 (5), Parallel3 (6)—commutative and associative rules for parallel operation;
- Nesting1 (7), Nesting2 (8)—associative rules for the choice operation between processes nested in another process.
- Distributive1 (9), Distributive2 (10)—distributive rules for parallel over choice are only available in sibling relations. If not, a sequencing problem occurs.
| Type | Rules | Index |
|---|---|---|
| Choice1 | (1) | |
| Choice2 | (2) | |
| Choice3 | (3) | |
| Parallel1 | (4) | |
| Parallel2 | (5) | |
| Parallel3 | (6) | |
| Nesting1 | (7) | |
| Nesting2 | (8) | |
| Distributive1 | (9) | |
| Distributive2 | (10) |
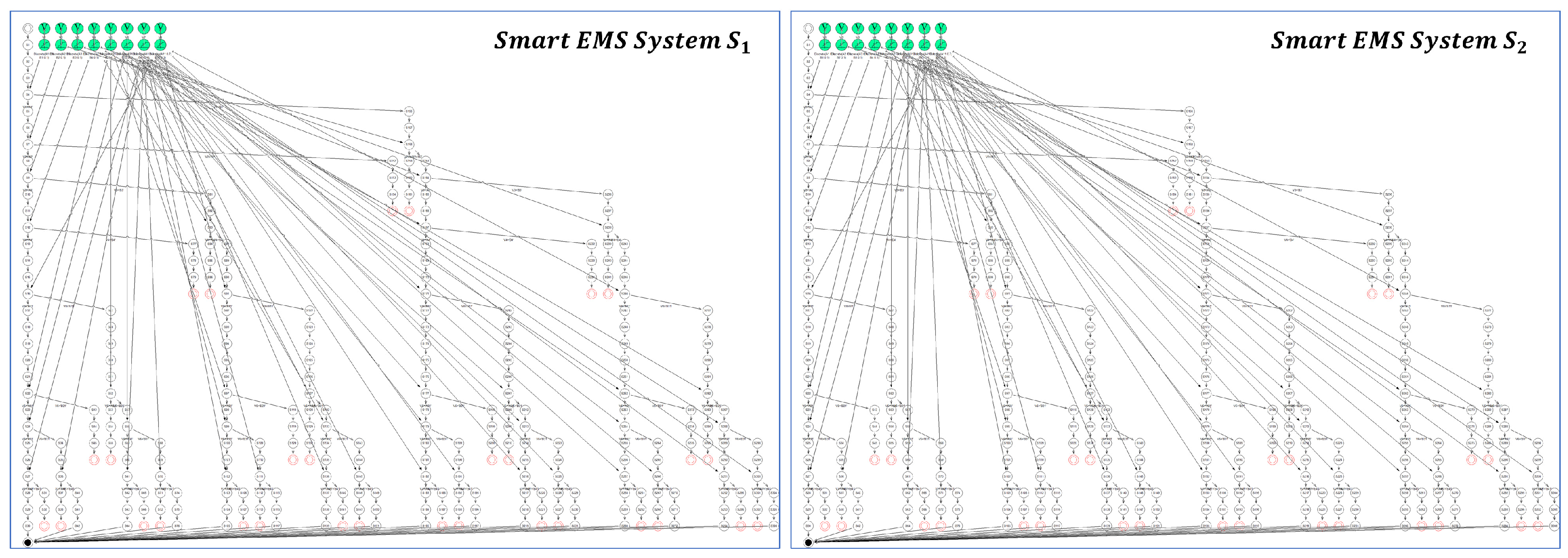
2.2. Probabilistic Equivalences
2.2.1. Probabilistic Process Equivalences

2.2.2. Probabilistic System Equivalences
3. Approach
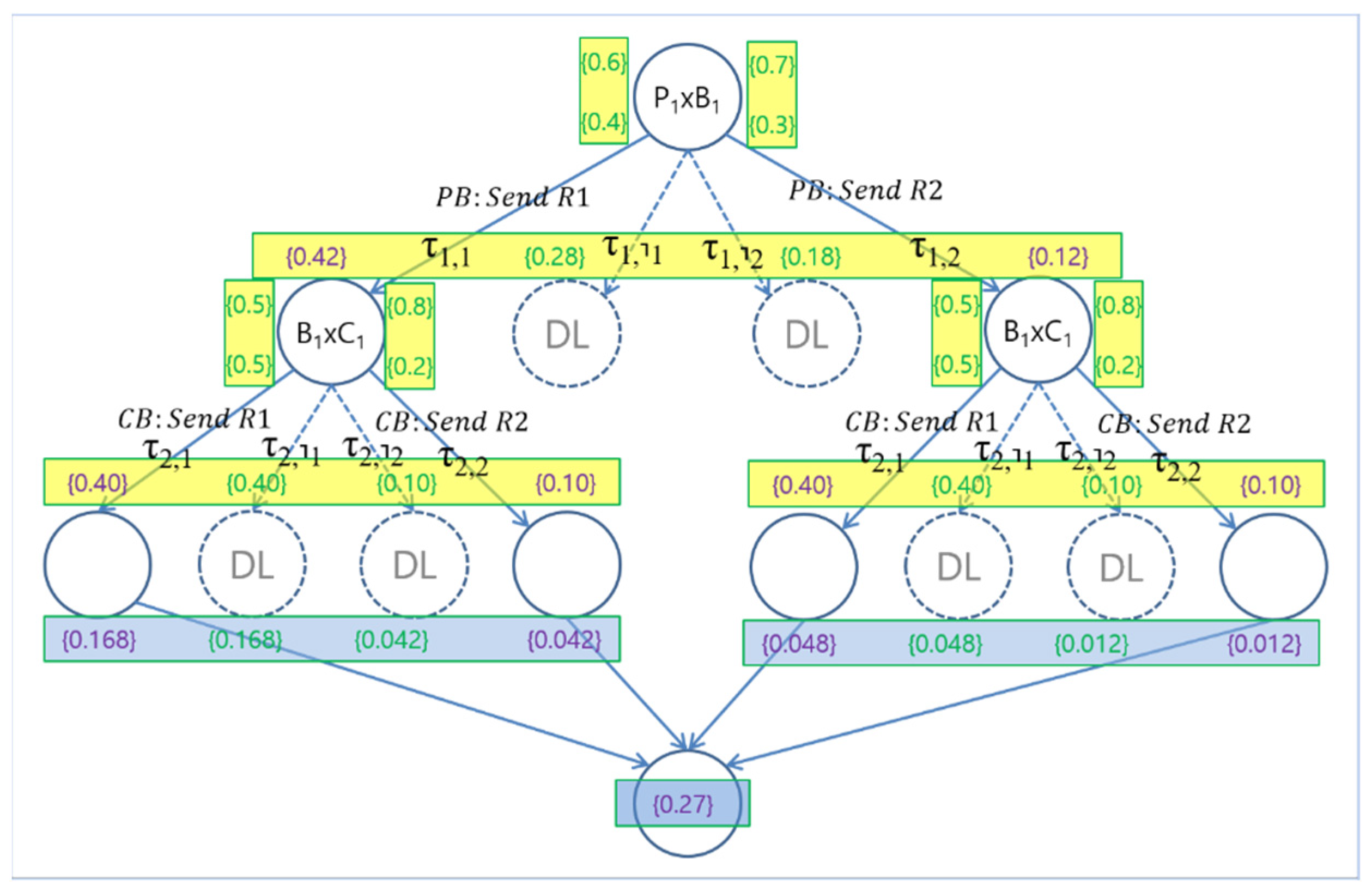
3.1. Probabilistic Verification
3.2. Probabilistic Validation
- ;
- ;
- ;
- .
| eP1 | eP2 | eP3 | eP4 | eP5 | eP6 | eP7 | eP8 | eP9 | eP10 | Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| τ1•τ2 | τ1,1•τ2,1 | τ1,1•τ2,⸣1 | τ1,1•τ2,⸣2 | τ1,1•τ2,2 | τ1, ⸣1 | τ1, ⸣2 | τ1,2•τ2,1 | τ1,2•τ2,⸣1 | τ1,2•τ2,⸣2 | τ1,2•τ2,2 | |
| Prob. | 0.168 | 0.168 | 0.042 | 0.042 | 0.28 | 0.28 | 0.048 | 0.048 | 0.012 | 0.012 | 1.00 |
| ◯ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ◯ | 0.18 | |
| ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | 0.27 | |
| ◯ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ◯ | 0.18 | |
| ✕ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ✕ | 0.09 |
3.3. Incremental Enhancement and Improvement
- ;
- ;
- ;
- .


| eP1 | eP2 | eP3 | eP4 | eP5 | eP6 | eP7 | eP8 | eP9 | eP10 | Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| τ1•τ2 | τ1,1•τ2,1 | τ1,1•τ2,⸣1 | τ1,1•τ2,⸣2 | τ1,1•τ2,2 | τ1, ⸣1 | τ1, ⸣2 | τ1,2•τ2,1 | τ1,2•τ2,⸣1 | τ1,2•τ2,⸣2 | τ1,2•τ2,2 | |
| Prob. | 0.196 | 0.196 | 0.049 | 0.049 | 0.21 | 0.21 | 0.036 | 0.036 | 0.009 | 0.009 | 1.00 |
| ◯ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ◯ | 0.205 | |
| ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | 0.290 | |
| ◯ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ◯ | 0.205 | |
| ✕ | ✕ | ✕ | ◯ | ✕ | ✕ | ◯ | ✕ | ✕ | ✕ | 0.085 |
4. Implementation
4.1. ADOxx Meta-Modeling Platform
- Meta-modeling languages—ADOxx provides a function to develop modeling languages for business domains. It is very useful to utilize the existing standard modeling languages or to develop completely new modeling languages;
- Meta-modeling modules—ADOxx provides a set of meta-modeling functions to define modeling languages and extend them, thorough which users can define modeling processes more effectively by defining the structures and rules of the modeling languages;
- Modeling tools—ADOxx provides a set of intuitive tools with which users can design and edit graphically the models and through which the users can understand more visually modeled processes and manage them more effectively.
- Plugin extension—It allows an extension of functions by supporting various plugin facilities through which the users can extend specific functions, if needed, and integrate the platform with other external systems.
4.2. SAVE
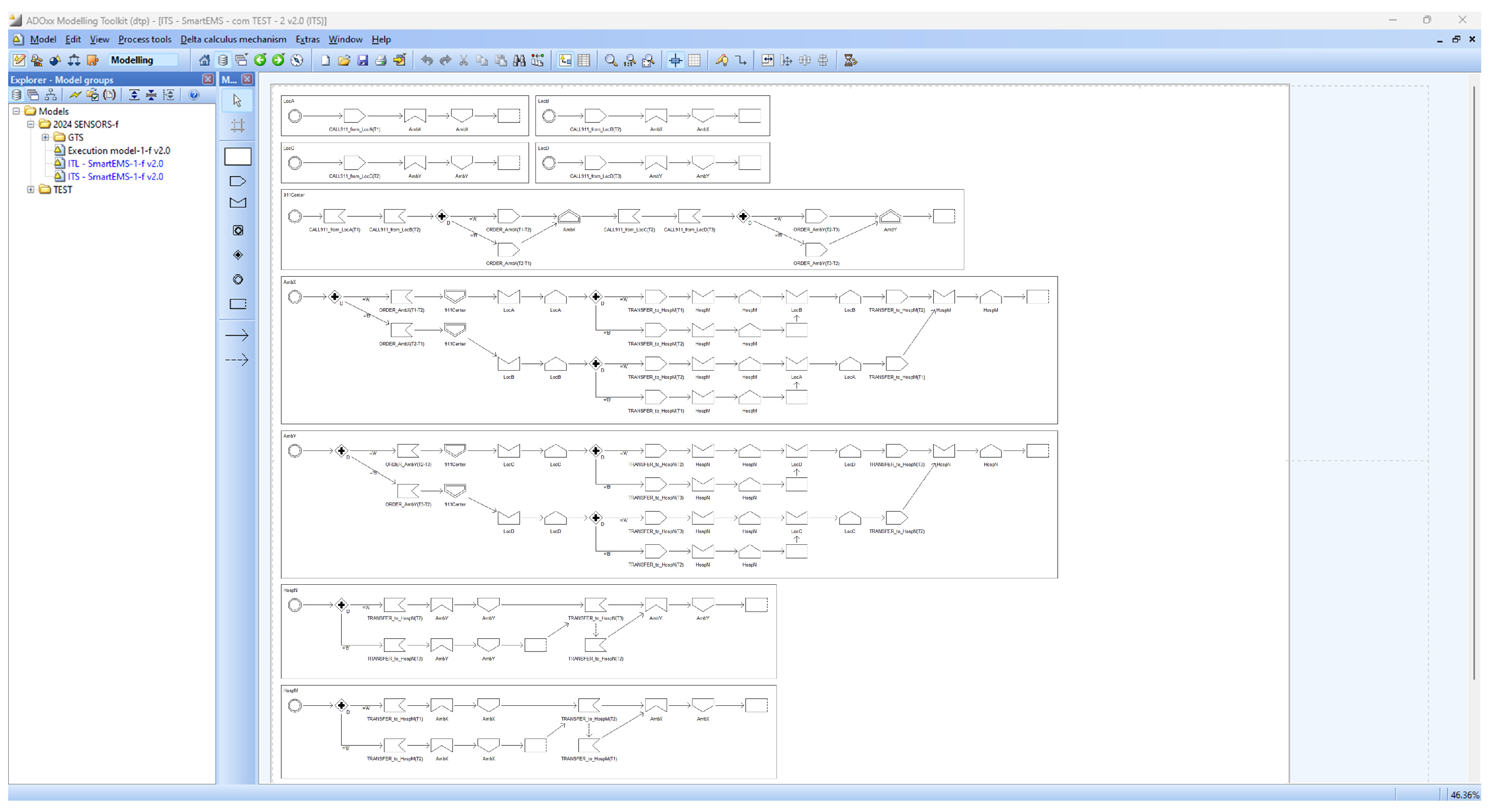
4.2.1. SAVE: Modeler
- The ITL model is a system view that visually shows a set of processes in a system connected by a set of channels for communication among the processes;
- The ITS model is a process view that visually shows the set of interactions, that is, communication or movement, to perform in a sequential or selective order.
- The ITL loader loads each ITL model on the SAVE model view screen and shows all the processes and their communication channels, as defined on the ADOxx meta-modeling platform;
- The ITS loader loads each ITS model on the SAVE model view screen and shows all the actions and their precedence relations, as defined on the ADOxx meta-modeling platform;
- ITL/ITS mapper—as the system defined, an ITL model contains a number of ITS models. It inspects the proper relations between the ITL model and their contained ITS models for their proper syntactical relations and performs a function to generate a set of preliminary data that will be used to generate a set of future data for the following execution model for the system, including processes;
- T2M parser performs the translation function from the specification for system with processes in dTP-Calculus to ITL and ITS models in SAVE on ADOxx;
- Syntactic checker—At the time of checking the T2M parser function, it performs the inspection function for the syntactic validity of the characters input to the parser;
- The probability specifier supports a function to support the specification of probabilities in the ITS model.
4.2.2. SAVE: Simulator
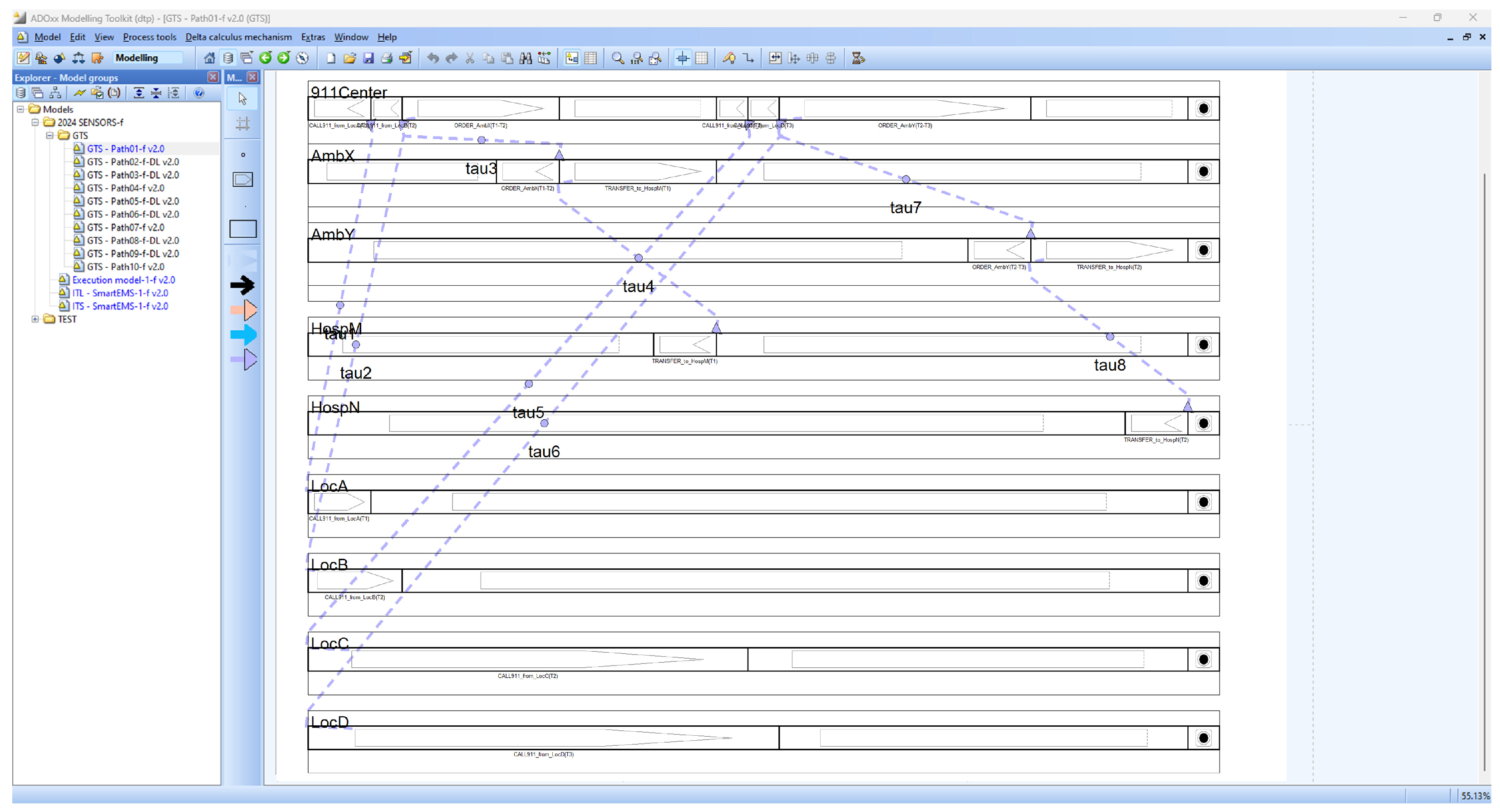
- The geo-temporal space (GTS) model is a graphical model that shows the processes in a system and their interactions, that is, communication and movement, on a two-dimensional geo-temporal space, as defined on the ADOxx meta-modeling platform for GTS models.
- EM Generator generates an EX model for a target ITL model with a set of ITS models;
- Simulation Core with Probability is a core engine to simulate each path of the target EX model with probability and visually shows the probabilistic branches of the EM model for simulation;
- EM Path Analyzer performs a set of probabilistic analysis on each path of the target EX model;
- GTS Generator generates a GTS model from the EX model.
4.2.3. SAVE: Analyzer and Verifier
- T2G Logic Parser checks the syntactical validity of the safety and security requirements and performs a function to generate the preliminary data needed for the analysis and verification;
- GTS Logic Verifier performs an analysis and verification of whether the target GTS model is satisfied for the specified SSReq or not from the data received from the T2G Logic Parser;
- GTS Logic Visualizer performs a function to visualize the results of analysis and verification from the GTS Logic Verifier;
- Coverage Analyzer/Verifier performs a set of analyses and verifications of SSReqs on all the paths of the EX model for the target system, including visualization.
4.3. Smart EMS System
- an 11.3% increase in transfer cases from 2020, which is 1,775,000 transfer cases;
- a 12.4% increase in transfer cases from 2020, which is 1,823,000 individual transferred patients.
4.3.1. Description
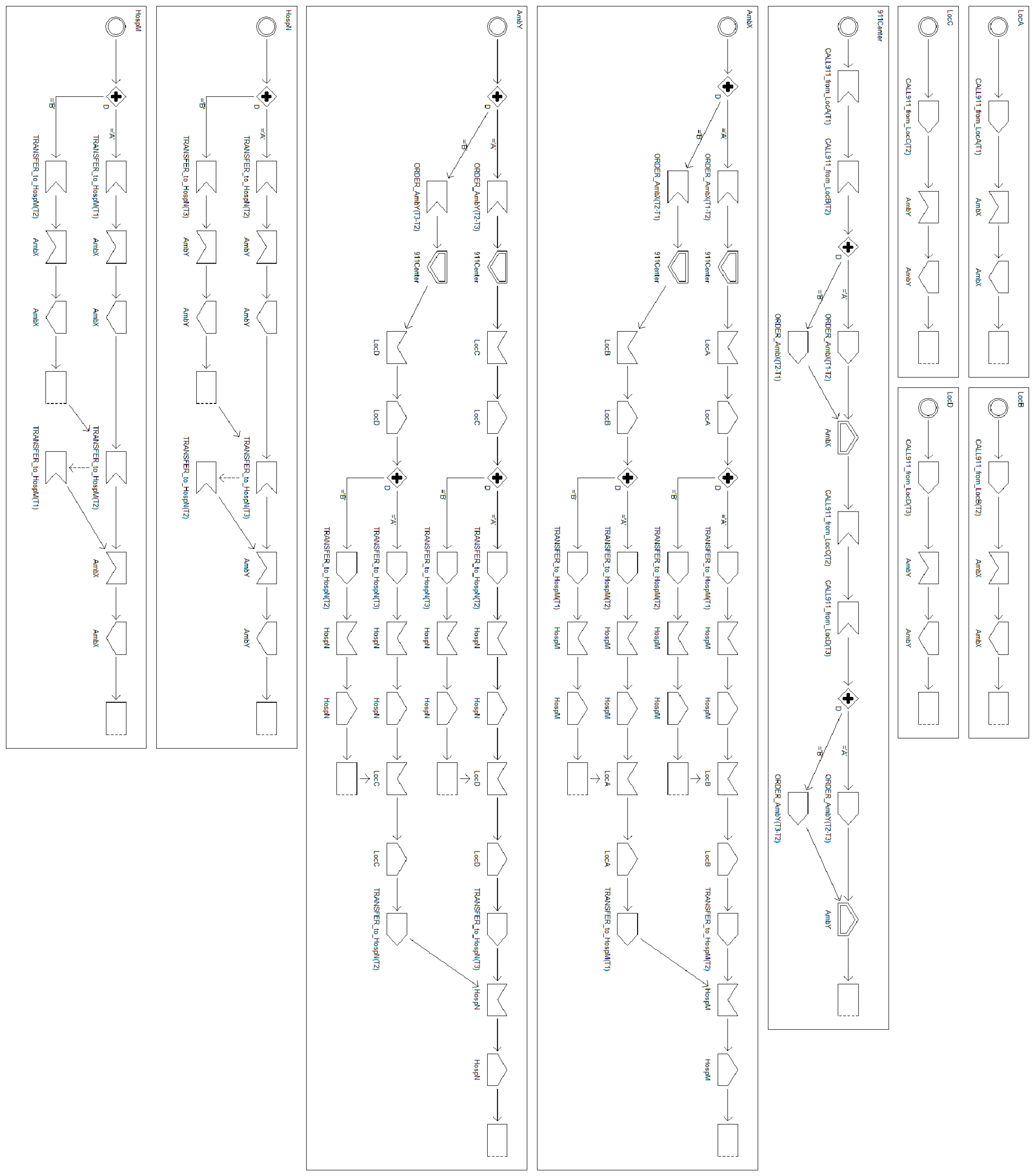
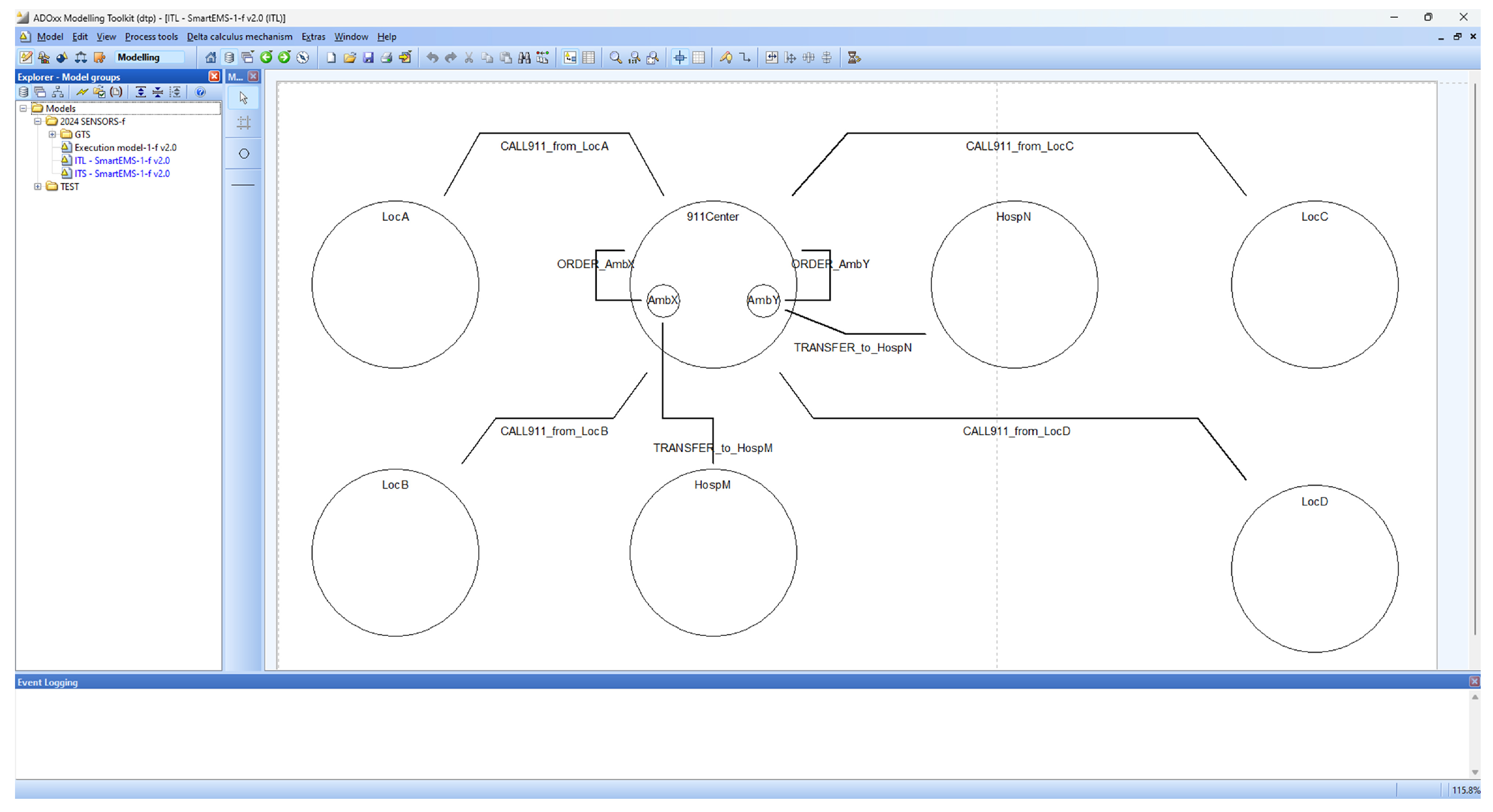
- (1)
- EMS consists of 911 (911Center1), ambulances (AmbX1, AmbY1), locations of patients (LocA, LocB, LocC, LocD), and hospitals (HospM1 and HospN1);
- (i)
- 911Center1 contains ambulances;
- (ii)
- Both AmbX1 and AmbY1 imply ambulances;
- (iii)
- LocA LocB, LocC and LocD imply locations;
- (iv)
- HospM1 and HospN1 imply hospitals.
- (2)
- Assuming that there is a T1 patient of Table 12 in LocA;
- (3)
- Assuming that there is a T2 patient of Table 12 in LocB;
- (4)
- Assuming that there is a T2 patient of Table 12 in LocC;
- (5)
- Assuming that there is a T3 patient of Table 12 in LocD;
- (6)
- 911Center1 receives patient information from locations LocA, LocB, LocC, and LocD;
- (7)
- AmbX1 moves to LocA and LocB, based on the information received from 911Center1;
- (i)
- In the case where AmbX1 moves to LocA first, it transfers the patient at the location to HospM1 after sending a message to the hospital and it moves to LocB, rescues the patient at the location, and transfers the patient to HospM1;
- (ii)
- In the case where AmbX1 moves to LocB first, instead of LocA, it transfers the patient at the location to HospM1 after sending a message to the hospital and it moves to LocA, rescues the patient at the location, and transfers the patient to HospM1.
- (8)
- AmbY1 moves to LocC and LocD, based on the information received from 911Center1;
- (i)
- In the case where AmbX1 moves to LocC first, it transfers the patient at the location to HospN1 after sending a message to the hospital and it moves to LocD, rescues the patient at the location, and transfers the patient to HospN1;
- (ii)
- In the case where AmbX1 moves to LocD first, instead of LocC, it transfers the patient at the location to HospN1 after sending a message to the hospital and it moves to LocC, rescues the patient at the location, and transfers the patient to HospN1.
- (9)
- HospM1 takes a patient from AmbX1.
- (10)
- HospN1 takes a patient from AmbY1.
4.3.2. Specification
- (1)
- shows the inclusion relations among the components of the EMS example;
- (2)
- LocA transmits the patient’s information to 911Center with ;
- (3)
- LocB transmits the patient’s information to 911Center with ;
- (4)
- LocC transmits the patient’s information to 911Center with ;
- (5)
- LocD transmits the patient’s information to 911Center with ;
- (6)
- 911Center1 sends the patients’ information to AmbX1 and AmbY1;
- (a)
- The probabilities that 911Center1 sends AmbX1 the rescue order for the patients are
- (i)
- —the probability that a T1 patient at LocA is rescued first (90%);
- (ii)
- —the probability that a T2 patient at LocB is rescued first (10%).
- (b)
- The probabilities that 911Center1 sends AmbY1 the rescue order for the patients are
- (i)
- —the probability that a T2 patient at LocC is rescued first (70%);
- (ii)
- —the probability that a T2 patient at Location LocC is rescued first (30%).
- (7)
- AmbX1 receives the patient’s information from 911Center1 and transfers the patient to HospM1 after rescuing the patient;
- (a)
- —the probability that AmbX1 moves first to LocA (90%);
- (b)
- —the probability that AmbX1 moves first to LocB (10%);
- (c)
- —the probability that AmbX1 transmits the information of a T1 patient at LocA to HospM1 (90%);
- (d)
- —the probability that AmbX1 transmits the information of a T2 patient at LocB to HospM1 (10%).
- (8)
- AmbY1 receives the patient’s information from 911Center1 and transfers the patient to HospN1 after rescuing the patient;
- (a)
- —the probability that AmbY1 moves first to LocC (70%);
- (b)
- —the probability that AmbY1 moves first to LocD (30%);
- (c)
- —the probability that AmbY1 transmits the information of a T2 patient at LocC to HospN1 (90%);
- (d)
- —the probability that AmbY1 transmits the information of a T3 patient at LocD to HospN1 (10%).
- (9)
- HospM1 receives the patient from AmbX1;
- (a)
- —the probability that HospM1 receives the information on a T1 patient at LocA (90%);
- (b)
- —the probability that HospM1 receives the information on a T2 patient at LocB (10%).
- (10)
- HospN1 receives the patient from AmbY1.
- (a)
- —the probability that HospN1 receives the information on a T2 patient at LocC (90%);
- (b)
- —the probability that HospN1 receives the information on a T3 patient at LocD (10%).

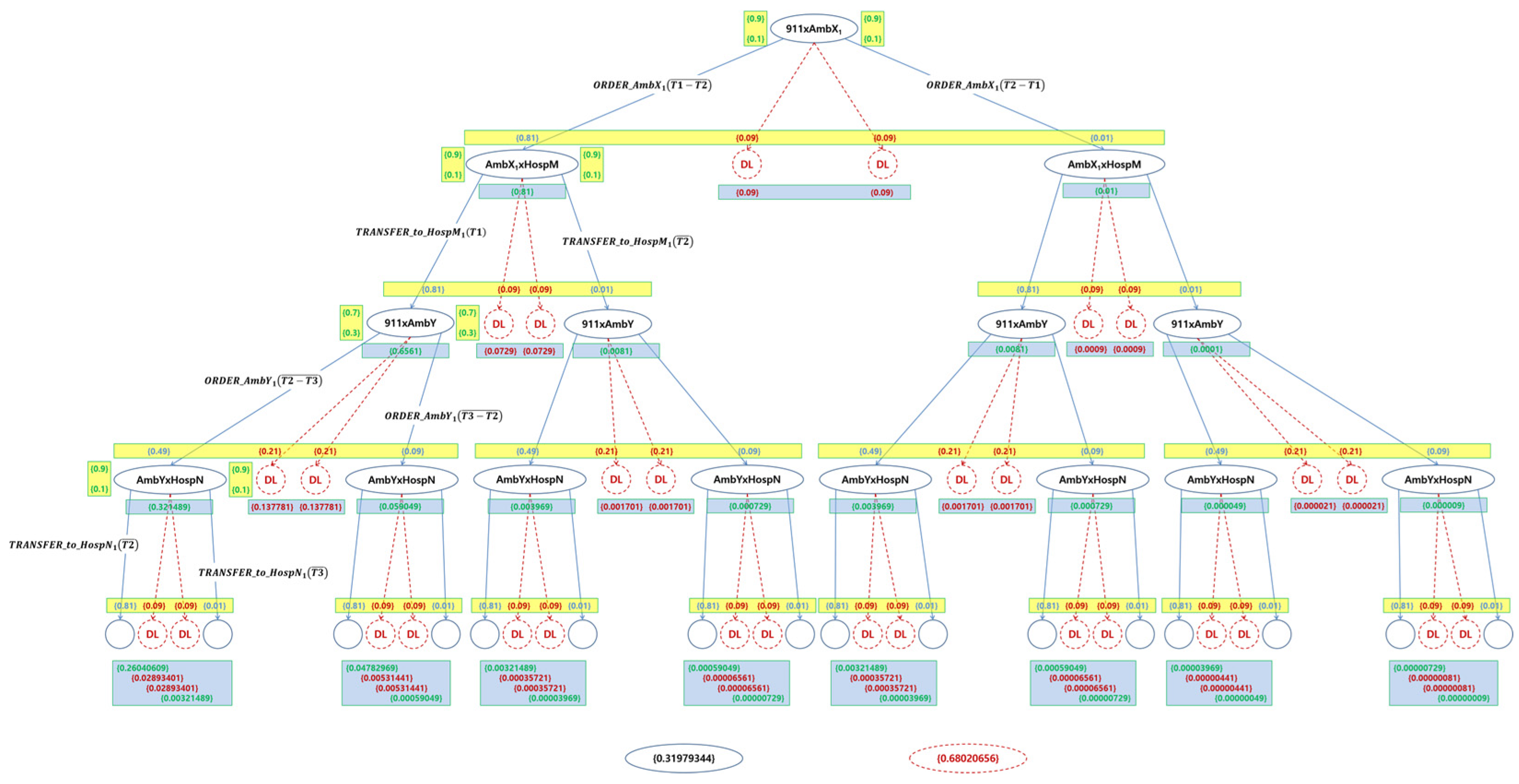
4.3.3. Probability Analysis
4.3.4. Safety and Security Requirements
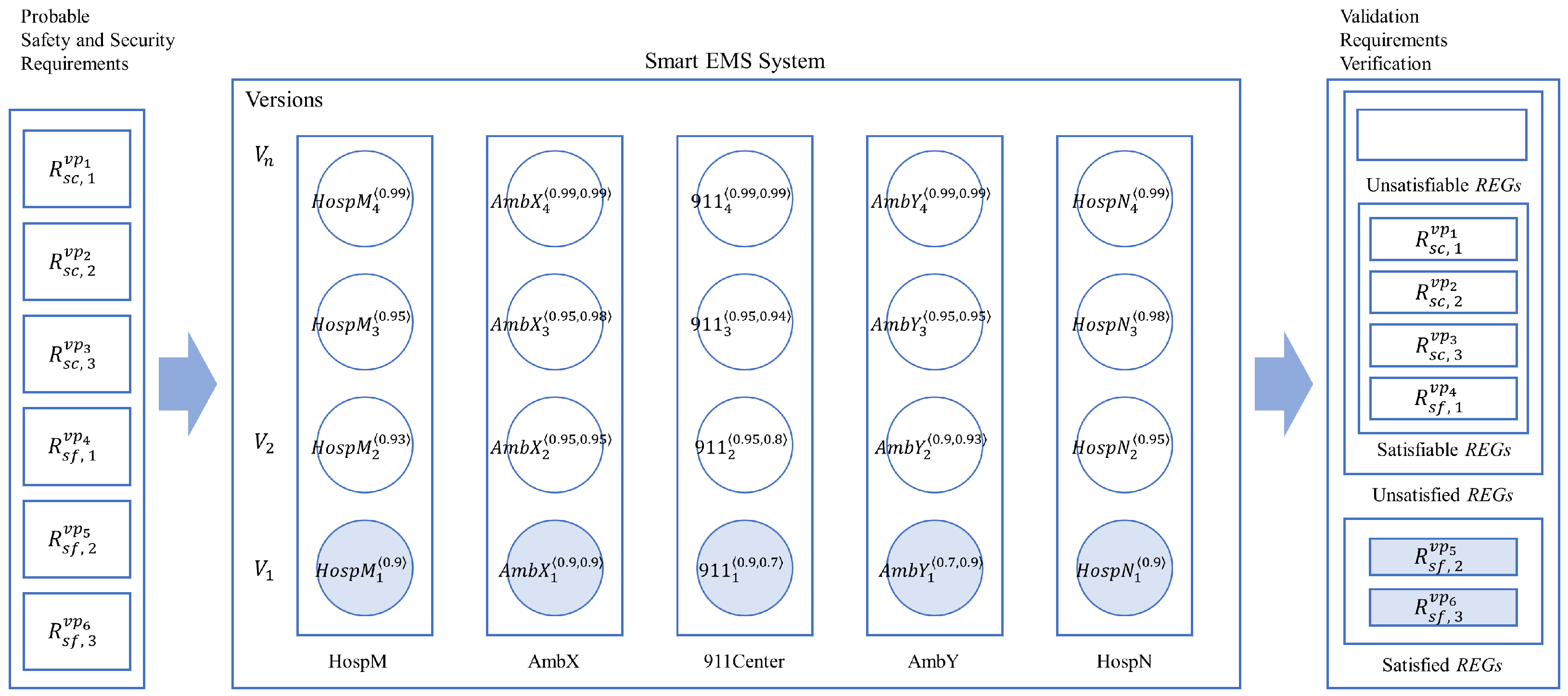
4.4. Smart EMS: Incremental System Improvement
4.4.1. Incremental System Improvement by Single Process Enhancement
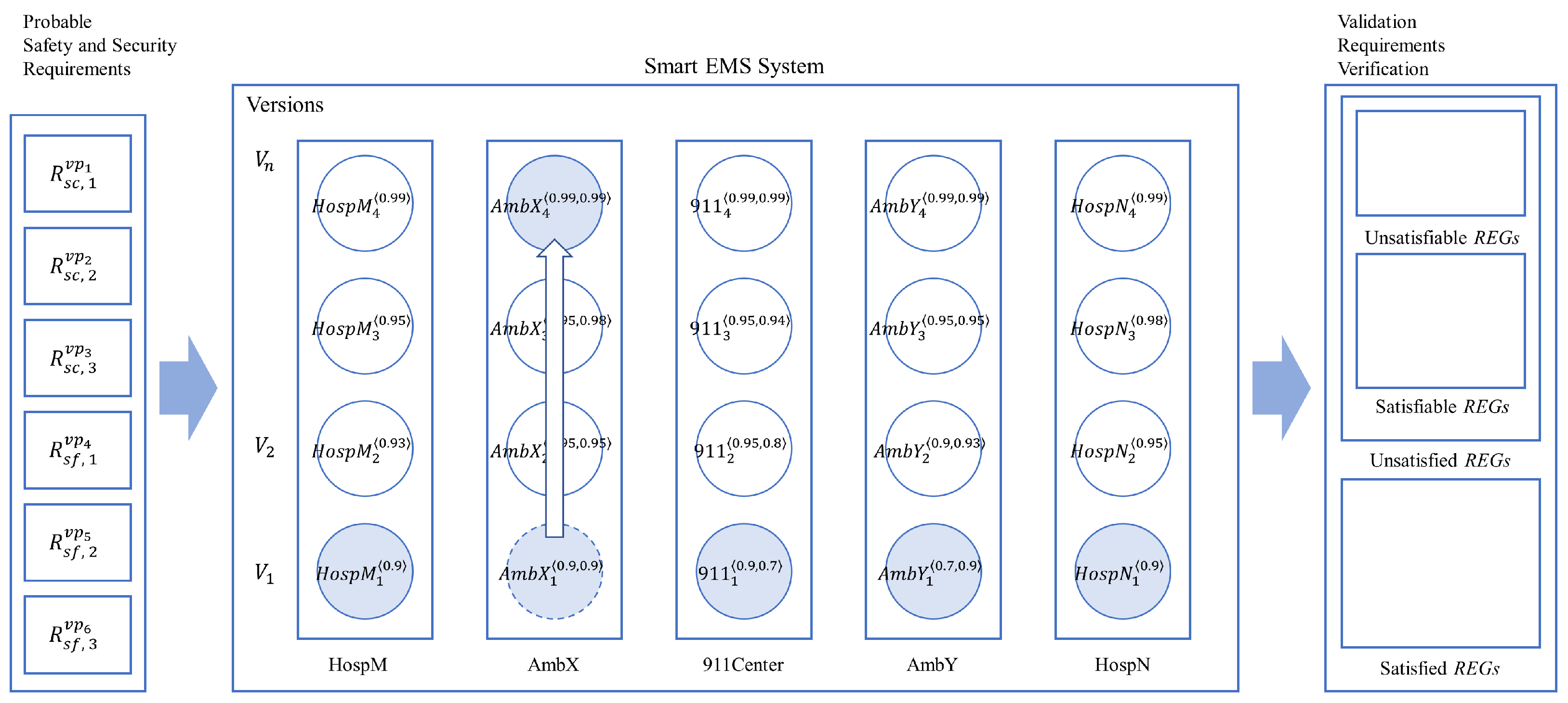
- (1)
- The probabilities that 911Center1 sends AmbX1 the rescue order for the patients are updated where
- —the probability that a T1 patient at LocA is rescued first (99%);
- —the probability that a T2 patient at LocB is rescued first (1%).
- (2)
- AmbX1 receives the patient’s information from 911Center1, and transfers the patient to HospM1 after rescuing the patient, with the updated probabilities.
- —the probability that AmbX1 moves first to LocA (99%);
- —the probability that AmbX1 moves first to LocB (1%).
4.4.2. Incremental System Improvement for Collective Process Enhancements
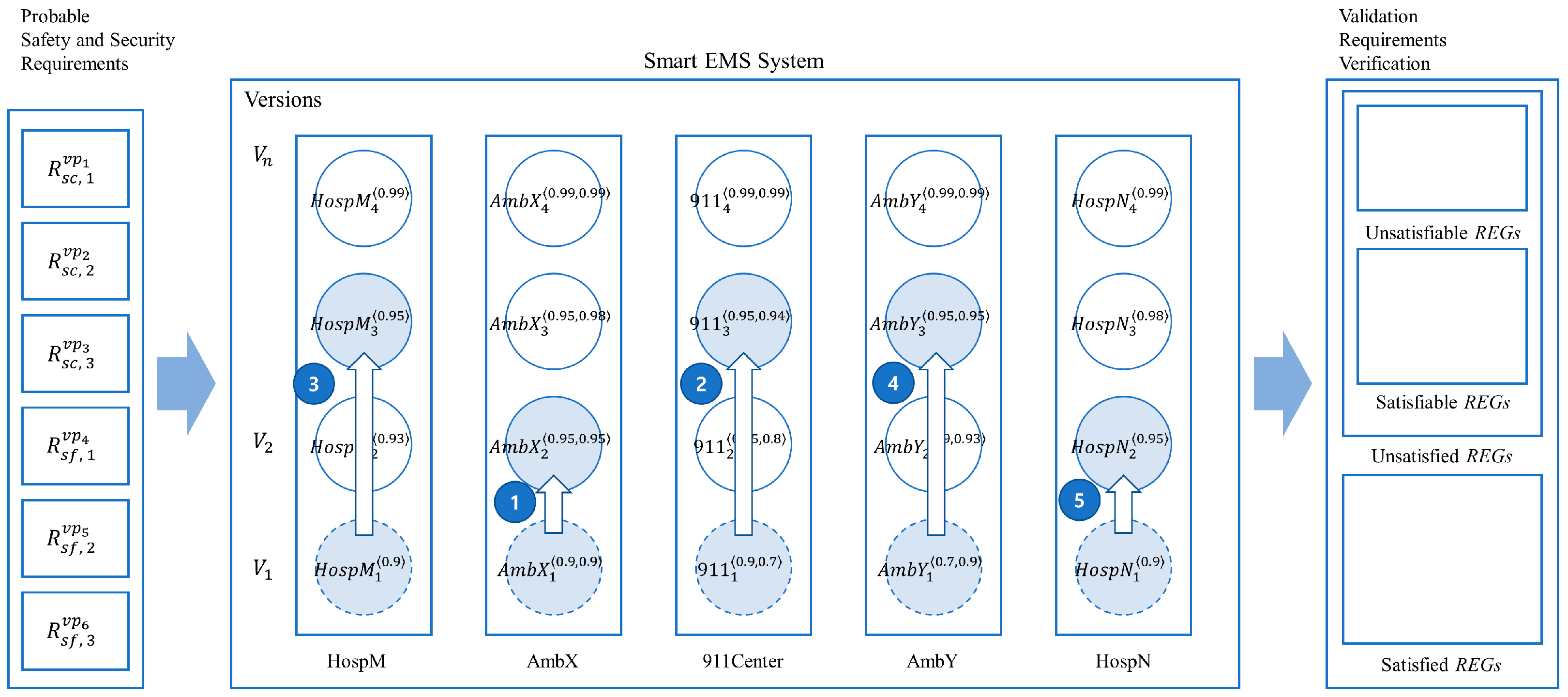
- (1)
- AmbX—assuming that AmbX has been upgraded one level up from AmbX1 to AmbX2;
- (2)
- 911Center—assuming that 911Center related to AmbX has been upgraded two levels up from 911Center1 to 911Center3;
- (3)
- HospM—assuming that HospM has been upgraded two levels up from HospM1 to HospM3;
- (4)
- AmbY—assuming that AmbY has been upgraded two levels up from AmbY1 to AmbY3;
- (5)
- HospN—assuming that HospN has been upgraded one level up from HospN1 to HospN2.
5. Comparative Study
5.1. Previous Research
- PCCS only relies on discrete probability models;
- PACSR only relies on discrete probability models, similar to PCCS;
- PALOMA only focuses exponential probability distribution models.
- Specification of nondeterministic behavior—the behavior of processes in a system is specified with probability so that the system become probabilistically predictable and controllable;
- Verification of probabilistic requirements—the safety and security requirements can be both analyzed and verified probabilistically;
- Control of nondeterministic behavior—the nondeterministic behavior of a system becomes controllable with dynamically controllable probability.
- Probabilistic equivalences—the probabilities for operational requirements on nondeterministic operators are defined by the incremental levels reflecting the capacities of the real IoT devices;
- Incremental improvement—the devices can be improved by incremental steps to satisfy the probabilistic safety and security requirements.
5.2. Related Research
- A linear process-algebraic format with data for probabilistic automata (Katoen, J. P., van de Pol, J., Stoelinga, M., & Timmer, M, 2012) that proposes an algebraic approach to verify bisimulation on data-dependent models and presents a method to inspect equivalence among processes based on data dependencies [36];
- Probabilistic bisimulation: Naturally on distributions (Hermanns, H., Krčál, J., & Křetínský, J, 2014) that deals with similar bisimulation from probabilistic process algebra and introduces a method to limit the size of state space in probabilistic process algebra and a method to reduce the state space effectively by applying the bisimulation [37].
6. Conclusions and Future Research
- (1)
- Defining the notion of weighted integration of interrelated processes for incremental improvement—the approach in this paper assumes that all the processes in the system are considered to be candidates for improvement. However, it could be better to include only the ones influence by the main processes that cause the major and direct improvement of performance of the systems, based on some degree of weighted interrelationships. In this way, the redundant repetition of increments may be reduced dramatically by applying them simultaneously at once;
- (2)
- Systematic evaluation mechanism for the versionization of processes—in the approach, the capabilities of IoT devices are represented with versions with some discrete probabilities. In the future, we need some systematic way of representing their capabilities in terms of discrete probability;
- (3)
- Field application—currently, SAVE has been applied to conceptual model examples. A real example from the field of smart IoT systems needs to be selected to prove the feasibility of the approach in this paper with the SAVE tool suite.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A




| Version | CPU Speed | RAM Capacity | Price |
|---|---|---|---|
| Raspberry Pi 1 | 700 MHz Single Core | 256 MB~512 MB | $5~$20 |
| Raspberry Pi 2 | 900 MHz Multi Core | 512 MB~1 GB | $25~$35 |
| Raspberry Pi 3 | 1.2 GHz Multi Core | 512 MB~1 GB | $25~$45 |
| Raspberry Pi 4 | 1.5 GHz Multi Core | 2 GB~8 GB | $45~$75 |
| Raspberry Pi 1 vs. 2 | Raspberry Pi 2 vs. 3 | Raspberry Pi 3 vs. 4 | ||||
|---|---|---|---|---|---|---|
| CPU Speed | 700 MHz | 900 MHz | 900 MHz | 1.2 GHz | 1.2 GHz | 1.5 GHz |
| Approx. 28.57% | Approx. 33.33% | Approx. 25% | ||||
| RAM Capacity | 256 MB | 1 GB | 1 GB | 1 GB | 1 GB | 8 GB |
| Approx. 290.63% | Approx. 0% | Approx. 700% | ||||
| Accumulative Improvement | Approx. 159.6% | Approx. 16.67% | Approx. 362.5% | |||
| Adjusted Improvement | Approx. 64.29% | Approx. 16.67% | Approx. 62.5% | |||
References
- Manimuthu, A.; Dharshini, V.; Zografopoulos, I.; Priyan, M.K.; Konstantinou, C. Contactless technologies for smart cities: Big data, IoT, and cloud infrastructures. SN Comput. Sci. 2021, 2, 334. [Google Scholar] [CrossRef] [PubMed]
- Arshi, O.; Mondal, S. Advancements in sensors and actuators technologies for smart cities: A comprehensive review. Smart Constr. Sustain. Cities 2023, 1, 18. [Google Scholar] [CrossRef]
- Arya, S.; Dwivedi, S.K.; Ansar, S.A.; Sharma, K.; Pandey, D. Integrating IoT with cloud computing and big data analytics: Security perspective. In Proceedings of the AIP Conference Proceedings, Penang, Malaysia, 11–12 November 2022; AIP Publishing: Melville, NY, USA, 2023; Volume 2954. [Google Scholar] [CrossRef]
- Bibri, S.E.; Alexandre, A.; Sharifi, A.; Krogstie, J. Environmentally sustainable smart cities and their converging AI, IoT, and big data technologies and solutions: An integrated approach to an extensive literature review. Energy Inform. 2023, 6, 9. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shang, S. Managing uncertainty in AI-enabled decision making and achieving sustainability. Sustainability 2020, 12, 8758. [Google Scholar] [CrossRef]
- N’Guyen, S.; Moulin-Frier, C.; Droulez, J. Decision making under uncertainty: A quasimetric approach. PLoS ONE 2013, 8, e83411. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kurniawati, H. Partially observable markov decision processes (pomdps) and robotics. arXiv 2021, arXiv:2107.07599. [Google Scholar] [CrossRef]
- Misra, A.; Mittal, A.; Misra, V.; Pandey, D. Improving non-deterministic uncertainty modelling in Industry 4.0 scheduling. arXiv 2021, arXiv:2101.05677. [Google Scholar] [CrossRef]
- AlSalem, T.S.; Almaiah, M.A.; Lutfi, A. Cybersecurity Risk Analysis in the IoT: A Systematic Review. Electronics 2023, 12, 3958. [Google Scholar] [CrossRef]
- Kandasamy, K.; Srinivas, S.; Achuthan, K.; Rangan, V.P. IoT cyber risk: A holistic analysis of cyber risk assessment frameworks, risk vectors, and risk ranking process. EURASIP J. Inf. Secur. 2020, 2020, 8. [Google Scholar] [CrossRef]
- Song, J.; Lee, S.; Karagiannis, D.; Lee, M. Process Algebraic Approach for Probabilistic Verification of Safety and Security Requirements of Smart IoT (Internet of Things) Systems in Digital Twin. Sensors 2024, 24, 767. [Google Scholar] [CrossRef]
- Song, J.; Karagiannis, D.; Lee, M. Modeling Method to Abstract Collective Behavior of Smart IoT Systems in CPS. Sensors 2022, 22, 5057. [Google Scholar] [CrossRef] [PubMed]
- Karagiannis, D.; Mayr, H.C.; Mylopoulos, J. (Eds.) Domain-Specific Conceptual Modeling: Concepts, Methods and Tools; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Karagiannis, D.; Kühn, H. Metamodelling platforms. In E-Commerce and Web Technologies; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2455, p. 182. [Google Scholar] [CrossRef]
- Karagiannis, D.; Lee, M.; Hinkelmann, K.; Utz, W. (Eds.) Domain-Specific Conceptual Modeling: Concepts, Methods and ADOxx Tools; Springer Nature: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Whitbeck, J.; Dias de Amorim, M.; Conan, V.; Guillaume, J.L. Temporal reachability graphs. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012; pp. 377–388. [Google Scholar] [CrossRef]
- Zhang, C.; Bonifati, A.; Özsu, M.T. Indexing Techniques for Graph Reachability Queries. arXiv 2023, arXiv:2311.03542. [Google Scholar] [CrossRef]
- Quer, S.; Calabrese, A. Graph reachability on parallel many-core architectures. Computation 2020, 8, 103. [Google Scholar] [CrossRef]
- National Fire Department of Korea. Available online: https://www.index.go.kr/unity/potal/main/EachDtlPageDetail.do?idx_cd=1634 (accessed on 23 March 2024).
- Noor, T.H. Human Action Recognition-Based IoT Services for Emergency Response Management. Mach. Learn. Knowl. Extr. 2023, 5, 20. [Google Scholar] [CrossRef]
- Edoh, T. Internet of things in emergency medical care and services. In Medical Internet of Things (m-IoT)-Enabling Technologies and Emerging Applications; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Damaševičius, R.; Bacanin, N.; Misra, S. From sensors to safety: Internet of Emergency Services (IoES) for emergency response and disaster management. J. Sens. Actuator Netw. 2023, 12, 41. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kaisar, S.; Khoda, M.E.; Naha, R.; Khoshkholghi, M.A.; Aiash, M. IoT-based emergency vehicle services in intelligent transportation system. Sensors 2023, 23, 5324. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.L.; Chou, Y.H.; Chang, L.C. An intelligent IoT emergency vehicle warning system using RFID and Wi-Fi technologies for emergency medical services. Technol. Health Care 2018, 26, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chen, Z.; Cui, F. Collaborative and secure transmission of medical data applied to mobile healthcare. BioMedical Eng. OnLine 2019, 18, 60. [Google Scholar] [CrossRef] [PubMed]
- Refaee, E.; Parveen, S.; Begum KM, J.; Parveen, F.; Raja, M.C.; Gupta, S.K.; Krishnan, S. Secure and scalable healthcare data transmission in IoT based on optimized routing protocols for mobile computing applications. Wirel. Commun. Mob. Comput. 2022, 2022, 5665408. [Google Scholar] [CrossRef]
- Hansson, H.A. Time and Probability in Formal Design of Distributed Systems. Ph.D. Thesis, Department of Computer Systems, Uppsala University, Uppsala, Sweden, 1994. [Google Scholar]
- Lee, I.; Brémond-Grégoire, P.; Gerber, R. A process algebraic approach to the specification and analysis of resource-bound real-time systems. Proc. IEEE 1994, 82, 158–171. [Google Scholar] [CrossRef]
- Feng, C.; Hillston, J. PALOMA: A process algebra for located markovian agents. In International Conference on Quantitative Evaluation of Systems; Springer: Cham, Switzerland, 2014; pp. 265–280. [Google Scholar] [CrossRef]
- Baeten, J.C.; Reniers, M.A. Process Algebra: Equational Theories of Communicating Processes; Cambridge University Press: Cambridge, UK, 2010; Volume 50. [Google Scholar]
- Garavel, H.; Lang, F. Equivalence checking 40 years after: A review of bisimulation tools. In A Journey from Process Algebra via Timed Automata to Model Learning; Springer: Cham, Switerland, 2022; pp. 213–265. [Google Scholar] [CrossRef]
- Hirshfeld, Y.; Jerrum, M. Bisimulation equivalence is decidable for normed process algebra. In Automata, Languages and Programming: 26th International Colloquium, ICALP’99 Prague, Czech Republic, 11–15 July 1999 Proceedings; Springer: Berlin/Heidelberg, Germany, 2002; pp. 412–421. [Google Scholar] [CrossRef]
- Jancar, P. Bisimilarity on basic process algebra is in 2-exptime (an explicit proof). Log. Methods Comput. Sci. 2013, 9, 1–19. [Google Scholar] [CrossRef]
- Milner, R. (Ed.) A Calculus of Communicating Systems; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Lee, I.; Philippou, A.; Sokolsky, O. Resources in process algebra. J. Log. Algebr. Program. 2007, 72, 98–122. [Google Scholar] [CrossRef][Green Version]
- Katoen, J.P.; van de Pol, J.; Stoelinga, M.; Timmer, M. A linear process-algebraic format with data for probabilistic automata. Theor. Comput. Sci. 2012, 413, 36–57. [Google Scholar] [CrossRef]
- Hermanns, H.; Krčál, J.; Křetínský, J. Probabilistic bisimulation: Naturally on distributions. In International Conference on Concurrency Theory; Springer: Berlin/Heidelberg, Germany, 2014; pp. 249–265. [Google Scholar] [CrossRef]
- OMiLAB. OMiLAB NPO. Available online: https://www.omilab.org (accessed on 10 April 2024).






| Movements | Request | Permision | Results |
|---|---|---|---|
| In | |||
 | 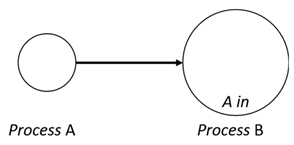 | 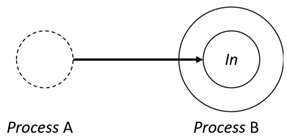 | |
| Out | |||
 | 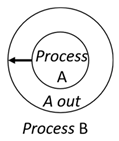 |  | |
| Get | |||
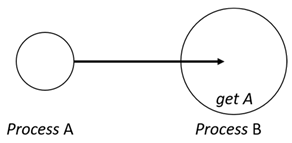 |  |  | |
| Put | |||
 |  |  |
| Construct | Name | Index | |
|---|---|---|---|
| Action | (1) | ||
| Timed Action | (2) | ||
| Timed Process | (3) | ||
| Priority | (4) | ||
| Nesting | (5) | ||
| Channel | (6) | ||
| Choice | (7) | ||
| Probabilistic Choice | (8) | ||
| Parallel | (9) | ||
| Exception | (10) | ||
| Sequence | (11) | ||
| Discrete Distribution | (12) | ||
| Normal Distribution | (13) | ||
| Exponential Distribution | (14) | ||
| Uniform Distribution | (15) | ||
| Empty | (16) | ||
| Send | (17) | ||
| Receive | (18) | ||
| Movement | (19) | ||
| Control | (20) | ||
| Movement Request | (21) | ||
| Movement Permission | (22) | ||
| In Movement | (23) | ||
| Out Movement | (24) | ||
| Get Movement | (25) | ||
| Put Movement | (26) | ||
| Create Process | (27) | ||
| Kill Process | (28) | ||
| Exit Process | (29) | ||
| Name | Transition Rules | Index |
|---|---|---|
| Sequence | (1) | |
| ChoiceL ChoiceR | , | (2) |
| Prob. Choice | (3) | |
| ParallelL ParallelR | , | (4) |
| ParallelCom | (5) | |
| NestingO NestingI | , | (6) |
| NestingCom | (7) | |
| In | (8) | |
| Out | (9) | |
| Get | (10) | |
| Put | (11) | |
| InP | (12) | |
| OutP | (13) | |
| GetP | (14) | |
| PutP | (15) | |
| TickTime R | (16) | |
| TickTime TO | (17) | |
| TickTime End | (18) | |
| TickTime SyncE | (19) | |
| TickTime AsyncE | (20) | |
| Timeout | (21) | |
| Deadline | (22) | |
| Period | (23) | |
| Period End | (24) |
| SSReq | VaReg | Validation | ||
|---|---|---|---|---|
| The order of the resources, that is, R1–R2 or R2–R1, should not be violated because the security information is contained in the first resource (R1) to decode the second resource (R2) or vice versa. | 0.10 | To be Validated | ||
| The propagation between the first (R1) and second (R2), or vice versa, should not be more than 3 time units. | 0.15 | |||
| The deadline for the consumption of the second resource (R2) by should not be more than 10 time units for the order of the resources R1–R2. | 0.10 | To be Validated | ||
| The deadline for consumption of the second resource (R2) by should not be more than 11 time units for the order of the resources R2–R1. | 0.05 | |||
| SSReq | Case 1 | |||
|---|---|---|---|---|
| 0.10 | Satisfied | 0.18 | ||
| 0.15 | Satisfied | 0.27 | ||
| 0.10 | Satisfied | 0.18 | ||
| 0.05 | Satisfied | 0.09 | ||
| SSReq | Case 2 | |||
|---|---|---|---|---|
| 0.20 | Unsatisfied | 0.18 | ||
| 0.25 | Satisfied | 0.27 | ||
| 0.20 | Unsatisfied | 0.18 | ||
| 0.05 | Satisfied | 0.09 | ||
| SSReq | Case 2 | ||||
|---|---|---|---|---|---|
| 0.20 | Unsatisfied, but Satisfiable | 0.18 | 0.205 | ||
| 0.25 | Satisfied | 0.27 | 0.290 | ||
| 0.20 | Unsatisfied, but Satisfiable | 0.18 | 0.205 | ||
| 0.05 | Satisfied | 0.09 | 0.085 | ||
| Status | Meaning | Example |
|---|---|---|
| T1 | Immediate | 1st Transfer Priority: Patient whose life is threatened if not treated meediately (e.g., heart attack, ceretral hemorrhage, major amputation, etc.). |
| T2 | Delayed | 2nd Transfer Priority: Patient who is under observation for immediate medical treatment if necessary, but not needed immediately (e.g., fracture, dislocation, food poisoning, etc.). |
| T3 | Minimal | 3rd Transfer Priority: Patient without any life-threaning or physical disabilities (e.g., minor lacerated wound, sprain, scratch, etc.). |
| Path | Probability | Path | Probability |
|---|---|---|---|
| 1 | 0.260514 | 24 (Deadlock) | 0.090095 |
| 2 (Deadlock) | 0.028985 | 25 | 0.003193 |
| 3 (Deadlock) | 0.028968 | 26 (Deadlock) | 0.000362 |
| 4 | 0.003227 | 27 (Deadlock) | 0.000355 |
| 5 (Deadlock) | 0.137511 | 28 | 0.000042 |
| 6 (Deadlock) | 0.137929 | 29 (Deadlock) | 0.001706 |
| 7 | 0.047687 | 30 (Deadlock) | 0.001679 |
| 8 (Deadlock) | 0.005240 | 31 | 0.000601 |
| 9 (Deadlock) | 0.005317 | 32 (Deadlock) | 0.000071 |
| 10 | 0.000629 | 33 (Deadlock) | 0.000073 |
| 11 (Deadlock) | 0.072801 | 34 | 0.000008 |
| 12 (Deadlock) | 0.073120 | 35 (Deadlock) | 0.000840 |
| 13 | 0.003201 | 36 (Deadlock) | 0.000924 |
| 14 (Deadlock) | 0.000347 | 37 | 0.000037 |
| 15 (Deadlock) | 0.000358 | 38 (Deadlock) | 0.000005 |
| 16 | 0.000034 | 39 (Deadlock) | 0.000005 |
| 17 (Deadlock) | 0.001706 | 40 | 0.000002 |
| 18 (Deadlock) | 0.001695 | 41 (Deadlock) | 0.000021 |
| 19 | 0.000589 | 42 (Deadlock) | 0.000019 |
| 20 (Deadlock) | 0.000062 | 43 | 0.000008 |
| 21 (Deadlock) | 0.000065 | 44 (Deadlock) | 0.000001 |
| 22 | 0.000005 | 45 (Deadlock) | 0.000002 |
| 23 (Deadlock) | 0.089958 | 46 | 0.000003 |
| Total | 1.000000 | ||
| Security | Requirements | VaProb | |
|---|---|---|---|
| All patients are to be transferred to hospitals. | 0.35 | ||
| A T1 patient should be transferred before a T2 patient. | 0.40 | ||
| A T2 patient should be transferred before a T3 patient. | 0.30 | ||
| Safety | |||
| The deadline for a T1 patient is in 10 unit times. | 0.50 | ||
| The deadline for a T2 patient is in 20 unit times. | 0.30 | ||
| The deadline for a T3 patient is in 30 unit times. | 0.20 | ||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | Prob. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prob. | Succ. | 0.26 | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.32 | ||||||||||||||||||||||||||||||
| Fail | 0.03 | 0.03 | 0.14 | 0.14 | 0.01 | 0.01 | 0.07 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.68 | |||||||||||||||||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.32 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.32 | ||
| O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | 0.27 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.31 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | 0.32 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.32 | ||
| Requirements | Va Probabilities | System Probabilities | Verification Results | ||
|---|---|---|---|---|---|
| 0.35 | 0.32 | X | Unsatisfied, but Satisfiable | ||
| 0.40 | 0.32 | X | Unsatisfied, but Satisfiable | ||
| 0.30 | 0.27 | X | Unsatisfied, but Satisfiable | ||
| 0.50 | 0.31 | X | Unsatisfied, but Satisfiable | ||
| 0.30 | 0.32 | O | Satisfied | ||
| 0.20 | 0.32 | O | Satisfied | ||
| Versions | dTP-Calculus | |
|---|---|---|
| AmbX | AmbX1 |  |
| AmbX4 |  | |
| Probabilistic Process Equivalence | ||
| BR | Reachability Table | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||
| 3 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||
| 4 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||
| 5 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||||||||||
| 6 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||
| 7 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||
| 8 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |
| Prob. | 0.26 | 0.03 | 0.03 | 0.00 | 0.14 | 0.14 | 0.06 | 0.01 | 0.01 | 0.00 | 0.07 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Total | 0.32 (Success) + 0.68 (Fail) = 1 | |||||||||||||||||||||||||||||||||||||||||||||
| BR | Reachability Table | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0.99 | 0.01 | 0.99 | 0.01 | ||||||||||||||||||||||||||||||||||||||||||
| 3 | 0.99 | 0.01 | 0.99 | 0.01 | ||||||||||||||||||||||||||||||||||||||||||
| 4 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||
| 5 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||||||||||
| 6 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||
| 7 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||
| 8 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |
| Prob. | 0.32 | 0.04 | 0.04 | 0.00 | 0.16 | 0.16 | 0.06 | 0.01 | 0.01 | 0.00 | 0.09 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Total | 0.38 (Success) + 0.62 (Fail) = 1 | |||||||||||||||||||||||||||||||||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | Prob. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prob. | Succ. | 0.32 | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.38 | ||||||||||||||||||||||||||||||
| Fail | 0.04 | 0.04 | 0.16 | 0.16 | 0.01 | 0.01 | 0.09 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.62 | |||||||||||||||||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.38 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.38 | ||
| O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | 0.32 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.38 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | 0.38 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.38 | ||
| Requirements | Va Probabilities | System Probabilities | Verification Results | ||
|---|---|---|---|---|---|
| 0.35 | 0.38 | O | Satisfied | ||
| 0.40 | 0.38 | X | Unsatisfied, but Satisfiable | ||
| 0.30 | 0.32 | O | Satisfied | ||
| 0.50 | 0.38 | X | Unsatisfied, but Satisfiable | ||
| 0.30 | 0.38 | O | Satisfied | ||
| 0.20 | 0.38 | O | Satisfied | ||
| Process | Probabilistic Process Equivalence | Imterpertation |
|---|---|---|
| HospM | 0.05% improvement from HospM1 to HospM3 | |
| AmbX | 0.05% improvement from 911Center1 to 911Center3 | |
| 911Center | 0.05% improvement from AmbX1 to AmbX2 | |
| AmbY | 0.25% improvement from AmbY1 to AmbY3 | |
| HospN | 0.05% improvement from HospN1 to HospN2 |
| BR | Reachability Table | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||
| 3 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||||||
| 4 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||||||||||
| 5 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||||||||||
| 6 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | 0.7 | 0.3 | ||||||||||||||||||||||||||||||
| 7 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||||||||||||||||||
| 8 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |
| Prob. | 0.26 | 0.03 | 0.03 | 0.00 | 0.14 | 0.14 | 0.06 | 0.01 | 0.01 | 0.00 | 0.07 | 0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Total | 0.32 (Success) + 0.68 (Fail) = 1 | |||||||||||||||||||||||||||||||||||||||||||||
| BR | Reachability Table | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0.95 | 0.05 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||||||||||||||
| 3 | 0.95 | 0.05 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||||||||||||||
| 4 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||||||||||
| 5 | 0.94 | 0.06 | 0.94 | 0.06 | 0.94 | 0.06 | 0.94 | 0.06 | ||||||||||||||||||||||||||||||||||||||
| 6 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||
| 7 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | 0.95 | 0.05 | ||||||||||||||||||||||||||||||
| 8 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | 0.9 | 0.1 | ||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |
| Prob. | 0.64 | 0.04 | 0.04 | 0.01 | 0.04 | 0.04 | 0.01 | 0.00 | 0.00 | 0.00 | 0.04 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Total | 0.66 (Success) + 0.34 (Fail) = 1 | |||||||||||||||||||||||||||||||||||||||||||||
| Path | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | Prob. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prob. | Succ. | 0.64 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.66 | ||||||||||||||||||||||||||||||
| Fail | 0.04 | 0.04 | 0.04 | 0.04 | 0.00 | 0.00 | 0.04 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.34 | |||||||||||||||||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.66 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.66 | ||
| O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | X | X | O | X | X | O | X | X | X | X | X | X | 0.66 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.65 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | X | X | X | X | X | X | X | X | X | X | 0.66 | ||
| O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | X | X | O | 0.66 | ||
| Requirements | Va Probabilities | System Probabilities | Verification Results | ||
|---|---|---|---|---|---|
| 0.35 | 0.66 | O | Satisfied | ||
| 0.40 | 0.66 | O | Satisfied | ||
| 0.30 | 0.66 | O | Satisfied | ||
| 0.50 | 0.65 | O | Satisfied | ||
| 0.30 | 0.66 | O | Satisfied | ||
| 0.20 | 0.66 | O | Satisfied | ||
| Previous Research | Present Research | |
|---|---|---|
| Probability Enhancement | Arbitrary | Deterministic |
| Incremental Improvement | Arbitrary | Step-wise |
| Other Research | Present Research | |
|---|---|---|
| Probabilistic Equivalence | System-Level Probabilistic Equivalence Continuous and Sequential Equivalence | Process Equivalence: Incremental and Discrete Equivalence System Equivalence: Step-wise Integrated Equivalence |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Karagiannis, D.; Lee, M. A Process Algebraic Approach to Predict and Control Uncertainty in Smart IoT Systems for Smart Cities Based on Permissible Probabilistic Equivalence. Sensors 2024, 24, 3881. https://doi.org/10.3390/s24123881
Song J, Karagiannis D, Lee M. A Process Algebraic Approach to Predict and Control Uncertainty in Smart IoT Systems for Smart Cities Based on Permissible Probabilistic Equivalence. Sensors. 2024; 24(12):3881. https://doi.org/10.3390/s24123881
Chicago/Turabian StyleSong, Junsup, Dimitris Karagiannis, and Moonkun Lee. 2024. "A Process Algebraic Approach to Predict and Control Uncertainty in Smart IoT Systems for Smart Cities Based on Permissible Probabilistic Equivalence" Sensors 24, no. 12: 3881. https://doi.org/10.3390/s24123881
APA StyleSong, J., Karagiannis, D., & Lee, M. (2024). A Process Algebraic Approach to Predict and Control Uncertainty in Smart IoT Systems for Smart Cities Based on Permissible Probabilistic Equivalence. Sensors, 24(12), 3881. https://doi.org/10.3390/s24123881






